How to Develop LSTM Models for Time Series Forecasting

By Jason Brownlee on November 14, 2018 in Deep Learning for Time Series

Last Updated on August 28, 2020

Long Short-Term Memory networks, or LSTMs for short, can be applied to time series forecasting.

There are many types of LSTM models that can be used for each specific type of time series forecasting problem.

In this tutorial, you will discover how to develop a suite of LSTM models for a range of standard time series forecasting problems.

The objective of this tutorial is to provide standalone examples of each model on each type of time series problem as a template that you can copy and adapt for your specific time series forecasting problem.

After completing this tutorial, you will know:

How to develop LSTM models for univariate time series forecasting.
How to develop LSTM models for multivariate time series forecasting.
How to develop LSTM models for multi-step time series forecasting.

This is a large and important post; you may want to bookmark it for future reference.

Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

How to Develop LSTM Models for Time Series Forecasting
Photo by N i c o l a, some rights reserved.

Tutorial Overview

In this tutorial, we will explore how to develop a suite of different types of LSTM models for time series forecasting.

The models are demonstrated on small contrived time series problems intended to give the flavor of the type of time series problem being addressed. The chosen configuration of the models is arbitrary and not optimized for each problem; that was not the goal.

This tutorial is divided into four parts; they are:

Univariate LSTM Models
1. Data Preparation
2. Vanilla LSTM
3. Stacked LSTM
4. Bidirectional LSTM
5. CNN LSTM
6. ConvLSTM
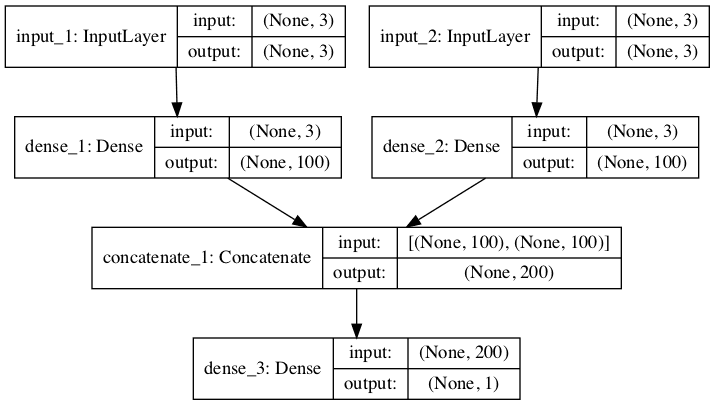
Multivariate LSTM Models
1. Multiple Input Series.
2. Multiple Parallel Series.
Multi-Step LSTM Models
1. Data Preparation
2. Vector Output Model
3. Encoder-Decoder Model
Multivariate Multi-Step LSTM Models
1. Multiple Input Multi-Step Output.
2. Multiple Parallel Input and Multi-Step Output.

Univariate LSTM Models

LSTMs can be used to model univariate time series forecasting problems.

These are problems comprised of a single series of observations and a model is required to learn from the series of past observations to predict the next value in the sequence.

We will demonstrate a number of variations of the LSTM model for univariate time series forecasting.

This section is divided into six parts; they are:

Data Preparation
Vanilla LSTM
Stacked LSTM
Bidirectional LSTM
CNN LSTM
ConvLSTM

Each of these models are demonstrated for one-step univariate time series forecasting, but can easily be adapted and used as the input part of a model for other types of time series forecasting problems.

Data Preparation

Before a univariate series can be modeled, it must be prepared.

The LSTM model will learn a function that maps a sequence of past observations as input to an output observation. As such, the sequence of observations must be transformed into multiple examples from which the LSTM can learn.

Consider a given univariate sequence:

[10, 20, 30, 40, 50, 60, 70, 80, 90]

1	[10, 20, 30, 40, 50, 60, 70, 80, 90]

We can divide the sequence into multiple input/output patterns called samples, where three time steps are used as input and one time step is used as output for the one-step prediction that is being learned.

X,				y
10, 20, 30		40
20, 30, 40		50
30, 40, 50		60
...

X, y

10, 20, 30 40

20, 30, 40 50

30, 40, 50 60

...

The split_sequence() function below implements this behavior and will split a given univariate sequence into multiple samples where each sample has a specified number of time steps and the output is a single time step.

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# split a univariate sequence into samples

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

We can demonstrate this function on our small contrived dataset above.

The complete example is listed below.

# univariate data preparation
from numpy import array

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 3
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# summarize the data
for i in range(len(X)):
	print(X[i], y[i])

# univariate data preparation

from numpy import array

# split a univariate sequence into samples

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps = 3

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# summarize the data

for i in range(len(X)):

print(X[i], y[i])

Running the example splits the univariate series into six samples where each sample has three input time steps and one output time step.

[10 20 30] 40
[20 30 40] 50
[30 40 50] 60
[40 50 60] 70
[50 60 70] 80
[60 70 80] 90

[10 20 30] 40

[20 30 40] 50

[30 40 50] 60

[40 50 60] 70

[50 60 70] 80

[60 70 80] 90

Now that we know how to prepare a univariate series for modeling, let’s look at developing LSTM models that can learn the mapping of inputs to outputs, starting with a Vanilla LSTM.

Need help with Deep Learning for Time Series?

Take my free 7-day email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Vanilla LSTM

A Vanilla LSTM is an LSTM model that has a single hidden layer of LSTM units, and an output layer used to make a prediction.

We can define a Vanilla LSTM for univariate time series forecasting as follows.

...
# define model
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

Key in the definition is the shape of the input; that is what the model expects as input for each sample in terms of the number of time steps and the number of features.

We are working with a univariate series, so the number of features is one, for one variable.

The number of time steps as input is the number we chose when preparing our dataset as an argument to the split_sequence() function.

The shape of the input for each sample is specified in the input_shape argument on the definition of first hidden layer.

We almost always have multiple samples, therefore, the model will expect the input component of training data to have the dimensions or shape:

[samples, timesteps, features]

1	[samples, timesteps, features]

Our split_sequence() function in the previous section outputs the X with the shape [samples, timesteps], so we easily reshape it to have an additional dimension for the one feature.

...
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))

...

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

In this case, we define a model with 50 LSTM units in the hidden layer and an output layer that predicts a single numerical value.

The model is fit using the efficient Adam version of stochastic gradient descent and optimized using the mean squared error, or ‘mse‘ loss function.

Once the model is defined, we can fit it on the training dataset.

...
# fit model
model.fit(X, y, epochs=200, verbose=0)

...

# fit model

model.fit(X, y, epochs=200, verbose=0)

After the model is fit, we can use it to make a prediction.

We can predict the next value in the sequence by providing the input:

[70, 80, 90]

1	[70, 80, 90]

And expecting the model to predict something like:

[100]

[100]

The model expects the input shape to be three-dimensional with [samples, timesteps, features], therefore, we must reshape the single input sample before making the prediction.

...
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)

...

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

We can tie all of this together and demonstrate how to develop a Vanilla LSTM for univariate time series forecasting and make a single prediction.

# univariate lstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 3
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
# define model
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=200, verbose=0)
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate lstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

# split a univariate sequence into samples

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps = 3

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

# define model

model = Sequential()

model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=200, verbose=0)

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example prepares the data, fits the model, and makes a prediction.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the model predicts the next value in the sequence.

[[102.09213]]

1	[[102.09213]]

Stacked LSTM

Multiple hidden LSTM layers can be stacked one on top of another in what is referred to as a Stacked LSTM model.

An LSTM layer requires a three-dimensional input and LSTMs by default will produce a two-dimensional output as an interpretation from the end of the sequence.

We can address this by having the LSTM output a value for each time step in the input data by setting the return_sequences=True argument on the layer. This allows us to have 3D output from hidden LSTM layer as input to the next.

We can therefore define a Stacked LSTM as follows.

...
# define model
model = Sequential()
model.add(LSTM(50, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))
model.add(LSTM(50, activation='relu'))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(LSTM(50, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))

model.add(LSTM(50, activation='relu'))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

We can tie this together; the complete code example is listed below.

# univariate stacked lstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# split a univariate sequence
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 3
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
# define model
model = Sequential()
model.add(LSTM(50, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))
model.add(LSTM(50, activation='relu'))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=200, verbose=0)
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate stacked lstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

# split a univariate sequence

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps = 3

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

# define model

model = Sequential()

model.add(LSTM(50, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))

model.add(LSTM(50, activation='relu'))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=200, verbose=0)

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example predicts the next value in the sequence, which we expect would be 100.

[[102.47341]]

1	[[102.47341]]

Bidirectional LSTM

On some sequence prediction problems, it can be beneficial to allow the LSTM model to learn the input sequence both forward and backwards and concatenate both interpretations.

This is called a Bidirectional LSTM.

We can implement a Bidirectional LSTM for univariate time series forecasting by wrapping the first hidden layer in a wrapper layer called Bidirectional.

An example of defining a Bidirectional LSTM to read input both forward and backward is as follows.

...
# define model
model = Sequential()
model.add(Bidirectional(LSTM(50, activation='relu'), input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(Bidirectional(LSTM(50, activation='relu'), input_shape=(n_steps, n_features)))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

The complete example of the Bidirectional LSTM for univariate time series forecasting is listed below.

# univariate bidirectional lstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import Bidirectional

# split a univariate sequence
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 3
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
# define model
model = Sequential()
model.add(Bidirectional(LSTM(50, activation='relu'), input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=200, verbose=0)
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate bidirectional lstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

from keras.layers import Bidirectional

# split a univariate sequence

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps = 3

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

# define model

model = Sequential()

model.add(Bidirectional(LSTM(50, activation='relu'), input_shape=(n_steps, n_features)))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=200, verbose=0)

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example predicts the next value in the sequence, which we expect would be 100.

[[101.48093]]

1	[[101.48093]]

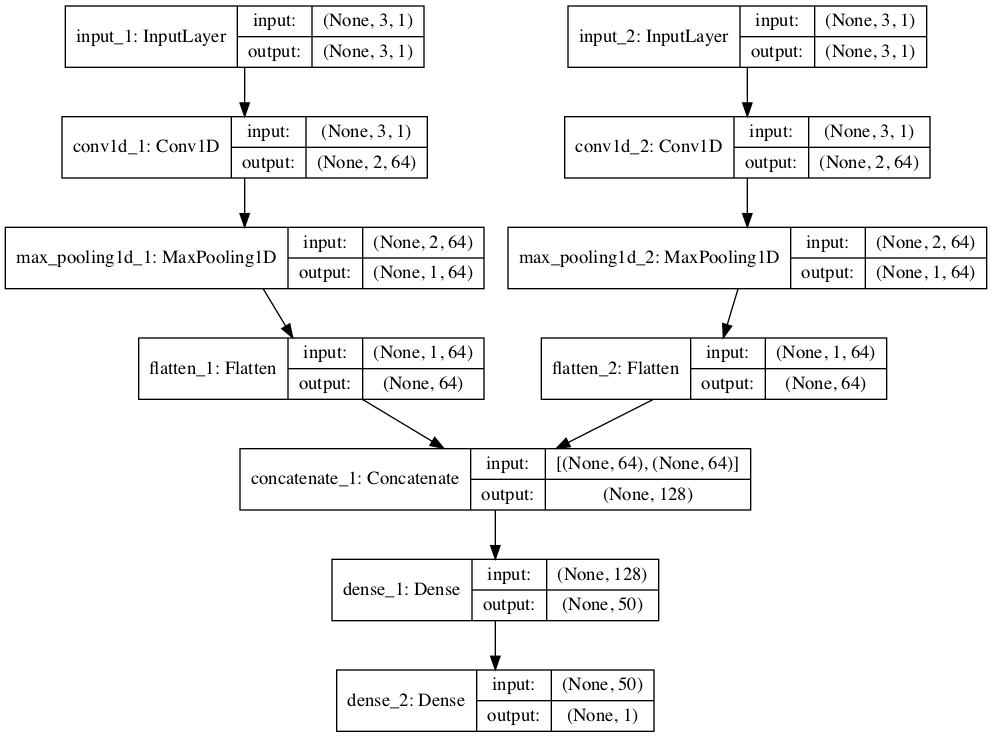
CNN LSTM

A convolutional neural network, or CNN for short, is a type of neural network developed for working with two-dimensional image data.

The CNN can be very effective at automatically extracting and learning features from one-dimensional sequence data such as univariate time series data.

A CNN model can be used in a hybrid model with an LSTM backend where the CNN is used to interpret subsequences of input that together are provided as a sequence to an LSTM model to interpret. This hybrid model is called a CNN-LSTM.

The first step is to split the input sequences into subsequences that can be processed by the CNN model. For example, we can first split our univariate time series data into input/output samples with four steps as input and one as output. Each sample can then be split into two sub-samples, each with two time steps. The CNN can interpret each subsequence of two time steps and provide a time series of interpretations of the subsequences to the LSTM model to process as input.

We can parameterize this and define the number of subsequences as n_seq and the number of time steps per subsequence as n_steps. The input data can then be reshaped to have the required structure:

[samples, subsequences, timesteps, features]

1	[samples, subsequences, timesteps, features]

For example:

...
# choose a number of time steps
n_steps = 4
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, subsequences, timesteps, features]
n_features = 1
n_seq = 2
n_steps = 2
X = X.reshape((X.shape[0], n_seq, n_steps, n_features))

...

# choose a number of time steps

n_steps = 4

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, subsequences, timesteps, features]

n_features = 1

n_seq = 2

n_steps = 2

X = X.reshape((X.shape[0], n_seq, n_steps, n_features))

We want to reuse the same CNN model when reading in each sub-sequence of data separately.

This can be achieved by wrapping the entire CNN model in a TimeDistributed wrapper that will apply the entire model once per input, in this case, once per input subsequence.

The CNN model first has a convolutional layer for reading across the subsequence that requires a number of filters and a kernel size to be specified. The number of filters is the number of reads or interpretations of the input sequence. The kernel size is the number of time steps included of each ‘read’ operation of the input sequence.

The convolution layer is followed by a max pooling layer that distills the filter maps down to 1/2 of their size that includes the most salient features. These structures are then flattened down to a single one-dimensional vector to be used as a single input time step to the LSTM layer.

...
model.add(TimeDistributed(Conv1D(filters=64, kernel_size=1, activation='relu'), input_shape=(None, n_steps, n_features)))
model.add(TimeDistributed(MaxPooling1D(pool_size=2)))
model.add(TimeDistributed(Flatten()))

...

model.add(TimeDistributed(Conv1D(filters=64, kernel_size=1, activation='relu'), input_shape=(None, n_steps, n_features)))

model.add(TimeDistributed(MaxPooling1D(pool_size=2)))

model.add(TimeDistributed(Flatten()))

Next, we can define the LSTM part of the model that interprets the CNN model’s read of the input sequence and makes a prediction.

...
model.add(LSTM(50, activation='relu'))
model.add(Dense(1))

...

model.add(LSTM(50, activation='relu'))

model.add(Dense(1))

We can tie all of this together; the complete example of a CNN-LSTM model for univariate time series forecasting is listed below.

# univariate cnn lstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import TimeDistributed
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 4
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, subsequences, timesteps, features]
n_features = 1
n_seq = 2
n_steps = 2
X = X.reshape((X.shape[0], n_seq, n_steps, n_features))
# define model
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=64, kernel_size=1, activation='relu'), input_shape=(None, n_steps, n_features)))
model.add(TimeDistributed(MaxPooling1D(pool_size=2)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(50, activation='relu'))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=500, verbose=0)
# demonstrate prediction
x_input = array([60, 70, 80, 90])
x_input = x_input.reshape((1, n_seq, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate cnn lstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

from keras.layers import Flatten

from keras.layers import TimeDistributed

from keras.layers.convolutional import Conv1D

from keras.layers.convolutional import MaxPooling1D

# split a univariate sequence into samples

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps = 4

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, subsequences, timesteps, features]

n_features = 1

n_seq = 2

n_steps = 2

X = X.reshape((X.shape[0], n_seq, n_steps, n_features))

# define model

model = Sequential()

model.add(TimeDistributed(Conv1D(filters=64, kernel_size=1, activation='relu'), input_shape=(None, n_steps, n_features)))

model.add(TimeDistributed(MaxPooling1D(pool_size=2)))

model.add(TimeDistributed(Flatten()))

model.add(LSTM(50, activation='relu'))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=500, verbose=0)

# demonstrate prediction

x_input = array([60, 70, 80, 90])

x_input = x_input.reshape((1, n_seq, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example predicts the next value in the sequence, which we expect would be 100.

[[101.69263]]

1	[[101.69263]]

ConvLSTM

A type of LSTM related to the CNN-LSTM is the ConvLSTM, where the convolutional reading of input is built directly into each LSTM unit.

The ConvLSTM was developed for reading two-dimensional spatial-temporal data, but can be adapted for use with univariate time series forecasting.

The layer expects input as a sequence of two-dimensional images, therefore the shape of input data must be:

[samples, timesteps, rows, columns, features]

1	[samples, timesteps, rows, columns, features]

For our purposes, we can split each sample into subsequences where timesteps will become the number of subsequences, or n_seq, and columns will be the number of time steps for each subsequence, or n_steps. The number of rows is fixed at 1 as we are working with one-dimensional data.

We can now reshape the prepared samples into the required structure.

...
# choose a number of time steps
n_steps = 4
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, timesteps, rows, columns, features]
n_features = 1
n_seq = 2
n_steps = 2
X = X.reshape((X.shape[0], n_seq, 1, n_steps, n_features))

...

# choose a number of time steps

n_steps = 4

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, timesteps, rows, columns, features]

n_features = 1

n_seq = 2

n_steps = 2

X = X.reshape((X.shape[0], n_seq, 1, n_steps, n_features))

We can define the ConvLSTM as a single layer in terms of the number of filters and a two-dimensional kernel size in terms of (rows, columns). As we are working with a one-dimensional series, the number of rows is always fixed to 1 in the kernel.

The output of the model must then be flattened before it can be interpreted and a prediction made.

...
model.add(ConvLSTM2D(filters=64, kernel_size=(1,2), activation='relu', input_shape=(n_seq, 1, n_steps, n_features)))
model.add(Flatten())

...

model.add(ConvLSTM2D(filters=64, kernel_size=(1,2), activation='relu', input_shape=(n_seq, 1, n_steps, n_features)))

model.add(Flatten())

The complete example of a ConvLSTM for one-step univariate time series forecasting is listed below.

# univariate convlstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import ConvLSTM2D

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the sequence
		if end_ix > len(sequence)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 4
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# reshape from [samples, timesteps] into [samples, timesteps, rows, columns, features]
n_features = 1
n_seq = 2
n_steps = 2
X = X.reshape((X.shape[0], n_seq, 1, n_steps, n_features))
# define model
model = Sequential()
model.add(ConvLSTM2D(filters=64, kernel_size=(1,2), activation='relu', input_shape=(n_seq, 1, n_steps, n_features)))
model.add(Flatten())
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=500, verbose=0)
# demonstrate prediction
x_input = array([60, 70, 80, 90])
x_input = x_input.reshape((1, n_seq, 1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate convlstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

from keras.layers import Flatten

from keras.layers import ConvLSTM2D

# split a univariate sequence into samples

def split_sequence(sequence, n_steps):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the sequence

if end_ix > len(sequence)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps = 4

# split into samples

X, y = split_sequence(raw_seq, n_steps)

# reshape from [samples, timesteps] into [samples, timesteps, rows, columns, features]

n_features = 1

n_seq = 2

n_steps = 2

X = X.reshape((X.shape[0], n_seq, 1, n_steps, n_features))

# define model

model = Sequential()

model.add(ConvLSTM2D(filters=64, kernel_size=(1,2), activation='relu', input_shape=(n_seq, 1, n_steps, n_features)))

model.add(Flatten())

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=500, verbose=0)

# demonstrate prediction

x_input = array([60, 70, 80, 90])

x_input = x_input.reshape((1, n_seq, 1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example predicts the next value in the sequence, which we expect would be 100.

[[103.68166]]

1	[[103.68166]]

Now that we have looked at LSTM models for univariate data, let’s turn our attention to multivariate data.

Multivariate LSTM Models

Multivariate time series data means data where there is more than one observation for each time step.

There are two main models that we may require with multivariate time series data; they are:

Multiple Input Series.
Multiple Parallel Series.

Let’s take a look at each in turn.

Multiple Input Series

A problem may have two or more parallel input time series and an output time series that is dependent on the input time series.

The input time series are parallel because each series has an observation at the same time steps.

We can demonstrate this with a simple example of two parallel input time series where the output series is the simple addition of the input series.

...
# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

...

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

We can reshape these three arrays of data as a single dataset where each row is a time step, and each column is a separate time series. This is a standard way of storing parallel time series in a CSV file.

...
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))

...

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

The complete example is listed below.

# multivariate data preparation
from numpy import array
from numpy import hstack
# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
print(dataset)

# multivariate data preparation

from numpy import array

from numpy import hstack

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

print(dataset)

Running the example prints the dataset with one row per time step and one column for each of the two input and one output parallel time series.

[[ 10  15  25]
 [ 20  25  45]
 [ 30  35  65]
 [ 40  45  85]
 [ 50  55 105]
 [ 60  65 125]
 [ 70  75 145]
 [ 80  85 165]
 [ 90  95 185]]

[[ 10 15 25]

[ 20 25 45]

[ 30 35 65]

[ 40 45 85]

[ 50 55 105]

[ 60 65 125]

[ 70 75 145]

[ 80 85 165]

[ 90 95 185]]

As with the univariate time series, we must structure these data into samples with input and output elements.

An LSTM model needs sufficient context to learn a mapping from an input sequence to an output value. LSTMs can support parallel input time series as separate variables or features. Therefore, we need to split the data into samples maintaining the order of observations across the two input sequences.

If we chose three input time steps, then the first sample would look as follows:

Input:

10, 15
20, 25
30, 35

10, 15

20, 25

30, 35

Output:

65

That is, the first three time steps of each parallel series are provided as input to the model and the model associates this with the value in the output series at the third time step, in this case, 65.

We can see that, in transforming the time series into input/output samples to train the model, that we will have to discard some values from the output time series where we do not have values in the input time series at prior time steps. In turn, the choice of the size of the number of input time steps will have an important effect on how much of the training data is used.

We can define a function named split_sequences() that will take a dataset as we have defined it with rows for time steps and columns for parallel series and return input/output samples.

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the dataset
		if end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the dataset

if end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

We can test this function on our dataset using three time steps for each input time series as input.

The complete example is listed below.

# multivariate data preparation
from numpy import array
from numpy import hstack

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the dataset
		if end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps = 3
# convert into input/output
X, y = split_sequences(dataset, n_steps)
print(X.shape, y.shape)
# summarize the data
for i in range(len(X)):
	print(X[i], y[i])

# multivariate data preparation

from numpy import array

from numpy import hstack

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the dataset

if end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps = 3

# convert into input/output

X, y = split_sequences(dataset, n_steps)

print(X.shape, y.shape)

# summarize the data

for i in range(len(X)):

print(X[i], y[i])

Running the example first prints the shape of the X and y components.

We can see that the X component has a three-dimensional structure.

The first dimension is the number of samples, in this case 7. The second dimension is the number of time steps per sample, in this case 3, the value specified to the function. Finally, the last dimension specifies the number of parallel time series or the number of variables, in this case 2 for the two parallel series.

This is the exact three-dimensional structure expected by an LSTM as input. The data is ready to use without further reshaping.

We can then see that the input and output for each sample is printed, showing the three time steps for each of the two input series and the associated output for each sample.

(7, 3, 2) (7,)

[[10 15]
 [20 25]
 [30 35]] 65
[[20 25]
 [30 35]
 [40 45]] 85
[[30 35]
 [40 45]
 [50 55]] 105
[[40 45]
 [50 55]
 [60 65]] 125
[[50 55]
 [60 65]
 [70 75]] 145
[[60 65]
 [70 75]
 [80 85]] 165
[[70 75]
 [80 85]
 [90 95]] 185

(7, 3, 2) (7,)

[[10 15]

[20 25]

[30 35]] 65

[[20 25]

[30 35]

[40 45]] 85

[[30 35]

[40 45]

[50 55]] 105

[[40 45]

[50 55]

[60 65]] 125

[[50 55]

[60 65]

[70 75]] 145

[[60 65]

[70 75]

[80 85]] 165

[[70 75]

[80 85]

[90 95]] 185

We are now ready to fit an LSTM model on this data.

Any of the varieties of LSTMs in the previous section can be used, such as a Vanilla, Stacked, Bidirectional, CNN, or ConvLSTM model.

We will use a Vanilla LSTM where the number of time steps and parallel series (features) are specified for the input layer via the input_shape argument.

...
# define model
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

When making a prediction, the model expects three time steps for two input time series.

We can predict the next value in the output series providing the input values of:

80,	 85
90,	 95
100, 105

80, 85

90, 95

100, 105

The shape of the one sample with three time steps and two variables must be [1, 3, 2].

We would expect the next value in the sequence to be 100 + 105, or 205.

...
# demonstrate prediction
x_input = array([[80, 85], [90, 95], [100, 105]])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)

...

# demonstrate prediction

x_input = array([[80, 85], [90, 95], [100, 105]])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

The complete example is listed below.

# multivariate lstm example
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the dataset
		if end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps = 3
# convert into input/output
X, y = split_sequences(dataset, n_steps)
# the dataset knows the number of features, e.g. 2
n_features = X.shape[2]
# define model
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=200, verbose=0)
# demonstrate prediction
x_input = array([[80, 85], [90, 95], [100, 105]])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# multivariate lstm example

from numpy import array

from numpy import hstack

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the dataset

if end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps = 3

# convert into input/output

X, y = split_sequences(dataset, n_steps)

# the dataset knows the number of features, e.g. 2

n_features = X.shape[2]

# define model

model = Sequential()

model.add(LSTM(50, activation='relu', input_shape=(n_steps, n_features)))

model.add(Dense(1))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=200, verbose=0)

# demonstrate prediction

x_input = array([[80, 85], [90, 95], [100, 105]])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example prepares the data, fits the model, and makes a prediction.

[[208.13531]]

1	[[208.13531]]

Multiple Parallel Series

An alternate time series problem is the case where there are multiple parallel time series and a value must be predicted for each.

For example, given the data from the previous section:

[[ 10  15  25]
 [ 20  25  45]
 [ 30  35  65]
 [ 40  45  85]
 [ 50  55 105]
 [ 60  65 125]
 [ 70  75 145]
 [ 80  85 165]
 [ 90  95 185]]

[[ 10 15 25]

[ 20 25 45]

[ 30 35 65]

[ 40 45 85]

[ 50 55 105]

[ 60 65 125]

[ 70 75 145]

[ 80 85 165]

[ 90 95 185]]

We may want to predict the value for each of the three time series for the next time step.

This might be referred to as multivariate forecasting.

Again, the data must be split into input/output samples in order to train a model.

The first sample of this dataset would be:

Input:

10, 15, 25
20, 25, 45
30, 35, 65

10, 15, 25

20, 25, 45

30, 35, 65

Output:

40, 45, 85

1	40, 45, 85

The split_sequences() function below will split multiple parallel time series with rows for time steps and one series per column into the required input/output shape.

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the dataset
		if end_ix > len(sequences)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the dataset

if end_ix > len(sequences)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

We can demonstrate this on the contrived problem; the complete example is listed below.

# multivariate output data prep
from numpy import array
from numpy import hstack

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the dataset
		if end_ix > len(sequences)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps = 3
# convert into input/output
X, y = split_sequences(dataset, n_steps)
print(X.shape, y.shape)
# summarize the data
for i in range(len(X)):
	print(X[i], y[i])

# multivariate output data prep

from numpy import array

from numpy import hstack

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the dataset

if end_ix > len(sequences)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps = 3

# convert into input/output

X, y = split_sequences(dataset, n_steps)

print(X.shape, y.shape)

# summarize the data

for i in range(len(X)):

print(X[i], y[i])

Running the example first prints the shape of the prepared X and y components.

The shape of X is three-dimensional, including the number of samples (6), the number of time steps chosen per sample (3), and the number of parallel time series or features (3).

The shape of y is two-dimensional as we might expect for the number of samples (6) and the number of time variables per sample to be predicted (3).

The data is ready to use in an LSTM model that expects three-dimensional input and two-dimensional output shapes for the X and y components of each sample.

Then, each of the samples is printed showing the input and output components of each sample.

(6, 3, 3) (6, 3)

[[10 15 25]
 [20 25 45]
 [30 35 65]] [40 45 85]
[[20 25 45]
 [30 35 65]
 [40 45 85]] [ 50  55 105]
[[ 30  35  65]
 [ 40  45  85]
 [ 50  55 105]] [ 60  65 125]
[[ 40  45  85]
 [ 50  55 105]
 [ 60  65 125]] [ 70  75 145]
[[ 50  55 105]
 [ 60  65 125]
 [ 70  75 145]] [ 80  85 165]
[[ 60  65 125]
 [ 70  75 145]
 [ 80  85 165]] [ 90  95 185]

(6, 3, 3) (6, 3)

[[10 15 25]

[20 25 45]

[30 35 65]] [40 45 85]

[[20 25 45]

[30 35 65]

[40 45 85]] [ 50 55 105]

[[ 30 35 65]

[ 40 45 85]

[ 50 55 105]] [ 60 65 125]

[[ 40 45 85]

[ 50 55 105]

[ 60 65 125]] [ 70 75 145]

[[ 50 55 105]

[ 60 65 125]

[ 70 75 145]] [ 80 85 165]

[[ 60 65 125]

[ 70 75 145]

[ 80 85 165]] [ 90 95 185]

We are now ready to fit an LSTM model on this data.

Any of the varieties of LSTMs in the previous section can be used, such as a Vanilla, Stacked, Bidirectional, CNN, or ConvLSTM model.

We will use a Stacked LSTM where the number of time steps and parallel series (features) are specified for the input layer via the input_shape argument. The number of parallel series is also used in the specification of the number of values to predict by the model in the output layer; again, this is three.

...
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))
model.add(LSTM(100, activation='relu'))
model.add(Dense(n_features))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))

model.add(LSTM(100, activation='relu'))

model.add(Dense(n_features))

model.compile(optimizer='adam', loss='mse')

We can predict the next value in each of the three parallel series by providing an input of three time steps for each series.

70, 75, 145
80, 85, 165
90, 95, 185

70, 75, 145

80, 85, 165

90, 95, 185

The shape of the input for making a single prediction must be 1 sample, 3 time steps, and 3 features, or [1, 3, 3]

...
# demonstrate prediction
x_input = array([[70,75,145], [80,85,165], [90,95,185]])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)

...

# demonstrate prediction

x_input = array([[70,75,145], [80,85,165], [90,95,185]])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

We would expect the vector output to be:

[100, 105, 205]

1	[100, 105, 205]

We can tie all of this together and demonstrate a Stacked LSTM for multivariate output time series forecasting below.

# multivariate output stacked lstm example
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps
		# check if we are beyond the dataset
		if end_ix > len(sequences)-1:
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps = 3
# convert into input/output
X, y = split_sequences(dataset, n_steps)
# the dataset knows the number of features, e.g. 2
n_features = X.shape[2]
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))
model.add(LSTM(100, activation='relu'))
model.add(Dense(n_features))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=400, verbose=0)
# demonstrate prediction
x_input = array([[70,75,145], [80,85,165], [90,95,185]])
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# multivariate output stacked lstm example

from numpy import array

from numpy import hstack

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps

# check if we are beyond the dataset

if end_ix > len(sequences)-1:

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps = 3

# convert into input/output

X, y = split_sequences(dataset, n_steps)

# the dataset knows the number of features, e.g. 2

n_features = X.shape[2]

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps, n_features)))

model.add(LSTM(100, activation='relu'))

model.add(Dense(n_features))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=400, verbose=0)

# demonstrate prediction

x_input = array([[70,75,145], [80,85,165], [90,95,185]])

x_input = x_input.reshape((1, n_steps, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example prepares the data, fits the model, and makes a prediction.

[[101.76599 108.730484 206.63577 ]]

1	[[101.76599 108.730484 206.63577 ]]

Multi-Step LSTM Models

A time series forecasting problem that requires a prediction of multiple time steps into the future can be referred to as multi-step time series forecasting.

Specifically, these are problems where the forecast horizon or interval is more than one time step.

There are two main types of LSTM models that can be used for multi-step forecasting; they are:

Vector Output Model
Encoder-Decoder Model

Before we look at these models, let’s first look at the preparation of data for multi-step forecasting.

Data Preparation

As with one-step forecasting, a time series used for multi-step time series forecasting must be split into samples with input and output components.

Both the input and output components will be comprised of multiple time steps and may or may not have the same number of steps.

For example, given the univariate time series:

[10, 20, 30, 40, 50, 60, 70, 80, 90]

1	[10, 20, 30, 40, 50, 60, 70, 80, 90]

We could use the last three time steps as input and forecast the next two time steps.

The first sample would look as follows:

Input:

[10, 20, 30]

1	[10, 20, 30]

Output:

[40, 50]

[40, 50]

The split_sequence() function below implements this behavior and will split a given univariate time series into samples with a specified number of input and output time steps.

# split a univariate sequence into samples
def split_sequence(sequence, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the sequence
		if out_end_ix > len(sequence):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# split a univariate sequence into samples

def split_sequence(sequence, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the sequence

if out_end_ix > len(sequence):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

We can demonstrate this function on the small contrived dataset.

The complete example is listed below.

# multi-step data preparation
from numpy import array

# split a univariate sequence into samples
def split_sequence(sequence, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the sequence
		if out_end_ix > len(sequence):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# split into samples
X, y = split_sequence(raw_seq, n_steps_in, n_steps_out)
# summarize the data
for i in range(len(X)):
	print(X[i], y[i])

# multi-step data preparation

from numpy import array

# split a univariate sequence into samples

def split_sequence(sequence, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the sequence

if out_end_ix > len(sequence):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# split into samples

X, y = split_sequence(raw_seq, n_steps_in, n_steps_out)

# summarize the data

for i in range(len(X)):

print(X[i], y[i])

Running the example splits the univariate series into input and output time steps and prints the input and output components of each.

[10 20 30] [40 50]
[20 30 40] [50 60]
[30 40 50] [60 70]
[40 50 60] [70 80]
[50 60 70] [80 90]

[10 20 30] [40 50]

[20 30 40] [50 60]

[30 40 50] [60 70]

[40 50 60] [70 80]

[50 60 70] [80 90]

Now that we know how to prepare data for multi-step forecasting, let’s look at some LSTM models that can learn this mapping.

Vector Output Model

Like other types of neural network models, the LSTM can output a vector directly that can be interpreted as a multi-step forecast.

This approach was seen in the previous section were one time step of each output time series was forecasted as a vector.

As with the LSTMs for univariate data in a prior section, the prepared samples must first be reshaped. The LSTM expects data to have a three-dimensional structure of [samples, timesteps, features], and in this case, we only have one feature so the reshape is straightforward.

...
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))

...

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

With the number of input and output steps specified in the n_steps_in and n_steps_out variables, we can define a multi-step time-series forecasting model.

Any of the presented LSTM model types could be used, such as Vanilla, Stacked, Bidirectional, CNN-LSTM, or ConvLSTM. Below defines a Stacked LSTM for multi-step forecasting.

...
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps_in, n_features)))
model.add(LSTM(100, activation='relu'))
model.add(Dense(n_steps_out))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps_in, n_features)))

model.add(LSTM(100, activation='relu'))

model.add(Dense(n_steps_out))

model.compile(optimizer='adam', loss='mse')

The model can make a prediction for a single sample. We can predict the next two steps beyond the end of the dataset by providing the input:

[70, 80, 90]

1	[70, 80, 90]

We would expect the predicted output to be:

[100, 110]

1	[100, 110]

As expected by the model, the shape of the single sample of input data when making the prediction must be [1, 3, 1] for the 1 sample, 3 time steps of the input, and the single feature.

...
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps_in, n_features))
yhat = model.predict(x_input, verbose=0)

...

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps_in, n_features))

yhat = model.predict(x_input, verbose=0)

Tying all of this together, the Stacked LSTM for multi-step forecasting with a univariate time series is listed below.

# univariate multi-step vector-output stacked lstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# split a univariate sequence into samples
def split_sequence(sequence, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the sequence
		if out_end_ix > len(sequence):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# split into samples
X, y = split_sequence(raw_seq, n_steps_in, n_steps_out)
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps_in, n_features)))
model.add(LSTM(100, activation='relu'))
model.add(Dense(n_steps_out))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=50, verbose=0)
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps_in, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate multi-step vector-output stacked lstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

# split a univariate sequence into samples

def split_sequence(sequence, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the sequence

if out_end_ix > len(sequence):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# split into samples

X, y = split_sequence(raw_seq, n_steps_in, n_steps_out)

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps_in, n_features)))

model.add(LSTM(100, activation='relu'))

model.add(Dense(n_steps_out))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=50, verbose=0)

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps_in, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example forecasts and prints the next two time steps in the sequence.

[[100.98096 113.28924]]

1	[[100.98096 113.28924]]

Encoder-Decoder Model

A model specifically developed for forecasting variable length output sequences is called the Encoder-Decoder LSTM.

The model was designed for prediction problems where there are both input and output sequences, so-called sequence-to-sequence, or seq2seq problems, such as translating text from one language to another.

This model can be used for multi-step time series forecasting.

As its name suggests, the model is comprised of two sub-models: the encoder and the decoder.

The encoder is a model responsible for reading and interpreting the input sequence. The output of the encoder is a fixed length vector that represents the model’s interpretation of the sequence. The encoder is traditionally a Vanilla LSTM model, although other encoder models can be used such as Stacked, Bidirectional, and CNN models.

...
model.add(LSTM(100, activation='relu', input_shape=(n_steps_in, n_features)))

1 2	... model.add(LSTM(100, activation='relu', input_shape=(n_steps_in, n_features)))

The decoder uses the output of the encoder as an input.

First, the fixed-length output of the encoder is repeated, once for each required time step in the output sequence.

...
model.add(RepeatVector(n_steps_out))

1 2	... model.add(RepeatVector(n_steps_out))

This sequence is then provided to an LSTM decoder model. The model must output a value for each value in the output time step, which can be interpreted by a single output model.

...
model.add(LSTM(100, activation='relu', return_sequences=True))

1 2	... model.add(LSTM(100, activation='relu', return_sequences=True))

We can use the same output layer or layers to make each one-step prediction in the output sequence. This can be achieved by wrapping the output part of the model in a TimeDistributed wrapper.

....
model.add(TimeDistributed(Dense(1)))

1 2	.... model.add(TimeDistributed(Dense(1)))

The full definition for an Encoder-Decoder model for multi-step time series forecasting is listed below.

...
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', input_shape=(n_steps_in, n_features)))
model.add(RepeatVector(n_steps_out))
model.add(LSTM(100, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(1)))
model.compile(optimizer='adam', loss='mse')

...

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', input_shape=(n_steps_in, n_features)))

model.add(RepeatVector(n_steps_out))

model.add(LSTM(100, activation='relu', return_sequences=True))

model.add(TimeDistributed(Dense(1)))

model.compile(optimizer='adam', loss='mse')

As with other LSTM models, the input data must be reshaped into the expected three-dimensional shape of [samples, timesteps, features].

...
X = X.reshape((X.shape[0], X.shape[1], n_features))

1 2	... X = X.reshape((X.shape[0], X.shape[1], n_features))

In the case of the Encoder-Decoder model, the output, or y part, of the training dataset must also have this shape. This is because the model will predict a given number of time steps with a given number of features for each input sample.

...
y = y.reshape((y.shape[0], y.shape[1], n_features))

1 2	... y = y.reshape((y.shape[0], y.shape[1], n_features))

The complete example of an Encoder-Decoder LSTM for multi-step time series forecasting is listed below.

# univariate multi-step encoder-decoder lstm example
from numpy import array
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import RepeatVector
from keras.layers import TimeDistributed

# split a univariate sequence into samples
def split_sequence(sequence, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequence)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the sequence
		if out_end_ix > len(sequence):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# split into samples
X, y = split_sequence(raw_seq, n_steps_in, n_steps_out)
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
y = y.reshape((y.shape[0], y.shape[1], n_features))
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', input_shape=(n_steps_in, n_features)))
model.add(RepeatVector(n_steps_out))
model.add(LSTM(100, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(1)))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=100, verbose=0)
# demonstrate prediction
x_input = array([70, 80, 90])
x_input = x_input.reshape((1, n_steps_in, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# univariate multi-step encoder-decoder lstm example

from numpy import array

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

from keras.layers import RepeatVector

from keras.layers import TimeDistributed

# split a univariate sequence into samples

def split_sequence(sequence, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequence)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the sequence

if out_end_ix > len(sequence):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# split into samples

X, y = split_sequence(raw_seq, n_steps_in, n_steps_out)

# reshape from [samples, timesteps] into [samples, timesteps, features]

n_features = 1

X = X.reshape((X.shape[0], X.shape[1], n_features))

y = y.reshape((y.shape[0], y.shape[1], n_features))

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', input_shape=(n_steps_in, n_features)))

model.add(RepeatVector(n_steps_out))

model.add(LSTM(100, activation='relu', return_sequences=True))

model.add(TimeDistributed(Dense(1)))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=100, verbose=0)

# demonstrate prediction

x_input = array([70, 80, 90])

x_input = x_input.reshape((1, n_steps_in, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example forecasts and prints the next two time steps in the sequence.

[[[101.9736  
  [116.213615]]]

1 2	[[[101.9736 [116.213615]]]

Multivariate Multi-Step LSTM Models

In the previous sections, we have looked at univariate, multivariate, and multi-step time series forecasting.

It is possible to mix and match the different types of LSTM models presented so far for the different problems. This too applies to time series forecasting problems that involve multivariate and multi-step forecasting, but it may be a little more challenging.

In this section, we will provide short examples of data preparation and modeling for multivariate multi-step time series forecasting as a template to ease this challenge, specifically:

Multiple Input Multi-Step Output.
Multiple Parallel Input and Multi-Step Output.

Perhaps the biggest stumbling block is in the preparation of data, so this is where we will focus our attention.

Multiple Input Multi-Step Output

There are those multivariate time series forecasting problems where the output series is separate but dependent upon the input time series, and multiple time steps are required for the output series.

For example, consider our multivariate time series from a prior section:

[[ 10  15  25]
 [ 20  25  45]
 [ 30  35  65]
 [ 40  45  85]
 [ 50  55 105]
 [ 60  65 125]
 [ 70  75 145]
 [ 80  85 165]
 [ 90  95 185]]

[[ 10 15 25]

[ 20 25 45]

[ 30 35 65]

[ 40 45 85]

[ 50 55 105]

[ 60 65 125]

[ 70 75 145]

[ 80 85 165]

[ 90 95 185]]

We may use three prior time steps of each of the two input time series to predict two time steps of the output time series.

Input:

10, 15
20, 25
30, 35

10, 15

20, 25

30, 35

Output:

65
85

The split_sequences() function below implements this behavior.

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out-1
		# check if we are beyond the dataset
		if out_end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out-1

# check if we are beyond the dataset

if out_end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

We can demonstrate this on our contrived dataset.

The complete example is listed below.

# multivariate multi-step data preparation
from numpy import array
from numpy import hstack

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out-1
		# check if we are beyond the dataset
		if out_end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# covert into input/output
X, y = split_sequences(dataset, n_steps_in, n_steps_out)
print(X.shape, y.shape)
# summarize the data
for i in range(len(X)):
	print(X[i], y[i])

# multivariate multi-step data preparation

from numpy import array

from numpy import hstack

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out-1

# check if we are beyond the dataset

if out_end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# covert into input/output

X, y = split_sequences(dataset, n_steps_in, n_steps_out)

print(X.shape, y.shape)

# summarize the data

for i in range(len(X)):

print(X[i], y[i])

Running the example first prints the shape of the prepared training data.

We can see that the shape of the input portion of the samples is three-dimensional, comprised of six samples, with three time steps, and two variables for the 2 input time series.

The output portion of the samples is two-dimensional for the six samples and the two time steps for each sample to be predicted.

The prepared samples are then printed to confirm that the data was prepared as we specified.

(6, 3, 2) (6, 2)

[[10 15]
 [20 25]
 [30 35]] [65 85]
[[20 25]
 [30 35]
 [40 45]] [ 85 105]
[[30 35]
 [40 45]
 [50 55]] [105 125]
[[40 45]
 [50 55]
 [60 65]] [125 145]
[[50 55]
 [60 65]
 [70 75]] [145 165]
[[60 65]
 [70 75]
 [80 85]] [165 185]

(6, 3, 2) (6, 2)

[[10 15]

[20 25]

[30 35]] [65 85]

[[20 25]

[30 35]

[40 45]] [ 85 105]

[[30 35]

[40 45]

[50 55]] [105 125]

[[40 45]

[50 55]

[60 65]] [125 145]

[[50 55]

[60 65]

[70 75]] [145 165]

[[60 65]

[70 75]

[80 85]] [165 185]

We can now develop an LSTM model for multi-step predictions.

A vector output or an encoder-decoder model could be used. In this case, we will demonstrate a vector output with a Stacked LSTM.

The complete example is listed below.

# multivariate multi-step stacked lstm example
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out-1
		# check if we are beyond the dataset
		if out_end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# covert into input/output
X, y = split_sequences(dataset, n_steps_in, n_steps_out)
# the dataset knows the number of features, e.g. 2
n_features = X.shape[2]
# define model
model = Sequential()
model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps_in, n_features)))
model.add(LSTM(100, activation='relu'))
model.add(Dense(n_steps_out))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=200, verbose=0)
# demonstrate prediction
x_input = array([[70, 75], [80, 85], [90, 95]])
x_input = x_input.reshape((1, n_steps_in, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# multivariate multi-step stacked lstm example

from numpy import array

from numpy import hstack

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out-1

# check if we are beyond the dataset

if out_end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# covert into input/output

X, y = split_sequences(dataset, n_steps_in, n_steps_out)

# the dataset knows the number of features, e.g. 2

n_features = X.shape[2]

# define model

model = Sequential()

model.add(LSTM(100, activation='relu', return_sequences=True, input_shape=(n_steps_in, n_features)))

model.add(LSTM(100, activation='relu'))

model.add(Dense(n_steps_out))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=200, verbose=0)

# demonstrate prediction

x_input = array([[70, 75], [80, 85], [90, 95]])

x_input = x_input.reshape((1, n_steps_in, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example fits the model and predicts the next two time steps of the output sequence beyond the dataset.

We would expect the next two steps to be: [185, 205]

It is a challenging framing of the problem with very little data, and the arbitrarily configured version of the model gets close.

[[188.70619 210.16513]]

1	[[188.70619 210.16513]]

Multiple Parallel Input and Multi-Step Output

A problem with parallel time series may require the prediction of multiple time steps of each time series.

For example, consider our multivariate time series from a prior section:

[[ 10  15  25]
 [ 20  25  45]
 [ 30  35  65]
 [ 40  45  85]
 [ 50  55 105]
 [ 60  65 125]
 [ 70  75 145]
 [ 80  85 165]
 [ 90  95 185]]

[[ 10 15 25]

[ 20 25 45]

[ 30 35 65]

[ 40 45 85]

[ 50 55 105]

[ 60 65 125]

[ 70 75 145]

[ 80 85 165]

[ 90 95 185]]

We may use the last three time steps from each of the three time series as input to the model and predict the next time steps of each of the three time series as output.

The first sample in the training dataset would be the following.

Input:

10, 15, 25
20, 25, 45
30, 35, 65

10, 15, 25

20, 25, 45

30, 35, 65

Output:

40, 45, 85
50, 55, 105

1 2	40, 45, 85 50, 55, 105

The split_sequences() function below implements this behavior.

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the dataset
		if out_end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the dataset

if out_end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

We can demonstrate this function on the small contrived dataset.

The complete example is listed below.

# multivariate multi-step data preparation
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import RepeatVector
from keras.layers import TimeDistributed

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the dataset
		if out_end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# covert into input/output
X, y = split_sequences(dataset, n_steps_in, n_steps_out)
print(X.shape, y.shape)
# summarize the data
for i in range(len(X)):
	print(X[i], y[i])

# multivariate multi-step data preparation

from numpy import array

from numpy import hstack

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

from keras.layers import RepeatVector

from keras.layers import TimeDistributed

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the dataset

if out_end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# covert into input/output

X, y = split_sequences(dataset, n_steps_in, n_steps_out)

print(X.shape, y.shape)

# summarize the data

for i in range(len(X)):

print(X[i], y[i])

Running the example first prints the shape of the prepared training dataset.

We can see that both the input (X) and output (Y) elements of the dataset are three dimensional for the number of samples, time steps, and variables or parallel time series respectively.

The input and output elements of each series are then printed side by side so that we can confirm that the data was prepared as we expected.

(5, 3, 3) (5, 2, 3)

[[10 15 25]
 [20 25 45]
 [30 35 65]] [[ 40  45  85]
 [ 50  55 105]]
[[20 25 45]
 [30 35 65]
 [40 45 85]] [[ 50  55 105]
 [ 60  65 125]]
[[ 30  35  65]
 [ 40  45  85]
 [ 50  55 105]] [[ 60  65 125]
 [ 70  75 145]]
[[ 40  45  85]
 [ 50  55 105]
 [ 60  65 125]] [[ 70  75 145]
 [ 80  85 165]]
[[ 50  55 105]
 [ 60  65 125]
 [ 70  75 145]] [[ 80  85 165]
 [ 90  95 185]]

(5, 3, 3) (5, 2, 3)

[[10 15 25]

[20 25 45]

[30 35 65]] [[ 40 45 85]

[ 50 55 105]]

[[20 25 45]

[30 35 65]

[40 45 85]] [[ 50 55 105]

[ 60 65 125]]

[[ 30 35 65]

[ 40 45 85]

[ 50 55 105]] [[ 60 65 125]

[ 70 75 145]]

[[ 40 45 85]

[ 50 55 105]

[ 60 65 125]] [[ 70 75 145]

[ 80 85 165]]

[[ 50 55 105]

[ 60 65 125]

[ 70 75 145]] [[ 80 85 165]

[ 90 95 185]]

We can use either the Vector Output or Encoder-Decoder LSTM to model this problem. In this case, we will use the Encoder-Decoder model.

The complete example is listed below.

# multivariate multi-step encoder-decoder lstm example
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import RepeatVector
from keras.layers import TimeDistributed

# split a multivariate sequence into samples
def split_sequences(sequences, n_steps_in, n_steps_out):
	X, y = list(), list()
	for i in range(len(sequences)):
		# find the end of this pattern
		end_ix = i + n_steps_in
		out_end_ix = end_ix + n_steps_out
		# check if we are beyond the dataset
		if out_end_ix > len(sequences):
			break
		# gather input and output parts of the pattern
		seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :]
		X.append(seq_x)
		y.append(seq_y)
	return array(X), array(y)

# define input sequence
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convert to [rows, columns] structure
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# horizontally stack columns
dataset = hstack((in_seq1, in_seq2, out_seq))
# choose a number of time steps
n_steps_in, n_steps_out = 3, 2
# covert into input/output
X, y = split_sequences(dataset, n_steps_in, n_steps_out)
# the dataset knows the number of features, e.g. 2
n_features = X.shape[2]
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_steps_in, n_features)))
model.add(RepeatVector(n_steps_out))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(n_features)))
model.compile(optimizer='adam', loss='mse')
# fit model
model.fit(X, y, epochs=300, verbose=0)
# demonstrate prediction
x_input = array([[60, 65, 125], [70, 75, 145], [80, 85, 165]])
x_input = x_input.reshape((1, n_steps_in, n_features))
yhat = model.predict(x_input, verbose=0)
print(yhat)

# multivariate multi-step encoder-decoder lstm example

from numpy import array

from numpy import hstack

from keras.models import Sequential

from keras.layers import LSTM

from keras.layers import Dense

from keras.layers import RepeatVector

from keras.layers import TimeDistributed

# split a multivariate sequence into samples

def split_sequences(sequences, n_steps_in, n_steps_out):

X, y = list(), list()

for i in range(len(sequences)):

# find the end of this pattern

end_ix = i + n_steps_in

out_end_ix = end_ix + n_steps_out

# check if we are beyond the dataset

if out_end_ix > len(sequences):

break

# gather input and output parts of the pattern

seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :]

X.append(seq_x)

y.append(seq_y)

return array(X), array(y)

# define input sequence

in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])

in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])

out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

# convert to [rows, columns] structure

in_seq1 = in_seq1.reshape((len(in_seq1), 1))

in_seq2 = in_seq2.reshape((len(in_seq2), 1))

out_seq = out_seq.reshape((len(out_seq), 1))

# horizontally stack columns

dataset = hstack((in_seq1, in_seq2, out_seq))

# choose a number of time steps

n_steps_in, n_steps_out = 3, 2

# covert into input/output

X, y = split_sequences(dataset, n_steps_in, n_steps_out)

# the dataset knows the number of features, e.g. 2

n_features = X.shape[2]

# define model

model = Sequential()

model.add(LSTM(200, activation='relu', input_shape=(n_steps_in, n_features)))

model.add(RepeatVector(n_steps_out))

model.add(LSTM(200, activation='relu', return_sequences=True))

model.add(TimeDistributed(Dense(n_features)))

model.compile(optimizer='adam', loss='mse')

# fit model

model.fit(X, y, epochs=300, verbose=0)

# demonstrate prediction

x_input = array([[60, 65, 125], [70, 75, 145], [80, 85, 165]])

x_input = x_input.reshape((1, n_steps_in, n_features))

yhat = model.predict(x_input, verbose=0)

print(yhat)

Running the example fits the model and predicts the values for each of the three time steps for the next two time steps beyond the end of the dataset.

We would expect the values for these series and time steps to be as follows:

90, 95, 185
100, 105, 205

1 2	90, 95, 185 100, 105, 205

We can see that the model forecast gets reasonably close to the expected values.

[[[ 91.86044   97.77231  189.66768 ]
  [103.299355 109.18123  212.6863  ]]]

1 2	[[[ 91.86044 97.77231 189.66768 ] [103.299355 109.18123 212.6863 ]]]

Summary

In this tutorial, you discovered how to develop a suite of LSTM models for a range of standard time series forecasting problems.

Specifically, you learned:

How to develop LSTM models for univariate time series forecasting.
How to develop LSTM models for multivariate time series forecasting.
How to develop LSTM models for multi-step time series forecasting.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

951 Responses to How to Develop LSTM Models for Time Series Forecasting

Jenna Ma November 16, 2018 at 12:09 am # Edit

This tutorial is so helpful to me. Thank you very much!
It will be more helpful in the real projects if the dataset is split into batches. Hope you will mention this in the future.

Reply
- Jason Brownlee November 16, 2018 at 6:16 am # Edit
  
  Keras will split the dataset into batches.
  
  Reply
  - Jenna Ma November 16, 2018 at 7:27 pm # Edit
    
    I think this blog ( https://machinelearningmastery.com/use-different-batch-sizes-training-predicting-python-keras/) may answer my question. I will do more research. Thanks a lot.
    
    Reply
    - Jason Brownlee November 17, 2018 at 5:45 am # Edit
      
      Great!
      
      Reply
    - Ahmed Saif February 11, 2021 at 9:51 pm # Edit
      
      Thank you
      
      Reply
  - maria October 8, 2019 at 8:52 pm # Edit
    
    Hi!
    
    i would like to cite your book “Deep Learning for Time Series Forecasting: Predict the Future
    with MLPs, CNNs and LSTMs in Python.” Is there an appropriate format for doing this?
    
    Reply
    - Jason Brownlee October 9, 2019 at 8:12 am # Edit
      
      Yes, see here:
      https://machinelearningmastery.com/faq/single-faq/how-do-i-reference-or-cite-a-book-or-blog-post
      
      Reply
  - H October 31, 2019 at 2:31 am # Edit
    
    Hi Jason,
    I want please an example of Sliding window-based support vector regression for prediction.
    have you this example .
    
    Thanks a lot
    
    Reply
    - Jason Brownlee October 31, 2019 at 5:35 am # Edit
      
      Thanks for the suggestion.
      
      Reply
      - Sruthi March 29, 2021 at 11:14 pm # Edit
        
        Hi Jason, It was a great tutorial
        I have a question :
        
        IN Multiple Parallel inputs, the output of the LSTM Encdoer 0Decoder model will be 3D, how do we transform it back to 2D? I am asking this because I have performed scaling on the data using minmaxscaler() and it expects the input to be a 2d array.
        
        In order to compare the predicted values with the original values, I need to perform inverse scaling, but I am stuck at how to reshape the 3d input and output back to 2d without losing any data.
      - Jason Brownlee March 30, 2021 at 6:05 am # Edit
        
        You might need to write custom code to collect values for each variable before inverting the scale.
- chi August 27, 2019 at 7:07 am # Edit
  
  Hello Jason,
  
  Thank you so so much for your post, it was super helpful. For the multiple timesteps output LSTM model, I am wondering what will be the difference of the performance between model-1 and model-2? Model-1 is your multiple timesteps output LSTM model, for example, we input last 7 days data features, and the output is the next 5 days prices. Model-2 is the simple 1-timstep output LSTM model, where the input is last 7 days data features, output is the next day price. Then we use our predicted price as the new input to predict future prices until we predict all next 5 days prices.
  I am wondering what are the key differences between those 2 strategies to predict the next 5 days prices? What are the advantages and disadvantages of those 2 LSTM models?
  
  Thank you,
  
  Reply
  - Jason Brownlee August 27, 2019 at 2:06 pm # Edit
    
    Good question, the differences really depend on the choice of model and complexity of the dataset.
    
    This post compares the different approaches:
    https://machinelearningmastery.com/multi-step-time-series-forecasting/
    
    Reply
- Rick March 28, 2020 at 5:45 pm # Edit
  
  Hey Jason,
  Thanks for the blogs. They are really helpful and I have learned a lot from machinelearningmastery.
  This blog about LSTM is very informative, but I have a question
  
  I have a set of amplitude scans, and I want to predict next scan (many to one problem). So my data is of (6,590) and the result should be (1,590). 590 are the amplitude values in the scan.
  
  A. Is it possible to address this problem with LSTM and
  B. Even if possible how much accurate do you think the system might perform given the number of time steps and features it is predicting.
  
  Thanks
  
  Reply
  - Jason Brownlee March 29, 2020 at 5:50 am # Edit
    
    You’re welcome.
    
    Try it and see. This framework will help:
    https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
    
    Reply
- annemarieke May 8, 2021 at 2:33 am # Edit
  
  [email protected]
  
  Reply
Amy November 16, 2018 at 7:17 am # Edit

Thanks Jason for this good tutorial. I have a question. When we have two different time series, 1 and 2. Time series 1 will influence time series 2 and our goal is to predict the future value of time series 2. How can we use LSTM for this case?

Reply
- Jason Brownlee November 16, 2018 at 1:55 pm # Edit
  
  I call this a dependent time series problem. I given an example of how to model it on this post:
  https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/
  
  Reply
  - Amy November 16, 2018 at 2:21 pm # Edit
    
    The link is the link of the current page, Do you mean that?
    
    Reply
    - Jason Brownlee November 17, 2018 at 5:41 am # Edit
      
      Yes, I give an example above.
      
      Reply
Kwan November 22, 2018 at 8:03 pm # Edit

Thanks Jason for this good tutorial, I have read your tutorial for a long time , I have a question. How to use LSTM model forecasting Multi-Site Multivariate Time Series, such as EMC Data Science Global Hackathon dataset, thank you very much!

Reply
- Jason Brownlee November 23, 2018 at 7:48 am # Edit
  
  I have advice for multi-site forecasting here:
  https://machinelearningmastery.com/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites
  
  Reply
Caiyuan November 29, 2018 at 1:33 pm # Edit

Thank you for sharing. I found that the results of time series prediction using LSTM are similar to the results of one step behind the original sequence. What do you think?

Reply
- Jason Brownlee November 29, 2018 at 2:40 pm # Edit
  
  Sounds like the model has learned a persistance model and may not be skillful.
  
  Reply
  - Sudrit Saisa-ing August 9, 2019 at 8:48 pm # Edit
    
    I have some question?
    If I have model from LSTM,I want to know percent of accurate of new prediction.
    
    How to know percent accurate for new forcast?
    
    Thank you
    
    Reply
    - Jason Brownlee August 10, 2019 at 7:16 am # Edit
      
      If your model is predicting a class label, you can specify the accuracy measure as a metric in the call to compile() then use the evaluate() model to calculate the accuracy.
      
      You can learn how for an MLP in this post which will be the same for an LSTM:
      https://machinelearningmastery.com/tutorial-first-neural-network-python-keras/
      
      Reply
WLF December 5, 2018 at 6:04 pm # Edit

Thanks a lot! I have read your websites for a long time!
I have a question, in “Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras” you said that:
“LSTMs are sensitive to the scale of the input data, specifically when the sigmoid (default) or tanh activation functions are used. It can be a good practice to rescale the data to the range of 0-to-1, also called normalizing. ”
So why don’t you normalize input here?
Because you used relu? Because the data is increasing (so we can’t normalize the future input)? Or because you just give us an example?
Do you suggest normalizing here?

Reply
- Jason Brownlee December 6, 2018 at 5:51 am # Edit
  
  It would be a good idea to prepare the data with normalization or similar here.
  
  I chose not to because it seems to confuse more readers than it helps. Also, choice of relu does make the model a lot more robust to unscaled data.
  
  Reply
rkk621 December 6, 2018 at 2:27 am # Edit

Thanks for a great article. Minor typo or confusion:

For the Multiple input case in Multivariate series, if we use three time steps and

10,15
20,25
30,35

as our inputs, shouldn’t the output (predicted val used for training) be

85

instead of 65?

Reply
- Jason Brownlee December 6, 2018 at 5:57 am # Edit
  
  In the chosen framing of the problem, we want to predict the output at t not t+1, given inputs up to and including t.
  
  You can choose to frame the problem differently if you like. It is arbitrary.
  
  Reply
- WLF December 6, 2018 at 11:02 pm # Edit
  
  You can also reference ‘Multiple Parallel …’
  
  So you can find the differences in function ‘split_sequences’
  
  if you want to predict 85, you can change the code to:
  
  if end_ix > len(sequences)-1:
  break
  seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix, -1]
  
  Notice ‘len(sequences)-1’, and ‘sequences[end_ix, -1]’
  
  Reply
Ida December 10, 2018 at 7:55 pm # Edit

Thanks sooooo much Jason.
It helped me a lot.

Reply
- Jason Brownlee December 11, 2018 at 7:42 am # Edit
  
  I’m happy to hear that.
  
  Reply
John December 12, 2018 at 9:21 am # Edit

Hi Jason,

Thanks for this nice blog! I am new to LSTM in time-series, and I need your help.

Most info on internet is for a single time series and for next-step forecasting. I want to produce 6 months ahead forecast using previous 15 months for 100 different time series, each of length 54 months.

So, there is 34 windows for each time-series if we use sliding windows. So, my initial X_train has a shape of (3400,15). Then. I am reshaping my X_train [samples, timesteps, features] as follows: (3400, 15, 1). Is this reshaping correct? In genera, how can we choose “timesteps” and “features” arguments in this multi-input multi-step forecast?

Also, how can I choose “batch_size” and “units”? Since I want 6 months ahead forecast, my output should be a matrix with dimensions (100,6). I chose units=6, and batch_size=1. Are these numbers correct?

Thanks for your help!

Reply
- Jason Brownlee December 12, 2018 at 2:14 pm # Edit
  
  Looks good.
  
  Time steps is really problem specific – e.g. how much history do you need to make a prediction. Perhaps test with your data.
  
  Batch size and units – again, depends on your problem. Test. 6 units is too few. Start with 100, try 500, 1000, etc. Batch size of 1 seems small, perhaps also try 32, 64, etc.
  
  Let me know how you go.
  
  Reply
  - John December 13, 2018 at 2:06 am # Edit
    
    Hi Jason,
    
    Thanks for your response.
    
    I don’t understand “6 units is too few”. In documentation of lstm functions in R, units is defined as “dimensionality of the output space”. Since I need an output with 6 columns (6 months forecast), I define units=6. Any other number does not produce the output I want. Is there anything wrong in my interpretation?
    
    Reply
    - Jason Brownlee December 13, 2018 at 7:55 am # Edit
      
      I recommend using a Dense layer as the output rather than the outputting from the LSTM directly.
      
      Then dramatically increase the capacity of the model by increasing the number of LSTM units.
      
      Reply
- Ravi Varma Injeti December 18, 2019 at 12:55 am # Edit
  
  Hii Jason that’s great tutorial. I have time series data of the size 2245 where timings of bus from starting station to destination station. I want to find the pattern is it possible through LSTM WITHOUT THE CATEGORICAL RESPONSES.
  
  Reply
  - Jason Brownlee December 18, 2019 at 6:08 am # Edit
    
    Perhaps start here:
    https://machinelearningmastery.com/start-here/#deep_learning_time_series
    
    Reply
Shaifali December 16, 2018 at 1:21 am # Edit

Bidirectional LSTM works better than LSTM. Can you please explain the working of bidirectional LSTM. Since we do not know future values. How do we do prediction?

Reply
- Jason Brownlee December 16, 2018 at 5:23 am # Edit
  
  It has two LSTM layers, one that processes the sequences forwards, and one that processes it backwards.
  
  You can learn more here:
  https://machinelearningmastery.com/develop-bidirectional-lstm-sequence-classification-python-keras/
  
  Reply
Jenna Ma December 16, 2018 at 4:24 pm # Edit

In the last encoder-decoder model, if I have different features of input and output, is it correct that I change the code like this?
model = Sequential()
model.add(LSTM(200, activation=’relu’, input_shape=(n_steps_in, n_features_in)))
model.add(RepeatVector(n_steps_out))
model.add(LSTM(200, activation=’relu’, return_sequences=True))
model.add(TimeDistributed(Dense(n_features_out)))
model.compile(optimizer=’adam’, loss=’mse’)

Reply
- Jason Brownlee December 17, 2018 at 6:19 am # Edit
  
  I’m sure I understand, what do you mean exactly?
  
  Reply
  - Jenna Ma December 18, 2018 at 1:50 pm # Edit
    
    I am sorry for not expressing my question clearly.
    In the last part of your tutorial, you gave an example like this:
    [[10 15 25]
    [20 25 45]
    [30 35 65]]
    [[ 40 45 85]
    [ 50 55 105]]
    Then, you introduced the Encoder-Decoder LSTM to model this problem.
    If I want to use the last three time steps from each of the three time series as input to the model and predict the next two time steps of the third time series as output. Namely, my input and output elements are like the following. The shapes of input and output are (5, 3, 3) and (5, 2, 1) respectively.
    [[10 15 25]
    [20 25 45]
    [30 35 65]]
    [[85]
    [105]]
    When I define the Encoder-Decoder LSTM model, the code will be like this:
    model = Sequential()
    model.add(LSTM(200, activation=’relu’, input_shape=(3,3)))
    model.add(RepeatVector(2))
    model.add(LSTM(200, activation=’relu’, return_sequences=True))
    model.add(TimeDistributed(Dense(1)))
    model.compile(optimizer=’adam’, loss=’mse’)
    Is it correct?
    Thank you very much!
    
    Reply
    - Jason Brownlee December 18, 2018 at 2:36 pm # Edit
      
      It looks correct, but I don’t have the capacity to test the code to be sure.
      
      Reply
      - Jenna Ma December 18, 2018 at 6:05 pm # Edit
        
        Thank you!
        I test the code, and I want to show you what I got.
        I assume the input sequence:
        in_seq1 = np.arange(10,1000,10)
        in_seq2 = np.arange(15,1005,10)
        Define the prediction input:
        x_input = np.array([[960, 965, 1925], [970, 975, 1945], [980, 985, 1965]])
        I expect the output values would be as follows:
        [ [1985] [2005] ]
        And the model forecasts: [ [1997.1425] [2026.6136] ]
        I think this means that the model can work.
      - Jason Brownlee December 19, 2018 at 6:31 am # Edit
        
        Nice work! Now you can start tuning the model to lift skill.
dani December 19, 2018 at 12:55 pm # Edit

how we can test these examples if have big excel data set?and its time series data, kindly refer to a link?

Reply

Navigation

How to Develop LSTM Models for Time Series Forecasting

Tutorial Overview

Univariate LSTM Models

Data Preparation

Need help with Deep Learning for Time Series?

Vanilla LSTM

Stacked LSTM

Bidirectional LSTM

CNN LSTM

ConvLSTM

Multivariate LSTM Models

Multiple Input Series

Multiple Parallel Series

Multi-Step LSTM Models

Data Preparation

Vector Output Model

Encoder-Decoder Model

Multivariate Multi-Step LSTM Models

Multiple Input Multi-Step Output

Multiple Parallel Input and Multi-Step Output

Further Reading

Summary

Develop Deep Learning models for Time Series Today!

Develop Your Own Forecasting models in Minutes

Finally Bring Deep Learning to your Time Series Forecasting Projects

More On This Topic

951 Responses to How to Develop LSTM Models for Time Series Forecasting