Ever looked at your data and thought something was missing or it’s hiding something from you? This is a deep dive guide on revealing those hidden connections and unknown relationships between the variables in your dataset.
Why should you care?
Machine learning algorithms like linear regression hate surprises.
It is essential to discover and quantify the degree to which variables in your dataset are dependent upon each other. This knowledge can help you better prepare your data to meet the expectations of machine learning algorithms, such as linear regression, whose performance will degrade with these interdependencies.
In this guide, you will discover that correlation is the statistical summary of the relationship between variables and how to calculate it for different types of variables and relationships.
After completing this tutorial, you will know:
Covariance Matrix Magic: Summarize the linear bond between multiple variables.
Pearson’s Power: Decode the linear ties between two variables.
Spearman’s Insight: Unearth the unique monotonic rhythm between variables.
Kick-start your project with my new book Statistics for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
Update May/2018: Updated description of the sign of the covariance (thanks Fulya).
Update Nov/2023: Updated some wording for clarity and additional insights.
How to Use Correlation to Understand the Relationship Between Variables Photo by Fraser Mummery, some rights reserved.
Tutorial Overview
This tutorial is divided into 5 parts; they are:
What is Correlation?
Test Dataset
Covariance
Pearson’s Correlation
Spearman’s Correlation
Need help with Statistics for Machine Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
What is Correlation?
Ever wondered how your data variables are linked to one another? Variables within a dataset can be related for lots of reasons.
For example:
One variable could cause or depend on the values of another variable.
One variable could be lightly associated with another variable.
Two variables could depend on a third unknown variable.
All of these aspects of correlation and how data variables are dependent or can relate to one another get us thinking about their use. Correlation is very useful in data analysis and modelling to better understand the relationships between variables. The statistical relationship between two variables is referred to as their correlation.
A correlation could be presented in different ways:
Positive Correlation: both variables change in the same direction.
Neutral Correlation: No relationship in the change of the variables.
Negative Correlation: variables change in opposite directions.
The performance of some algorithms can deteriorate if two or more variables are tightly related, called multicollinearity. An example is linear regression, where one of the offending correlated variables should be removed in order to improve the skill of the model.
We may also be interested in the correlation between input variables with the output variable in order to provide insight into which variables may or may not be relevant as input for developing a model.
The structure of the relationship may be known, e.g. it may be linear, or we may have no idea whether a relationship exists between two variables or what structure it may take. Depending on what is known about the relationship and the distribution of the variables, different correlation scores can be calculated.
In this tutorial guide, we will delve into a correlation score tailored for variables with a Gaussian distribution and a linear relationship. We will also explore another score that does not rely on a specific distribution and captures any monotonic (either increasing or decreasing) relationship.
Test Dataset
Before we go diving into correlation methods, let’s define a dataset we can use to test the methods.
We will generate 1,000 samples of two variables with a strong positive correlation. The first variable will be random numbers drawn from a Gaussian distribution with a mean of 100 and a standard deviation of 20. The second variable will be values from the first variable with Gaussian noise added with a mean of 50 and a standard deviation of 10.
We will use the randn() function to generate random Gaussian values with a mean of 0 and a standard deviation of 1, then multiply the results by our own standard deviation and add the mean to shift the values into the preferred range.
The pseudorandom number generator is seeded to ensure that we get the same sample of numbers each time the code is run.
Executing the above code initially outputs the mean and standard deviation for both variables:
1
2
data1: mean=100.776 stdv=19.620
data2: mean=151.050 stdv=22.358
A scatter plot of the two variables will be created. Because we contrived the dataset, we know there is a relationship between the two variables. This is clear when we review the generated scatter plot where we can see an increasing trend.
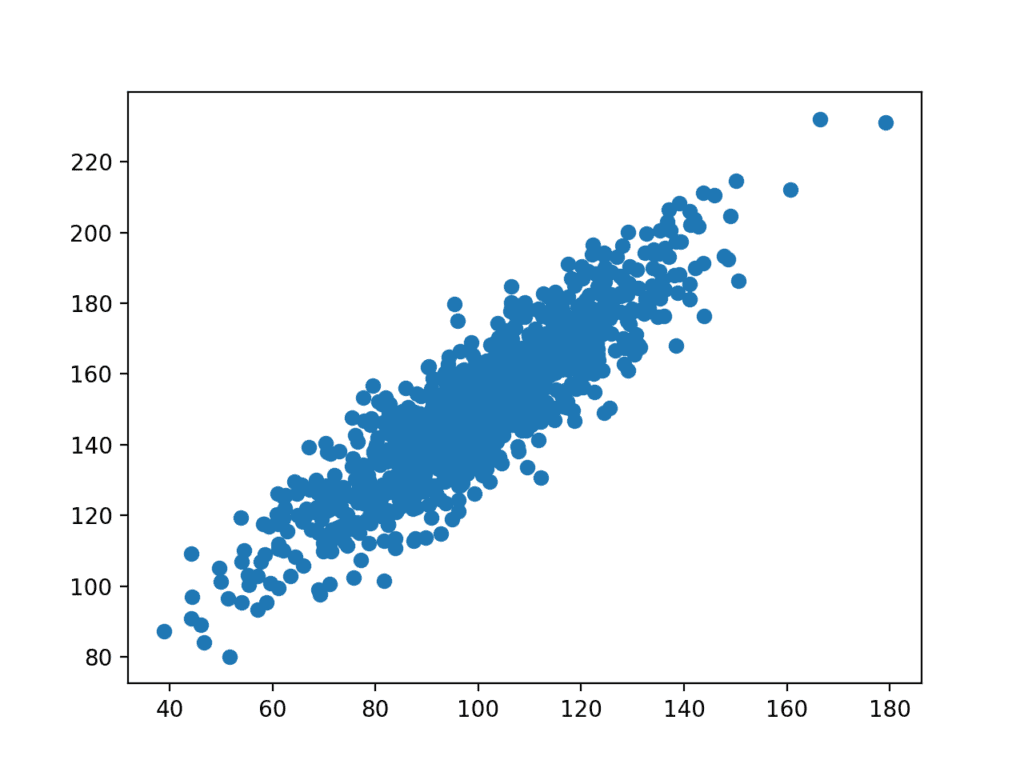
Scatter plot of the test correlation dataset
Before we look at calculating some correlation scores, it’s imperative to first comprehend a fundamental statistical concept known as covariance.
Covariance
You may have heard of linear relationships at school and also a lot in the world of data science. At the core of many statistical analyses is the concept of linear relationships between variables. This is a relationship that is consistently additive across the two data samples.
This relationship can be summarized between two variables, called the covariance. It is calculated as the average of the product between the values from each sample, where the values have been centred (by subtracting their respective means).
The calculation of the sample covariance is as follows:
The use of the mean in the calculation implies that each data should ideally adhere to a Gaussian or Gaussian-like distribution.
The covariance sign can be interpreted as whether the two variables change in the same direction (positive) or change in different directions (negative). The magnitude of the covariance is not easily interpreted. A covariance value of zero indicates that both variables are completely independent.
The cov() NumPy function can be used to calculate a covariance matrix between two or more variables.
1
covariance=cov(data1,data2)
The diagonal of the matrix contains the covariance between each variable and itself. The other values in the matrix represent the covariance between the two variables; in this case, the remaining two values are the same given that we are calculating the covariance for only two variables.
We can calculate the covariance matrix for the two variables in our test problem.
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
# calculate the covariance between two variables
from numpy.random import randn
from numpy.random import seed
from numpy import cov
# seed random number generator
seed(1)
# prepare data
data1=20*randn(1000)+100
data2=data1+(10*randn(1000)+50)
# calculate covariance matrix
covariance=cov(data1,data2)
print(covariance)
The covariance and covariance matrix are used widely within statistics and multivariate analysis to characterize the relationships between two or more variables.
Running the example calculates and prints the covariance matrix.
Because the dataset was contrived with each variable drawn from a Gaussian distribution and the variables linearly correlated, covariance is a reasonable method for describing the relationship.
The covariance between the two variables is 389.75. We can see that it is positive, suggesting the variables change in the same direction as we expect.
1
2
[[385.33297729 389.7545618 ]
[389.7545618 500.38006058]]
A problem with covariance as a statistical tool alone is that it is challenging to interpret. This leads us to Pearson’s correlation coefficient next.
Pearson’s Correlation
Named after Karl Pearson, The Pearson correlation coefficient can be used to summarize the strength of the linear relationship between two data samples.
Pearson’s correlation coefficient is calculated by dividing the covariance of the two variables by the product of their respective standard deviations. It is the normalization of the covariance between the two variables to give an interpretable score.
The use of mean and standard deviation in the calculation suggests the need for the two data samples to have a Gaussian or Gaussian-like distribution.
The result of the calculation, the correlation coefficient can be interpreted to understand the relationship.
The coefficient returns a value between -1 and 1, symbolizing the full spectrum of correlation: from a complete negative correlation to a total positive correlation. A value of 0 means no correlation. The value must be interpreted, where often a value below -0.5 or above 0.5 indicates a notable correlation, and values below those values suggests a less notable correlation.
The pearsonr() SciPy function can be used to calculate the Pearson’s correlation coefficient between two data samples with the same length.
We can calculate the correlation between the two variables in our test problem.
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
# calculate the Pearson's correlation between two variables
from numpy.random import randn
from numpy.random import seed
from scipy.stats import pearsonr
# seed random number generator
seed(1)
# prepare data
data1=20*randn(1000)+100
data2=data1+(10*randn(1000)+50)
# calculate Pearson's correlation
corr,_=pearsonr(data1,data2)
print('Pearsons correlation: %.3f'%corr)
Upon execution, Pearson’s correlation coefficient is determined and displayed. The evident positive correlation of 0.888 between the two variables is strong, as it surpasses the 0.5 threshold and approaches 1.0.
1
Pearsons correlation: 0.888
Pearson’s correlation coefficient can be used to evaluate the relationship between more than two variables.
This can be done by calculating a matrix of the relationships between each pair of variables in the dataset. The result is a symmetric matrix called a correlation matrix with a value of 1.0 along the diagonal as each column always perfectly correlates with itself.
Spearman’s Correlation
While many data relationships can be linear, some may be nonlinear. These nonlinear relationships are stronger or weaker across the distribution of the variables. Further, the two variables being considered may have a non-Gaussian distribution.
Named after Charles Spearman, Spearman’s correlation coefficient can be used to summarize the strength between the two data samples. This test of relationship can also be used if there is a linear relationship between the variables but will have slightly less power (e.g. may result in lower coefficient scores).
As with the Pearson correlation coefficient, the scores are between -1 and 1 for perfectly negatively correlated variables and perfectly positively correlated respectively.
Instead of directly working with the data samples, it operates on the relative ranks of data values. This is a common approach used in non-parametric statistics, e.g. statistical methods where we do not assume a distribution of the data such as Gaussian.
A linear relationship between the variables is not assumed, although a monotonic relationship is assumed. This is a mathematical name for an increasing or decreasing relationship between the two variables.
If you are unsure of the distribution and possible relationships between two variables, the Spearman correlation coefficient is a good tool to use.
The spearmanr() SciPy function can be used to calculate the Spearman’s correlation coefficient between two data samples with the same length.
We can calculate the correlation between the two variables in our test problem.
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
# calculate the spearmans's correlation between two variables
from numpy.random import randn
from numpy.random import seed
from scipy.stats import spearmanr
# seed random number generator
seed(1)
# prepare data
data1=20*randn(1000)+100
data2=data1+(10*randn(1000)+50)
# calculate spearman's correlation
corr,_=spearmanr(data1,data2)
print('Spearmans correlation: %.3f'%corr)
Running the example calculates and prints the Spearman’s correlation coefficient.
We know that the data is Gaussian and that the relationship between the variables is linear. Nevertheless, the nonparametric rank-based approach shows a strong correlation between the variables of 0.8.
1
Spearmans correlation: 0.872
As with the Pearson’s correlation coefficient, the coefficient can be calculated pair-wise for each variable in a dataset to give a correlation matrix for review.
For more help with non-parametric correlation methods in Python, see:
In this tutorial, you discovered that correlation is the statistical summary of the relationship between variables and how to calculate it for different types variables and relationships.
Specifically, you learned:
How to calculate a covariance matrix to summarize the linear relationship between two or more variables.
How to calculate the Pearson’s correlation coefficient to summarize the linear relationship between two variables.
How to calculate the Spearman’s correlation coefficient to summarize the monotonic relationship between two variables.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
Thank you very much for the article!
Maybe I’m wrong. But it seems to me that the covariance formula should be with an additional left bracket:
cov(X, Y) = sum ((x – mean(X)) * (y – mean(Y)) * 1/(n-1)).
Please correct me if I’m not right.
Hi Jason, thank you for yet again another awesome tutorial, this is exactly what I was looking for in the past few days. I have a question, in case that we are interested in the correlation between our input variables and the output variable, can we simply compute it similarly only by using one of the correlation metrics, the desired input variable and the output variable? or is there a different procedure to follow when considering the output?
Svp quelle approche peut on nous utiliser si on veut étudier la corrélation entre la variable qualitative par rapport à la variable quantitative. c’est à dire si je veux voir le changement de la variable qualitative suite au changement à la variable quantitative.
Dear Dr Jason,.
Many apologies for this. The tutorial was not obvious in distinguishing the ‘random’ and ‘randn’ functions.
The difference are:
‘randn’ generates standard normal distributions from -1 to 1. Further help see
1
help('numpy.random.randn')
And ‘random’ is a versatile function which allows one to generate values from various distributions such as uniform, and gaussian(mu, sigma) just to name a few.
1
help('random');# If you use the 'Idle' program in Windows, press F1
Sorry for ignoring the subtlety of importing ‘randn’. At the same time I did learn something.
Hi Jason,
Thanks for your post. Here is my case, there are many candidate input variables, and I’d like to predict one output. And I want to select some related variables as input from all the variables. So can I use the Normalized Mutual Information (NMI) method to do the selection?
Is there an example using this simple dataset to separate the two gaussian distributions, showing a resulting scatterplot using two colors for each distribution ?
Thanks for the nice post. I have a small suggestion. It is my understanding that “relationship” is meant to be used between people (e.g., “they have a close relationship), while “relation” is meant to be used for more abstract concepts (such as between two variables).
I am working on kaggle dataset and I want to check non-linear correlation between 2 features.
So according to you Spearman’s Correlation can be used for my purpose right?
What are the other ways to calculate non-linear relationships ?
According to my knowledge Spearman’s Correlation needs monotonic correlation between 2 features which similar to linear relationships(less restrictive though).
Please correct me if I am wrong.
How would I go about determining relationships between several variables (dependency is unknown at this time) to come up with a metric that will be used as an indicator for some output variable? Which parameters have a correlation to the output (workload over time). And how does this metric compare against the Bedford workload scale indicator.
Nice Article thumbs Up. I have Question does correlation among different variables affect the performance of the regression model other than linear regression? Like SVM or Random forest regression?
Could you help me to understand when should I use Theil’s U [https://en.m.wikipedia.org/wiki/Uncertainty_coefficient] and pearson’s/spearman’s Coefficient to compute the coefficient between categorical variables?
Thank you. Your article is always great and good to read. To me the best part of your blog is the Q&A where I have great admire of your patience to revert all the questions raise (hope including mine 🙂 ).
My question is what particular type of correlation we are look at in our feature selection for classification problem? is it Positive Correlation? Neutral Correlation? Negative Correlation?
For a binary classification task, with a numerical data set having continuous values for all variables other than target. Can we use corr() to determine relationship among variables?
Need Quick help!!
To Measure similarity, Is the Cross correlation only way?. I know Dynamic Time Warping(DTW) which is time consuming for the signal classification problem I am working on. I need an algorithm which can work on time related instead of frequency stuff like Fast Fourier Transform.
I have created a spearman rank correlation matrix where each comparison is between randomly sampled current density maps. The 10 maps have been generated via Circuitscape (using circuit theory) each with a unique range of cost values (all with three ranks: low, medium, high.Eg. 1,2,3 or 10,100,1000) used to generate each current density map. To summarize, overall mean correlation was 0.79 with an overall range of 0.52 to 0.99 within the matrix. The 4 maps with cost value ranges where the factorial change from medium to high is a fraction, and is also smaller than the low to medium factorial change (eg 1,2,3 (2 & 1.5) or 1,150,225 (150 & 1.5) or 1,1.5,2.25 (1.5 & 1.5), had mean ranges of .67 to .75. The 6 others were whole numbers with either increasing or even factorial changes ranging from 0.82 to .85 as mean correlation values.
Is there a particular reason why, in the cost value ranges, the second factorial change being smaller than the first and also being a fraction (or containing a decimal place, if you will) would lower the correlation values?
How do we find a correlation between two rows or two columns of the dataset If we do not have any domain knowledge and there are high numbers of rows and columns in the dataset?
I know the question above is dumb since correlation might produce NaN. My intended question was: How to find correlation between classification accuracies of different classifiers and compare?
In this case say for example the accuracy of Knn is 0.59 and that of DT is 0.67.
Please tell me a way to do so in order to choose best few classifiers for creating an ensemble from many.
In choosing models for an ensemble, we would monitor the correlation between classifiers based on their prediction error on a test set, not on their summary statistics like accuracy scores.
For classification, we might look at the correlation across the predicted probabilities for example.
I have a sensor data set. The sensor data is strongly (positively) correlated with temperature. As temperature moves, the sensor values drift with the temperature. I need to compensate for this temperature-induced drift. I therefore need an algorithm to offset (neutralize) the effect of the temperature on the primary variable I am measuring.
Thank you very much for your useful tutorial post.
I do not have a strong base of statistics, i would like to ask which coefficient is suitable for the case that considers both categorical and continuous variables in a correletation matrix?
Hi, is there any method to select non-correlated variables from a future space with hundreds of them? I mean how to select non-correlated variables from 100 variables.
Thanks in advance
Hi Jason.
I studied your article. It is very interesting, congrats.
I have a question. Spearman method can be used in both cases: in the case of linear relation, indicating if there is such a relation or not, and in the case of non linear relation, indicating if there is no relation of two vars or that there is a relation (linear or not).
How can I identify which kind of relation the two vars have, in the case that Spearman coefficient is higly positive, meaning that there is indeed a relation? In other words, in the case of two variables being related, how can I know if the relation is quadratic, or qubic e.t.c
Thanks for your time.
Thanks, but I am afraid I didn’t get you. To be more exact, in the case the two datasets have a Gaussian distribution, the linear method will reveal whether there is a linear relation or not (a linear relation). But if there is no linear relation, it does not points whether there is any other relation and the kind of it. Same situation is observed in the case the two datasets do not have the Gaussian distribution. The ranking method will reveal if there is a relation or not, indicating by no way the kind of relation the may have. Is it quadratic, qubic or what?
I appologize for insisting and for asking such a probably “naive” question.
Regards
Hey Jason,
Wanted to ask that i am using logistic regression for binary classification of the data.Now the dataset is created by me and for classification purpose,i am going to use 3 columns as features which are [‘DESCRIPTION’,’NUMBER OF CASUALTIES’,’CLASSIFY’].Now the ‘DESCRIPTION’ has text data, ‘NUMBER OF CASUALTIES’ has numerical data and the last column ‘CLASSIFY’ is a column filled with 0/1 for helping in classification.Now i have already classified the data into 0/1 in ‘CLASSIFY’ column i.e i have already given the answers of classification.Now for LOGISTIC REGRESSION MODEL,i am thinking of using these 3 columns so that my testing data will be classified correctly.What do you think about this approach ?
thank you very much for the article, please advise during data preparation selection for the formula for calculating the correlation coefficient not between all pairs of real-valued variables but the cumulative correlation coefficient between one variable with all the others. these variables are input numerical and categorical variables for a regression model.
thank you in advance
Thanks Jason, for another superb post. One of the applications of correlation is for feature selection/reduction, in case you have multiple variables highly correlated between themselves which ones do you remove or keep?
Thanks, Jason, for helping us understand, with this and other tutorials. Just thinking broader about correlation (and regression) in non-machine-learning versus machine learning contexts. I mean: what if I’m not interested in predicting unseen data, what if I’m only interested to fully describe the data in hand? Would overfitting become good news, so long as I’m not fitting to outliers? One could then question why use Scikit/Keras/boosters for regression if there is no machine learning intent — presumably I can justify/argue saying these machine learning tools are more powerful and flexible compared to traditional statistical tools (many of which require/assume Gaussian distribution etc)?
Perhaps contact the authors of the material directly?
Perhaps find the name of the metric you want to calculate and see if it is available directly in scipy?
Perhaps find a metric that is similar and modify the implementation to match your preferred metric?
Hi Jason. thank you for the post.
If I am working on a time series forecasting problem, can I use these methods to see if my input time series 1 is correlated with my input time series 2 for example?
Thank you so much for explaining Correlation topic so easy.
I have few doubts, please clear them.
1. If we know two variable have linear relationship then we should consider Covariance or Pearson’s Correlation Coefficient. Or is there any other parameter we should consider?
2. Would it be advisable to always go with Spearman Correlation coefficient?
Thank you so much for your article, it is enlightening.
I have a question : I have a lot of features (around 900) and a lot of rows (about a million), and I want to find the correlation between my features to get rid of some of them. Since I Don’t know how they are linked I tried to use the Spearman correlation matrix but it doesn’t work well (almost all the coeficient are NaN values…). I think that it is because there is a lot of zeros in my dataset.
Do you know a way to deal with this issue ?
Hi Jason, thanks for this wonderful tutorial. I’m just wondering about the section where you explain the calculation of sample covariance, and you mentioned that “The use of the mean in the calculation suggests the need for each data sample to have a Gaussian or Gaussian-like distribution”. I’m not sure why the sample have necessarily to be Gaussian-like if we use its mean. Could you elaborate a bit, or point me to some additional resources? Thanks.
If the data has a skewed distribution or exponential, the mean as calculated normally would not be the central tendency (mean for an exponential is 1 over lambda from memory) and would throw off the covariance.
As per your book, I am trying to develop a standard workflow of tasks/recipes to perform during EDA on any dataset before I then try to make any predictions or classifications using ML.
Say I have a dataset that is a mix of numeric and categoric variables, I am trying to work out the correct logic for step 3 below.
Here is my current proposed workflow:
1. Produce histograms & KDE plots for all of the attributes so that I can see which ones are normally distributed.
2. Produce a scatterplot matrix so that I can see if each attribute pair has a linear, monotonic or no obvious relationship. If I plan to perform a classification task then additionally hue on the target variable so that I can see if there is any additional pattern for each class within each attribute pairing.
3. Then for each attribute pair in my scatterplot matrix:
3.1. If the attribute pair is 2 numeric attributes AND they have a linear relationship AND are both normally distributed, then use Pearson correlation for this attribute pair.
3.2. If the attribute pair is 2 numeric attributes BUT they have a monotonic relationship that is non linear eg exponential AND are both normally distributed, then use Spearman correlation for this attribute pair.
3.3. If the attribute pair is 2 numeric attributes AND they have a linear relationship BUT ONE/BOTH are NOT normally distributed, then use Spearman correlation for this attribute pair.
3.4. If the attribute pair is 2 numeric attributes BUT they have a monotonic relationship that is non linear eg exponential AND ONE OR NEITHER are normally distributed, then use Spearman correlation for this attribute pair.
3.5. If the attribute pair is 2 categoric attributes then use Spearman correlation for this attribute pair.
4. Identify all attribute pairs where Pearson was identified as the appropriate choice – produce a correlation matrix for these attributes only.
5. Identify all attribute pairs where Spearman was identified as the appropriate choice – produce a correlation matrix for these attributes only.
Questions:
A. Can Spearman correlation only be used for ordinal categoric variables or can it be used for any type of categoric variable? If it is the formal only then what choice do I have – should I instead use chi squared for 2 nominal categoric variables rather than correlation?
B. If I have identified that Spearman is the appropriate choice, then should I also just produce an identical correlation matrix using Kendall tau instead and see which produces the strongest correlation value between the two?
C. If one attribute is numeric and one is ordinal categoric then do I just use Spearman correlation for this attribute pair?
Thanks for providing such an excellent practical resource.
D. The above workflow that I describe seems quite involved for datasets that contain a lot of features.
Instead of messing about with a mix of numeric and categoric features (some of which will be ordinal and some nominal), would I be better off first changing all categoric attributes to numeric dtype (eg using get_dummies or some other type of encoding) and then following the rest of the workflow as described?
Apolgies if this is too big a question, loving your articles but I feel like the more I read the more questions that I have!
I have a question, if my input variable is continuous and output variable is binary, how can I check the correlation between the 2? should I use Spearman’s correlation? and in this case should I measure a correlation at all?
Dear Jason,
I have referred to many of your tutorials, which have always helped me to improve my understanding about ML concepts.
Your work is an Inspiration. Thanking you.
Thanks for the post, I have a question. The values you generate are for a Gaussian distribution. My question is how would you go about generating random values in a PERT distribution? Thanks in advance
do you have any pointers on how to perform NLP topic correlation with Python. I have used pyLDAvis for a visual topic correlation but am unable to find a method to get the correlation in tabular format?
Thanks so much for providing these brilliant materials. I have a question regarding my current project.
I have this scenario(https://ibb.co/F0WBtJq) which a car publishes a message through wireless network to a broker and an App, then after processing, the App sends the same message to another car via wireless network.
Now I am supposed to analyses delays. All of them are fine, except delay5 which has high and abnormal values. I want to find underlying causes of this behavior, but I don’t know how or what ML/non-ML technique is suitable for such problem. Do you have any idea or reference to guide me?
HI
my question is about revers this article
how we can define or assign correlation between two random variable?
for example i need to use of lognormal distribution many times and generate dataset from it; but in paper it is written correlation between dataset is 0.6
how i can assign correlation to my data?
thanks
Thanks for this. Now I know what is correlation and how to calculate it and everything. But what I do no understand is what do I do with that information? Like, how can I use that information to better my model?
I have partitioned a dataframe into five subsets based on the values of a categorical variable. I have calculated the correlation coefficient between each of the corresponding subsets of a predictor variable and the target variable; resulting in 5 correlation coefficients. I wish to compare the 5 correlation coefficients to determine whether there are any statistically significant differences between the 5 groups. I would like to use either One Way ANOVA or Fisher’s Z Test to evaluate the null hypothesis that all 5 coefficients are all equal. Please advise w,r,t, methdology and Code. Thanks
Hi Jason, Thanks for your article. I heard about the Hypothesis testing. Can’t we check this or decide by hypothesis testing that these 2 variables are related or not? If so when to use Hypo testing and when to use this covariance and correlation to decide the relationship?
Hi Kenneth…Yes, hypothesis testing, covariance, and correlation are all statistical tools used to assess relationships between variables, but they serve different purposes and are used in different contexts.
1. **Hypothesis Testing**: Hypothesis testing is a statistical method used to make inferences about the population parameter based on sample data. It can be used to test whether there is a significant difference between two groups or whether a relationship exists between variables. In the context of relationships between variables, hypothesis testing can be used to test whether the correlation coefficient (which measures the strength and direction of the linear relationship between two variables) is significantly different from zero. This can help determine whether there is a significant linear relationship between two variables.
2. **Covariance**: Covariance measures the extent to which two variables change together. A positive covariance indicates that as one variable increases, the other variable tends to increase as well, while a negative covariance indicates that as one variable increases, the other variable tends to decrease. However, the magnitude of covariance depends on the units of the variables, making it difficult to interpret. Therefore, covariance is often standardized to give correlation.
3. **Correlation**: Correlation is a standardized measure of the strength and direction of the linear relationship between two variables. Unlike covariance, correlation is unitless and ranges from -1 to 1. A correlation coefficient of 1 indicates a perfect positive linear relationship, -1 indicates a perfect negative linear relationship, and 0 indicates no linear relationship. Correlation is often preferred over covariance because it provides a standardized measure that is easier to interpret and compare across different datasets.
So, when deciding whether two variables are related, you can use both correlation and hypothesis testing. Correlation gives you a measure of the strength and direction of the relationship, while hypothesis testing helps you determine whether that relationship is statistically significant. If you find a strong correlation between two variables, you can use hypothesis testing to determine whether that correlation is significant or due to random chance.
Hi, Jason!
Thank you very much for the article!
Maybe I’m wrong. But it seems to me that the covariance formula should be with an additional left bracket:
cov(X, Y) = sum ((x – mean(X)) * (y – mean(Y)) * 1/(n-1)).
Please correct me if I’m not right.
Fixed, thanks.
Hello Jason,
It is a very good article on correlation for beginners like me.
I think you missed one more bracket in covariance function.
cov(X,Y) = sum((x-mean(X)) * (y-mean(Y))) * 1/(n-1)
Thanks.
Hi Jason, thank you for yet again another awesome tutorial, this is exactly what I was looking for in the past few days. I have a question, in case that we are interested in the correlation between our input variables and the output variable, can we simply compute it similarly only by using one of the correlation metrics, the desired input variable and the output variable? or is there a different procedure to follow when considering the output?
Yes, it is a helpful way for finding relevant/irrelevant input variables.
It does ignore interactions between multiple inputs and the output though, so always experiment and use resulting model skill to guide you.
Hi Jason.
I am curious, do you have a preferred measure to measure “correlation” between your inputs and a binary target value?
Good question.
For two categorial variables, we can use the chi squared test.
Generally, I would be looking at feature selection methods instead.
Svp quelle approche peut on nous utiliser si on veut étudier la corrélation entre la variable qualitative par rapport à la variable quantitative. c’est à dire si je veux voir le changement de la variable qualitative suite au changement à la variable quantitative.
Hi Bennani…Please translate to English so that we may better assist you.
Hi Jason! Great article! I look forward to reading your stats book. And I love API section at the end of the blog! Cheers!
Thanks!
Hi Jason!
Wow really thank you for your articles. Great articles.
Do you have a plan to add Grandure causality analysis, which is also a way to measure a correlation between variables?
Have a great day~
What is “grandure causality analysis”?
Dear Dr Jason,
I wish to report typo two errors under “Test Dataset”, “Covariance” , “Pearson’s Correlation” and “Spearman’s Correlation”,
where it respectively says in lines 11 & 12, 8 & 9, 8 & 9 and 8 & 9.
it should be
This is because under the former, you will get an error if using ‘randn’..
Regards
Anthony of exciting Belfield.
Dear Dr Jason,.
Many apologies for this. The tutorial was not obvious in distinguishing the ‘random’ and ‘randn’ functions.
The difference are:
‘randn’ generates standard normal distributions from -1 to 1. Further help see
And ‘random’ is a versatile function which allows one to generate values from various distributions such as uniform, and gaussian(mu, sigma) just to name a few.
Sorry for ignoring the subtlety of importing ‘randn’. At the same time I did learn something.
Thank you,
Anthony of exciting Belfield
No problem.
Teaching you something was the goal of this site!
It does not give an error on Py3 and the latest numpy.
What version of Numpy/Python were you using?
Dear Dr Jason.
It was my fault I did not include
No problems after that.
The versions are:
All’s well that ends well,
Anthony from downtown Belfield
Glad to hear it.
Hi Jason,
Thanks for your post. Here is my case, there are many candidate input variables, and I’d like to predict one output. And I want to select some related variables as input from all the variables. So can I use the Normalized Mutual Information (NMI) method to do the selection?
I would recommend testing a suite of feature selection methods:
https://machinelearningmastery.com/an-introduction-to-feature-selection/
Hi Jason,
Can I apply the pearson correlation with two time series in order to find how two time series depend with each other?
If not, could you please give some source or your another blog post to read.
cheers
Good question.
For correlation with prior time steps, we normally use auto-correlation plots:
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
For correlation between series, we use cross-correlation:
https://en.wikipedia.org/wiki/Cross-correlation
Is there an example using this simple dataset to separate the two gaussian distributions, showing a resulting scatterplot using two colors for each distribution ?
I’m not sure I follow, what do you mean exactly?
Hi Jason,
Thanks for the nice post. I have a small suggestion. It is my understanding that “relationship” is meant to be used between people (e.g., “they have a close relationship), while “relation” is meant to be used for more abstract concepts (such as between two variables).
For more details, see http://www.learnersdictionary.com/qa/relations-and-relationship
Cheers!
Very nice, thanks!
I am working on kaggle dataset and I want to check non-linear correlation between 2 features.
So according to you Spearman’s Correlation can be used for my purpose right?
What are the other ways to calculate non-linear relationships ?
Thank you in advance.
Yes. I list more here:
https://machinelearningmastery.com/statistical-hypothesis-tests-in-python-cheat-sheet/
According to my knowledge Spearman’s Correlation needs monotonic correlation between 2 features which similar to linear relationships(less restrictive though).
Please correct me if I am wrong.
Thanks
Yes, a monotonic relationship.
Excellent article jason!
How would I go about determining relationships between several variables (dependency is unknown at this time) to come up with a metric that will be used as an indicator for some output variable? Which parameters have a correlation to the output (workload over time). And how does this metric compare against the Bedford workload scale indicator.
Perhaps start by measuring simple linear correlations between variables and whether the results are significant.
Please can anyone help me with the formula for correlation between variables?
Thank you
Best regards,
Sure:
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
Nice Article thumbs Up. I have Question does correlation among different variables affect the performance of the regression model other than linear regression? Like SVM or Random forest regression?
Yes, it can impact other models. Perhaps SVM, probably not random forest.
Hi Jason,
Could you help me to understand when should I use Theil’s U [https://en.m.wikipedia.org/wiki/Uncertainty_coefficient] and pearson’s/spearman’s Coefficient to compute the coefficient between categorical variables?
Thank you!
Thanks for the suggestion, I may cover the topic in the future
Dear Jason,
Thank you. Your article is always great and good to read. To me the best part of your blog is the Q&A where I have great admire of your patience to revert all the questions raise (hope including mine 🙂 ).
My question is what particular type of correlation we are look at in our feature selection for classification problem? is it Positive Correlation? Neutral Correlation? Negative Correlation?
Hope my question make sense to you.
Thank you again.
Positive or negative linear correlation is a good start.
Thanks Jason. Good to know your thought on the matter.
HI Jason,
For a binary classification task, with a numerical data set having continuous values for all variables other than target. Can we use corr() to determine relationship among variables?
In a few places applying corr() was questioned.
Thanks.
Yes.
Can we calculate Pearson’s Correlation Co-efficient if the target is binary? I have seen it being used in many places. But how does it work?
Also, does it make sense to calculate the correlation between categorical features with the target (binary or continuous)?
In Python, to calculate correlation, we can use corr() or pearsonr(). What is the difference?
No, you can use a chi squared estimate in that case:
https://machinelearningmastery.com/chi-squared-test-for-machine-learning/
Hi Jason! Great work. I was wondering, can you propose a media source that presents a relationship between two variables?
What do you mean exactly?
Need Quick help!!
To Measure similarity, Is the Cross correlation only way?. I know Dynamic Time Warping(DTW) which is time consuming for the signal classification problem I am working on. I need an algorithm which can work on time related instead of frequency stuff like Fast Fourier Transform.
Sorry, I don’t have any tutorials on calculating the similarity between time series. I hope to cover the topic in the future.
Hi Jason,
I have created a spearman rank correlation matrix where each comparison is between randomly sampled current density maps. The 10 maps have been generated via Circuitscape (using circuit theory) each with a unique range of cost values (all with three ranks: low, medium, high.Eg. 1,2,3 or 10,100,1000) used to generate each current density map. To summarize, overall mean correlation was 0.79 with an overall range of 0.52 to 0.99 within the matrix. The 4 maps with cost value ranges where the factorial change from medium to high is a fraction, and is also smaller than the low to medium factorial change (eg 1,2,3 (2 & 1.5) or 1,150,225 (150 & 1.5) or 1,1.5,2.25 (1.5 & 1.5), had mean ranges of .67 to .75. The 6 others were whole numbers with either increasing or even factorial changes ranging from 0.82 to .85 as mean correlation values.
Is there a particular reason why, in the cost value ranges, the second factorial change being smaller than the first and also being a fraction (or containing a decimal place, if you will) would lower the correlation values?
Thank you
I don’t know, sorry.
Hi Jason,
It was a great article. For a quick correlation, I found this tool:
https://www.answerminer.com/calculators/correlation-test
Thanks
Thanks.
Hello James,
How do we find a correlation between two rows or two columns of the dataset If we do not have any domain knowledge and there are high numbers of rows and columns in the dataset?
*Jason
You can find correlation between columns, e.g. features.
Not between rows, but across rows for two features.
Thank you Jason.
Could you please give an example of how to find a correlation between the columns?
Yes, the above tutorial shows how.
hi Jason,
suppose given two variable
data1 = 20 * randn(1000) + 100
data2 = data1 + (10 * randn(1000) + 50)
i am confuse when i get 0.8 mean high correlation if i get 0 then which one variable will discard?
If they are not correlated, keep both.
Hi Jason,
Thanks for the wonderful article.I am a newbie.
Is the following LoC correct ?
corr,_ =pearsonr(0.599122807018,0.674224021592)
What is LoC?
Line of Code
Hi Jason,
I know the question above is dumb since correlation might produce NaN. My intended question was: How to find correlation between classification accuracies of different classifiers and compare?
In this case say for example the accuracy of Knn is 0.59 and that of DT is 0.67.
Please tell me a way to do so in order to choose best few classifiers for creating an ensemble from many.
Thank You
In choosing models for an ensemble, we would monitor the correlation between classifiers based on their prediction error on a test set, not on their summary statistics like accuracy scores.
For classification, we might look at the correlation across the predicted probabilities for example.
Hi Jason
I have a sensor data set. The sensor data is strongly (positively) correlated with temperature. As temperature moves, the sensor values drift with the temperature. I need to compensate for this temperature-induced drift. I therefore need an algorithm to offset (neutralize) the effect of the temperature on the primary variable I am measuring.
Can you help?
Perhaps try a linear regression as a first step?
Hi Jason,
Thank you very much for your useful tutorial post.
I do not have a strong base of statistics, i would like to ask which coefficient is suitable for the case that considers both categorical and continuous variables in a correletation matrix?
Thank you!
You must use different measures.
Maybe Pearson correlation for real-valued variables and maybe chi-squared for categorical variables.
How to perform a one-side test? When you know the type of correlation (psotive for example) you should looking for?
Thanks for your help
Perhaps some of the examples here will help:
https://machinelearningmastery.com/statistical-hypothesis-tests-in-python-cheat-sheet/
Hi, is there any method to select non-correlated variables from a future space with hundreds of them? I mean how to select non-correlated variables from 100 variables.
Thanks in advance
Typically we do the reverse and find the most correlated variables and remove then, this is called feature selection:
https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/
Hi Jason.
I studied your article. It is very interesting, congrats.
I have a question. Spearman method can be used in both cases: in the case of linear relation, indicating if there is such a relation or not, and in the case of non linear relation, indicating if there is no relation of two vars or that there is a relation (linear or not).
How can I identify which kind of relation the two vars have, in the case that Spearman coefficient is higly positive, meaning that there is indeed a relation? In other words, in the case of two variables being related, how can I know if the relation is quadratic, or qubic e.t.c
Thanks for your time.
Thanks.
Good question. When the two datasets have a Gaussian distribution use the linear method, otherwise use the ranking method.
Thanks, but I am afraid I didn’t get you. To be more exact, in the case the two datasets have a Gaussian distribution, the linear method will reveal whether there is a linear relation or not (a linear relation). But if there is no linear relation, it does not points whether there is any other relation and the kind of it. Same situation is observed in the case the two datasets do not have the Gaussian distribution. The ranking method will reveal if there is a relation or not, indicating by no way the kind of relation the may have. Is it quadratic, qubic or what?
I appologize for insisting and for asking such a probably “naive” question.
Regards
It’s a great question.
Yes, in that case a rank correlation may be required.
If we are unsure, we can plot that data and inspect, or calculate both approaches and review their findings, and perhaps p-values.
Hey Jason,
Wanted to ask that i am using logistic regression for binary classification of the data.Now the dataset is created by me and for classification purpose,i am going to use 3 columns as features which are [‘DESCRIPTION’,’NUMBER OF CASUALTIES’,’CLASSIFY’].Now the ‘DESCRIPTION’ has text data, ‘NUMBER OF CASUALTIES’ has numerical data and the last column ‘CLASSIFY’ is a column filled with 0/1 for helping in classification.Now i have already classified the data into 0/1 in ‘CLASSIFY’ column i.e i have already given the answers of classification.Now for LOGISTIC REGRESSION MODEL,i am thinking of using these 3 columns so that my testing data will be classified correctly.What do you think about this approach ?
Try it and see.
What are the application of correlation in real life
Some ideas:
– Insight into the domain.
– Feature selection/removal.
– Model selection.
– Data preparation selection.
thank you very much for the article, please advise during data preparation selection for the formula for calculating the correlation coefficient not between all pairs of real-valued variables but the cumulative correlation coefficient between one variable with all the others. these variables are input numerical and categorical variables for a regression model.
thank you in advance
Yes, I recommend using the sklearn library to do it for you:
https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/
Thanks Jason, for another superb post. One of the applications of correlation is for feature selection/reduction, in case you have multiple variables highly correlated between themselves which ones do you remove or keep?
Good question, see this:
https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/
Thanks, Jason, for helping us understand, with this and other tutorials. Just thinking broader about correlation (and regression) in non-machine-learning versus machine learning contexts. I mean: what if I’m not interested in predicting unseen data, what if I’m only interested to fully describe the data in hand? Would overfitting become good news, so long as I’m not fitting to outliers? One could then question why use Scikit/Keras/boosters for regression if there is no machine learning intent — presumably I can justify/argue saying these machine learning tools are more powerful and flexible compared to traditional statistical tools (many of which require/assume Gaussian distribution etc)?
Yes, the objective of a descriptive model is very different from a predictive model.
Hi Jason, thank you for explanation.I have a affine transformation parameters with size 6×1, and I want to do correlation analysis between this parameters.I found the formula below (I’m not sure if it’s the right formula for my purpose).However,I don’t understand how to implement this formula.In general, the result I want to achieve should be like this.(https://lh3.googleusercontent.com/proxy/kbh85HHtDQJ0WLnemcxeGprtL6MJ7DgEs8banlEmGF5dh5Cjy1BGjrYGmhewbE8y99jzja64-8vC-KQ0Nld48HBFMU7EsgS4eAKFRvIQg1F9aXXr5rY6EbIRCY2gcbkiDjcMCgIgYVelwLKat4VAgje9N0I-x3rJgq5dD1XAu6pim_LWTatU8Py0cls)
How can I do this implement,please help me?
formula: https://wikimedia.org/api/rest_v1/media/math/render/svg/2b9c2079a3ffc1aacd36201ea0a3fb2460dc226f
I don’t have the capacity to code things for you.
Some ideas:
Perhaps contact the authors of the material directly?
Perhaps find the name of the metric you want to calculate and see if it is available directly in scipy?
Perhaps find a metric that is similar and modify the implementation to match your preferred metric?
Hi Jason. thank you for the post.
If I am working on a time series forecasting problem, can I use these methods to see if my input time series 1 is correlated with my input time series 2 for example?
Yes, this is called an ACF and PACF plot:
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
Thank you so much for explaining Correlation topic so easy.
I have few doubts, please clear them.
1. If we know two variable have linear relationship then we should consider Covariance or Pearson’s Correlation Coefficient. Or is there any other parameter we should consider?
2. Would it be advisable to always go with Spearman Correlation coefficient?
Yes, use Pearson’s or covariance if you expect a linear relationship.
No, you want the most powerful test for your data.
Hi Jason,
Thank you so much for your article, it is enlightening.
I have a question : I have a lot of features (around 900) and a lot of rows (about a million), and I want to find the correlation between my features to get rid of some of them. Since I Don’t know how they are linked I tried to use the Spearman correlation matrix but it doesn’t work well (almost all the coeficient are NaN values…). I think that it is because there is a lot of zeros in my dataset.
Do you know a way to deal with this issue ?
Thank you very much
You’re welcome!
I recommend using an automated feature selection method:
https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/
Hi Jason, thanks for this wonderful tutorial. I’m just wondering about the section where you explain the calculation of sample covariance, and you mentioned that “The use of the mean in the calculation suggests the need for each data sample to have a Gaussian or Gaussian-like distribution”. I’m not sure why the sample have necessarily to be Gaussian-like if we use its mean. Could you elaborate a bit, or point me to some additional resources? Thanks.
If the data has a skewed distribution or exponential, the mean as calculated normally would not be the central tendency (mean for an exponential is 1 over lambda from memory) and would throw off the covariance.
Hi Jason,
Thanks for this excellent article.
As per your book, I am trying to develop a standard workflow of tasks/recipes to perform during EDA on any dataset before I then try to make any predictions or classifications using ML.
Say I have a dataset that is a mix of numeric and categoric variables, I am trying to work out the correct logic for step 3 below.
Here is my current proposed workflow:
1. Produce histograms & KDE plots for all of the attributes so that I can see which ones are normally distributed.
2. Produce a scatterplot matrix so that I can see if each attribute pair has a linear, monotonic or no obvious relationship. If I plan to perform a classification task then additionally hue on the target variable so that I can see if there is any additional pattern for each class within each attribute pairing.
3. Then for each attribute pair in my scatterplot matrix:
3.1. If the attribute pair is 2 numeric attributes AND they have a linear relationship AND are both normally distributed, then use Pearson correlation for this attribute pair.
3.2. If the attribute pair is 2 numeric attributes BUT they have a monotonic relationship that is non linear eg exponential AND are both normally distributed, then use Spearman correlation for this attribute pair.
3.3. If the attribute pair is 2 numeric attributes AND they have a linear relationship BUT ONE/BOTH are NOT normally distributed, then use Spearman correlation for this attribute pair.
3.4. If the attribute pair is 2 numeric attributes BUT they have a monotonic relationship that is non linear eg exponential AND ONE OR NEITHER are normally distributed, then use Spearman correlation for this attribute pair.
3.5. If the attribute pair is 2 categoric attributes then use Spearman correlation for this attribute pair.
4. Identify all attribute pairs where Pearson was identified as the appropriate choice – produce a correlation matrix for these attributes only.
5. Identify all attribute pairs where Spearman was identified as the appropriate choice – produce a correlation matrix for these attributes only.
Questions:
A. Can Spearman correlation only be used for ordinal categoric variables or can it be used for any type of categoric variable? If it is the formal only then what choice do I have – should I instead use chi squared for 2 nominal categoric variables rather than correlation?
B. If I have identified that Spearman is the appropriate choice, then should I also just produce an identical correlation matrix using Kendall tau instead and see which produces the strongest correlation value between the two?
C. If one attribute is numeric and one is ordinal categoric then do I just use Spearman correlation for this attribute pair?
Thanks for providing such an excellent practical resource.
Maleko
I expect spearman can be used for ordinal data. Perhaps check a textbook listed in further reading section.
If you like.
Perhaps, or perhaps an anova or mutual information would be more appropriate. This might help:
https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/
Sorry I missed one other question:
D. The above workflow that I describe seems quite involved for datasets that contain a lot of features.
Instead of messing about with a mix of numeric and categoric features (some of which will be ordinal and some nominal), would I be better off first changing all categoric attributes to numeric dtype (eg using get_dummies or some other type of encoding) and then following the rest of the workflow as described?
Apolgies if this is too big a question, loving your articles but I feel like the more I read the more questions that I have!
Thanks
Probably not.
Here is a great article explaining the diff betw Covariance and Correlation :
https://www.surveygizmo.com/resources/blog/variance-covariance-correlation/
Thanks for sharing.
I have a question, if my input variable is continuous and output variable is binary, how can I check the correlation between the 2? should I use Spearman’s correlation? and in this case should I measure a correlation at all?
No, it would not be valid, see this:
https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/
I have a question, in the line,
corr, _ = pearsonr(data1, data2)
why is it necessary to put the , _ after corr, i know it wont work otherwise but why?
To ignore one of the values returned from the function.
Using an underscore (“_”) is a python idiom for ignore a variable.
Dear Jason,
I have referred to many of your tutorials, which have always helped me to improve my understanding about ML concepts.
Your work is an Inspiration. Thanking you.
You’re very welcome!
Awesome tutorial!
Thanks!
“A covariance value of zero indicates that both variables are completely independent.”
Actually independent variables have 0 correlation, but 0 correlation does not imply independence always.
Great catch!
Thanks for the post, I have a question. The values you generate are for a Gaussian distribution. My question is how would you go about generating random values in a PERT distribution? Thanks in advance
You can check the numpy API for generating random numbers in arbitrary distributions.
Hello Dr. Jason,
do you have any pointers on how to perform NLP topic correlation with Python. I have used pyLDAvis for a visual topic correlation but am unable to find a method to get the correlation in tabular format?
Below is a reference link to the subject to make it clearer: https://towardsdatascience.com/end-to-end-topic-modeling-in-python-latent-dirichlet-allocation-lda-35ce4ed6b3e0
Thank you!
Luxman
I think you’re looking for this function in scikit-learn: https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.LatentDirichletAllocation.html
Hello dear Jason,
Thanks so much for providing these brilliant materials. I have a question regarding my current project.
I have this scenario(https://ibb.co/F0WBtJq) which a car publishes a message through wireless network to a broker and an App, then after processing, the App sends the same message to another car via wireless network.
Now I am supposed to analyses delays. All of them are fine, except delay5 which has high and abnormal values. I want to find underlying causes of this behavior, but I don’t know how or what ML/non-ML technique is suitable for such problem. Do you have any idea or reference to guide me?
Thanks
Hi Eshan…You may wish to analyze your system for anomalies and outliers to better understand causation and effect:
https://machinelearningmastery.com/how-to-identify-outliers-in-your-data/
https://machinelearningmastery.com/model-based-outlier-detection-and-removal-in-python/
HI
my question is about revers this article
how we can define or assign correlation between two random variable?
for example i need to use of lognormal distribution many times and generate dataset from it; but in paper it is written correlation between dataset is 0.6
how i can assign correlation to my data?
thanks
Hi javad…you may find the following of interest:
https://www.projectguru.in/how-to-improve-the-correlation-between-the-variables/
Thanks for this. Now I know what is correlation and how to calculate it and everything. But what I do no understand is what do I do with that information? Like, how can I use that information to better my model?
Hi Nikhil…You may find the following helpful:
https://medium.com/analytics-vidhya/what-is-correlation-4fe0c6fbed47
Hello, Thank you for Your explanations.
When the data set has missing value, correlation is reliable?
Hi Ali…The following resource may be of interest to you:
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4145345/
I have partitioned a dataframe into five subsets based on the values of a categorical variable. I have calculated the correlation coefficient between each of the corresponding subsets of a predictor variable and the target variable; resulting in 5 correlation coefficients. I wish to compare the 5 correlation coefficients to determine whether there are any statistically significant differences between the 5 groups. I would like to use either One Way ANOVA or Fisher’s Z Test to evaluate the null hypothesis that all 5 coefficients are all equal. Please advise w,r,t, methdology and Code. Thanks
Hi Jon…You may find the following location of interest:
https://machinelearningmastery.com/start-here/#statistical_methods
Hi Jason, Thanks for your article. I heard about the Hypothesis testing. Can’t we check this or decide by hypothesis testing that these 2 variables are related or not? If so when to use Hypo testing and when to use this covariance and correlation to decide the relationship?
Hi Kenneth…Yes, hypothesis testing, covariance, and correlation are all statistical tools used to assess relationships between variables, but they serve different purposes and are used in different contexts.
1. **Hypothesis Testing**: Hypothesis testing is a statistical method used to make inferences about the population parameter based on sample data. It can be used to test whether there is a significant difference between two groups or whether a relationship exists between variables. In the context of relationships between variables, hypothesis testing can be used to test whether the correlation coefficient (which measures the strength and direction of the linear relationship between two variables) is significantly different from zero. This can help determine whether there is a significant linear relationship between two variables.
2. **Covariance**: Covariance measures the extent to which two variables change together. A positive covariance indicates that as one variable increases, the other variable tends to increase as well, while a negative covariance indicates that as one variable increases, the other variable tends to decrease. However, the magnitude of covariance depends on the units of the variables, making it difficult to interpret. Therefore, covariance is often standardized to give correlation.
3. **Correlation**: Correlation is a standardized measure of the strength and direction of the linear relationship between two variables. Unlike covariance, correlation is unitless and ranges from -1 to 1. A correlation coefficient of 1 indicates a perfect positive linear relationship, -1 indicates a perfect negative linear relationship, and 0 indicates no linear relationship. Correlation is often preferred over covariance because it provides a standardized measure that is easier to interpret and compare across different datasets.
So, when deciding whether two variables are related, you can use both correlation and hypothesis testing. Correlation gives you a measure of the strength and direction of the relationship, while hypothesis testing helps you determine whether that relationship is statistically significant. If you find a strong correlation between two variables, you can use hypothesis testing to determine whether that correlation is significant or due to random chance.