It is common to have missing observations from sequence data.
Data may be corrupt or unavailable, but it is also possible that your data has variable length sequences by definition. Those sequences with fewer timesteps may be considered to have missing values.
In this tutorial, you will discover how you can handle data with missing values for sequence prediction problems in Python with the Keras deep learning library.
After completing this tutorial, you will know:
- How to remove rows that contain a missing timestep.
- How to mark missing timesteps and force the network to learn their meaning.
- How to mask missing timesteps and exclude them from calculations in the model.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

A Gentle Introduction to Linear Algebra
Photo by Steve Corey, some rights reserved.
Overview
This section is divided into 3 parts; they are:
- Echo Sequence Prediction Problem
- Handling Missing Sequence Data
- Learning With Missing Sequence Values
Environment
This tutorial assumes you have a Python SciPy environment installed. You can use either Python 2 or 3 with this example.
This tutorial assumes you have Keras (v2.0.4+) installed with either the TensorFlow (v1.1.0+) or Theano (v0.9+) backend.
This tutorial also assumes you have scikit-learn, Pandas, NumPy, and Matplotlib installed.
If you need help setting up your Python environment, see this post:
Echo Sequence Prediction Problem
The echo problem is a contrived sequence prediction problem where the objective is to remember and predict an observation at a fixed prior timestep, called a lag observation.
For example, the simplest case is to predict the observation from the previous timestep that is, echo it back. For example:
|
1 2 3 4 |
Time 1: Input 45 Time 2: Input 23, Output 45 Time 3: Input 73, Output 23 ... |
The question is, what do we do about timestep 1?
We can implement the echo sequence prediction problem in Python.
This involves two steps: the generation of random sequences and the transformation of random sequences into a supervised learning problem.
Generate Random Sequence
We can generate sequences of random values between 0 and 1 using the random() function in the random module.
We can put this in a function called generate_sequence() that will generate a sequence of random floating point values for the desired number of timesteps.
This function is listed below.
|
1 2 3 |
# generate a sequence of random values def generate_sequence(n_timesteps): return [random() for _ in range(n_timesteps)] |
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Frame as Supervised Learning
Sequences must be framed as a supervised learning problem when using neural networks.
That means the sequence needs to be divided into input and output pairs.
The problem can be framed as making a prediction based on a function of the current and previous timesteps.
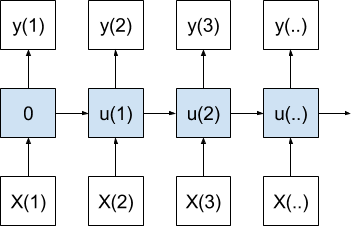
Or more formally:
|
1 |
y(t) = f(X(t), X(t-1)) |
Where y(t) is the desired output for the current timestep, f() is the function we are seeking to approximate with our neural network, and X(t) and X(t-1) are the observations for the current and previous timesteps.
The output could be equal to the previous observation, for example, y(t) = X(t-1), but it could as easily be y(t) = X(t). The model that we train on this problem does not know the true formulation and must learn this relationship.
This mimics real sequence prediction problems where we specify the model as a function of some fixed set of sequenced timesteps, but we don’t know the actual functional relationship from past observations to the desired output value.
We can implement this framing of an echo problem as a supervised learning problem in python.
The Pandas shift() function can be used to create a shifted version of the sequence that can be used to represent the observations at the prior timestep. This can be concatenated with the raw sequence to provide the X(t-1) and X(t) input values.
|
1 2 |
df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) |
We can then take the values from the Pandas DataFrame as the input sequence (X) and use the first column as the output sequence (y).
|
1 2 |
# specify input and output data X, y = values, values[:, 0] |
Putting this all together, we can define a function that takes the number of timesteps as an argument and returns X,y data for sequence learning called generate_data().
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# generate data for the lstm def generate_data(n_timesteps): # generate sequence sequence = generate_sequence(n_timesteps) sequence = array(sequence) # create lag df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) values = df.values # specify input and output data X, y = values, values[:, 0] return X, y |
Sequence Problem Demonstration
We can tie the generate_sequence() and generate_data() code together into a worked example.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
from random import random from numpy import array from pandas import concat from pandas import DataFrame # generate a sequence of random values def generate_sequence(n_timesteps): return [random() for _ in range(n_timesteps)] # generate data for the lstm def generate_data(n_timesteps): # generate sequence sequence = generate_sequence(n_timesteps) sequence = array(sequence) # create lag df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) values = df.values # specify input and output data X, y = values, values[:, 0] return X, y # generate sequence n_timesteps = 10 X, y = generate_data(n_timesteps) # print sequence for i in range(n_timesteps): print(X[i], '=>', y[i]) |
Running this example generates a sequence, converts it to a supervised representation, and prints each X,y pair.
|
1 2 3 4 5 6 7 8 9 10 |
[ nan 0.18961404] => nan [ 0.18961404 0.25956078] => 0.189614044109 [ 0.25956078 0.30322084] => 0.259560776929 [ 0.30322084 0.72581287] => 0.303220844801 [ 0.72581287 0.02916655] => 0.725812865047 [ 0.02916655 0.88711086] => 0.0291665472554 [ 0.88711086 0.34267107] => 0.88711086298 [ 0.34267107 0.3844453 ] => 0.342671068373 [ 0.3844453 0.89759621] => 0.384445299683 [ 0.89759621 0.95278264] => 0.897596208691 |
We can see that we have NaN values on the first row.
This is because we do not have a prior observation for the first value in the sequence. We have to fill that space with something.
But we cannot fit a model with NaN inputs.
Handling Missing Sequence Data
There are two main ways to handle missing sequence data.
They are to remove rows with missing data and to fill the missing timesteps with another value.
For more general methods for handling missing data, see the post:
The best approach for handling missing sequence data will depend on your problem and your chosen network configuration. I would recommend exploring each method and see what works best.
Remove Missing Sequence Data
In the case where we are echoing the observation in the previous timestep, the first row of data does not contain any useful information.
That is, in the example above, given the input:
|
1 |
[ nan 0.18961404] |
and the output:
|
1 |
nan |
There is nothing meaningful that can be learned or predicted.
The best case here is to delete this row.
We can do this during the formulation of the sequence as a supervised learning problem by removing all rows that contain a NaN value. Specifically, the dropna() function can be called prior to splitting the data into X and y components.
The complete example is listed below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
from random import random from numpy import array from pandas import concat from pandas import DataFrame # generate a sequence of random values def generate_sequence(n_timesteps): return [random() for _ in range(n_timesteps)] # generate data for the lstm def generate_data(n_timesteps): # generate sequence sequence = generate_sequence(n_timesteps) sequence = array(sequence) # create lag df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) # remove rows with missing values df.dropna(inplace=True) values = df.values # specify input and output data X, y = values, values[:, 0] return X, y # generate sequence n_timesteps = 10 X, y = generate_data(n_timesteps) # print sequence for i in range(len(X)): print(X[i], '=>', y[i]) |
Running the example results in 9 X,y pairs instead of 10, with the first row removed.
|
1 2 3 4 5 6 7 8 9 |
[ 0.60619475 0.24408238] => 0.606194746194 [ 0.24408238 0.44873712] => 0.244082383195 [ 0.44873712 0.92939547] => 0.448737123424 [ 0.92939547 0.74481645] => 0.929395472523 [ 0.74481645 0.69891311] => 0.744816453809 [ 0.69891311 0.8420314 ] => 0.69891310578 [ 0.8420314 0.58627624] => 0.842031399202 [ 0.58627624 0.48125348] => 0.586276240292 [ 0.48125348 0.75057094] => 0.481253484036 |
Replace Missing Sequence Data
In the case when the echo problem is configured to echo the observation at the current timestep, then the first row will contain meaningful information.
For example, we can change the definition of y from values[:, 0] to values[:, 1] and re-run the demonstration to produce a sample of this problem, as follows:
|
1 2 3 4 5 6 7 8 9 10 |
[ nan 0.50513289] => 0.505132894821 [ 0.50513289 0.22879667] => 0.228796667421 [ 0.22879667 0.66980995] => 0.669809946421 [ 0.66980995 0.10445146] => 0.104451463568 [ 0.10445146 0.70642423] => 0.70642422679 [ 0.70642423 0.10198636] => 0.101986362328 [ 0.10198636 0.49648033] => 0.496480332278 [ 0.49648033 0.06201137] => 0.0620113728356 [ 0.06201137 0.40653087] => 0.406530870804 [ 0.40653087 0.63299264] => 0.632992635565 |
We can see that the first row is given the input:
|
1 |
[ nan 0.50513289] |
and the output:
|
1 |
0.505132894821 |
Which could be learned from the input.
The problem is, we still have a NaN value to handle.
Instead of removing the rows with NaN values, we can replace all NaN values with a specific value that does not appear naturally in the input, such as -1. To do this, we can use the fillna() Pandas function.
The complete example is listed below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
from random import random from numpy import array from pandas import concat from pandas import DataFrame # generate a sequence of random values def generate_sequence(n_timesteps): return [random() for _ in range(n_timesteps)] # generate data for the lstm def generate_data(n_timesteps): # generate sequence sequence = generate_sequence(n_timesteps) sequence = array(sequence) # create lag df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) # replace missing values with -1 df.fillna(-1, inplace=True) values = df.values # specify input and output data X, y = values, values[:, 1] return X, y # generate sequence n_timesteps = 10 X, y = generate_data(n_timesteps) # print sequence for i in range(len(X)): print(X[i], '=>', y[i]) |
Running the example, we can see that the NaN value in the first column of the first row was replaced with a -1 value.
|
1 2 3 4 5 6 7 8 9 10 |
[-1. 0.94641256] => 0.946412559807 [ 0.94641256 0.11958645] => 0.119586451733 [ 0.11958645 0.50597771] => 0.505977714614 [ 0.50597771 0.92496641] => 0.924966407025 [ 0.92496641 0.15011979] => 0.150119790096 [ 0.15011979 0.69387197] => 0.693871974256 [ 0.69387197 0.9194518 ] => 0.919451802966 [ 0.9194518 0.78690337] => 0.786903370269 [ 0.78690337 0.17017999] => 0.170179993691 [ 0.17017999 0.82286572] => 0.822865722747 |
Learning with Missing Sequence Values
There are two main options when learning a sequence prediction problem with marked missing values.
The problem can be modeled as-is and we can encourage the model to learn that a specific value means “missing.” Alternately, the special missing values can be masked and explicitly excluded from the prediction calculations.
We will take a look at both cases for the contrived “echo the current observation” problem with two inputs.
Learning Missing Values
We can develop an LSTM for the prediction problem.
The input is defined by 2 timesteps with 1 feature. A small LSTM with 5 memory units in the first hidden layer is defined and a single output layer with a linear activation function.
The network will be fit using the mean squared error loss function and the efficient ADAM optimization algorithm with default configuration.
|
1 2 3 4 5 |
# define model model = Sequential() model.add(LSTM(5, input_shape=(2, 1))) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') |
To ensure that the model learns a generalized solution to the problem, that is to always returns the input as output (y(t) == X(t)), we will generate a new random sequence every epoch. The network will be fit for 500 epochs and updates will be performed after each sample in each sequence (batch_size=1).
|
1 2 3 4 |
# fit model for i in range(500): X, y = generate_data(n_timesteps) model.fit(X, y, epochs=1, batch_size=1, verbose=2) |
Once fit, another random sequence will be generated and the predictions from the model will be compared to the expected values. This will provide a concrete idea of the skill of the model.
|
1 2 3 4 5 |
# evaluate model on new data X, y = generate_data(n_timesteps) yhat = model.predict(X) for i in range(len(X)): print('Expected', y[i,0], 'Predicted', yhat[i,0]) |
Tying all of this together, the complete code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
from random import random from numpy import array from pandas import concat from pandas import DataFrame from keras.models import Sequential from keras.layers import LSTM from keras.layers import Dense # generate a sequence of random values def generate_sequence(n_timesteps): return [random() for _ in range(n_timesteps)] # generate data for the lstm def generate_data(n_timesteps): # generate sequence sequence = generate_sequence(n_timesteps) sequence = array(sequence) # create lag df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) # replace missing values with -1 df.fillna(-1, inplace=True) values = df.values # specify input and output data X, y = values, values[:, 1] # reshape X = X.reshape(len(X), 2, 1) y = y.reshape(len(y), 1) return X, y n_timesteps = 10 # define model model = Sequential() model.add(LSTM(5, input_shape=(2, 1))) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit model for i in range(500): X, y = generate_data(n_timesteps) model.fit(X, y, epochs=1, batch_size=1, verbose=2) # evaluate model on new data X, y = generate_data(n_timesteps) yhat = model.predict(X) for i in range(len(X)): print('Expected', y[i,0], 'Predicted', yhat[i,0]) |
Running the example prints the loss each epoch and compares the expected vs. the predicted output at the end of a run for one sequence.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Reviewing the final predictions, we can see that the network learned the problem and predicted “good enough” outputs, even in the presence of missing values.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
... Epoch 1/1 0s - loss: 1.5992e-04 Epoch 1/1 0s - loss: 1.3409e-04 Epoch 1/1 0s - loss: 1.1581e-04 Epoch 1/1 0s - loss: 2.6176e-04 Epoch 1/1 0s - loss: 8.8303e-05 Expected 0.390784174343 Predicted 0.394238 Expected 0.688580469278 Predicted 0.690463 Expected 0.347155799665 Predicted 0.329972 Expected 0.345075533266 Predicted 0.333037 Expected 0.456591840482 Predicted 0.450145 Expected 0.842125610156 Predicted 0.839923 Expected 0.354087132135 Predicted 0.342418 Expected 0.601406667694 Predicted 0.60228 Expected 0.368929815424 Predicted 0.351224 Expected 0.716420996314 Predicted 0.719275 |
You could experiment further with this example and mark 50% of the t-1 observations for a given sequence as -1 and see how that affects the skill of the model over time.
Masking Missing Values
The marked missing input values can be masked from all calculations in the network.
We can do this by using a Masking layer as the first layer to the network.
When defining the layer, we can specify which value in the input to mask. If all features for a timestep contain the masked value, then the whole timestep will be excluded from calculations.
This provides a middle ground between excluding the row completely and forcing the network to learn the impact of marked missing values.
Because the Masking layer is the first in the network, it must specify the expected shape of the input, as follows:
|
1 |
model.add(Masking(mask_value=-1, input_shape=(2, 1))) |
We can tie all of this together and re-run the example. The complete code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
from random import random from numpy import array from pandas import concat from pandas import DataFrame from keras.models import Sequential from keras.layers import LSTM from keras.layers import Dense from keras.layers import Masking # generate a sequence of random values def generate_sequence(n_timesteps): return [random() for _ in range(n_timesteps)] # generate data for the lstm def generate_data(n_timesteps): # generate sequence sequence = generate_sequence(n_timesteps) sequence = array(sequence) # create lag df = DataFrame(sequence) df = concat([df.shift(1), df], axis=1) # replace missing values with -1 df.fillna(-1, inplace=True) values = df.values # specify input and output data X, y = values, values[:, 1] # reshape X = X.reshape(len(X), 2, 1) y = y.reshape(len(y), 1) return X, y n_timesteps = 10 # define model model = Sequential() model.add(Masking(mask_value=-1, input_shape=(2, 1))) model.add(LSTM(5)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') # fit model for i in range(500): X, y = generate_data(n_timesteps) model.fit(X, y, epochs=1, batch_size=1, verbose=2) # evaluate model on new data X, y = generate_data(n_timesteps) yhat = model.predict(X) for i in range(len(X)): print('Expected', y[i,0], 'Predicted', yhat[i,0]) |
Again, the loss is printed each epoch and the predictions are compared to expected values for a final sequence.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Again, the predictions appear good enough to a few decimal places.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
... Epoch 1/1 0s - loss: 1.0252e-04 Epoch 1/1 0s - loss: 6.5545e-05 Epoch 1/1 0s - loss: 3.0831e-05 Epoch 1/1 0s - loss: 1.8548e-04 Epoch 1/1 0s - loss: 7.4286e-05 Expected 0.550889403319 Predicted 0.538004 Expected 0.24252028132 Predicted 0.243288 Expected 0.718869927574 Predicted 0.724669 Expected 0.355185878917 Predicted 0.347479 Expected 0.240554707978 Predicted 0.242719 Expected 0.769765554707 Predicted 0.776608 Expected 0.660782450416 Predicted 0.656321 Expected 0.692962017672 Predicted 0.694851 Expected 0.0485233839401 Predicted 0.0722362 Expected 0.35192019185 Predicted 0.339201 |
Which Method to Choose?
These one-off experiments are not sufficient to evaluate what would work best on the simple echo sequence prediction problem.
They do provide templates that you can use on your own problems.
I would encourage you to explore the 3 different ways of handling missing values in your sequence prediction problems. They were:
- Removing rows with missing values.
- Mark and learn missing values.
- Mask and learn without missing values.
Try each approach on your sequence prediction problem and double down on what appears to work best.
Summary
It is common to have missing values in sequence prediction problems if your sequences have variable lengths.
In this tutorial, you discovered how to handle missing data in sequence prediction problems in Python with Keras.
Specifically, you learned:
- How to remove rows that contain a missing value.
- How to mark missing values and force the model to learn their meaning.
- How to mask missing values to exclude them from calculations in the model.
Do you have any questions about handling missing sequence data?
Ask your questions in the comments and I will do my best to answer.







Fantastic !
I’m glad it helps Nader.
I really like your books, they have really helped me, I’m using 4 of them Time Series Forecasting, Machine Learning, Deep Learning, and, Machine Learning from scratch. Especially the Machine Learning from scratch has helped a lot with my python skills. I hope the Deep Learning from scratch, not using Tensor Flow and Keras will be coming soon. Thanks a lot.
Thanks for your support James.
If I want to normalize input data, I should replace Missing data first or normalizing input data?
Yes, I would impute before scaling.
Hi Jason
Thanks for the tutorials.
Not sure if I understand your answer to Adam correctly: Do you recommend that we first replace the nan’s with a value (say “-1”) and then scale?
1) If so, the data will be scaled taking the -1 value into account: i.e.: If my data has a range of 10 to 50, but contains NaNs, then 10 will no longer be the minimum; -1 would be.
2) Also, if I replace prior to scaling, I will need to change the “mask_value=-1” from -1 to the value to which -1 has now been scaled. Is that correct?
Would it not be better to first scale and then replace the NaN’s?
If you replace missing with a value, like the average, do it first then scale.
If you want to mask them out, scale first in a way that ignores the missing values.
On Replace Missing Sequence Data, we should change the definition of y from values[:, 0] to values[:, 1], right?
Yes, from the post:
if we change generate_sequence:
def generate_sequence(n_timesteps):
return random.randint(34,156,n_timesteps)
The results and the real value will be a lot of error
why?
Because neural networks cannot predict a pseudo random series.
What if I collect values from internet every 5 minutes, but sometimes there are server issues and I miss some values. Could solution be to add another feature as input as timestamp of time when each set of features were captured? Would LSTM would make sense than features usually go every 300n but somtimes number is different.
You could add zero values to get the required length and use a mask in your model to ignore them.
I am missing methods to sensibly impute missing data of uni- or multivariate time series and their pythonic implementation. I’m thinking of interpolation, autocorrelation or maybe other sophisticated unsupervised learning methods. Have you written about this somewhere?
Perhaps try a few different methods and see what works best for your specific problem.
Also see this post:
https://machinelearningmastery.com/handle-missing-data-python/
I hope to cover more sophisticated methods in the future.
Just noting that stateless Sequential model (RNN) in Keras can be constructed with unspecified batch size. This allows train / validate / predict with different batch sizes:
https://stackoverflow.com/questions/43702481/why-does-keras-lstm-batch-size-used-for-prediction-have-to-be-the-same-as-fittin
Thanks, I also give an example here:
https://machinelearningmastery.com/develop-encoder-decoder-model-sequence-sequence-prediction-keras/
Does masking work for missing values in output sequence?
Not in the same way. You can use a “I don’t know” output, e.g. predict a 0 or something. Very useful in NLP problems.
Hi Jason,
Thank you for this.
How do you feel about imputing a Time Series using and Iterative Imputer or a KNN model, in a Sklearn Pipeline during training?
Missing values will have probably have been imputed from data in the future.
Thanks
It really depends on the time series.
Often simple persistence is better.
“When defining the layer, we can specify which value in the input to mask. If all features for a timestep contain the masked value, then the whole timestep will be excluded from calculations.”
Does this mean all featrures would be excluded? Or features with Nan value only?
We tell the Masking layer what to ignore, e.g. 0.0 by default.
Thanks, helpful post! Though in your examples you have a relatively small gap, compared to the total amount of data. I am facing a problem where I have a data set of 450 vectors and a gap between them of 250 consequent missing vectors. Do you have a recommended templates, examples, some other blog posts you would point at in such a case?
Perhaps try zero padding with a masking layer?
Perhaps try ignoring the gap?
Perhaps try imputing?
Perhaps try splitting samples in such a way that the missing space is one sample you can skip?
Let me know how you go.
For example, we can change the definition of y from values[:, 0] to values[:, 0] and re-run the demonstration to produce a sample of this problem, as follows:
It should be revised as below:
For example, we can change the definition of y from values[:, 0] to values[:, -1] and re-run the demonstration to produce a sample of this problem, as follows:
Is it right?
Nearly, I think values[:,1] from the complete example.
Thanks, fixed.
Great tutorial. I have a question. I am using keras to do a sequence tagging work (Bi-LSTM + CRF model) with different sequence lengths. I use masking layer to mask 0 value and sequence.pad_sequences() to pad training data with 0. I trained the model successfully, however, I met a problem when I predict the test data.
I pad the test instances with 0, e.g., 23 -> 100(maxlen). In theory, the model will ignore the 77 “0” and only predict the 23 timesteps. But I get 100 prediction results and the latter 77 results are not 0 or null. I am confused. Have you met this situation before ? Is the masking layer in use ? Or I just need to ignore the latter 77 results. Thanks.
I’m not sure I follow, are you talking about masking inputs or making predictions with padding or both?
Both. If you mask inputs when you train your model, you must mask the test data in the same way when the model makes the prediction. Here is part of my model code:
model = Sequential()
model.add(Masking(mask_value=0, input_shape=(seq_length, features_length)))
model.add(Bidirectional(LSTM(lstm_units_num, return_sequences=True)))
model.add(Dropout(dropout_rate))
model.add(Bidirectional(LSTM(lstm_units_num, return_sequences=True)))
model.add(Dropout(dropout_rate))
model.add(TimeDistributed(Dense(num_class, activation=”softmax”)))
crf_layer = CRF(num_class)
model.add(crf_layer).
When I use the model to make the prediction, I get 100(seq_length) prediction results(all are not 0 or null), however, 77 of these 100 input timesteps are masked, they should not be predicted with a not-0 result. So I am very confused. I am not sure whether the prediction results are correct…
Predictions that are all 0 might suggest that the model has not yet learned the problem. Perhaps try training longer or an alternate model configuration?
Sorry, what you said is not my question… Let’s take an example, in my experiment, maxlen is 100, now the model has already been trained successfully (with masking layer). Assume there is a test instance(length is 23) and the model wants to predict it. First I use padding to pad this test case with 0 and then length of the test instance becomes 100 (latter 77 values are all 0). Then the model will get the prediction results with length 100. The model masks 0 value, so in theory, the latter 77 of these 100 prediction results should be all 0, because they should not be predicted (being masked). However, in my experiment, the latter 77 prediction results are not 0, it seems they are also predicted and the masking has no effect. Have you met this problem before ? Or in your experiments, the latter “77” prediction results are all 0 ?
Here is a link (https://groups.google.com/forum/#!topic/keras-users/M7BVggL7cG0) talking about the same question. Thanks.
We cannot mask predictions, only pad them.
Perhaps your model requires further tuning.
I searched in google and found someone has the same question with me. (https://groups.google.com/forum/#!topic/keras-users/M7BVggL7cG0). Hope it can help you to understand my question. Many thanks.
evaluate model on new data
X, y = generate_data(n_timesteps)
so.in this caes ,you should know 10 data to evaluate model , but if you know the result, Why Predict?
THIS model how to predict new data
To demonstrate to beginners how to do it.
Hi Jason, in the function generate_data(), there is a line that looks like this:
X, y = values, values[:, 1]
It appears that this includes the value that we want to predict, ‘y’, as the 2nd column in X. Doesn’t that make it very easy for the model to predict ‘y’ (it would simply need to pull out the value in the 2nd column of X)? Shouldn’t this line look like this instead?:
X, y = values[:, 0], values[:, 1]
Of course, we’d need to change the input_shape() for the first layer in the Keras model.
Yes and now, perhaps this post will make things clearer:
https://machinelearningmastery.com/convert-time-series-supervised-learning-problem-python/
And this on walk forward validation:
https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
Here is a CMU paper that uses a modified version of LSTM called “Phased LSTM”, with various manipulations of the data.
https://www.cs.cmu.edu/~epxing/Class/10708-17/project-reports/project8.pdf
One of the data manipulations involves construction of a mask (Equation 1), and then adds this mask as NEW COLUMNS in the input matrix of predictor values ‘X’. This is CMU’s “PLSTM-Masking” model, (see Table 1 in the paper). This effectively DOUBLES the number of columns in the matrix X. (This may be very similar to an earlier comment you made in this thread: https://machinelearningmastery.com/handle-missing-timesteps-sequence-prediction-problems-python/#comment-424701 in response to Darius’ question. It may also be related to White’s earlier question: https://machinelearningmastery.com/handle-missing-timesteps-sequence-prediction-problems-python/#comment-452953)
In the section of the above tutorial entitled “Masking Missing Values”, a Masking layer is added. If this were essentially doing the same thing as PLSTM-Masking in the CMU paper, I would have expected the output of the Masking layer to have double the number of columns, i.e., 4. But when I run
model.summary()
to inspect the shape of the output, I see that the Masking layer’s output still has only 2 columns: “(None, 2, 1)”. Am I right to infer that the Masking layer is not implementing the same masking approach as is done in the PLSTM-Masking model in the CMU paper? I think the answer is “yes”, that the Masking layer is simply “skipping over” rows in the input matrix X where all values have the masking value “-1”.
Even though a row of missing values is skipped, does the LSTM “know” that it must still cause its memory to decay by one time step? (Values further back in time should be weighted less than more recent values.)
I believe the masked inputs are excluded from all forward/backward computation through each lstm unit.
You could consult the Keras API/code to confirm.
Hey Jason – many thanks for the article. You mention that that masking is somewhere in between completely removing missing values/rows and Imputing/learning missing values. Could you please explain why masking is any different to just removing the values from the time series? The way I understand it so far is that: if all values in input tensor equal the mask value then that time step will be skipped and the state transferred (if stateful is true). How is this different to excluding the row from the time series?
Yes, masked values are skipped.
But the row is not skipped if it contains sparse values.
Hey Jason,
Consider I have a dataset wherein there are 4 input features what if there are Nans only in 2 of the 4 input features, I don’t want the rows to be skipped and also I do not want to replace Nans with a value that is out of range. Forward filling can be done for the data points which lie in between. How to handle the missing values if they are at the beginning of the dataset without backfilling.
You fill or skip them. After that you’re out of options I think.
Thanks, Jason
I was wondering the same, And I do have another question wrt to the above example, if I am replacing Nans with a value that is out of range, will the model(Assuming LSTM) recognise that 2 of 4 input features are meaningless and use the other 2 input features.
It may, if you mark them with a special value or mark them as missing and use a masking layer. Try it and see.
Hello Master Brownlee, was trying to implement a mask in a multi-headed MLP, after flattening the inputs, I keep getting the error Layer dense does not support masking but was passed an input_mask…any idea on how to get over the problem? Thanks in advance
Yes, I think only RNNs support masking.
Hello ,
Could you please clarify one thing
You defined the timesteps to be 2,
But in the code you are generating the sequences of 10 timesteps for fitting the model. What is the difference between this things
The code example has 10 observations, split into subsequences of two lag observations as input and one observation as output.
More about this here:
https://machinelearningmastery.com/time-series-forecasting-supervised-learning/
Hi Jason,
thank you very much for this. That’s always fantastic !!
One question about time-series and lstm :
I work with time-series (daily physical values from sensors from factory in fonction of time) and I have to deal with missing data. That’s not “real’ missing data, we don’t have values because factory is stopped…cleaning for example. I have long periods with no values (several days). For you, what’s the best solution to deal with that ?
Thank you
Christophe
I have some suggestions here:
https://machinelearningmastery.com/faq/single-faq/how-do-i-handle-discontiguous-time-series-data
Hi Jason,
I have a time series data, but there are several interrupts in the time series, and the interrupts are actually quite long, which means it is not reasonable to say a data can be forecasted by the data before an interrupt.
If I want to train an LSTM using this data. How can I deal with those interrupts?
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/how-do-i-handle-discontiguous-time-series-data
Thx!
No problem.
One of my input features has about 50% of missing data, what could be done in such case?
Try a range of different imputing schemes and see what works best for your specific dataset?
Using the mean or median might be a good start?
Hello,
Thank you for your helpful material.
I am trying to use ANN to complete my time series, in which there are missing data, using another compete data set. I realized that first I need to drop the missing values and their correspondent values in both data sets, then train the model with these data sets. My question here is how can I enter those correspondent values as new data set to my trained model to predict the missing values?
Excellent question.
There are many ways to handle missing data in a time series.
You can create a fake missing values in real data and have your model learn to fill the gaps. These would be one-step predictions I would expect using complete or partial input. Data can be “removed” e.g. fake missing randomly.
Does that help?
Thank you for your response.
Actually my question is how we can enter new data as input to a trained model to predict the output.
Good question, I believe this will help:
https://machinelearningmastery.com/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
And this:
https://machinelearningmastery.com/make-predictions-long-short-term-memory-models-keras/
hi!
the maskig need to be propagate?
https://www.tensorflow.org/guide/keras/masking_and_padding
Thanks!
Keras will handle it for you. Not all layers support it, but I believe LSTMs do.
Hi Jason,
I have fed web traffic data to Keras RNN and it seems the model is mis-predicting the data on weekends. 🙁
Here is link to screenshot:
https://github.com/RSwarnkar/temporary/blob/master/RNN-Mis-Predict-Weekends.jpg
Should I remove the data on weekends so that the RNN does not mis-learns it?
regards, Rajesh
Perhaps use controlled experiments to discover what works best for your specific dataset.
Hi Jason,
Thanks for all the good work. Your blogs and newsletters are always welcomed.
I have not read all the replies but I have spotted a missing command? If I followed correctly the masking approach, are we supposed to insert
” model.add(Masking(mask_value=-1, input_shape=(2, 1))) ”
after the ” model.add(Dense(1)) ” command
and before ” model.compile(loss=’mean_squared_error’, optimizer=’adam’) ” ?
The code runs fine like that.
Cheers,
Loïc
Damn, missed it at L.35… !!
Sorry about this. Does the position of the command matter?
Thanks a lot for your work!
Yes, this will help you copy-paste the code example:
https://machinelearningmastery.com/faq/single-faq/how-do-i-copy-code-from-a-tutorial
Thanks.
Copy the whole code example – it executes directly.
Hi Jason
I have hourly recorded time series data so i need to predict missing values from data set and refill it so which technique or algorithm are best fitted can you please suggest me
Perhaps try a suite of methods and see which results in a dataset that when used to fit a model achieves the best performance on new data.
Hi, Jason, is there any other way to fill time series missing values other than the neural network. like using any other machine learning model (algorithm) like regression etc.
Kindly share any links or posts.
Yes, mean, median, persistence, a ml model, etc.
Perhaps test a suite of methods and see what works best.
Can you please tell me which are the ML model ?and if you have any post on that plz share me thanks so much Jason I love your articles
For example:
https://scikit-learn.org/stable/modules/impute.html
Hi Jason,
I am working on some missing data in csv file. So, I want to use Masking Missing Values in LSTM method. In your code, you generated random data, how can I put my own data as csv file to predict the missing value in it?
This will show you how to load a CSV file:
https://machinelearningmastery.com/load-machine-learning-data-python/
Hi Jason,
I have multivariate time-series problem but I have missing target values not the input values. Any idea about that.
How about masking those predictions which are missing and using only those predictions which correspond to available values. In this way, we can calculate the loss and back-propagate this loss at each mini-batch although this loss is calculated based on only few values within a mini-batch. But as over available observations are representative of overall function i.e. it captures most aspects of the function, we get reasonable predictions.
Do you consider this approach reasonable?
I will greatly appreciate your feedback.
Some missing data can be imputed. All missing data means you want to make predictions – and you need to fit a model on data where you do have predictions available.
Perhaps try your approach and compare to other methods.
Hi Ather
I have the same problem here, have you tried your approach? Did it work?
I use fillna() first to replace the Nan to a value, then I use a fit_transform() to change all the training data to spare matrix, can I mask the replacing after fit_transform()? Since I want to get accuracy, I need to replace the Nan to a value, but I want to know which one is better, 1-just replacing the Nan to a value, 2-after replacing, make the model learn the missing data using mask?
Most algorithms and transforms will require that you remove rows with nan or impute the nan values prior to their use.
Can a LSTM Time series prediction model return NA values as prediction even when there is no NA in the input data. If yes, why would that happen
Maybe not NA, but you can train it to predict an “I don’t know”.
Hi Jason,
My encoder decoder LSTM model is forecasting NA for a multistep timeseries prediction even though the historical timeseries has no NA values. This is happen only for a few cases , other cases its giving proper values (i am parallely training multiple timeseries using multicores). I was wondering why would that happen. In the cases where i am getting NAs, The historical timeseries has a long sequence of 0s though. Could that be causing this
The gradients may have overflowed/exploded. Perhaps add some gradient clipping and ensuring you are using relu activations in hidden layers.
Hi, Jason!
“When defining the layer, we can specify which value in the input to mask.
If all features for a timestep contain the masked value, then the whole timestep will be excluded from calculations.””
According to the definition; when I have 5 timesteps like “2, 4, 7, 1, 0” and the masking value is 0. I understood that this timestep will not be excluded and 0 value will not be excluded from calculations. Am I right? According to definition it should be “0, 0, 0, 0, 0” to be excluded.
By the way, thanks for the great post.
Yes, the mask layer lets you specify which value to mask.
Thank you for your answer. However something is not clear for me. I need to mask 0 and My all timesteps for timesteps 5 look like “8, 6, 7, 0, 0” , “7, 9, 23, 5, 0″ ,”1, 2,0, 0,0 ” because of padding but none of them look like “0, 0,0,0,0” . Does masking will be helpful for me? The sentence below in the definition confused me.
“If all features for a timestep contain the masked value, then the whole timestep will be excluded from calculations.” Does it excludes masking values when some features (but not all of them)have masking values ?
Yes, any time steps that have your masked value will be skipped. It does not matter if it is a sequence of masked values or sporadic.
Hello,
I am trying to fit a CNN model but I have NA data in the output dataset, how can I tell the model to omit this pixels with NA data during the training. I have tried several things but I always get a loss: nan.
Perhaps mark the N/A as 0 values?
good morning , I have real data set. I have al lot missing values. Above programmed are available for synthetic data. How to use “fill” command for real datasets.
Perhaps start with a simple persistence of the last observation.
from pandas import concat
# create lag
df = concat([df.shift(1), df],axis=1)
# replace missing values with -1
df.fillna(-1, inplace=True)
values = df.values
###Get the Independent Features
X=df.drop(‘rating’, axis=1)
# specify input
X = values
# reshape
X = X.reshape(len(X), 100836, 5)
return X
#################
ValueError Traceback (most recent call last)
in ()
10 X = values
11 # reshape
—> 12 X = X.reshape(len(X), 100836, 5)
13 return X
ValueError: cannot reshape array of size 2420064 into shape (201672,100836,5)
###########################
Hello, I have response variable in real dataset. how to operate above code. please correct
my code.
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/can-you-read-review-or-debug-my-code
hello, please share specific link.
Jason – I have read your LSTM book and (it feels like) every post on here about LSTM models. I have a problem with varying time sequences and have used your advice here to pad_sequences and use a Masking layer.
Since I am building an LSTM autoencoder, I realized that RepeatVector layers, and any LSTM layer that has return_sequences=False will lose the mask. After some research, I came across this post (https://stackoverflow.com/questions/58144336/how-to-mask-the-inputs-in-an-lstm-autoencoder-having-a-repeatvector-layer). I took the recommended approach with the custom bottleneck layer.
Do you agree with the approach in this post? Is this over-complicating the process, or is there another way to deal with Masking and autoencoders?
Thanks in advance – this site has been incredible for all my ML tasks, not just LSTMs.
It won’t matter/is not needed (as far as I think off the cuff) as the compressed signal at the repeatlayer/bottleneck has masked values excluded.
thank you – intuitively, that makes sense. For a reconstruction autoencoder, I shouldn’t need the mask after the RepeatVector, as the learning of the input has been accomplished up to that point.
One more question – for an autoencoder, does that also imply feature compression, and therefore, you should have multiple stacked layers where you reduce the number of neurons in each layer leading up to the bottleneck? I’m assuming you use the reduced neurons to compress the “features”.
Yes, the autoencoder compresses input to the bottleneck vector.
please help me with this Jason. so suppose i have an electricity time series data sampled at 30 minutes interval with some missing time stamps, say there is data for December 12, 2:30pm but no data for December 12, 3pm, 3:30pm, to about 6pm, then the data continues at 6:30pm. These missing time stamps would not be recorded as missing if i use the conventional pandas isna() function. So my question is that is there a way i can view discontinuity in my time series data? i.e a way to see if any time periods were skipped?
please i would really appreciate an answer to this.
Here are some ideas:
https://machinelearningmastery.com/ufaqs/how-do-i-handle-discontiguous-time-series-data/
Hi!
Many thanks for this. It’s very helpful! But there’s just this one little thing…
Replacing NaN with a number is falsification of data.
I came here for your masking example. Masking seems like a marginally acceptable kludge to exclude NaN from the computations in a library that can’t handle NaN competently… except that it’s dangerous. You ARE falsifying data, and then (hopefully) ignoring the falsified bit. How do you guarantee that the falsified data don’t corrupt the real data?
How about we invent a special value that represents “not a number” and then correctly propagate it through computations?
Back to your “Masking” code, NaN is ignored by being converted to -1 and then ignoring the -1. Since it’s just a placeholder for masking, it will make no difference if we replace the -1 with some other value like 99999999, right? Is that what you see? In my rather banal, fairly recent, stock Python environment, the “falsify and mask” technique you show here results in the falsified data corrupting the result, not with NaN, but with numbers, which would happily enter the next 18 stages of my collaborators’ data-processing pipelines. Or is the problem due to non-masked input normalisation, or something else entirely? Who knows when the problem would be caught?
I came here because I didn’t know the answer, and I still don’t. Do you see a better way around this that can be implemented by the end-user?
Again, thank you for all I’ve learned here!
Using -1 or using 9999999 should just be the same if it is a mask, but most transfer functions would prefer values with smaller magnitude. Also, falsifying may not be bad because it helps prevent the model to overfit. If the data still contain some information even there are NaN, I want the model to point that out. Example in image recognition may help explain this: Changing a few pixels in the image should not affect what you identify. So you shouldn’t care how I change those few pixels.
Hello Jason,
thank you very much for your endless efforts on making machine learning algorithms very easy to learn through your useful posts.
I have a question regarding the learning with missing values, my question is What if we don’t want -1 as a value in our time series data because it’s not logical for example to have a pressure value that is -1 and also if we have as a feature wind speed value. and also assigning 0 would be an outlier compared to the available range of features values. in that case, is it useful to run these options on my dataset?
I tried actually, regression techniques and they give reasonable results to fill the gaps of my multivariate time series though i have obvious outliers in some features. I am just not sure if it’s needed to try your suggested approaches as well.
thanks
You may also try interpolation, i.e., consider what is the value before and after the missing value in a time series and take the average to fill in.
Hi!
Fantastic post!
Is there any technique to handle missing data in an image sequence problem? i.e. what can I do if a whole image is missing in the sequence?
Thanks