Human activity recognition is the problem of classifying sequences of accelerometer data recorded by specialized harnesses or smart phones into known well-defined movements.
Classical approaches to the problem involve hand crafting features from the time series data based on fixed-sized windows and training machine learning models, such as ensembles of decision trees. The difficulty is that this feature engineering requires deep expertise in the field.
Recently, deep learning methods such as recurrent neural networks and one-dimensional convolutional neural networks, or CNNs, have been shown to provide state-of-the-art results on challenging activity recognition tasks with little or no data feature engineering, instead using feature learning on raw data.
In this tutorial, you will discover how to develop one-dimensional convolutional neural networks for time series classification on the problem of human activity recognition.
After completing this tutorial, you will know:
- How to load and prepare the data for a standard human activity recognition dataset and develop a single 1D CNN model that achieves excellent performance on the raw data.
- How to further tune the performance of the model, including data transformation, filter maps, and kernel sizes.
- How to develop a sophisticated multi-headed one-dimensional convolutional neural network model that provides an ensemble-like result.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to Develop 1D Convolutional Neural Network Models for Human Activity Recognition
Photo by Wolfgang Staudt, some rights reserved.
Tutorial Overview
This tutorial is divided into four parts; they are:
- Activity Recognition Using Smartphones Dataset
- Develop 1D Convolutional Neural Network
- Tuned 1D Convolutional Neural Network
- Multi-Headed 1D Convolutional Neural Network
Activity Recognition Using Smartphones Dataset
Human Activity Recognition, or HAR for short, is the problem of predicting what a person is doing based on a trace of their movement using sensors.
A standard human activity recognition dataset is the ‘Activity Recognition Using Smart Phones Dataset’ made available in 2012.
It was prepared and made available by Davide Anguita, et al. from the University of Genova, Italy and is described in full in their 2013 paper “A Public Domain Dataset for Human Activity Recognition Using Smartphones.” The dataset was modeled with machine learning algorithms in their 2012 paper titled “Human Activity Recognition on Smartphones using a Multiclass Hardware-Friendly Support Vector Machine.”
The dataset was made available and can be downloaded for free from the UCI Machine Learning Repository:
The data was collected from 30 subjects aged between 19 and 48 years old performing one of six standard activities while wearing a waist-mounted smartphone that recorded the movement data. Video was recorded of each subject performing the activities and the movement data was labeled manually from these videos.
Below is an example video of a subject performing the activities while their movement data is being recorded.
The six activities performed were as follows:
- Walking
- Walking Upstairs
- Walking Downstairs
- Sitting
- Standing
- Laying
The movement data recorded was the x, y, and z accelerometer data (linear acceleration) and gyroscopic data (angular velocity) from the smart phone, specifically a Samsung Galaxy S II. Observations were recorded at 50 Hz (i.e. 50 data points per second). Each subject performed the sequence of activities twice, once with the device on their left-hand-side and once with the device on their right-hand side.
The raw data is not available. Instead, a pre-processed version of the dataset was made available. The pre-processing steps included:
- Pre-processing accelerometer and gyroscope using noise filters.
- Splitting data into fixed windows of 2.56 seconds (128 data points) with 50% overlap.
- Splitting of accelerometer data into gravitational (total) and body motion components.
Feature engineering was applied to the window data, and a copy of the data with these engineered features was made available.
A number of time and frequency features commonly used in the field of human activity recognition were extracted from each window. The result was a 561 element vector of features.
The dataset was split into train (70%) and test (30%) sets based on data for subjects, e.g. 21 subjects for train and nine for test.
Experiment results with a support vector machine intended for use on a smartphone (e.g. fixed-point arithmetic) resulted in a predictive accuracy of 89% on the test dataset, achieving similar results as an unmodified SVM implementation.
The dataset is freely available and can be downloaded from the UCI Machine Learning repository.
The data is provided as a single zip file that is about 58 megabytes in size. The direct link for this download is below:
Download the dataset and unzip all files into a new directory in your current working directory named “HARDataset”.
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Develop 1D Convolutional Neural Network
In this section, we will develop a one-dimensional convolutional neural network model (1D CNN) for the human activity recognition dataset.
Convolutional neural network models were developed for image classification problems, where the model learns an internal representation of a two-dimensional input, in a process referred to as feature learning.
This same process can be harnessed on one-dimensional sequences of data, such as in the case of acceleration and gyroscopic data for human activity recognition. The model learns to extract features from sequences of observations and how to map the internal features to different activity types.
The benefit of using CNNs for sequence classification is that they can learn from the raw time series data directly, and in turn do not require domain expertise to manually engineer input features. The model can learn an internal representation of the time series data and ideally achieve comparable performance to models fit on a version of the dataset with engineered features.
This section is divided into 4 parts; they are:
- Load Data
- Fit and Evaluate Model
- Summarize Results
- Complete Example
Load Data
The first step is to load the raw dataset into memory.
There are three main signal types in the raw data: total acceleration, body acceleration, and body gyroscope. Each has three axes of data. This means that there are a total of nine variables for each time step.
Further, each series of data has been partitioned into overlapping windows of 2.65 seconds of data, or 128 time steps. These windows of data correspond to the windows of engineered features (rows) in the previous section.
This means that one row of data has (128 * 9), or 1,152, elements. This is a little less than double the size of the 561 element vectors in the previous section and it is likely that there is some redundant data.
The signals are stored in the /Inertial Signals/ directory under the train and test subdirectories. Each axis of each signal is stored in a separate file, meaning that each of the train and test datasets have nine input files to load and one output file to load. We can batch the loading of these files into groups given the consistent directory structures and file naming conventions.
The input data is in CSV format where columns are separated by whitespace. Each of these files can be loaded as a NumPy array. The load_file() function below loads a dataset given the file path to the file and returns the loaded data as a NumPy array.
|
1 2 3 4 |
# load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values |
We can then load all data for a given group (train or test) into a single three-dimensional NumPy array, where the dimensions of the array are [samples, time steps, features].
To make this clearer, there are 128 time steps and nine features, where the number of samples is the number of rows in any given raw signal data file.
The load_group() function below implements this behavior. The dstack() NumPy function allows us to stack each of the loaded 3D arrays into a single 3D array where the variables are separated on the third dimension (features).
|
1 2 3 4 5 6 7 8 9 |
# load a list of files into a 3D array of [samples, timesteps, features] def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded |
We can use this function to load all input signal data for a given group, such as train or test.
The load_dataset_group() function below loads all input signal data and the output data for a single group using the consistent naming conventions between the train and test directories.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y |
Finally, we can load each of the train and test datasets.
The output data is defined as an integer for the class number. We must one hot encode these class integers so that the data is suitable for fitting a neural network multi-class classification model. We can do this by calling the to_categorical() Keras function.
The load_dataset() function below implements this behavior and returns the train and test X and y elements ready for fitting and evaluating the defined models.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy |
Fit and Evaluate Model
Now that we have the data loaded into memory ready for modeling, we can define, fit, and evaluate a 1D CNN model.
We can define a function named evaluate_model() that takes the train and test dataset, fits a model on the training dataset, evaluates it on the test dataset, and returns an estimate of the models performance.
First, we must define the CNN model using the Keras deep learning library. The model requires a three-dimensional input with [samples, time steps, features].
This is exactly how we have loaded the data, where one sample is one window of the time series data, each window has 128 time steps, and a time step has nine variables or features.
The output for the model will be a six-element vector containing the probability of a given window belonging to each of the six activity types.
These input and output dimensions are required when fitting the model, and we can extract them from the provided training dataset.
|
1 |
n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] |
The model is defined as a Sequential Keras model, for simplicity.
We will define the model as having two 1D CNN layers, followed by a dropout layer for regularization, then a pooling layer. It is common to define CNN layers in groups of two in order to give the model a good chance of learning features from the input data. CNNs learn very quickly, so the dropout layer is intended to help slow down the learning process and hopefully result in a better final model. The pooling layer reduces the learned features to 1/4 their size, consolidating them to only the most essential elements.
After the CNN and pooling, the learned features are flattened to one long vector and pass through a fully connected layer before the output layer used to make a prediction. The fully connected layer ideally provides a buffer between the learned features and the output with the intent of interpreting the learned features before making a prediction.
For this model, we will use a standard configuration of 64 parallel feature maps and a kernel size of 3. The feature maps are the number of times the input is processed or interpreted, whereas the kernel size is the number of input time steps considered as the input sequence is read or processed onto the feature maps.
The efficient Adam version of stochastic gradient descent will be used to optimize the network, and the categorical cross entropy loss function will be used given that we are learning a multi-class classification problem.
The definition of the model is listed below.
|
1 2 3 4 5 6 7 8 9 |
model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=64, kernel_size=3, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) |
The model is fit for a fixed number of epochs, in this case 10, and a batch size of 32 samples will be used, where 32 windows of data will be exposed to the model before the weights of the model are updated.
Once the model is fit, it is evaluated on the test dataset and the accuracy of the fit model on the test dataset is returned.
The complete evaluate_model() function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=64, kernel_size=3, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate(testX, testy, batch_size=batch_size, verbose=0) return accuracy |
There is nothing special about the network structure or chosen hyperparameters; they are just a starting point for this problem.
Summarize Results
We cannot judge the skill of the model from a single evaluation.
The reason for this is that neural networks are stochastic, meaning that a different specific model will result when training the same model configuration on the same data.
This is a feature of the network in that it gives the model its adaptive ability, but requires a slightly more complicated evaluation of the model.
We will repeat the evaluation of the model multiple times, then summarize the performance of the model across each of those runs. For example, we can call evaluate_model() a total of 10 times. This will result in a population of model evaluation scores that must be summarized.
|
1 2 3 4 5 6 7 |
# repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy) score = score * 100.0 print('>#%d: %.3f' % (r+1, score)) scores.append(score) |
We can summarize the sample of scores by calculating and reporting the mean and standard deviation of the performance. The mean gives the average accuracy of the model on the dataset, whereas the standard deviation gives the average variance of the accuracy from the mean.
The function summarize_results() below summarizes the results of a run.
|
1 2 3 4 5 |
# summarize scores def summarize_results(scores): print(scores) m, s = mean(scores), std(scores) print('Accuracy: %.3f%% (+/-%.3f)' % (m, s)) |
We can bundle up the repeated evaluation, gathering of results, and summarization of results into a main function for the experiment, called run_experiment(), listed below.
By default, the model is evaluated 10 times before the performance of the model is reported.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# run an experiment def run_experiment(repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy) score = score * 100.0 print('>#%d: %.3f' % (r+1, score)) scores.append(score) # summarize results summarize_results(scores) |
Complete Example
Now that we have all of the pieces, we can tie them together into a worked example.
The complete code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 |
# cnn model from numpy import mean from numpy import std from numpy import dstack from pandas import read_csv from matplotlib import pyplot from keras.models import Sequential from keras.layers import Dense from keras.layers import Flatten from keras.layers import Dropout from keras.layers.convolutional import Conv1D from keras.layers.convolutional import MaxPooling1D from keras.utils import to_categorical # load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # load a list of files and return as a 3d numpy array def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded # load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y # load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy # fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=64, kernel_size=3, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate(testX, testy, batch_size=batch_size, verbose=0) return accuracy # summarize scores def summarize_results(scores): print(scores) m, s = mean(scores), std(scores) print('Accuracy: %.3f%% (+/-%.3f)' % (m, s)) # run an experiment def run_experiment(repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy) score = score * 100.0 print('>#%d: %.3f' % (r+1, score)) scores.append(score) # summarize results summarize_results(scores) # run the experiment run_experiment() |
Running the example first prints the shape of the loaded dataset, then the shape of the train and test sets and the input and output elements. This confirms the number of samples, time steps, and variables, as well as the number of classes.
Next, models are created and evaluated and a debug message is printed for each.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Finally, the sample of scores is printed followed by the mean and standard deviation. We can see that the model performed well achieving a classification accuracy of about 90.9% trained on the raw dataset, with a standard deviation of about 1.3.
This is a good result, considering that the original paper published a result of 89%, trained on the dataset with heavy domain-specific feature engineering, not the raw dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
(7352, 128, 9) (7352, 1) (2947, 128, 9) (2947, 1) (7352, 128, 9) (7352, 6) (2947, 128, 9) (2947, 6) >#1: 91.347 >#2: 91.551 >#3: 90.804 >#4: 90.058 >#5: 89.752 >#6: 90.940 >#7: 91.347 >#8: 87.547 >#9: 92.637 >#10: 91.890 [91.34713267729894, 91.55072955548015, 90.80420766881574, 90.05768578215134, 89.75229046487954, 90.93993892093654, 91.34713267729894, 87.54665761791652, 92.63657957244655, 91.89005768578215] Accuracy: 90.787% (+/-1.341) |
Now that we have seen how to load the data and fit a 1D CNN model, we can investigate whether we can further lift the skill of the model with some hyperparameter tuning.
Tuned 1D Convolutional Neural Network
In this section, we will tune the model in an effort to further improve performance on the problem.
We will look at three main areas:
- Data Preparation
- Number of Filters
- Size of Kernel
Data Preparation
In the previous section, we did not perform any data preparation. We used the data as-is.
Each of the main sets of data (body acceleration, body gyroscopic, and total acceleration) have been scaled to the range -1, 1. It is not clear if the data was scaled per-subject or across all subjects.
One possible transform that may result in an improvement is to standardize the observations prior to fitting a model.
Standardization refers to shifting the distribution of each variable such that it has a mean of zero and a standard deviation of 1. It really only makes sense if the distribution of each variable is Gaussian.
We can quickly check the distribution of each variable by plotting a histogram of each variable in the training dataset.
A minor difficulty in this is that the data has been split into windows of 128 time steps, with a 50% overlap. Therefore, in order to get a fair idea of the data distribution, we must first remove the duplicated observations (the overlap), then remove the windowing of the data.
We can do this using NumPy, first slicing the array and only keeping the second half of each window, then flattening the windows into a long vector for each variable. This is quick and dirty and does mean that we lose the data in the first half of the first window.
|
1 2 3 4 5 |
# remove overlap cut = int(trainX.shape[1] / 2) longX = trainX[:, -cut:, :] # flatten windows longX = longX.reshape((longX.shape[0] * longX.shape[1], longX.shape[2])) |
The complete example of loading the data, flattening it, and plotting a histogram for each of the nine variables is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
# plot distributions from numpy import dstack from pandas import read_csv from keras.utils import to_categorical from matplotlib import pyplot # load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # load a list of files and return as a 3d numpy array def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded # load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y # load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy # plot a histogram of each variable in the dataset def plot_variable_distributions(trainX): # remove overlap cut = int(trainX.shape[1] / 2) longX = trainX[:, -cut:, :] # flatten windows longX = longX.reshape((longX.shape[0] * longX.shape[1], longX.shape[2])) print(longX.shape) pyplot.figure() xaxis = None for i in range(longX.shape[1]): ax = pyplot.subplot(longX.shape[1], 1, i+1, sharex=xaxis) ax.set_xlim(-1, 1) if i == 0: xaxis = ax pyplot.hist(longX[:, i], bins=100) pyplot.show() # load data trainX, trainy, testX, testy = load_dataset() # plot histograms plot_variable_distributions(trainX) |
Running the example creates a figure with nine histogram plots, one for each variable in the training dataset.
The order of the plots matches the order in which the data was loaded, specifically:
- Total Acceleration x
- Total Acceleration y
- Total Acceleration z
- Body Acceleration x
- Body Acceleration y
- Body Acceleration z
- Body Gyroscope x
- Body Gyroscope y
- Body Gyroscope z
We can see that each variable has a Gaussian-like distribution, except perhaps the first variable (Total Acceleration x).
The distributions of total acceleration data is flatter than the body data, which is more pointed.
We could explore using a power transform on the data to make the distributions more Gaussian, although this is left as an exercise.
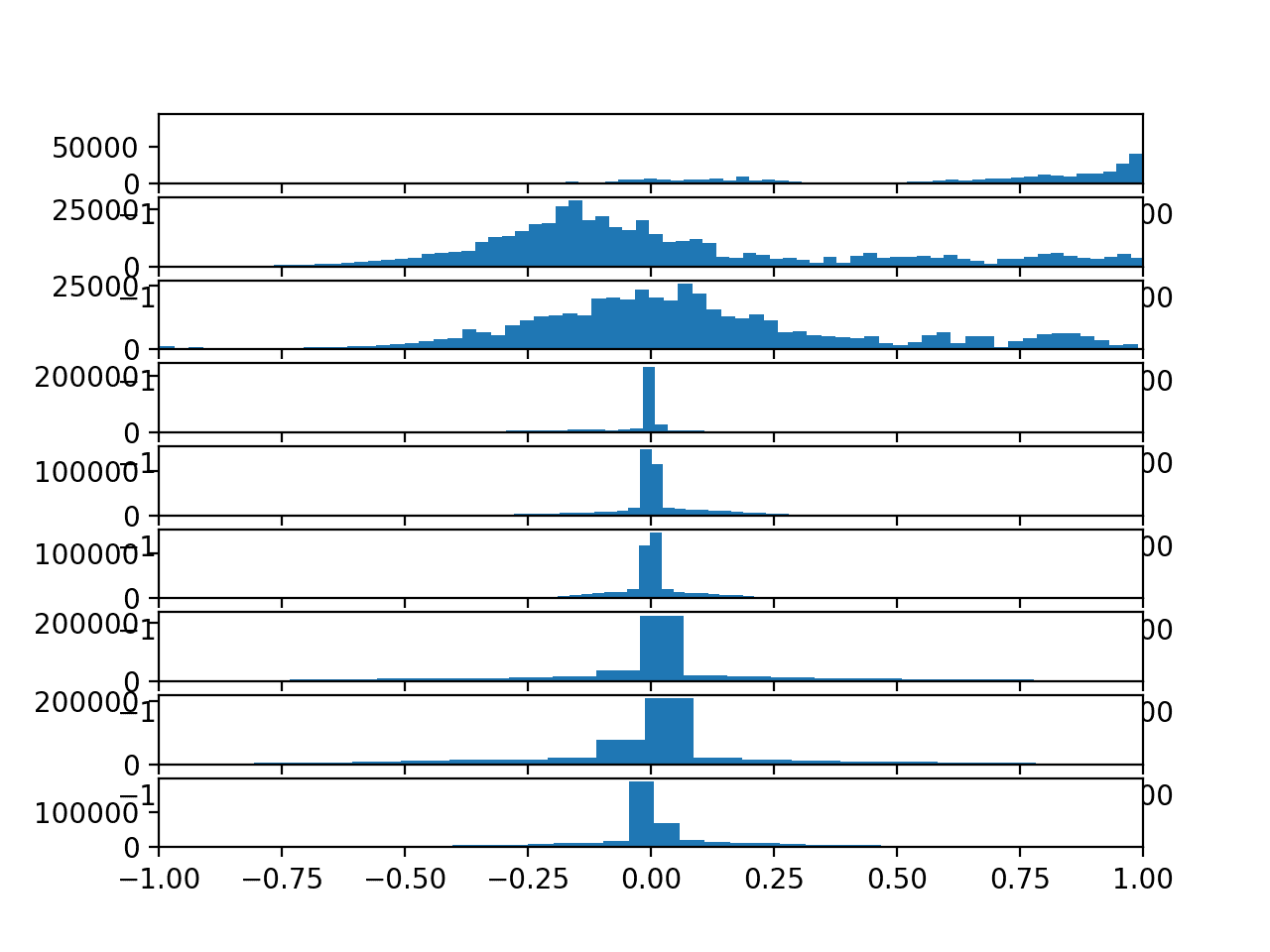
Histograms of each variable in the training data set
The data is sufficiently Gaussian-like to explore whether a standardization transform will help the model extract salient signal from the raw observations.
The function below named scale_data() can be used to standardize the data prior to fitting and evaluating the model. The StandardScaler scikit-learn class will be used to perform the transform. It is first fit on the training data (e.g. to find the mean and standard deviation for each variable), then applied to the train and test sets.
The standardization is optional, so we can apply the process and compare the results to the same code path without the standardization in a controlled experiment.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# standardize data def scale_data(trainX, testX, standardize): # remove overlap cut = int(trainX.shape[1] / 2) longX = trainX[:, -cut:, :] # flatten windows longX = longX.reshape((longX.shape[0] * longX.shape[1], longX.shape[2])) # flatten train and test flatTrainX = trainX.reshape((trainX.shape[0] * trainX.shape[1], trainX.shape[2])) flatTestX = testX.reshape((testX.shape[0] * testX.shape[1], testX.shape[2])) # standardize if standardize: s = StandardScaler() # fit on training data s.fit(longX) # apply to training and test data longX = s.transform(longX) flatTrainX = s.transform(flatTrainX) flatTestX = s.transform(flatTestX) # reshape flatTrainX = flatTrainX.reshape((trainX.shape)) flatTestX = flatTestX.reshape((testX.shape)) return flatTrainX, flatTestX |
We can update the evaluate_model() function to take a parameter, then use this parameter to decide whether or not to perform the standardization.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy, param): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] # scale data trainX, testX = scale_data(trainX, testX, param) model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=64, kernel_size=3, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate(testX, testy, batch_size=batch_size, verbose=0) return accuracy |
We can also update the run_experiment() to repeat the experiment 10 times for each parameter; in this case, only two parameters will be evaluated [False, True] for no standardization and standardization respectively.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# run an experiment def run_experiment(params, repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # test each parameter all_scores = list() for p in params: # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy, p) score = score * 100.0 print('>p=%d #%d: %.3f' % (p, r+1, score)) scores.append(score) all_scores.append(scores) # summarize results summarize_results(all_scores, params) |
This will result in two samples of results that can be compared.
We will update the summarize_results() function to summarize the sample of results for each configuration parameter and to create a boxplot to compare each sample of results.
|
1 2 3 4 5 6 7 8 9 10 |
# summarize scores def summarize_results(scores, params): print(scores, params) # summarize mean and standard deviation for i in range(len(scores)): m, s = mean(scores[i]), std(scores[i]) print('Param=%d: %.3f%% (+/-%.3f)' % (params[i], m, s)) # boxplot of scores pyplot.boxplot(scores, labels=params) pyplot.savefig('exp_cnn_standardize.png') |
These updates will allow us to directly compare the results of a model fit as before and a model fit on the dataset after it has been standardized.
It is also a generic change that will allow us to evaluate and compare the results of other sets of parameters in the following sections.
The complete code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 |
# cnn model with standardization from numpy import mean from numpy import std from numpy import dstack from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import StandardScaler from keras.models import Sequential from keras.layers import Dense from keras.layers import Flatten from keras.layers import Dropout from keras.layers.convolutional import Conv1D from keras.layers.convolutional import MaxPooling1D from keras.utils import to_categorical # load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # load a list of files and return as a 3d numpy array def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded # load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y # load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy # standardize data def scale_data(trainX, testX, standardize): # remove overlap cut = int(trainX.shape[1] / 2) longX = trainX[:, -cut:, :] # flatten windows longX = longX.reshape((longX.shape[0] * longX.shape[1], longX.shape[2])) # flatten train and test flatTrainX = trainX.reshape((trainX.shape[0] * trainX.shape[1], trainX.shape[2])) flatTestX = testX.reshape((testX.shape[0] * testX.shape[1], testX.shape[2])) # standardize if standardize: s = StandardScaler() # fit on training data s.fit(longX) # apply to training and test data longX = s.transform(longX) flatTrainX = s.transform(flatTrainX) flatTestX = s.transform(flatTestX) # reshape flatTrainX = flatTrainX.reshape((trainX.shape)) flatTestX = flatTestX.reshape((testX.shape)) return flatTrainX, flatTestX # fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy, param): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] # scale data trainX, testX = scale_data(trainX, testX, param) model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=64, kernel_size=3, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate(testX, testy, batch_size=batch_size, verbose=0) return accuracy # summarize scores def summarize_results(scores, params): print(scores, params) # summarize mean and standard deviation for i in range(len(scores)): m, s = mean(scores[i]), std(scores[i]) print('Param=%s: %.3f%% (+/-%.3f)' % (params[i], m, s)) # boxplot of scores pyplot.boxplot(scores, labels=params) pyplot.savefig('exp_cnn_standardize.png') # run an experiment def run_experiment(params, repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # test each parameter all_scores = list() for p in params: # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy, p) score = score * 100.0 print('>p=%s #%d: %.3f' % (p, r+1, score)) scores.append(score) all_scores.append(scores) # summarize results summarize_results(all_scores, params) # run the experiment n_params = [False, True] run_experiment(n_params) |
Running the example may take a few minutes, depending on your hardware.
The performance is printed for each evaluated model. At the end of the run, the performance of each of the tested configurations is summarized showing the mean and the standard deviation.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that it does look like standardizing the dataset prior to modeling does result in a small lift in performance from about 90.4% accuracy (close to what we saw in the previous section) to about 91.5% accuracy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
(7352, 128, 9) (7352, 1) (2947, 128, 9) (2947, 1) (7352, 128, 9) (7352, 6) (2947, 128, 9) (2947, 6) >p=False #1: 91.483 >p=False #2: 91.245 >p=False #3: 90.838 >p=False #4: 89.243 >p=False #5: 90.193 >p=False #6: 90.465 >p=False #7: 90.397 >p=False #8: 90.567 >p=False #9: 88.938 >p=False #10: 91.144 >p=True #1: 92.908 >p=True #2: 90.940 >p=True #3: 92.297 >p=True #4: 91.822 >p=True #5: 92.094 >p=True #6: 91.313 >p=True #7: 91.653 >p=True #8: 89.141 >p=True #9: 91.110 >p=True #10: 91.890 [[91.48286392941975, 91.24533423820834, 90.83814048184594, 89.24329826942655, 90.19341703427214, 90.46487953851374, 90.39701391245333, 90.56667797760434, 88.93790295215473, 91.14353579911774], [92.90804207668816, 90.93993892093654, 92.29725144214456, 91.82219205972176, 92.09365456396336, 91.31319986426874, 91.65252799457076, 89.14149983033593, 91.10960298608755, 91.89005768578215]] [False, True] Param=False: 90.451% (+/-0.785) Param=True: 91.517% (+/-0.965) |
A box and whisker plot of the results is also created.
This allows the two samples of results to be compared in a nonparametric way, showing the median and the middle 50% of each sample.
We can see that the distribution of results with standardization is quite different from the distribution of results without standardization. This is likely a real effect.
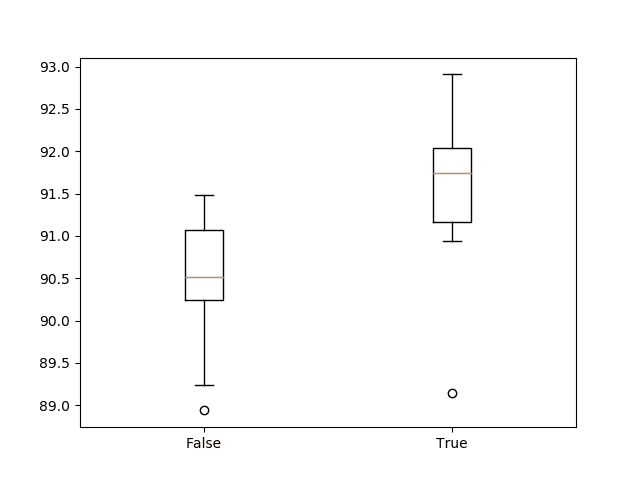
Box and whisker plot of 1D CNN with and without standardization
Number of Filters
Now that we have an experimental framework, we can explore varying other hyperparameters of the model.
An important hyperparameter for the CNN is the number of filter maps. We can experiment with a range of different values, from less to many more than the 64 used in the first model that we developed.
Specifically, we will try the following numbers of feature maps:
|
1 |
n_params = [8, 16, 32, 64, 128, 256] |
We can use the same code from the previous section and update the evaluate_model() function to use the provided parameter as the number of filters in the Conv1D layers. We can also update the summarize_results() function to save the boxplot as exp_cnn_filters.png.
The complete code example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
# cnn model with filters from numpy import mean from numpy import std from numpy import dstack from pandas import read_csv from matplotlib import pyplot from keras.models import Sequential from keras.layers import Dense from keras.layers import Flatten from keras.layers import Dropout from keras.layers.convolutional import Conv1D from keras.layers.convolutional import MaxPooling1D from keras.utils import to_categorical # load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # load a list of files and return as a 3d numpy array def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded # load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y # load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy # fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy, n_filters): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] model = Sequential() model.add(Conv1D(filters=n_filters, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=n_filters, kernel_size=3, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate(testX, testy, batch_size=batch_size, verbose=0) return accuracy # summarize scores def summarize_results(scores, params): print(scores, params) # summarize mean and standard deviation for i in range(len(scores)): m, s = mean(scores[i]), std(scores[i]) print('Param=%d: %.3f%% (+/-%.3f)' % (params[i], m, s)) # boxplot of scores pyplot.boxplot(scores, labels=params) pyplot.savefig('exp_cnn_filters.png') # run an experiment def run_experiment(params, repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # test each parameter all_scores = list() for p in params: # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy, p) score = score * 100.0 print('>p=%d #%d: %.3f' % (p, r+1, score)) scores.append(score) all_scores.append(scores) # summarize results summarize_results(all_scores, params) # run the experiment n_params = [8, 16, 32, 64, 128, 256] run_experiment(n_params) |
Running the example repeats the experiment for each of the specified number of filters.
At the end of the run, a summary of the results with each number of filters is presented.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see perhaps a trend of increasing average performance with the increase in the number of filter maps. The variance stays pretty constant, and perhaps 128 feature maps might be a good configuration for the network.
|
1 2 3 4 5 6 7 |
... Param=8: 89.148% (+/-0.790) Param=16: 90.383% (+/-0.613) Param=32: 90.356% (+/-1.039) Param=64: 90.098% (+/-0.615) Param=128: 91.032% (+/-0.702) Param=256: 90.706% (+/-0.997) |
A box and whisker plot of the results is also created, allowing the distribution of results with each number of filters to be compared.
From the plot, we can see the trend upward in terms of median classification accuracy (orange line on the box) with the increase in the number of feature maps. We do see a dip at 64 feature maps (the default or baseline in our experiments), which is surprising, and perhaps a plateau in accuracy across 32, 128, and 256 filter maps. Perhaps 32 would be a more stable configuration.
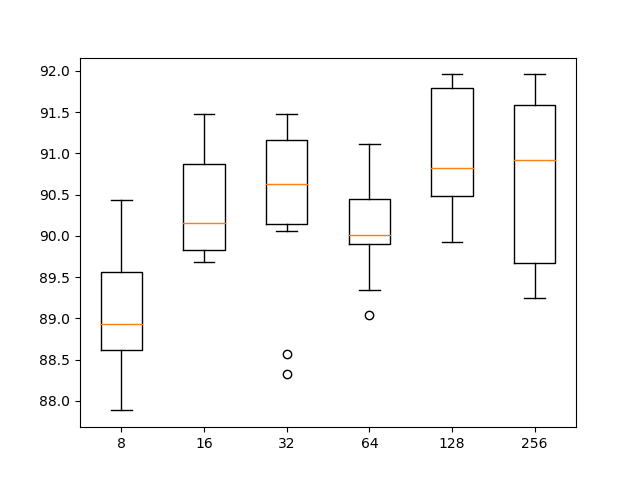
Box and whisker plot of 1D CNN with different numbers of filter maps
Size of Kernel
The size of the kernel is another important hyperparameter of the 1D CNN to tune.
The kernel size controls the number of time steps consider in each “read” of the input sequence, that is then projected onto the feature map (via the convolutional process).
A large kernel size means a less rigorous reading of the data, but may result in a more generalized snapshot of the input.
We can use the same experimental set-up and test a suite of different kernel sizes in addition to the default of three time steps. The full list of values is as follows:
|
1 |
n_params = [2, 3, 5, 7, 11] |
The complete code listing is provided below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
# cnn model vary kernel size from numpy import mean from numpy import std from numpy import dstack from pandas import read_csv from matplotlib import pyplot from keras.models import Sequential from keras.layers import Dense from keras.layers import Flatten from keras.layers import Dropout from keras.layers.convolutional import Conv1D from keras.layers.convolutional import MaxPooling1D from keras.utils import to_categorical # load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # load a list of files and return as a 3d numpy array def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded # load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y # load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy # fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy, n_kernel): verbose, epochs, batch_size = 0, 15, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] model = Sequential() model.add(Conv1D(filters=64, kernel_size=n_kernel, activation='relu', input_shape=(n_timesteps,n_features))) model.add(Conv1D(filters=64, kernel_size=n_kernel, activation='relu')) model.add(Dropout(0.5)) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dense(n_outputs, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate(testX, testy, batch_size=batch_size, verbose=0) return accuracy # summarize scores def summarize_results(scores, params): print(scores, params) # summarize mean and standard deviation for i in range(len(scores)): m, s = mean(scores[i]), std(scores[i]) print('Param=%d: %.3f%% (+/-%.3f)' % (params[i], m, s)) # boxplot of scores pyplot.boxplot(scores, labels=params) pyplot.savefig('exp_cnn_kernel.png') # run an experiment def run_experiment(params, repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # test each parameter all_scores = list() for p in params: # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy, p) score = score * 100.0 print('>p=%d #%d: %.3f' % (p, r+1, score)) scores.append(score) all_scores.append(scores) # summarize results summarize_results(all_scores, params) # run the experiment n_params = [2, 3, 5, 7, 11] run_experiment(n_params) |
Running the example tests each kernel size in turn.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
The results are summarized at the end of the run. We can see a general increase in model performance with the increase in kernel size.
The results suggest a kernel size of 5 might be good with a mean skill of about 91.8%, but perhaps a size of 7 or 11 may also be just as good with a smaller standard deviation.
|
1 2 3 4 5 6 |
... Param=2: 90.176% (+/-0.724) Param=3: 90.275% (+/-1.277) Param=5: 91.853% (+/-1.249) Param=7: 91.347% (+/-0.852) Param=11: 91.456% (+/-0.743) |
A box and whisker plot of the results is also created.
The results suggest that a larger kernel size does appear to result in better accuracy and that perhaps a kernel size of 7 provides a good balance between good performance and low variance.
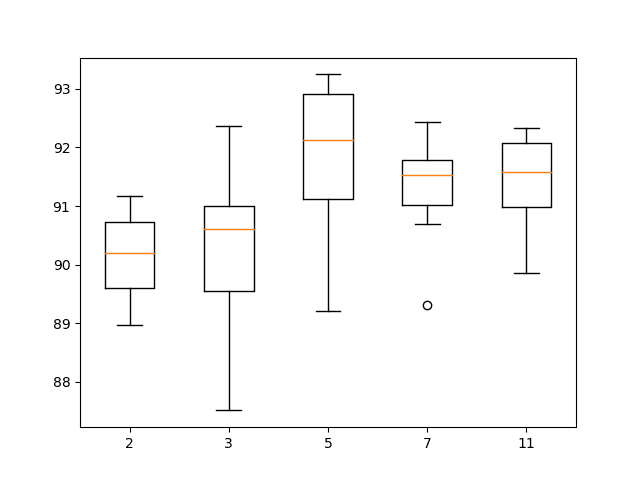
Box and whisker plot of 1D CNN with different numbers of kernel sizes
This is just the beginning of tuning the model, although we have focused on perhaps the more important elements. It might be interesting to explore combinations of some of the above findings to see if performance can be lifted even further.
It may also be interesting to increase the number of repeats from 10 to 30 or more to see if it results in more stable findings.
Multi-Headed Convolutional Neural Network
Another popular approach with CNNs is to have a multi-headed model, where each head of the model reads the input time steps using a different sized kernel.
For example, a three-headed model may have three different kernel sizes of 3, 5, 11, allowing the model to read and interpret the sequence data at three different resolutions. The interpretations from all three heads are then concatenated within the model and interpreted by a fully-connected layer before a prediction is made.
We can implement a multi-headed 1D CNN using the Keras functional API. For a gentle introduction to this API, see the post:
The updated version of the evaluate_model() function is listed below that creates a three-headed CNN model.
We can see that each head of the model is the same structure, although the kernel size is varied. The three heads then feed into a single merge layer before being interpreted prior to making a prediction.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] # head 1 inputs1 = Input(shape=(n_timesteps,n_features)) conv1 = Conv1D(filters=64, kernel_size=3, activation='relu')(inputs1) drop1 = Dropout(0.5)(conv1) pool1 = MaxPooling1D(pool_size=2)(drop1) flat1 = Flatten()(pool1) # head 2 inputs2 = Input(shape=(n_timesteps,n_features)) conv2 = Conv1D(filters=64, kernel_size=5, activation='relu')(inputs2) drop2 = Dropout(0.5)(conv2) pool2 = MaxPooling1D(pool_size=2)(drop2) flat2 = Flatten()(pool2) # head 3 inputs3 = Input(shape=(n_timesteps,n_features)) conv3 = Conv1D(filters=64, kernel_size=11, activation='relu')(inputs3) drop3 = Dropout(0.5)(conv3) pool3 = MaxPooling1D(pool_size=2)(drop3) flat3 = Flatten()(pool3) # merge merged = concatenate([flat1, flat2, flat3]) # interpretation dense1 = Dense(100, activation='relu')(merged) outputs = Dense(n_outputs, activation='softmax')(dense1) model = Model(inputs=[inputs1, inputs2, inputs3], outputs=outputs) # save a plot of the model plot_model(model, show_shapes=True, to_file='multichannel.png') model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit([trainX,trainX,trainX], trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate([testX,testX,testX], testy, batch_size=batch_size, verbose=0) return accuracy |
When the model is created, a plot of the network architecture is created; provided below, it gives a clear idea of how the constructed model fits together.
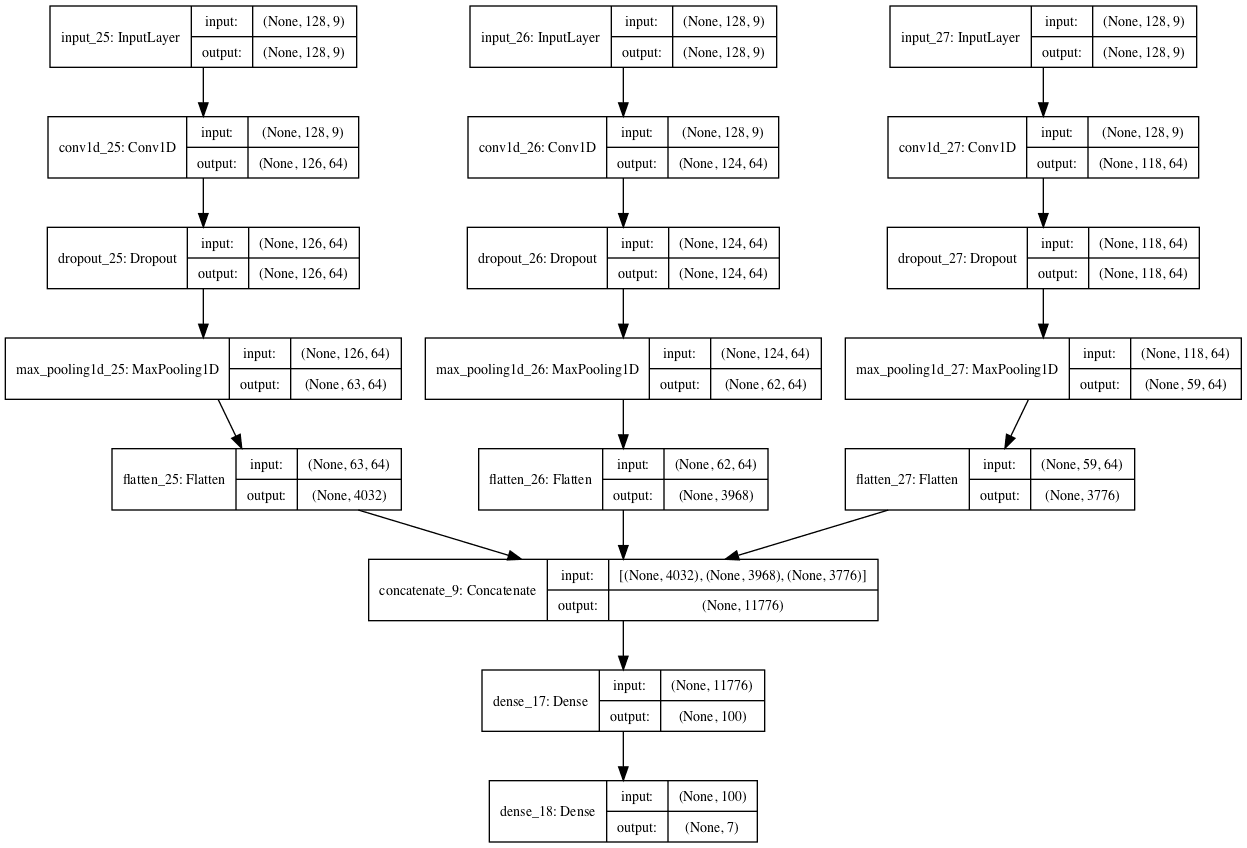
Plot of the Multi-Headed 1D Convolutional Neural Network
Other aspects of the model could be varied across the heads, such as the number of filters or even the preparation of the data itself.
The complete code example with the multi-headed 1D CNN is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 |
# multi-headed cnn model from numpy import mean from numpy import std from numpy import dstack from pandas import read_csv from matplotlib import pyplot from keras.utils import to_categorical from keras.utils.vis_utils import plot_model from keras.models import Model from keras.layers import Input from keras.layers import Dense from keras.layers import Flatten from keras.layers import Dropout from keras.layers.convolutional import Conv1D from keras.layers.convolutional import MaxPooling1D from keras.layers.merge import concatenate # load a single file as a numpy array def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # load a list of files and return as a 3d numpy array def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # stack group so that features are the 3rd dimension loaded = dstack(loaded) return loaded # load a dataset group, such as train or test def load_dataset_group(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # load all 9 files as a single array filenames = list() # total acceleration filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # body acceleration filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # body gyroscope filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # load input data X = load_group(filenames, filepath) # load class output y = load_file(prefix + group + '/y_'+group+'.txt') return X, y # load the dataset, returns train and test X and y elements def load_dataset(prefix=''): # load all train trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/') print(trainX.shape, trainy.shape) # load all test testX, testy = load_dataset_group('test', prefix + 'HARDataset/') print(testX.shape, testy.shape) # zero-offset class values trainy = trainy - 1 testy = testy - 1 # one hot encode y trainy = to_categorical(trainy) testy = to_categorical(testy) print(trainX.shape, trainy.shape, testX.shape, testy.shape) return trainX, trainy, testX, testy # fit and evaluate a model def evaluate_model(trainX, trainy, testX, testy): verbose, epochs, batch_size = 0, 10, 32 n_timesteps, n_features, n_outputs = trainX.shape[1], trainX.shape[2], trainy.shape[1] # head 1 inputs1 = Input(shape=(n_timesteps,n_features)) conv1 = Conv1D(filters=64, kernel_size=3, activation='relu')(inputs1) drop1 = Dropout(0.5)(conv1) pool1 = MaxPooling1D(pool_size=2)(drop1) flat1 = Flatten()(pool1) # head 2 inputs2 = Input(shape=(n_timesteps,n_features)) conv2 = Conv1D(filters=64, kernel_size=5, activation='relu')(inputs2) drop2 = Dropout(0.5)(conv2) pool2 = MaxPooling1D(pool_size=2)(drop2) flat2 = Flatten()(pool2) # head 3 inputs3 = Input(shape=(n_timesteps,n_features)) conv3 = Conv1D(filters=64, kernel_size=11, activation='relu')(inputs3) drop3 = Dropout(0.5)(conv3) pool3 = MaxPooling1D(pool_size=2)(drop3) flat3 = Flatten()(pool3) # merge merged = concatenate([flat1, flat2, flat3]) # interpretation dense1 = Dense(100, activation='relu')(merged) outputs = Dense(n_outputs, activation='softmax')(dense1) model = Model(inputs=[inputs1, inputs2, inputs3], outputs=outputs) # save a plot of the model plot_model(model, show_shapes=True, to_file='multichannel.png') model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # fit network model.fit([trainX,trainX,trainX], trainy, epochs=epochs, batch_size=batch_size, verbose=verbose) # evaluate model _, accuracy = model.evaluate([testX,testX,testX], testy, batch_size=batch_size, verbose=0) return accuracy # summarize scores def summarize_results(scores): print(scores) m, s = mean(scores), std(scores) print('Accuracy: %.3f%% (+/-%.3f)' % (m, s)) # run an experiment def run_experiment(repeats=10): # load data trainX, trainy, testX, testy = load_dataset() # repeat experiment scores = list() for r in range(repeats): score = evaluate_model(trainX, trainy, testX, testy) score = score * 100.0 print('>#%d: %.3f' % (r+1, score)) scores.append(score) # summarize results summarize_results(scores) # run the experiment run_experiment() |
Running the example prints the performance of the model each repeat of the experiment and then summarizes the estimated score as the mean and standard deviation, as we did in the first case with the simple 1D CNN.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that the average performance of the model is about 91.6% classification accuracy with a standard deviation of about 0.8.
This example may be used as the basis for exploring a variety of other models that vary different model hyperparameters and even different data preparation schemes across the input heads.
It would not be an apples-to-apples comparison to compare this result with a single-headed CNN given the relative tripling of the resources in this model. Perhaps an apples-to-apples comparison would be a model with the same architecture and the same number of filters across each input head of the model.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
>#1: 91.788 >#2: 92.942 >#3: 91.551 >#4: 91.415 >#5: 90.974 >#6: 91.992 >#7: 92.162 >#8: 89.888 >#9: 92.671 >#10: 91.415 [91.78825924669155, 92.94197488971835, 91.55072955548015, 91.41499830335935, 90.97387173396675, 91.99185612487275, 92.16152019002375, 89.88802171700034, 92.67051238547675, 91.41499830335935] Accuracy: 91.680% (+/-0.823) |
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Date Preparation. Explore other data preparation schemes such as data normalization and perhaps normalization after standardization.
- Network Architecture. Explore other network architectures, such as deeper CNN architectures and deeper fully-connected layers for interpreting the CNN input features.
- Diagnostics. Use simple learning curve diagnostics to interpret how the model is learning over the epochs and whether more regularization, different learning rates, or different batch sizes or numbers of epochs may result in a better performing or more stable model.
If you explore any of these extensions, I’d love to know.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
- A Public Domain Dataset for Human Activity Recognition Using Smartphones, 2013.
- Human Activity Recognition on Smartphones using a Multiclass Hardware-Friendly Support Vector Machine, 2012.
Articles
- Human Activity Recognition Using Smartphones Data Set, UCI Machine Learning Repository
- Activity recognition, Wikipedia
- Activity Recognition Experiment Using Smartphone Sensors, Video.
Summary
In this tutorial, you discovered how to develop one-dimensional convolutional neural networks for time series classification on the problem of human activity recognition.
Specifically, you learned:
- How to load and prepare the data for a standard human activity recognition dataset and develop a single 1D CNN model that achieves excellent performance on the raw data.
- How to further tune the performance of the model, including data transformation, filter maps, and kernel sizes.
- How to develop a sophisticated multi-headed one-dimensional convolutional neural network model that provides an ensemble-like result.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.





Hi Jason,
Both this post and your book are great! I have a question though:
In my case, although the database has similar structure to the one of the example, due to the nature of the environment the dataset is small.
I have been digging but I could not find a nice approach for the data augmentation problem where the case of study are multivariate time series.
Any suggestion?
Thanks for your work!
Thanks.
A good starting point might be to add Gaussian noise to the input samples.
Hi sir, I have a question for you. For example, I want to use 4 IMU data to classify human movements into four types of sports: running, walking, going up stairs, going down stairs. Each IMU has 9 features, so there are 4 * 9 in the same time step. Can this classification use LSTM model? Or make predictions?
Perhaps try it and see?
Jason,
I am dying to understand one question that I can not find any answer to:
When doing Conv1D on a multivariate time-series – is the KERNEL convolved across ALL dimensions or for each dimension individually?
The thing is that I input a 900 by 10 time series into a Conv1D(filter =16,kernel_size=6)
And I get 800 by 16 as output, whereas I would expect to get 800 by 16 by 10 , because each time series dimension is convolved with the filter individually.
What is the case?
Across each time series separately from memory.
Hi Jason,
I made a data set and trained it with CNN. The training accuracy was close to 1, but the verification accuracy remained around 0.55. Loss of verification decreased first and then increased. Is this an over-fitting problem? However, data augmentation and regularization have no effect. Do you have any good suggestions?.
Look forward to your reply!
Sounds like overfitting.
Try a large model and use weight regularization and early stopping against a validation dataset.
Weight regularization can stabilize the loss of the validation, but the validation accuracy has not been improved, keeping about 0.55. And The validation accuracyis around 0.55 during of the whole training process, so early stopping also have no effect. How to improve the verification accuracy?
I have some suggestions here:
https://machinelearningmastery.com/improve-deep-learning-performance/
Hi,
First of all – thanks for this amazing post. I am stuck with a certain problem at the moment and was wondering whether you could give me your thoughts on this.
I am analyzing a Time Series with only 1 feature. The Keras 1D Convolutional Layer does, however, require a matrix as the input. Does it make sense to split the 1D Time Series up in smaller Subvectors? And what exactly are the implications of this?
Thanks in advance!
Yes, it can make sense. The implications can only be assessed in the context of your specific problem.
you have 9 features but they are not independent. body Acc = Total Acc – gravity
where gravity is constant. So this should have led to errors ?
Not errors so much as redundancy.
Thanks Jason for this amazing post! I have a pretty similar dataset with over 1700 samples, each has 9 features (orientation,acceleration, velocity in x,y,z) over 128 timestamps and I need to predict the surface (concrete, tiles, carpet…9 in total) that the sample is moving in
I have taken the who dataset as it is and apply CNN. The acc and val_acc doesn’t increase from 60% after around 20 epochs.
Do you have any idea how should I work with these type of sensor data? Your insights can make a difference in my project.
Generally, I recommend testing a suite of models and different configurations for each approach in order to discover what works best for your specific problem.
I’m eager to hear how you go with your project.
Hi Jason,
Thanks for an amazing post. I’m currently working on a similar-ish problem using vehicle acceleration and exploring the use of 1D Covnets. What I want to know is why didn’t you use a validation set during the model fitting?
Brevity.
Also, this may help:
https://machinelearningmastery.com/faq/single-faq/why-do-you-use-the-test-dataset-as-the-validation-dataset
Hi sir,
We are evaluating neural models here say 10 times to get the accuracy and stddev because of their stochastic nature….if i want to plot a confusion matrix then how to proceed abt that here since we have trained 10 models here…
Also if i want to plot loss vs epochs to check overfitting how to do here?
You can plot the learning curve for a single run, or plot all the curves for multiple runs on a single plot.
Hello Mr. Brownlee,
I want to thank you for these clear and very useful tutorials.
Do you have an example of plotting the learning curve or other graphics that show the performance of 1D CNN models? I saw boxplots for the number of filters and kernels.
I’m new to python and I need to see an example of code 🙁 Please help me!
Yes, many examples of plotting learning curves on the blog, start here:
https://machinelearningmastery.com/display-deep-learning-model-training-history-in-keras/
Good question.
A confusion matrix is based on a single run of the model and evaluation against a single test dataset.
So it means sir here it is not feasible to plot confusion matrix as we are evaluating the model 10 times…because every time confusion matrix will be different?
It would not make sense.
Hi Sir,
In all the above analysis how u r sure that the model is not overfitting without plotting it?
I’m not 100% sure now.
I did inspect plots of loss when developing the code though.
Sir, if i evaluate the model say 30 times and take the mean accuracy as done above but say out of those 30 evaluations my model overfitted in some cases( by seeing loss vs epoch plot) then shall i still take the mean accuracy as my final outcome?
Yes.
Sir one more doubt…we are saying that the model is stochastic and everytime it is giving different results…but why is so?
is it because of the weights we are assigning in the beginning as it changes everytime?
keras by default uses glorot uniform….so everytime we assign a different weight from glorot uniform and that is why our model is stochastic?
Yes, different model weights and different order of samples when estimating the gradient during training.
This is a feature, not a bug:
https://machinelearningmastery.com/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
Sir, we can also use gridsearch cv here with keras wrapper for tuning paramters like kernals and size of kernals right?
any difference then in both the approaches….shown above and the gridsearch one ? apart from cross validation that we can use in grid search….
Yes.
I recommend grid searching manually with neural nets to have more control over the process.
Hi Jason,
First of all many thanks for sharing all your knowledge and insights.
I have a question for you. What are the default filters/kernel used by Keras in the case of a 1D CNN ?
There are no defaults for these hyperparameters, you must specify filter size and number of filters.
Hi Jason
Is it possible to have a prediction for the regression problem regarding your script? if so, can you please explain what exactly should be changed in the code? Thanks.
Regards,
Matt
Yes, you can call model.predict() to make a prediction.
Perhaps this post will help:
https://machinelearningmastery.com/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
Hi, nice blog post, can we use conv2d for this problem, if not why? can you explain briefly?
No, because each series/variable is 1D.
Dear Jason,
Am I missing something because this network should give result to be something of those 6 activities, from this example accuracy is very good, how to use this model on new dataset with no labels so we can see how it predicts activities ?
You can fit the model on available data, then use the model to make predictions via model.predict()
More here:
https://machinelearningmastery.com/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
Hi Jason,
Can we use TimeDistributed layer after Flatten instead of Dense layer? Have you got any example about it. Because When I try to use it, always I get different errors.
Thanks.
Perhaps try it and see?
This may not be the place to ask this, but it’s driving me crazy. Pandas is giving me FileNotFoundError even though the files are definitely in place. Anybody else having this issue? I’ve tried using absolute paths instead but not change.
Try running the code from the command line in the same location as the python file and data file:
https://machinelearningmastery.com/faq/single-faq/how-do-i-run-a-script-from-the-command-line
Thank you for the great tutorial.
I notice that a lot of papers or tutorials visually depict their models from input to convolution to output and everything in between. I was trying to recreate one of these diagrams but was having difficulty visualizing this one.
For example:
http://alexlenail.me/NN-SVG/LeNet.html
Have you created something like this for this model?
I have not, sorry Eric.
Hi Jason,
Thanks for your helpful post. May I ask whether there is any source for the theoretical aspects of CNN 1D? Any kinds of help are much appreciated.
Like what exactly?
Perhaps the deep learning textbook.
Hi Jason,
Your tutorials are very helpful and informative too. It solved a lot of doubts that I had. However, most of the examples are based on image datasets. I am not so sure going about parameters passing for tabular data. Could you please make a tutorial for CNN and LSTM on binary classification and external dataset testing with K fold validation?
Thanks a lot.
CNN and LSTM are not appropriate for tabular data, you can learn more here:
https://machinelearningmastery.com/when-to-use-mlp-cnn-and-rnn-neural-networks/
Hi Jason, thanks for your post.
why use an LSTM for the same set of data (as you showed in another post) you get a worse result?
The tutorials show how to use the models, rather than how to get the best result for a standard dataset.
I’m sorry, maybe I didn’t explain myself well.
In this article you use a CNN, obtaining an accuracy = 90.78
In another article you used an LSTM network, but you got less accuracy (89.78).
My questions are:
1. Was this result (CNN offers better accuracy) predictable on a theoretical basis, before training the model, taking into consideration only TYPE OF THE NETWORK and the TYPE OF DATASET?
2. If we built a new neural network, using both LSTM layer and CNN layer, would we probably get better results? Why?
Thanks for your attention. This information is very important to me.
Models were not selected for the dataset not tuned for the dataset. They were demonstrated in the context of a complex multivariate multi-step forecasting problem. The problem was a backdrop for the models.
Yes, I recommend testing a suite of models, tuning them carefully and discover what works well/best for your specific dataset. See this framework:
https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
Thank you so much for this tutorial.
I have a question please. I am new in Deep learning.
can I do this part for cross-validation? I will shuffle the data for performing this.. is it ok?
————————————————–
# run an experiment
def run_experiment(repeats=10):
# load data
trainX, trainy, testX, testy = load_dataset()
# repeat experiment
scores = list()
for r in range(repeats):
score = evaluate_model(trainX, trainy, testX, testy)
score = score * 100.0
print(‘>#%d: %.3f’ % (r+1, score))
scores.append(score)
# summarize results
summarize_results(scores)
# run the experiment
run_experiment()
———————————
We typically cannot use cross-validation for sequence prediction. Instead we use walk-forward validation.
Thank you so much for this tutorial.
I want to build a predictive model for evaluating breast cancer survivability (Binary classification ) based on CSV a file dataset, using 1D CNN as the above model, what is the inpute_shape?
knowing that the dataset.shape = (237124, 37)
You’re welcome.
A 1D CNN us only appropriate for time series data, not regular tabular data.
Ok, is there another Deep learning techniques that we can predict on the regular tabular data and give good results?
Techniques other than Deep neural networks(DNN).
Thanks for your cooperation.
Yes, you can use an MLP, a good place to start is here:
https://machinelearningmastery.com/tutorial-first-neural-network-python-keras/
I’m sorry, maybe I didn’t explain myself well.
I have a tabular data set in CSV format. How can I use LSTM and CNN or (any other deep learning technique ) on it for customer churn prediction in order to compare the Accuracy, Specificity, Sensitivity…. I have used MLP
Is MLP one of the deep learning techniques or Machine learning?!
Because the concepts mixed up for me.
Is (MLP) the same as (DNN) technique?
Thank you for your understanding and cooperation
CNN and LSTM are inappropriate for tabular data, you can use an MLP, which is a type of deep learning model.
This explains further:
https://machinelearningmastery.com/when-to-use-mlp-cnn-and-rnn-neural-networks/
Hi Jason,
I have column vectors representing signatures of users. For each user I have 60 samples. Having 60 samples I have generated 1D vectors and plotted. I am attaching the outputs. Red is real and blue is GAN generated. Now with as low as 60 samples per user, is it posible to generate high quality images or 1D vectors from GANs.
https://drive.google.com/file/d/1aJE_ugzhJcfayJwOGNYu5uGofV2jPAZ6/view?usp=sharing
Nice work.
Perhaps try it and see?
Hello Jason,
Thank you for the tutorial.
Instead of the to_categorical() for y_train, could we use an Embedding layer here, like
Flatten()(Embedding(n_classes, n_features)(y)) ?
A second question,
Could we use multiply instead of concatenate? Why choose one versus the other?
I have not tried that, not sure what you would achieve exactly.
Concat gives more context, you can try to multiply and compare results.
I have a numpy array shape (9339,16384 )
how to give the convolutional 1d layers for that input size
it is the image
This explains how to prepare data for CNN and RNNs:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
I got the accurate result and the errors for both p value and params from your code (case : 141 lines ) after complied by Jupyter notebook python3.6
How to correct it ?
_________
7352, 128, 9) (7352, 1)
(2947, 128, 9) (2947, 1)
(7352, 128, 9) (7352, 6) (2947, 128, 9) (2947, 6)
—————————————————————————
TypeError Traceback (most recent call last)
in ()
139 # run the experiment
140 n_params = [False, True]
–> 141 run_experiment(n_params)
in run_experiment(params, repeats)
129 scores = list()
130 for r in range(repeats):
–> 131 score = evaluate_model(trainX, trainy, testX, testy, p)
132 score = score * 100.0
133 print(‘>p=%s #%d: %.3f’ % (p, r+1, score))
in evaluate_model(trainX, trainy, testX, testy, param)
100 model.add(Flatten())
101 model.add(Dense(100, activation=’relu’))
–> 102 model.add(Dense(n_outputs, activation=’softmax’))
103 model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])
104 # fit network
c:\users\tanunchai.j\appdata\local\programs\python\python36\lib\site-packages\keras\engine\sequential.py in add(self, layer)
179 self.inputs = network.get_source_inputs(self.outputs[0])
180 elif self.outputs:
–> 181 output_tensor = layer(self.outputs[0])
182 if isinstance(output_tensor, list):
183 raise TypeError(‘All layers in a Sequential model ‘
c:\users\tanunchai.j\appdata\local\programs\python\python36\lib\site-packages\keras\engine\base_layer.py in __call__(self, inputs, **kwargs)
455 # Actually call the layer,
456 # collecting output(s), mask(s), and shape(s).
–> 457 output = self.call(inputs, **kwargs)
458 output_mask = self.compute_mask(inputs, previous_mask)
459
c:\users\tanunchai.j\appdata\local\programs\python\python36\lib\site-packages\keras\layers\core.py in call(self, inputs)
881 output = K.bias_add(output, self.bias, data_format=’channels_last’)
882 if self.activation is not None:
–> 883 output = self.activation(output)
884 return output
885
c:\users\tanunchai.j\appdata\local\programs\python\python36\lib\site-packages\keras\activations.py in softmax(x, axis)
29 raise ValueError(‘Cannot apply softmax to a tensor that is 1D’)
30 elif ndim == 2:
—> 31 return K.softmax(x)
32 elif ndim > 2:
33 e = K.exp(x – K.max(x, axis=axis, keepdims=True))
c:\users\tanunchai.j\appdata\local\programs\python\python36\lib\site-packages\keras\backend\tensorflow_backend.py in softmax(x, axis)
3229 A tensor.
3230 “””
-> 3231 return tf.nn.softmax(x, axis=axis)
3232
3233
TypeError: softmax() got an unexpected keyword argument ‘axis’
I recommend running from the command line, not a notebook:
https://machinelearningmastery.com/faq/single-faq/why-dont-use-or-recommend-notebooks
The previous message is error because I used keras version 2.2.4 that was not compatible with function softmax() in your program.
then i changed keras version from 2.2.4 to 2.1.3 , and unstalled keras 2.2.4
then it work very well with keras version 2.1.3 for softmax() in your program
Tanunchai
The example was tested with TensorFlow 2.1 and Keras 2.2.4.
Perhaps this will help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
This is the result from Keras version 2.1.4 ( but version 2.2.4 is error for softmax() function)
(7352, 128, 9) (7352, 1)
(2947, 128, 9) (2947, 1)
(7352, 128, 9) (7352, 6) (2947, 128, 9) (2947, 6)
>p=False #1: 88.599
>p=False #2: 88.293
>p=False #3: 90.770
>p=False #4: 87.784
>p=False #5: 91.686
>p=False #6: 89.820
>p=False #7: 92.501
>p=False #8: 89.990
>p=False #9: 87.309
>p=False #10: 91.585
>p=True #1: 91.144
>p=True #2: 88.836
>p=True #3: 91.619
>p=True #4: 91.449
>p=True #5: 93.146
>p=True #6: 92.026
>p=True #7: 91.822
>p=True #8: 88.734
>p=True #9: 92.128
>p=True #10: 92.162
[[88.59857482185272, 88.29317950458093, 90.77027485578554, 87.78418730912793, 91.68646080760095, 89.82015609093995, 92.50084832032576, 89.98982015609094, 87.30912792670512, 91.58466236851035], [91.14353579911774, 88.83610451306413, 91.61859518154056, 91.44893111638956, 93.14557176789955, 92.02578893790296, 91.82219205972176, 88.73430607397353, 92.12758737699356, 92.16152019002375]] [False, True]
Param=False: 89.834% (+/-1.703)
Param=True: 91.306% (+/-1.358)
What if the model.fit has a dimension of (7352, 128, 9) samples and (7352, 6) classes and model.evaluate has (7352, 128, 5) with the same classes
Input data must have the same shape for both training and inference.
Hello,
Could you please let me know how exactly to load the data, the zip files do not contain any csv files!
Thank you!
The above tutorial shows you exactly how to load the dataset.
hi Jason,
i want to ask a question for 2d cnn
i see in implementations that are add on more dimension
lets say that in this initial layer model.add(Conv2D(128, (2, 2), activation = ‘relu’, input_shape = X_train[0].shape))
the initial X_train[0].shape is 200, 6 and they reshape in order to add one more dimension
X_train = X_train.reshape(7062, 200, 6, 1)
X_test = X_test.reshape(1766, 200, 6, 1)
what is the purpose of the extra dimension?
is the cnn 2d expects 3d input?
For rows and cols – like an image. You can learn more here:
https://machinelearningmastery.com/convolutional-layers-for-deep-learning-neural-networks/
hi jason thanks for your answer.
so when we use data from an accelerometer that has 3 axes (x,y ,z) then we use three channels as a color image?
Different channels for features but we are using a 1D CNN, not a 2D CNN – so not like an image.
Hi Jason,
Do you have any example how to implement this type of 1D CNN in the form of an autoencoder?
I don’t think so, but you could adapt the examples here:
https://machinelearningmastery.com/lstm-autoencoders/
Hi Jason, in your Multi-Headed CNN example, how could I use model.fit_generator rather model.fit
I have this error, ValueError: Error when checking model input: the list of Numpy arrays that you are passing to your model is not the size the model expected. Expected to see 3 array(s), but instead got the following list of 1 arrays
in your code you have model = Model(inputs=[inputs1, inputs2, inputs3], outputs=outputs)
in mine: model.fit_generator(generator=generator, epochs=epochs, steps_per_epoch=timesteps, workers=3, verbose=2)
The error suggests the data does not meet your model’s expectations. Change the model or change the data.
Hi jason
Thank you very much for this issue
I have one question. Is this code appropriate only for human activity? I have a problem in civil engineering with acceleration time series. Is this code helpful?
No, you can apply to any sequence prediction problem, here are examples:
https://machinelearningmastery.com/how-to-develop-convolutional-neural-network-models-for-time-series-forecasting/
How the major drawbacks of CNN, i.e., dealing with finite context length, computational inefficiency for time-series data, handling time stretching effectively, etc. can be addressed in the model trained with 1D time-series sensor data?
Is finite context length, time-stretching really the major drawback of CNN for 1D time series classification.
1D cnn is magic, it has these limitations.
Hi Jason, Thanks for the quick response.
How can we make sure the trained CNN model is not having the finite context length, time-stretching? Because I feel if we are using the 1D CNN model for classification then it doesn’t have any impact of finite context length and time-stretching. I might be wrong in this so could you please help me in understanding the finite context length and time stretching with respect to 1D CNN? It will be a great help.
Thanks
The CNN implementation for Keras expects a fixed length.
To over come this, you might need to write custom code. I don’t have an example, sorry.
Hi Jason, Thanks for the response.
Could you please provide some insight into the strategies I can follow for the same so that I can overcome the finite context length issue. If you could have some good material which can help in understanding finite context length and time stretching with respect to CNN.
Thanks
You can use a dynamic rnn that does not require fixed length inputs. Perhaps you can adapt a dyanmic rnn to be a dynamic 1d cnn… I have not done this.
do you know how to extract variable importance in cnn?
No, sorry.
Hello . Thanks for this tutorial.
Is it possible in this dataset to calculate accuracy based on each separate activity?
For example, the cnn model is 90% accurate for walking and 89% for standing.
Is it possible to do this with the same data and code that you have taught?
Yes. You can calculate the confusion matrix for predictions and then calculate the accuracy of each class.
Thanks for the great advice.
Can you advise me on how to do this?
Yes, I will prepare a tutorial on the topic.
Until then, this may help you get started:
https://machinelearningmastery.com/confusion-matrix-machine-learning/
Hi Jason,
I was just curious if this was out yet. I know that the confusion matrix requires a predicted score and an expected score so in this case, how would we know what the expected score would be ?
Your training data should have all the information you needed to compute these expected scores.
Thank you for this tutorial!
What do we mean by (MaxPooling1D(pool_size=2)) what happens for the convolutional layer?
and
kernel_size=1 ?
Pooling reduces the dimensionality of the feature maps, you can learn more here:
https://machinelearningmastery.com/pooling-layers-for-convolutional-neural-networks/
To see the effect, you can summarize the shapes of data through the layers:
Hello Jason, thank you for the tutorial.
I have a dataset of my own in which it contains 64 time-series files. 1 file is a signal broken into 12 features and ~200 time steps, hence 1 file has ~200 rows of data with 1 row having 12 elements each. The 64 files categorize into 4 different groups and are labelled. How would you advice me to fit the dataset into 1d CNN? How can I change from your tutorial given to fit the dataset?
You’re welcome.
Good question, this will help you understand how the CNN (and LSTM) expect to receive input data:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hi Jason, thank you again for preparing a question bank about ML, but I’m still uncertain about how the dimensions of train_y and test_y data should look like when fitting into CNN 1D. I tried checking the y files from the zip folder but they contain foreign characters and I attempted fitting 2d train_y and test_y files (only have 1 column) but to no avail. What can you advice me on this? ????
It can be tricky, the advice here will help with input data for both 1d cnns and LSTMs:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hi Dr. Brownlee,
I’m having a bit of an issue with a similar 1D CNN for time based data that I am using to classify gestures in EMG data.
After working with my data to get it to the correct shape, I followed your example and created a list of arrays that would work for my particular model. Then I followed your tutorial for a basic model architecture, using my own input shape(863 time steps by 8 channels of EMG) and tried to compile and run the model. I ran into an error during compilation, which states that the model expects a 3D input, not a 2D one.
When I checked the TF documentation, I found it needed a batch size. This is where it gets a bit weird. After entering the batch size into the input layer and the optimizer, I got a separate error, saying that I had input too many dimensions. It returned the input shapes, and it appeared like so:
[None, 10, 863, 8], while I had input [10, 863, 8] into the input shape in my code.
Do you have any insights into what I could do to correct this error? I’d be happy to send you more information on my code if you think that it would help.
That is surprising as a 1D CNN expects 3d input, not 4d input. Perhaps you are using a different model or API.
Hello . Excellent tutorial .
I have one question :
Could we have as trainX the 3d ndarray (128, 9, 7352) instead of (7352, 128, 9)) ?
You said “The model requires a three-dimensional input with [samples, time steps, features].”
Is that standard and if yes , why that is ?
I run a similar project and i got ValueError: Input 0 of layer sequential is incompatible with the layer: : expected min_ndim=3, found ndim=2. Full shape received: [None, 3] .
Good question, this description for LSTMs applies just as equally to 1D CNNs, it will help a lot:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hi Jason, thanks for such great tutorial. However I’ve some confusion here.
1. What is the difference using 1 Input over 3 Inputs (like you have)?
I mean:
inputs = Input(shape=(n_timesteps,n_features))
# layer 1
conv1 = Conv1D(filters=64, kernel_size=3, activation=’relu’)(inputs)
# layer 2
conv2 = Conv1D(filters=64, kernel_size=5, activation=’relu’)(inputs)
# layer 3
conv3 = Conv1D(filters=64, kernel_size=11, activation=’relu’)(inputs)
2. and basically, you’re building MNN (Multilayer Neural Network) here, right?
3. What is the difference using output with 1 sigmoid output over 10 softmax (sorry I don’t know how to say). I mean, what is the difference:
Output 10, softmax, categorical_crossentropy
vs
Output 1, sigmoid, binary_crossentropy
I know we are dealing with multi-class, but is it possible to just have 1 output?
You’re welcome.
The 3 input model allows the input sequences to be considered at different resolutions. It may or may not help depending on the complexity of your dataset.
All the models are multi-layer. This is a multi-input model.
softmax output is required when there are more than 2 classes to be predicted. You can have one output for a two class problem. You can also interpret the multi-class output as a single integer class label using argmax:
https://machinelearningmastery.com/argmax-in-machine-learning/
Still don’t get it. What about when I use WordEmbedding before Convolutional? Do I need to have 3 inputs or just 1 input?
# layer 1
inputs1 = Input(shape=(n_timesteps,n_features))
embedding = layers.Embedding(vocab_size, embedding_dim, input_length=maxlen)(inputs1)
conv1 = Conv1D(filters=64, kernel_size=3, activation=’relu’)(embedding)
# layer 2
inputs2 = Input(shape=(n_timesteps,n_features))
embedding = layers.Embedding(vocab_size, embedding_dim, input_length=maxlen)(inputs2)
conv2 = Conv1D(filters=64, kernel_size=5, activation=’relu’)(embedding)
# layer 3
inputs3 = Input(shape=(n_timesteps,n_features))
embedding = layers.Embedding(vocab_size, embedding_dim, input_length=maxlen)(inputs3)
conv3 = Conv1D(filters=64, kernel_size=11, activation=’relu’)(embedding)
Sorry, I mean Multichannel Neural Network. Since I’ve a little bit confuse these days about Multichannel Neural Network (MNN) and Multilayer Neural Network (MNN). Can you give me the intuition about it? Or any article from you maybe..
Okay my question now, can I have 1 output for more than 2 class problem? I mean why not just 1 output, then we don’t need to use np.argmax?
You don’t need 3 input models, you can change the model to have one input if you like.
This may help to understand a multi-input model:
https://machinelearningmastery.com/develop-n-gram-multichannel-convolutional-neural-network-sentiment-analysis/
You cannot have one output for a multi-class problem given the choice of loss function used to train the model.
Thanks for the wonderful tutorial..
I have data from a manufacturing plant in set of 10 sec and sampled at 10ms. The data has 5 signals as input and one signal as output.
How can I develop a model for predicting the time behavior of the output signal. Can I follow similar approach. I need the output as a time vector.
I have developed point wise model fro same the same data but how can I develop vectorised output model
pls suggest some methods.
This can help you prepare your data (it applies for 1D CNN just as well for LSTM):
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Nice and helpful tutorial .
I used your CNN model architecture but my validation loss graph does not seems like i expected .
I noticed that (from model.summary()) my total parameters are 3,249,676 (too many ?). Could be that a problem ?
Perhaps try adding some regularization, or try alternate model architectures and compare the results.
Hi Jason,
Thanks for the great tutorial!
I have a multivariate time series data from 19 sensors (each sensor as a feature). I want to perform a binary classification. I am thinking of using both 1D conventional with LSTM as follows:
—
model = Sequential()
model.add(
TimeDistributed(Conv1D(filters=32, kernel_size=2, activation=’relu’,padding=’same’)
, input_shape=(None,timesteps,n_features)))
model.add(TimeDistributed(Conv1D(filters=64, kernel_size=2, activation=’relu’)))
model.add(TimeDistributed(MaxPooling1D(pool_size=2)))
model.add(TimeDistributed(Flatten()))
model.add(Dropout(0.2))
model.add(LSTM(64,activation=’relu’,return_sequences=True))
model.add(LSTM(64,activation=’relu’))
model.add(Dense(1, activation=’sigmoid’))
—
I just have two questions if it possible:
1) Is it fine (from theoretical point of view) to use those model together (Conv1D with LSTM)?
2) I am still working on it, but I have not got good results yet. Is there anything that I might miss in the code? I mean does it look fine or did I miss something that I need to add or remove?
Thank you very much!
It is important to test a suite of model types and model architectures and discover what works best for your dataset. Theory cannot answer this question.
Yes, here are some suggestions for improving model performance:
https://machinelearningmastery.com/improve-deep-learning-performance/
Thank you very much for your prompt reply!
Yes I agree with you and thanks for providing me the link. I will have a look at it.
Thanks Jason.
You’re welcome.
Hi Jason,
Thank you for your helpful tutorial!
I applied your code to simulated data that has 500 time steps, one feature, and 3 outputs. I replaced n_features in the evaluated function by 1 and directly put the data inside of the experiment function as below, but got the error message,
” ValueError: Input 0 of layer sequential_23 is incompatible with the layer: : expected min_ndim=3, found ndim=2. Full shape received: [None, 500].” I would really appreciate it if you could help me find what went wrong.
Thank you in advance.
###data ##
np.random.seed(1234)
#Group 1
Group1=np.reshape(np.random.normal(0,1,50000),(100,500))
#Group 2
Group2=np.reshape(np.random.normal(100,1,50000),(100,500))
#Group 3
Group3=np.reshape(np.random.normal(200,1,50000),(100,500))
sns.boxplot(data=[Group1,Group2,Group3])
stacked_mean0=np.stack(Group1)
stacked_mean100=np.stack(Group2)
stacked_mean200=np.stack(Group3)
labels = [0] * len(stacked_mean0)
labels += [1] * len(stacked_mean100)
labels += [2] * len(stacked_mean200)
labels = np.array(labels)
data=np.concatenate((stacked_mean0,stacked_mean100,stacked_mean200))
np.random.seed(151)
## indexing
training = np.random.choice(len(labels), round(0.7*len(labels)), replace=False)
test= [i for i in range(len(labels)) if i not in training]
training_labels = labels[training]
train_data1 = data[training]
test_labels=labels[test]
test_data1=data[test]
trainy = training_labels – 1
testy = test_labels – 1
# one hot encode y
trainy2 = to_categorical(trainy)
testy2 = to_categorical(testy)
print(train_data1.shape, trainy2.shape, test_data1.shape, testy2.shape)
# run an experiment
def run_experiment(repeats=10):
# load data
trainX, trainy, testX, testy = train_data1, trainy2, test_data1, testy2
# repeat experiment
scores = list()
for r in range(repeats):
score = evaluate_model(trainX, trainy, testX, testy)
score = score * 100.0
print(‘>#%d: %.3f’ % (r+1, score))
scores.append(score)
# summarize results
summarize_results(scores)
# run the experiment
run_experiment()
Perhaps some of these tips will help:
https://machinelearningmastery.com/faq/single-faq/can-you-read-review-or-debug-my-code
Hello, professor Jason
I sent you comment in another post is related to the subject but only for visualizations, you told me that X_train is a training set why do we use the inertial_Signals preprocessed data as training data to fit the model? And What is the importance of X_train?
We fit the model on the raw data in this tutorial. X_train is the training dataset.
I got the idea inertial Signals are raw data and preprocessed and made available. It’s split into 2.56 seconds of windows data. Applying feature engineering on the 128 data points to extract the X_train. Let’s referring to the question, why didn’t we use the X_train while training stacked with the inertial signals ?
X_train is loaded from internal signals.
But there is X_train alone with 561 feature and you didn’t use it as the training. you loaded only the data with 128 data points and 9 features.
which features 9(inertial Signals) or 561(X_train) will clear and support the model to distinguish the pattern of different activities. I’m sorry about the many questions,
we can use the (7532,128, 561) as a training set instead of (7532,128,9)? Why did you use the 9 features only?
There are only 9 features in the raw data – inspect it yourself in a text editor.
Sir my question is about the reason for leaving the data with 561 features why didn’t you load it ?
I said that it might be this data(561 features) helped the model train.
I’ve tried in earnest to answer your questions and I’m failing to make progress.
I don’t think I am the best person to help you, sorry.
I found prof. Jason that the accuracy was increasing by using training data(7352,561,1) to 99% on validation using CONV1. And using Robust Scaler as preprocessing.
Nice work.
Hi Jason.
A very nice article, as always.
When it comes to image classification, I realized that the input_shape in the first convLayer can be like that:
input_shape = (None, None,3))
Which means that the model will be able to classify variable input size images.
Let’s say I want to know when a couple of time series are 1 (first_label) or 0 (second_label).
And the time series lengths can be in range(5, 50).
In the previously mentioned input_shape =(None, None,3)), “3” is actually the number of channels.
In this situation: a=[0, 1, 2, 3, 4], b=[2, 3, 4, 5, 6].
My input would be c=[a, b]. My label would be [0].
My input_shape is: input_shape=(n_timesteps,n_features) which is actually input_shape=(2,5).
In this case, n_timesteps is 2 because I got a couple of time series to look at. n_features is 5, because each of them has 5 elements.
How would be possible to make things work, by changing the function input_shape=(n_timesteps,n_features) or either the dataset, in order to give the model the possibility to train from any couple of two same-length series?
I mean, one input could be c =[[1, 2, 3], [2, 3, 4]. d =[[1, 2, 3, 4], [1, 2, 3, 4]] and so on.
Thanks in advance! A variable input size il always interesting, evei if some layers may not be compatible (such as Dense or Flatten)
Thanks.
Preparing data for 1D CNNs is identical to preparing data for LSTMs, this will help:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
That is what I was looking for, thank you Jason.
I’m happy to hear that.
Hi Jason,
Since the time steps= 128 and features = 9 and the input size is [samples, time steps, features]
does this mean each input sample consist of 9 channels and each channel has 128 lengths?
in other words, is the input sample a metric of 128 rows and 9 columns or it is 9 vectors (i.e. channel) and 128 rows for each channel.
the difference in the two cases is the filter size; is it vector or matrix.
Thanks
Yes.
sorry.
is it
a) 9 channels and each channel has 128 length vector (i.e. the filters are vectors)
or
b) matrix of 128 rows and 9 columns (i.e. the filtres are matrix)
Thanks
This can help you understand input for CNNs, it’s the same as for LSTMs:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Thanks
Hi, Thank you for your tutorial.
I still have doubts about:
in a Conv1d for a time serie binary classification, how/where to visualize the extracted features by layer. I had found information for Conv2d, but still nothing clear where it is describe how to visualize features in Conv1d.
I was reading your tutorial, but still is not clear to me if in the validation section that was done.
Cheers
Generally, would not visualize the layers of a 1d layer.
Hi Jasson. May i ask why not?
What if for example i am working with an inout that was in time series and i would like to observe what the model extract as features. Would that be reasonable?
You can and I recommend go for it – as an experiment.
My thinking is that unlike images any plots of the filters or filter-generated outputs would be hard to interpret.
Hello Jason. Thank you for all of your articles. I stumbled here because like Lara I was searching for a way to visualize convolution results.
Like Lara, I think that visualization could be helpful.
For example, I am analyzing some series where I already know that smoothed versions of the series enhance the prediction results (I’m doing forecasting, not classification). Then, for my personal understanding, I am experimenting if Conv1d filters are going to extract any smoothed version of the series.
I would also be curious to see if Conv1d filters will extract a differentiated version of the series.
All of this would be easy to interpret visually.
I’m learning and I’m not an expert so maybe I just have the wrong expectations.
Your thoughts on these concerns would be very insightful.
Thank you!
Outstanding feedback Luca! We greatly appreciate your support!
train_X(5993,250,6) as train_Y(5993,250,12) where 5993 are number of windows,250 is my window size and 6 are my input features and 12 are the one-hot-coded output.
How can i give this as an inputshape to my ConvLSTM2D model as its creating an error with shapes compatibility.
model.build(input_shape=(None,5,50,1,6))
model.fit(train_X,train_Y ,epochs=epochs, batch_size=batch_size)
I believe the input shape for a convlstm2d will be 4d, perhaps you can use the above example as a starting point?
Hello Jason,
Thank you for the amazing posts as always.
I have question regarding the output from Conv1D layer. In multi headed 1D CNN, in the image(Plot of the Multi-Headed 1D Convolutional Neural Network). Input is 9 features each of 128 time steps. Here each time series(each feature) is convoluted along time axis by 64 different filter kernels. But the output of 1D CNN is 126,64, I understand that 128 time step is reduced to 126 after 1D convolution and 64 refers to number of features maps. But this corresponds to output of 1 feature(or 1 time series)where is the output for remaining 8 features?
Thank You in Advance
You’re welcome!
Good question, off the cuff – I believe the features are consolidated down to single feature maps.
Thank You. Let me find out more and confirm.
I have few more questions(perhaps these questions are for UCL guys who uploaded the data. However if you have answer that would be great)
1. What is the rationale behind overlapping 128 sample window? I assume, this is because time series is periodic in nature, and if we take 1 window, it would be sufficient to find the signature of the time series.we don’t need to look at the entire time series at once.
2.How do decide the window size ? I assume it is based on the max frequency of the data,
suppose 25Hz is the max frequency(let us assume no noise in the data). This means that after 25 samples max frequency component repeats itself. So if we take 128 samples we are in safe zone i.e we have all the primary periods of the all frequencies covered. And fortunately, we need windowed(max 400samples/window I suppose) time series for 1D CNN/LSTM networks.
Let me know your thoughts.
Thanks in Advance.
Overlapping the windows might help the model detect patterns at the edge of the window.
Determine window size or history length based on the results from systematic experiments.
I just found my answer to my previous question. The features are consolidated to single features. Basically they are added together.
Great work as always.
Even though I have a question. I am looking to a classification problem, where I have 3D multivariate input vector and a 2d univariate output vector. I don’t understand the functionality of the layers:
– Dropout.
– Max Pooling.
– Flatern.
– Dense.
I don’t know if could explain me why are this layers necessaries in this model or if you could point me in the direction of an explanation.
Thanks in advance.
Thanks.
It works well in practice, but try different combinations and see what works well for your specific dataset.
hi Jason,
Great tutorial, as always.
well, I have a question about input_shape in Conv1d layer. I’m working on a dataset that has 3000 samples and each sample has about 6300 features. in fact 6300 features are extracted from each .wav file.
I want to feed the data to a Conv1d layer. is it reasonable to reshape the data to (3000, 1, 6300) with input_shape of (1, 6300)? because as you said, input_shape must be (n_timesteps, n_features) and in this case there is only 1 timestep or sequence. in fact samples are not sequences of features.
so which one is true for input_shape? (1, n_features) or (n_features, 1) ?
thanks a million!
Using one time step is probably not appropriate or the 1d CNN is not appropriate for your model.
This may help (preparing data for 1d cnns is the same as preparing for lstms):
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hi Jason,
regarding the multi head model.
If i have a timeline were i have to detect short downward impulses, could it be usefull to use a min pool instead of a maxpool for the kernel size 3 route?
Is it common to use the dropout layer after the conv layer? I always thought that dropout should only be used after a dense/linear layer.
Thanks in advance
Perhaps try it.
Yes, it is common to use dropout after conv layers.
How do you infer that there are 128 time steps from 2.65 seconds of data?
It’s not an inference. I believe I looked at the data itself and counted.
Good morning,
how do you infer that overlapping windows of 2.65 seconds of data equals to 128 time steps?
Kind regards,
F.
I looked at the data.
Can the exact same codes be used on Colab? I am very new to the entire field and have a project in this. I was hoping you may have had a video on this. I tried downloading the dataset and tried the load function on Colab to load the test data for the body acc x. It didnt seem to go through so was curious if the same code could be used without change on Colab ?
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/do-code-examples-run-on-google-colab
Where should I give the path of the dataset? Could you please specify the location? I am unable to do it. Please reply as soon as possible.
You must place the dataset in the same directory as your python file, then you can run the above code in the tutorial to load the dataset for you.
How can I print the graph for the CNN code? Can you please tell me?
What do you mean by a graph? Do you mean epoch vs loss, if so then see this:
https://machinelearningmastery.com/display-deep-learning-model-training-history-in-keras/
how to plot validation curve and print confusion matrix for your code?
You can find these topics via the search box.
Plot validation curves:
https://machinelearningmastery.com/display-deep-learning-model-training-history-in-keras/
Confusion matrix:
https://machinelearningmastery.com/confusion-matrix-machine-learning/
how can I Show the result/detection performance on the test dataset?
Make a prediction on the test set and compare predictions to expected values with a metric.
can we use this code for the other dataset?
If yes, where should we give the path or change the syntax. Please tell us in detail.
If you need help loading data files, perhaps start here:
https://machinelearningmastery.com/load-machine-learning-data-python/
Yes, that is the intent.
Which formula did you use to calculate the accuracy for the CNN model?
There is only one way to calculate accuracy: total correct predictions / total predictions made.
thank you Jason but I am asking the prediction formula that you uses in your algorithm.
We use a neural net, not a formula.
Please give me the pseudo-code of your algorithm for activity recognition.
Sorry, I don’t have it.
how to print loss for your code
set verbose=1 when calling model.fit()
Thanks! I’m looking for article like this!
I’m going to detect transportation by sensor sequence data, so first I tried LSTM to recognize time sequential feature, but it didn’t go well… So I tried CNN-LSTM model, but still didn’t go well too! Finally, I removed LSTM on my model, then it makes sense! Now I’m so confused to how 1D-Conv can do well, so I’m searching for why, then I found this article.
In Human activity recognition area, I thought sequence data have no meaning in time, didn’t it? So LSTM couldn’t go well, but CNN could, because CNN can extract feature and can mine patterns. Is my thought correct?
In the above problem, the input is a sequence of observations which is a good fit for an LSTM or 1D CNN.
Then, what’s an difference between LSTM and 1D-CNN in detect sensor data? In my intuition, 1-D CNN is less sensitive to time than LSTM which deal with recursive network. Also I thought time is not much important on sensor data detection problems because they are not predictive models. So I thought 1D-CNN is more fit for them.
If I use LSTM on this problem, how can I deal with? My goal is not predicting the next sequences, but classifying sequences. To achieve it, I have to add softmax layer, and then previous layer should find patterns of each sequence. Then it can find such patterns, through LSTM? To find such patterns, I added 1D-CNN before LSTM, which called CNN-LSTM, but it works worse. What’s problem of this modelling?
Internally the two methods operate very differently.
Practically, I recommend evaluating each and use whatever works best for your specific dataset, as well as hybrid methods and a suite of different data preparations and model configurations.
so can you provide me the algorithm for this task using 1D CNN
You can adapt the 1D CNN models here:
https://machinelearningmastery.com/how-to-develop-convolutional-neural-network-models-for-time-series-forecasting/
I tried to run your code with a different dataset, but it did not work. Please suggest to me some datasets except UCI HAR. and let me know if it is required, any specific changes
You will have to adapt the code and model for any other dataset.
can you please tell me the size of all the layers of your architecture (filter size and all the details )
It is listed directly in the above code.
Hi Jason,
Thank you so much for this. It is fairly clear. However, I seem to be having trouble running this code as I am fairly new to Python. I am trying to understand Human Activity Recognition with deep learning but am unable to simulate this code. You wouldn’t happen to have a video tutorial of running this code step by step with the dataset labels that need to be put into the code, would you? I tried to run this on Google Colab and there one of the errors I couldn’t debug was that ‘group’ isn’t defined. I hope you can assist with this.
Cheers
No, we don’t have video tutorial. The group isn’t defined error means you use group as a variable and read from it before you have written anything into it.
Thanks so much for this tutorial! I am still a bit confused about the input shape required for Conv1D. I want to do a binary classification with EEG data, and the dataset has the following shape: 500, 1250, 6 (where 500 is the number of epochs, 1250 are the timesteps in milliseconds and 6 is the number of frontal electrodes). Then, the y/label dataset has a shape of 500. Would it be correct to feed an input shape equal to (1250, 6)?
Good question, it is the same as an LSTM, this will help:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
model.add(Dense(100, activation=’relu’))
Why did we use 100 always as output for fc dense layer?
No particular reason. Just an easy number to use in examples.
Hi, I am running a similar 1D convolutional model. I have my samples and features ready to be fed into the model as X_train but I am unsure what the train_y & test_y data is in the case of 1D data. Could you elaborate in your example
What do you expect from the network output? That is your “y” value.
Could you share how you derived your y_train and test? It is difficult to follow the path through the functions.Is it just how the data was pre-formatted and it was just brought into the code or was it formated in the code.
Yes, those are pre-formatted.
Really thanks for the post sir,
One doubt I’m having is usually 1D CNN work on 1 dimensional data, here you are using it on a 2d data that is (timesteps,no_features). But how these kernel of dimension 64*1 do convolution on the the 2d data, is it column wise or row wise.
Please provide me with this answer I have been searching this concept many places but was unable to understand.
And for one of my project, I have made it a 1d data by separating all the features, so input to the model is (timesteps,1), so my doubt is that, will the results change if I send the input as (1,timesteps).
this is the reason for my earlier doubt.
Thank you
In case of 1D data, the only convolution possible is on time axis. Hence you are more like taking average of previous n steps, for example. If you do convolution across n_features axis, you did nothing, just like the convolution does not exist.
Good Evening Sir,
I have gone through the UCI HAR Dataset.zip but was unable to identify y_test.txt and y_train.txt, which shows some symbols whereas X_test.txt and X_train.txt show some values. I request you kindly provide some details regarding y_test.txt and y_train.tx.
Thank you.
If they are symbols, just use label encoding to convert them into numbers. See here for details: https://machinelearningmastery.com/one-hot-encoding-for-categorical-data/
Dr. Brownlee,
Good morning, sir, and thanks for writing this article! I am going to dig into the DL for Time Series book later today, but am hoping you can answer something. I am experimenting with adding more convolution/pooling layers per head. However, I keep running into a Keras error. Here is a single sample:
inputs1 = Input(shape=(n_timesteps,n_features))
conv1 = Conv1D(filters=128, kernel_size=3, activation=’relu’)(inputs1)
pool1 = MaxPooling1D(pool_size=2)(conv1)
conv1a = Conv1D(filters=64, kernel_size=5, activation=’relu’)(pool1)
pool1a = MaxPooling1D(pool_size=2)(conv1a)
drop1a = Dropout(0.5)(pool1a)
flat1 = Flatten()(drop1a)
Does anything stick out as a glaring issue? I’ve seen this sort of style used in the Sequential API, but I can’t find a good example using Functional instead. Thank you very much for your time and help, sir!
Never mind, sir. I figured out where the problem was. I tried adding another metric besides accuracy and Tensorflow was not happy. Your page on how to use the Functional API was unbelievably helpful. Thanks for posting all of this great stuff!
What is your error?
Hi Jason,
This example is excellent. However, do you have some simpler examples with the time series classification of just two-dimensional signals (x=time, y=value)? Such an example could be a nice intro to this one. Also, I would say there are more such problems in real situations.
Thank you
Hi Mark…You may find the following resource of interest:
https://machinelearningmastery.com/indoor-movement-time-series-classification-with-machine-learning-algorithms/
Hello Jason,
Great article and a great discussion.
I have a question regarding the prerequisites on data for applying time series classification.
Is there a summary of prerequisites for data appropriate for time series classification?
Also, what should we do in case when the sensors don’t give signals at the same timestamp?
For example:
timestamp#signal1_value#signal2_value#signal3_value
————————————————————————-
timestamp1#value11#N/A#value31
timestamp2#value12#value22#value32
timestamp3#N/A#N/A#value33
timestamp4#value13#value24#N/A
…
Hi Filip…The following resource provides a practical guide that should add clarity:
https://www.analyticsvidhya.com/blog/2021/01/image-classification-using-convolutional-neural-networks-a-step-by-step-guide/
Hi James,
Thank you. My question was related to time series univariate multiclass classification. The link is related to image classification. Could you suggest some other resources?
Thank you
Hi James,
what about validation data in model.fit([train_X,train_X,train_X], train_y, epochs=50, batch_size=1024, verbose=1)
Can you tell me how to pass validation data???
Thank you
Hi Hasnat…The following resource may be of interest:
https://machinelearningmastery.com/update-neural-network-models-with-more-data/
okay, it’s done now. I was loading data in wrong format.
Hi james
Thanks for cnn1d with this info
I ask
If use optuna or pso to auto tuning filter or kernal whats update in your code
Can u write change part in code ??? Please
Do anyone help me to understand the idea of time steps? I have signals from 64 samples, which I need to classified in 4 classes. Each signals are recorded for 300 s. After that I divide the 300s signal into 10s time window. As some windows contain noises, I removed them manually. Now each sample has different time windows. Now how can I find out my time steps? If I chose time steps randomly will it be a problem?
Hi Paromita…The following resource may be of interest to you:
https://machinelearningmastery.com/use-timesteps-lstm-networks-time-series-forecasting/
hi James. Good tutorial you got there. Can i ask you 1 question?
I’m having a dataset include 4 files, represents for 4 fault in machine, and each file has 1000 csv consist of accelerometer in 3 axis x, y and z. The csv is times-series sampling 1KHz for 1 seconds. Do you think i can use this CNN 1D for this dataset. I’m new to this field. Looking forward to receiving your reply soon.
Thank you so much!
Hi Quan…You are very welcome! Yes! In general, CNNs are great options for time-series classification. If you are also wanting to perform regression you could consider a hybrid model with CNNs and LSTMs.
https://machinelearningmastery.com/how-to-develop-convolutional-neural-network-models-for-time-series-forecasting/
Hi James,
In google colab I’ve received the following error:
ModuleNotFoundError: No module named ‘keras.layers.convolutional’
How can I solve it?