Navigation

LSTMs for Human Activity Recognition Time Series Classification

By on September 24, 2018 in Deep Learning for Time Series

Last Updated on August 28, 2020

Human activity recognition is the problem of classifying sequences of accelerometer data recorded by specialized harnesses or smart phones into known well-defined movements.

Classical approaches to the problem involve hand crafting features from the time series data based on fixed-sized windows and training machine learning models, such as ensembles of decision trees. The difficulty is that this feature engineering requires strong expertise in the field.

Recently, deep learning methods such as recurrent neural networks like as LSTMs and variations that make use of one-dimensional convolutional neural networks or CNNs have been shown to provide state-of-the-art results on challenging activity recognition tasks with little or no data feature engineering, instead using feature learning on raw data.

In this tutorial, you will discover three recurrent neural network architectures for modeling an activity recognition time series classification problem.

After completing this tutorial, you will know:

  • How to develop a Long Short-Term Memory Recurrent Neural Network for human activity recognition.
  • How to develop a one-dimensional Convolutional Neural Network LSTM, or CNN-LSTM, model.
  • How to develop a one-dimensional Convolutional LSTM, or ConvLSTM, model for the same problem.

Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

How to Develop RNN Models for Human Activity Recognition Time Series Classification

How to Develop RNN Models for Human Activity Recognition Time Series Classification
Photo by Bonnie Moreland, some rights reserved.

Tutorial Overview

This tutorial is divided into four parts; they are:

  1. Activity Recognition Using Smartphones Dataset
  2. Develop an LSTM Network Model
  3. Develop a CNN-LSTM Network Model
  4. Develop a ConvLSTM Network Model

Activity Recognition Using Smartphones Dataset

Human Activity Recognition, or HAR for short, is the problem of predicting what a person is doing based on a trace of their movement using sensors.

A standard human activity recognition dataset is the ‘Activity Recognition Using Smart Phones Dataset’ made available in 2012.

It was prepared and made available by Davide Anguita, et al. from the University of Genova, Italy and is described in full in their 2013 paper “A Public Domain Dataset for Human Activity Recognition Using Smartphones.” The dataset was modeled with machine learning algorithms in their 2012 paper titled “Human Activity Recognition on Smartphones using a Multiclass Hardware-Friendly Support Vector Machine.”

The dataset was made available and can be downloaded for free from the UCI Machine Learning Repository:

The data was collected from 30 subjects aged between 19 and 48 years old performing one of six standard activities while wearing a waist-mounted smartphone that recorded the movement data. Video was recorded of each subject performing the activities and the movement data was labeled manually from these videos.

Below is an example video of a subject performing the activities while their movement data is being recorded.

The six activities performed were as follows:

  1. Walking
  2. Walking Upstairs
  3. Walking Downstairs
  4. Sitting
  5. Standing
  6. Laying

The movement data recorded was the x, y, and z accelerometer data (linear acceleration) and gyroscopic data (angular velocity) from the smart phone, specifically a Samsung Galaxy S II. Observations were recorded at 50 Hz (i.e. 50 data points per second). Each subject performed the sequence of activities twice; once with the device on their left-hand-side and once with the device on their right-hand side.

The raw data is not available. Instead, a pre-processed version of the dataset was made available. The pre-processing steps included:

  • Pre-processing accelerometer and gyroscope using noise filters.
  • Splitting data into fixed windows of 2.56 seconds (128 data points) with 50% overlap.Splitting of accelerometer data into gravitational (total) and body motion components.

Feature engineering was applied to the window data, and a copy of the data with these engineered features was made available.

A number of time and frequency features commonly used in the field of human activity recognition were extracted from each window. The result was a 561 element vector of features.

The dataset was split into train (70%) and test (30%) sets based on data for subjects, e.g. 21 subjects for train and nine for test.

Experiment results with a support vector machine intended for use on a smartphone (e.g. fixed-point arithmetic) resulted in a predictive accuracy of 89% on the test dataset, achieving similar results as an unmodified SVM implementation.

The dataset is freely available and can be downloaded from the UCI Machine Learning repository.

The data is provided as a single zip file that is about 58 megabytes in size. The direct link for this download is below:

Download the dataset and unzip all files into a new directory in your current working directory named “HARDataset”.

Need help with Deep Learning for Time Series?

Take my free 7-day email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Develop an LSTM Network Model

In this section, we will develop a Long Short-Term Memory network model (LSTM) for the human activity recognition dataset.

LSTM network models are a type of recurrent neural network that are able to learn and remember over long sequences of input data. They are intended for use with data that is comprised of long sequences of data, up to 200 to 400 time steps. They may be a good fit for this problem.

The model can support multiple parallel sequences of input data, such as each axis of the accelerometer and gyroscope data. The model learns to extract features from sequences of observations and how to map the internal features to different activity types.

The benefit of using LSTMs for sequence classification is that they can learn from the raw time series data directly, and in turn do not require domain expertise to manually engineer input features. The model can learn an internal representation of the time series data and ideally achieve comparable performance to models fit on a version of the dataset with engineered features.

This section is divided into four parts; they are:

  1. Load Data
  2. Fit and Evaluate Model
  3. Summarize Results
  4. Complete Example

Load Data

The first step is to load the raw dataset into memory.

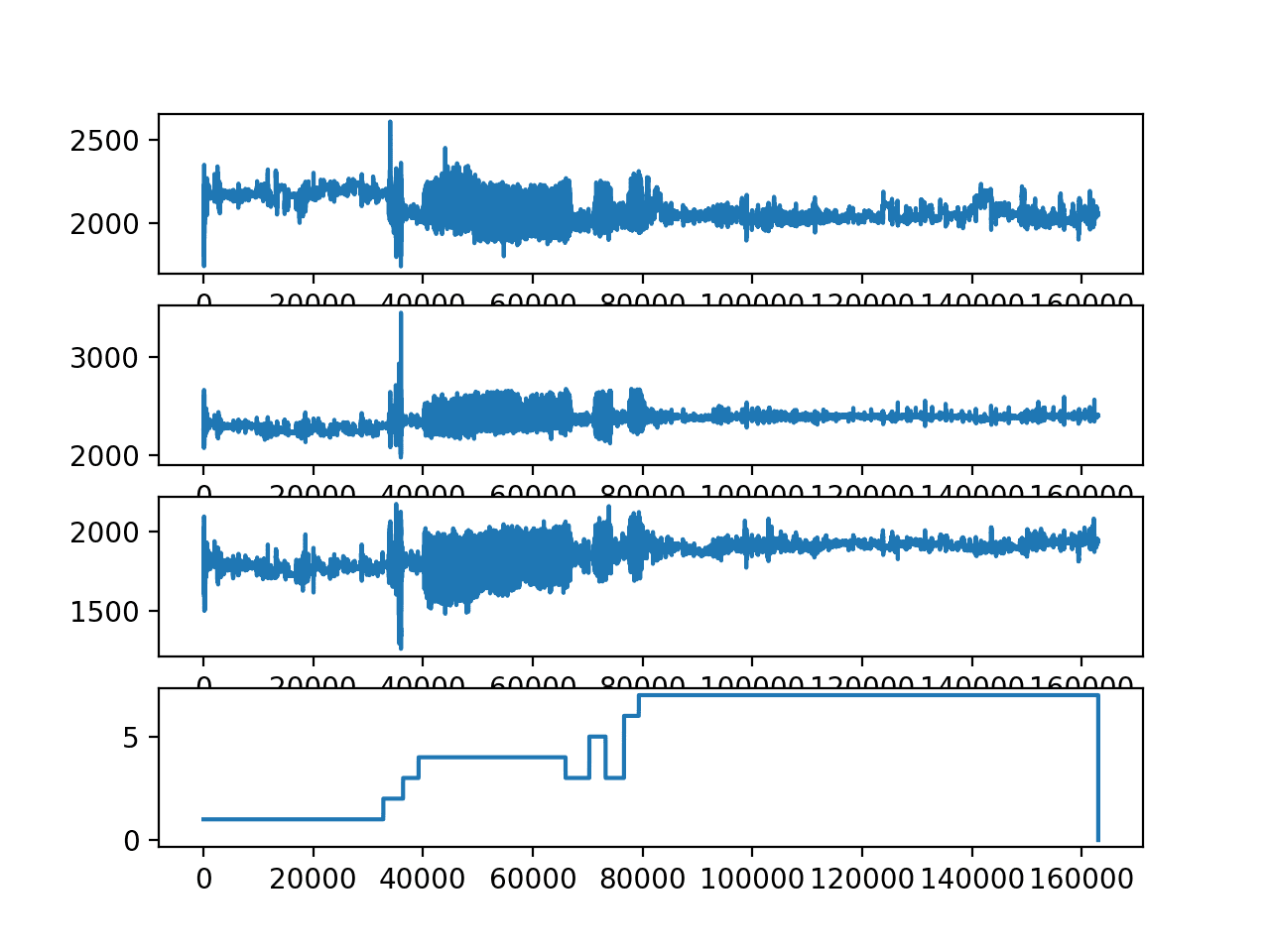
There are three main signal types in the raw data: total acceleration, body acceleration, and body gyroscope. Each has 3 axises of data. This means that there are a total of nine variables for each time step.

Further, each series of data has been partitioned into overlapping windows of 2.56 seconds of data, or 128 time steps. These windows of data correspond to the windows of engineered features (rows) in the previous section.

This means that one row of data has (128 * 9), or 1,152 elements. This is a little less than double the size of the 561 element vectors in the previous section and it is likely that there is some redundant data.

The signals are stored in the /Inertial Signals/ directory under the train and test subdirectories. Each axis of each signal is stored in a separate file, meaning that each of the train and test datasets have nine input files to load and one output file to load. We can batch the loading of these files into groups given the consistent directory structures and file naming conventions.

The input data is in CSV format where columns are separated by whitespace. Each of these files can be loaded as a NumPy array. The load_file() function below loads a dataset given the fill path to the file and returns the loaded data as a NumPy array.

We can then load all data for a given group (train or test) into a single three-dimensional NumPy array, where the dimensions of the array are [samples, time steps, features].

To make this clearer, there are 128 time steps and nine features, where the number of samples is the number of rows in any given raw signal data file.

The load_group() function below implements this behavior. The dstack() NumPy function allows us to stack each of the loaded 3D arrays into a single 3D array where the variables are separated on the third dimension (features).

We can use this function to load all input signal data for a given group, such as train or test.

The load_dataset_group() function below loads all input signal data and the output data for a single group using the consistent naming conventions between the directories.

Finally, we can load each of the train and test datasets.

The output data is defined as an integer for the class number. We must one hot encode these class integers so that the data is suitable for fitting a neural network multi-class classification model. We can do this by calling the to_categorical() Keras function.

The load_dataset() function below implements this behavior and returns the train and test X and y elements ready for fitting and evaluating the defined models.

Fit and Evaluate Model

Now that we have the data loaded into memory ready for modeling, we can define, fit, and evaluate an LSTM model.

We can define a function named evaluate_model() that takes the train and test dataset, fits a model on the training dataset, evaluates it on the test dataset, and returns an estimate of the model’s performance.

First, we must define the LSTM model using the Keras deep learning library. The model requires a three-dimensional input with [samples, time steps, features].

This is exactly how we have loaded the data, where one sample is one window of the time series data, each window has 128 time steps, and a time step has nine variables or features.

The output for the model will be a six-element vector containing the probability of a given window belonging to each of the six activity types.

Thees input and output dimensions are required when fitting the model, and we can extract them from the provided training dataset.

The model is defined as a Sequential Keras model, for simplicity.

We will define the model as having a single LSTM hidden layer. This is followed by a dropout layer intended to reduce overfitting of the model to the training data. Finally, a dense fully connected layer is used to interpret the features extracted by the LSTM hidden layer, before a final output layer is used to make predictions.

The efficient Adam version of stochastic gradient descent will be used to optimize the network, and the categorical cross entropy loss function will be used given that we are learning a multi-class classification problem.

The definition of the model is listed below.

The model is fit for a fixed number of epochs, in this case 15, and a batch size of 64 samples will be used, where 64 windows of data will be exposed to the model before the weights of the model are updated.

Once the model is fit, it is evaluated on the test dataset and the accuracy of the fit model on the test dataset is returned.

Note, it is common to not shuffle sequence data when fitting an LSTM. Here we do shuffle the windows of input data during training (the default). In this problem, we are interested in harnessing the LSTMs ability to learn and extract features across the time steps in a window, not across windows.

The complete evaluate_model() function is listed below.

There is nothing special about the network structure or chosen hyperparameters, they are just a starting point for this problem.

Summarize Results

We cannot judge the skill of the model from a single evaluation.

The reason for this is that neural networks are stochastic, meaning that a different specific model will result when training the same model configuration on the same data.

This is a feature of the network in that it gives the model its adaptive ability, but requires a slightly more complicated evaluation of the model.

We will repeat the evaluation of the model multiple times, then summarize the performance of the model across each of those runs. For example, we can call evaluate_model() a total of 10 times. This will result in a population of model evaluation scores that must be summarized.

We can summarize the sample of scores by calculating and reporting the mean and standard deviation of the performance. The mean gives the average accuracy of the model on the dataset, whereas the standard deviation gives the average variance of the accuracy from the mean.

The function summarize_results() below summarizes the results of a run.

We can bundle up the repeated evaluation, gathering of results, and summarization of results into a main function for the experiment, called run_experiment(), listed below.

By default, the model is evaluated 10 times before the performance of the model is reported.

Complete Example

Now that we have all of the pieces, we can tie them together into a worked example.

The complete code listing is provided below.

Running the example first prints the shape of the loaded dataset, then the shape of the train and test sets and the input and output elements. This confirms the number of samples, time steps, and variables, as well as the number of classes.

Next, models are created and evaluated and a debug message is printed for each.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

Finally, the sample of scores is printed, followed by the mean and standard deviation. We can see that the model performed well, achieving a classification accuracy of about 89.7% trained on the raw dataset, with a standard deviation of about 1.3.

This is a good result, considering that the original paper published a result of 89%, trained on the dataset with heavy domain-specific feature engineering, not the raw dataset.

Now that we have seen how to develop an LSTM model for time series classification, let’s look at how we can develop a more sophisticated CNN LSTM model.

Develop a CNN-LSTM Network Model

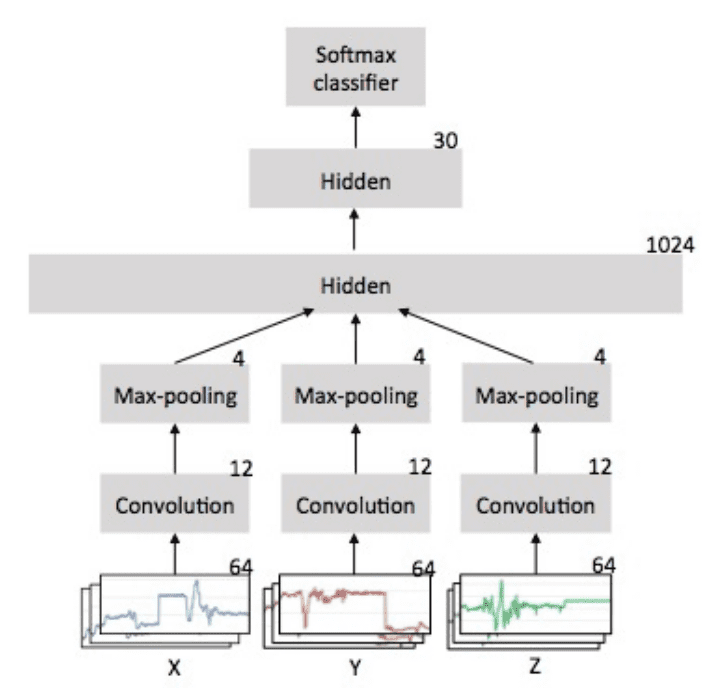
The CNN LSTM architecture involves using Convolutional Neural Network (CNN) layers for feature extraction on input data combined with LSTMs to support sequence prediction.

CNN LSTMs were developed for visual time series prediction problems and the application of generating textual descriptions from sequences of images (e.g. videos). Specifically, the problems of:

  • Activity Recognition: Generating a textual description of an activity demonstrated in a sequence of images.
  • Image Description: Generating a textual description of a single image.
  • Video Description: Generating a textual description of a sequence of images.

You can learn more about the CNN LSTM architecture in the post:

To learn more about the consequences of combining these models, see the paper:

The CNN LSTM model will read subsequences of the main sequence in as blocks, extract features from each block, then allow the LSTM to interpret the features extracted from each block.

One approach to implementing this model is to split each window of 128 time steps into subsequences for the CNN model to process. For example, the 128 time steps in each window can be split into four subsequences of 32 time steps.

We can then define a CNN model that expects to read in sequences with a length of 32 time steps and nine features.

The entire CNN model can be wrapped in a TimeDistributed layer to allow the same CNN model to read in each of the four subsequences in the window. The extracted features are then flattened and provided to the LSTM model to read, extracting its own features before a final mapping to an activity is made.

It is common to use two consecutive CNN layers followed by dropout and a max pooling layer, and that is the simple structure used in the CNN LSTM model here.

The updated evaluate_model() is listed below.

We can evaluate this model as we did the straight LSTM model in the previous section.

The complete code listing is provided below.

Running the example summarizes the model performance for each of the 10 runs before a final summary of the models performance on the test set is reported.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the model achieved a performance of about 90.6% with a standard deviation of about 1%.

Develop a ConvLSTM Network Model

A further extension of the CNN LSTM idea is to perform the convolutions of the CNN (e.g. how the CNN reads the input sequence data) as part of the LSTM.

This combination is called a Convolutional LSTM, or ConvLSTM for short, and like the CNN LSTM is also used for spatio-temporal data.

Unlike an LSTM that reads the data in directly in order to calculate internal state and state transitions, and unlike the CNN LSTM that is interpreting the output from CNN models, the ConvLSTM is using convolutions directly as part of reading input into the LSTM units themselves.

For more information for how the equations for the ConvLSTM are calculated within the LSTM unit, see the paper:

The Keras library provides the ConvLSTM2D class that supports the ConvLSTM model for 2D data. It can be configured for 1D multivariate time series classification.

The ConvLSTM2D class, by default, expects input data to have the shape:

Where each time step of data is defined as an image of (rows * columns) data points.

In the previous section, we divided a given window of data (128 time steps) into four subsequences of 32 time steps. We can use this same subsequence approach in defining the ConvLSTM2D input where the number of time steps is the number of subsequences in the window, the number of rows is 1 as we are working with one-dimensional data, and the number of columns represents the number of time steps in the subsequence, in this case 32.

For this chosen framing of the problem, the input for the ConvLSTM2D would therefore be:

  • Samples: n, for the number of windows in the dataset.
  • Time: 4, for the four subsequences that we split a window of 128 time steps into.
  • Rows: 1, for the one-dimensional shape of each subsequence.
  • Columns: 32, for the 32 time steps in an input subsequence.
  • Channels: 9, for the nine input variables.

We can now prepare the data for the ConvLSTM2D model.

The ConvLSTM2D class requires configuration both in terms of the CNN and the LSTM. This includes specifying the number of filters (e.g. 64), the two-dimensional kernel size, in this case (1 row and 3 columns of the subsequence time steps), and the activation function, in this case rectified linear (ReLU).

As with a CNN or LSTM model, the output must be flattened into one long vector before it can be interpreted by a dense layer.

We can then evaluate the model as we did the LSTM and CNN LSTM models before it.

The complete example is listed below.

As with the prior experiments, running the model prints the performance of the model each time it is fit and evaluated. A summary of the final model performance is presented at the end of the run.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the model does consistently perform well on the problem achieving an accuracy of about 90%, perhaps with fewer resources than the larger CNN LSTM model.

Extensions

This section lists some ideas for extending the tutorial that you may wish to explore.

  • Data Preparation. Consider exploring whether simple data scaling schemes can further lift model performance, such as normalization, standardization, and power transforms.
  • LSTM Variations. There are variations of the LSTM architecture that may achieve better performance on this problem, such as stacked LSTMs and Bidirectional LSTMs.
  • Hyperparameter Tuning. Consider exploring tuning of model hyperparameters such as the number of units, training epochs, batch size, and more.

If you explore any of these extensions, I’d love to know.

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Papers

Articles

Summary

In this tutorial, you discovered three recurrent neural network architectures for modeling an activity recognition time series classification problem.

Specifically, you learned:

  • How to develop a Long Short-Term Memory Recurrent Neural Network for human activity recognition.
  • How to develop a one-dimensional Convolutional Neural Network LSTM, or CNN LSTM, model.
  • How to develop a one-dimensional Convolutional LSTM, or ConvLSTM, model for the same problem.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

Develop Deep Learning models for Time Series Today!

Deep Learning for Time Series Forecasting

Develop Your Own Forecasting models in Minutes

...with just a few lines of python code

Discover how in my new Ebook:
Deep Learning for Time Series Forecasting

It provides self-study tutorials on topics like:
CNNs, LSTMs, Multivariate Forecasting, Multi-Step Forecasting and much more...

Finally Bring Deep Learning to your Time Series Forecasting Projects

Skip the Academics. Just Results.

See What's Inside

More On This Topic

419 Responses to LSTMs for Human Activity Recognition Time Series Classification

  1. Avatar
    Tin September 28, 2018 at 9:20 am #

    Hi Jason,

    So enjoy reading with your stuff, very helpful. As we can use CNN+LSTM to predict the spatial-temporal data, can we reverse the architecture as LSTM+CNN to do the same job? Any examples for LSTM + CNN?

    Reply
  2. Avatar
    Akilesh October 29, 2018 at 12:40 pm #

    Hi Jason,
    Can you please explain the choice of parameters for the LSTM network?
    Especially the LSTM layer and the dense layer?
    What does the value 100 signify?

    Reply
    • Avatar
      Jason Brownlee October 29, 2018 at 2:14 pm #

      The model was configured via trial and error.

      There is no analytical way to calculate how to configure a neural network model, more details here:
      https://machinelearningmastery.mystagingwebsite.com/faq/single-faq/how-many-layers-and-nodes-do-i-need-in-my-neural-network

      Reply
      • Avatar
        Kiran April 3, 2019 at 12:33 am #

        Hi Jason, I’m just trying to understand correct me if I am wrong, does this value 100 in LSTM layer equal to 100 LSTM units in input layer? and each LSTM layer is fed with a sequence of length 128 (Time steps), right?

        Reply
        • Avatar
          Jason Brownlee April 3, 2019 at 6:44 am #

          Yes, 100 is refers to the number of parallel units or nodes. It is unrelated to the number of timesteps.

          Each node gets the full input sequence, not each layer.

          Reply
          • Avatar
            Kiran April 3, 2019 at 6:57 pm #

            Thank you for clarifying and I have one more question regarding dense layer. what is the input that dense layer is receiving from LSTM layer?( is it the time series itself or the last time step) and what happens if # of nodes in dense layer is not equal to # of nodes in LSTM(I mean is it possible to have more nodes in dense layer )?

          • Avatar
            Jason Brownlee April 4, 2019 at 7:46 am #

            The LSTM creates an internal representation / extracted features from the entire input sequence.

          • Avatar
            Jaroslaw Goslinski August 2, 2019 at 2:32 am #

            The term: „LSTM units” is very misleading. When it comes to the number of units we actually speak about the size of an internal state vector (either hidden, input or forget), so in the end it is just a mathematical thing. In my opinion it should not be called parallel because everything is done in one place at the same time (simple matrix-vector multiplication, where both are dimensionally-extended due to the number of “LSTM units”). BTW: Very good tutorial

          • Avatar
            Jason Brownlee August 2, 2019 at 6:53 am #

            Thanks!

            Perhaps “nodes” would be more appropriate?

          • Avatar
            Jaroslaw Goslinski August 2, 2019 at 10:04 pm #

            Definitely!

          • Avatar
            Jason Brownlee August 3, 2019 at 8:04 am #

            Note that I took the “unit” nomenclature from the original LSTM paper, and use it all the time across this site and my books:
            https://www.bioinf.jku.at/publications/older/2604.pdf

      • Avatar
        Najoua February 21, 2020 at 7:13 am #

        Hi Jason. Could you please explain me the purpose of the first dense layer in the LSTM approach. Is it because of the dropout layer in front of it? Thanks.

        Reply
        • Avatar
          Jason Brownlee February 21, 2020 at 8:31 am #

          Perhaps to interpet the output of the LSTM layers.

          Reply
  3. Avatar
    Amir October 31, 2018 at 8:13 pm #

    Thanks for such a comprehensive tutorial
    I try it and it worked as expressed in the tutorial.

    Now, I’m going to try it with my data that comes from a single axis accelerometer. It means I have only one feature so I don’t need a 3D array but a 2D.
    You mentioned “The model (RNN LSTM) requires a three-dimensional input with [samples, time steps, features]. This is exactly how we have loaded the data.”
    Then, it means that it won’t work with a 2D array? or I can consider a 3D array but the 3rd dimension has only one member?

    and my second question is:
    I need the model for a real-time classification, so I need to train once and then save the model and use it in my web application.
    how can I save the model after training and use it?

    Reply
    • Avatar
      Jason Brownlee November 1, 2018 at 6:05 am #

      Yes, even if the 3rd dimension has 1 parameter, it is still a 3D array.

      You can call model.save() to save the model.

      Reply
  4. Avatar
    Daniel Aguilera Garcia November 21, 2018 at 10:24 am #

    Hello Jason.

    In my case I have 2 time series from EGG and I have to diseign a model that classify in two types de signal. I dont understand exactly how should i reshape the data.

    The freq is 256 values per second so i could divide in windows like you did before. The problem is that i dont know how to put the 3rd dimension of caracteristics. From each window I have 7 caracteristics not from each moment (max, min, std, fft bandwidths, fft centroids, Arima 1, Arima 2)

    Please, how could I do what you mean [samples, time steps, features] in my case??

    Reply
    • Avatar
      Jason Brownlee November 21, 2018 at 2:10 pm #

      Perhaps those 7 characteristics are 7 features.

      If you have 256 samples per section, you can choose how many samples/seconds to use as time steps and perhaps change the resolution via averaging or removing samples.

      Reply
      • Avatar
        Daniel Aguilera Garcia November 21, 2018 at 9:16 pm #

        Let’s see im going to make an easy example:

        channel1 (values in one second)=2,5,6,8,54,2,8,4,7,8,…,5,7,8 (in total 256 values per second)

        channel2 (values in one second)=2,5,6,8,54,2,8,4,7,8,…,5,7,8 (in total 256 values per second)

        7 diferent features

        [samples,timesteps,features]=[2, 256, 7]?

        and another questions, for example the mean feature:

        chanel 1:

        feat_mean[0]=2
        feat_mean[1]=(2+5)/2=3.5
        feat_mean[2]=(2+5+6)/3=4.33
        etc…

        is it correct? what I understood is that I have to substract features for each each moment?

        Reply
  5. Avatar
    coolyj November 22, 2018 at 5:21 pm #

    where does the “561 element vector of features” apply to?

    Reply
    • Avatar
      Jason Brownlee November 23, 2018 at 7:44 am #

      That vector was the pre-processed data, prepared by the authors of the study that we do not use in this tutorial.

      Reply
  6. Avatar
    Daniel Aguilera Garcia November 26, 2018 at 8:29 pm #

    hello jason!

    should we normalize each feature??

    Reply
    • Avatar
      Jason Brownlee November 27, 2018 at 6:33 am #

      Perhaps try it and evaluate how it impacts model performance.

      Reply
      • Avatar
        Asif Nawaz May 21, 2019 at 3:09 am #

        Does Batch Normalization layer serves the same purpose?

        Reply
        • Avatar
          Jason Brownlee May 21, 2019 at 6:39 am #

          Not really, it is used to normalize a batch of activations between layers.

          Reply
  7. Avatar
    Leon December 3, 2018 at 7:05 am #

    Hi Jason, thanks for the great article.
    I notice in your load data section, you probably mean 2.56 seconds instead of 2.65, since 128(time step) * 1/50(record sampling rate) = 2.56.

    Reply
  8. Avatar
    Daniel Aguilera Garcia December 12, 2018 at 11:06 pm #

    Hello Jason,

    Why in Conv LSTM kernel_size=(1,3)? I don’t understand

    Reply
    • Avatar
      Jason Brownlee December 13, 2018 at 7:53 am #

      For 1 row and 3 columns.

      Reply
      • Avatar
        Daniel Aguilera Garcia December 14, 2018 at 6:53 am #

        what what represents this in this example?

        Reply
        • Avatar
          Jason Brownlee December 14, 2018 at 2:34 pm #

          We split each sequence into sub-sequences. Perhaps re-read the section titled “Develop a ConvLSTM Network Model” and note the configuration that chooses these parameters.

          Reply
      • Avatar
        Asif Nawaz May 9, 2019 at 3:47 am #

        Why we used 1 row? and why we used convLSTM2D? Can’t we model this problem like Conv1D?

        Reply
        • Avatar
          Jason Brownlee May 9, 2019 at 6:47 am #

          A convlstm2d is not required, the tutorial demonstrates how to create different types of models for time series classification.

          Reply
  9. Avatar
    beomyoung January 3, 2019 at 5:37 pm #

    In dataset file, there aren’t label file (about y) Can i earn that files??

    Reply
    • Avatar
      Jason Brownlee January 4, 2019 at 6:27 am #

      They are in a separate file with “y” in the filename.

      Reply
  10. Avatar
    beomyoung January 7, 2019 at 5:02 pm #

    i found it thank you!!

    Reply
    • Avatar
      Jason Brownlee January 8, 2019 at 6:45 am #

      Glad to hear that.

      Reply
      • Avatar
        beomyoung January 8, 2019 at 1:31 pm #

        thank you for answering me. I have one more question! you have 30 subjects in this experiment. so when you handle data, for example, in ‘body_acc_x_train’ all of the 30 subjects data is just merged?

        Reply
        • Avatar
          Jason Brownlee January 9, 2019 at 8:37 am #

          Yes.

          Also note, I did not run the experiment, I just analyzed the freely available data.

          Reply
          • Avatar
            beomyoung January 9, 2019 at 1:05 pm #

            Oh thanks. Nowadays, i’m doing task about rare activity detection using sensor data, RNN&CRNN.
            For example, i wanna detect scratch activity and non-scratch activity. But in my experiment, ratio of scratch and non-scratch window is not balanced (scratch is so rare..) then how to put my input ? Can you give me some advices?

          • Avatar
            Jason Brownlee January 10, 2019 at 7:43 am #

            Perhaps you can oversample the rare events? E.g. train more on the rare cases?

  11. Avatar
    Jemshit January 17, 2019 at 7:41 pm #

    Hi Jason, i have question regarding to feeding feature data to LSTM. I have not used CNN, but if i use regular Auto encoder (sandwich like structure) instead of CNN for feature extraction, and if i define the time step of LSTM to be lets say 128,
    1) should i extract feature from each time step and concatenate them to form a window before feeding to LSTM or
    2) should i extract feature from window itself and feed the vector to LSTM

    Thanks

    Reply
    • Avatar
      Jason Brownlee January 18, 2019 at 5:33 am #

      The CNN must extract features from a sequence of obs (multiple time steps), not from a single observation (time step).

      Reply
      • Avatar
        Jemshit January 18, 2019 at 6:18 am #

        But LSTM will interpret features of each time step, not of a whole window right?

        Reply
  12. Avatar
    Kiran Krishna February 11, 2019 at 11:28 pm #

    Hi Jason,

    Thank you for the great material. My question is on data preprocessing. I have a squence of pressure data every 5 seconds with timestamp. How can I convert the 2D dataframe(Sample, feature) into 3D (Sample, Timestep, feature).

    Reply
  13. Avatar
    P.Y Lee February 12, 2019 at 1:57 pm #

    Hi Jason,

    In CNN LSTM model part, why we need to split the 128 time steps into 4 subsequences of 32 time steps?
    Can’t we do this model with 128 time step directly?

    Thank you

    Reply
    • Avatar
      Jason Brownlee February 12, 2019 at 2:00 pm #

      No, as this specific model expects sequences of sequences as input.

      Reply
  14. Avatar
    imGaboy February 19, 2019 at 11:48 pm #

    Hi there,

    I have a question about your first model.

    You set the batch_size for 64.
    When I run your model (with verbose = 1), I got this :
    Epoch 1/15
    7352/7352 [==============================] – 12s 2ms/step – loss: 1.2669 – acc: 0.4528

    It is mean 7352 * 64 ?

    I ask this, because I want to overwrite your example which woulduse fit_generator, and I didn’t get the same results.

    Here is my code:

    ………………

    Reply
    • Avatar
      Jason Brownlee February 20, 2019 at 8:08 am #

      I don’t recall sorry, perhaps check the data file to confirm the number of instances?

      Reply
  15. Avatar
    cora March 22, 2019 at 5:30 am #

    any one cannot load the data? help, I think I follow the guide, unzip and rename in the working directory

    Reply
  16. Avatar
    Adim April 11, 2019 at 11:35 pm #

    Hi Jason,

    thank you for this tutorial. I am little be confused about the load the data set. Why we read_csv since no CVS files in the dataset. Sorry for this question because I am new to this subject. Also, I applied the code for (load_group), (load_dataset_group) and (load_dataset) ? Can you tell me if there is something need to add ?

    Reply
    • Avatar
      Jason Brownlee April 12, 2019 at 7:47 am #

      In this tutorial we are loading datasets from CSV files, multiple files.

      Reply
  17. Avatar
    Manisha April 12, 2019 at 4:40 pm #

    Sir, LSTM(100) means 100 LSTM cells with each cell having forget,input and output gate and each LSTM cell sends the output to other LSTM cells also and dinally every cell will give a 100 D vector as output..m i right?

    Reply
    • Avatar
      Jason Brownlee April 13, 2019 at 6:23 am #

      100 cells or units means that each unit gets the output and creates an activation for the next layer.

      The units in one layer do not communicate with each other.

      Reply
      • Avatar
        Manisha April 13, 2019 at 6:48 am #

        Sorry Sir I didn’t get this.

        1: Does these LSTM 100 cells communicate with each other?

        2:If say we have 7352 samples with 128 timesteps and 9 features and my batch size is 64 then can i say that at time= 1 we will input first timestep of 64 samples to all the 100 LSTM cells then at time=2 we will input second time step of 64 samples and so on till we input 128th time step of 64 samples at time= 128 and then do BPTT and each lstm preserves its state from time =1 to time=128 ?

        Reply
        • Avatar
          Jason Brownlee April 13, 2019 at 6:53 am #

          No, cells in one layer do not communicate with each other.

          No, each sample is processed one at a time, at time step 1, all 100 cells would get the first time step of data with all 9 features.

          BPTT refers to the end of the batch when model weights are updated. One way to think about it is to unroll each cell back through time into a deep network, more here:
          https://machinelearningmastery.mystagingwebsite.com/rnn-unrolling/

          Reply
          • Avatar
            Manisha April 13, 2019 at 7:17 am #

            “No, each sample is processed one at a time, at time step 1, all 100 cells would get the first time step of data with all 9 features”

            sir batch size means how many samples to show to network before weight updates.

            If i have 64 as batch size….then is it that at time step 1, all 100 cells would get the first time step of each 64 data points with all 9 features?then at next time step =2, all 10 cells would get the second time step of each 64 data points with all 9 features and so on.

            or is it like at time step 1, all cells get the first time step of one data point with all 9 features then at time step =2 all cells get the second time step of that data point and when all the 128 time steps of that point is fed to the network we compute the loss and do this same for remaining 63 points and then updates weights?

            I am getting confused how batch size is working here..what i am visualizing wrong here ?

          • Avatar
            Jason Brownlee April 13, 2019 at 1:42 pm #

            If the batch size is 64, then 64 samples are shown to the network before weights are updated and state is reset.

            In a batch, samples are processed one at a time, e.g. all time steps of sample 1, then all time steps of samples 2, etc.

            I strongly recommend reading this:
            https://machinelearningmastery.mystagingwebsite.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input

  18. Avatar
    Manisha April 12, 2019 at 6:31 pm #

    Also here we are using dropout after lstm 100 means only 50 values will be passed to a dense 100 layer right sir?

    Reply
  19. Avatar
    Avani Pitre April 13, 2019 at 12:19 am #

    hello
    I am beginner in area.. thanks for wonderful tutorial..
    I wanted to workout your LSTM and CNN RNN example, I have downloaded HARDataset but
    I have simple question here how to give input CSV file at the beginning ?
    Do I have to generate that file? if so how to do that?

    # load a single file as a numpy array
    def load_file(filepath):
    dataframe = read_csv(filepath, header=None, delim_whitespace=True)
    return dataframe.values

    Please help me
    thanks in advance

    Reply
    • Avatar
      Jason Brownlee April 13, 2019 at 6:33 am #

      You can follow the tutorial to learn how to load the CSV file.

      Reply
    • Avatar
      MELIKA December 17, 2020 at 5:32 am #

      Did you get your answer?

      Reply
  20. Avatar
    Manisha April 13, 2019 at 8:12 am #

    Sir i printed the model summary for CNN_LSTM output dimensions for timedistributed came as 4dimensions like (None,None,30,64)…it is 4D because we have partioned the windows into 4 subwindows of 32 size?

    what is None,None representing here….30,64 I got that it is the output after 1st convolution

    Reply
    • Avatar
      Jason Brownlee April 13, 2019 at 1:43 pm #

      The “None” sized dimension means that the provided dataset will define the other dimensions.

      Reply
  21. Avatar
    Manisha April 13, 2019 at 9:02 am #

    Sir https://machinelearningmastery.mystagingwebsite.com/cnn-long-short-term-memory-networks/ u have mentioned that…

    “In both of these cases, conceptually there is a single CNN model and a sequence of LSTM models, one for each time step. We want to apply the CNN model to each input image and pass on the output of each input image to the LSTM as a single time step.”

    So here we are dividing the 128 time steps into 4 subblocks..we will give each block to the CNN at once and our CNN model will give the output features.

    means we have converted 128 time sequences to 4 time sequences here whih we will feed to our LSTM model now.

    so earlier we were feeding 128 time steps to the LSTM(in simple LSTM) and now we will feed 4…am i right?

    Reply
    • Avatar
      Jason Brownlee April 13, 2019 at 1:47 pm #

      Yes, but the “4 time steps” are distilled from many more real time steps via the CNN model.

      Reply
      • Avatar
        Manisha April 13, 2019 at 5:50 pm #

        and sir CNN will process each of the 32 windows parallelly or will it first process first 32 sized window and feed it to lstm then another 32 and so on

        Reply
        • Avatar
          Jason Brownlee April 14, 2019 at 5:45 am #

          Each window of data is processed by the n filters in the CNN layer in parallel – if that is what you mean.

          Reply
          • Avatar
            Manisha April 14, 2019 at 8:35 am #

            yes sir go it ..thanks a lot

  22. Avatar
    Manisha April 14, 2019 at 9:07 am #

    Sir means all four 32 sized windows from one 128 time step window are processed by th CNN parallelly then at time step 1 what we will input into our lstm?

    like in normal lstm with 128 timesteps we input 1st time step with 9 features then 2nd timestep and so on..

    here since we have processed 4 time steps parallely what we will input to lstm?

    Reply
    • Avatar
      Jason Brownlee April 15, 2019 at 7:49 am #

      The LSTM takes the CNN activations (feature maps) as input. You can see the output shapes of each layer via the model.summary() output.

      Reply
      • Avatar
        Manisha April 15, 2019 at 12:20 pm #

        Sir I did that but getting a little confused….this is te summary

        None,None,30,64….1st convoution
        None,None,28,64….2nd convolution
        None,None,28,64…dropout
        None,None,896…maxpool
        None,100…lstm 100
        None,100…dropout
        None,100…dense 100
        None,6…softmax

        Sir,My doubt is we input 32 sized window from 128 sized original window to lstm…so does lstm here predicting the activity for each 32 sized window treating it as one time sequence?

        Reply
      • Avatar
        Alex Szameitat March 16, 2020 at 10:24 am #

        Dear Mr. Brownlee,

        I was also trying to get behind the idea of how the data flows in the CNN-LSTM model, sadly I didn’t fully understand it yet. I was reading through the comment section and found a few helpful questions and answers! Still though, I’m stuck at this very exact point between the Flatten layer and the LSTM layer. How exactly are the flattened (invariant) features from the max pooling layer getting fed into the LSTM layer?

        I tried to dig a little deeper and made some extra research on the internet. There I found these three posts

        https://stackoverflow.com/questions/43237124/what-is-the-role-of-flatten-in-keras

        https://medium.com/smileinnovation/how-to-work-with-time-distributed-data-in-a-neural-network-b8b39aa4ce00

        https://datascience.stackexchange.com/questions/24909/the-model-of-lstm-with-more-than-one-unit

        These three posts helped me to visualize the data flow in the network. Have I understood everything correctly?… So Keras will distribute the input in layers step by step to the LSTM cells. This means that it’ll first present the invariant flattened layers of the first subsequence to the LSTMs, then the features from the second subsequence…

        To clearly show what I mean I made this visualization that also includes a short numerical example of the forwardpass from a smaller subsequence:

        https://filebin.net/0kywmitsq5u0qgy5

        In the numerical example I take the 2 first subsequences and show how they change from input, then through first and second convolution (here I just picked some random numbers), next the max-pooling operation and the flatten operation (note that here I was trying to correctly max-pool the random numbers from the previous convolution layers. Also I was flattening the max-pooled features, how they should be flattened according to the second post-link).
        Is this understandable and correct what I visualized here?

        And another questions that came up. If I feed the flattened features to the 100 LSTM cells (that are all in one layer, meaning that they are not stacked or not connected with each other or something like that). What is the exact benefit of using more then just one LSTM cell in one layer?

        Reply
  23. Avatar
    Sàçha April 30, 2019 at 9:40 pm #

    Do you have an idea about the multi-class classification with the algorithm ECOC algorithm.

    Can we use it for unsupervised classification (clustering)

    Reply
  24. Avatar
    Asif Nawaz May 16, 2019 at 11:15 pm #

    Does it makes sense to use dropout and maxpooling after convlstm layer, like we did in cnn?

    Reply
    • Avatar
      Jason Brownlee May 17, 2019 at 5:54 am #

      Hmmm, maybe.

      Always test, and use a configuration that gives best performance.

      Reply
  25. Avatar
    Alicia May 21, 2019 at 11:56 pm #

    Hi Jason,

    thank you for this tutorial.
    Why is it necessary to perform signal windowing before training the neural network?
    Can we consider the full signal instead?

    Reply
    • Avatar
      Jason Brownlee May 22, 2019 at 8:09 am #

      We must transform the series into a supervised learning problem:
      https://machinelearningmastery.mystagingwebsite.com/time-series-forecasting-supervised-learning/

      Reply
      • Avatar
        Alicia May 22, 2019 at 7:12 pm #

        Let’s assume that the original signal is an acceleration representing a person walking and that the aim is to establish wheter the person fell on the floor.
        Let’s say the original signal is composed by 1000 samples belonging to class1. The signal is processed and divided into fixed windows of N data points: now I have sub-signals each one labelled with class1. Is that correct to consider different windows even if the peak of the falling is present only in one of the them?

        Reply
        • Avatar
          Jason Brownlee May 23, 2019 at 5:58 am #

          Perhaps. There are many ways to frame a given prediction problem, perhaps experiment with a few approaches and see what works best for your specific dataset?

          Reply
  26. Avatar
    Khan May 26, 2019 at 3:09 am #

    Is their any role of LSTM units in convlstm. parameters of convlstm layer are similar to CNN, but nothing related to LSTM can be seen. In LSTM model, 100 LSTM units are used. How can we see convlstm in this context?

    Reply
    • Avatar
      Jason Brownlee May 26, 2019 at 6:48 am #

      Not sure I follow what you’re asking, can you elaborate?

      Reply
      • Avatar
        Khan May 26, 2019 at 6:22 pm #

        Following are input layers used in three different models.

        model.add(LSTM(100, input_shape=(n_timesteps,n_features)))
        model.add(TimeDistributed(Conv1D(filters=64, kernel_size=3, activation=’relu’), input_shape=(None,n_length,n_features)))
        model.add(ConvLSTM2D(filters=64, kernel_size=(1,3), activation=’relu’, input_shape=(n_steps, 1, n_length, n_features)))

        ConvLSTM2D layer I believe should be a mixture of CNN and LSTM. All parameters in convlstm layers are parameters of cnn like no of filters, filter size, activation function etc. LSTM as standalone uses 100 LSTM cells. My question was how many LSTM cells will be used by convlstm model? I believe convlstm operates with only one lstm cell?

        Reply
        • Avatar
          Jason Brownlee May 27, 2019 at 6:48 am #

          I believe each filter is a cell – the idea behind these two concepts is merged.

          Reply
  27. Avatar
    Riddy June 4, 2019 at 1:27 am #

    I am generating sine and cosine curves for classification. However, I am not sure whether I need to pre-process data or just load it to the model. My understanding is further confounded by the following state in your post “Further, each series of data has been partitioned into overlapping windows of 2.56 seconds of data, or 128 time step”

    Reply
  28. Avatar
    Amy June 7, 2019 at 11:12 am #

    Jason thanks a lot for his wonderful tutorial.

    I want to use your approach for my problem. But my data set is a little different than what you used here.
    I have 75 time series. Each of them shows two classes. From time 0 until time t ( which is different for each time series) is data for class 1 and from time t until the end of time series is class 2. Then, I want for test time series predict the time at which the class has changed from 1 to 2, or at each time the class is 1 or 2. can you help me how I can use your approach for my problem?

    Reply
  29. Avatar
    Amy June 8, 2019 at 10:32 pm #

    I mean each time series shows two classes, healthy and unhealthy, for one system. From time 0 until time t, it shows healthy state and from time t until the failure of the system, it shows unhealthy state. We have 75 time series like that with different lengths for both classess. Now We want to determine for a test system, the time that it switches from healthy to unhealthy state.

    Thanks

    Reply
    • Avatar
      Jason Brownlee June 9, 2019 at 6:21 am #

      Perhaps you can predict the class value for each input time step, if you have the data?

      Reply
      • Avatar
        Amy June 9, 2019 at 10:42 am #

        May you please explain more? Do you think I can use your approach ?

        Reply
        • Avatar
          Jason Brownlee June 10, 2019 at 7:35 am #

          I was suggesting perhaps try modeling the problem as a one-to-one mapping so each input time step has a classification.

          More on sequence prediction here:
          https://machinelearningmastery.mystagingwebsite.com/models-sequence-prediction-recurrent-neural-networks/

          Reply
          • Avatar
            Christian Post September 7, 2019 at 12:19 am #

            I applied your tutorial to data similar to Amy’s (I guessed) where I tried to predict disease events, and for training and validation I used the n days before a disease event, and as comparison n days from an individual without disease events, and each window classified as either 1 (sick) or 0 (healthy).
            The model was performing okay with an AUC of >0.85, but I’m not sure how I would apply this in practice because the time windows for the validation data were designed with a priori knowledge.
            In practice one would have to construct a new input vector every time step, and I don’t think the classification of those vectors would be as good. But I did not try that out yet.

            What I didn’t understand is how would I apply the on-to-one mapping from your article here? You state that the one-to-one approach isn’t appropriate for RNNs since it doesn’t capture the dependencies between time points.

            @Amy you could investigate on heart rate classification with neural networks, I think that is a somewhat similar problem.

          • Avatar
            Jason Brownlee September 7, 2019 at 5:35 am #

            Not sure I follow the question completely.

            Generally, you must frame the problem around the way the model is intended to be used, then evaluate under those constraints. If you build/evaluate a model based on a framing that you cannot use in practice, then the evaluation is next to useless.

            Using training info or domain knowledge in the framing is fine, as long as you expect it to generalize. Again, this too can be challenged with experiments.

            If I’ve missed the point, perhaps you can elaborate here, or email me?
            https://machinelearningmastery.mystagingwebsite.com/contact/

      • Avatar
        Amy June 9, 2019 at 10:43 am #

        May you please explain more?

        Reply
  30. Avatar
    vinodh June 21, 2019 at 2:55 pm #

    Hello sir,
    Great tutorial, how to normalize or standardize this data.

    Reply
  31. Avatar
    Simon June 22, 2019 at 9:05 pm #

    Dear Mr. Brownlee,

    I am a student from Germany and first of all: thank you for your great Blog! It is so much better than all the lectures I have been visited so far!

    I had a question regarding the 3D array and I hope you could help me. Let’s assume we have the following case, which is similar to the one from your example:

    We measure the velocity in 3 dimensions (x,y,z direction) with a frequency of 50 Hz over one minute. We measure the velocity of 5 people in total.

    – Would the 3D array have the following form: (5*60*50; 1 ; 3)?

    – What do you mean by time steps? I am referring to “[samples, time steps, features]”.

    – Is the form of the 3D array related to the batch size of our LSTM model?

    Thank you in advance. I would really appreciate your help as I am currently stuck…

    Best regards,
    Simon

    Reply
  32. Avatar
    jai July 3, 2019 at 6:18 pm #

    what is the use of those 561 features?

    Reply
  33. Avatar
    jai July 3, 2019 at 6:29 pm #

    if in those 128*9 data, 64*9 represent standing and other 64*9 represent walking then how do i label that 128*9 data?

    Reply
    • Avatar
      Jason Brownlee July 4, 2019 at 7:43 am #

      You can model the problem as a sequence classification problem, and try different length sequence inputs to see what works best for your specific dataset.

      Reply
  34. Avatar
    jonniej393 August 9, 2019 at 7:21 pm #

    Amazing!

    But how do I train the network with additional new data? I’m working on a project to detect suspicious activity from surveillance videos.

    I have no idea on how to prepare such dataset. Appreciate your help!

    Reply
    • Avatar
      Jason Brownlee August 10, 2019 at 7:14 am #

      You can save the model, load it later and update/train it on the new data or a mix of old and new. Or throw away the model and fit it anew.

      Perhaps test diffrent approaches and compare the results.

      Reply
  35. Avatar
    nisha August 28, 2019 at 9:46 pm #

    Hi Jason,

    Do you have the link for trained model? I would like to quickly check that how well it works on my data.

    Also, what is size of your model? I am looking for the models which are less in size so as to be able to deploy on edge?

    Reply
    • Avatar
      Jason Brownlee August 29, 2019 at 6:07 am #

      Sorry, I don’t share trained models.

      Perhaps try fitting the model yourself, it only takes a few minutes.

      Reply
  36. Avatar
    Tommy September 2, 2019 at 1:45 pm #

    what is the purpose of ‘prefix’ when loading the file?

    Reply
    • Avatar
      Jason Brownlee September 2, 2019 at 1:52 pm #

      In case you have the data located elsewhere and need to specify that location.

      Reply
  37. Avatar
    Shivamani Patil September 3, 2019 at 9:32 pm #

    Hi Jason,

    If I export this model to an android app should I do any preprocessing on input data from mobile sensors?

    Reply
  38. Avatar
    Tommy September 14, 2019 at 5:11 pm #

    Hi Jason,
    the first LSTM example, you mentioned that the multiple times of evaluation due to stochastic reason. BUT, how did you get the best performance parameter weights?

    Reply
  39. Avatar
    Pranav Gundewar September 18, 2019 at 7:59 am #

    Hi Jason, thanks for the great article. I am currently working on human activity recognition (Kinetics-600) and I wanted to connect LSTM with 3D ResNet head for action prediction. Can you please tell how can I use LSTM on 1024 vectors obtained from the last layer and feed it to RNN-LSTM for action prediction?

    Thank you.

    Reply
  40. Avatar
    Tanveer October 7, 2019 at 10:08 pm #

    model = Sequential()
    model.add(LSTM(100, input_shape=(n_timesteps,n_features)))
    model.add(Dropout(0.5))
    model.add(Dense(100, activation=’relu’))
    model.add(Dense(n_outputs, activation=’softmax’))
    model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])
    In this code i am getting an this traceback

    Traceback (most recent call last):
    File “C:\Users\Tanveer\AppData\Local\Programs\Python\Python37-32\HARUP.py”, line 54, in
    model = Sequential()
    NameError: name ‘Sequential’ is not defined
    How can resolve this issue kindly guide me

    Reply
    • Avatar
      Jason Brownlee October 8, 2019 at 8:02 am #

      You may have skipped some lines from the full example.

      Reply
      • Avatar
        Tanveer December 19, 2019 at 8:06 pm #

        Dear Sir i didn’t skipped any code which is given above but this problem still occuring kindly give me some guideline or hint to solve this issue

        Reply
        • Avatar
          Jason Brownlee December 20, 2019 at 6:43 am #

          I recommend copying the complete code example, rather than the partial code examples.

          Reply
  41. Avatar
    AGGELOS PAPOUTSIS October 18, 2019 at 11:44 pm #

    hi Jason. I am running the code from here https://medium.com/@curiousily/human-activity-recognition-using-lstms-on-android-tensorflow-for-hackers-part-vi-492da5adef64 on anaconda and notebook and pycharm with TensorFlow at 1.4 version (i had to downgrade due to the fact that the author is using placeholders which are incompatible with TensorFlow 2) and python at 3.6. The problem here is that I always get train loss: nan

    can you please suggest some ideas here because I cannot find anything when I search for the problem (there are some articles but are not helpful)

    Reply
    • Avatar
      Jason Brownlee October 19, 2019 at 6:40 am #

      Sorry, i am not familiar with that tutorial, perhaps contact the authors?

      Reply
  42. Avatar
    Dhiren November 12, 2019 at 6:50 pm #

    Hello Jason,
    Amazing tutorial. I am doing something very similar to this. My problem is: “If I am given a set of 128 time steps with 9 features data, i.e. an ndarray of the shape (128,9), how can I use the model.predict() method to make a prediction for the 128 time steps data?” Currently when I do model.predict( ndarray of shape (128, 9)), I get the error that “expected lstm_1_input to have 3 dimensions, but got array with shape (128, 9)”. From my understanding, I will be provided a time steps data with its feature values, and I have to predict the class for it. How can this data be 3d since I have to predict only one sample?
    Thank you

    Reply
  43. Avatar
    Alex November 17, 2019 at 11:58 pm #

    hey Jason,

    Thanks for the useful tutorial 🙂

    I don’t really get how the data is shaped into windows of size 128. I know here the data has already been shaped but I am asking if you have a tutorial showing how this shaping is done for a classification problem.

    Thanks,

    Reply
  44. Avatar
    john November 22, 2019 at 5:13 am #

    Hi,

    do you think your CNN+LSTM example would achieve good results for pose estimation ? what necessary changes would have to be done to accomplish this ? thanks in advance

    Reply
  45. Avatar
    Marvi Waheed December 3, 2019 at 8:36 pm #

    Hello,
    my dataset has dimensions (170,200,9) and i want to assign one class label to one sample/window of 200 timesteps, not individual labels to each of the 200 time steps in one window.
    How can i do this? so my target class output has dimensions (170,1)

    Reply
    • Avatar
      Jason Brownlee December 4, 2019 at 5:35 am #

      Yes, this is called time series classification.

      The above tutorial does this.

      Reply
  46. Avatar
    John December 7, 2019 at 5:45 pm #

    Hello,
    Can you please tell me which files do I need to load in the code below for stacking?

    Thanks.

    Reply
    • Avatar
      Jason Brownlee December 8, 2019 at 6:08 am #

      Sorry, I don’t understand your question. Perhaps you can elaborate?

      Reply
  47. Avatar
    John December 8, 2019 at 10:48 am #

    I meant that which files in the dataset should I load and stack so that the features are in 3 dimensions?

    I mean for applying the Numpy’s dstack function in the code above which files from the dataset should I load?

    Thanks in advance.

    Reply
    • Avatar
      Jason Brownlee December 9, 2019 at 6:43 am #

      The example in the tutorial shows exactly how to call this function to stack the dataset.

      No need to invent anything – just copy the full code example.

      Reply
  48. Avatar
    Devon December 8, 2019 at 1:42 pm #

    Hello,

    Can you please tell me why are we subtracting 1 in the code below?

    # zero-offset class values
    trainy = trainy – 1
    testy = testy – 1

    Thank you.

    Reply
    • Avatar
      Jason Brownlee December 9, 2019 at 6:45 am #

      As the comment suggests, to change the integers for the class label to have a zero offset. To start at 0 and not 1.

      Reply
  49. Avatar
    Ahmed Mubarak January 5, 2020 at 12:18 am #

    Hi Jason, Have a good day.

    Thank you for this tutorial. I have one question. I have data to online learning students, I want to prepare data to CNN LSTM, the data form ( students, weeks, videos for every week, video features ). now, I want to make inputs data(samples,n_steps,n_length, features) where n_length is Variable length such as ( first week 8 videos, second week of 13 videos, so on,). these data form as inputs data to CNN then LSTM. as like CNN-LSTM. Please, Can you guide me, how to prepare this data? my especially question, how can make n_length is variable length?

    Reply
  50. Avatar
    Charles Yu January 25, 2020 at 7:14 am #

    Hi Jason,

    I used this tutorial to do my time-series-classification / prediction.
    Basically, I only use 1st part of this tutorial, the LSTM.
    The predicted result should be either 0, 1, or 2

    I had 3 classes in Y, the integer values are 0, 1, 2.
    So after a calling to_categorical(), that will be:
    0 –> [1, 0, 0]
    1 –> [0, 1, 0]
    2 –> [0, 0, 1]

    However, after I make this kind of function call:
    yhat = model.predict(test_X, verbose=verbose)

    I got these kind of values:
    …
    [0.95416844 0.00828072 0.03755087]
    [0.9620431 0.00921117 0.02874582]
    [0.9660313 0.01018358 0.02378514]
    [0.9682437 0.01118453 0.02057172]
    [0.96942824 0.01226482 0.01830701]
    [0.9697388 0.01347514 0.0167861 ]
    …

    Can you elaborate that a little bit about how to convert my predicted values back to one-hot form or integer form?

    Thanks a lot

    Reply
    • Avatar
      Jason Brownlee January 25, 2020 at 8:46 am #

      Calculate the argmax() to get the index of the class label with the largest probability for each predicted sample.

      Reply
      • Avatar
        Charles Yu January 26, 2020 at 12:27 pm #

        Thank you so much. It solved my problem.
        However, I got a second question.

        For this kind of predicting results,
        [0.95416844 0.00828072 0.03755087]
        [0.9620431 0.00921117 0.02874582]
        [0.9660313 0.01018358 0.02378514]
        [0.9682437 0.01118453 0.02057172]
        [0.96942824 0.01226482 0.01830701]
        [0.9697388 0.01347514 0.0167861 ]

        if I use the argmax(), I will have all of events classified to class 1 which is “0”

        I was just wondering if there is anything wrong with my model?
        model.add(LSTM(100, input_shape=(train_X.shape[1], train_X.shape[2])))
        model.add(Dropout(0.5))
        model.add(Dense(100, activation=’relu’))
        model.add(Dense(n_outputs, activation=’softmax’))
        model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])

        Or anything I need to do in data pre-processing?
        For example, this is my raw data piece for the feature I’m predicting on:
        0
        0
        0
        0
        0
        1
        0
        0
        0
        0
        0
        1
        0
        0
        0
        0
        0
        0
        0
        0
        0
        0
        2
        0
        0
        0
        0
        0
        0
        1
        0
        0
        0
        0
        0
        1
        0
        0
        0
        0
        0
        0
        0
        0
        0
        0
        2
        0

        Reply
  51. Avatar
    AGGELOS PAPOUTSIS January 26, 2020 at 2:50 am #

    HI Sir,

    if we want to test the lstm model to new data, let’s say fro here(https://sensor.informatik.uni-mannheim.de/#dataset_realworld) which will be the procedure?

    1. we will stop after the train and then we will go to evaluate to new data (model.evaluate(new_data), without some pre-processing?

    2. or we must turn the data in a format that our lstm model understand

    Thank you so much for giving me the opportunity to ask my question.

    Reply
    • Avatar
      Jason Brownlee January 26, 2020 at 5:25 am #

      You must prepare all data the same way, including test data and new data when making a predictions.

      Reply
      • Avatar
        AGGELOS PAPOUTSIS January 26, 2020 at 8:56 pm #

        thank you fo the answer,

        when the model performs well on test data but not in new data what you think is the case?

        it depends on the quality of the new data, or maybe some hyperparameters change will lead to better accuracy?

        Reply
        • Avatar
          Jason Brownlee January 27, 2020 at 7:05 am #

          Perhaps the test dataset is too small or not representative of the problem.

          Reply
          • Avatar
            AGGELOS PAPOUTSIS January 27, 2020 at 6:36 pm #

            thank you so much for your answers

          • Avatar
            Jason Brownlee January 28, 2020 at 7:51 am #

            You’re welcome.

  52. Avatar
    AGGELOS PAPOUTSIS February 5, 2020 at 1:05 am #

    as I do not find anywhere in the site I will ask here. what is the procedure for downsampling sensor signal?

    if say we have a dataframe with same columns like

    acticity, accx, accy, accz, gurx, gury, gurz

    and the sampling array is 100hz. How can I downsample to 50 Hz?

    I find pandas replace but I have not seen anywhere how is applied.

    Reply
  53. Avatar
    Simon February 13, 2020 at 4:24 am #

    Hi,

    I have a classification problem in which the transitions from one state to the next happen very abruptly. I can classify the sequences well with the above example but is there a way to accurately identify when the system changes from one state to the next?

    Thanks

    Reply
    • Avatar
      Jason Brownlee February 13, 2020 at 5:43 am #

      Good question.

      I recommend looking into models for “regime changes” in time series.

      Reply
  54. Avatar
    Pritam February 16, 2020 at 10:49 pm #

    Hello Sir,
    Running your LSTM code yields me a shape of
    (7352, 128, 1) (7352, 1)
    (2947, 128, 1) (2947, 1)
    (7352, 128, 1) (7352, 6) (2947, 128, 1) (2947, 6)

    instead of

    (7352, 128, 9) (7352, 1)
    (2947, 128, 9) (2947, 1)
    (7352, 128, 9) (7352, 6) (2947, 128, 9) (2947, 6)..
    Can you please clarify the reason?

    Reply
  55. Avatar
    Aggelos Papoutsis February 17, 2020 at 5:19 am #

    hi,

    when the signal from the accelerometer or gyroscope data does not capture properly (i.e sharp peaks, edges, flat lines, etc), do you think that a auto-encoder lstm network will get read of this permutations?

    Reply
  56. Avatar
    AGGELOS PAPOUTSIS February 25, 2020 at 10:57 pm #

    hi Jason,

    thank you for your answers in my previous posts.

    can i use the suggestion from here https://machinelearningmastery.mystagingwebsite.com/diagnose-overfitting-underfitting-lstm-models/

    in order to check for overfitting or underfitting? and how i decide to the number of validation split during train?

    Reply
    • Avatar
      Jason Brownlee February 26, 2020 at 8:20 am #

      Yes, but you may have to create the curve manually.

      Depends on the problem and what you want to validate. E.g. perhaps try different size validation sets and see what is stable.

      Reply
      • Avatar
        AGGELOS PAPOUTSIS February 26, 2020 at 5:06 pm #

        thank you Jason. What do you mean to create the curve manually. I usually use this code

        def plot_learningCurve(history, epochs):
        # Plot training & validation accuracy values
        epoch_range = range(1, epochs+1)
        plt.plot(epoch_range, history.history[‘accuracy’])
        plt.plot(epoch_range, history.history[‘val_accuracy’])
        plt.title(‘Model accuracy’)
        plt.ylabel(‘Accuracy’)
        plt.xlabel(‘Epoch’)
        plt.legend([‘Train’, ‘Val’], loc=’upper left’)
        plt.show()

        # Plot training & validation loss values
        plt.plot(epoch_range, history.history[‘loss’])
        plt.plot(epoch_range, history.history[‘val_loss’])
        plt.title(‘Model loss’)
        plt.ylabel(‘Loss’)
        plt.xlabel(‘Epoch’)
        plt.legend([‘Train’, ‘Val’], loc=’upper left’)
        plt.show()

        Reply
        • Avatar
          Jason Brownlee February 27, 2020 at 5:39 am #

          But calculating validation accuracy via fit() might not be correct, instead we might want to estimate it using walk-forward validation.

          Reply
          • Avatar
            AGGELOS PAPOUTSIS February 27, 2020 at 6:11 am #

            ok thanks, i will try your suggestions

          • Avatar
            Jason Brownlee February 27, 2020 at 1:30 pm #

            You’re welcome.

  57. Avatar
    AGGELOS PAPOUTSIS February 26, 2020 at 1:56 am #

    hi,

    what will happen if someone omits this layer model.add(Dense(100, activation=’relu’))

    i am performing different experiments with a dataset that i record (accelerometer, gyroscope signals at 100hz).

    when i do not use the above layer the accuracy raises to 1.00 and all classes are property classified

    when i use the layer the accuracy drops at 78% and some static activities like sitting can not be classified

    what you think is the case here?

    Reply
    • Avatar
      Jason Brownlee February 26, 2020 at 8:25 am #

      The dense layer interprets the output from the LSTM.

      Try other configs and see if you can lift the skill of the model.

      Reply
      • Avatar
        AGGELOS PAPOUTSIS February 26, 2020 at 5:11 pm #

        ok i see thanks. so it seems mandatory to have a dense layer before your final dense layer where you make predictions

        Reply
        • Avatar
          Jason Brownlee February 27, 2020 at 5:39 am #

          No, some people use an global pooling layer.

          Reply
          • Avatar
            AGGELOS PAPOUTSIS February 27, 2020 at 6:01 am #

            oo I thought that global pooling layer is only for CNN.

            Thanks i gonna search for this

  58. Avatar
    AGGELOS PAPOUTSIS February 26, 2020 at 6:21 pm #

    hi ,

    one more question, please

    how do you decide the number of hidden units?

    model.add(LSTM(100, input_shape=(n_timesteps,n_features)))

    why 100 and not 200 or 50 etc? Are you aware of any paper that discusses this issue

    Reply
  59. Avatar
    PRIYANKA March 3, 2020 at 8:20 pm #

    I wish to form a model which could detect yawn of the driver. I wish to know how and by using what algorithm I can do that??

    Reply
  60. Avatar
    zohre March 6, 2020 at 10:34 am #

    Great work Jason!

    I am doing video classification for action detection using Keras (v.2.3.1). My model is CNN and LSTM. My dataset consists of videos of 3-7 seconds, each representing specific action. I use OpenCv to get frames from each video. But since video lengths are different, I get different number of frames for each video. However, I need to have the same number of frames for the LSTM layer. I searched a little bit and looks like padding along with a masking layer should do it, but I can’t figure out how to do this with Keras. Could you please provide some clues on how to achieve this?

    Reply
  61. Avatar
    Anon March 9, 2020 at 3:56 am #

    Is it possible to classify activities detected by bounding boxes ?

    Reply
    • Avatar
      Anon March 9, 2020 at 7:16 am #

      To elaborate on my above comment,

      how to build a model to classify a multi-class video sequence? instead of the whole video as you show in the above tutor.

      For example, let us imagine we have a video with 4 different clocks moving at varying speeds. I have folders as following:

      Folder 1: 1000 multi-clocks in a Video

      Folder 2: 1000 corresponding annotated JSON/XML files with the co-ordinates of the clocks with their respective labels (“Slow Speed”, “Normal Speed”, “Fast Speed”, “Varying Speed”).

      How to build a model to classify such videos?

      Reply
      • Avatar
        Jason Brownlee March 9, 2020 at 7:19 am #

        I don’t have examples of working with video, sorry.

        Reply
        • Avatar
          Anon March 9, 2020 at 8:22 am #

          Hi Jason, I found that you have

          https://machinelearningmastery.mystagingwebsite.com/how-to-develop-rnn-models-for-human-activity-recognition-time-series-classification/

          Is there an expansion on that tutorial so that instead of recognition on the whole video, there are several recognitions on the same video multiple activities? i.e. Bounding with Slow Speed, Bounding box with Normal speed etc…

          It will not be sufficient to do only “object recognition” since it needs the next frames in order to predict the clock speed.

          Some methods I found online are:

          1) 3D CNN
          2) ConvNets + RNN
          3) COnvent + MLP
          4) Two steam convolutional networks

          Do you cover any of these methods in one of your books perhaps with a video example?

          Thank you for your prompt reply, and thank you for all your fantastic work.

          Reply
          • Avatar
            Jason Brownlee March 9, 2020 at 11:06 am #

            I don’t have any examples of working with video.

    • Avatar
      Jason Brownlee March 9, 2020 at 7:18 am #

      In images? Yes, that is called “object recognition”:
      https://machinelearningmastery.mystagingwebsite.com/object-recognition-with-deep-learning/

      Reply
  62. Avatar
    Tanveer March 29, 2020 at 1:57 am #

    Hello Dear,

    I want to plot time series graph single activity..

    For Example,
    def plot_activity(activity, df):
    data = df[df[‘activity’] == activity][[‘x-axis’, ‘y-axis’, ‘z-axis’]][:200]
    axis = data.plot(subplots=True, figsize=(16, 12),
    title=activity)
    Can i plot this by using HARDataset?
    Pleaze Guide me

    Reply
  63. Avatar
    Tanveer March 30, 2020 at 10:44 pm #

    Ok Dear, Can you give me some hint; HARDataset has many files, how can i relate to them so as it will be possible for me to solve above problem

    Reply
  64. Avatar
    aggelos April 1, 2020 at 6:59 pm #

    hi Jason,

    do you have any examples in order to synchronize and interpolate accelerometer and gyroscope data

    let’s say that we have a data frame
    activity timestamp accx accy accz timestamp gurx gury gurz
    0 walking 1585564269527 -0.625122 -0.343262 0.357971 1585564269513 10.785061 3.288872 -5.015244

    the timestamps form the two sensors are in different scale

    Reply
  65. Avatar
    aggelos April 2, 2020 at 7:19 am #

    yeah, i have already seen this. First, i must convert the unix time into date and time and then use the examples

    thanks Jason

    Reply
  66. Avatar
    Kinjal April 13, 2020 at 3:13 am #

    Hi Jason,
    Nice explanation, as always. I have a query that how to do the same (video classification) with multiple videos. I mean, any suggestion for one label for one video?

    Reply
    • Avatar
      Jason Brownlee April 13, 2020 at 6:20 am #

      Perhaps explore a CNN-LSTM and ConvLSTM for this type of problem.

      Reply
  67. Avatar
    Kinjal April 13, 2020 at 10:39 pm #

    Any good resource/tutorial if you can please suggest?

    Reply
  68. Avatar
    Ahmad April 16, 2020 at 1:32 am #

    Hello Jason,

    Thank you for this tutorial. In fact I have a question:

    I can see that the size of the sliding window is 128. I can also see that the sliding window is moving by 64 values in the data (50% overlap). So in the new window, there is 128 / 2 = 64 redundant data. Do you have an explanation for the choice of 50%? What is the effect of choosing other options?

    Thank you for your answer.

    Reply
    • Avatar
      Jason Brownlee April 16, 2020 at 6:02 am #

      The choice of framing is arbitrary. Find what works well/best for your specific model and dataset.

      Reply
  69. Avatar
    Thilan April 16, 2020 at 1:37 am #

    sir how does this use for live data.

    Reply
    • Avatar
      Jason Brownlee April 16, 2020 at 6:03 am #

      First fit your model on all available data, then make predictions on new data by calling model.predict()

      Reply
  70. Avatar
    Alex April 23, 2020 at 6:26 pm #

    Hey Jason,

    I also enjoyed this article. I am currently working on a similar project and I wanted to know if the sliding window is always necessary in a time series classification problem, where the idea is to predict the classes of one multivariate time series data?
    To be concrete, lets say I have 9 subjects, each of them has 22 features extracted and from the measurements i get for every feature 376 data points, which makes 22*376=8272 datapoints for each person. Each subject then belongs to either class 1,2,3 or 4. How do I decide on the window size and why is this necessary? I actually also read you articles about how to convert a Time Series to a supervised learning problem, but I did not see how this is applicable for my problem.

    Thanks a lot!

    Reply
    • Avatar
      Jason Brownlee April 24, 2020 at 5:38 am #

      Yes it is.

      Choose the window size based on the size that results in the best performing models on your data.

      Reply
  71. Avatar
    zitoun May 2, 2020 at 6:50 pm #

    Great tuto,

    Is there any transfert learning to be applied in the CNN part of the CNN-LSTM model (like VGG, RestNet, Inception…) in order to make time series classification ?

    Reply
    • Avatar
      Jason Brownlee May 3, 2020 at 6:07 am #

      You could. I don’t recall writing an example of exactly this, sorry.

      Reply
  72. Avatar
    Shida May 8, 2020 at 3:17 am #

    Hi Jason, I stuck at loading the data. Should I include the directory of the workspace for example C:\Users\… ? I’ve done everything but the dataset just could not load.
    Thank you in advance!

    Reply
    • Avatar
      Jason Brownlee May 8, 2020 at 6:40 am #

      Yes, have the dataset and code in the same directory.

      Reply
  73. Avatar
    khandu May 9, 2020 at 5:46 pm #

    Sir, i am adapting the your example using my data. I have 4 input features and 1 target.

    The target value is in 0s and 1s , y= [0,1,0]

    and the input shapes is (timestep, features) [7,4] and output[1] since i have got only one target i.e num_y-signals.

    The proposed model is:
    model.add(LSTM(100, activation=’relu’, return_sequences=True,
    input_shape=(X_train.shape[1], X_train.shape[2])))

    model.add(Dense(num_y_signals, activation=’softmax’))

    I am getting the following error
    ValueError: A target array with shape (14388, 1) was passed for an output of shape (None, 7, 1) while using as loss binary_crossentropy.
    This loss expects targets to have the same shape as the output.

    Can you please help me where i have got wrong please

    Reply
  74. Avatar
    khandu May 10, 2020 at 12:57 pm #

    Sir,
    Thank you for the response

    I have y classes with 0s and 1s and how to get the predicted label classes for the corresponding feature.

    I got this output but donot know how to interpret.

    # define vector
    probs = np.array(yhat)
    print(probs.shape)
    # get argmax
    labels = np.argmax(probs, axis=-1)
    print(labels)

    Output
    (3592, 7, 2)
    [[1 1 1 … 1 1 1]
    [1 1 1 … 1 1 1]
    [1 1 1 … 1 1 1]
    …
    [1 1 1 … 1 1 1]
    [1 1 1 … 1 1 1]
    [1 1 1 … 1 1 1]]

    Thank You

    Reply
  75. Avatar
    kGao May 18, 2020 at 6:59 am #

    Hi Jason,

    Thanks for the great tutorial.

    I want to play with CNN based model to make a Rank list. I have student’s profile(20 students) in a class and I want to create a model, which is able to make a rang list in the class.
    The student profile is only one row with 10 features (grades from different curriculum and achievements).

    Dou you have any idea, or suggestion for me?

    Reply
  76. Avatar
    AGGELOS PAPOUTSIS May 20, 2020 at 10:01 pm #

    Hi, Jason,

    I have a question, please. The samples and the timestamps are the same? I mean that when we have 50hz frequency and we decide to take 2s we then take 100-timestep which is equal to 100 samples. Am I write?

    Reply
  77. Avatar
    sacoras June 3, 2020 at 1:04 am #

    Hello. It was a great post, thank you.
      When I use the following code to predict the model:

    pred = model.predict( testX )

    I get the following error for convlstm:
    ——————————————ERROR——————————————————————————–
    ValueError: Error when checking input: expected conv_lst_m2d_4_input to have 5 dimensions, but got array with shape (2947, 128, 9)
    ————————————————————————————————————————–

    and for cnn-lstm is:

    ——————————————————ERROR——————————————————————–
    ValueError: Error when checking input: expected time_distributed_21_input to have 4 dimensions, but got array with shape (2947, 128, 9)

    ————————————————————————————————————————–

    How can I fix it? Thank You

    Reply
    • Avatar
      Jason Brownlee June 3, 2020 at 8:03 am #

      You need to change the shape of your data to match the expectation of your model or change your model to meet the shape of your data.

      Reply
  78. Avatar
    Alix June 4, 2020 at 2:00 pm #

    Sir I was trying to apply CNN+LSTM on EEG data whose X shape is (11540,20). How should I reshape it to feed into neural network? Thank you.

    Reply
  79. Avatar
    Vaishnavee Sharma June 25, 2020 at 12:11 pm #

    Hi Jason, amazing article for novices. I had a question regarding the Zero-one offset. Why there is a need to do it? Why do you want the class labels to start from zero and not from one? Also it changes the dimension of the “trainy” and “testy” to (7352, 6) and (2947, 6) respectively. Why is that happening?

    Reply
  80. Avatar
    fah July 8, 2020 at 3:42 pm #

    Hi,
    Thank you for your good tutorial.

    I read your previous article.
    https://machinelearningmastery.mystagingwebsite.com/cnn-models-for-human-activity-recognition-time-series-classification/

    Could you please explain the differences between 1D Convolutional Neural Network Models and CNN-LSTM / ConvLSTM?

    if I understand correctly, there are 4 types:

    recurrent neural networks include:
    LSTM
    CNN-LSTM
    ConvLSTM

    and one-dimensional convolutional neural networks include:
    CNN

    Am I correct? Thank you very much.

    Reply
  81. Avatar
    keerthan July 13, 2020 at 12:25 am #

    I have one doubt, my work is similar to this. But instead of human activity, I have to tell whether the vehicle is moving straight or zigzag path. I have sensor readings, how can I implement it with neural network model? Thanks in advance

    Reply
    • Avatar
      Jason Brownlee July 13, 2020 at 6:04 am #

      Perhaps you can use the tutorial as a starting point and adapt it for your specific dataset.

      Reply
  82. Avatar
    Vinit Hegiste August 4, 2020 at 11:39 pm #

    Hello, I want to apply RNN on data extract from 2D skeleton of openpose. So I have 36 features (body co ordinates) and a label for that pose. So my X_train has a shape of (4000,36) and Y_train has a shape of (4000,5). How can I use RNN to classify this data?
    I am currently using a dense network for pose estimation in real time

    Reply
  83. Avatar
    Yasmin August 18, 2020 at 12:55 am #

    Hello,
    I trained my LSTM network given the all vector (time series vector of n samples).
    But what I need is to feed my network sample by sample and get the results after each sample and not to give the whole vector,
    How do I do that?

    Reply
    • Avatar
      Jason Brownlee August 18, 2020 at 6:05 am #

      Use a loop over your samples and pass them in one at a time and make a prediction.

      Reply
      • Avatar
        yasmin August 19, 2020 at 2:10 am #

        Thank you, this is what I am doing now.

        what do you mean by ‘samples’? sample of a given series?
        if so:
        1. I will do prediction sample after sample, but when I get new series what should I do?
        The default is stateful = false, so there is reset between batches.

        2. should I used stateful = True?
        How do I use it ? should I use it during training\predication?
        2. if I set return_sequences = true, than I get the hidden state… is it the outputs of the prediction for each sample in my series?

        I

        Reply
      • Avatar
        yasmin August 19, 2020 at 2:20 am #

        If just ” pass them in one at a time and make a prediction” than after every predication the states will be reset, no? because every predication is like a new batch, no?

        Reply
        • Avatar
          Jason Brownlee August 19, 2020 at 6:05 am #

          Correct.

          Test if this matters or not for your model/data.

          If not, you may as well use a CNN or MLP as it will be faster.

          Reply
  84. Avatar
    AGGELOS PAPOUTSIS August 20, 2020 at 2:57 am #

    Hi jason,

    i have a question please,

    you said above that:

    1. The model learns to extract features from sequences of observations and how to map the internal features to different activity types.

    2. we do feature learning on raw data.

    3. The benefit of using LSTMs for sequence classification is that they can learn from the raw time series data directly, and in turn do not require domain expertise to manually engineer input features. The model can learn an internal representation of the time series data and ideally achieve comparable performance to models fit on a version of the dataset with engineered features.

    How can this possible? How can LSTM learn that in this timestep the activity is let’s say walking? which features it recognize in order to come to that decision,

    any help will be higly valuable.

    Thank you

    Reply
    • Avatar
      Jason Brownlee August 20, 2020 at 6:51 am #

      It learns the unknown underlying function that maps patterns in the input data to a target class.

      This is called function approximation and it is what neural nets do well, perhaps this will help:
      https://machinelearningmastery.mystagingwebsite.com/neural-networks-are-function-approximators/

      Reply
      • Avatar
        AGGELOS PAPOUTSIS August 20, 2020 at 5:31 pm #

        oh so LSTM does not calculate ant features like min-max etc? Is function approximation valid in the unsupervised scenario right?

        Reply
        • Avatar
          Jason Brownlee August 21, 2020 at 6:25 am #

          Unsupervised algorithms like clustering methods do a type of function approximation, e.g. best separation of data by natural groupings.

          Reply
  85. Avatar
    RobinF August 31, 2020 at 11:23 pm #

    Hello,

    First of all thanks for this code !!

    I have a question, where did you write the path of your dataset location ?

    I’m trying to run it but it always says : ‘FileNotFoundError: [Errno 2] File HARDataset/train/Inertial Signals/total_acc_x_train.txt does not exist: ‘HARDataset/train/Inertial Signals/total_acc_x_train.txt”

    Thanks for your help,

    Robin

    Reply
    • Avatar
      Jason Brownlee September 1, 2020 at 6:33 am #

      The code is expecting to run in the same directory as the unzipped dataset.

      You can change the path to the dataset in the code if you like.

      Reply
  86. Avatar
    RobinF September 8, 2020 at 8:07 pm #

    Thanks ! It’s working 🙂

    Reply
  87. Avatar
    Tanveer September 12, 2020 at 5:15 am #

    Greetings!

    Would you like to explain to me the number of layers, cells, and type of LSTM that you have performed in the first model HAR LSTM-RNN?

    Reply
  88. Avatar
    Kerry September 13, 2020 at 12:33 am #

    Hi Jason,

    Hopefully this is a quick question, but I haven’t been able to find an answer anywhere.

    What is the best way to preprocess timestamp data for an LSTM?

    Should timestamps be scaled or normalised like other continuous variables? Or is there a more appropriate approach?

    Specific context: I’m using an LSTM sequential model (from Keras in Python) for time series anomaly detection (classification) on network packet captures from a simulated network

    Reply
  89. Avatar
    Yasmin Tsiprun September 19, 2020 at 5:19 pm #

    Hello,
    In this example you set lstm unit =100.
    Does it means that the memory of the lstm is only of 100 time stamps?
    It will forget what happend 101 time stamps before?

    I found the following defenistion for units:
    STM with units=1 the key values (f, i, C, h) are scalar; and with units=n they’ll be vectors of length n

    I am confuzed because diagram of unrolled lstm network looks like a chain of lstm units…. is this the same unit above?
    Thx
    Yasmin

    Reply
  90. Avatar
    AGGELOS PAPOUTSIS September 28, 2020 at 11:50 pm #

    Hi jason,

    i have two questions, please. In the setting of human activity recognition, we have the many to one sequence? Meaning that in each time step we input a window of data and we have a prediction y hat.

    also, I see that there been used different models like encoders-decoders, bidirectional lstm, transformer, models with attentions etc. Are these models applicable to the human activity recognition area?

    Reply
    • Avatar
      Jason Brownlee September 29, 2020 at 5:41 am #

      In this case, one to one, e.g. one input observation, one classification.

      Yes, try a suite of models and see what works best for your dataset.

      Reply
  91. Avatar
    Safynaz October 7, 2020 at 2:14 am #

    Dear Jason,
    Really V.good material thank you for it,

    i want to apply the same ideas of the tutorial to my problem. I have raw data for 385 patients, each 2 hours i take some measurements for this patients to predict his state want to enter ICU or not where each patient has 2 rows of measurements. the shape of data for LSTM was (385, 2, 85) where 385 is number of samples/ patients, 2 is number of sequences for each patient, and 85 is a group of measurements as features that calculated for each sequence of time.

    my problem is the shape of input for CNNLSTM model, i don’t know how to get n_steps, n_length because my problem is simple than the problem in the tutorial .

    please help me to know how to reshape trainx and what is n_steps, n_length in my problem?
    Also, what is the input shape of CNNLSTM for CONV1D layer?
    the same thing for ConvLSTM Network Model???

    Thanks

    Reply
  92. Avatar
    ganesh October 9, 2020 at 6:12 am #

    Hi Jason,

    In the similar way i am trying to implement Time series classification using keras. It is 33000×251 size data for each instance.

    Training data is about 18x33000x251
    test data is about 12x33000x251

    When trained with model, validation accuracy is not going beyond 60%

    Can you please suggest what we can do in this case to improve validation accuracy. my model is as below:

    from tensorflow.keras.layers import Dropout
    from tensorflow.keras.callbacks import EarlyStopping
    early_stop=EarlyStopping(monitor=”val_loss”, mode=”min”, verbose=1, patience=25)
    from tensorflow.keras.regularizers import l2

    model3=Sequential()
    model3.add(LSTM(256, input_shape=(seq_len, 251), kernel_regularizer=l2(0.01), recurrent_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
    model3.add(Dense(150, activation=”relu”))
    model3.add(Dense(50, activation=”relu”))
    model3.add(Dense(1, activation=”sigmoid”))
    model3.compile(loss=”binary_crossentropy”, optimizer=”adam”, metrics=[“accuracy”])

    model3.fit(x=train,
    y=train_target,
    epochs=600,
    callbacks=[early_stop],
    validation_data=(test, test_target))

    Reply
  93. Avatar
    Asish November 11, 2020 at 2:49 am #

    Hi Jason,

    I’m using the following model for eye tracking time series data but accuracy is only 64%.Any suggestions how to improve it?

    model = Sequential()
    model.add(TimeDistributed(Conv1D(filters=128, kernel_size=1, activation=’relu’), input_shape=(1,3, 3)))
    model.add(TimeDistributed(Conv1D(filters=128, kernel_size=1, activation=’relu’)))
    model.add(TimeDistributed(Dropout(0.5)))
    model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
    model.add(TimeDistributed(Flatten()))
    model.add(LSTM(250))
    model.add(Dropout(0.5))
    model.add(Dense(100, activation=’relu’))
    model.add(Dense(3, activation=’softmax’))
    model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])
    model.fit(X_train, y_train, epochs=30, validation_split=0.2)
    _, accuracy = model.evaluate(X_test, y_test, batch_size=64, verbose=0)
    print(“accuracy”, accuracy)

    Reply
  94. Avatar
    Laurent December 10, 2020 at 9:47 pm #

    Hello Jason,

    Thank you for this amazing tutorial, as always.

    Out of curiosity, a simple logistic regression with l1 penalty trained on the features (training set) provides 95.9% accuracy on the test set, while the whole LSTM one seems to be at around 92% max.

    What are your thoughts on this?

    Thank you in advance !

    Reply
    • Avatar
      Jason Brownlee December 11, 2020 at 6:38 am #

      The tutorial is teaching how to use a method, not solve a specific standard dataset in the most effective manner.

      Use the model that performs the best on your problem.

      Reply
  95. Avatar
    Omar January 5, 2021 at 12:31 am #

    Hi, Jason:

    In “model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’]” , is it possible to change ‘accuray’ by ‘f1_macro’ or something similar? (I have an imbalanced dataset). I tried it but got an error.

    Thanks in advance

    Reply
  96. Avatar
    Cass January 18, 2021 at 3:38 am #

    Hi Mr. Jason,

    I’m new to machine learning and I have some questions.

    I’m trying to plot a confusion matrix, displaying classification report for the CNN-LSTM model.
    I comment the line #_, accuracy = model.evaluate(testX, testy, batch_size=batch_size)
    and add this line
    history = model.fit(trainX, trainy, epochs=epochs, batch_size=batch_size, validation_split=0.2)

    then I add a function

    But I keep getting errors like name ‘history’ is not defined

    Even I write the plotting codes out of function it also return the same error, do you know how to solve this error please?
    Or perhaps do you know how can I plot confusion matrix and display classification report?

    Your reply will be highly appreciated, thank you very much.

    Reply
  97. Avatar
    Mike January 27, 2021 at 1:07 pm #

    Great article, I used the LSTM approach you highlighted and successfully could distinguish among 3 different activities. I created my own data from essentially multiple “runs” of executing an activity (e.g. throwing a ball). In a recording I would do the activity multiple times. As I converted sensor data (accelerometer, gyroscope) into the right shape using your series_to_supervised with ~30 lags and 100 observations. My question to you is once I successfully characterize the activity, how can I count the number of times the activity occurred in my original data. To clear my original sequence may represent say 10 instances of an activity (e.g. throwing a ball 10 times), the conversion of this sequence may with lags and observations create roughly 500-1000 samples. So though I classify the activity successfully I don’t understand how to count the number of times I did the activity. Any suggestions?

    Reply
    • Avatar
      Jason Brownlee January 27, 2021 at 1:24 pm #

      Well done!

      You may need to write code to interpret the predictions from your model. E.g. classical programming/software engineering where the model is just one piece.

      Reply
  98. Avatar
    Mike January 28, 2021 at 1:13 am #

    I guess I don’t understand what you are suggestion. For example if an original sequence of sensor data is say 20 seconds and you do an activity every 5 seconds (say throw a ball in my example) I would like to count “4 times a ball was thrown). Are you suggesting I should somehow understand there are 4 cycles of data in this 20 seconds? How? Furthermore if mixed kicking a ball versus throwing a ball the cycles would look different (and the model would see that) but again how to equate it back to original data.

    Can you expand on your suggestion? Maybe an equivalent example would be if the activity was walking and model accurately determined walking, how would one go about counting the number of steps in that walking sequence?

    Reply
    • Avatar
      Jason Brownlee January 28, 2021 at 6:02 am #

      I don’t know the full extent of your project, but it sounds like you are using the model to classify sequences of data.

      Once classified, you can write some if-statements to interpret the predictions, e.g. in this interval there were this many of this and that actions.

      If that is not the case, perhaps I don’t follow.

      Reply
  99. Avatar
    Mike January 28, 2021 at 7:12 am #

    Let me explain. Say you ask a person to wear a sensor and perform a series of different activities. Example throw a football 10 times, then shoot a basketball 10 times, then hit a tennis ball with a racquet ten times. Say each sequence takes ~ 25 -30 seconds. Using your blog concepts I can create sequences of times series data with known labels and converting these time series with series_to_supervised. That is I can get convert these into samples, timesteps, features. Building a model on this gives great accuracy with LSTM. And if I then have the person repeat one aspect say throw the football 5 times, convert the data and do a model.predict the model accurately determines the person’s activity is throwing a football. The problem is I know the person is throwing a football but I don’t know how many times the person is throwing the football (other than I told them to throw it n times). So once I know what the person’s activity is I’d like to count the discrete number of times the person does that activity? Does this better explain the challenge?

    Reply
    • Avatar
      Jason Brownlee January 28, 2021 at 8:02 am #

      Thanks for elaborating, I think you can address your concern by redefining the problem.

      Some ideas:

      Perhaps you can re-define what you classify from the activity to the identification of a specific sub-action of an activity, like catching the ball. Then count catches

      Perhaps you can train the model to identify the beginning and end of each activity so you can count iterations?

      Perhaps you can train the model to identify the activity performed between repetitions (e.g. standing waiting to throw/catch football before actually doing it)?

      Reply
  100. Avatar
    Sampat February 12, 2021 at 8:21 am #

    I have a query , is this for a sequence to label or for sequence to sequence classification problem.

    Beacuse i too have a similar windowed input i.e trainX(462,250,6) and its corresponding trainY(462,250.12) where in trainX there are 6 features(3 accelerometer + 3 gyrometer) and 12 output classes in trainY.

    So i am having an error with input shapes of the Conv + Lstm architecture which you were using beacuse i think i need to change the shape of trainY(as i a doing sequence to sequence prediction).

    Could you please throw some light on it?

    Reply
  101. Avatar
    JC February 14, 2021 at 10:25 am #

    Instead of classifying individual data point, what would be a good approach towards classifying the entire time series?

    Reply
    • Avatar
      Jason Brownlee February 14, 2021 at 2:16 pm #

      I recommend evaluating a suite of approaches in order to discover what works well or best for your dataset.

      Reply
  102. Avatar
    Sarker March 21, 2021 at 2:35 pm #

    How can I use LSTM for real-time data classification?

    Reply
  103. Avatar
    Sarker March 23, 2021 at 2:02 pm #

    Thanks Jason for quick response.
    I’m collecting data from EEG and model is already pre-trianed, so I need to get real-time output every 10 seconds. How can I do this real-time classification output every 10 or 20 seconds?

    TIA

    Reply
    • Avatar
      Jason Brownlee March 24, 2021 at 5:48 am #

      Perhaps you can fit a model on historical data then make predictions on new data as it comes it. Try it and compare it to a model that is updated frequently.

      Reply
  104. Avatar
    Jake April 7, 2021 at 2:26 am #

    Hey Jason,

    I have adapted this example for a research project where I take in keypoints from a body instead of acceleration data.

    I am a new to Keras and I was wondering if you know the syntax to print out each individual result in the LSTM. For example, I want to see which results are wrong and which are correctly estimated. Thanks!

    Reply
    • Avatar
      Jason Brownlee April 7, 2021 at 5:12 am #

      The LSTM will output a matrix with one row per sample. You can print each row to get the output foe each input sample.

      Reply
  105. Avatar
    Abid Abdul Azeez April 11, 2021 at 7:57 pm #

    Hi Jason, I have a total of 16 simulation runs (Time Series) for a healthy and 15 faulty cases. I want to build a classifier to differentiate the type of fault. There are a total of 8 features (sensor signals) for each simulation run and each data set consists of 20,000 data points. I would like to know if any of the above mentioned methods can help to build this classifier.

    Reply
    • Avatar
      Jason Brownlee April 12, 2021 at 5:07 am #

      Perhaps try an LSTM and compare results to other models to see if they have skill.

      Reply
  106. Avatar
    ali April 12, 2021 at 10:34 pm #

    i am looking for similar data to the dataset used in this toturiel please

    Reply
  107. Avatar
    kevin May 14, 2021 at 4:07 pm #

    Hello jason, first this article is very helpful for my studying keras lstm.

    And i have a question

    In dataset there are 6 label, but why did you make zero-offset class value?
    (trainy = trainy – 1
    testy = testy – 1)
    because i want to classify all of label.

    Reply
    • Avatar
      Jason Brownlee May 15, 2021 at 6:27 am #

      We use a one hot encoding for class labels, requiring the data to be first ordinal encoded with a zero-offset.

      Reply
  108. Avatar
    Fatemeh Esfahani June 18, 2021 at 8:29 am #

    hi Jason, Thank you for your post. I have a question about preparing dataset for training. I have a wide range of time series files, let say filename1, filename2, …. The sample rate is the same, but these files may be of different length. For instance, filename1 may contain 20 min of the data, and filename2 can contain 10 min of the data. I mean my data is not continuous and also it is coming from different sensors. To prepare my files as input for lstm/cnn I should merge them together and assign the class that each data point belongs to? is that right?

    Reply
      • Avatar
        Fatemeh Esfahani July 4, 2021 at 3:30 am #

        Thank you. Whether a window in one row of the train dataset should be necessarily related to the next row? I mean should windows have overlap or they can be from different data files?

        Reply
        • Avatar
          Jason Brownlee July 4, 2021 at 6:05 am #

          It’s your choice whether windows overlap or not.

          Perhaps test a few approaches and compare results.

          Reply
          • Avatar
            Fatemeh Esfahani July 6, 2021 at 5:37 am #

            Thank you for your reply. Based on what I understand from lstm windows can contain a discontinues time intervals as well. Is that right? For instance, first window can contain time 0,…,128 and the second one can contain time 200, 328.

          • Avatar
            Jason Brownlee July 6, 2021 at 5:51 am #

            There is nothing stopping you.

            It may or may not impact the performance of your model on your dataset.

  109. Avatar
    sinfer June 23, 2021 at 4:14 pm #

    Hi Jason, Thanks a lot for the valuable tutorial. I have a question though. I have a data set collected from a cooling water system sensors and there are 64 features/variables and nearly 12000 records to train with 7 types of faulty data. I’m working on conducting a fault detection & diagnosis on this data set with LSTM approach for multi-class classification(7 fault types and normal).

    But Iim finding a bit confused here how to decide the number of time steps that i should use when shaping the input to the LSTM layer since it is now a two dimensional data with the shape of (12000,64). If i do this with a single time step am i not gonna get the full use out of LSTM due to there will be not recurrence of the same cell?

    and secondly do i need to conduct a optimal feature extraction for the LSTM before the input layer setup. Or is it something that LSTM will take care of by it self? ( i can use all 64 features without having to do any selection?)

    Reply
    • Avatar
      Jason Brownlee June 24, 2021 at 5:59 am #

      Perhaps you can evaluate different numbers of time steps and discover what works well or best for your specific model and dataset.

      LSTM will perform feature extraction automatically.

      Reply
  110. Avatar
    Nayab July 6, 2021 at 4:46 am #

    Hi Jason,

    I have dataset of a uni-axial accelerometer. The raw dataset only have one feature and class and the total datapoints are 36000. I injected sensor faults via simulations and added 5 more classes. Now, I have a dataset with one feature, 6 classes and total datapoints 216000.

    With the help of your tutorials I made samples of the dataset, each sample has 1000 datapoints. I did sampling in two ways; one with no overlap in this case data shape is [samples= 216, n_timesteps=1000, n_features=1] and the second with overlap skipping just one step and the data shape in this case is [samples= 12006, n_timesteps=1000, n_features=1]. And each sample of the dataset is labeled.

    I want to build a classification model using LSTM. I build a single layers LSTM with input layer having the shapes mentioned above and the output layer with 6 nodes/cells. But it’s not working I am getting the following error:
    ValueError: Shapes (None, 1) and (None, 6) are incompatible

    First, I was thinking to use auto-encoder (for feature extraction) with LSTM (for classification). But, then I decided to train a LSTM first and then go for a hybrid kinda model so that I have clear picture whether the autoencoder is useful or not.

    I want to know if there is a problem with my dataset or the choice of algorithm?

    I really need your help. Any sort of help and guidance would be great.

    Thanks.

    Reply
  111. Avatar
    sinfer July 8, 2021 at 10:44 pm #

    can’t i predict only one label output if i make multiple time steps in LSTM (which makes return a whole sequence). I think i find it very vague and unclear what the time step is and how we can use it in LSTM.

    Reply
    • Avatar
      Jason Brownlee July 9, 2021 at 5:09 am #

      If the model is designed to predict a sequence, then you will always get a sequence as output for each input sample.

      Reply
      • Avatar
        sinfer July 11, 2021 at 1:40 am #

        Thanks alot

        Reply
  112. Avatar
    sinfer July 14, 2021 at 7:11 pm #

    Hi Jason,
    One more question. I’m a little worried about if i have structured my data set in a way it is suitable for a LSTM time series multi-class classification problem. I have different machinery conditions (7 faults and normal condition) logged in 8 different times. And i have setup my data frame by appending all these 8 data files. each data file has 3000 records with 65 columns(sensors) with a label to mention which condition that certain data point falls into.

    So i split this data set into x and y and reshape if i want to go with more than one time step.
    Is this sort of a scenario valid with such a dataset for LSTM? Really appreciate if you can give me a help on this
    Thanks

    Reply
    • Avatar
      Jason Brownlee July 15, 2021 at 5:25 am #

      Perhaps try an LSTM and compare results to other models like 1d cnn and mlp, and other ml models like random forest.

      Reply
      • Avatar
        sinfer July 15, 2021 at 10:11 pm #

        I tried both LSTM and 1D CNN and I get a testing data accuracy of 97.59% for 1D CNN and 98.11 % for LSTM. Training accuracies of both of them are more than 99.20 %. Guess i should go with LSTM.

        In LSTM I have done the classification by reshaping both X and Y into 3D with 100 time steps. So I have to take predicted value for the last time step returned from the prediction function as the output right? becoz i get a array of predicted values (many to many). Those should be the states calculate at each time steps with the effect of previous time step state ?

        Reply
        • Avatar
          Jason Brownlee July 16, 2021 at 5:24 am #

          Not sure I follow your question, sorry.

          Your model will make one prediction per input sample.

          Perhaps this will help if you’re confused with the predictions:
          https://machinelearningmastery.mystagingwebsite.com/how-to-connect-model-input-data-with-predictions-for-machine-learning/

          Reply
          • Avatar
            sinfer July 16, 2021 at 10:26 am #

            Hi Jason,

            this is my input data shape for X and Y data.

            X_train.shape, y_train.shape
            ((816, 100, 65), (816, 100, 8))

            following is the model

            model.add(LSTM(100, dropout=0.1, input_shape=(X_train.shape[1],
            X_train.shape[2]),return_sequences=True))
            model.add(LSTM(100, return_sequences=True))
            model.add(Dense(100, activation=’relu’))
            model.add(Dense(8,activation=’softmax’))
            model.compile(loss=’categorical_crossentropy’,
            optimizer=’adam’, metrics=[‘accuracy’])

            Here I have to return the sequence since i have reshaped the Y also into 3D. Then calling the predict function for this i get a result like following for a prediction input of a 10 samples in a sequence
            [[2,2,2,2,2,2,3,3,2,3]]

            So here i get states for the each time step i have send to predict function right. and what should i get as the output value from these values as the predicted class label for my input sequence? Hope it is clear now
            Thanks

          • Avatar
            Jason Brownlee July 17, 2021 at 5:18 am #

            Not sure I follow.

            The output of your model is a vector of class predictions for a given input.

            Also, your model is odd, e.g. it has return_sequences=true for the last LSTM layer, I would not recommend this.

  113. Avatar
    sinfer July 17, 2021 at 10:37 am #

    Hi Jason,

    I had to return the sequences since I have reshaped not only X_train to ((816, 100, 65) but also y_train to (816, 100, 8)) since I want to train my model using multi time steps (multiple recurrence). Other wise I will get an error saying Invalid output shapes since y output is defined with time steps (816, 100, 8).
    Anyway thanks a lot for your response 😉

    Reply
  114. Avatar
    Nathan H. July 26, 2021 at 3:41 am #

    For sequence classification, when would you use an autoencoder first, and feed the compressed representation (from the trained encoder) into a subsequent classification model?

    When the training datasets are “noisy”?

    I’m just trying to synthesize across the various LSTM-based sequence classification articles you have presented?

    Reply
    • Avatar
      Jason Brownlee July 26, 2021 at 5:32 am #

      That approach can be effective in many cases, noisy data as you say, also sequences with variable lengths. Try it and see.

      Reply
  115. Avatar
    Don August 2, 2021 at 5:40 pm #

    Dear Jason,

    Thanks for the post!

    My data set was not obtained in a complete constant rate. For example, it is 50Hz but only for 5 seconds in every minute. What should I do?

    Thanks,
    Don

    Reply
  116. Avatar
    Don August 4, 2021 at 4:31 pm #

    Helpful, thanks for the quick reply!

    Reply
  117. Avatar
    Josh August 11, 2021 at 9:32 pm #

    Hi Jason,

    Quick question. Is it normal that using my own data and running experiment 20 times it’s getting the same accuracy in all cases? What could be a possible reason for this? Increasing the training data obviously increases the accuracy but it’s not changing from run to run.

    Thank you in advance.

    Reply
    • Avatar
      Adrian Tam August 12, 2021 at 5:54 am #

      If you get the same accuracy, may be you reset your random seed every time? You should not. See this FAQ on random seed https://machinelearningmastery.mystagingwebsite.com/faq/single-faq/what-value-should-i-set-for-the-random-number-seed

      Reply
      • Avatar
        Josh August 12, 2021 at 10:01 pm #

        Hi Adrian,

        It’s solved thank you for your help. I would like to ask something related with input data.

        I’m not too sure how should I address the problem of doing the same classification as I have done but instead of using a csv file using more csv’s files with completely different variables.

        I’m not sure if I should create 3 different models and combine later or if there’s a different way to solve this. Any hint with this would help me a lot.

        Thank you in advance.

        Reply
        • Avatar
          Adrian Tam August 13, 2021 at 2:22 am #

          “Bagging” or “ensemble learning” is a technique in machine learning doing exactly like what you said. You can definitely create different models and train them independently, and later combine them, such as by taking their average.

          Reply
  118. Avatar
    Misha August 13, 2021 at 6:32 pm #

    Dear Jason,

    I am trying to implement a CNN network + LSTM to be able to predict the class based on the sequence of images. My X-train shape is (10, 256, 150, 150, 3). Images’ size is 150*150*3, and each image sequence includes 256 images (so I have 10 image sequences). I defined time-steps to be 256, channels (features) to be 3. This is a part of my code:

    X_data = np.reshape(X_data, (10, 256, 150, 150, 3))
    Y_data = np.reshape(Y_data, (10, 256, 1))

    model = tf.keras.models.Sequential()
    model.add(TimeDistributed(Conv2D(filters=64, kernel_size=3, activation=’relu’), input_shape=(None, 256, 150, 150,3)))
    model.add(TimeDistributed(Conv2D(filters=64, kernel_size=3, activation=’relu’)))
    model.add(TimeDistributed(Dropout(0.5)))
    model.add(TimeDistributed(MaxPool2D(pool_size=2)))
    model.add(TimeDistributed(Flatten()))
    model.add(LSTM(100))
    model.add(Dropout(0.5))
    model.add(Dense(100, activation=’relu’))
    model.add(Dense(3, activation=’softmax’))
    model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])

    model.fit(X_data, Y_data, verbose=1, epochs=epochs, callbacks=callbacks)

    And I get this error:

    ValueError: Input 0 of layer max_pooling2d is incompatible with the layer: expected ndim=4, found ndim=5. Full shape received: (None, 256, 146, 146, 64)

    Can you please tell me What is the problem with input_shape and how can I give the network the desired input()?

    I tried several different input shapes but every time I get an error regarding the dimension of input.

    Reply
    • Avatar
      Adrian Tam August 14, 2021 at 3:11 am #

      Sorry I can’t debug your code but what it might help is that the max_pooling2d layer in the error message is not your input layer. Please see if you can trace back where is causing that. One way to do is to remove some layers in the model until you see the error goes away. That can tell you which layer is configured wrong.

      Reply
  119. Avatar
    Don August 19, 2021 at 7:45 am #

    Dear Jason,

    Thanks again for the post!

    I have another question. In my case, I have only 10 time steps (vs. 128 in this post) with no overlap between the time windows, and I have only 2-3 features (vs. 9 in this post). How many LSTM units I should take (in this post 100 units were taken)? Any rule I should follow maybe even some thumb rule? And a similar question regarding the units in the dense layer, which number should I take? Any rules here?

    Many thanks,
    Don

    Reply
    • Avatar
      Adrian Tam August 20, 2021 at 1:09 am #

      No rules here. The best bet is to read other people’s code, especially those with similar problem as yours, and try to tweak around their design. Hyperparameters like the number of units can also be underfit or overfit. If you get too few units, for example, your model learn nothing. If you get too much, your model may take too long time to converge and fail to generalize.

      Reply
  120. Avatar
    Don August 20, 2021 at 5:16 pm #

    Thanks Adrian for the quick reply!

    I guess that when Jason set the number of LSTM units to be 100 it was not a random number, and there are reasons he didn’t set it to 10 or 1000. For example, the amount of data puts constraints on the number of free parameters (which are connected to the number of units). Is it possible to get Jason’s view on my question?

    Thanks a lot,
    Don

    Reply
    • Avatar
      Adrian Tam August 21, 2021 at 5:03 am #

      Checked with Jason. That’s arbitrary as it is just a demonstration. In reality, as I mentioned before, you need to try out different values and evaluate. Often it is a trade off between model complexity and output accuracy.

      Reply
      • Avatar
        Don August 21, 2021 at 5:14 pm #

        Thanks for checking with Jason! Ok, then I’ll try different values.

        Thanks again,
        Don

        Reply
  121. Avatar
    Micheal August 21, 2021 at 3:15 am #

    Thank you for this wonderful explanation.

    Please, I am working on an experiment and would love to know if using LSTM algorithm will be most suitable for my experiment.

    I am trying to learn the behavioral pattern of a single individual living in a 4 room house. I can get data (movement from one door to another and the time spent in each room) from the simulation using PIR sensors. I want to be able to predict when the occupant generates an abnormal behavior like, spending more time in the kitchen than usual (maybe he has fallen down and requires the Ambulance).

    Also, if the sequence of data collected over a period of time seems normal and all of a sudden a sequence of some seemingly inaccurate data is generated over a short time period and then correct data sequence starts coming in again; I need to be able to predict that this would be a possible sensor malfunction. For instance. If all previous readings are normal and I notice a move from room1 to room4 which is clearly abnormal but all other subsequent readings continues normally; the prediction algorithm should be able to infer this situation as caused by the sensors in doors 2 and 3 not capturing when the occupant passed through them.

    Thank you.

    Reply
    • Avatar
      Adrian Tam August 21, 2021 at 5:20 am #

      I cannot really tell because you didn’t give any design on how you would use the LSTM. This kind of problem can also be applied using other techniques. But if you’re using LSTM, you are remembering some pattern in the network and producing output based on input. If you can quantify what is your input, what would be the output, and why remembering something is required, then you should easily see whether LSTM is a good fit.

      Reply
  122. Avatar
    Josh August 23, 2021 at 9:11 pm #

    Hi Adrian,

    I have three models using this method that are exactly the same. In each of these models the input has the same 3 dimensions (changing the values because data is different, but following the same structure of: time steps, 1 ,and features).

    The problem I’m facing is that following all of them the same structure, only 2 of those 3 models work. I’m not sure why but in one of them it’s printing the same accuracy all the time, I didn’t really touch anything, the models are the same and the structure of input data is as well.

    The only difference I see from this input data compared with the rest is that there are way more variables (160, while on the other cases it’s 2 or just 40 variables), can this be the reason? if not what do you think it could be?

    Thank you in advance.

    Reply
    • Avatar
      Adrian Tam August 24, 2021 at 8:36 am #

      160 vs 2 is very imbalanced. Of course this will hurt (usually, also depends on variation of the data, e.g., whether the 160 are binary variables or floating point values).

      Reply
  123. Avatar
    alireza karimi August 31, 2021 at 1:57 am #

    Hi Adrian Tam

    first of all I really appreciate your precious effort sharing the materials with us. As a beginner I have two questions,
    1. the way to use the model for prediction of a new input or a test case.

    2. <for another case using ategorical_crossentropy and sofmax, the output of the prediction was like this [[0.08681168 0.11935446 0.09112465 0.09589134 0.10852194 0.08946144
    0.10187661 0.11885039 0.0876272 0.10048036]] while I expected to see the integer. I was wondering if you could answer my questions

    Reply
    • Avatar
      Adrian Tam September 1, 2021 at 8:16 am #

      (1) I think you just borrow the code from this post should work; (2) that’s the nature of softmax. It gives you a list of probability-like value and usually we just pick the one with highest “probability” as the classification output.

      Reply
  124. Avatar
    Josh September 7, 2021 at 6:48 pm #

    Hi Adrian,

    I’m not sure why but accuracy is always the same, no matter if I change the data set always sets to a 25% or 0%. I had to make a padding of 0’s to make the second dimension the same in train and test and I’m not sure of this can be the reason for the model to not work properly.

    So the structure (and input adding to the model) I have is trainX = (10,1000,140) trainy = (10,8) testX = (3,1000,140) testy = (3,8)

    The majority of rows from that 1000 are the padding of 0’s, I got this 1000 because it was the max number of labels of a specific class from the 8 I have to classify, so we include all the data.

    I believe this has nothing to do with reseting the seed, if you could please give me some idea of what can be happening I would be very thankful.

    Thank you in advance.

    Reply
    • Avatar
      Josh September 7, 2021 at 9:00 pm #

      I forgot to say that with a different data set of structure trainX = (43, 369, 49) trainy = (43, 8)
      testX = (8, 369, 49) testy = (8, 8), the accuracy is always the same but in this case 12.5%. So it shouldn’t be a problem of having a high value on the second dimension.

      Here I did a padding of 0’s as well, since originally the input was trainX = (15867, 49)
      trainy = (43,8) testX = (2952, 49) testy = (8, 8) after reshaping it.

      The original labels have been subdivided in “groups” of 8 (testy) and 43 (trainy) respectively because each group has actions happening many times

      I’m looking forward for your response.

      Reply
    • Avatar
      Adrian Tam September 8, 2021 at 1:37 am #

      Can you explain what are each of the dimension (10,1000,140) means?

      Reply