The choice of optimization algorithm for your deep learning model can mean the difference between good results in minutes, hours, and days.
The Adam optimization algorithm is an extension to stochastic gradient descent that has recently seen broader adoption for deep learning applications in computer vision and natural language processing.
In this post, you will get a gentle introduction to the Adam optimization algorithm for use in deep learning.
After reading this post, you will know:
- What the Adam algorithm is and some benefits of using the method to optimize your models.
- How the Adam algorithm works and how it is different from the related methods of AdaGrad and RMSProp.
- How the Adam algorithm can be configured and commonly used configuration parameters.
Kick-start your project with my new book Better Deep Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
What is the Adam optimization algorithm?
Adam is an optimization algorithm that can be used instead of the classical stochastic gradient descent procedure to update network weights iterative based in training data.
Adam was presented by Diederik Kingma from OpenAI and Jimmy Ba from the University of Toronto in their 2015 ICLR paper (poster) titled “Adam: A Method for Stochastic Optimization“. I will quote liberally from their paper in this post, unless stated otherwise.
The algorithm is called Adam. It is not an acronym and is not written as “ADAM”.
… the name Adam is derived from adaptive moment estimation.
When introducing the algorithm, the authors list the attractive benefits of using Adam on non-convex optimization problems, as follows:
- Straightforward to implement.
- Computationally efficient.
- Little memory requirements.
- Invariant to diagonal rescale of the gradients.
- Well suited for problems that are large in terms of data and/or parameters.
- Appropriate for non-stationary objectives.
- Appropriate for problems with very noisy/or sparse gradients.
- Hyper-parameters have intuitive interpretation and typically require little tuning.
Want Better Results with Deep Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
How Does Adam Work?
Adam is different to classical stochastic gradient descent.
Stochastic gradient descent maintains a single learning rate (termed alpha) for all weight updates and the learning rate does not change during training.
A learning rate is maintained for each network weight (parameter) and separately adapted as learning unfolds.
The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients.
The authors describe Adam as combining the advantages of two other extensions of stochastic gradient descent. Specifically:
- Adaptive Gradient Algorithm (AdaGrad) that maintains a per-parameter learning rate that improves performance on problems with sparse gradients (e.g. natural language and computer vision problems).
- Root Mean Square Propagation (RMSProp) that also maintains per-parameter learning rates that are adapted based on the average of recent magnitudes of the gradients for the weight (e.g. how quickly it is changing). This means the algorithm does well on online and non-stationary problems (e.g. noisy).
Adam realizes the benefits of both AdaGrad and RMSProp.
Instead of adapting the parameter learning rates based on the average first moment (the mean) as in RMSProp, Adam also makes use of the average of the second moments of the gradients (the uncentered variance).
Specifically, the algorithm calculates an exponential moving average of the gradient and the squared gradient, and the parameters beta1 and beta2 control the decay rates of these moving averages.
The initial value of the moving averages and beta1 and beta2 values close to 1.0 (recommended) result in a bias of moment estimates towards zero. This bias is overcome by first calculating the biased estimates before then calculating bias-corrected estimates.
The paper is quite readable and I would encourage you to read it if you are interested in the specific implementation details.
If you would like to learn how to code Adam from scratch in Python, see the tutorial:
Adam is Effective
Adam is a popular algorithm in the field of deep learning because it achieves good results fast.
Empirical results demonstrate that Adam works well in practice and compares favorably to other stochastic optimization methods.
In the original paper, Adam was demonstrated empirically to show that convergence meets the expectations of the theoretical analysis. Adam was applied to the logistic regression algorithm on the MNIST digit recognition and IMDB sentiment analysis datasets, a Multilayer Perceptron algorithm on the MNIST dataset and Convolutional Neural Networks on the CIFAR-10 image recognition dataset. They conclude:
Using large models and datasets, we demonstrate Adam can efficiently solve practical deep learning problems.
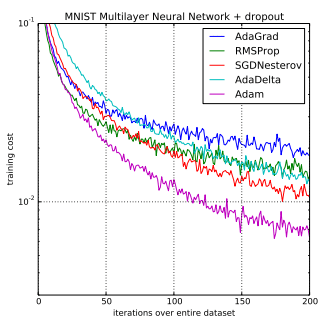
Comparison of Adam to Other Optimization Algorithms Training a Multilayer Perceptron
Taken from Adam: A Method for Stochastic Optimization, 2015.
Sebastian Ruder developed a comprehensive review of modern gradient descent optimization algorithms titled “An overview of gradient descent optimization algorithms” published first as a blog post, then a technical report in 2016.
The paper is basically a tour of modern methods. In his section titled “Which optimizer to use?“, he recommends using Adam.
Insofar, RMSprop, Adadelta, and Adam are very similar algorithms that do well in similar circumstances. […] its bias-correction helps Adam slightly outperform RMSprop towards the end of optimization as gradients become sparser. Insofar, Adam might be the best overall choice.
In the Stanford course on deep learning for computer vision titled “CS231n: Convolutional Neural Networks for Visual Recognition” developed by Andrej Karpathy, et al., the Adam algorithm is again suggested as the default optimization method for deep learning applications.
In practice Adam is currently recommended as the default algorithm to use, and often works slightly better than RMSProp. However, it is often also worth trying SGD+Nesterov Momentum as an alternative.
And later stated more plainly:
The two recommended updates to use are either SGD+Nesterov Momentum or Adam.
Adam is being adapted for benchmarks in deep learning papers.
For example, it was used in the paper “Show, Attend and Tell: Neural Image Caption Generation with Visual Attention” on attention in image captioning and “DRAW: A Recurrent Neural Network For Image Generation” on image generation.
Do you know of any other examples of Adam? Let me know in the comments.
Adam Configuration Parameters
- alpha. Also referred to as the learning rate or step size. The proportion that weights are updated (e.g. 0.001). Larger values (e.g. 0.3) results in faster initial learning before the rate is updated. Smaller values (e.g. 1.0E-5) slow learning right down during training
- beta1. The exponential decay rate for the first moment estimates (e.g. 0.9).
- beta2. The exponential decay rate for the second-moment estimates (e.g. 0.999). This value should be set close to 1.0 on problems with a sparse gradient (e.g. NLP and computer vision problems).
- epsilon. Is a very small number to prevent any division by zero in the implementation (e.g. 10E-8).
Further, learning rate decay can also be used with Adam. The paper uses a decay rate alpha = alpha/sqrt(t) updted each epoch (t) for the logistic regression demonstration.
The Adam paper suggests:
Good default settings for the tested machine learning problems are alpha=0.001, beta1=0.9, beta2=0.999 and epsilon=10−8
The TensorFlow documentation suggests some tuning of epsilon:
The default value of 1e-8 for epsilon might not be a good default in general. For example, when training an Inception network on ImageNet a current good choice is 1.0 or 0.1.
We can see that the popular deep learning libraries generally use the default parameters recommended by the paper.
- TensorFlow: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08.
Keras: lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0. - Blocks: learning_rate=0.002, beta1=0.9, beta2=0.999, epsilon=1e-08, decay_factor=1.
- Lasagne: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08
- Caffe: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08
- MxNet: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8
- Torch: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8
Do you know of any other standard configurations for Adam? Let me know in the comments.
Further Reading
This section lists resources to learn more about the Adam optimization algorithm.
- Adam: A Method for Stochastic Optimization, 2015.
- Stochastic gradient descent on Wikipedia
- An overview of gradient descent optimization algorithms, 2016.
- ADAM: A Method for Stochastic Optimization (a review)
- Optimization for Deep Networks (slides)
- Adam: A Method for Stochastic Optimization (slides).
- Code Adam Gradient Descent Optimization From Scratch
Do you know of any other good resources on Adam? Let me know in the comments.
Summary
In this post, you discovered the Adam optimization algorithm for deep learning.
Specifically, you learned:
- Adam is a replacement optimization algorithm for stochastic gradient descent for training deep learning models.
- Adam combines the best properties of the AdaGrad and RMSProp algorithms to provide an optimization algorithm that can handle sparse gradients on noisy problems.
- Adam is relatively easy to configure where the default configuration parameters do well on most problems.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.







The name thing is a little strange. What was so wrong with AdaMomE? The abbreviated name is only useful if it encapsulates the name, adaptive moment estimation. I think part of the process of writing useful papers is coming up with an abbreviation that will not irritate others in the field, such as anyone named Adam.
Adam is catchy.
hehe ur name is adam
Lol! Why do you take it personally? Well, you do look like a character from THE ADDAMS FAMILY. Something to ponder upon!
Yes of course daddy what’s the problem 🙁 I like your name, I think it’s efficient even in this EPOCH;)
Salut frangin ! Ne renie pas ton prénom, à bon entendeur
Using it already for a year , don’t see any reason to use anything different . My main issue with deep learning remains the fact that a lot of efficiency is lost due to the fact that neural nets have a lot of redundant symmetry built in that leads to multiple equivalent local optima . There must be a way to address this mathematically . It puzzles me that nobody had done anything about . If you did this in combinatorics (Traveling Salesman Problems type of problems ), this would qualify as a horrendous model formulation .
It would be great to see what you can dig up on the topic. Neural nets have been studied for a long time by some really bright people.
Those bright people may excel in statistics , but non linear non convex optimization is a very specialized field where other very bright people excel . The same applies to Integer and Combinatorial optimization : very specialized field .The days of “homo universalis” are long gone . By the way , although I am impressed by recent results in deep learning , I am not so deeply impressed by the technology . It’s just an unconstrained very big non linear optimization problem , so what ? And the thing is , you should not even try to find the true optimum , because that is 100% sure to overfit . So , in the end , we have to conclude that true learning aka generalization is not the same as optimizing some objective function , Basically , we still don’t know what “learning is” , but we know that iit s not “deep learning” . I have a hunch that this (deep learning) approach to “general AI” will fail .
I would argue deep learning methods only address the perception part of AI.
But what you describe is a result of using to many nodes, you fear over-fitting.
With the proper amount of nodes they dont become ‘beasts’ of redundant logic.
But i guess a lot of people are missing the point about what to train, with what data, and with the best neural network for that task.
I just red an article in which someone improved natural language to text, because he thought about those thinks, and as a result he didnt require deep nets , he was also able to train easily for any language (as in contrast to the most common 5). With a better speech to text score.
I think with the advancement in hardware people forget often about the ‘beauty’ of properly efficient coding, the same counts for neural network designs
I often say that the points of biggest leverage are in the framing of the problem.
Could you share that ref?
Perhaps the lottery ticket hypothesis is relevant here?
@Gerrit I have been wondering about the exact same thing – are there maybe ways to find symmetry or canonical forms that would reduce the search space significantly. Besides potentially speeding up learning, such representations could maybe enable better transfer learning or give us better insights into learning in general. It seems that the theory of DL is way behind practice. I must say that the results are often amazing, but I’m not comfortable with the almost entirely empirical approach.
Hi Jason. Thanks for you amazing tutorials. I have already read some, and already putting some into practice as well. As many other blogs on the net, I found yours by searching on google “how to predict data after training a model”, since I am trying to work on a personal project using LSTM. Surely enough I ran into your great informational blog.
One thing I wanted to comment on, is the fact that you mention about not being necessary to get a phd to become a master in machine learning, which I find to be a biased proposition all depending on the goal of the reader. However, most phd graduates I have found online – to mention some, yourself, Sebastian as you recommended in this post, Andrew Ng, Matt Mazur, Michael Nielsen, Adrian Rosebrock, some of the people I follow and write amazing content all have phd’s. Excluding Siraj, a current youtube blogger that makes amazing videos on machine learning – one of the few I have seen thus far that does not hold a phd, not even a bachelors. My point and question to you is.. Without a phd, would you have had the skills to make all this content found in your website? And I’m not referring to just being adept in the topic of AI, but also writing amazing in depth topics, creating amazing design for the site, book for others to read, and even clean codes in python?
As a different note, about me, for the past ten years, my profession has been in Information technology. I currently work as a systems administrator for a medium size enterprise, but for the past three years since I started college, I grew this passion toward programming, which eventually grew into machine learning. I became obsessed with Neural Networks and its back prop, and currently are now obsessed with learning more about LSTM’s. I have been testing with one of your codes. Although I still struggle with knowing how to predict data. Without being able to predict data, I feel lost. For example, most articles I find, including yours (Sorry if I haven’t found my answer yet in your site), only show how to train data, and test data. So for example, this is what I find;
x= 0001 y= 0010
x= 0010 y= 0011
x[m1,,,,,,m]
y[m1,,,,,,m]
—Usually the output I get printer—
But to this day, I haven’t learned how to feed unknown data to a network and it to predict the next unknown output such as;
if x== 0100, then, what will ‘y’ be? that is, without feeding the network the next possible, rather its suppose to tell me based on the pattern learned before.
If a training set == m, and test set also == m, then I should be able to ask for a result == n. Maybe you can guide towards the right direction?
I am currently in the first semester of a bachelor in Computer Science, and always have in the back of my head in pursuing all the way towards a phd, this is, to become an amazing writer of my own content in the field of machine learning – not Just become a “so so” data scientist, although I am still very far from getting to that level. Frankly, what really calls my attention in pursuing a higher degree, is the fact that the math learned in school, is harder to pick up as a hobby. Which is my case; this is my every day hobby.
Thanks for everything Jason, its now time to continue reading through your blog… :-p.
Making a site and educational material like this is not the same as delivering results with ML at work.
The same as the difference from a dev and a college professor teaching development. Very different skill sets.
Consider this post on finalizing a model in order to make predictions:
https://machinelearningmastery.com/train-final-machine-learning-model/
Does that help?
Hey Jason! What about Nadam vs Adam?
Nadam si a Keras optimizer which is essentially ‘Adam’+ Nesterov momentum.
Also what is Nesterov momentum?
And how can we figure out a good epsilon for a particular problem?
Thanks a lot!
Great question. I don’t know much about it sorry.
https://i.stack.imgur.com/wBIpz.png
hope this helps 🙂
here http://cs229.stanford.edu/proj2015/054_report.pdf you can find the paper
Thanks for sharing.
Thank you for your great article. If I use Adam as an optimizer, do I still need to do learning rate scheduleing during the training?
Thanks a lot
No. I don’t believe so.
In a particular case of MNIST, I achieved better results while using adam +learning rate scheduler(test accuracy 99.71) as compared to only using adam(test accuracy 99.2).
Not sure that makes sense as each weight has its own learning rate in adam.
I also thought about this the same way, but then I made some optimization with different learning rates (unsheduled) and it had a substantial influence on the convergence rate. This is sort of the same, since I could say ‘Any (global) learning rate will just be compensated by the individual learning rate’. Look at it this way:
If you look at the implementation, the ‘individual learning rate’ you mentioned (in the original paper it is
(m/sqrt(v))_i) is build up by the magnitude of the gradient. This is totally independent of the learning rate! (Of course only if the gradients at the previous steps are the same). But a different learning rate under the same gradient-history will scale all step sizes and so make larger steps for larger alpha.Think about it this way: you optimize a linear slope. The momentum is picked up but there is a maximum, since the previous steps have exponentially less influence. Let’s say, the
min the original paper tends to 1. This is independent of thelearning_rate. This means, that varying it will change the convergence speed (yes, in this casextends to infinity, but forget about that…). Let’s return to a problem with a solution: What this means is thatlearning_ratewill limit the maximum convergence speed in the beginning. But in closer proximity to the solution, a large learning rate will increase the actual step size (despite a small m/sqrt(v)), which might still lead to an overshoot. Definitely not as big as if there was no automatic adaptation.I used the OperatorDiscretizationLibrary (ODL: https://github.com/odlgroup/odl) and it has the same default parameters, as mentioned in the original paper (or as Tensorflow)
Thanks for sharing.
As a prospective author who very likely will suggest a gentleman named Adam as a possible reviewer, I reject the author’s spelling of “Adam” and am using ADAM, which I call an optimization, “Algorithm to Decay by Average Moments” which uses the original authors’ term “decay” for what Tensorflow calls “loss.”
The variance here seems incorrect. I don’t mean incorrect as in different from the paper; I mean that it doesn’t truly seem to resemble variance; shouldn’t variance take into account the mean as well?
Here it appears the variance will continue to grow throughout the entire process of training. Wouldn’t we want the variance to shrink when we encounter hyper-surfaces with little change and growing variance on hyper-surfaces that are volatile?
H2o deep learning package use ADADELTA as the default adaptive rate.
It has rho, epsilon and rate parameters.
rho: Specifies the adaptive learning rate time decay factor. This parameter
is similar to momentum and relates to the memory for prior weight updates.
Typical values are between 0.9 and 0.999. The default value is 0.99. Refer to
Adaptive Learning for more details.
epsilon: When enabled, specifies the second of two hyperparameters for the
adaptive learning rate. This parameter is similar to learning rate annealing
during initial training and momentum at later stages where it assists progress.
Typical values are between 1e-10 and 1e-4. This parameter is only active if
adaptive rate is enabled. The default is 1e-8. Refer to Adaptive Learning
for more details.
rate: Specifies the learning rate. Higher values lead to less stable models,
while lower values result in slower convergence. The default is 0.005.
Can we map the rho to beta2, rate to alpha?
How do these parameters affects the adaptive rate? (proportional or inversely proportional)
Good question, I’m not sure off the cuff, perhaps experiment a little?
Every time I’m glad I find this blog whenever I’m trying to understand some machine learning topic. The fact that I have access to this concise and useful information restores my faith in humanity. Thank you!
Thanks Daniel, I’m happy to help.
You wrote: “should be set close to 1.0 on problems with a sparse gradient”. What’s the definition of “sparse gradient”?
A gradient that has lots of zero values, e.g. flat spots.
“Instead of adapting the parameter learning rates based on the average first moment (the mean) as in RMSProp, Adam also makes use of the average of the second moments of the gradients (the uncentered variance).”
shouldn’t this be:
“Instead of adapting the parameter learning rates based on the average second moment (the uncentered variance) as in RMSProp, Adam also makes use of the average of the first moments of the gradients (the mean).”
I think that RMSprop is using second moment, or am I mixing things up?
Why do you say that exactly?
I don’t recall the specifics.
Since RMSprop is using the SQUARED gradient to update the learning rate, this relates to the second moment, as far as I understand.
(see equations for example at https://en.wikipedia.org/wiki/Stochastic_gradient_descent#RMSProp)
I was expecting to see some wallpaper in the beginning of this page 🙂
That wallpaper is important. looks like you forgot to include it here.
What do you mean?
Hi Jason,
Thanks for this great article that helped me a lot 🙂
Just so you know, I am using Keras with Python 2.7, and default epsilon is set to 1e-7 instead of 1e-8 as you state (I know I am fussy).
Also, there is a “decay” parameter I don’t really catch. Do you know how to set it please (default is None… if it helps) ?
Again, thank you !
Florian
Thanks.
Sorry, I don’t have good advice for the decay parameter. Perhaps decay is mentioned in the paper to give some ideas?
No, unfortunately. It’s not.
If it helps someone, I dug into the code and I found out that the “decay” parameter allows the “learning_rate” parameter to vanish. The current decay value is computed as 1 / (1 + decay*iteration). And then, the current learning rate is simply multiplied by this current decay value.
As a result, the steps get more and more little to converge.
Florian
A learning rate decay.
thanks for a great effort
I have one question please about the decay with optimizer.adam such as
optimizer.adam(lr=0.01, decay=1e-6) does the decay here means the weight decay which is also used as regulization ?!
thanks in advance
Hi Jason,
Could you also provide an implementation of ADAM in python (preferably from scratch) just like you have done for stochastic SGD. It would help in understanding ADAM optimization for beginners.
Thanks for the great gist.
Thanks for the suggestion.
Python using Optimizer = Adam
https://github.com/llSourcell/How_to_simulate_a_self_driving_car/blob/master/model.py
Thanks for sharing.
do I understand it right: in backpropagation during training my gradient of my activation function is optimized by adam or adaelta etc, and stochastict gradient descent is also a method like adam or how does this affect backpropagation ?
The weights are optimized via an algorithm called stochastic gradient descent.
A version of gradient descent that works well is Adam.
The update to the weights is performed using a method called the ‘backpropagation of error’ or backpropagation for short.
Hi, As far as I know the Adam optimizer is also responsible for updating the weights. It may use a method like the backpropagation to do so.
Adam is used in “Scalable and accurate deep learning with electronic health records”, described here: https://ai.googleblog.com/2018/03/making-healthcare-data-work-better-with.html . The reference to Adam, though, is in the Supplementary Material of the paper, https://static-content.springer.com/esm/art%3A10.1038%2Fs41746-018-0029-1/MediaObjects/41746_2018_29_MOESM1_ESM.pdf
Thanks for sharing.
Adam is also used in “End-to-end driving via Conditional Imitation Learning” by Codevilla, Müller, Lopez et al. https://arxiv.org/pdf/1710.02410.pdf
Thanks.
hi Jason, thanks for the article!
I hadn’t understand a part.
You say: “A learning rate is maintained for each network weight (parameter) and separately adapted as learning unfolds.”
The paper says: “The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients.”
I’m not sure that i really understand it: basically the algorithm compute a specific learning rate for each weight, so if we had a network with 255m of parameters, it compute 255m of learning rates?
But how is possible? we had alpha that’s the learning rate..
Seeing the pseudocode in the paper i suppose that maybe it’s work as follows: its use the learning rate alpha as static, multiplied for (mt/(vt + e)) that generates in practice a new learning rate for a specific iterations of the algorithm, but i’m not sure about this.
I totally don’t understand this part: “and separately adapted as learning unfolds.”
Could you explain this more clearly?
Thanks!
Sorry for the confusion.
I am highlighting that indeed, a separate learning rate is maintained for each parameter and that each learning rate is adapted in response to the specific gradients observed flowing through the network at that point – e.g. relevant for that weight, that the learning rates are adapted separately.
This is based on my reading of the paper.
Does that help?
Maybe, i will try to explain what i think now:
basically, we had a learning rate alpha (that we set manually), then we got another learning rate alpha2 internal the algorithm, and when there’s the update of the weights, it’s consider our learning rate alpha (fixed) and also the learning rate calculated for this specific iteration (alpha2).
Next iteration we had our fixed learning rate alpha, but the previous learning rate alpha2 will get updated with another value, so we lost the previous value for alpha2.
It’s a correct interpretation?
By the way, looking for the “alpha2”, i noticed that in the pseudo code (https://arxiv.org/pdf/1412.6980.pdf, page 2) the only thing that suggest me is alpha2 is that mt/(root(vt) – epsilon), otherwise i don’t know which can be.
I’ve built a classical backpropagation ANN using Keras for a regression problem, which has two hidden layers with a low amount of neurons (max. 8 per layer). The optimizer I use is ADAM. The amount of samples for training and validating is 20000, divided 90% and 10% respectively.
Is there anything wrong with those graphs?
https://i.imgur.com/wrP18WR.jpg
Is it normal to have this kind of dropdown at the beginning of VAL_LOSS? Too low batch size (currently 128)? Any overfitting/underfitting?
Well done.
I have some suggestions or interpreting the learning curves here:
https://machinelearningmastery.com/learning-curves-for-diagnosing-machine-learning-model-performance/
Thank you for the link. Can you please give some comment on my graphs? Is it a good learning curve? Learning rate too fast (default)?
Looks like a fast convergence. Perhaps try slowing down the rate of learning and see how that impacts the final result?
Hi Jason,
Thanks for the intro to Adam .It is very helpful and clear to understand.
I am currently using the MATLAB neural network tool to classify spectra. Do you know if
(i) MATLAB produces a template for classification using Adam?
(ii) Are there any preferred starting parameters to use (alpha, beta 1 , beta 2 ) when classifying spectra on an Adam based system?
Sorry, I don’t have examples for matlab.
Yes, there are sensible defaults for Adam and they are set in Keras:
https://keras.io/optimizers/
Hi Jason,
I hope you can do a comparison for some optimizers, e.g. SGD, Adam and AdaBound, with different batch size, learning rate, momentum etc.
Currently I am running a grid search for these three. I use AdaBound for Keras:
https://github.com/titu1994/keras-adabound
Nice work.
Hello Jason, Since Adam divides the update √v, which of the model parameters will get larger updates? Why might this help with with learning?
To clarify, why is the first moment divided by the square root of the second moment when the learning parameters are updated?
Hi Jason, thanks for your always awesome articles. Short question, why does it matter which initial learning rate to set for adam, if it adapts it during training anyway? It seems like the individual learning rates for each parameters are not even bounded by 1 so anyhow it shouldn’t matter much no? thanks for your answer.
Good question, starting point is a big deal in optimization problems.
Hi Jason,
Thanks for your post. I have few basic questions in which I am confused.
1) For Adam what will be our cost function? Will it be (1/N)(cross-entropy) or just cross entropy, if N is batch size.
2) I followed this post and here author is using batch size but during update of parameters he is not using the average of parameters neither sum. May be I am not able to understand it clearly. Can you help me here.
3) Does Adam works well with higher batch size?
Adam can work with any loss you like.
Adam will work with any batch size you like.
Adam is just the optimization procedure, a type of stochastic gradient decent with adaptive learning rate.
I forgot to ask one more question. Do we need to decay lambda the penalty for weights and learning rate during Adam optimization processing?
You can try using Adam with and without a weight penalty.
Hello Dear Jason
Kindly tell me how to add ” Adam version of stochastic gradient descent ” in python
In Keras, you specify the optimizer as ‘adam’, there is an example here:
https://machinelearningmastery.com/tutorial-first-neural-network-python-keras/
Hello Sir,
Greetings of the Day!
Currently i am using adam in my cnn model for image classification.
Can i customize adam or use some features/data as optimizer in CNN? is it possible or not?
plz help.
Not sure I understand, what do you mean exactly?
Adam is just an optimization algorithm. It does not use features.
sir actually i calculated feature correlation loss in my cnn model and i want to use it as an optimizer to improve accuracy of model. so is it possible or not?
No idea, perhaps try it and see?
Hi Jason,
what would be reasonable ranges for HyperTunning to Beta1, Beta2 and epsilon?
thanks a lot for all the amazing content that you share with us!
Great question.
lrate perhaps on a log scale
beta1 perhaps 0.5 to 0.9 in 0.1 increments
beta2 perhaps 0.90 to 0.99 in 0.01 increments?
eps – na.
Lrate has all the leverage – that would be my guess.
In the sentence “The Adam optimization algorithm is an extension to stochastic gradient descent”, ” stochastic gradient descent” should be “mini-batch gradient descent”. right?
Not really. Mini-batch/batch gradient descent are simply configurations of stochastic gradient descent.
dragonfly optimizer is that possible on Keras compiler?
I mean model.compile(loss=’binary_crossentropy’,optimizer=’adam’,metrics=[‘accuracy’])
use that line ( optimizer=’adam’).
What is “dragonfly optimizer”?
Dragonfly is an open-source python library for scalable Bayesian optimisation.
Bayesian optimisation is used for optimising black-box functions whose evaluations are usually expensive. Beyond vanilla optimisation techniques, Dragonfly provides an array of tools to scale up Bayesian optimisation to expensive large scale problems. These include features/functionality that are especially suited for high dimensional optimisation (optimising for a large number of variables), parallel evaluations in synchronous or asynchronous settings (conducting multiple evaluations in parallel), multi-fidelity optimisation (using cheap approximations to speed up the optimisation process), and multi-objective optimisation (optimising multiple functions simultaneously).
https://github.com/dragonfly/dragonfly
https://dragonfly-opt.readthedocs.io/en/master/getting_started_py/
Thanks for sharing!
This is possible or not
Not directly, no. You would have to integrate it yourself and I would not expect it to perform well.
Hello Jason,
Is it fair to say that Adam, only optimizes the “Learning Rate”? If not, can you give a brief about what other areas does it touch other than the learning rate itself?
It aims to optimize the optimization process itself.
Hi Jason, Clear illustration for a complex topic
you mentioned “Instead of adapting the parameter learning rates based on the average first moment (the mean) as in RMSProp, Adam also makes use of the average of the second moments of the gradients (the uncentered variance)”.
I belive RMSProp is the one “makes use of the average of the second moments of the gradients (the uncentered variance)”.
Am I right?
Thanks.
See the variancecounter balancing alternative.
https://www.worldscientific.com/doi/abs/10.1142/S0218213020500104
Thanks for sharing.
“Again, depending on the specifics of the problem, the division of columns into X and Y components can be chosen arbitrarily, such as if the current observation of var1 was also provided as input and only var2 was to be predicted.”
In the case where we want to predict var2(t) and var1(t) is also available.
var1(t-2),var2(t-2),var1(t-1) ,var2(t-1),var1(t),var2(t)
Lstm networks want a 3D input. What shape should we give to the train_X?
Do i have to give shape [X,1,5] ?
In case we had an even number for train_X (when we dont have var1(t)), we had to shape like this,
[X,2,2]
But now its not an even number and i cannot shape like this because we have 5 features for train_X
The only solution is to give shape [X,1,5]?
*X length of dataset
Please ignore this comment i posted on the wrong article.
Good question, see this:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
I like the way you explain things – it is very focused, short and precise.
Keep doing, thanks.
Thank you!
The model size is huge different with different optimizers,right? model trained by adam is huge bigger than sgd model. Adam model is more better than sgd model,except model size problem. i want to know if you have any advise about this problem.
The size of the model does not change under diffrent optimizers.
The role of an optimizer is to find a set of parameters (weights) in a fixed sized model using a fixed training dataset.
Does Adam need the learning rate to be annealed?
Yes and no, it adapts the learning rate automatically for each parameter and part of this automatic adaptation involves some annealing of the momentum.
Thanks. You are truly my teacher who answered all the questions I had.
You’re welcome, I’m happy to hear that.
If I want to choose the best optimizer for my deep learning model (from ADAM, Sgdm,…) , how can I compare between performance to them , If any suggestion to compare between them , by figures , values,….?….
and, if I choose learning rate first and then optimizer?
actually, How I can choose best learning rate and best optimizer for the model , whom to choose first and How???
Perhaps test each in turn with a range of configurations and see which results in the best performing model.
It might be more cost effective to run Adam once, then run SGD and tune it to see if it can do better.
Hello! Do you cover Adam in your book ‘Better Deep Learning’? If not, do you cover it in another one of your books?
No, not really. I hope to have a book dedicated to “optimization” in the future.
Thanks. Very good an paper.
Thanks.
Your articles, as always, clarify topics beautifully. Minor typos:
“Adam is an optimization algorithm that can be used instead of the classical stochastic gradient descent procedure to update network weights iterative based in training data.”
Do you mean “iterativeLY based ON training data”?
Thanks.
Your articles, as always, clarify topics beautifully. Minor typos:
“Adam is an optimization algorithm that can be used instead of the classical stochastic gradient descent procedure to update network weights iterative based in training data.”
Do you mean “iterativeLY based ON training data”?
“Adam is different to classical stochastic gradient descent.”
I presume you mean “FROM classical…”
“A learning rate is maintained for each network weight (parameter) and separately adapted as learning unfolds.” – Suggest adding the words, “With Adam, a learning rate…”
“updted each epoch” –>”updated”
Thanks.
Dear Jason Brownlee
Thanks for your amazing contents.
Here I have one question, as in original paper it is stated that each weight has its own learning rate but I am getting far better result using adam+Learning rate scheduler (ReduceLROnPlateau).
You can have look at it https://imgur.com/a/P2mkQWy
In theory there is no such material to prove, can you please explain the possible reason for it?
Thank you.
Hi Shah…My recommendation would be to work through the examples presented in the following resource:
https://machinelearningmastery.com/optimization-for-machine-learning/
Hey Jason,
Thanks for your amazing articles.
I would like to tell you that I am using learning scheduling (ReduceLROnPlateau with adam. I can clearly see, it does effect the model performance. You can check it by visiting the following link.
https://imgur.com/a/P2mkQWy
Can you please explain the logic behind it?
I will be very thankful you
regards,
Hi Zuheer,
I am able to better assist you with specific questions regarding concepts presented in our materials.
Regards,
Ok. Got it.
Thank you so much
“Sebastian Ruder developed a comprehensive review of modern gradient descent optimization algorithms titled “An overview of gradient descent optimization algorithms” published first as a blog post, then a technical report in 2016.”
-> The link to the blog post does not work. Is this the correct one?
https://ruder.io/optimizing-gradient-descent/