Stacking Ensemble for Deep Learning Neural Networks in Python

Last Updated on August 28, 2020

Model averaging is an ensemble technique where multiple sub-models contribute equally to a combined prediction.

Model averaging can be improved by weighting the contributions of each sub-model to the combined prediction by the expected performance of the submodel. This can be extended further by training an entirely new model to learn how to best combine the contributions from each submodel. This approach is called stacked generalization, or stacking for short, and can result in better predictive performance than any single contributing model.

In this tutorial, you will discover how to develop a stacked generalization ensemble for deep learning neural networks.

After completing this tutorial, you will know:

• Stacked generalization is an ensemble method where a new model learns how to best combine the predictions from multiple  existing models.
• How to develop a stacking model using neural networks as a submodel and a scikit-learn classifier as the meta-learner.
• How to develop a stacking model where neural network sub-models are embedded in a larger stacking ensemble model for training and prediction.

Kick-start your project with my new book Better Deep Learning, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

• Updated Oct/2019: Updated for Keras 2.3 and TensorFlow 2.0.
• Update Jan/2020: Updated for changes in scikit-learn v0.22 API.
• Update Aug/2020: Updated for Keras 2.4.3 and TensorFlow 2.3

How to Develop a Stacking Ensemble for Deep Learning Neural Networks in Python With Keras
Photo by David Law, some rights reserved.

Tutorial Overview

This tutorial is divided into six parts; they are:

1. Stacked Generalization Ensemble
2. Multi-Class Classification Problem
3. Multilayer Perceptron Model
4. Train and Save Sub-Models
5. Separate Stacking Model
6. Integrated Stacking Model

Stacked Generalization Ensemble

A model averaging ensemble combines the predictions from multiple trained models.

A limitation of this approach is that each model contributes the same amount to the ensemble prediction, regardless of how well the model performed. A variation of this approach, called a weighted average ensemble, weighs the contribution of each ensemble member by the trust or expected performance of the model on a holdout dataset. This allows well-performing models to contribute more and less-well-performing models to contribute less. The weighted average ensemble provides an improvement over the model average ensemble.

A further generalization of this approach is replacing the linear weighted sum (e.g. linear regression) model used to combine the predictions of the sub-models with any learning algorithm. This approach is called stacked generalization, or stacking for short.

In stacking, an algorithm takes the outputs of sub-models as input and attempts to learn how to best combine the input predictions to make a better output prediction.

It may be helpful to think of the stacking procedure as having two levels: level 0 and level 1.

• Level 0: The level 0 data is the training dataset inputs and level 0 models learn to make predictions from this data.
• Level 1: The level 1 data takes the output of the level 0 models as input and the single level 1 model, or meta-learner, learns to make predictions from this data.

Stacked generalization works by deducing the biases of the generalizer(s) with respect to a provided learning set. This deduction proceeds by generalizing in a second space whose inputs are (for example) the guesses of the original generalizers when taught with part of the learning set and trying to guess the rest of it, and whose output is (for example) the correct guess.

— Stacked generalization, 1992.

Unlike a weighted average ensemble, a stacked generalization ensemble can use the set of predictions as a context and conditionally decide to weigh the input predictions differently, potentially resulting in better performance.

Interestingly, although stacking is described as an ensemble learning method with two or more level 0 models, it can be used in the case where there is only a single level 0 model. In this case, the level 1, or meta-learner, model learns to correct the predictions from the level 0 model.

… although it can also be used when one has only a single generalizer, as a technique to improve that single generalizer

— Stacked generalization, 1992.

It is important that the meta-learner is trained on a separate dataset to the examples used to train the level 0 models to avoid overfitting.

A simple way that this can be achieved is by splitting the training dataset into a train and validation set. The level 0 models are then trained on the train set. The level 1 model is then trained using the validation set, where the raw inputs are first fed through the level 0 models to get predictions that are used as inputs to the level 1 model.

A limitation of the hold-out validation set approach to training a stacking model is that level 0 and level 1 models are not trained on the full dataset.

A more sophisticated approach to training a stacked model involves using k-fold cross-validation to develop the training dataset for the meta-learner model. Each level 0 model is trained using k-fold cross-validation (or even leave-one-out cross-validation for maximum effect); the models are then discarded, but the predictions are retained. This means for each model, there are predictions made by a version of the model that was not trained on those examples, e.g. like having holdout examples, but in this case for the entire training dataset.

The predictions are then used as inputs to train the meta-learner. Level 0 models are then trained on the entire training dataset and together with the meta-learner, the stacked model can be used to make predictions on new data.

In practice, it is common to use different algorithms to prepare each of the level 0 models, to provide a diverse set of predictions.

… stacking is not normally used to combine models of the same type […] it is applied to models built by different learning algorithms.

— Practical Machine Learning Tools and Techniques, Second Edition, 2005.

It is also common to use a simple linear model to combine the predictions. Because use of a linear model is common, stacking is more recently referred to as “model blending” or simply “blending,” especially in machine learning competitions.

… the multi-response least squares linear regression technique should be employed as the high-level generalizer. This technique provides a method of combining level-0 models’ confidence

— Issues in Stacked Generalization, 1999.

A stacked generalization ensemble can be developed for regression and classification problems. In the case of classification problems, better results have been seen when using the prediction of class probabilities as input to the meta-learner instead of class labels.

… class probabilities should be used instead of the single predicted class as input attributes for higher-level learning. The class probabilities serve as the confidence measure for the prediction made.

— Issues in Stacked Generalization, 1999.

Now that we are familiar with stacked generalization, we can work through a case study of developing a stacked deep learning model.

Multi-Class Classification Problem

We will use a small multi-class classification problem as the basis to demonstrate the stacking ensemble.

The scikit-learn class provides the make_blobs() function that can be used to create a multi-class classification problem with the prescribed number of samples, input variables, classes, and variance of samples within a class.

The problem has two input variables (to represent the x and y coordinates of the points) and a standard deviation of 2.0 for points within each group. We will use the same random state (seed for the pseudorandom number generator) to ensure that we always get the same data points.

The results are the input and output elements of a dataset that we can model.

In order to get a feeling for the complexity of the problem, we can graph each point on a two-dimensional scatter plot and color each point by class value.

The complete example is listed below.

Running the example creates a scatter plot of the entire dataset. We can see that the standard deviation of 2.0 means that the classes are not linearly separable (separable by a line) causing many ambiguous points.

This is desirable as it means that the problem is non-trivial and will allow a neural network model to find many different “good enough” candidate solutions, resulting in a high variance.

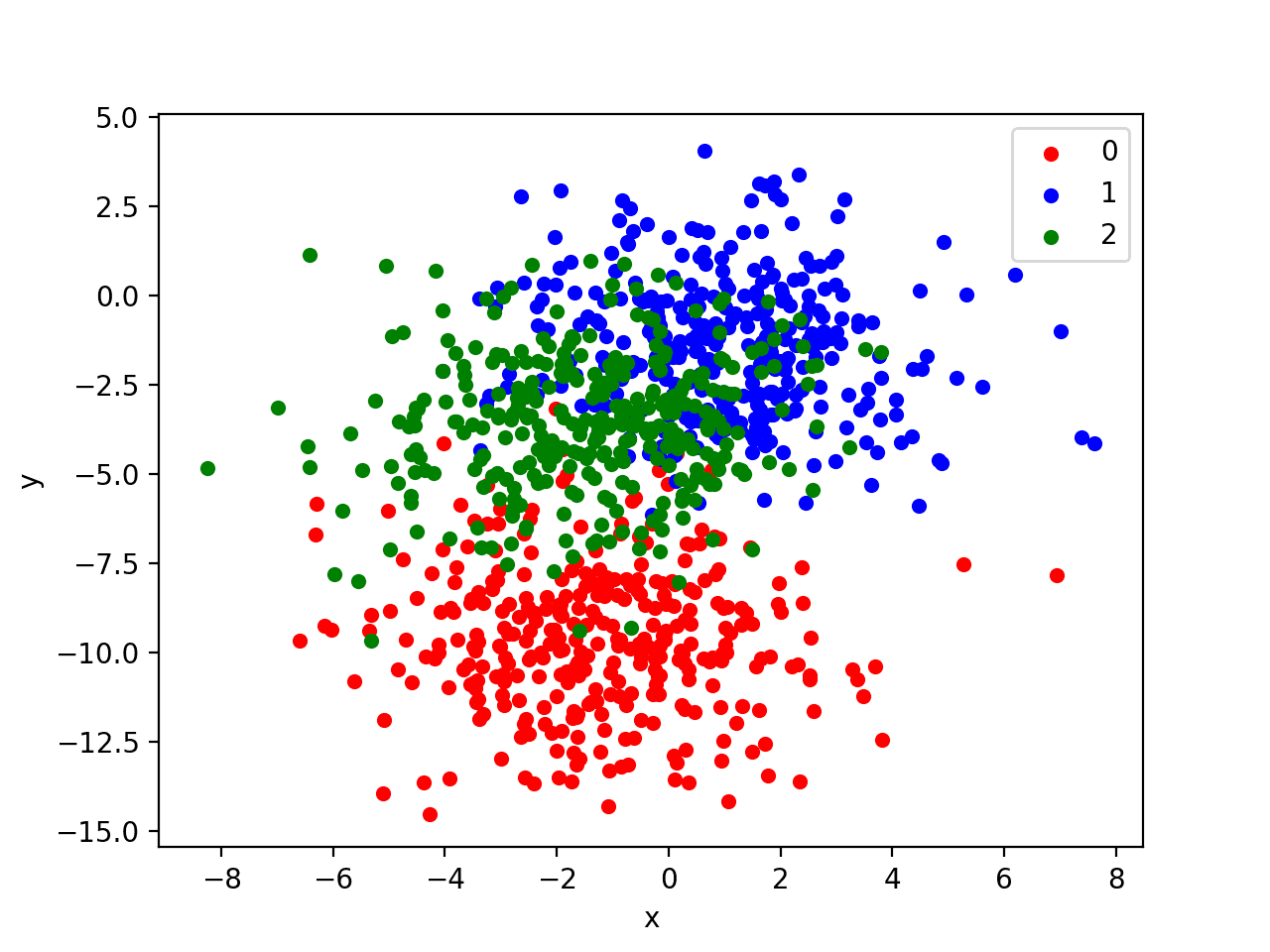
Scatter Plot of Blobs Dataset With Three Classes and Points Colored by Class Value

Multilayer Perceptron Model

Before we define a model, we need to contrive a problem that is appropriate for the stacking ensemble.

In our problem, the training dataset is relatively small. Specifically, there is a 10:1 ratio of examples in the training dataset to the holdout dataset. This mimics a situation where we may have a vast number of unlabeled examples and a small number of labeled examples with which to train a model.

We will create 1,100 data points from the blobs problem. The model will be trained on the first 100 points and the remaining 1,000 will be held back in a test dataset, unavailable to the model.

The problem is a multi-class classification problem, and we will model it using a softmax activation function on the output layer. This means that the model will predict a vector with three elements with the probability that the sample belongs to each of the three classes. Therefore, we must one hot encode the class values before we split the rows into the train and test datasets. We can do this using the Keras to_categorical() function.

Next, we can define and combine the model.

The model will expect samples with two input variables. The model then has a single hidden layer with 25 nodes and a rectified linear activation function, then an output layer with three nodes to predict the probability of each of the three classes and a softmax activation function.

Because the problem is multi-class, we will use the categorical cross entropy loss function to optimize the model and the efficient Adam flavor of stochastic gradient descent.

The model is fit for 500 training epochs and we will evaluate the model each epoch on the test set, using the test set as a validation set.

At the end of the run, we will evaluate the performance of the model on the train and test sets.

Then finally, we will plot learning curves of the model accuracy over each training epoch on both the training and validation datasets.

Tying all of this together, the complete example is listed below.

Running the example first prints the shape of each dataset for confirmation, then the performance of the final model on the train and test datasets.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

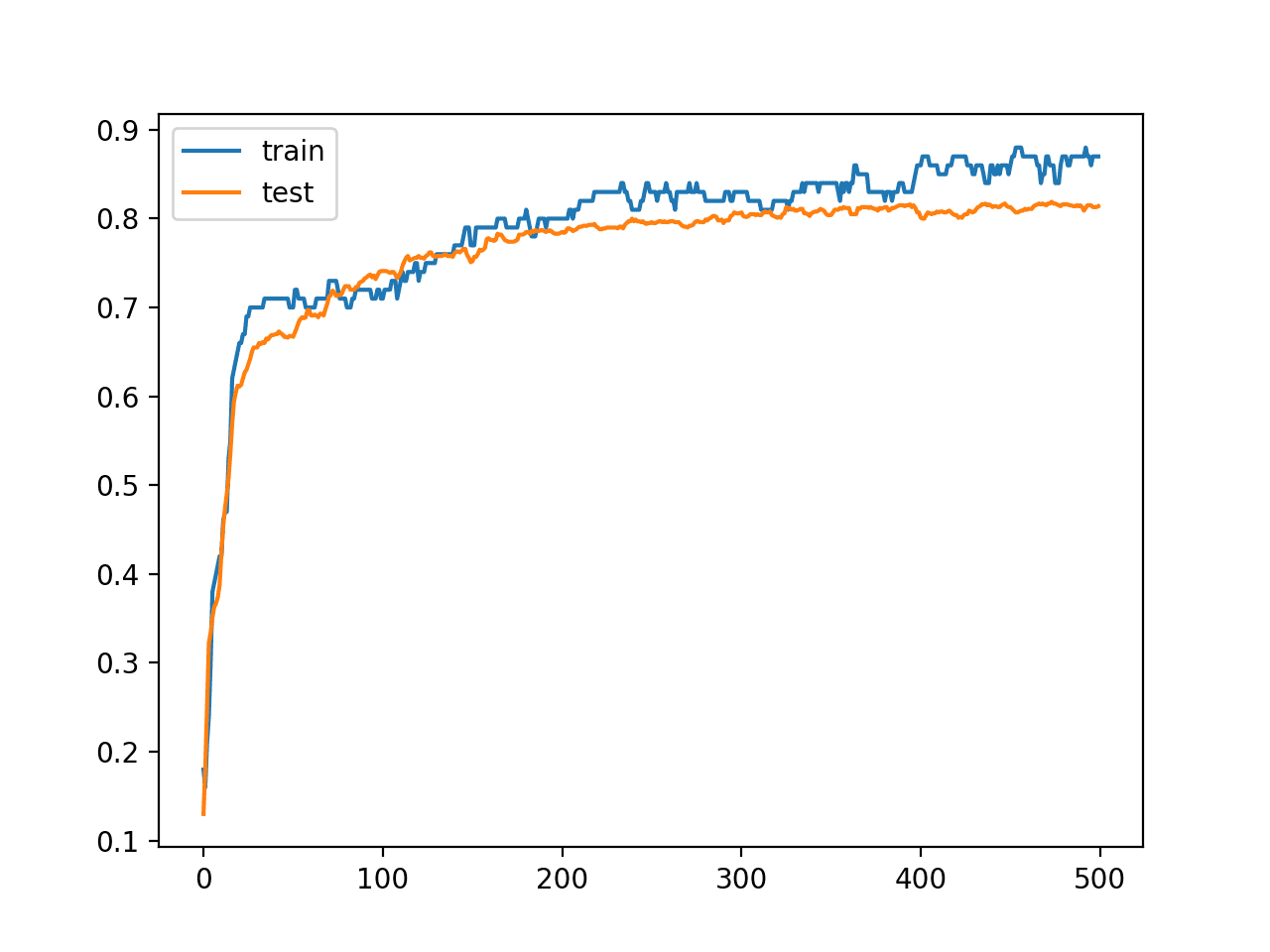
In this case, we can see that the model achieved about 85% accuracy on the training dataset, which we know is optimistic, and about 80% on the test dataset, which we would expect to be more realistic.

A line plot is also created showing the learning curves for the model accuracy on the train and test sets over each training epoch.

We can see that training accuracy is more optimistic over most of the run as we also noted with the final scores.

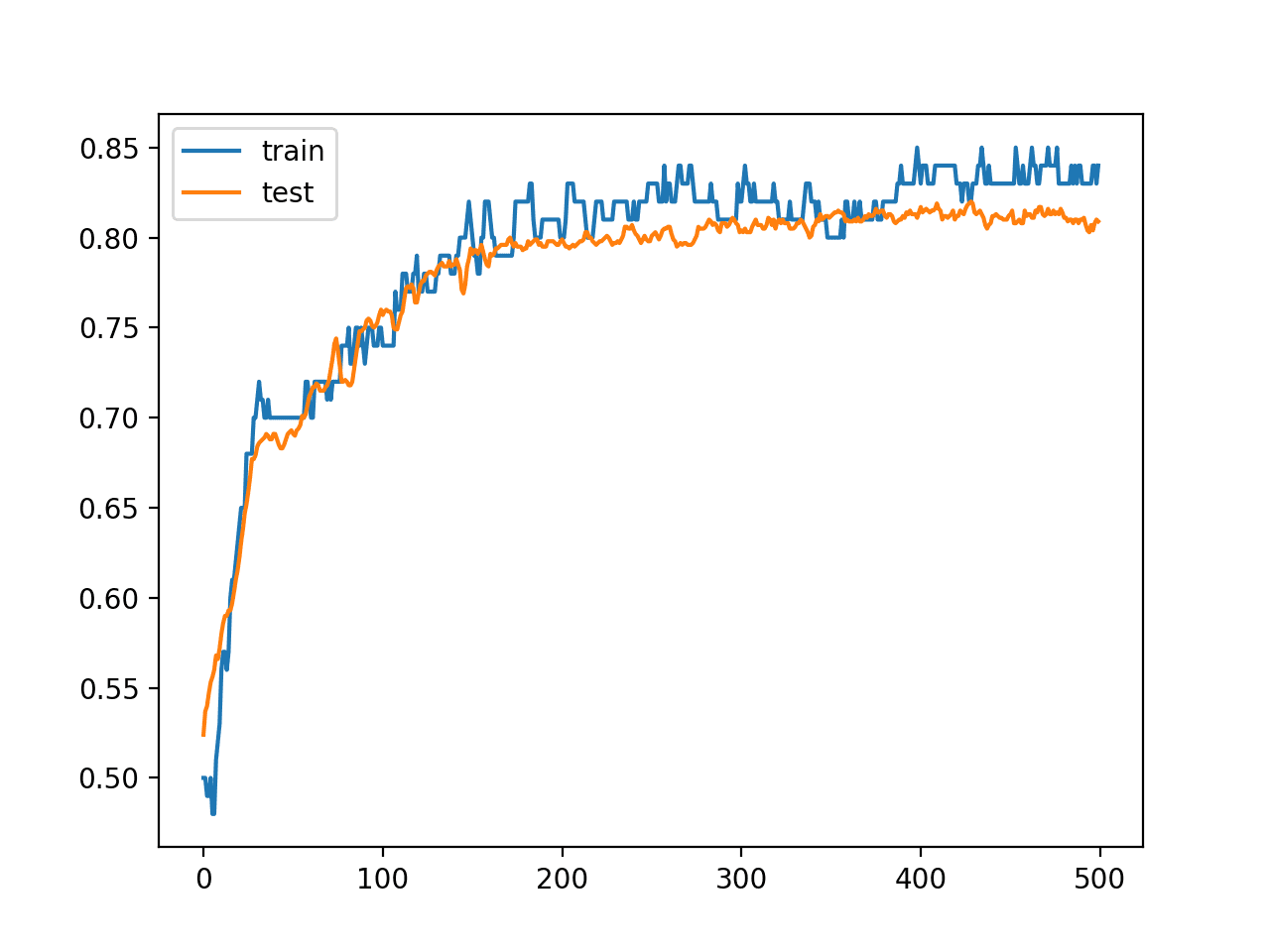
Line Plot Learning Curves of Model Accuracy on Train and Test Dataset Over Each Training Epoch

We can now look at using instances of this model as part of a stacking ensemble.

Train and Save Sub-Models

To keep this example simple, we will use multiple instances of the same model as level-0 or sub-models in the stacking ensemble.

We will also use a holdout validation dataset to train the level-1 or meta-learner in the ensemble.

A more advanced example may use different types of MLP models (deeper, wider, etc.) as sub-models and train the meta-learner using k-fold cross-validation.

In this section, we will train multiple sub-models and save them to file for later use in our stacking ensembles.

The first step is to create a function that will define and fit an MLP model on the training dataset.

Next, we can create a sub-directory to store the models.

Note, if the directory already exists, you may have to delete it when re-running this code.

Finally, we can create multiple instances of the MLP and save each to the “models/” subdirectory with a unique filename.

In this case, we will create five sub-models, but you can experiment with a different number of models and see how it impacts model performance.

We can tie all of these elements together; the complete example of training the sub-models and saving them to file is listed below.

Running the example creates the “models/” subfolder and saves five trained models with unique filenames.

Next, we can look at training a meta-learner to make best use of the predictions from these submodels.

Separate Stacking Model

We can now train a meta-learner that will best combine the predictions from the sub-models and ideally perform better than any single sub-model.

The first step is to load the saved models.

We can use the load_model() Keras function and create a Python list of loaded models.

We can call this function to load our five saved models from the “models/” sub-directory.

It would be useful to know how well the single models perform on the test dataset as we would expect a stacking model to perform better.

We can easily evaluate each single model on the training dataset and establish a baseline of performance.

Next, we can train our meta-learner. This requires two steps:

• Prepare a training dataset for the meta-learner.
• Use the prepared training dataset to fit a meta-learner model.

We will prepare a training dataset for the meta-learner by providing examples from the test set to each of the submodels and collecting the predictions. In this case, each model will output three predictions for each example for the probabilities that a given example belongs to each of the three classes. Therefore, the 1,000 examples in the test set will result in five arrays with the shape [1000, 3].

We can combine these arrays into a three-dimensional array with the shape [1000, 5, 3] by using the dstack() NumPy function that will stack each new set of predictions.

As input for a new model, we will require 1,000 examples with some number of features. Given that we have five models and each model makes three predictions per example, then we would have 15 (3 x 5) features for each example provided to the submodels. We can transform the [1000, 5, 3] shaped predictions from the sub-models into a [1000, 15] shaped array to be used to train a meta-learner using the reshape() NumPy function and flattening the final two dimensions. The stacked_dataset() function implements this step.

Once prepared, we can use this input dataset along with the output, or y part, of the test set to train a new meta-learner.

In this case, we will train a simple logistic regression algorithm from the scikit-learn library.

Logistic regression only supports binary classification, although the implementation of logistic regression in scikit-learn in the LogisticRegression class supports multi-class classification (more than two classes) using a one-vs-rest scheme. The function fit_stacked_model() below will prepare the training dataset for the meta-learner by calling the stacked_dataset() function, then fit a logistic regression model that is then returned.

We can call this function and pass in the list of loaded models and the training dataset.

Once fit, we can use the stacked model, including the members and the meta-learner, to make predictions on new data.

This can be achieved by first using the sub-models to make an input dataset for the meta-learner, e.g. by calling the stacked_dataset() function, then making a prediction with the meta-learner. The stacked_prediction() function below implements this.

We can use this function to make a prediction on new data; in this case, we can demonstrate it by making predictions on the test set.

Tying all of these elements together, the complete example of fitting a linear meta-learner for the stacking ensemble of MLP sub-models is listed below.

Running the example first loads the sub-models into a list and evaluates the performance of each.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the best performing model is the final model with an accuracy of about 81.3%.

Next, a logistic regression meta-learner is trained on the predicted probabilities from each sub-model on the test set, then the entire stacking model is evaluated on the test set.

We can see that in this case, the meta-learner out-performed each of the sub-models on the test set, achieving an accuracy of about 82.4%.

Integrated Stacking Model

When using neural networks as sub-models, it may be desirable to use a neural network as a meta-learner.

Specifically, the sub-networks can be embedded in a larger multi-headed neural network that then learns how to best combine the predictions from each input sub-model. It allows the stacking ensemble to be treated as a single large model.

The benefit of this approach is that the outputs of the submodels are provided directly to the meta-learner. Further, it is also possible to update the weights of the submodels in conjunction with the meta-learner model, if this is desirable.

This can be achieved using the Keras functional interface for developing models.

After the models are loaded as a list, a larger stacking ensemble model can be defined where each of the loaded models is used as a separate input-head to the model. This requires that all of the layers in each of the loaded models be marked as not trainable so the weights cannot be updated when the new larger model is being trained. Keras also requires that each layer has a unique name, therefore the names of each layer in each of the loaded models will have to be updated to indicate to which ensemble member they belong.

Once the sub-models have been prepared, we can define the stacking ensemble model.

The input layer for each of the sub-models will be used as a separate input head to this new model. This means that k copies of any input data will have to be provided to the model, where k is the number of input models, in this case, 5.

The outputs of each of the models can then be merged. In this case, we will use a simple concatenation merge, where a single 15-element vector will be created from the three class-probabilities predicted by each of the 5 models.

We will then define a hidden layer to interpret this “input” to the meta-learner and an output layer that will make its own probabilistic prediction. The define_stacked_model() function below implements this and will return a stacked generalization neural network model given a list of trained sub-models.

A plot of the network graph is created when this function is called to give an idea of how the ensemble model fits together.

Creating the plot requires that pygraphviz is installed.

If this is a challenge on your workstation, you can comment out the call to the plot_model() function.

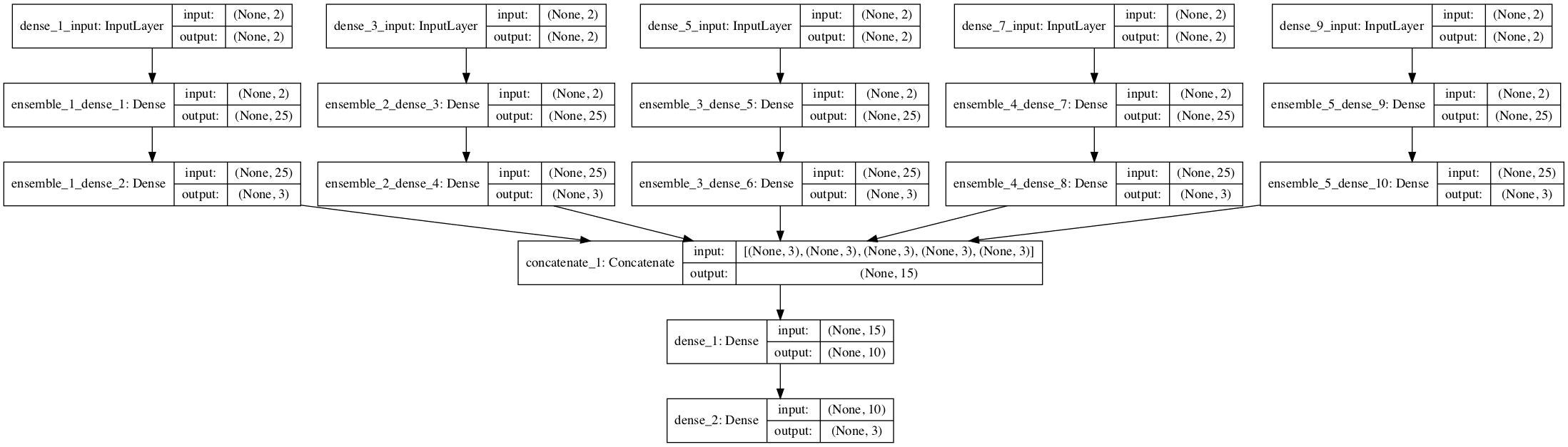
Visualization of Stacked Generalization Ensemble of Neural Network Models

Once the model is defined, it can be fit. We can fit it directly on the holdout test dataset.

Because the sub-models are not trainable, their weights will not be updated during training and only the weights of the new hidden and output layer will be updated. The fit_stacked_model() function below will fit the stacking neural network model on for 300 epochs.

We can call this function providing the defined stacking model and the test dataset.

Once fit, we can use the new stacked model to make a prediction on new data.

This is as simple as calling the predict() function on the model. One minor change is that we require k copies of the input data in a list to be provided to the model for each of the k sub-models. The predict_stacked_model() function below simplifies this process of making a prediction with the stacking model.

We can call this function to make a prediction for the test dataset and report the accuracy.

We would expect the performance of the neural network learner to be better than any individual submodel and perhaps competitive with the linear meta-learner used in the previous section.

Tying all of these elements together, the complete example is listed below.

Running the example first loads the five sub-models.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

A larger stacking ensemble neural network is defined and fit on the test dataset, then the new model is used to make a prediction on the test dataset. We can see that, in this case, the model achieved an accuracy of about 83.3%, out-performing the linear model from the previous section.

Extensions

This section lists some ideas for extending the tutorial that you may wish to explore.

• Alternate Meta-Learner. Update the example to use an alternate meta-learner classifier model to the logistic regression model.
• Single Level 0 Model. Update the example to use a single level-0 model and compare the results.
• Vary Level 0 Models. Develop a study that demonstrates the relationship between test classification accuracy and the number of sub-models used in the stacked ensemble.
• Cross-Validation Stacking Ensemble. Update the example to use k-fold cross-validation to prepare the training dataset for the meta-learner model.
• Use Raw Input in Meta-Learner. Update the example so that the meta-learner algorithms take the raw input data for the sample as well as the output from the sub-models and compare performance.

If you explore any of these extensions, I’d love to know.

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Books

• Section 8.8 Model Averaging and Stacking, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition, 2016.
• Section 7.5 Combining multiple models, Data Mining: Practical Machine Learning Tools and Techniques, Second Edition, 2005.
• Section 9.8.2 Stacked Generalization, Neural Networks for Pattern Recognition, 1995.

Papers

• Stacked generalization, 1992.
• Issues in Stacked Generalization, 1999.

API

• Getting started with the Keras Sequential model
• Keras Core Layers API
• numpy.argmax API
• sklearn.datasets.make_blobs API
• numpy.dstack API
• sklearn.linear_model.LogisticRegression API

Articles

• Stacked Generalization (Stacking) Bibliography.
• Ensemble learning, Wikipedia.

Posts

• How to Implement Stacked Generalization From Scratch With Python

Summary

In this tutorial, you discovered how to develop a stacked generalization ensemble for deep learning neural networks.

Specifically, you learned:

• Stacked generalization is an ensemble method where a new model learns how to best combine the predictions from multiple existing models.
• How to develop a stacking model using neural networks as a submodel and a scikit-learn classifier as the meta-learner.
• How to develop a stacking model where neural network sub-models are embedded in a larger stacking ensemble model for training and prediction.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

Develop Better Deep Learning Models Today!

Train Faster, Reduce Overftting, and Ensembles

...with just a few lines of python code

Discover how in my new Ebook:
Better Deep Learning

It provides self-study tutorials on topics like:
weight decay, batch normalization, dropout, model stacking and much more...

Bring better deep learning to your projects!

Skip the Academics. Just Results.

See What's Inside