Stacking or Stacked Generalization is an ensemble machine learning algorithm.
It uses a meta-learning algorithm to learn how to best combine the predictions from two or more base machine learning algorithms.
The benefit of stacking is that it can harness the capabilities of a range of well-performing models on a classification or regression task and make predictions that have better performance than any single model in the ensemble.
In this tutorial, you will discover the stacked generalization ensemble or stacking in Python.
After completing this tutorial, you will know:
- Stacking is an ensemble machine learning algorithm that learns how to best combine the predictions from multiple well-performing machine learning models.
- The scikit-learn library provides a standard implementation of the stacking ensemble in Python.
- How to use stacking ensembles for regression and classification predictive modeling.
Kick-start your project with my new book Ensemble Learning Algorithms With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Aug/2020: Improved code examples, added more references.

Stacking Ensemble Machine Learning With Python
Photo by lamoix, some rights reserved.
Tutorial Overview
This tutorial is divided into four parts; they are:
- Stacked Generalization
- Stacking Scikit-Learn API
- Stacking for Classification
- Stacking for Regression
Stacked Generalization
Stacked Generalization or “Stacking” for short is an ensemble machine learning algorithm.
It involves combining the predictions from multiple machine learning models on the same dataset, like bagging and boosting.
Stacking addresses the question:
- Given multiple machine learning models that are skillful on a problem, but in different ways, how do you choose which model to use (trust)?
The approach to this question is to use another machine learning model that learns when to use or trust each model in the ensemble.
- Unlike bagging, in stacking, the models are typically different (e.g. not all decision trees) and fit on the same dataset (e.g. instead of samples of the training dataset).
- Unlike boosting, in stacking, a single model is used to learn how to best combine the predictions from the contributing models (e.g. instead of a sequence of models that correct the predictions of prior models).
The architecture of a stacking model involves two or more base models, often referred to as level-0 models, and a meta-model that combines the predictions of the base models, referred to as a level-1 model.
- Level-0 Models (Base-Models): Models fit on the training data and whose predictions are compiled.
- Level-1 Model (Meta-Model): Model that learns how to best combine the predictions of the base models.
The meta-model is trained on the predictions made by base models on out-of-sample data. That is, data not used to train the base models is fed to the base models, predictions are made, and these predictions, along with the expected outputs, provide the input and output pairs of the training dataset used to fit the meta-model.
The outputs from the base models used as input to the meta-model may be real value in the case of regression, and probability values, probability like values, or class labels in the case of classification.
The most common approach to preparing the training dataset for the meta-model is via k-fold cross-validation of the base models, where the out-of-fold predictions are used as the basis for the training dataset for the meta-model.
The training data for the meta-model may also include the inputs to the base models, e.g. input elements of the training data. This can provide an additional context to the meta-model as to how to best combine the predictions from the meta-model.
Once the training dataset is prepared for the meta-model, the meta-model can be trained in isolation on this dataset, and the base-models can be trained on the entire original training dataset.
Stacking is appropriate when multiple different machine learning models have skill on a dataset, but have skill in different ways. Another way to say this is that the predictions made by the models or the errors in predictions made by the models are uncorrelated or have a low correlation.
Base-models are often complex and diverse. As such, it is often a good idea to use a range of models that make very different assumptions about how to solve the predictive modeling task, such as linear models, decision trees, support vector machines, neural networks, and more. Other ensemble algorithms may also be used as base-models, such as random forests.
- Base-Models: Use a diverse range of models that make different assumptions about the prediction task.
The meta-model is often simple, providing a smooth interpretation of the predictions made by the base models. As such, linear models are often used as the meta-model, such as linear regression for regression tasks (predicting a numeric value) and logistic regression for classification tasks (predicting a class label). Although this is common, it is not required.
- Regression Meta-Model: Linear Regression.
- Classification Meta-Model: Logistic Regression.
The use of a simple linear model as the meta-model often gives stacking the colloquial name “blending.” As in the prediction is a weighted average or blending of the predictions made by the base models.
The super learner may be considered a specialized type of stacking.
Stacking is designed to improve modeling performance, although is not guaranteed to result in an improvement in all cases.
Achieving an improvement in performance depends on the complexity of the problem and whether it is sufficiently well represented by the training data and complex enough that there is more to learn by combining predictions. It is also dependent upon the choice of base models and whether they are sufficiently skillful and sufficiently uncorrelated in their predictions (or errors).
If a base-model performs as well as or better than the stacking ensemble, the base model should be used instead, given its lower complexity (e.g. it’s simpler to describe, train and maintain).
Want to Get Started With Ensemble Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Stacking Scikit-Learn API
Stacking can be implemented from scratch, although this can be challenging for beginners.
For an example of implementing stacking from scratch in Python, see the tutorial:
For an example of implementing stacking from scratch for deep learning, see the tutorial:
The scikit-learn Python machine learning library provides an implementation of stacking for machine learning.
It is available in version 0.22 of the library and higher.
First, confirm that you are using a modern version of the library by running the following script:
|
1 2 3 |
# check scikit-learn version import sklearn print(sklearn.__version__) |
Running the script will print your version of scikit-learn.
Your version should be the same or higher. If not, you must upgrade your version of the scikit-learn library.
|
1 |
0.22.1 |
Stacking is provided via the StackingRegressor and StackingClassifier classes.
Both models operate the same way and take the same arguments. Using the model requires that you specify a list of estimators (level-0 models), and a final estimator (level-1 or meta-model).
A list of level-0 models or base models is provided via the “estimators” argument. This is a Python list where each element in the list is a tuple with the name of the model and the configured model instance.
For example, below defines two level-0 models:
|
1 2 3 |
... models = [('lr',LogisticRegression()),('svm',SVC()) stacking = StackingClassifier(estimators=models) |
Each model in the list may also be a Pipeline, including any data preparation required by the model prior to fitting the model on the training dataset. For example:
|
1 2 3 |
... models = [('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC())) stacking = StackingClassifier(estimators=models) |
The level-1 model or meta-model is provided via the “final_estimator” argument. By default, this is set to LinearRegression for regression and LogisticRegression for classification, and these are sensible defaults that you probably do not want to change.
The dataset for the meta-model is prepared using cross-validation. By default, 5-fold cross-validation is used, although this can be changed via the “cv” argument and set to either a number (e.g. 10 for 10-fold cross-validation) or a cross-validation object (e.g. StratifiedKFold).
Sometimes, better performance can be achieved if the dataset prepared for the meta-model also includes inputs to the level-0 models, e.g. the input training data. This can be achieved by setting the “passthrough” argument to True and is not enabled by default.
Now that we are familiar with the stacking API in scikit-learn, let’s look at some worked examples.
Stacking for Classification
In this section, we will look at using stacking for a classification problem.
First, we can use the make_classification() function to create a synthetic binary classification problem with 1,000 examples and 20 input features.
The complete example is listed below.
|
1 2 3 4 5 6 |
# test classification dataset from sklearn.datasets import make_classification # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and summarizes the shape of the input and output components.
|
1 |
(1000, 20) (1000,) |
Next, we can evaluate a suite of different machine learning models on the dataset.
Specifically, we will evaluate the following five algorithms:
- Logistic Regression.
- k-Nearest Neighbors.
- Decision Tree.
- Support Vector Machine.
- Naive Bayes.
Each algorithm will be evaluated using default model hyperparameters. The function get_models() below creates the models we wish to evaluate.
|
1 2 3 4 5 6 7 8 9 |
# get a list of models to evaluate def get_models(): models = dict() models['lr'] = LogisticRegression() models['knn'] = KNeighborsClassifier() models['cart'] = DecisionTreeClassifier() models['svm'] = SVC() models['bayes'] = GaussianNB() return models |
Each model will be evaluated using repeated k-fold cross-validation.
The evaluate_model() function below takes a model instance and returns a list of scores from three repeats of stratified 10-fold cross-validation.
|
1 2 3 4 5 |
# evaluate a given model using cross-validation def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') return scores |
We can then report the mean performance of each algorithm and also create a box and whisker plot to compare the distribution of accuracy scores for each algorithm.
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# compare standalone models for binary classification from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.naive_bayes import GaussianNB from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1) return X, y # get a list of models to evaluate def get_models(): models = dict() models['lr'] = LogisticRegression() models['knn'] = KNeighborsClassifier() models['cart'] = DecisionTreeClassifier() models['svm'] = SVC() models['bayes'] = GaussianNB() return models # evaluate a given model using cross-validation def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean and standard deviation accuracy for each model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that in this case, SVM performs the best with about 95.7 percent mean accuracy.
|
1 2 3 4 5 |
>lr 0.866 (0.029) >knn 0.931 (0.025) >cart 0.821 (0.050) >svm 0.957 (0.020) >bayes 0.833 (0.031) |
A box-and-whisker plot is then created comparing the distribution accuracy scores for each model, allowing us to clearly see that KNN and SVM perform better on average than LR, CART, and Bayes.
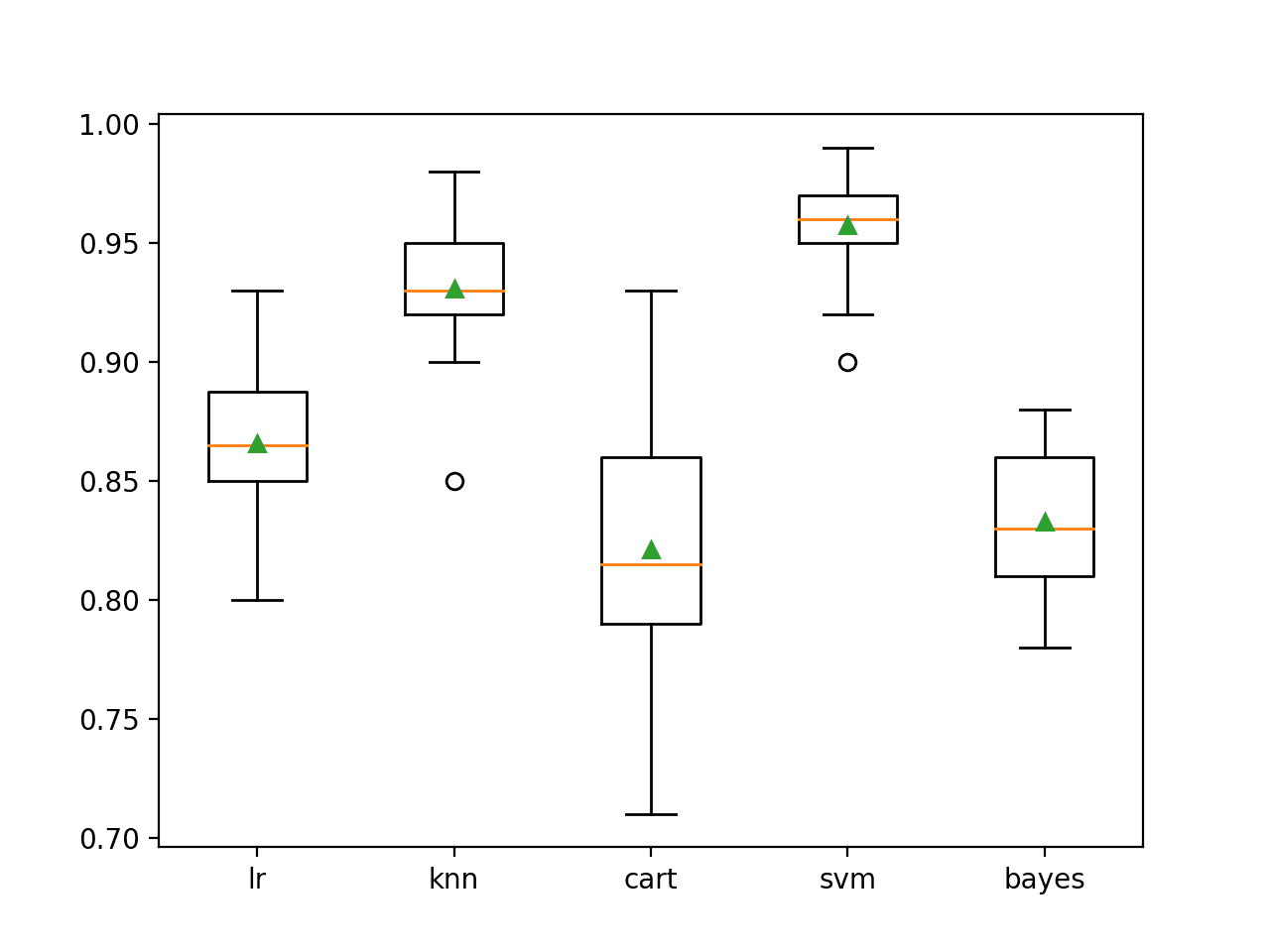
Box Plot of Standalone Model Accuracies for Binary Classification
Here we have five different algorithms that perform well, presumably in different ways on this dataset.
Next, we can try to combine these five models into a single ensemble model using stacking.
We can use a logistic regression model to learn how to best combine the predictions from each of the separate five models.
The get_stacking() function below defines the StackingClassifier model by first defining a list of tuples for the five base models, then defining the logistic regression meta-model to combine the predictions from the base models using 5-fold cross-validation.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# get a stacking ensemble of models def get_stacking(): # define the base models level0 = list() level0.append(('lr', LogisticRegression())) level0.append(('knn', KNeighborsClassifier())) level0.append(('cart', DecisionTreeClassifier())) level0.append(('svm', SVC())) level0.append(('bayes', GaussianNB())) # define meta learner model level1 = LogisticRegression() # define the stacking ensemble model = StackingClassifier(estimators=level0, final_estimator=level1, cv=5) return model |
We can include the stacking ensemble in the list of models to evaluate, along with the standalone models.
|
1 2 3 4 5 6 7 8 9 10 |
# get a list of models to evaluate def get_models(): models = dict() models['lr'] = LogisticRegression() models['knn'] = KNeighborsClassifier() models['cart'] = DecisionTreeClassifier() models['svm'] = SVC() models['bayes'] = GaussianNB() models['stacking'] = get_stacking() return models |
Our expectation is that the stacking ensemble will perform better than any single base model.
This is not always the case and if it is not the case, then the base model should be used in favor of the ensemble model.
The complete example of evaluating the stacking ensemble model alongside the standalone models is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
# compare ensemble to each baseline classifier from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.naive_bayes import GaussianNB from sklearn.ensemble import StackingClassifier from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1) return X, y # get a stacking ensemble of models def get_stacking(): # define the base models level0 = list() level0.append(('lr', LogisticRegression())) level0.append(('knn', KNeighborsClassifier())) level0.append(('cart', DecisionTreeClassifier())) level0.append(('svm', SVC())) level0.append(('bayes', GaussianNB())) # define meta learner model level1 = LogisticRegression() # define the stacking ensemble model = StackingClassifier(estimators=level0, final_estimator=level1, cv=5) return model # get a list of models to evaluate def get_models(): models = dict() models['lr'] = LogisticRegression() models['knn'] = KNeighborsClassifier() models['cart'] = DecisionTreeClassifier() models['svm'] = SVC() models['bayes'] = GaussianNB() models['stacking'] = get_stacking() return models # evaluate a give model using cross-validation def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the performance of each model. This includes the performance of each base model, then the stacking ensemble.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the stacking ensemble appears to perform better than any single model on average, achieving an accuracy of about 96.4 percent.
|
1 2 3 4 5 6 |
>lr 0.866 (0.029) >knn 0.931 (0.025) >cart 0.820 (0.044) >svm 0.957 (0.020) >bayes 0.833 (0.031) >stacking 0.964 (0.019) |
A box plot is created showing the distribution of model classification accuracies.
Here, we can see that the mean and median accuracy for the stacking model sits slightly higher than the SVM model.
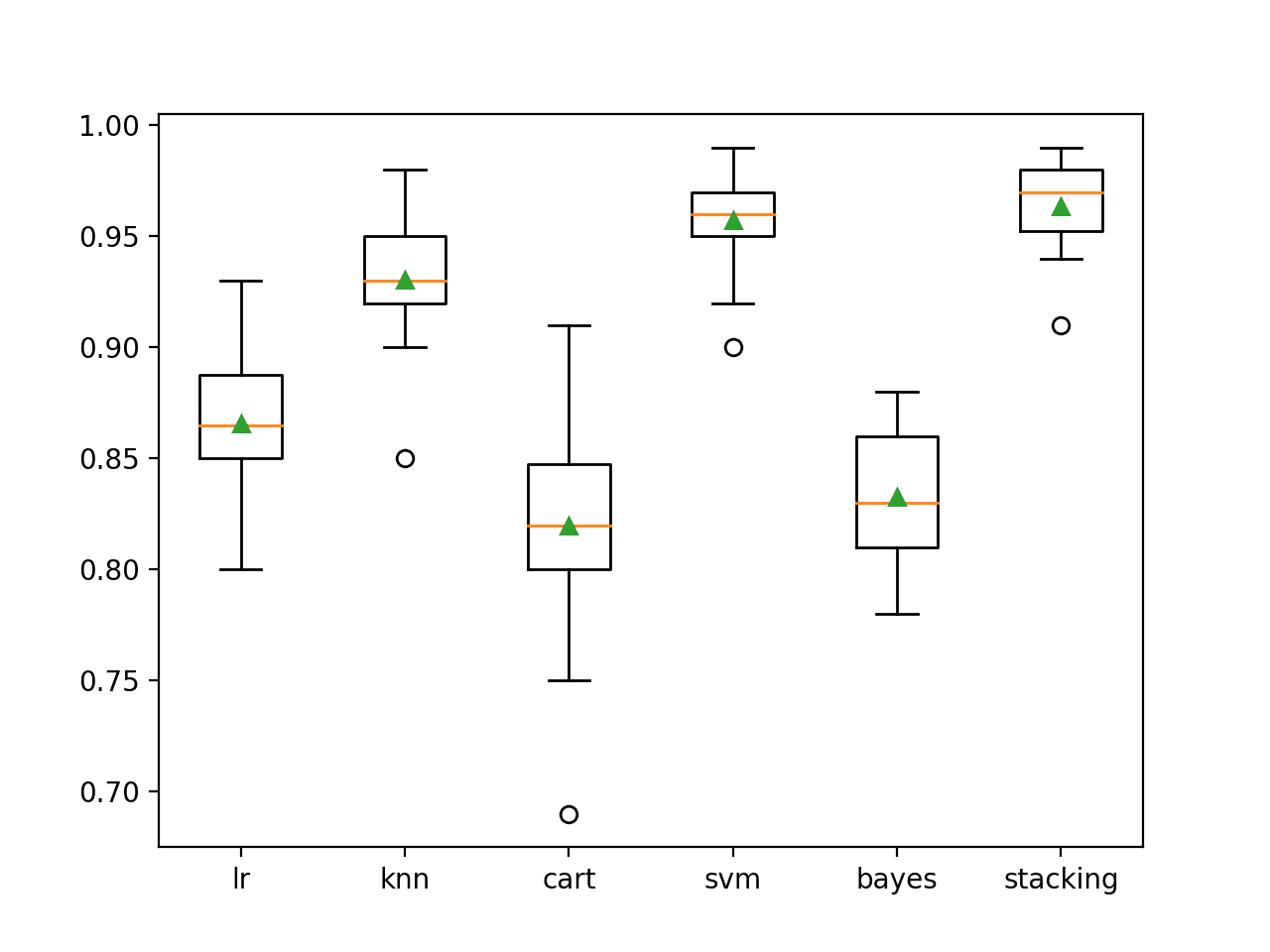
Box Plot of Standalone and Stacking Model Accuracies for Binary Classification
If we choose a stacking ensemble as our final model, we can fit and use it to make predictions on new data just like any other model.
First, the stacking ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our binary classification dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# make a prediction with a stacking ensemble from sklearn.datasets import make_classification from sklearn.ensemble import StackingClassifier from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.naive_bayes import GaussianNB # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1) # define the base models level0 = list() level0.append(('lr', LogisticRegression())) level0.append(('knn', KNeighborsClassifier())) level0.append(('cart', DecisionTreeClassifier())) level0.append(('svm', SVC())) level0.append(('bayes', GaussianNB())) # define meta learner model level1 = LogisticRegression() # define the stacking ensemble model = StackingClassifier(estimators=level0, final_estimator=level1, cv=5) # fit the model on all available data model.fit(X, y) # make a prediction for one example data = [[2.47475454,0.40165523,1.68081787,2.88940715,0.91704519,-3.07950644,4.39961206,0.72464273,-4.86563631,-6.06338084,-1.22209949,-0.4699618,1.01222748,-0.6899355,-0.53000581,6.86966784,-3.27211075,-6.59044146,-2.21290585,-3.139579]] yhat = model.predict(data) print('Predicted Class: %d' % (yhat)) |
Running the example fits the stacking ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Predicted Class: 0 |
Stacking for Regression
In this section, we will look at using stacking for a regression problem.
First, we can use the make_regression() function to create a synthetic regression problem with 1,000 examples and 20 input features.
The complete example is listed below.
|
1 2 3 4 5 6 |
# test regression dataset from sklearn.datasets import make_regression # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and summarizes the shape of the input and output components.
|
1 |
(1000, 20) (1000,) |
Next, we can evaluate a suite of different machine learning models on the dataset.
Specifically, we will evaluate the following three algorithms:
- k-Nearest Neighbors.
- Decision Tree.
- Support Vector Regression.
Note: The test dataset can be trivially solved using a linear regression model as the dataset was created using a linear model under the covers. As such, we will leave this model out of the example so we can demonstrate the benefit of the stacking ensemble method.
Each algorithm will be evaluated using the default model hyperparameters. The function get_models() below creates the models we wish to evaluate.
|
1 2 3 4 5 6 7 |
# get a list of models to evaluate def get_models(): models = dict() models['knn'] = KNeighborsRegressor() models['cart'] = DecisionTreeRegressor() models['svm'] = SVR() return models |
Each model will be evaluated using repeated k-fold cross-validation. The evaluate_model() function below takes a model instance and returns a list of scores from three repeats of 10-fold cross-validation.
|
1 2 3 4 5 |
# evaluate a given model using cross-validation def evaluate_model(model, X, y): cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise') return scores |
We can then report the mean performance of each algorithm and also create a box and whisker plot to compare the distribution of accuracy scores for each algorithm.
In this case, model performance will be reported using the mean absolute error (MAE). The scikit-learn library inverts the sign on this error to make it maximizing, from -infinity to 0 for the best score.
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# compare machine learning models for regression from numpy import mean from numpy import std from sklearn.datasets import make_regression from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedKFold from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.svm import SVR from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) return X, y # get a list of models to evaluate def get_models(): models = dict() models['knn'] = KNeighborsRegressor() models['cart'] = DecisionTreeRegressor() models['svm'] = SVR() return models # evaluate a given model using cross-validation def evaluate_model(model, X, y): cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean and standard deviation MAE for each model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that in this case, KNN performs the best with a mean negative MAE of about -100.
|
1 2 3 |
>knn -101.019 (7.161) >cart -148.100 (11.039) >svm -162.419 (12.565) |
A box-and-whisker plot is then created comparing the distribution negative MAE scores for each model.
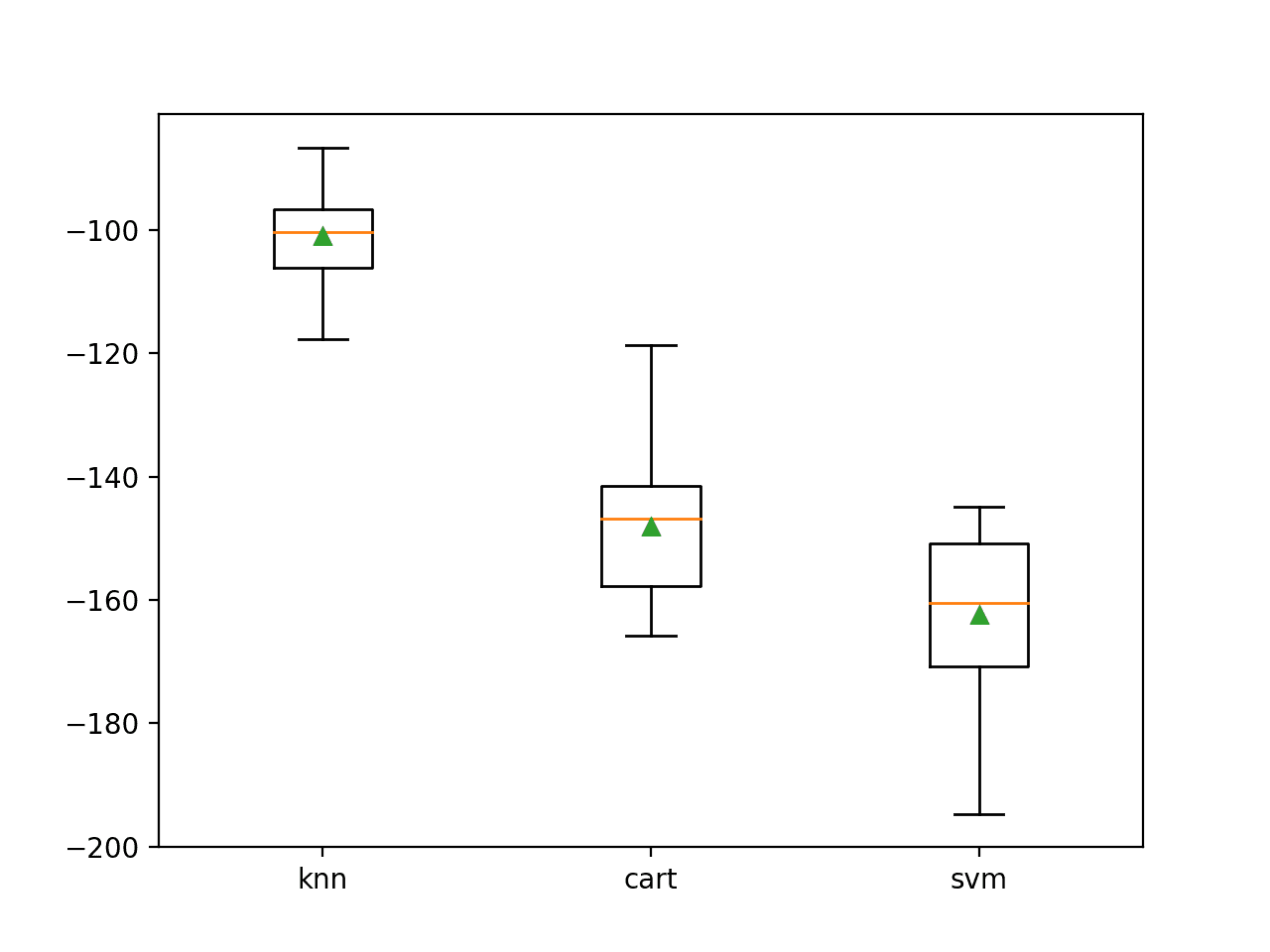
Box Plot of Standalone Model Negative Mean Absolute Error for Regression
Here we have three different algorithms that perform well, presumably in different ways on this dataset.
Next, we can try to combine these three models into a single ensemble model using stacking.
We can use a linear regression model to learn how to best combine the predictions from each of the separate three models.
The get_stacking() function below defines the StackingRegressor model by first defining a list of tuples for the three base models, then defining the linear regression meta-model to combine the predictions from the base models using 5-fold cross-validation.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# get a stacking ensemble of models def get_stacking(): # define the base models level0 = list() level0.append(('knn', KNeighborsRegressor())) level0.append(('cart', DecisionTreeRegressor())) level0.append(('svm', SVR())) # define meta learner model level1 = LinearRegression() # define the stacking ensemble model = StackingRegressor(estimators=level0, final_estimator=level1, cv=5) return model |
We can include the stacking ensemble in the list of models to evaluate, along with the standalone models.
|
1 2 3 4 5 6 7 8 |
# get a list of models to evaluate def get_models(): models = dict() models['knn'] = KNeighborsRegressor() models['cart'] = DecisionTreeRegressor() models['svm'] = SVR() models['stacking'] = get_stacking() return models |
Our expectation is that the stacking ensemble will perform better than any single base model.
This is not always the case, and if it is not the case, then the base model should be used in favor of the ensemble model.
The complete example of evaluating the stacking ensemble model alongside the standalone models is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
# compare ensemble to each standalone models for regression from numpy import mean from numpy import std from sklearn.datasets import make_regression from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedKFold from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.svm import SVR from sklearn.ensemble import StackingRegressor from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) return X, y # get a stacking ensemble of models def get_stacking(): # define the base models level0 = list() level0.append(('knn', KNeighborsRegressor())) level0.append(('cart', DecisionTreeRegressor())) level0.append(('svm', SVR())) # define meta learner model level1 = LinearRegression() # define the stacking ensemble model = StackingRegressor(estimators=level0, final_estimator=level1, cv=5) return model # get a list of models to evaluate def get_models(): models = dict() models['knn'] = KNeighborsRegressor() models['cart'] = DecisionTreeRegressor() models['svm'] = SVR() models['stacking'] = get_stacking() return models # evaluate a given model using cross-validation def evaluate_model(model, X, y): cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the performance of each model. This includes the performance of each base model, then the stacking ensemble.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the stacking ensemble appears to perform better than any single model on average, achieving a mean negative MAE of about -56.
|
1 2 3 4 |
>knn -101.019 (7.161) >cart -148.017 (10.635) >svm -162.419 (12.565) >stacking -56.893 (5.253) |
A box plot is created showing the distribution of model error scores. Here, we can see that the mean and median scores for the stacking model sit much higher than any individual model.
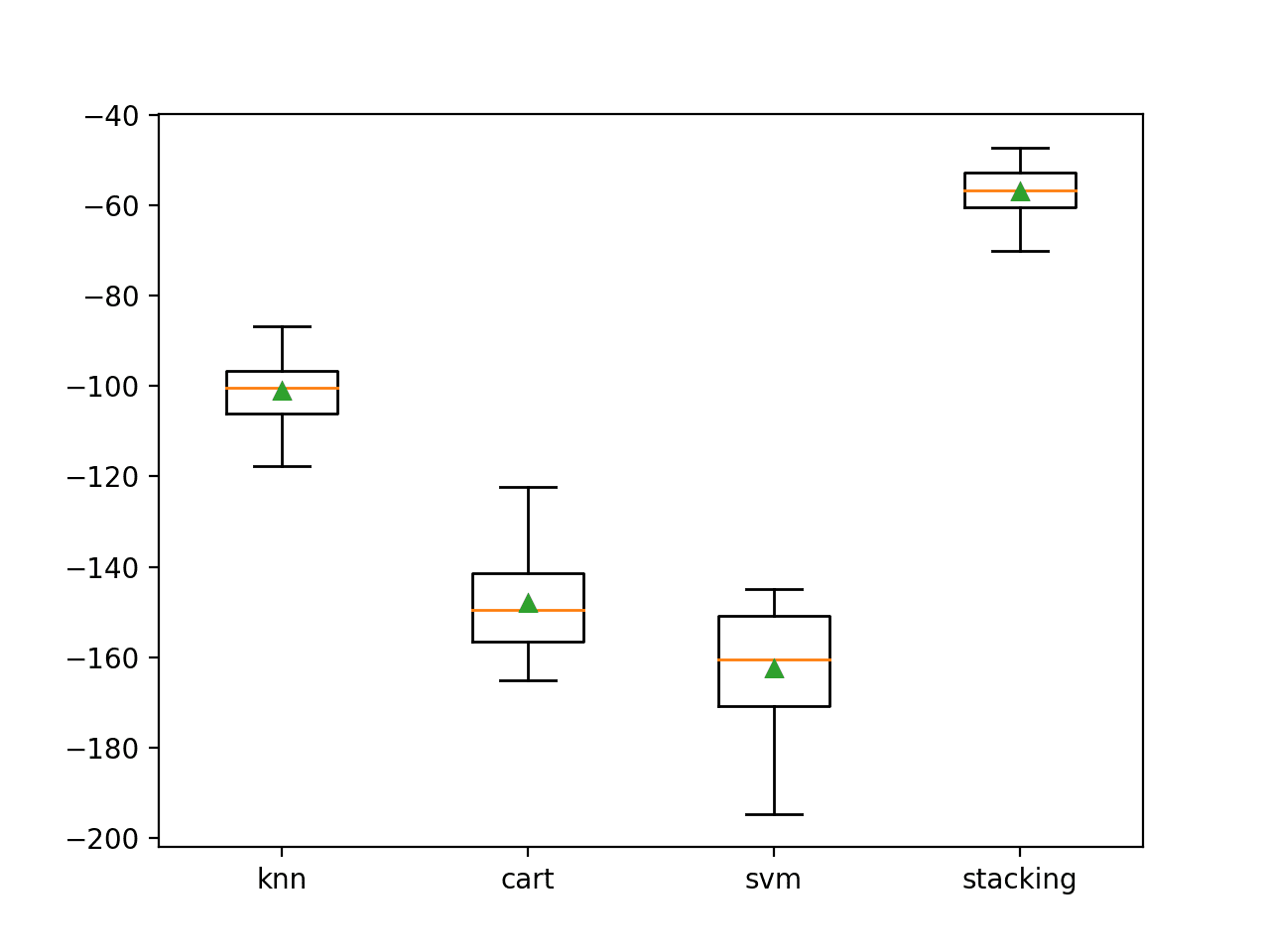
Box Plot of Standalone and Stacking Model Negative Mean Absolute Error for Regression
If we choose a stacking ensemble as our final model, we can fit and use it to make predictions on new data just like any other model.
First, the stacking ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our regression dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# make a prediction with a stacking ensemble from sklearn.datasets import make_regression from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.svm import SVR from sklearn.ensemble import StackingRegressor # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) # define the base models level0 = list() level0.append(('knn', KNeighborsRegressor())) level0.append(('cart', DecisionTreeRegressor())) level0.append(('svm', SVR())) # define meta learner model level1 = LinearRegression() # define the stacking ensemble model = StackingRegressor(estimators=level0, final_estimator=level1, cv=5) # fit the model on all available data model.fit(X, y) # make a prediction for one example data = [[0.59332206,-0.56637507,1.34808718,-0.57054047,-0.72480487,1.05648449,0.77744852,0.07361796,0.88398267,2.02843157,1.01902732,0.11227799,0.94218853,0.26741783,0.91458143,-0.72759572,1.08842814,-0.61450942,-0.69387293,1.69169009]] yhat = model.predict(data) print('Predicted Value: %.3f' % (yhat)) |
Running the example fits the stacking ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Predicted Value: 556.264 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Related Tutorials
- How to Implement Stacked Generalization (Stacking) From Scratch With Python
- How to Develop a Stacking Ensemble for Deep Learning Neural Networks in Python With Keras
- How to Develop Super Learner Ensembles in Python
- How to Use Out-of-Fold Predictions in Machine Learning
- A Gentle Introduction to k-fold Cross-Validation
Papers
- Stacked Generalization, 1992.
- Stacked Generalization: When Does It Work?, 1997.
- Issues in Stacked Generalization, 1999.
Books
- Data Mining: Practical Machine Learning Tools and Techniques, 2016.
- The Elements of Statistical Learning, 2017.
- Machine Learning: A Probabilistic Perspective, 2012.
APIs
- sklearn.ensemble.StackingClassifier API.
- sklearn.ensemble.StackingRegressor API.
- sklearn.datasets.make_classification API.
- sklearn.datasets.make_regression API.
Articles
Summary
In this tutorial, you discovered the stacked generalization ensemble or stacking in Python.
Specifically, you learned:
- Stacking is an ensemble machine learning algorithm that learns how to best combine the predictions from multiple well-performing machine learning models.
- The scikit-learn library provides a standard implementation of the stacking ensemble in Python.
- How to use stacking ensembles for regression and classification predictive modeling.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.







Thanks for this great explanation.
I have a question, how can I pass a specific type of data (e.g. specific class) to a specific algorithm, where each model learns from its particular data. then gathering all models (stacking) to predict
best regards,
You can fit different models perhaps manually, then use another model to combine the predictions. E.g. all maually.
Hi Jason, thanks for the blog and all the information in a digested form, I am a beginner in all aspects and I can really see the advantages of using the method of stacking. I am yet to start doing my first project but before that I plan on reading as much as possible from your articles.
Thank you and be safe, I hope to learn as much as posible from you.
Cheers from Mexico!!
You’re welcome.
that’s a lot of coding which can be reduce into just several lines of code n AutoMLPipeline: https://github.com/IBM/AutoMLPipeline.jl
Thanks for sharing.
Great article, Jason! Keep these coming. Thanks!
You’re welcome!
Thanks for sharing. I suppose when cv=n argument provided to the StackingClassifier, it implicitly trains base models on training data and then trains StackingClassifier with predictions of base models on out-of-sample data right?
It finds params via an internal cv process.
Thanks a lot for the info! though I have a question:
I have tried your stacking for classification on the given dataset, I took the first 800 samples for training and produced the box plot, however, when I test each model’s accuracy results on the 200 test samples the stacking model doesn’t provide the best results, do you have an explanation for this?
Yes, stacking is not guaranteed to outperform base models.
This is why we must use controlled experiments as the basis for model selection.
Hi Jason Brownlee, your articles really helped a lot many times.
In a paragraph you stated that ” That is, data not used to train the base models is fed to the base models, predictions are made, and these predictions, along with the expected outputs, provide the input and output pairs of the training dataset used to fit the meta-model.”
Here what do you mean by expected outputs ??
I’m happy to hear that!
Expected outputs are target values in the dataset.
So you mean that during model.fit(x_train,y_train) (training phase), the meta-model will not learn anything, only at the time of model.score(x_test,y_test) (testing phase),the meta-model trains on the test inputs and predicted values/labels made by base estimator.
Is my understand correct ?
No, I don’t quite follow your summary.
The stacking model is fit during the call to fit(). The call to cross_val_score() will fit and evaluate k models which internally involves calls to fit().
Great article!
I’m trying to follow the previous questions and I got another one:
Why not fitting level 0 models with a train_0, then train the meta model with level 0 predictions (trained with train_0, validated with train_1), and evaluated the meta model with a X_valid?
Would that be a better way since the we woud be training with not seen data all the time?
Hi Victor…You are very welcome! You make a great point! We would be interested in learning how your models perform based upon your suggestion.
hi Jason, thank you for your great tutorials!
I want to use CalibratedClassifier in Level0 estimators, then stacking them. I tried this one but not sure. Is it true?
model1=XGBClassifier()
model2=…..
calibrated1 = CalibratedClassifierCV(model1, cv=5)
calibrated1.fit(X_train, y_train)
calibrated2 = ….
calibrated2.fit(….)
estimators = [(‘xgb’, calibrated1),(‘…’, calibrated2)]
clf = StackingClassifier(estimators=estimators, final_estimator=LogisticRegression())
Thanks.
Calibrating level0 classifiers does not make sense to me, sorry. You might have to use some trial and error to make it work.
Hi,Jason!Thanks for your sharing. I used this tutorial for my binary classification task.I have 1000 image samples,and each sample has 4000 dimmensions that extrcted by CNN. However, the stacking result is lower than lr or bayes classifier, and also the super learning in your another tutorial. Could you tell me the reason? Hope for your reply.Many thanks!
Answering “why” questions it too hard/intractable.
Often the best we can do is use controlled experiments and present results to support decision of what model or modeling pipeline works well/best.
Thanks for the wonderful tutorial.
I see in this tutorial each base learner evaluated using default model hyperparameters. In real time, can I implement the base learner with hyperparameters tuning so I might get a better accuracy from meta-model?
Can we use boosting and bagging classifiers in level 0 or as base learners?
Thanks!
Yes, tuning is a good idea.
You can use ensembles as base models if you like.
Thank you.
1. From below piece of code which you used in this tutorial, I believe we are getting accuracy on Test data set, please confirm?
# evaluate a given model using cross-validation
def evaluate_model(model):
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X, y, scoring=’neg_mean_absolute_error’, cv=cv, n_jobs=-1, error_score=’raise’)
return scores
2. I am working on a classification problem and please find my different classification algorithm results below.
Method Train Acuracy Test Acuracy
0 Logistic Regression 0.8504762 0.8426966
1 KNN 0.9330952 0.9550562
2 Naive Bayes 0.7882540 0.7640449
3 SVM 0.9573810 0.9775281
4 Decision Tree 1.0000000 0.9438202
5 Random Forest 0.9477778 0.9550562
6 Stacking 1.0000000 0.9775281
Base learners – 0 to 5, Meta model – 6
If you look at Stacking classifier, it is completely over-fit on training data and I don’t think this is best model to consider, is that right?
Note: I tried removing Decision tree from my base learners list because it’s over-fit on training data and but still I get below results from stacking classifier.So again this is not best model, is that right?
Accuracy of Training data set: 1.0000 %
Accuracy of Test data set: 0.9888 %
Perhaps I will go for SVM as my final model.
There is no train/test sets. Instead, we are using repeated k-fold cross-validation to estimate model performance.
Not sure I would agree it is overfit. You can focus on hold out set performance to select a model.
Sorry, could you please clarify what is “hold out set performance”?
Also, please answer below question.
1. From below piece of code which you used in this tutorial, I believe we are getting accuracy on Test data set, please confirm?
# evaluate a given model using cross-validation
def evaluate_model(model):
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X, y, scoring=’neg_mean_absolute_error’, cv=cv, n_jobs=-1, error_score=’raise’)
return scores
No, we are using cross-validation.
Yes, you can learn more about how cross-validation works here:
https://machinelearningmastery.com/k-fold-cross-validation/
You can learn more about out of fold predictions (on the hold out set) here:
https://machinelearningmastery.com/out-of-fold-predictions-in-machine-learning/
Hello,
First of all, great guide. I found it really useful.
If I use predict_proba for the stacking classifier, will it use the probabilities for the whole data set for the level1 model? Or will it use only the ones from each test split in each cross validation run. Im not sure I am making a lot of sense. I am looking at this guide and the out of folds prediction part for ensemble and I want to understand if it is the same idea, or if it isnt, which one is preferable? Also, can both of them be integrated in a pipeline that also does feature selection?
Im a bit new to machine learning and python in general.
Thanks a lot!
Thank you.
Regardless of predicting labels or probabilities, the meta model is fit on the out of fold predictions from the base models.
Does that help?
Yes, thanks. So, tell me if I understand corectly because I want to be sure: in this guide the meta model is fitted on the out of fold predictions, just like in your other guide for out of folds. Im asking because in this guide you dont create the meta dataset like in that one. Is this being done by the stacking classifier?
Correct on both accounts.
The sklearn hides the complexity away and makes this complex ensemble algorithm “routine”. I love it!
Working on a multiclass classification problem and the dataset is imbalanced I have used SMOTE to over sample. Using xgboost I could achieve an f1 score of about 90.67 affer tuning as well. Would stacked classifiers along with xgboost help increase the f1 score.
Perhaps try it and see.
Thank you Mr. Jason for your guide. I used the codes above to implement a stacking model on Titanic datasets. For the hyperparameter tunning I used GrisearchCV. How can I extract the best stacking model? How will I use it to predict outcome on the test set?
Thank you.
You’re welcome.
Well done! The gridsearchcv will provide access to the best configuration as follows:
You can then fit a new model using the printed configuration, fit your model on all available data and call predict() for new data.
If making predictions is new for you, see this:
https://machinelearningmastery.com/make-predictions-scikit-learn/
Dear Dr Jason,
Again many thanks for your tutorials.
I understand the listing directly under the heading “The complete example of evaluating the stacking ensemble model alongside the standalone models is listed below”
What I have learned from the model from the get_models() and get_stacking().
* get_stacking is a model.
* get_models gets a list of models. That includes the get_stacking which is a model.
* I could use the code under “The complete example of evaluating the stacking ensemble model alongside the standalone models is listed below” to make a prediction.
* So making the prediction can be done underneath the lines for the boxplot.
Conclusion by following the example at “The complete example of evaluating the stacking ensemble model alongside the standalone models is listed below” we can understand that the get_stacked() is a stacked model consisting of level 0 models and level1 LR model.
Thank you,
Anthony from Sydney
Thanks.
Dear Dr Jason,
Thanks for your explain about stacking. I have a question about it. Several days ago I did a experiment that made the best params for every base model and the default params for every base model. In my opinion, if every base model could achieve a better performance, so that the meta model would get a higher accuracy by the training data combined by the predictions generated the base models. But in fact, the result was a little worse. So could you help me to explain the complex phenomenon?
Best regards,
This is common.
The reason is highly tuned models are fragile to small changes.
Hi Jason
I found your script and explanation very helful and as I am new in the feild.
Not really sure how to cite your script in my manuscript.
Do i just cite it as any mormal website is cited or is there there some other method?
Best,
Neeraj Gaur
Thanks!
This can help you cite a blog post:
https://machinelearningmastery.com/faq/single-faq/how-do-i-reference-or-cite-a-book-or-blog-post
Hello..
How to obtain feature importance from a Stacking Ensemble?
I tried but it was not possible.
Off hand, I don’t think stacking offers this capability.
How do you think I can do this?
I am a beginner, please help me how to write the code
Yes!
This will help you install what you need:
https://machinelearningmastery.com/setup-python-environment-machine-learning-deep-learning-anaconda/
This will help you copy the code:
https://machinelearningmastery.com/faq/single-faq/how-do-i-copy-code-from-a-tutorial
This will help you run it:
https://machinelearningmastery.com/faq/single-faq/how-do-i-run-a-script-from-the-command-line
Hi Jason,
Thank you very much for your tutorials. Please help me here
I want to stack 3 different algorithms after performing feature selection. But, the algorithms selected slightly different features..
Do I need to train my sub-models using same features?
The response variable is crop yield. I have 24 different predictors. The best fit model with Random Forest (%IncMSE) takes 8 variables out of the 24. Lasso takes 10 variables, and Xgboost takes 6…. How do I train these models if I want to stack them?
No, as long as the 3 models have the same training data, you can then transform the training data any way you like for each model.
Thank you for your prompt reply…But, I am not sure if you understand what I am saying. My data has 24 independent variables. Feature selection resulted in 8 variables for Random Forest, 10 variables for lasso, and 6 for XGBoost…..my question is: Do I need to use the same number and the same independent variables in each of my 3 models before I stack the models.
my best-fit models(RF, Lasso, & XGB) were trained on different independent variables: RF with 8 independent variables, Lasso with 10 independent variables, and XGB with 6 independent variables…. I am not referring to data splitting.
QUESTION: .do I need to use the same independent variables across the 3 models? Instead of 8, 6, and 10…must I train the models using the same independent variables…same across the 3 models??
The response variable is Corn Yield. RF is trained with 8 variables: Fertilizer, rainfall, temperature, seed type, Field size, Altitude, Slope, soil pH, Farmer’s gender
Must I use the same variables in all the 3 sub-models?….is it ok to train the other models with 10 and 6 variables as I have explained above?
I believe I understood.
No you do not need to use the same independent variables for each model, as long as each model starts with the same training dataset (rows) – even if each model uses different independent variables (columns).
Random Forest drew 8variables out of 24
Lasso selected 10 variables out of 24
Xgb selected 10 variables out of 24
The 24 has nothing to do with the 8,the 6, and the 10….except that I had a total of 24 independent variables. Different feature selection methods were applied and they selected 8, 10, and 6 variables respectively
Yes, that is fine. As long as you test the model on data not used during training.
Hello dr jason, is it correct based on your code that you split/cv the data into 5 parts. I still cannot understand why there is 2 times of cross fold validation on stacking and cross_val
Hi Fara…The following resource may be of interest to you:
https://machinelearningmastery.com/repeated-k-fold-cross-validation-with-python/
Hi Jason,
Thanks very you much for the detailed explanation on Stacking; it was very helpful to me.
Please I have a question concerning this paragraph in your article:
“The meta-model is trained on the predictions made by base models on out-of-sample data. That is, data not used to train the base models is fed to the base models, predictions are made, and these predictions, along with the expected outputs, provide the input and output pairs of the training dataset used to fit the meta-model.”
From the above paragraph, this is my understanding:
1. Given a training dataset, (X_{train}, Y_{train}), during training the base-models are only fed with X_{train}.
2. The base models make predictions, Xbase_{prediction} based on the fed data X_{train}.
3. Xbase_{prediction} is then fed to the meta-model as input. However, it will also have the desired output for the predictions Y_{train}. This way, the meta-model is fit on the training dataset.
4. Sets 1 to 3 is then repeated several times.
Please is my understanding of the above paragraph in your article right?
Thanks
Mark
Cross-validation is used where the out of sample predictions from base models are taken as input for the stacked model.
Okay, thanks.
Let’s say that I have used RandomSearchCV to identify the best hyperparameters for my models – but I set the scoring parameter to optimize for ‘precision’. (I ONLY care about eliminating false positives; I am unharmed by the existence of false negatives).
The docs for StackingClassifier don’t include a scoring parameter. The docs only mention training the ensemble to get the best *accuracy*.
Does this mean that StackingClassifier will optimize for a metric I don’t want to optimize (accuracy) instead of the metric I do want to optimize (precision)?
If that is the case predict the positive class in all cases and achieve the best precision.
The stacking ensemble itself does not optimize a score. I think you are referring to the score() function, which is one way to evaluate the model.
how to remove this error as sklearn is already installed and uptodate
No module named ‘sklearn.cross_validation’
You must update your version of the scikit-learn library.
Thank you very much for this. This is no doubt the best way I’ve seen it explained.
Thanks!
Instead of cross validation cv=5 can we use train test split instead 60:40 for stacking model ?
If you like.
It would be called blending:
https://machinelearningmastery.com/blending-ensemble-machine-learning-with-python/
Hi Jason,
How it would be the best way for ensemble 3 Random Forests with 3 different datasets? Could you help me?
Thanks!
Sorry again, the problem has 3 classes
Perhaps start using an average of the models.
Hi Jason,
I have an imbalanced dataset multiclass, and I have balanced the dataset en 3 dataset, after I apply methods for feature selection. Thus, i want to do 3 Random Forests which will have differents data and different column number and after ensemble this three datasets. What is the best way? Could you help me please?
Evaluate a suite of approaches and discover what works best on your dataset.
Hi Jason Brownlee
can i ask how to use RMSE to evaluate the results?
could give me some example?
See this tutorial on how to calculate metrics like RMSE:
https://machinelearningmastery.com/regression-metrics-for-machine-learning/
Hi Dr. Brownlee,
Thank you for your excellent tutorials. I am working on a stacking architecture and I’m stuck on a particular idea. All of my level 0 models require different threshholds to predict optimally. Is there anyway to set the threshholds individually in a stacking architecture or to work around this issue?
Thanks!
You’re welcome.
Not as far as I know.
You can implement the stacking manually and use threshold values that pass on to the next level.
Alternately, you could drop your thresholds and let the level 1 model learn how to best use the predictions from level 0.
Thanks for sharing
You’re welcome!
Thanks for sharing such a wonderful tutorial. How do you save the model for later use? Joblib or pickle gives an error when trying to reuse the model to predict in another code.
Good question, this will show you how:
https://machinelearningmastery.com/save-load-keras-deep-learning-models/
Thank you Jason for this amazing article. It helped me a lot with my research.
I would like to leave here a link about a paper we wrote related to Stacked Generalization. Specifically, it is about how you could combine base models with the guidance from visualizations in order to build powerful and diverse Stacking ensembles.
StackGenVis: https://doi.org/10.1109/TVCG.2020.3030352
Thanks for sharing.
Hi Jason,
Thanks for the tutorial it’s really interesting.
Could you do a tutorial to show how to Random Search and Grid Search after stacking models for regression please ?
Thanks !
Thanks for the suggestion!
You’re welcome !
Hi Jason! so much for your tutorial!
I have a question- if I were to use a base model that requires evaluation set for early stopping, how would I used it inside the stacked ensemble?
You might just have to use a separate dataset as the validation set.
thanks Jason,
just to clarify- you mean to use a seperate validation to find the right number of estimators required beforehand right? and then run the stack model using this number
Perhaps. Some experimentation may be required.
Dear Dr Jason,
I varied the number of folds = cv from 2 to 20 in the line
and found that there was very little variation in mean and std dev of scores when cv = 2. 5. 10, 20.
Mean varied between 0.962 when cv=2, and 0.964 when cv = 5, 10, 20
Thank you
Anthony of Sydney
Nice work! Sounds like the system is stable.
Dear Dr Jason,
I combined the evaluation and prediction for each model by combining the last two segments of the stacked regressor:
The respective output produced significantly different predictions:
Range of predictions from 31 to 556
Lesson: have to use a range of models with the least score. In this case the stacked regression model produced the smallest score.
Thank you,
Anthony of Sydney
Thanks for sharing.
Dear Dr Jason,
Another observation on when to use the RepeatedKFold and RepeatedStratifiedKFold when using resampling techniques for cv.
RepeatedKFold – use for output which is continuous, eg for stacked regressor
RepeatedStratifiedKFold – use for output which is discrete, eg for stacked classifier
Thank you,
Anthony of Sydney
Yes, these descriptions are likely in the API docs.
Hi, love your work. Is it possible to use stack regressor with pretrained regression models such as XGBoost and Catboost. I am working on optimizing predictions and i have a set of models that perform well when it comes to errror metrics mae, mape. How could i combine it to get an optimized prediction? Is is possible to use pretrained models? Would linear regression work?
Thanks.
You may have to write custom code, I don’t think sklearn can handle pre-trained models.
Hi, Can you point in the direction on how I could it Jason? Im kind of new to the whole concept. Any code that i could refer? Thanks in advance!
Sorry, I don’t think I have examples close to this. You may need to develop some prototypes in order to discover the best path forward.
Hi,
Can we display confusion matrix after applying stacking ? if yes how ? As here only accuracy parameter is displayed if we want to display other performance metrices how to get these?
Yes, use the entire model to make predictions on new data and calculate the confusion matrix for the predictions.
Great lesson! Thanks.
You’re welcome.
Hi Jason,
Thank you so much for the guidance. this was indeed helpful to me. However, I tried implementing stacking emsemble classification on Isloationforest, OCSVM, and LOF.
But I usually got the following error.
“ValueError: The estimator IsolationForest should be a classifier”.
My question is: Does that mean Isolation Forest and OneClass SVM are not classifiers like KNN, Logistic Regression, SVM, Decision Tree classifiers?
Hope someone will respond as soon as possible. Thank you
Those models are not classifiers, you may need to write custom code to stack their output.
Hi Jason
Your articles are always helpful, so thanks!
do you have any insights on how to tune the hyperparameters of a stacking model? (for eg. if the base models need to be tuned first and then the meta model).
thanks!
You’re welcome!
Yes, it would just be different level 0 models and different level 1 models.
Great post! One question – If I wish to check the statistical significance between performance (accuracy) differences between each base model & stacked model, how would I do that? That is, if we have 5 base models, then how significantly does each of these 5 base models differ from stacked model performance. Please guide. Thanks
Thanks!
This will help:
https://machinelearningmastery.com/statistical-significance-tests-for-comparing-machine-learning-algorithms/
Good evening sir,
I am working on stacked ensemble learning. Can you please tell me what are the research challenges about this algorithm in classification .
I don’t know. Perhaps you can read the literature to discover current challenges.
Great content, as always!
I believe that the main drawback in this algorithm is that the parameters of the meta-model and each of the base models, are estimated separately (in our example there are six different optimizations). Single optimization for the whole structure will probably improve accuracy. How can we implement this approach?
thanks,
Assaf
I don’t think scikit-learn allows this. After all, having all models independent to each other in training is the idea of ensemble.
I got tpeError from this line:????
print(‘>%s %.3f (%.3f)’ % (name, mean(scores), std(scores)))
not all arguments converted during string formatting.
Please how can I resolved this challenge?
Just do print(name, mean(scores), std(scores)) and see what cannot be converted.
Thank you sir.
Finally it works for me.
????
Instead of using cross_val_score(), how can you implement GridSearchCV and use its custom scoring metrics?
Surely, check out: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html
Look at the “scoring” parameter.
If base learner A significantly outperform base learner B, whether the stacking cannot further improve the performance. Here, ‘significantly’ means that the ROC curve of A enclosed that of B.
Thank you for the feedback Jian! Keep up the great work!
Hi, Thanks for the great article, I found almost all the information about the stacking at one place with a very nice explanation. I have one doubt though, is it wise to use stacking models for a dataset that is big enough?
Hi James thank you so much for your efforts for the researcher like us.
I have one question let say we ensemble XGBOOST + LGBM regression models for level 0 and we want to stack their result with LSTM on Level 1 meta-layer for regression problem.
any of your thoughts would be appreciated.
Thanks
Hi Muhammad…You are very welcome! Please elaborate on your question so that I may better assist you. Have you implemented this idea or are you experiencing a specific error?
Hi, love your work!
This idea works well for my project. but I have one question.
Is it possible to retrain in a production environment?
I tried ‘partial_fit’, ‘refit’, etc, but couldn`t apply it to model(stacking)
Any ideas to solve this?
Hi Kang…The following may be of interest to you:
https://machinelearningmastery.com/update-neural-network-models-with-more-data/
Hi Jason. Great post.
How would one find the best combination of models for stacking? We have various different models/algorithms available and we can use any combination of them in stacking. So how would I choose which particular combination performs the best for a given task?
Hi Ankit…We greatly appreciate your support and feedback! The following resource may be of interest to you:
https://www.analyticsvidhya.com/blog/2015/10/trick-right-model-ensemble/
Hi Mr. James Carmichael
Why do we use “negative” in MAE ?
Hello Mr. James Carmichael
How do we use ‘negative’ for MAE
Hi Vahid…Some model evaluation metrics such as mean squared error (MSE) or MAE are negative when calculated in scikit-learn.
This is confusing, because error scores like MSE cannot actually be negative, with the smallest value being zero or no error.
The scikit-learn library has a unified model scoring system where it assumes that all model scores are maximized. In order this system to work with scores that are minimized, like MSE and other measures of error, the sores that are minimized are inverted by making them negative.
This can also be seen in the specification of the metric, e.g. ‘neg‘ is used in the name of the metric ‘neg_mean_squared_error‘.
When interpreting the negative error scores, you can ignore the sign and use them directly.
You can learn more here:
Model evaluation: quantifying the quality of predictions
Hello Jason,
Thanks for the tutorial. Cureently, I am conducting a regression study of household expenditure (target variable) from a set of determiants (income, household size, …) using OLS and Random Forest. In my study, result shows that OLS regression (0.853) performs slightly better than Random Forest regresion (0.850) using r2 score. However, Random Forest is another good choice as part of my determinants having non-linear relationships with target variable, which are classified as insignifcant variables (using t-test) in OLS.
I am looking for a tutorial to develop a hybrid model that utilize both strengths from OLS (accuracy) and Random Forest (able to distinguish non-linear relationship). I have tried the stacking regression mentioned in this tutorial and the r2 score improved a litte(0.855) using Random Forest as base and OLS as final estimators. I am wondering do the stacking regression actually integrated both strengths that I mentioned, or should I refer to the other tutorial/literature about developing a hybrid model?
Thanks
Hello Jason,
Thanks for the tutorial. Cureently, I am conducting a regression study of household expenditure (target variable) from a set of determiants (income, household size, …) using OLS and Random Forest. In my study, result shows that OLS regression (0.853) performs slightly better than Random Forest regresion (0.850) using r2 score. However, Random Forest is another good choice as part of my determinants having non-linear relationships with target variable, which are classified as insignifcant variables (using t-test) in OLS.
I am looking for a tutorial to develop a hybrid model that utilize both strengths from OLS (accuracy) and Random Forest (able to distinguish non-linear relationship). I have tried the stacking regression mentioned in this tutorial and the r2 score improved a litte(0.855) using Random Forest as base and OLS as final estimators. I am wondering do the stacking regression actually integrated both strengths that I mentioned, or should I refer to the other tutorial/literature about developing a hybrid model?
Hi agario…The following resource is a great starting point to answer your questions:
https://machinelearningmastery.com/ensemble-machine-learning-with-python-7-day-mini-course/
Hi James,
Thanks a lot for the tutorial. I have a question. Assume I’m gonna use a neural network as the meta model. As you mentioned, we can include the original input (the one we feed to the base models) in the input of the meta model alongside the base models outputs. Can you please explain how can I do this? I mean how do you think I should combine these two types of input and feed it to the meta model.
I am talking based on this paragraph ” The training data for the meta-model may also include the inputs to the base models, e.g. input elements of the training data. This can provide an additional context to the meta-model as to how to best combine the predictions from the meta-model.”
Thanks in advance
Hi Mike…You are very welcome! I recommend the followin resource as a starting point to clarify some of the topics of your query:
https://machinelearningmastery.com/ensemble-machine-learning-with-python-7-day-mini-course/
Hi Jason,
Thank you for doing this great work.
You mentioned that “The outputs from the base models used as input to the meta-model may be real value in the case of regression, and probability values, probability like values, or class labels in the case of classification.”
Is the a way to ensure that the base models outputs “probability values, probability like values” ONLY for classification?
I do not see such a parameter in the Scikit-learn documentation of StackingClassifiier.
Hi ARM…You are very welcome! The softmax function may be beneficial:
https://machinelearningmastery.com/softmax-activation-function-with-python/