Selecting a machine learning algorithm for a predictive modeling problem involves evaluating many different models and model configurations using k-fold cross-validation.
The super learner is an ensemble machine learning algorithm that combines all of the models and model configurations that you might investigate for a predictive modeling problem and uses them to make a prediction as-good-as or better than any single model that you may have investigated.
The super learner algorithm is an application of stacked generalization, called stacking or blending, to k-fold cross-validation where all models use the same k-fold splits of the data and a meta-model is fit on the out-of-fold predictions from each model.
In this tutorial, you will discover the super learner ensemble machine learning algorithm.
After completing this tutorial, you will know:
Super learner is the application of stacked generalization using out-of-fold predictions during k-fold cross-validation.
The super learner ensemble algorithm is straightforward to implement in Python using scikit-learn models.
The ML-Ensemble (mlens) library provides a convenient implementation that allows the super learner to be fit and used in just a few lines of code.
Kick-start your project with my new book Ensemble Learning Algorithms With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
Update Jan/2020: Updated for changes in scikit-learn v0.22 API.
How to Develop Super Learner Ensembles in Python Photo by Mark Gunn, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
What Is the Super Learner?
Manually Develop a Super Learner With scikit-learn
Super Learner With ML-Ensemble Library
What Is the Super Learner?
There are many hundreds of models to choose from for a predictive modeling problem; which one is best?
Then, after a model is chosen, how do you best configure it for your specific dataset?
These are open questions in applied machine learning. The best answer we have at the moment is to use empirical experimentation to test and discover what works best for your dataset.
In practice, it is generally impossible to know a priori which learner will perform best for a given prediction problem and data set.
This involves selecting many different algorithms that may be appropriate for your regression or classification problem and evaluating their performance on your dataset using a resampling technique, such as k-fold cross-validation.
The algorithm that performs the best on your dataset according to k-fold cross-validation is then selected, fit on all available data, and you can then start using it to make predictions.
There is an alternative approach.
Consider that you have already fit many different algorithms on your dataset, and some algorithms have been evaluated many times with different configurations. You may have many tens or hundreds of different models of your problem. Why not use all those models instead of the best model from the group?
This is the intuition behind the so-called “super learner” ensemble algorithm.
The super learner algorithm involves first pre-defining the k-fold split of your data, then evaluating all different algorithms and algorithm configurations on the same split of the data. All out-of-fold predictions are then kept and used to train an algorithm that learns how to best combine the predictions.
The algorithms may differ in the subset of the covariates used, the basis functions, the loss functions, the searching algorithm, and the range of tuning parameters, among others.
The results of this model should be no worse than the best performing model evaluated during k-fold cross-validation and has the likelihood of performing better than any single model.
The super learner algorithm was proposed by Mark van der Laan, Eric Polley, and Alan Hubbard from Berkeley in their 2007 paper titled “Super Learner.” It was published in a biological journal, which may be sheltered from the broader machine learning community.
The super learner technique is an example of the general method called “stacked generalization,” or “stacking” for short, and is known in applied machine learning as blending, as often a linear model is used as the meta-model.
The super learner is related to the stacking algorithm introduced in neural networks context …
We can think of the “super learner” as a specific configuration of stacking specifically to k-fold cross-validation.
I have sometimes seen this type of blending ensemble referred to as a cross-validation ensemble.
The procedure can be summarized as follows:
1. Select a k-fold split of the training dataset.
2. Select m base-models or model configurations.
3. For each basemodel:
a. Evaluate using k-fold cross-validation.
b. Store all out-of-fold predictions.
c. Fit the model on the full training dataset and store.
4. Fit a meta-model on the out-of-fold predictions.
5. Evaluate the model on a holdout dataset or use model to make predictions.
The image below, taken from the original paper, summarizes this data flow.
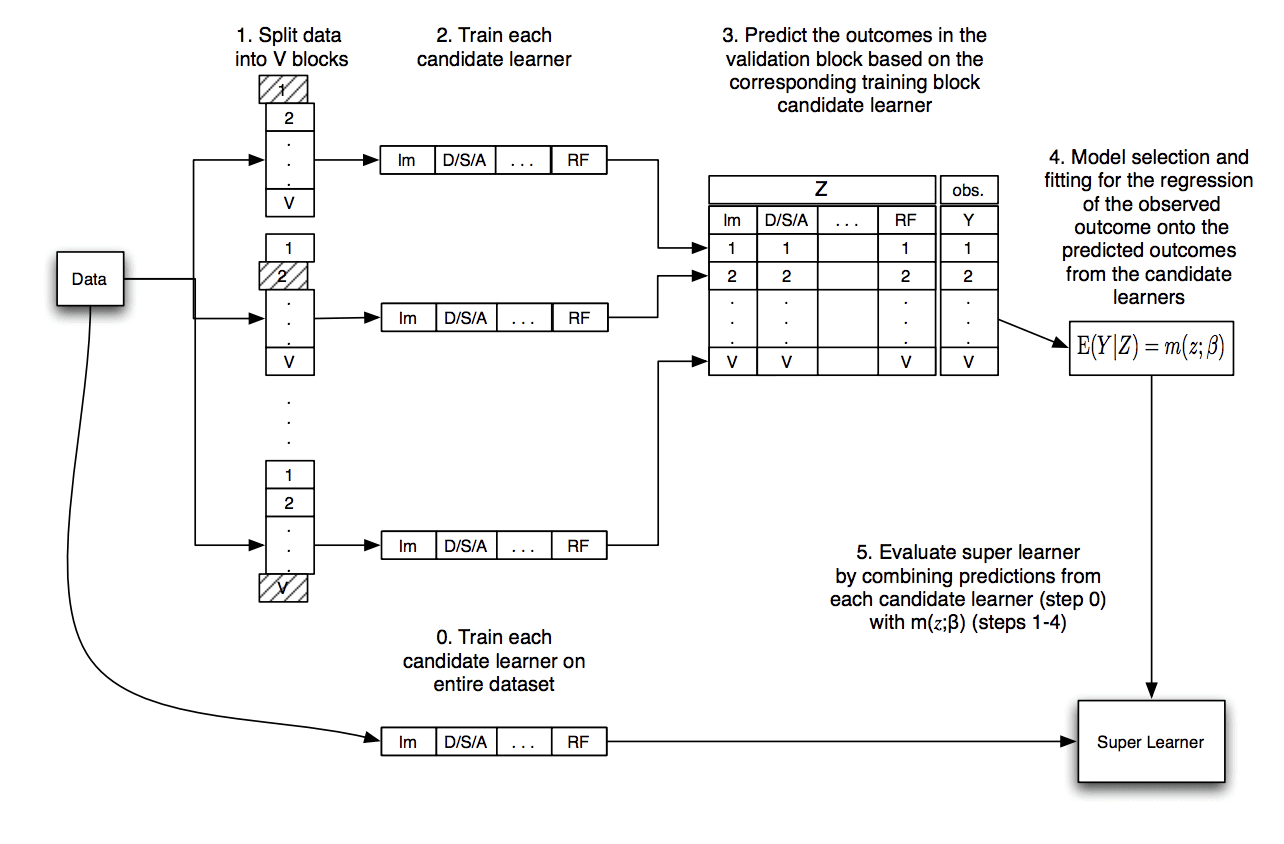
Diagram Showing the Data Flow of the Super Learner Algorithm Taken from “Super Learner.”
Let’s take a closer look at some common sticking points you may have with this procedure.
Q. What are the inputs and outputs for the meta-model?
The meta-model takes in predictions from base-models as input and predicts the target for the training dataset as output:
Input: Predictions from base-models.
Output: Prediction for training dataset.
For example, if we had 50 base-models, then one input sample would be a vector with 50 values, each value in the vector representing a prediction from one of the base-models for one sample of the training dataset.
If we had 1,000 examples (rows) in the training dataset and 50 models, then the input data for the meta-model would be 1,000 rows and 50 columns.
Q. Won’t the meta-model overfit the training data?
Probably not.
This is the trick of the super learner, and the stacked generalization procedure in general.
The input to the meta-model is the out-of-fold (out-of-sample) predictions. In aggregate, the out-of-fold predictions for a model represent the model’s skill or capability in making predictions on data not seen during training.
By training a meta-model on out-of-sample predictions of other models, the meta-model learns how to both correct the out-of-sample predictions for each model and to best combine the out-of-sample predictions from multiple models; actually, it does both tasks at the same time.
Importantly, to get an idea of the true capability of the meta-model, it must be evaluated on new out-of-sample data. That is, data not used to train the base models.
Q. Can this work for regression and classification?
Yes, it was described in the papers for regression (predicting a numerical value).
It can work just as well for classification (predicting a class label), although it is probably best to predict probabilities to give the meta-model more granularity when combining predictions.
Q. Why do we fit each base-model on the entire training dataset?
Each base-model is fit on the entire training dataset so that the model can be used later to make predictions on new examples not seen during training.
This step is strictly not required until predictions are needed by the super learner.
Q. How do we make a prediction?
To make a prediction on a new sample (row of data), first, the row of data is provided as input to each base model to generate a prediction from each model.
The predictions from the base-models are then concatenated into a vector and provided as input to the meta-model. The meta-model then makes a final prediction for the row of data.
We can summarize this procedure as follows:
1. Take a sample not seen by the models during training.
2. For each base-model:
a. Make a prediction given the sample.
b. Store prediction.
3. Concatenate predictions from submodel into a single vector.
4. Provide vector as input to the meta-model to make a final prediction.
Now that we are familiar with the super learner algorithm, let’s look at a worked example.
Want to Get Started With Ensemble Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Manually Develop a Super Learner With scikit-learn
The Super Learner algorithm is relatively straightforward to implement on top of the scikit-learn Python machine learning library.
In this section, we will develop an example of super learning for both regression and classification that you can adapt to your own problems.
Super Learner for Regression
We will use the make_regression() test problem and generate 1,000 examples (rows) with 100 features (columns). This is a simple regression problem with a linear relationship between input and output, with added noise.
We will split the data so that 50 percent is used for training the model and 50 percent is held back to evaluate the final super model and base-models.
Next, we will use k-fold cross-validation to make out-of-fold predictions that will be used as the dataset to train the meta-model or “super learner.”
This involves first splitting the data into k folds; we will use 10. For each fold, we will fit the model on the training part of the split and make out-of-fold predictions on the test part of the split. This is repeated for each model and all out-of-fold predictions are stored.
Each out-of-fold prediction will be a column for the meta-model input. We will collect columns from each algorithm for one fold of the data, horizontally stacking the rows. Then for all groups of columns we collect, we will vertically stack these rows into one long dataset with 500 rows and nine columns.
The get_out_of_fold_predictions() function below does this for a given test dataset and list of models; it will return the input and output dataset required to train the meta-model.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# collect out of fold predictions form k-fold cross validation
def get_out_of_fold_predictions(X,y,models):
meta_X,meta_y=list(),list()
# define split of data
kfold=KFold(n_splits=10,shuffle=True)
# enumerate splits
fortrain_ix,test_ix inkfold.split(X):
fold_yhats=list()
# get data
train_X,test_X=X[train_ix],X[test_ix]
train_y,test_y=y[train_ix],y[test_ix]
meta_y.extend(test_y)
# fit and make predictions with each sub-model
formodel inmodels:
model.fit(train_X,train_y)
yhat=model.predict(test_X)
# store columns
fold_yhats.append(yhat.reshape(len(yhat),1))
# store fold yhats as columns
meta_X.append(hstack(fold_yhats))
returnvstack(meta_X),asarray(meta_y)
We can then call the function to get the models and the function to prepare the meta-model dataset.
Running the example first reports the shape of the prepared dataset, then the shape of the dataset for the meta-model.
Next, the performance of each base-model is reported on the holdout dataset, and finally, the performance of the super learner on the holdout dataset.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the linear models perform well on the dataset and the nonlinear algorithms not so well.
We can also see that the super learner out-performed all of the base-models.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Train (500, 100) (500,) Test (500, 100) (500,)
Meta (500, 9) (500,)
LinearRegression: RMSE 0.548
ElasticNet: RMSE 67.142
SVR: RMSE 172.717
DecisionTreeRegressor: RMSE 159.137
KNeighborsRegressor: RMSE 154.064
AdaBoostRegressor: RMSE 98.422
BaggingRegressor: RMSE 108.915
RandomForestRegressor: RMSE 115.637
ExtraTreesRegressor: RMSE 105.749
Super Learner: RMSE 0.546
You can imagine plugging in all kinds of different models into this example, including XGBoost and Keras deep learning models.
Now that we have seen how to develop a super learner for regression, let’s look at an example for classification.
Super Learner for Classification
The super learner algorithm for classification is much the same.
The inputs to the meta learner can be class labels or class probabilities, with the latter more likely to be useful given the increased granularity or uncertainty captured in the predictions.
As before, the shape of the dataset and the prepared meta dataset is reported, followed by the performance of the base-models on the holdout dataset and finally the super model itself on the holdout dataset.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the super learner has slightly better performance than the base learner algorithms.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Train (500, 100) (500,) Test (500, 100) (500,)
Meta (500, 18) (500,)
LogisticRegression: 96.600
DecisionTreeClassifier: 74.400
SVC: 97.400
GaussianNB: 97.800
KNeighborsClassifier: 95.400
AdaBoostClassifier: 93.200
BaggingClassifier: 84.400
RandomForestClassifier: 82.800
ExtraTreesClassifier: 82.600
Super Learner: 98.000
Super Learner With ML-Ensemble Library
Implementing the super learner manually is a good exercise but is not ideal.
We may introduce bugs in the implementation and the example as listed does not make use of multiple cores to speed up the execution.
Thankfully, Sebastian Flennerhag provides an efficient and tested implementation of the Super Learner algorithm and other ensemble algorithms in his ML-Ensemble (mlens) Python library. It is specifically designed to work with scikit-learn models.
First, the library must be installed, which can be achieved via pip, as follows:
1
sudo pip install mlens
Next, a SuperLearner class can be defined, models added via a call to the add() function, the meta learner added via a call to the add_meta() function, then the model used like any other scikit-learn model.
1
2
3
4
5
6
7
8
...
# configure model
ensemble=SuperLearner(...)
# add list of base learners
ensemble.add(...)
# add meta learner
ensemble.add_meta(...)
# use model ...
We can use this class on the regression and classification problems from the previous section.
Super Learner for Regression With the ML-Ensemble Library
First, we can define a function to calculate RMSE for our problem that the super learner can use to evaluate base-models.
1
2
3
# cost function for base models
def rmse(yreal,yhat):
returnsqrt(mean_squared_error(yreal,yhat))
Next, we can configure the SuperLearner with 10-fold cross-validation, our evaluation function, and the use of the entire training dataset when preparing out-of-fold predictions to use as input for the meta-model.
The get_super_learner() function below implements this.
We can then fit the model on the training dataset.
1
2
3
...
# fit the super learner
ensemble.fit(X,y)
Once fit, we can get a nice report of the performance of each of the base-models on the training dataset using k-fold cross-validation by accessing the “data” attribute on the model.
1
2
3
...
# summarize base learners
print(ensemble.data)
And that’s all there is to it.
Tying this together, the complete example of evaluating a super learner using the mlens library for regression is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# example of a super learner for regression using the mlens library
from math import sqrt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVR
from sklearn.ensemble import AdaBoostRegressor
from sklearn.ensemble import BaggingRegressor
from sklearn.ensemble import RandomForestRegressor
Running the example first reports the RMSE for (score-m) for each base-model, then reports the RMSE for the super learner itself.
Fitting and evaluating is very fast given the use of multi-threading in the backend allowing all cores of your machine to be used.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the super learner performs well.
Note that we cannot compare the base learner scores in the table to the super learner as the base learners were evaluated on the training dataset only, not the holdout dataset.
Running the example summarizes the shape of the dataset, the performance of the base-models, and finally the performance of the super learner on the holdout dataset.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Again, we can see that the super learner performs well on this test problem, and more importantly, is fit and evaluated very quickly as compared to the manual example in the previous section.
I’m a total beginner in coding the ML. However, I know the concepts of modelling.
Could you throw out the libraries you import in the code because I’m very interested in Super Learner and I would like to use a Spyder IDE to better understand what is happening here.
Carlos
You might want to take this same data set and try with H2O AutoML and Auto_ViML and compare their performance against the Super Learner. You might want to play back results here.
Readers should note Stacking Classifier and Regressor are new features in scikit-learn 0.22, released December 3, 2019. The link to the Classifier is below.
venkatesh siddamsettiDecember 14, 2019 at 6:47 pm#
Nice Article Jason.
I am just a beginner in ensemble learning. In the above example(Classification) did you considered probability predictions of base models as training data to the 2nd level logistic regression? or have you taken direct predictions of base model as training set ?
I just would like to ask how can I incorporate another model which would not be a machine learning model. This model is very powerful for my problem and I would like to incorporate it into the get_model() part.
Dear Jason
thank you so much for your generous work (Blog).
I am looking forward to understanding the math behind SL. I mean the methodology behind Super Learning. how it starts with the regression dataset and goes with CV and ends with the best-predicted value. If possible, could you enlight me, please?
Great Information on how to Develop Super Learner Ensembles in Python. It’s very practical and helpful in developing machine learning algorithms. Thanks for sharing such a piece of wonderful information.
Hi Jason, thanks for the great content. You have helped me so much the last few years.
In regard to this problem, predict_proba does not seem to work with the SuperLearner. No matter what, it only seems to return discrete values (ints that I converted from my string labels).
I think I might have to engineer it myself from your code, but maybe you could point out what I’m missing?
A rough and simple approach would be to sum the probability scores from each model for each class then normalize the values to give a probability-like score.
A better approach would be to combine the probabilities systematically, perhaps dip into the sklearn code to see how this is done in stacking or voting ensebles when predict_proba() is called.
Hi Jason, this is a very useful information.
Thank you for sharing.
For binary classification, I want to consider Artificial Neural Networks as one of the base models along with Catboost, LASSO and Random forest classifier. Can you help me with the same?
Thank you
Hi Jason, I have a question related to ensemble method for classification. how can i apply it with multi-class classification? and for meta_model, we can choose which classification we prefer or what? Thank you.
Jason, thank you so much! I’m trying to incorporate my own dataset into this. I have 1,875 rows (including headers) and 19 columns (18 of which are actual features). I’m trying to set X and y like this:
# create the inputs and outputs
X = dataframe.iloc[0:1874]
Y = dataframe.iloc[:,0:18]
But I keep getting this error:
ValueError: Found input variables with inconsistent numbers of samples: [1874, 1875]
Thank you so much if you can help me (or if anyone else in this comments thread can help me).
actually, my friend helped me to fix this; she said to do this:
# create the inputs and outputs
X = dataframe.iloc[0:1875].values #CHANGED THIS LINE FROM 0:1874 TO 0:1875 AND ADDED .VALUES <–she helped me here.
y = dataframe.iloc[:,-1].values # CHANGED THIS LINE, ADDED .VALUES <–she helped me here.
I would like to do hyperparameter tuning for each base model before using them in the super learner. I would like to ask that using the best configuration hyperparameter values rather than the default parameters for each base model in the super Learner model would be reasonable?
from the super learner, how do i extract the weights assigned to the base models? The source paper and the R package is able to say “the super learner is a combination of 20% ElasticNet, 80% LinearRegression” for example. How to get these combination weights from the python implementation, i.e. your fit_meta_model function. I don’t think they are the fit_meta_model regression coefficients because some are negative and don’t sum to 1. thanks
The R package of super learner uses NNLS (non-negative least squares) to estimate the super learner’s regression coefficients, and also ensures the coefs sum to 1. The python implementation here, on the other hand, is allowing the coefs to be negative and do not sum to 1.
Checking the source papers, they also say that the super learner combines the base learners by making coefs from OLS positive and sum to 1 so that they represent the weights assigned to the individual base learners (Polley and van der Laan, 2010 “Super Learner In Prediction”, p. 16 and van der Laan et al 2008 “Super Learner” p. 7).
how to implement NNLS in python? Using sci-kit learn’s Lasso with positive=True often gives errors because it is built for coordinate descent, while scipy.optimize.nnls is not wrapped for sci-kit learn, making it inconvenient.
Tried to apply the superlearner for classification on own data, but apparently I am missing out on a detail. The data is stored in a csv file, and when attempting to relate data load to the part named ‘# create the inputs and outputs’ I experience that the algorithm does not integrate the data. I was of the notion that e.g. using ‘data = pd.read_csv(path + file)’ and then defining X = data[‘Column’] and y = data[‘target’] would relate to the super learner for classification. What am I doing wrong? Thx, Jens
I did inspect several times, yet I do not seem to be able to spot the error, re below. My data is in fact 1,000 entries long, corresponding to the n_samples=1000. But when I try to double check, e.g. changing n_samples=10000 or n_samples=2000 I wouldn’t expect the algo to run properly. However, it does, telling me that I am not relating the algorithm correctly to my own data. Thx.
# create the inputs and outputs
data = pd.read_csv(path + file) # data entries = 1,000
X = data[‘Column’]
y = data[‘target’]
X, y = make_blobs(n_samples=1000, centers=2, n_features=100, cluster_std=20)
# split
X, X_val, y, y_val = train_test_split(X, y, test_size=0.1)
print(‘Train’, X.shape, y.shape, ‘Test’, X_val.shape, y_val.shape)
The code demonstrates that Linear Regression wins everytime because the process used to generate the data in the one example shown is itself a linear model (sklearn’s make_regression function).
When the data X and y are changed to randn() data generating processes, or time series, the R2 measures for the base models all turn negative and Linear regression no longer wins within the ensemble. Because of the change in data, the ensemble starts mixing more with the other base models instead.
What explains the ensemble kicking in when the data generating process is changed to something that OLS clearly can’t fully capture? If the underlying true model (data) is no longer OLS-compliant, isn’t R2 irrelevant? Some examples with other data besides this OLS one would help.
I would guess that the challenge of the problem forces diversity in the sub-models, and mixing allows for a lift in skill over the submodels – e.g. why we want to use ensembles in the first place.
Why is cross-validation being done twice? First in the get_out_of_fold_predictions() function and again within super_learner_predictions()? Both of these are generating their own meta_X matrix from the base models. Shouldn’t meta_X only be generated once by the first function while the second function, the superlearner, merely weights the columns of that first meta_X?
Thank you for article and useful examples! Question: if super learner ensemble has “likelihood of performing better” shall it be always checked out in Machine Learning projects as a part of the pipeline? Or maybe we should test it only in specific conditions? If the aim is only to boost KPI’s of the projects, then super learner cannot be neglected, I guess.
Hi Jason
thanks for your articles and useful examples!
I have sucessessful run the above cobe,and alse use my own data.
i have a question that what’s the meaning of the output score-m score-s ft-m ft-s pt-m pt-s
Hi, thanks for such a useful tutorial. I have a question regarding example of a super learner model for regression where I have a multi input multi output MIMO and I am going to use
modelchain = LinearSVR()
wrapperSVRchain = RegressorChain(modelchain)
Can I use such resembing using RegressorChain(LinearSVR())?
Even when I just try to reuse your code using my data (X and Y are based on PCA and normalization):
instead of
# create the inputs and outputs
X, y = make_regression(n_samples=1000, n_features=100, noise=0.5)
# split
X, X_val, y, y_val = train_test_split(X, y, test_size=0.50)
I use:
X = XPCA
X_val = X_testPCA
y = YPCA
y_val = Y_testPCA
and just using models.append(RandomForestRegressor(n_estimators=5)) :
# create a list of base-models
def get_models():
models = list()
# models.append(LinearRegression())
# models.append(ElasticNet())
# models.append(SVR(gamma=’scale’))
# models.append(DecisionTreeRegressor())
# models.append(KNeighborsRegressor())
# models.append(AdaBoostRegressor())
# models.append(BaggingRegressor(n_estimators=10))
models.append(RandomForestRegressor(n_estimators=5))
# models.append(ExtraTreesRegressor(n_estimators=10))
return models
I always recieved the follwoing error in line “ensemble.fit(X, y)”
Train (11, 6) (11, 6) Test (3, 6) (3, 6)
ValueError: could not broadcast input array from shape (2,6) into shape (2,1)
It works using your created data but not using my MIMO data.
Could you please let me know your opinion?
Thanks in advance
I just replace the created data code with the followiing to make it MIMO(multi-input-output):
# create datasets
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, n_targets=2, random_state=1, noise=0.5)
and commented:
# models.append(LinearRegression())
# models.append(ElasticNet())
# models.append(SVR(gamma=’scale’))
then it gave me this error in line ensemble.fit(X, y):
ValueError: bad input shape (500, 2)
and with the following changes:
# create a list of base-models
def get_models():
models = list()
models.append(LinearRegression())
# models.append(ElasticNet())
# models.append(SVR(gamma=’scale’))
models.append(DecisionTreeRegressor())
# models.append(KNeighborsRegressor())
# models.append(AdaBoostRegressor())
# models.append(BaggingRegressor(n_estimators=10))
# models.append(RandomForestRegressor(n_estimators=10))
# models.append(ExtraTreesRegressor(n_estimators=10))
return models
I had this error again in line ensemble.fit(X, y):
ValueError: could not broadcast input array from shape (50,2) into shape (50,1)
I have read a lot of papers about the super learner. I have also studied on your blog and read the answer for ‘Why do we fit each base-model on the entire training dataset?’.
However, I could not understand step 5 in the diagram of the SL.
How do we combine predictions from step 0 and steps 1-4? Step 0 includes only training.
Are the predictions of step 0 a part of super learner or do we use them only for evaluation purposes?
In the manual example, line 95 fits the base models on all data (step 0), line 101 uses models and meta model to make predictions on new data (step 5).
This is a great article! It succinctly hits the important aspects of SuperLearner.
Coming from the R world using the original SuperLearner R package, I am not seeing how this python implementation is performing nested cross-validation (not simply k-folds) to evaluate estimator performance. Can you clarify a function similar to CV.superlearner in the R package that performs both an inner fold cross-validation and an out fold cross-validation?
This is a great article on SuperLearner implementation in Python. I have a question on saving the model for a later use. I tried with simple joblib save model but when I load the model again it gives me an error.
Could you explain a way to save the model and load it for later use?
Hi Jason. First, thanks for the amazing service of your website.
Question: Does this ML-ENS code you wrote (for classification) automatically use the meta-learners on the predicted *probabilities* instead of on the predicted class memberships?
Thanks so much for this great article and your amazing website.
Could you please elaborate more on how to use the inputs in order to develop a meta-learner?
For example, if we have the input data for the meta-model as a 1000 x 50 matrix (as shown in step 3 of the diagram), how do we actually use this input to create a meta-learner? Do we always use linear regression to combine the models?
Hi, as a meta-model you have used logistic regression , for multi-class classification as meta-model which model do I have to try? What would be your suggestion?
Thanks
Thank you. As a meta-model I tried logistic regression for multi-class dataset… still it has given better result on recall and accuracy also.How can this the logistic regression as a meta model works on multi-class dataset.
Hi Jason
In the section “What Is the Super Learner?”, in this sentence “All out-of-fold predictions are then kept and used to train a that learns how to best combine the predictions.”, after ‘a’ There must be something like ‘meta learner’ or so, that is dropped now! It is a typo!
U mean this step just for training the base models but no relation between this step and the meta learner ( super learner ) because in the flow chart step 5 ( evaluate super learner by combining the Predictions from step 0 and step from 1 to 4)
step 1 to 4 is to learn about the weight for the ensemble, and step 0 is to build the component models. The model you built in steps 1 to 4 are not used in the final ensemble.
That is mean that the the base models just used to predict the folds and the prediction used to training the meta learner and we trained the base model in the entire training set to evaluate them with the test set to compare the performance between the super learner and the base models but we can’t compare the performance between the super learner and the base model In the case of using ML ensemble library because the base model didn’t trained in the entire training set?
I mean the step 0 uses for training the base models at the full training set to evaluate the base models at the test set and the meta learner just train at the Predictions of the base models at kfolds step.
So we can compare the performance of super learner and the base models.
But if we used ML ensemble library we didn’t train the base models at the full training set and we just training the base models using kfold but the super learner training at the full training set so we can’t compare the performance between base models and the super learner performance.
And also I want to know what the mean of this sentence ( The ensemble can be used for prediction by mapping a new test set T into a prediction set Z′ using the learners fitted in (2), and then mapping Z′ to y′ using the fitted meta learner from (5).)
I believe due to the structure of the super learner that a partial dependence plot would connect the predictions with the base models’ outputs, right? The idea of having a standard PDP as in RF or SVM, where the data inputs are linked to the predictions of the final model would not be possible.
where to adjust the code, to make hybrid models like CNN-LSTM as a base learner, in which the hybrid model by itself have different hyperparameters to tune???
i want to know when i using mlens library are the following the right steps :
1- step 0 we fit the base learner in the training set and keep it
2- we divide the training set into kfolds as ( 10 ) and we train each base learner on the 10 kfolds and we get all the prediction of the 10 kfolds and put all together in matrix consist of number of row ( which are the number of row at the training set for example if the training set consist of 100 row so the number of row in the matrix are 100 and the number of column are the number of base learner )
3- we fit the( level two) in case of using more than one level or fit (the meta learner) in case of using one level and the meta learner in the matrix which consist of the number of rows and the columns which are the numbers of base learner
4- in case of prediction new data which aren’t in the training set the super learner call the predictions which were a result from step 0 and make the prediction
Hi James , I used mlens library but I wanna know if the steps are correct if I used superlearner in the library ?
But I tried it and it is good if u use multi level and change the parameter of base learner algorithms and u will get high accuracy
For more explaination the following steps are in the paper which cited by ml ensemble library
1- Fit each algorithm in L on the entire data set X = {Xi : i =1,…,n} to estimate ˆΨk(W),k= 1,…,K(n).
2. Split the data set X into a training and validation sample, according to a V-fold crossvalidation scheme: splits the ordered n observations into V -equal size groups, let the ν-th group be the validation sample, and the remaining group the training sample, ν =1,…,V. Define T(ν)tobetheνth training data split and V(ν) to be the corresponding validation data split. T(ν)=X\V(ν),ν=1,…,V.
3. For the νth fold, fit each algorithm in L on T(ν) and save the predictions on the corresponding validation data, ˆΨk,T(ν)(Wi), Xi ∈ V (ν)forν =1,…,V.
4. Stack the predictions from each algorithm together to create a n by K matrix, Z =ˆΨk,T(ν)(WV(ν)),ν=1,…,V&k =1,…,K, where we used the notation WV(ν) = (Wi : Xi ∈ V(ν)) for the covariate-vectors of the V (ν)-validation sample.
5. Propose a family of weighted combinations of the candidate estimators indexed by weightvector α: K m(z|α)= k=1 K αk ˆΨk,T(ν)(WV(ν)),αk ≥ 0 ∀k, k=1 αk =1.
6. Determine the α that minimizes the cross-validated risk of the candidate estimator K k=1 αk ˆΨk over all allowed α-combinations: n ˆ α =argmin α i=1 (Yi −m(zi|α))2.
7. Combine ˆα with ˆΨk(W),k=1,…,K accordingtothefamilym(z|α) of weighted combinations to create the final super learner fit: K ˆ ΨSL(W)= k=1 ˆ αk ˆΨk(W)
So the steps from 5 to 7 aren’t clear in the sudo code of the ML ensemble library
Is the library not consider the weights of the algorithm and use all of them ?
Hi Daniel…You are very welcome! Yes, but understand that all code and material on my site and in my books was developed and provided for educational purposes only.
I take no responsibility for the code, what it might do, or how you might use it.
If you use my code or material in your own project, please reference the source, including:
The Name of the author, e.g. “Jason Brownlee”.
The Title of the tutorial or book.
The Name of the website, e.g. “Machine Learning Mastery”.
The URL of the tutorial or book.
The Date you accessed or copied the code.
For example:
Jason Brownlee, Machine Learning Algorithms in Python, Machine Learning Mastery, Available from https://machinelearningmastery.com/machine-learning-with-python/, accessed April 15th, 2018.
Also, if your work is public, contact me, I’d love to see it out of general interest.
Hello Mr. James, can this method tackle multiple outputs (responses). For example, I am studying some laboratory experimental performance curves plotted within some limit. These curves are basically divided into four quadrants. Through theoretical analysis, the first quadrant can be obtained with almost perfect accuracy. I am exploring the use of machine learning to predict the other three 3 quadrants with the first quadrant as input and laboratory experimental complete performance curves as data training set. Could you please advise me?
In your examples all base models are trained on the same feature sets but would it possible to create a super learner algorithm for base models trained on different feature sets (i.e. using models trained on both categorical vs. numerical encoded data)? Furthermore, how would probability calibration work for a super learner algorithm? I would assume you can wrap the final super learner algorithm with sklearn’s CalibratedClassifierCV but can see how this could be complicated for super learner’s built from base models fit on different feature sets.
Assuming each base model within a super learner ensemble are trained on different feature sets and may utilize different features in making model predictions, how would one evaluate feature importance for the overarching super learner ensemble meta model?
Great article Jason, clear and very useful for me. Does the SuperLearner import split 50% as in your example ?
Thanks.
Yes, I split the data 50/50 in the final example.
Thanks a lot Jason!
Could you explain how could I make a prediction with already trained super learner model on single row?
All the best!
If you are using the custom code, then see the super_learner_predictions() function.
If you are using the lib, call ensemble.predict(…)
Apologies I can see that 0.5 is set, ignore last question
No problem.
Hi
Interestingly no matter how many times I run the first complete example, RMSE of LinearRegression is less than Super Learner!
Following one sample output:
Train (500, 100) (500,) Test (500, 100) (500,)
Meta (500, 9) (500,)
LinearRegression: RMSE 0.562
ElasticNet: RMSE 67.114
SVR: RMSE 176.879
DecisionTreeRegressor: RMSE 162.378
KNeighborsRegressor: RMSE 156.142
AdaBoostRegressor: RMSE 103.183
BaggingRegressor: RMSE 118.581
RandomForestRegressor: RMSE 121.637
ExtraTreesRegressor: RMSE 109.636
Super Learner: RMSE 0.571
Here another one:
Train (500, 100) (500,) Test (500, 100) (500,)
Meta (500, 9) (500,)
LinearRegression: RMSE 0.509
ElasticNet: RMSE 64.889
SVR: RMSE 173.591
DecisionTreeRegressor: RMSE 169.789
KNeighborsRegressor: RMSE 155.547
AdaBoostRegressor: RMSE 96.808
BaggingRegressor: RMSE 119.754
RandomForestRegressor: RMSE 112.420
ExtraTreesRegressor: RMSE 110.969
Super Learner: RMSE 0.519
And here the third one:
Train (500, 100) (500,) Test (500, 100) (500,)
Meta (500, 9) (500,)
LinearRegression: RMSE 0.540
ElasticNet: RMSE 51.105
SVR: RMSE 137.585
DecisionTreeRegressor: RMSE 126.397
KNeighborsRegressor: RMSE 122.300
AdaBoostRegressor: RMSE 73.785
BaggingRegressor: RMSE 79.778
RandomForestRegressor: RMSE 81.047
ExtraTreesRegressor: RMSE 74.907
Super Learner: RMSE 0.545
Thanks!
Had the same issue with classification.
XGB almost always was better than Super learner 🤔
Nice work!
Yes, the chosen task might be too trivial and the ensemble messes it up.
What impact would an unbalanced dataset have on choice of individual learner algorithms and the ability for the super learner to improve
Probably predict calibrated probabilities and use a model to best combine those probabilities.
That is my first off-the-cuff thought.
Also, use metrics that focus on what’s important, e.g. f-measure or g-mean, etc.
Hello,
I’m a total beginner in coding the ML. However, I know the concepts of modelling.
Could you throw out the libraries you import in the code because I’m very interested in Super Learner and I would like to use a Spyder IDE to better understand what is happening here.
This tutorial will show you how to setup your development environment:
https://machinelearningmastery.com/setup-python-environment-machine-learning-deep-learning-anaconda/
Thanks Jason,
Two questions:
+ Have you tried what could be the performance with H2O’s approach for the same classification example: http://docs.h2o.ai/h2o/latest-stable/h2o-docs/data-science/stacked-ensembles.html
+ And is this issue already covered in any of your books?.
Also, it could be worth to consider what is the performance of this new Python library AutoViML: https://towardsdatascience.com/why-automl-is-an-essential-new-tool-for-data-scientists-2d9ab4e25e46
Thanks a lot for everything you share!.
Carlos.
I have not used H20, sorry.
I am not familiar wth AutoViML. Thanks for sharing.
Carlos
You might want to take this same data set and try with H2O AutoML and Auto_ViML and compare their performance against the Super Learner. You might want to play back results here.
Great suggestion!
Very lucid explanations, as always! Thank you!
Readers should note Stacking Classifier and Regressor are new features in scikit-learn 0.22, released December 3, 2019. The link to the Classifier is below.
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.StackingClassifier.html
mlens looks like it has been around for years and is speed and memory optimized. It has some advanced model selection features.
mlens: https://github.com/flennerhag/mlens
Thanks Justin!
Yes, I hope to write a tutorial on the new stacking api.
Another great article, thanks Jason!
Could you explain the main difference between this model and the stacking ensemble model (https://machinelearningmastery.com/stacking-ensemble-for-deep-learning-neural-networks/). I mean rather than their different sub-models and meta-models architecture.
Thanks
Thanks!
Not much difference at all. In fact, the super learner is a type of stacking.
I mention this in the post.
Nice Article Jason.
I am just a beginner in ensemble learning. In the above example(Classification) did you considered probability predictions of base models as training data to the 2nd level logistic regression? or have you taken direct predictions of base model as training set ?
Thanks!
Yes predictions from first level models are fed as input to second level models.
Thank you so much for your contribution,
I just would like to ask how can I incorporate another model which would not be a machine learning model. This model is very powerful for my problem and I would like to incorporate it into the get_model() part.
Thank you in advance.
One approach would be to use a stacking ensemble directly and only take the predictions from your good model and combine them with the meta model.
Another approach might be to wrap your powerful model in a Classifier class from the scikit-learn library.
Thank you very much for your kind response.
Could you please give me some advice to wrap my model in a Classifier class from the scikit-learn library.
this issue is not familiar with me.
What are you trying to achieve exactly?
Dear Jason
thank you so much for your generous work (Blog).
I am looking forward to understanding the math behind SL. I mean the methodology behind Super Learning. how it starts with the regression dataset and goes with CV and ends with the best-predicted value. If possible, could you enlight me, please?
regards!
Suraj
You’re welcome.
See the “further reading” section for papers and books.
Great Information on how to Develop Super Learner Ensembles in Python. It’s very practical and helpful in developing machine learning algorithms. Thanks for sharing such a piece of wonderful information.
Thanks!
Hi Jason, thanks for the great content. You have helped me so much the last few years.
In regard to this problem, predict_proba does not seem to work with the SuperLearner. No matter what, it only seems to return discrete values (ints that I converted from my string labels).
I think I might have to engineer it myself from your code, but maybe you could point out what I’m missing?
Thanks
Interesting, thanks for pointing that out.
A rough and simple approach would be to sum the probability scores from each model for each class then normalize the values to give a probability-like score.
A better approach would be to combine the probabilities systematically, perhaps dip into the sklearn code to see how this is done in stacking or voting ensebles when predict_proba() is called.
Hi Jason, this is a very useful information.
Thank you for sharing.
For binary classification, I want to consider Artificial Neural Networks as one of the base models along with Catboost, LASSO and Random forest classifier. Can you help me with the same?
Thank you
Yes, you can use the ML-Ensemble library with sklearn models directly.
I cannot code this for you. Use the example in the post as a starting point.
Hi Jason, I have a question related to ensemble method for classification. how can i apply it with multi-class classification? and for meta_model, we can choose which classification we prefer or what? Thank you.
In the same way as binary classification.
Hi,
Ia it possible to add RBFNN to the Super Learner?
Thank you
Perhaps. I don’t have an example sorry.
Jason, thank you so much! I’m trying to incorporate my own dataset into this. I have 1,875 rows (including headers) and 19 columns (18 of which are actual features). I’m trying to set X and y like this:
# create the inputs and outputs
X = dataframe.iloc[0:1874]
Y = dataframe.iloc[:,0:18]
But I keep getting this error:
ValueError: Found input variables with inconsistent numbers of samples: [1874, 1875]
Thank you so much if you can help me (or if anyone else in this comments thread can help me).
i’m getting the error at this step:
meta_X, meta_y = get_out_of_fold_predictions(X, y, models)
What error?
Looks like X is selecting rows and y is selecting columns.
Perhaps this will help:
https://machinelearningmastery.com/index-slice-reshape-numpy-arrays-machine-learning-python/
when i finally fix that error, i get this one:
KeyError: “None of [Int64Index([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,\n …\n 926, 927, 928, 929, 930, 931, 933, 934, 935, 936],\n dtype=’int64′, length=843)] are in the [columns]”
Sorry to hear that, perhaps this will help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
actually, my friend helped me to fix this; she said to do this:
# create the inputs and outputs
X = dataframe.iloc[0:1875].values #CHANGED THIS LINE FROM 0:1874 TO 0:1875 AND ADDED .VALUES <–she helped me here.
y = dataframe.iloc[:,-1].values # CHANGED THIS LINE, ADDED .VALUES <–she helped me here.
now all works! 😀
Well done.
Do you think making hyperparameter tunning is logical for candidate learners?
Thank you so much!
Sorry, I don’t understand what you mean, can you please elaborate?
I would like to do hyperparameter tuning for each base model before using them in the super learner. I would like to ask that using the best configuration hyperparameter values rather than the default parameters for each base model in the super Learner model would be reasonable?
Nice idea.
Often using good enough models works better than highly optimized (fragile) models in an ensemble. At least in general.
Thank you very much for your great contribution!
You’re welcome.
from the super learner, how do i extract the weights assigned to the base models? The source paper and the R package is able to say “the super learner is a combination of 20% ElasticNet, 80% LinearRegression” for example. How to get these combination weights from the python implementation, i.e. your fit_meta_model function. I don’t think they are the fit_meta_model regression coefficients because some are negative and don’t sum to 1. thanks
Not sure off hand, sorry. You might have to dig into the API/code.
The R package of super learner uses NNLS (non-negative least squares) to estimate the super learner’s regression coefficients, and also ensures the coefs sum to 1. The python implementation here, on the other hand, is allowing the coefs to be negative and do not sum to 1.
Checking the source papers, they also say that the super learner combines the base learners by making coefs from OLS positive and sum to 1 so that they represent the weights assigned to the individual base learners (Polley and van der Laan, 2010 “Super Learner In Prediction”, p. 16 and van der Laan et al 2008 “Super Learner” p. 7).
how to implement NNLS in python? Using sci-kit learn’s Lasso with positive=True often gives errors because it is built for coordinate descent, while scipy.optimize.nnls is not wrapped for sci-kit learn, making it inconvenient.
Good question, I don’t have an off-hand solution. You may have to try a few things.
Hi Jason,
Tried to apply the superlearner for classification on own data, but apparently I am missing out on a detail. The data is stored in a csv file, and when attempting to relate data load to the part named ‘# create the inputs and outputs’ I experience that the algorithm does not integrate the data. I was of the notion that e.g. using ‘data = pd.read_csv(path + file)’ and then defining X = data[‘Column’] and y = data[‘target’] would relate to the super learner for classification. What am I doing wrong? Thx, Jens
Perhaps confirm that the data was loaded and split correctly – inspect what the operations did and that they are numpy arrays of numbers.
I did inspect several times, yet I do not seem to be able to spot the error, re below. My data is in fact 1,000 entries long, corresponding to the n_samples=1000. But when I try to double check, e.g. changing n_samples=10000 or n_samples=2000 I wouldn’t expect the algo to run properly. However, it does, telling me that I am not relating the algorithm correctly to my own data. Thx.
# create the inputs and outputs
data = pd.read_csv(path + file) # data entries = 1,000
X = data[‘Column’]
y = data[‘target’]
X, y = make_blobs(n_samples=1000, centers=2, n_features=100, cluster_std=20)
# split
X, X_val, y, y_val = train_test_split(X, y, test_size=0.1)
print(‘Train’, X.shape, y.shape, ‘Test’, X_val.shape, y_val.shape)
Sorry to hear that, perhaps try posting your code and error to stackoverflow.com
The code demonstrates that Linear Regression wins everytime because the process used to generate the data in the one example shown is itself a linear model (sklearn’s make_regression function).
When the data X and y are changed to randn() data generating processes, or time series, the R2 measures for the base models all turn negative and Linear regression no longer wins within the ensemble. Because of the change in data, the ensemble starts mixing more with the other base models instead.
What explains the ensemble kicking in when the data generating process is changed to something that OLS clearly can’t fully capture? If the underlying true model (data) is no longer OLS-compliant, isn’t R2 irrelevant? Some examples with other data besides this OLS one would help.
Good question.
I would guess that the challenge of the problem forces diversity in the sub-models, and mixing allows for a lift in skill over the submodels – e.g. why we want to use ensembles in the first place.
Why is cross-validation being done twice? First in the get_out_of_fold_predictions() function and again within super_learner_predictions()? Both of these are generating their own meta_X matrix from the base models. Shouldn’t meta_X only be generated once by the first function while the second function, the superlearner, merely weights the columns of that first meta_X?
One to prepare the sub models, one to evaluate the whole method.
Ideally a separate validation dataset would be used to evaluate the final model.
Good morning!
Thank you for article and useful examples! Question: if super learner ensemble has “likelihood of performing better” shall it be always checked out in Machine Learning projects as a part of the pipeline? Or maybe we should test it only in specific conditions? If the aim is only to boost KPI’s of the projects, then super learner cannot be neglected, I guess.
Regards!
It can be a good idea to check for your project.
What is Kpi?
Key performance indicator:
https://en.wikipedia.org/wiki/Performance_indicator
Hi Jason,
Is it possible to add NN to the Super Learner for Regression? Do you have an example?
Thank you.
I don’t see why not.
I don’t have an example, sorry.
Hi Jason
thanks for your articles and useful examples!
I have sucessessful run the above cobe,and alse use my own data.
i have a question that what’s the meaning of the output score-m score-s ft-m ft-s pt-m pt-s
Well done!
m and s would be mean and standard deviation, as for the rest, I don’t know off the cuff. Perhaps the documentation offers ideas.
Hi, thanks for such a useful tutorial. I have a question regarding example of a super learner model for regression where I have a multi input multi output MIMO and I am going to use
modelchain = LinearSVR()
wrapperSVRchain = RegressorChain(modelchain)
Can I use such resembing using RegressorChain(LinearSVR())?
Even when I just try to reuse your code using my data (X and Y are based on PCA and normalization):
instead of
# create the inputs and outputs
X, y = make_regression(n_samples=1000, n_features=100, noise=0.5)
# split
X, X_val, y, y_val = train_test_split(X, y, test_size=0.50)
I use:
X = XPCA
X_val = X_testPCA
y = YPCA
y_val = Y_testPCA
and just using models.append(RandomForestRegressor(n_estimators=5)) :
# create a list of base-models
def get_models():
models = list()
# models.append(LinearRegression())
# models.append(ElasticNet())
# models.append(SVR(gamma=’scale’))
# models.append(DecisionTreeRegressor())
# models.append(KNeighborsRegressor())
# models.append(AdaBoostRegressor())
# models.append(BaggingRegressor(n_estimators=10))
models.append(RandomForestRegressor(n_estimators=5))
# models.append(ExtraTreesRegressor(n_estimators=10))
return models
I always recieved the follwoing error in line “ensemble.fit(X, y)”
Train (11, 6) (11, 6) Test (3, 6) (3, 6)
ValueError: could not broadcast input array from shape (2,6) into shape (2,1)
It works using your created data but not using my MIMO data.
Could you please let me know your opinion?
Thanks in advance
Perhaps try using a pipeline for your transform?
I just replace the created data code with the followiing to make it MIMO(multi-input-output):
# create datasets
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, n_targets=2, random_state=1, noise=0.5)
and commented:
# models.append(LinearRegression())
# models.append(ElasticNet())
# models.append(SVR(gamma=’scale’))
then it gave me this error in line ensemble.fit(X, y):
ValueError: bad input shape (500, 2)
and with the following changes:
# create a list of base-models
def get_models():
models = list()
models.append(LinearRegression())
# models.append(ElasticNet())
# models.append(SVR(gamma=’scale’))
models.append(DecisionTreeRegressor())
# models.append(KNeighborsRegressor())
# models.append(AdaBoostRegressor())
# models.append(BaggingRegressor(n_estimators=10))
# models.append(RandomForestRegressor(n_estimators=10))
# models.append(ExtraTreesRegressor(n_estimators=10))
return models
I had this error again in line ensemble.fit(X, y):
ValueError: could not broadcast input array from shape (50,2) into shape (50,1)
Could you please let me know your idea?
Thanks in advance
Sorry, I don’t have the capacity to debug your changes, perhaps these tips will help:
https://machinelearningmastery.com/faq/single-faq/can-you-read-review-or-debug-my-code
Dear Jason
Thanks for your sharing.
I have read a lot of papers about the super learner. I have also studied on your blog and read the answer for ‘Why do we fit each base-model on the entire training dataset?’.
However, I could not understand step 5 in the diagram of the SL.
How do we combine predictions from step 0 and steps 1-4? Step 0 includes only training.
Are the predictions of step 0 a part of super learner or do we use them only for evaluation purposes?
Thanks in advance,
Kind regards,
Mehtap
The model is comprised of many submodels. The predictions from submodels are combined, e.g. via averaging or another model.
Which part is confusing exactly?
To simply ask, I could not understand the purpose of step 0 and the evaluation process in step 5.
and where are these steps (step 0 and step 5) in python code for regression example?
In the manual example, line 95 fits the base models on all data (step 0), line 101 uses models and meta model to make predictions on new data (step 5).
Good question.
We want models trained on all data (step 0).
The CV steps figure out how to weight the models (steps 1-4).
We then use the trained model and the weightings we learned to make predictions on new data (step 5)
Hello sir,
I used super learner for my project, but it is not give me result what i expected. Instead Another models give me Than super learner
Nice work, then use the other model.
Hi Jason,
This is a great article! It succinctly hits the important aspects of SuperLearner.
Coming from the R world using the original SuperLearner R package, I am not seeing how this python implementation is performing nested cross-validation (not simply k-folds) to evaluate estimator performance. Can you clarify a function similar to CV.superlearner in the R package that performs both an inner fold cross-validation and an out fold cross-validation?
Thank you,
Mark
Thanks!
Not sure the library supports that feature, you may need to check the documentation.
Or perform it manually with sklearn library:
https://machinelearningmastery.com/nested-cross-validation-for-machine-learning-with-python/
This is a great article on SuperLearner implementation in Python. I have a question on saving the model for a later use. I tried with simple joblib save model but when I load the model again it gives me an error.
Could you explain a way to save the model and load it for later use?
Yes, joblib or pickle would be what I would use.
Perhaps there is a fault with the lib, you could try contacting the author of the library directly:
http://ml-ensemble.com/
Dear Jason,
Thank you so much for sharing?
Do you think the weighted-based combination of ML algorithms is heuristic?
Thanks in advance.
Not really. Maybe. What do you mean exactly?
Thank you so much for your response,
I just wonder whether SL combines the candidate learner in the optimal way.
It tries to.
Hi Jason. First, thanks for the amazing service of your website.
Question: Does this ML-ENS code you wrote (for classification) automatically use the meta-learners on the predicted *probabilities* instead of on the predicted class memberships?
Thanks!
You’re welcome!
I did not create the ml-ens library, I’m just showing how to use it.
Yes, I believe internally it uses soft voting from level 0 models.
Hi Jason. First, thanks for the amazing service of your website.
Question: Can superlearner algorithm be used in multi-classification?
I have targets with 4 class.
Thanks.
You’re welcome.
Yes, super learner can be used for multi-class classification.
Hi Jason,
Thanks so much for this great article and your amazing website.
Could you please elaborate more on how to use the inputs in order to develop a meta-learner?
For example, if we have the input data for the meta-model as a 1000 x 50 matrix (as shown in step 3 of the diagram), how do we actually use this input to create a meta-learner? Do we always use linear regression to combine the models?
Thank you very much!
You’re welcome!
You fit a model on the predictions from the sub models – as we do in the tutorial.
Is there a specific aspect of this that you’re having trouble with?
Hi, as a meta-model you have used logistic regression , for multi-class classification as meta-model which model do I have to try? What would be your suggestion?
Thanks
Good question. Perhaps multinomial regression, perhaps lda, perhaps a small neural net?
Thank you. As a meta-model I tried logistic regression for multi-class dataset… still it has given better result on recall and accuracy also.How can this the logistic regression as a meta model works on multi-class dataset.
Logistic regression can be used in a one-vs-one (OVO) or one-vs-rest (OVR) manner, or the loss function can be changed to a multinomial distribution.
[MLENS] backend: threading
Train (500, 100) (500,) Test (500, 100) (500,)
score-m score-s ft-m ft-s pt-m pt-s
layer-1 adaboostclassifier 0.90 0.04 0.51 0.05 0.04 0.01
layer-1 baggingclassifier 0.83 0.06 0.21 0.01 0.01 0.00
layer-1 decisiontreeclassifier 0.68 0.07 0.03 0.00 0.00 0.00
layer-1 extratreesclassifier 0.80 0.05 0.09 0.01 0.00 0.00
layer-1 gaussiannb 0.96 0.04 0.01 0.00 0.00 0.00
layer-1 kneighborsclassifier 0.90 0.03 0.00 0.00 0.03 0.01
layer-1 logisticregression 0.93 0.03 0.01 0.00 0.00 0.00
layer-1 randomforestclassifier 0.81 0.06 0.09 0.03 0.00 0.00
layer-1 svc 0.96 0.03 0.10 0.01 0.00 0.00
Super Learner: 97.400
Can you please explain these terms – score-m score-s ft-m ft-s pt-m pt-s in the last result?
They are the mean and standard deviation of the score, fit time, and predict time
Hi Jason
In the section “What Is the Super Learner?”, in this sentence “All out-of-fold predictions are then kept and used to train a that learns how to best combine the predictions.”, after ‘a’ There must be something like ‘meta learner’ or so, that is dropped now! It is a typo!
Thanks. Fixed.
Hi Jason, after training the super learner, how can it be saved using pickle or as a json file for future use?
Pickle would work.
Hello , I’m using mlens super learner with 3 layers and metalearner I want to know the flowchart or the steps of the superlearner
Don’t you think the sample code here is sufficient?
i want to know what the use of step 0 ?
Train the learners with the entire training set and no hold out. So with more data, the resulting learner should be better and stronger.
U mean this step just for training the base models but no relation between this step and the meta learner ( super learner ) because in the flow chart step 5 ( evaluate super learner by combining the Predictions from step 0 and step from 1 to 4)
step 1 to 4 is to learn about the weight for the ensemble, and step 0 is to build the component models. The model you built in steps 1 to 4 are not used in the final ensemble.
That is mean that the the base models just used to predict the folds and the prediction used to training the meta learner and we trained the base model in the entire training set to evaluate them with the test set to compare the performance between the super learner and the base models but we can’t compare the performance between the super learner and the base model In the case of using ML ensemble library because the base model didn’t trained in the entire training set?
Sorry, can’t get what you’re asking. Can you rephrase?
I mean the step 0 uses for training the base models at the full training set to evaluate the base models at the test set and the meta learner just train at the Predictions of the base models at kfolds step.
So we can compare the performance of super learner and the base models.
But if we used ML ensemble library we didn’t train the base models at the full training set and we just training the base models using kfold but the super learner training at the full training set so we can’t compare the performance between base models and the super learner performance.
And also I want to know what the mean of this sentence ( The ensemble can be used for prediction by mapping a new test set T into a prediction set Z′ using the learners fitted in (2), and then mapping Z′ to y′ using the fitted meta learner from (5).)
Thank you for the article!
I believe due to the structure of the super learner that a partial dependence plot would connect the predictions with the base models’ outputs, right? The idea of having a standard PDP as in RF or SVM, where the data inputs are linked to the predictions of the final model would not be possible.
Not sure. As I believe PDP is agnostic to the model? You can always make a PDP to see how a feature affects the result.
where to adjust the code, to make hybrid models like CNN-LSTM as a base learner, in which the hybrid model by itself have different hyperparameters to tune???
Hi Eyob…The following is an excellent resource to add clarify on designing and tuning CNN-LSTM models.
https://link.springer.com/article/10.1007/s11227-021-03838-w
i want to know when i using mlens library are the following the right steps :
1- step 0 we fit the base learner in the training set and keep it
2- we divide the training set into kfolds as ( 10 ) and we train each base learner on the 10 kfolds and we get all the prediction of the 10 kfolds and put all together in matrix consist of number of row ( which are the number of row at the training set for example if the training set consist of 100 row so the number of row in the matrix are 100 and the number of column are the number of base learner )
3- we fit the( level two) in case of using more than one level or fit (the meta learner) in case of using one level and the meta learner in the matrix which consist of the number of rows and the columns which are the numbers of base learner
4- in case of prediction new data which aren’t in the training set the super learner call the predictions which were a result from step 0 and make the prediction
Hi Mohammed…The steps you have outlined are reasonable. Have you implemented this algorithm? Let me know how it works.
Hi James , I used mlens library but I wanna know if the steps are correct if I used superlearner in the library ?
But I tried it and it is good if u use multi level and change the parameter of base learner algorithms and u will get high accuracy
Hi Mohammed…Your approach is in fact reasonable.
I just want how mlens library choose the weights of the base learner
Is it using mse to choose the best combination?
Hi MohhAhmed…Yes, the super learn algorithm often utilizes mse. The following may be of interest to you:
https://shariq-mohammed.github.io/files/cbsa2019/Super-Learner-In-Prediction.pdf
I know it is on the source paper but I want to know when it is used .
Is it using at the prediction step or cross validation step
For more explaination the following steps are in the paper which cited by ml ensemble library
1- Fit each algorithm in L on the entire data set X = {Xi : i =1,…,n} to estimate ˆΨk(W),k= 1,…,K(n).
2. Split the data set X into a training and validation sample, according to a V-fold crossvalidation scheme: splits the ordered n observations into V -equal size groups, let the ν-th group be the validation sample, and the remaining group the training sample, ν =1,…,V. Define T(ν)tobetheνth training data split and V(ν) to be the corresponding validation data split. T(ν)=X\V(ν),ν=1,…,V.
3. For the νth fold, fit each algorithm in L on T(ν) and save the predictions on the corresponding validation data, ˆΨk,T(ν)(Wi), Xi ∈ V (ν)forν =1,…,V.
4. Stack the predictions from each algorithm together to create a n by K matrix, Z =ˆΨk,T(ν)(WV(ν)),ν=1,…,V&k =1,…,K, where we used the notation WV(ν) = (Wi : Xi ∈ V(ν)) for the covariate-vectors of the V (ν)-validation sample.
5. Propose a family of weighted combinations of the candidate estimators indexed by weightvector α: K m(z|α)= k=1 K αk ˆΨk,T(ν)(WV(ν)),αk ≥ 0 ∀k, k=1 αk =1.
6. Determine the α that minimizes the cross-validated risk of the candidate estimator K k=1 αk ˆΨk over all allowed α-combinations: n ˆ α =argmin α i=1 (Yi −m(zi|α))2.
7. Combine ˆα with ˆΨk(W),k=1,…,K accordingtothefamilym(z|α) of weighted combinations to create the final super learner fit: K ˆ ΨSL(W)= k=1 ˆ αk ˆΨk(W)
So the steps from 5 to 7 aren’t clear in the sudo code of the ML ensemble library
Is the library not consider the weights of the algorithm and use all of them ?
Hi Mohammed…The following source is a great start:
https://machinelearningmastery.com/ensemble-machine-learning-algorithms-python-scikit-learn/
Thanks alot James, but I’m just talking about ml ensemble library I want to know is it using any loss function or not
Hello Jason, Thanks for the tutorial. Do I have permission to use this for my work? If so, how do I cite you to give you the credit?
Thanks
Hi Daniel…You are very welcome! Yes, but understand that all code and material on my site and in my books was developed and provided for educational purposes only.
I take no responsibility for the code, what it might do, or how you might use it.
If you use my code or material in your own project, please reference the source, including:
The Name of the author, e.g. “Jason Brownlee”.
The Title of the tutorial or book.
The Name of the website, e.g. “Machine Learning Mastery”.
The URL of the tutorial or book.
The Date you accessed or copied the code.
For example:
Jason Brownlee, Machine Learning Algorithms in Python, Machine Learning Mastery, Available from https://machinelearningmastery.com/machine-learning-with-python/, accessed April 15th, 2018.
Also, if your work is public, contact me, I’d love to see it out of general interest.
Whats the difference between stacking and Super learning ?! are they the same thing?!
Hi Hosam…The following should add clarity:
https://towardsdatascience.com/super-learner-versus-deep-neural-network-aa78547aabd7
Thanks a lot for posting this tutorial, can I save the training results in the h5 file? Also plotting learning curves of meta model?
Hi Kholood…The following may be helpful:
https://machinelearningmastery.com/how-to-save-and-load-models-and-data-preparation-in-scikit-learn-for-later-use/
https://machinelearningmastery.com/learning-curves-for-diagnosing-machine-learning-model-performance/
https://www.adamsmith.haus/python/answers/how-to-save-and-load-keras-models-from-hdf5-files
Thanks alot. I have a question, by calling fit_base_models(), where the fit information of each model is stored to make predictions?
In this tutorial, you say can using many models except XGBoost and DNN. How do I when I want to ensemble with XGBoost and DNN?
Hi sonnguyen…the following resource may be of interest to you:
https://machinelearningmastery.com/ensemble-machine-learning-with-python-7-day-mini-course/
Hello Mr. James, can this method tackle multiple outputs (responses). For example, I am studying some laboratory experimental performance curves plotted within some limit. These curves are basically divided into four quadrants. Through theoretical analysis, the first quadrant can be obtained with almost perfect accuracy. I am exploring the use of machine learning to predict the other three 3 quadrants with the first quadrant as input and laboratory experimental complete performance curves as data training set. Could you please advise me?
Hi Emmanuel…The following resource may be of interest to you:
https://machinelearningmastery.com/ensemble-machine-learning-with-python-7-day-mini-course/
For classification, would it be better to use StratifiedKFold if the percentages of the output classes are imbalanced?
Hi salcc…The following resources elaborate on best practices of applying StratifiedKFold:
https://www.geeksforgeeks.org/stratified-k-fold-cross-validation/
https://www.quora.com/What-are-the-advantages-and-disadvantages-of-k-fold-cross-validation
Thanks for another great tutorial Jason!
In your examples all base models are trained on the same feature sets but would it possible to create a super learner algorithm for base models trained on different feature sets (i.e. using models trained on both categorical vs. numerical encoded data)? Furthermore, how would probability calibration work for a super learner algorithm? I would assume you can wrap the final super learner algorithm with sklearn’s CalibratedClassifierCV but can see how this could be complicated for super learner’s built from base models fit on different feature sets.
Thanks again!
Hi Jake…Some additional guidelines can be found in the following resource:
https://towardsdatascience.com/a-comprehensive-guide-on-model-calibration-part-1-of-4-73466eb5e09a
Assuming each base model within a super learner ensemble are trained on different feature sets and may utilize different features in making model predictions, how would one evaluate feature importance for the overarching super learner ensemble meta model?