Voting is an ensemble machine learning algorithm.
For regression, a voting ensemble involves making a prediction that is the average of multiple other regression models.
In classification, a hard voting ensemble involves summing the votes for crisp class labels from other models and predicting the class with the most votes. A soft voting ensemble involves summing the predicted probabilities for class labels and predicting the class label with the largest sum probability.
In this tutorial, you will discover how to create voting ensembles for machine learning algorithms in Python.
After completing this tutorial, you will know:
- A voting ensemble involves summing the predictions made by classification models or averaging the predictions made by regression models.
- How voting ensembles work, when to use voting ensembles, and the limitations of the approach.
- How to implement a hard voting ensemble and soft voting ensemble for classification predictive modeling.
Kick-start your project with my new book Ensemble Learning Algorithms With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to Develop Voting Ensembles With Python
Photo by Bureau of Land Management, some rights reserved.
Tutorial Overview
This tutorial is divided into four parts; they are:
- Voting Ensembles
- Voting Ensemble Scikit-Learn API
- Voting Ensemble for Classification
- Hard Voting Ensemble for Classification
- Soft Voting Ensemble for Classification
- Voting Ensemble for Regression
Voting Ensembles
A voting ensemble (or a “majority voting ensemble“) is an ensemble machine learning model that combines the predictions from multiple other models.
It is a technique that may be used to improve model performance, ideally achieving better performance than any single model used in the ensemble.
A voting ensemble works by combining the predictions from multiple models. It can be used for classification or regression. In the case of regression, this involves calculating the average of the predictions from the models. In the case of classification, the predictions for each label are summed and the label with the majority vote is predicted.
- Regression Voting Ensemble: Predictions are the average of contributing models.
- Classification Voting Ensemble: Predictions are the majority vote of contributing models.
There are two approaches to the majority vote prediction for classification; they are hard voting and soft voting.
Hard voting involves summing the predictions for each class label and predicting the class label with the most votes. Soft voting involves summing the predicted probabilities (or probability-like scores) for each class label and predicting the class label with the largest probability.
- Hard Voting. Predict the class with the largest sum of votes from models
- Soft Voting. Predict the class with the largest summed probability from models.
A voting ensemble may be considered a meta-model, a model of models.
As a meta-model, it could be used with any collection of existing trained machine learning models and the existing models do not need to be aware that they are being used in the ensemble. This means you could explore using a voting ensemble on any set or subset of fit models for your predictive modeling task.
A voting ensemble is appropriate when you have two or more models that perform well on a predictive modeling task. The models used in the ensemble must mostly agree with their predictions.
One way to combine outputs is by voting—the same mechanism used in bagging. However, (unweighted) voting only makes sense if the learning schemes perform comparably well. If two of the three classifiers make predictions that are grossly incorrect, we will be in trouble!
— Page 497, Data Mining: Practical Machine Learning Tools and Techniques, 2016.
Use voting ensembles when:
- All models in the ensemble have generally the same good performance.
- All models in the ensemble mostly already agree.
Hard voting is appropriate when the models used in the voting ensemble predict crisp class labels. Soft voting is appropriate when the models used in the voting ensemble predict the probability of class membership. Soft voting can be used for models that do not natively predict a class membership probability, although may require calibration of their probability-like scores prior to being used in the ensemble (e.g. support vector machine, k-nearest neighbors, and decision trees).
- Hard voting is for models that predict class labels.
- Soft voting is for models that predict class membership probabilities.
The voting ensemble is not guaranteed to provide better performance than any single model used in the ensemble. If any given model used in the ensemble performs better than the voting ensemble, that model should probably be used instead of the voting ensemble.
This is not always the case. A voting ensemble can offer lower variance in the predictions made over individual models. This can be seen in a lower variance in prediction error for regression tasks. This can also be seen in a lower variance in accuracy for classification tasks. This lower variance may result in a lower mean performance of the ensemble, which might be desirable given the higher stability or confidence of the model.
Use a voting ensemble if:
- It results in better performance than any model used in the ensemble.
- It results in a lower variance than any model used in the ensemble.
A voting ensemble is particularly useful for machine learning models that use a stochastic learning algorithm and result in a different final model each time it is trained on the same dataset. One example is neural networks that are fit using stochastic gradient descent.
For more on this topic, see the tutorial:
Another particularly useful case for voting ensembles is when combining multiple fits of the same machine learning algorithm with slightly different hyperparameters.
Voting ensembles are most effective when:
- Combining multiple fits of a model trained using stochastic learning algorithms.
- Combining multiple fits of a model with different hyperparameters.
A limitation of the voting ensemble is that it treats all models the same, meaning all models contribute equally to the prediction. This is a problem if some models are good in some situations and poor in others.
An extension to the voting ensemble to address this problem is to use a weighted average or weighted voting of the contributing models. This is sometimes called blending. A further extension is to use a machine learning model to learn when and how much to trust each model when making predictions. This is referred to as stacked generalization, or stacking for short.
Extensions to voting ensembles:
- Weighted Average Ensemble (blending).
- Stacked Generalization (stacking).
Now that we are familiar with voting ensembles, let’s take a closer look at how to create voting ensemble models.
Want to Get Started With Ensemble Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Voting Ensemble Scikit-Learn API
Voting ensembles can be implemented from scratch, although it can be challenging for beginners.
The scikit-learn Python machine learning library provides an implementation of voting for machine learning.
It is available in version 0.22 of the library and higher.
First, confirm that you are using a modern version of the library by running the following script:
|
1 2 3 |
# check scikit-learn version import sklearn print(sklearn.__version__) |
Running the script will print your version of scikit-learn.
Your version should be the same or higher. If not, you must upgrade your version of the scikit-learn library.
|
1 |
0.22.1 |
Voting is provided via the VotingRegressor and VotingClassifier classes.
Both models operate the same way and take the same arguments. Using the model requires that you specify a list of estimators that make predictions and are combined in the voting ensemble.
A list of base models is provided via the “estimators” argument. This is a Python list where each element in the list is a tuple with the name of the model and the configured model instance. Each model in the list must have a unique name.
For example, below defines two base models:
|
1 2 3 |
... models = [('lr',LogisticRegression()),('svm',SVC())] ensemble = VotingClassifier(estimators=models) |
Each model in the list may also be a Pipeline, including any data preparation required by the model prior to fitting the model on the training dataset.
For example:
|
1 2 3 |
... models = [('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC()))] ensemble = VotingClassifier(estimators=models) |
When using a voting ensemble for classification, the type of voting, such as hard voting or soft voting, can be specified via the “voting” argument and set to the string ‘hard‘ (the default) or ‘soft‘.
For example:
|
1 2 3 |
... models = [('lr',LogisticRegression()),('svm',SVC())] ensemble = VotingClassifier(estimators=models, voting='soft') |
Now that we are familiar with the voting ensemble API in scikit-learn, let’s look at some worked examples.
Voting Ensemble for Classification
In this section, we will look at using stacking for a classification problem.
First, we can use the make_classification() function to create a synthetic binary classification problem with 1,000 examples and 20 input features.
The complete example is listed below.
|
1 2 3 4 5 6 |
# test classification dataset from sklearn.datasets import make_classification # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and summarizes the shape of the input and output components.
|
1 |
(1000, 20) (1000,) |
Next, we will demonstrate hard voting and soft voting for this dataset.
Hard Voting Ensemble for Classification
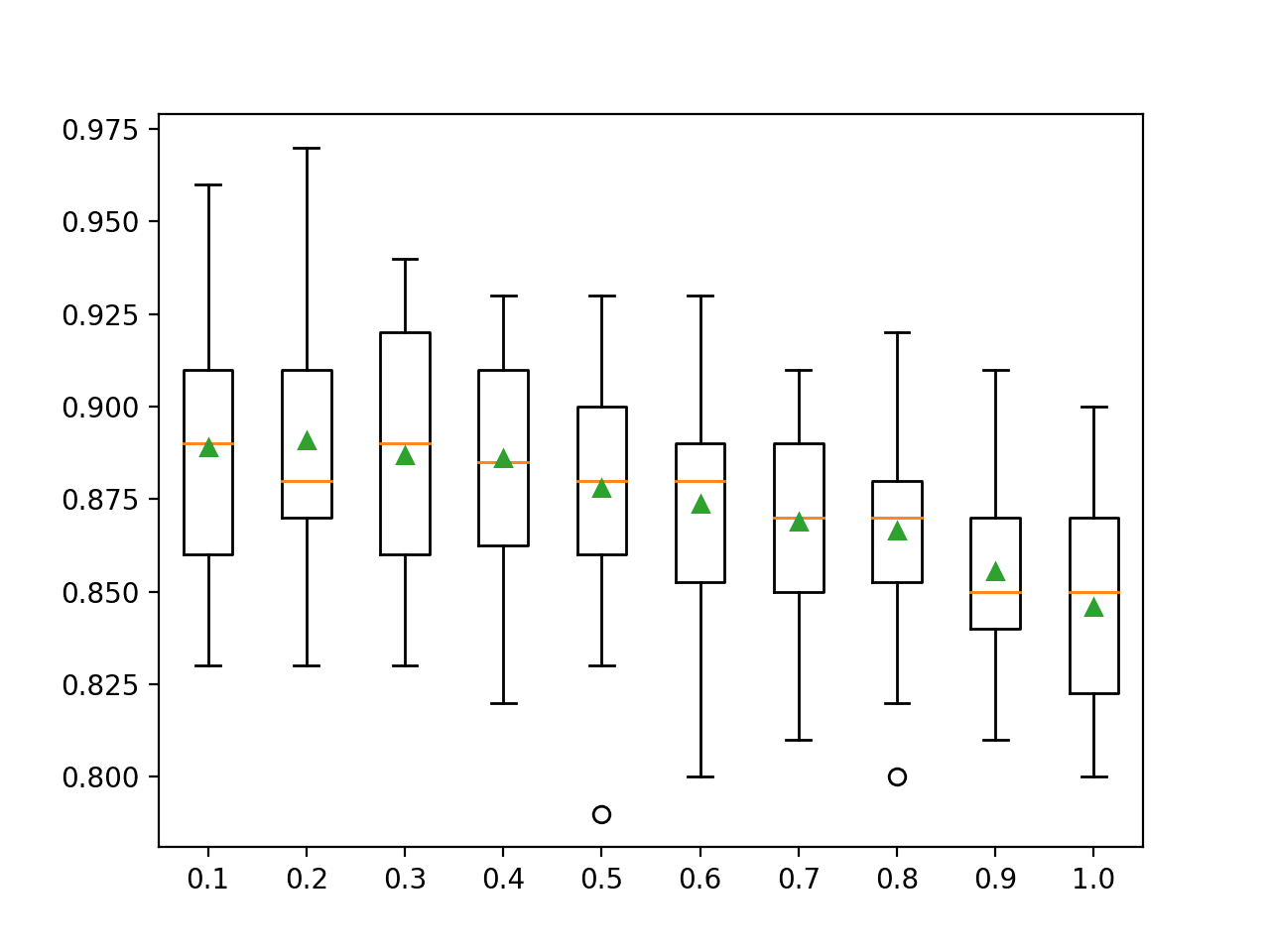
We can demonstrate hard voting with a k-nearest neighbor algorithm.
We can fit five different versions of the KNN algorithm, each with a different number of neighbors used when making predictions. We will use 1, 3, 5, 7, and 9 neighbors (odd numbers in an attempt to avoid ties).
Our expectation is that by combining the predicted class labels predicted by each different KNN model that the hard voting ensemble will achieve a better predictive performance than any standalone model used in the ensemble, on average.
First, we can create a function named get_voting() that creates each KNN model and combines the models into a hard voting ensemble.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# get a voting ensemble of models def get_voting(): # define the base models models = list() models.append(('knn1', KNeighborsClassifier(n_neighbors=1))) models.append(('knn3', KNeighborsClassifier(n_neighbors=3))) models.append(('knn5', KNeighborsClassifier(n_neighbors=5))) models.append(('knn7', KNeighborsClassifier(n_neighbors=7))) models.append(('knn9', KNeighborsClassifier(n_neighbors=9))) # define the voting ensemble ensemble = VotingClassifier(estimators=models, voting='hard') return ensemble |
We can then create a list of models to evaluate, including each standalone version of the KNN model configurations and the hard voting ensemble.
This will help us directly compare each standalone configuration of the KNN model with the ensemble in terms of the distribution of classification accuracy scores. The get_models() function below creates the list of models for us to evaluate.
|
1 2 3 4 5 6 7 8 9 10 |
# get a list of models to evaluate def get_models(): models = dict() models['knn1'] = KNeighborsClassifier(n_neighbors=1) models['knn3'] = KNeighborsClassifier(n_neighbors=3) models['knn5'] = KNeighborsClassifier(n_neighbors=5) models['knn7'] = KNeighborsClassifier(n_neighbors=7) models['knn9'] = KNeighborsClassifier(n_neighbors=9) models['hard_voting'] = get_voting() return models |
Each model will be evaluated using repeated k-fold cross-validation.
The evaluate_model() function below takes a model instance and returns as a list of scores from three repeats of stratified 10-fold cross-validation.
|
1 2 3 4 5 |
# evaluate a give model using cross-validation def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') return scores |
We can then report the mean performance of each algorithm, and also create a box and whisker plot to compare the distribution of accuracy scores for each algorithm.
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# compare hard voting to standalone classifiers from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.ensemble import VotingClassifier from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2) return X, y # get a voting ensemble of models def get_voting(): # define the base models models = list() models.append(('knn1', KNeighborsClassifier(n_neighbors=1))) models.append(('knn3', KNeighborsClassifier(n_neighbors=3))) models.append(('knn5', KNeighborsClassifier(n_neighbors=5))) models.append(('knn7', KNeighborsClassifier(n_neighbors=7))) models.append(('knn9', KNeighborsClassifier(n_neighbors=9))) # define the voting ensemble ensemble = VotingClassifier(estimators=models, voting='hard') return ensemble # get a list of models to evaluate def get_models(): models = dict() models['knn1'] = KNeighborsClassifier(n_neighbors=1) models['knn3'] = KNeighborsClassifier(n_neighbors=3) models['knn5'] = KNeighborsClassifier(n_neighbors=5) models['knn7'] = KNeighborsClassifier(n_neighbors=7) models['knn9'] = KNeighborsClassifier(n_neighbors=9) models['hard_voting'] = get_voting() return models # evaluate a give model using cross-validation def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean and standard deviation accuracy for each model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see the hard voting ensemble achieves a better classification accuracy of about 90.2% compared to all standalone versions of the model.
|
1 2 3 4 5 6 |
>knn1 0.873 (0.030) >knn3 0.889 (0.038) >knn5 0.895 (0.031) >knn7 0.899 (0.035) >knn9 0.900 (0.033) >hard_voting 0.902 (0.034) |
A box-and-whisker plot is then created comparing the distribution accuracy scores for each model, allowing us to clearly see that hard voting ensemble performing better than all standalone models on average.
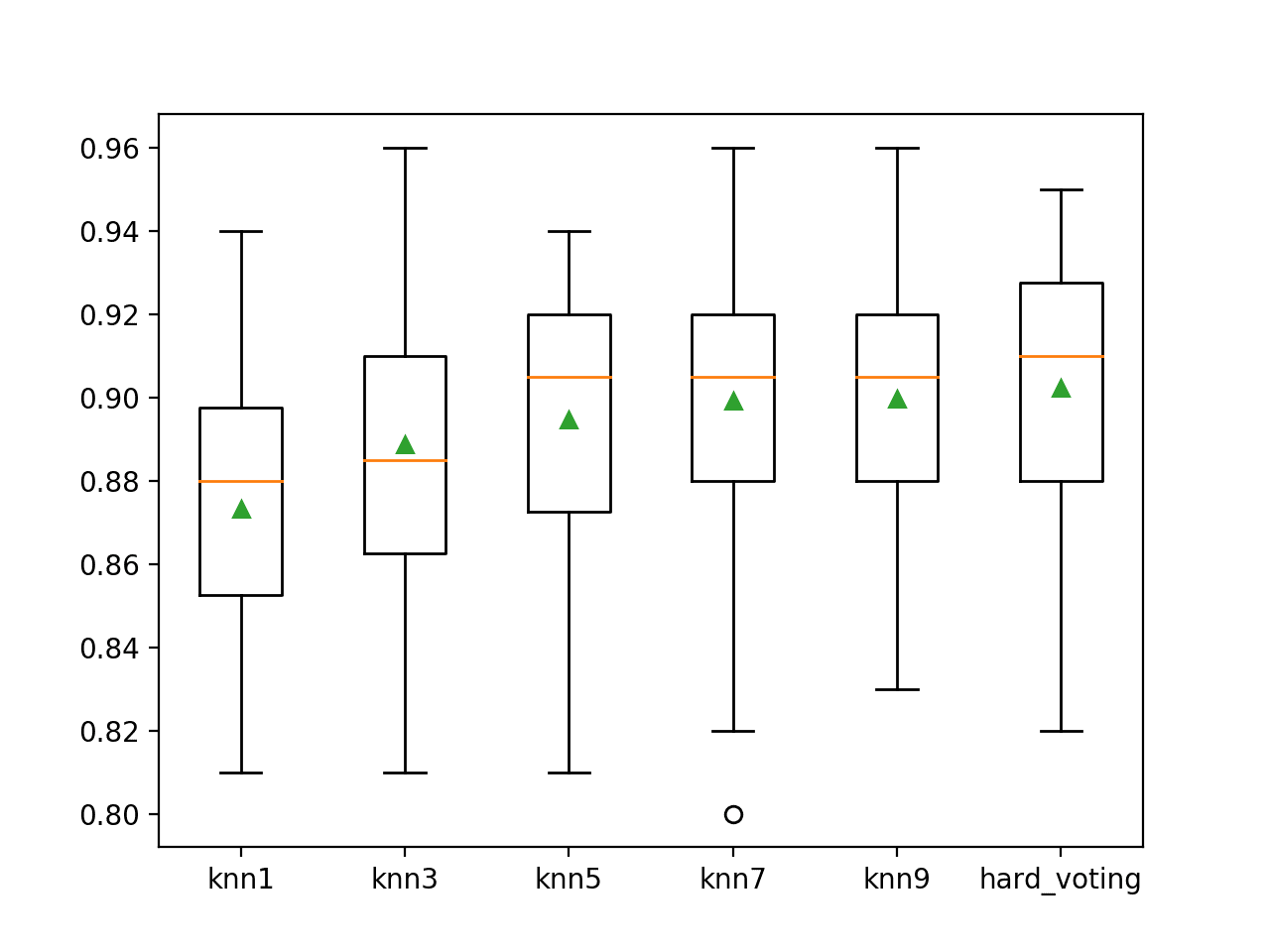
Box Plot of Hard Voting Ensemble Compared to Standalone Models for Binary Classification
If we choose a hard voting ensemble as our final model, we can fit and use it to make predictions on new data just like any other model.
First, the hard voting ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our binary classification dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# make a prediction with a hard voting ensemble from sklearn.datasets import make_classification from sklearn.ensemble import VotingClassifier from sklearn.neighbors import KNeighborsClassifier # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2) # define the base models models = list() models.append(('knn1', KNeighborsClassifier(n_neighbors=1))) models.append(('knn3', KNeighborsClassifier(n_neighbors=3))) models.append(('knn5', KNeighborsClassifier(n_neighbors=5))) models.append(('knn7', KNeighborsClassifier(n_neighbors=7))) models.append(('knn9', KNeighborsClassifier(n_neighbors=9))) # define the hard voting ensemble ensemble = VotingClassifier(estimators=models, voting='hard') # fit the model on all available data ensemble.fit(X, y) # make a prediction for one example data = [[5.88891819,2.64867662,-0.42728226,-1.24988856,-0.00822,-3.57895574,2.87938412,-1.55614691,-0.38168784,7.50285659,-1.16710354,-5.02492712,-0.46196105,-0.64539455,-1.71297469,0.25987852,-0.193401,-5.52022952,0.0364453,-1.960039]] yhat = ensemble.predict(data) print('Predicted Class: %d' % (yhat)) |
Running the example fits the hard voting ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Predicted Class: 1 |
Soft Voting Ensemble for Classification
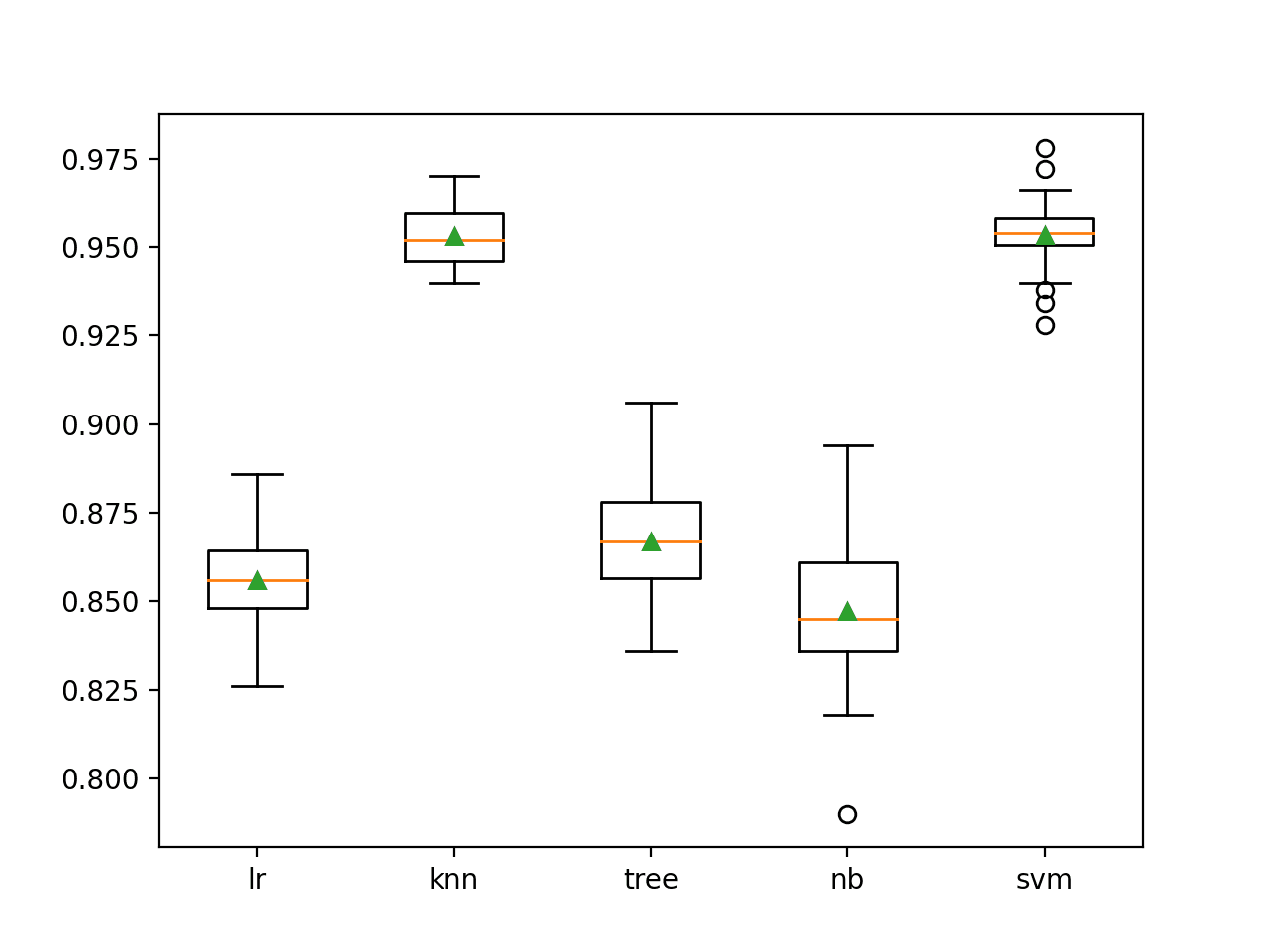
We can demonstrate soft voting with the support vector machine (SVM) algorithm.
The SVM algorithm does not natively predict probabilities, although it can be configured to predict probability-like scores by setting the “probability” argument to “True” in the SVC class.
We can fit five different versions of the SVM algorithm with a polynomial kernel, each with a different polynomial degree, set via the “degree” argument. We will use degrees 1-5.
Our expectation is that by combining the predicted class membership probability scores predicted by each different SVM model that the soft voting ensemble will achieve a better predictive performance than any standalone model used in the ensemble, on average.
First, we can create a function named get_voting() that creates the SVM models and combines them into a soft voting ensemble.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# get a voting ensemble of models def get_voting(): # define the base models models = list() models.append(('svm1', SVC(probability=True, kernel='poly', degree=1))) models.append(('svm2', SVC(probability=True, kernel='poly', degree=2))) models.append(('svm3', SVC(probability=True, kernel='poly', degree=3))) models.append(('svm4', SVC(probability=True, kernel='poly', degree=4))) models.append(('svm5', SVC(probability=True, kernel='poly', degree=5))) # define the voting ensemble ensemble = VotingClassifier(estimators=models, voting='soft') return ensemble |
We can then create a list of models to evaluate, including each standalone version of the SVM model configurations and the soft voting ensemble.
This will help us directly compare each standalone configuration of the SVM model with the ensemble in terms of the distribution of classification accuracy scores. The get_models() function below creates the list of models for us to evaluate.
|
1 2 3 4 5 6 7 8 9 10 |
# get a list of models to evaluate def get_models(): models = dict() models['svm1'] = SVC(probability=True, kernel='poly', degree=1) models['svm2'] = SVC(probability=True, kernel='poly', degree=2) models['svm3'] = SVC(probability=True, kernel='poly', degree=3) models['svm4'] = SVC(probability=True, kernel='poly', degree=4) models['svm5'] = SVC(probability=True, kernel='poly', degree=5) models['soft_voting'] = get_voting() return models |
We can evaluate and report model performance using repeated k-fold cross-validation as we did in the previous section.
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# compare soft voting ensemble to standalone classifiers from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.svm import SVC from sklearn.ensemble import VotingClassifier from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2) return X, y # get a voting ensemble of models def get_voting(): # define the base models models = list() models.append(('svm1', SVC(probability=True, kernel='poly', degree=1))) models.append(('svm2', SVC(probability=True, kernel='poly', degree=2))) models.append(('svm3', SVC(probability=True, kernel='poly', degree=3))) models.append(('svm4', SVC(probability=True, kernel='poly', degree=4))) models.append(('svm5', SVC(probability=True, kernel='poly', degree=5))) # define the voting ensemble ensemble = VotingClassifier(estimators=models, voting='soft') return ensemble # get a list of models to evaluate def get_models(): models = dict() models['svm1'] = SVC(probability=True, kernel='poly', degree=1) models['svm2'] = SVC(probability=True, kernel='poly', degree=2) models['svm3'] = SVC(probability=True, kernel='poly', degree=3) models['svm4'] = SVC(probability=True, kernel='poly', degree=4) models['svm5'] = SVC(probability=True, kernel='poly', degree=5) models['soft_voting'] = get_voting() return models # evaluate a give model using cross-validation def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean and standard deviation accuracy for each model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see the soft voting ensemble achieves a better classification accuracy of about 92.4% compared to all standalone versions of the model.
|
1 2 3 4 5 6 |
>svm1 0.855 (0.035) >svm2 0.859 (0.034) >svm3 0.890 (0.035) >svm4 0.808 (0.037) >svm5 0.850 (0.037) >soft_voting 0.924 (0.028) |
A box-and-whisker plot is then created comparing the distribution accuracy scores for each model, allowing us to clearly see that soft voting ensemble performing better than all standalone models on average.
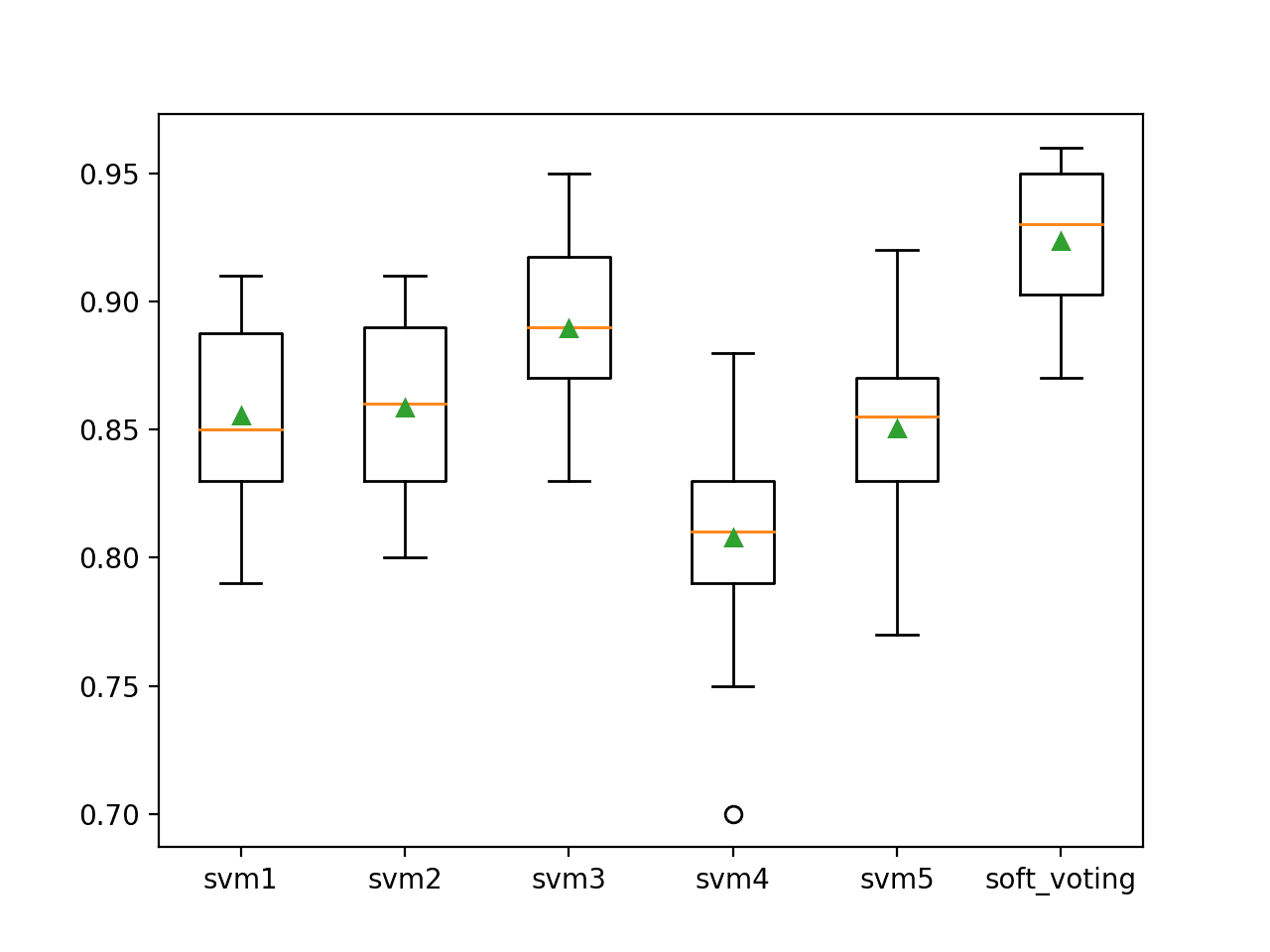
Box Plot of Soft Voting Ensemble Compared to Standalone Models for Binary Classification
If we choose a soft voting ensemble as our final model, we can fit and use it to make predictions on new data just like any other model.
First, the soft voting ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our binary classification dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# make a prediction with a soft voting ensemble from sklearn.datasets import make_classification from sklearn.ensemble import VotingClassifier from sklearn.svm import SVC # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=2) # define the base models models = list() models.append(('svm1', SVC(probability=True, kernel='poly', degree=1))) models.append(('svm2', SVC(probability=True, kernel='poly', degree=2))) models.append(('svm3', SVC(probability=True, kernel='poly', degree=3))) models.append(('svm4', SVC(probability=True, kernel='poly', degree=4))) models.append(('svm5', SVC(probability=True, kernel='poly', degree=5))) # define the soft voting ensemble ensemble = VotingClassifier(estimators=models, voting='soft') # fit the model on all available data ensemble.fit(X, y) # make a prediction for one example data = [[5.88891819,2.64867662,-0.42728226,-1.24988856,-0.00822,-3.57895574,2.87938412,-1.55614691,-0.38168784,7.50285659,-1.16710354,-5.02492712,-0.46196105,-0.64539455,-1.71297469,0.25987852,-0.193401,-5.52022952,0.0364453,-1.960039]] yhat = ensemble.predict(data) print('Predicted Class: %d' % (yhat)) |
Running the example fits the soft voting ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Predicted Class: 1 |
Voting Ensemble for Regression
In this section, we will look at using voting for a regression problem.
First, we can use the make_regression() function to create a synthetic regression problem with 1,000 examples and 20 input features.
The complete example is listed below.
|
1 2 3 4 5 6 |
# test regression dataset from sklearn.datasets import make_regression # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and summarizes the shape of the input and output components.
|
1 |
(1000, 20) (1000,) |
We can demonstrate ensemble voting for regression with a decision tree algorithm, sometimes referred to as a classification and regression tree (CART) algorithm.
We can fit five different versions of the CART algorithm, each with a different maximum depth of the decision tree, set via the “max_depth” argument. We will use depths of 1-5.
Our expectation is that by combining the values predicted by each different CART model that the voting ensemble will achieve a better predictive performance than any standalone model used in the ensemble, on average.
First, we can create a function named get_voting() that creates each CART model and combines the models into a voting ensemble.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# get a voting ensemble of models def get_voting(): # define the base models models = list() models.append(('cart1', DecisionTreeRegressor(max_depth=1))) models.append(('cart2', DecisionTreeRegressor(max_depth=2))) models.append(('cart3', DecisionTreeRegressor(max_depth=3))) models.append(('cart4', DecisionTreeRegressor(max_depth=4))) models.append(('cart5', DecisionTreeRegressor(max_depth=5))) # define the voting ensemble ensemble = VotingRegressor(estimators=models) return ensemble |
We can then create a list of models to evaluate, including each standalone version of the CART model configurations and the soft voting ensemble.
This will help us directly compare each standalone configuration of the CART model with the ensemble in terms of the distribution of error scores. The get_models() function below creates the list of models for us to evaluate.
|
1 2 3 4 5 6 7 8 9 10 |
# get a list of models to evaluate def get_models(): models = dict() models['cart1'] = DecisionTreeRegressor(max_depth=1) models['cart2'] = DecisionTreeRegressor(max_depth=2) models['cart3'] = DecisionTreeRegressor(max_depth=3) models['cart4'] = DecisionTreeRegressor(max_depth=4) models['cart5'] = DecisionTreeRegressor(max_depth=5) models['voting'] = get_voting() return models |
We can evaluate and report model performance using repeated k-fold cross-validation as we did in the previous section.
Models are evaluated using mean absolute error (MAE). The scikit-learn makes the score negative so that it can be maximized. This means that the reported MAE scores are negative, larger values are better, and 0 represents no error.
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# compare voting ensemble to each standalone models for regression from numpy import mean from numpy import std from sklearn.datasets import make_regression from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedKFold from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import VotingRegressor from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) return X, y # get a voting ensemble of models def get_voting(): # define the base models models = list() models.append(('cart1', DecisionTreeRegressor(max_depth=1))) models.append(('cart2', DecisionTreeRegressor(max_depth=2))) models.append(('cart3', DecisionTreeRegressor(max_depth=3))) models.append(('cart4', DecisionTreeRegressor(max_depth=4))) models.append(('cart5', DecisionTreeRegressor(max_depth=5))) # define the voting ensemble ensemble = VotingRegressor(estimators=models) return ensemble # get a list of models to evaluate def get_models(): models = dict() models['cart1'] = DecisionTreeRegressor(max_depth=1) models['cart2'] = DecisionTreeRegressor(max_depth=2) models['cart3'] = DecisionTreeRegressor(max_depth=3) models['cart4'] = DecisionTreeRegressor(max_depth=4) models['cart5'] = DecisionTreeRegressor(max_depth=5) models['voting'] = get_voting() return models # evaluate a give model using cross-validation def evaluate_model(model, X, y): cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise') return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean and standard deviation accuracy for each model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see the voting ensemble achieves a better mean squared error of about -136.338, which is larger (better) compared to all standalone versions of the model.
|
1 2 3 4 5 6 |
>cart1 -161.519 (11.414) >cart2 -152.596 (11.271) >cart3 -142.378 (10.900) >cart4 -140.086 (12.469) >cart5 -137.641 (12.240) >voting -136.338 (11.242) |
A box-and-whisker plot is then created comparing the distribution negative MAE scores for each model, allowing us to clearly see that voting ensemble performing better than all standalone models on average.
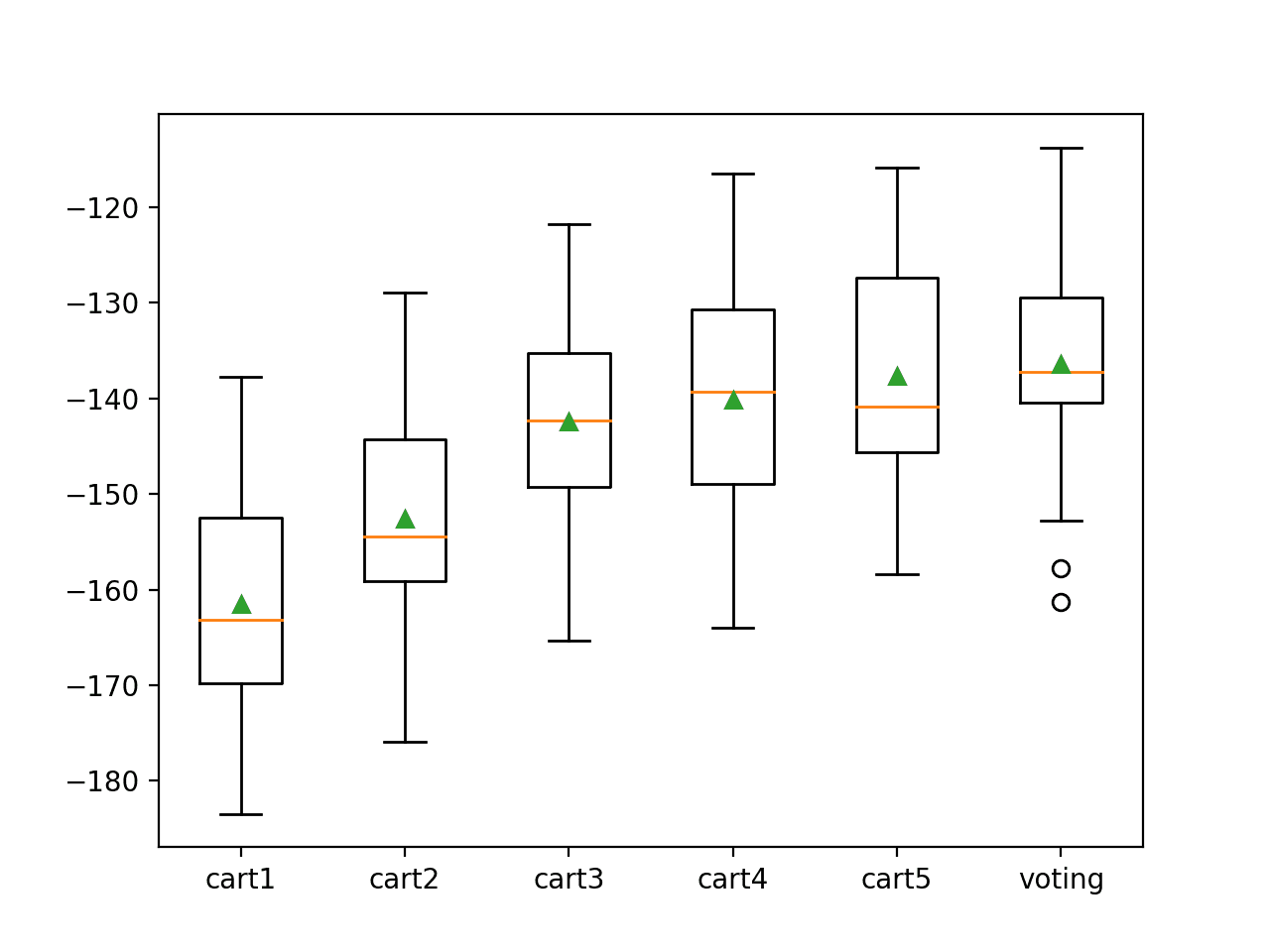
Box Plot of Voting Ensemble Compared to Standalone Models for Regression
If we choose a voting ensemble as our final model, we can fit and use it to make predictions on new data just like any other model.
First, the voting ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our binary classification dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# make a prediction with a voting ensemble from sklearn.datasets import make_regression from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import VotingRegressor # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=1) # define the base models models = list() models.append(('cart1', DecisionTreeRegressor(max_depth=1))) models.append(('cart2', DecisionTreeRegressor(max_depth=2))) models.append(('cart3', DecisionTreeRegressor(max_depth=3))) models.append(('cart4', DecisionTreeRegressor(max_depth=4))) models.append(('cart5', DecisionTreeRegressor(max_depth=5))) # define the voting ensemble ensemble = VotingRegressor(estimators=models) # fit the model on all available data ensemble.fit(X, y) # make a prediction for one example data = [[0.59332206,-0.56637507,1.34808718,-0.57054047,-0.72480487,1.05648449,0.77744852,0.07361796,0.88398267,2.02843157,1.01902732,0.11227799,0.94218853,0.26741783,0.91458143,-0.72759572,1.08842814,-0.61450942,-0.69387293,1.69169009]] yhat = ensemble.predict(data) print('Predicted Value: %.3f' % (yhat)) |
Running the example fits the voting ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Predicted Value: 141.319 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
- How to Develop a Weighted Average Ensemble for Deep Learning Neural Networks
- How to Develop a Stacking Ensemble for Deep Learning Neural Networks in Python With Keras
Books
APIs
- Ensemble methods scikit-learn API.
- sklearn.ensemble.VotingClassifier API.
- sklearn.ensemble.VotingRegressor API.
Summary
In this tutorial, you discovered how to create voting ensembles for machine learning algorithms in Python.
Specifically, you learned:
- A voting ensemble involves summing the predictions made by classification models or averaging the predictions made by regression models.
- How voting ensembles work, when to use voting ensembles, and the limitations of the approach.
- How to implement a hard voting ensemble and soft voting ensembles for classification predictive modeling.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.



This post gave me clarity on how to use voting for a classification problem I am working on right now. Thanks!
Thanks, I’m happy to hear that!
Hi jason
I am getting ” cannot import name ‘VotingRegressor’ error with this. Also, can you tell about some source to study ensemble for forecasting.Basically I got a VotingEnsemble model using azure automl but not able to figure out how to give input data for retraining. Since I want to automate my retraining, I wanted to check out the code myself. Thanks.
the error suggests you need to update your version of the scikit-learn library.
Hi Jason, how can we use Weighted votes in ensemble classification?
You can learn how to weight the models, this is called a stacking ensemble:
https://machinelearningmastery.com/stacking-ensemble-machine-learning-with-python/
In your opinion: Shall Voting Ensembles be considered as go-to step in standard pipeline of all ML projects?
Regards!
No, each project is different.
Hello,Jason. I have a question that how can I perform the multiple base-models learn different
features of same training and then ensemble?
Each could be a different model type of a model fit on different data (different subets of the same data).
Best source to understand ensemble learning. Keep up the good work!!!
Thanks!
Hey Jason, can we use same datasets (like the same datasets) for different models (based on different parameters or completely different algorithm models are required??)in ensemble learning??
Yes!
Hi, Jason. Thanks for the post, I enjoyed it. I am concerned; when should I use a hard voting regressor vs a soft voting regressor for regression problems?
If your models give good probabilities, like a logistic regression or naive bayes then soft is probably better than hard.
If in doubt, test both.
Hi Jason, this tutorial was so great and I give you a big thank you for that. I have a question for you, please. I’m dealing with skin disease images and I crop some patches from each image and feed to the classifier to grade the severity level for each patch. The presence of lesions influence the severity level. Then I’m going to combine the results of all patches to grade the severity of the whole image. But the problem is that the lesions don’t appear on all patches and only on a few so using voting ensemble of patches may not help as most of patches don’t have lesions so their severity will be normal or mild. So what strategy would you recommend in this case? Thank you so much
You’re welcome.
I would recommend using a CNN model on the whole input image, instead of ml models on patches of pixels.
Thanks for the response, Jason. Yes, that’s what I’m trying as another methodology but the problem with that is it needs high-resolution images which makes the training take time plus it needs an attention mechanism. I’m trying the stacking method you spoke in this post to learn the global grading from the local ones obtained from different patches, probably using SVM. Thank you!
Hello! I have the following issue. I am trying to use multi-output classification( I am trying to predict 3 values as an output) for stacking and voting. But Scikit learn doesn’t support voting and stacking for multi-output classification problems yet. Is there any way out of this situation?
Perhaps develop your own models manually?
Perhaps use an alternate model or API?
Perhaps extend the classes to achieve your desired outcome?
Hi! Thank you for this great topic.
I have one question, if I would like to test on different data sources (those data sources were extracted from the same origin), and I would like to know which data source and combination of them can yield the best performance. Can I use this technique? let’s say I’ve got 6 datasets. Can I fit the same SVM with these datasets individually, then I’ll get 6 models and also the combination of them i.e. mod1+mod2, mod1+mod3, …, and then do hard voting to evaluate the performances?
Voting does not compare the model, it will combine the predictions from the models. Does that make sense?
Hello Jason. Nice post. I am reading your posts from quite some time now. I need your suggestion.
II want to assign weights to the subsets of the training data according to their importance to test data. So, I tried voting ensemble where the models are same but trained on different subsets. I used hard voting for it, but I am not getting promising results.
The second scenario is that if I use different models for voting then is there a way to assign weights to the data. I have already tried with sample_weights.
I am using CNN.
Thanks!
I don’t believe voting would address your needs. Instead, I would recommend looking into sample weights for a single model.
Thanks for your prompt reply. I forgot to mention my dataset is the balanced dataset. I have tried using sample_weights for training data. Sample_weights are based on the importance of the sample. The problem I am facing now is what to pass as sample weights to the evaluate function. In my opinion the sample weights of the training data should not be passed as the size differs for training and test data. Kindly share your view.
Thank you once again for your suggestion and time:)
Sorry, I don’t understand the issue you are having, I don’t think I am the best person to help.
Perhaps post your question on stackoverflow.
Can ensembling be done with more than 1 type of algorithms ? I see that with one emsemble you have used 1 algorithm i.e. one with only KNN, one with only SVM etc. Can we use like KNN and SVM and CART etc in one ensemble ?
Yes. You can use any algorithms you like in an ensemble.
Thank you for this amazing tutorial, I would love to inform you that your book “Develop Deep Learning Models for Natural Language in Python” is included in the reading list for Text Mining course in my PhD.
Thanks, I’m happy to hear that!
Hello. Thank you for this useful tutorial
In a voting ensembles like Bagging, are models trained on subsets of train datasets?
In voting, each model is fit on all data.
In bagging, each model is fit on a subset of data.
Hello, mr. Jason
Please I have some questions
1- in case of multiclass classifier what is voting result if all estimator results are different?
eg: first estimator output is class 1
Second estimator output is class 2
Third estimator output is class 3
2 – in soft voting i know: what is the way to find the probability of each estimator? and how it work with multiclass classification?
3- we know random forest also use voting technique so what type of voting it used in the case of multiclass classification?
4- can i take random forest as estimator in voting classifier? Is it a practical?
Thanks
It will select the rounded mean I believe (1 + 2 + 3) / 3 = 2
You can use model.predict_proba() to get the probability of class membership from a given model/sub-model.
Random forest uses the rounded mean.
You could take random forest as a voting classifier, but we typically refer to it as a type of bagging – as that aspect is more important to the result.
thanks a lot, you helped me more.
You’re very welcome!
please, I have one more question. If I have even numbers of estimators e.g. 4 estimators and the outputs labels’ are text as follows [class2,class3, class2,class3] so what is the hard voting classifier output?
probably class2, e.g. floor of the rounded mean.
Test it and see.
I checked it, sometimes give the result as your mentioned procedure but other times it is unstable especially when the outputs are totally different like [class2,class3, class4,class1] it give class1 and accidentally class1 is the right class. so unfortunately I don’t know how it work till now.
According to the documentation, tie breaking is solved by sorting labels in ascending order and selecting the first label.
From here:
https://scikit-learn.org/stable/modules/ensemble.html#voting-classifier
ok, now that be so clear thank you so much with my best wishes
You’re welcome.
Hi Jason, Great article, quick question the take different algorithms and apply them to the same set of input features. What if you want an ensemble voting where each model may or may not be the same algorithm but are likely to be using different input features eg
Titanic
algo 1 inputs cabin deck, sex, age using GBM
algo 2 inputs Married, place boarded using XGBoost
etc
Can this be done with a voting ensemble library like sklearn or any other library you may no of
Thanks
Yes, see this example:
https://machinelearningmastery.com/feature-selection-subspace-ensemble-in-python/
excuse the typos
No problem.
Thank you for this tutorial Sir. With my code I have this :
ensemble = VotingClassifier(ensembles)
results_vc = cross_val_score(ensemble, X_train, y_train, cv=kfold)
print(results_vc.mean())
result_vc.mean() give me : 0.8838
but When I fit and predict I get a f1-score de 0.0560.
It’s good, not good. How I do to fix this problem ? According my data is very unbalanced. one class is 7 time more bigger than the other one
This can help you determine if the performance of your model is good or not:
https://machinelearningmastery.com/naive-classifiers-imbalanced-classification-metrics/
These suggestions may help:
https://machinelearningmastery.com/framework-for-imbalanced-classification-projects/
Hey Jason, Im trying to use this on my own dataset (70,15). Im wondering what the y that you have here is represented as. The data set is 1000 rows of what looks like a binary classification of 0s and 1s. So how can I use my dataset to represent a similar format for y? I tried to think through and it doesn’t make sense that these would be cluster identifiers right? So what is the binary/multiclass representation of for y?
Heres the code, Obviously I cannot use y as I have because it is continuous, but of course I implemented to see what would happen and to show for example purposes:
y = X_train_MinMax[:,1]
print(X_train_MinMax.shape, y.shape)
#(70,15)(70, )
# get a voting ensemble of models
def get_voting():
# define the base models
models = list()
models.append((‘knn1’, KNeighborsClassifier(n_neighbors=1)))
models.append((‘knn3’, KNeighborsClassifier(n_neighbors=3)))
models.append((‘knn5’, KNeighborsClassifier(n_neighbors=5)))
models.append((‘knn7’, KNeighborsClassifier(n_neighbors=7)))
models.append((‘knn9′, KNeighborsClassifier(n_neighbors=9)))
# define the voting ensemble
ensemble = VotingClassifier(estimators=models, voting=’hard’)
return ensemble
# get a list of models to evaluate
def get_models():
models = dict()
models[‘knn1’] = KNeighborsClassifier(n_neighbors=1)
models[‘knn3’] = KNeighborsClassifier(n_neighbors=3)
models[‘knn5’] = KNeighborsClassifier(n_neighbors=5)
models[‘knn7’] = KNeighborsClassifier(n_neighbors=7)
models[‘knn9’] = KNeighborsClassifier(n_neighbors=9)
models[‘hard_voting’] = get_voting()
return models
# evaluate a give model using cross-validation
def evaluate_model(model, X_train_MinMax, y):
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X_train_MinMax, y, scoring=’accuracy’, cv=cv, n_jobs=-1, error_score=’raise’)
return scores
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
scores = evaluate_model(model, X_train_MinMax, y)
results.append(scores)
names.append(name)
print(‘>%s %.3f (%.3f)’ % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()
This will help:
https://machinelearningmastery.com/faq/single-faq/what-are-x-and-y-in-machine-learning
hi jason,
Hard voting clasifier is applicable only for binary classification or multistage classification (Class of 5 stages)
Use whatever works best for your dataset.
Thank you very much for such a great tutorial sir
You’re welcome.
Hi Jason. Can you tell me the backend phenomena that how voting improves our accuracy score ? I am using 2 models which are MLP and ELM and having 4 labels.
Let’s assume I got these accuracies :
Mlp = 92
Elm = 94
Ensemble voting = 97
now the thing is . how ensemble voting improving our accuracy ? how it worked for that?
Sometimes it can help, sometimes not. Why – it depends on the model and the data. Try it and see.
Thanks for the post.
I have a question. I have used Adaboost, DT and Bagging in a voting classififer as classifier 1, classififer 2 and classifier 3, I used hard voting.The voting classifier obtained a result of 93.14% accuracy which is better than what DT gave me earlier (92.87%). Is it logical to use boosting and bagging in another ensemble method( voting classifier) ?
Sure. Perhaps try it and see.
Hi
Thank you for your useful content
I have a question. How to Machine learning(SVM,NB, KNN) and Lexicon (NRC) together to use majority voting؟
Please advise.
I don’t know what “Lexicon (NRC)” is sorry.
thanks!
How we can apply majority voting for 3 pre-trained language models?
Isn’t that you can always get a majority with 3 voters?
i can do with 3,4,5 and more, but how to apply it?
Simply count the result should work. That’s why you call it a voting.
Hi Jason,
thanks for this great post. I have a question about soft voting. How to calibrate models that do not natively predict a class probability like KNN to be used in ensemble with soft voting.
I don’t think we calibrate multiple models at once, but more to fine tune each model individually to make every one do good. If every one is doing good, the ensemble will be good too.
Hi Adrian,
just that I understand this correctly, you mean that first, I should tune and calibrate each algorithm individually and find the optimal parameters for each algorithm. The insert all calibrated models into the voting classifier and train the model based on the optimal parameters found for each individual algorithm?
Correct. But if the data you used for calibration is already the same as the data for your final model, you can save the calibrated model and skip the voting classifier function in sklearn, then build your own voting classifier in a loop. Of course, retrain the model with VotingClassifier function is simpler.
Hello, Jason,
Thanks for this tutorial.
I have a query as follows:
Suppose, I have two models (Model1 and Model2) trained on different image datasets say Data1 and Data2. Can I use these models in the voting-classifier function?
Nothing stop you from doing that. But does it makes sense in your problem?
Hi Adrian Tam
how can wee implement voting ensemble with extreme learning machine?
thank you
Hi abdou…You may find the following resource of interest:
https://analyticsindiamag.com/a-beginners-guide-to-extreme-learning-machine/
Dear Jason,
Dear Adrian,
Please, allow me to ask. Is there any theoretical background that limits the combination of some machine learning classifiers into voting meta-learners?
Say, I built a model from the X and y for each using Logistic regression with Lasso penalty, Logistic regression with ridge penalty, Decision Trees, Random Forest, AdaBoost, and XGboost with various accuracy results from each model.
Does it make sense to create a soft voting classifier (or weighted voting classifier) made from a combination of the Decision Trees model and Random Forest? (considering random forest itself is already a combination and voting of several decision trees). Does it make sense to create a voting classifier consisting of XGBoost and Adaboost?
I understand that we can combine as many SVM, KNN, ANN with their various hyperparameter into the voting classifier. Does the same apply to ensemble-based machine learning? (considering each ensemble method already implement a voting mechanism inside their algorithm).
Thank you for your patience. I am sorry for the beginner question. Peace.
Dear Jason,
Dear Adrian,
Please, allow me to ask. Is there any theoretical background that limits the combination of some machine learning classifiers into voting meta-learners?
Say, I built a model from the X and y for each using Logistic regression with Lasso penalty, Logistic regression with elastic net penalty, Decision Trees, Random Forest, AdaBoost, and XGboost with various accuracy results from each model using stratified kfold cross-validation.
Does it make sense to create a soft voting classifier (or weighted voting classifier) made from a combination of the Decision Trees model and Random Forest? (considering random forest itself is already a combination and voting of several decision trees).
Does it make sense to create a voting classifier consisting of XGBoost and Adaboost?
Does it make sense to create a voting classifier consisting of logistic regression with lasso penalty and other logistic regression with the elastic net penalty? (considering elastic net already a combination of lasso and ridge
I understand that we can combine as many SVM, KNN, and ANN with their various hyperparameter into the voting classifier. Does the same apply to ensemble-based machine learning? (considering each ensemble method already implement a voting mechanism inside their algorithm).
I understand that we are free to do anything with our data, I believe combining similar models will help narrowing the standard deviation from the cumulative average of the cross-validation loop. But, but, is it theoritically acceptable?
Thank you for your patience. I am sorry for the beginner question. Good luck to everyone.
Hi Jason,
Thank you for your useful content
I have a question. How to Machine learning(SVM,NB, RF) and Deep Learning(ANN) together to use majority voting?
Please advise.
Hi Sarvesh…The following resource may be of interest to you:
https://machinelearningmastery.com/ensemble-machine-learning-with-python-7-day-mini-course/
Dear Jason,
Dear Adrian,
Dear James,
Please, allow me to ask. Is there any theoretical background that limits the combination of some machine learning classifiers into voting classifiers?
Say, I built a model from the X and y using several models: Logistic regression with Lasso penalty, Logistic regression with elastic net penalty, Decision Trees, Random Forest, AdaBoost, and XGboost with various accuracy results from each model using stratified kfold cross-validation.
Does it make sense to create a soft voting classifier (or weighted voting classifier) made from a combination of the Decision Trees model and Random Forest? (considering random forest itself is already a combination and voting of several decision trees).
Does it make sense to create a voting classifier consisting of XGBoost and Adaboost?
Does it make sense to create a voting classifier consisting of logistic regression with lasso penalty and other logistic regression with the elastic net penalty? (considering elastic net already a combination of lasso and ridge
I understand that we can combine as many SVM, KNN, and ANN with their various hyperparameter into the voting classifier. Does the same apply to ensemble-based machine learning? (considering each ensemble method already implement a voting mechanism inside their algorithm).
I understand that we are free to do anything with our data, I believe combining similar models will help narrowing the standard deviation from the cumulative average of the cross-validation loop. But, but, is it theoritically acceptable?
Thank you for your patience. I am sorry for the beginner question. Good luck to everyone.
Thanks for the information, very educative. I want answers to some few questions.
1. Apart from voting, what other method can be adopted to combine algorithms to create an ensemble learner?
2. Is voting the same as stacking?
3. What is the difference between voting ensemble and blending?
Waiting for your quick response.
Thanks
Isaac
Hi Isaac…The following resource may be of interest to you:
https://towardsdatascience.com/ensemble-learning-stacking-blending-voting-b37737c4f483
Hi dear dr. Jason
I want to train some models (with same type or not) with different train data (but same number of classes) and vote between trained models for validation data. How can I do this in python?
Hi Ali…The following may be of interest to you in regard to training models on new data.
https://machinelearningmastery.com/update-neural-network-models-with-more-data/