Softmax Activation Function with Python

Softmax is a mathematical function that converts a vector of numbers into a vector of probabilities, where the probabilities of each value are proportional to the relative scale of each value in the vector.

The most common use of the softmax function in applied machine learning is in its use as an activation function in a neural network model. Specifically, the network is configured to output N values, one for each class in the classification task, and the softmax function is used to normalize the outputs, converting them from weighted sum values into probabilities that sum to one. Each value in the output of the softmax function is interpreted as the probability of membership for each class.

In this tutorial, you will discover the softmax activation function used in neural network models.

After completing this tutorial, you will know:

• Linear and Sigmoid activation functions are inappropriate for multi-class classification tasks.
• Softmax can be thought of as a softened version of the argmax function that returns the index of the largest value in a list.
• How to implement the softmax function from scratch in Python and how to convert the output into a class label.

Let’s get started.

Softmax Activation Function with Python
Photo by Ian D. Keating, some rights reserved.

Tutorial Overview

This tutorial is divided into three parts; they are:

1. Predicting Probabilities With Neural Networks
2. Max, Argmax, and Softmax
3. Softmax Activation Function

Predicting Probabilities With Neural Networks

Neural network models can be used to model classification predictive modeling problems.

Classification problems are those that involve predicting a class label for a given input. A standard approach to modeling classification problems is to use a model to predict the probability of class membership. That is, given an example, what is the probability of it belonging to each of the known class labels?

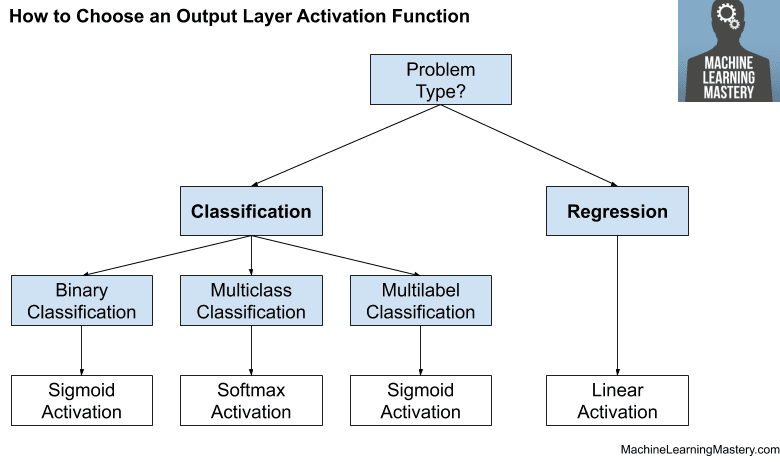
• For a binary classification problem, a Binomial probability distribution is used. This is achieved using a network with a single node in the output layer that predicts the probability of an example belonging to class 1.
• For a multi-class classification problem, a Multinomial probability is used. This is achieved using a network with one node for each class in the output layer and the sum of the predicted probabilities equals one.

A neural network model requires an activation function in the output layer of the model to make the prediction.

There are different activation functions to choose from; let’s look at a few.

Linear Activation Function

One approach to predicting class membership probabilities is to use a linear activation.

A linear activation function is simply the sum of the weighted input to the node, required as input for any activation function. As such, it is often referred to as “no activation function” as no additional transformation is performed.

Recall that a probability or a likelihood is a numeric value between 0 and 1.

Given that no transformation is performed on the weighted sum of the input, it is possible for the linear activation function to output any numeric value. This makes the linear activation function inappropriate for predicting probabilities for either the binomial or multinomial case.

Sigmoid Activation Function

Another approach to predicting class membership probabilities is to use a sigmoid activation function.

This function is also called the logistic function. Regardless of the input, the function always outputs a value between 0 and 1. The form of the function is an S-shape between 0 and 1 with the vertical or middle of the “S” at 0.5.

This allows very large values given as the weighted sum of the input to be output as 1.0 and very small or negative values to be mapped to 0.0.

The sigmoid activation is an ideal activation function for a binary classification problem where the output is interpreted as a Binomial probability distribution.

The sigmoid activation function can also be used as an activation function for multi-class classification problems where classes are non-mutually exclusive. These are often referred to as a multi-label classification rather than multi-class classification.

The sigmoid activation function is not appropriate for multi-class classification problems with mutually exclusive classes where a multinomial probability distribution is required.

Instead, an alternate activation is required called the softmax function.

Max, Argmax, and Softmax

Max Function

The maximum, or “max,” mathematical function returns the largest numeric value for a list of numeric values.

We can implement this using the max() Python function; for example:

Running the example returns the largest value “3” from the list of numbers.

Argmax Function

The argmax, or “arg max,” mathematical function returns the index in the list that contains the largest value.

Think of it as the meta version of max: one level of indirection above max, pointing to the position in the list that has the max value rather than the value itself.

We can implement this using the argmax() NumPy function; for example:

Running the example returns the list index value “1” that points to the array index [1] that contains the largest value in the list “3”.

Softmax Function

The softmax, or “soft max,” mathematical function can be thought to be a probabilistic or “softer” version of the argmax function.

The term softmax is used because this activation function represents a smooth version of the winner-takes-all activation model in which the unit with the largest input has output +1 while all other units have output 0.

— Page 238, Neural Networks for Pattern Recognition, 1995.

From a probabilistic perspective, if the argmax() function returns 1 in the previous section, it returns 0 for the other two array indexes, giving full weight to index 1 and no weight to index 0 and index 2 for the largest value in the list [1, 3, 2].

What if we were less sure and wanted to express the argmax probabilistically, with likelihoods?

This can be achieved by scaling the values in the list and converting them into probabilities such that all values in the returned list sum to 1.0.

This can be achieved by calculating the exponent of each value in the list and dividing it by the sum of the exponent values.

• probability = exp(value) / sum v in list exp(v)

For example, we can turn the first value “1” in the list [1, 3, 2] into a probability as follows:

• probability = exp(1) / (exp(1) + exp(3) + exp(2))
• probability = exp(1) / (exp(1) + exp(3) + exp(2))
• probability = 2.718281828459045 / 30.19287485057736
• probability = 0.09003057317038046

We can demonstrate this for each value in the list [1, 3, 2] in Python as follows:

Running the example converts each value in the list into a probability and reports the values, then confirms that all probabilities sum to the value 1.0.

We can see that most weight is put on index 1 (67 percent) with less weight on index 2 (24 percent) and even less on index 0 (9 percent).

This is the softmax function.

We can implement it as a function that takes a list of numbers and returns the softmax or multinomial probability distribution for the list.

The example below implements the function and demonstrates it on our small list of numbers.

Running the example reports roughly the same numbers with minor differences in precision.

Finally, we can use the built-in softmax() NumPy function to calculate the softmax for an array or list of numbers, as follows:

Running the example, again, we get very similar results with very minor differences in precision.

Now that we are familiar with the softmax function, let’s look at how it is used in a neural network model.

Softmax Activation Function

The softmax function is used as the activation function in the output layer of neural network models that predict a multinomial probability distribution.

That is, softmax is used as the activation function for multi-class classification problems where class membership is required on more than two class labels.

Any time we wish to represent a probability distribution over a discrete variable with n possible values, we may use the softmax function. This can be seen as a generalization of the sigmoid function which was used to represent a probability distribution over a binary variable.

— Page 184, Deep Learning, 2016.

The function can be used as an activation function for a hidden layer in a neural network, although this is less common. It may be used when the model internally needs to choose or weight multiple different inputs at a bottleneck or concatenation layer.

Softmax units naturally represent a probability distribution over a discrete variable with k possible values, so they may be used as a kind of switch.

— Page 196, Deep Learning, 2016.

In the Keras deep learning library with a three-class classification task, use of softmax in the output layer may look as follows:

By definition, the softmax activation will output one value for each node in the output layer. The output values will represent (or can be interpreted as) probabilities and the values sum to 1.0.

When modeling a multi-class classification problem, the data must be prepared. The target variable containing the class labels is first label encoded, meaning that an integer is applied to each class label from 0 to N-1, where N is the number of class labels.

The label encoded (or integer encoded) target variables are then one-hot encoded. This is a probabilistic representation of the class label, much like the softmax output. A vector is created with a position for each class label and the position. All values are marked 0 (impossible) and a 1 (certain) is used to mark the position for the class label.

For example, three class labels will be integer encoded as 0, 1, and 2. Then encoded to vectors as follows:

• Class 0: [1, 0, 0]
• Class 1: [0, 1, 0]
• Class 2: [0, 0, 1]

This is called a one-hot encoding.

It represents the expected multinomial probability distribution for each class used to correct the model under supervised learning.

The softmax function will output a probability of class membership for each class label and attempt to best approximate the expected target for a given input.

For example, if the integer encoded class 1 was expected for one example, the target vector would be:

• [0, 1, 0]

The softmax output might look as follows, which puts the most weight on class 1 and less weight on the other classes.

• [0.09003057 0.66524096 0.24472847]

The error between the expected and predicted multinomial probability distribution is often calculated using cross-entropy, and this error is then used to update the model. This is called the cross-entropy loss function.

For more on cross-entropy for calculating the difference between probability distributions, see the tutorial:

• A Gentle Introduction to Cross-Entropy for Machine Learning

We may want to convert the probabilities back into an integer encoded class label.

This can be achieved using the argmax() function that returns the index of the list with the largest value. Given that the class labels are integer encoded from 0 to N-1, the argmax of the probabilities will always be the integer encoded class label.

• class integer = argmax([0.09003057 0.66524096 0.24472847])
• class integer = 1

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Books

• Neural Networks for Pattern Recognition, 1995.
• Neural Networks: Tricks of the Trade: Tricks of the Trade, 2nd Edition, 2012.
• Deep Learning, 2016.

APIs

• numpy.argmax API.
• scipy.special.softmax API.

Articles

• Softmax function, Wikipedia.

Summary

In this tutorial, you discovered the softmax activation function used in neural network models.

Specifically, you learned:

• Linear and Sigmoid activation functions are inappropriate for multi-class classification tasks.
• Softmax can be thought of as a softened version of the argmax function that returns the index of the largest value in a list.
• How to implement the softmax function from scratch in Python and how to convert the output into a class label.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.