Activation functions are a critical part of the design of a neural network.
The choice of activation function in the hidden layer will control how well the network model learns the training dataset. The choice of activation function in the output layer will define the type of predictions the model can make.
As such, a careful choice of activation function must be made for each deep learning neural network project.
In this tutorial, you will discover how to choose activation functions for neural network models.
After completing this tutorial, you will know:
- Activation functions are a key part of neural network design.
- The modern default activation function for hidden layers is the ReLU function.
- The activation function for output layers depends on the type of prediction problem.
Let’s get started.

How to Choose an Activation Function for Deep Learning
Photo by Peter Dowley, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Activation Functions
- Activation for Hidden Layers
- Activation for Output Layers
Activation Functions
An activation function in a neural network defines how the weighted sum of the input is transformed into an output from a node or nodes in a layer of the network.
Sometimes the activation function is called a “transfer function.” If the output range of the activation function is limited, then it may be called a “squashing function.” Many activation functions are nonlinear and may be referred to as the “nonlinearity” in the layer or the network design.
The choice of activation function has a large impact on the capability and performance of the neural network, and different activation functions may be used in different parts of the model.
Technically, the activation function is used within or after the internal processing of each node in the network, although networks are designed to use the same activation function for all nodes in a layer.
A network may have three types of layers: input layers that take raw input from the domain, hidden layers that take input from another layer and pass output to another layer, and output layers that make a prediction.
All hidden layers typically use the same activation function. The output layer will typically use a different activation function from the hidden layers and is dependent upon the type of prediction required by the model.
Activation functions are also typically differentiable, meaning the first-order derivative can be calculated for a given input value. This is required given that neural networks are typically trained using the backpropagation of error algorithm that requires the derivative of prediction error in order to update the weights of the model.
There are many different types of activation functions used in neural networks, although perhaps only a small number of functions used in practice for hidden and output layers.
Let’s take a look at the activation functions used for each type of layer in turn.
Activation for Hidden Layers
A hidden layer in a neural network is a layer that receives input from another layer (such as another hidden layer or an input layer) and provides output to another layer (such as another hidden layer or an output layer).
A hidden layer does not directly contact input data or produce outputs for a model, at least in general.
A neural network may have zero or more hidden layers.
Typically, a differentiable nonlinear activation function is used in the hidden layers of a neural network. This allows the model to learn more complex functions than a network trained using a linear activation function.
In order to get access to a much richer hypothesis space that would benefit from deep representations, you need a non-linearity, or activation function.
— Page 72, Deep Learning with Python, 2017.
There are perhaps three activation functions you may want to consider for use in hidden layers; they are:
- Rectified Linear Activation (ReLU)
- Logistic (Sigmoid)
- Hyperbolic Tangent (Tanh)
This is not an exhaustive list of activation functions used for hidden layers, but they are the most commonly used.
Let’s take a closer look at each in turn.
ReLU Hidden Layer Activation Function
The rectified linear activation function, or ReLU activation function, is perhaps the most common function used for hidden layers.
It is common because it is both simple to implement and effective at overcoming the limitations of other previously popular activation functions, such as Sigmoid and Tanh. Specifically, it is less susceptible to vanishing gradients that prevent deep models from being trained, although it can suffer from other problems like saturated or “dead” units.
The ReLU function is calculated as follows:
- max(0.0, x)
This means that if the input value (x) is negative, then a value 0.0 is returned, otherwise, the value is returned.
You can learn more about the details of the ReLU activation function in this tutorial:
We can get an intuition for the shape of this function with the worked example below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# example plot for the relu activation function from matplotlib import pyplot # rectified linear function def rectified(x): return max(0.0, x) # define input data inputs = [x for x in range(-10, 10)] # calculate outputs outputs = [rectified(x) for x in inputs] # plot inputs vs outputs pyplot.plot(inputs, outputs) pyplot.show() |
Running the example calculates the outputs for a range of values and creates a plot of inputs versus outputs.
We can see the familiar kink shape of the ReLU activation function.
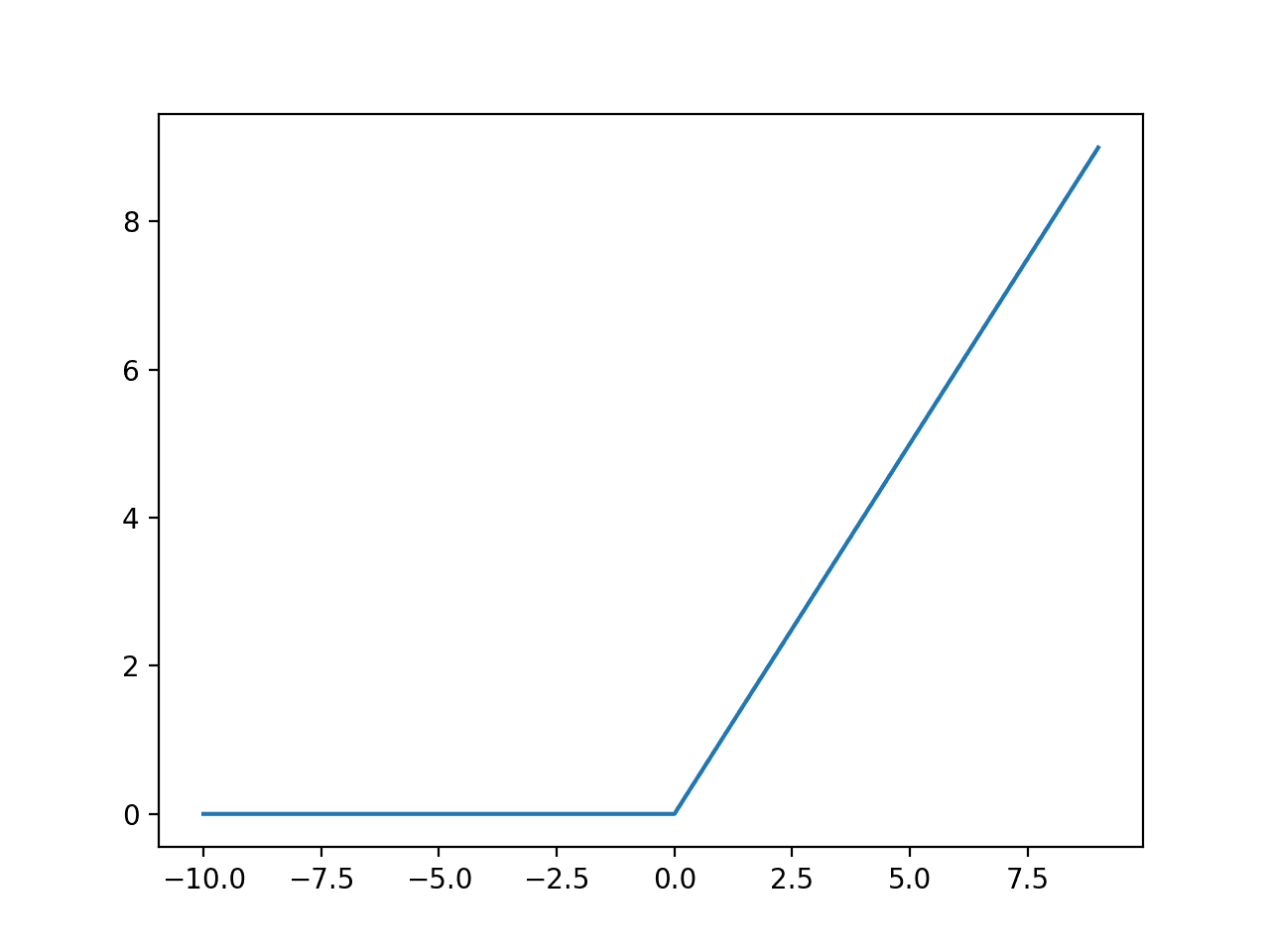
Plot of Inputs vs. Outputs for the ReLU Activation Function.
When using the ReLU function for hidden layers, it is a good practice to use a “He Normal” or “He Uniform” weight initialization and scale input data to the range 0-1 (normalize) prior to training.
Sigmoid Hidden Layer Activation Function
The sigmoid activation function is also called the logistic function.
It is the same function used in the logistic regression classification algorithm.
The function takes any real value as input and outputs values in the range 0 to 1. The larger the input (more positive), the closer the output value will be to 1.0, whereas the smaller the input (more negative), the closer the output will be to 0.0.
The sigmoid activation function is calculated as follows:
- 1.0 / (1.0 + e^-x)
Where e is a mathematical constant, which is the base of the natural logarithm.
We can get an intuition for the shape of this function with the worked example below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# example plot for the sigmoid activation function from math import exp from matplotlib import pyplot # sigmoid activation function def sigmoid(x): return 1.0 / (1.0 + exp(-x)) # define input data inputs = [x for x in range(-10, 10)] # calculate outputs outputs = [sigmoid(x) for x in inputs] # plot inputs vs outputs pyplot.plot(inputs, outputs) pyplot.show() |
Running the example calculates the outputs for a range of values and creates a plot of inputs versus outputs.
We can see the familiar S-shape of the sigmoid activation function.
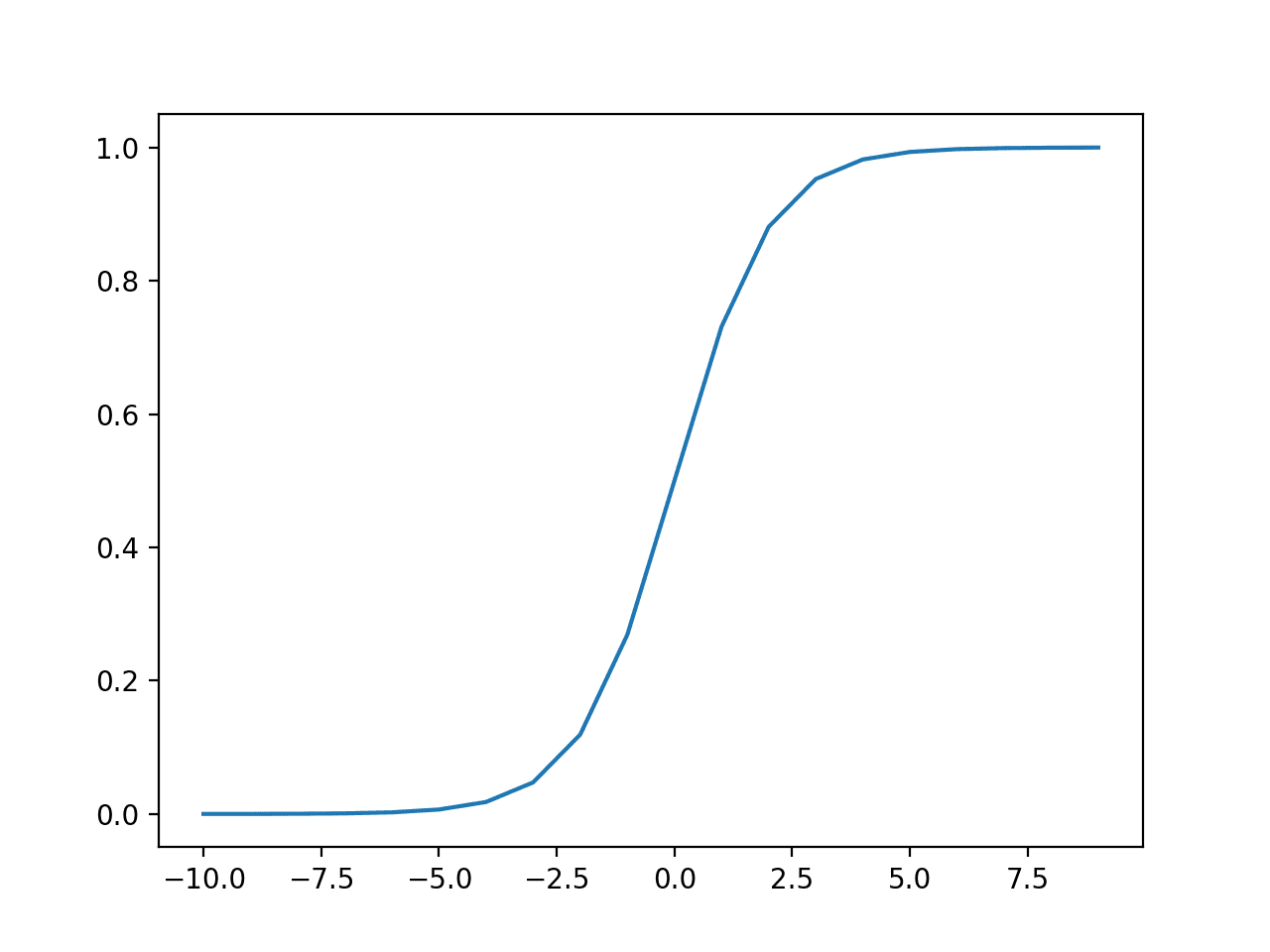
Plot of Inputs vs. Outputs for the Sigmoid Activation Function.
When using the Sigmoid function for hidden layers, it is a good practice to use a “Xavier Normal” or “Xavier Uniform” weight initialization (also referred to Glorot initialization, named for Xavier Glorot) and scale input data to the range 0-1 (e.g. the range of the activation function) prior to training.
Tanh Hidden Layer Activation Function
The hyperbolic tangent activation function is also referred to simply as the Tanh (also “tanh” and “TanH“) function.
It is very similar to the sigmoid activation function and even has the same S-shape.
The function takes any real value as input and outputs values in the range -1 to 1. The larger the input (more positive), the closer the output value will be to 1.0, whereas the smaller the input (more negative), the closer the output will be to -1.0.
The Tanh activation function is calculated as follows:
- (e^x – e^-x) / (e^x + e^-x)
Where e is a mathematical constant that is the base of the natural logarithm.
We can get an intuition for the shape of this function with the worked example below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# example plot for the tanh activation function from math import exp from matplotlib import pyplot # tanh activation function def tanh(x): return (exp(x) - exp(-x)) / (exp(x) + exp(-x)) # define input data inputs = [x for x in range(-10, 10)] # calculate outputs outputs = [tanh(x) for x in inputs] # plot inputs vs outputs pyplot.plot(inputs, outputs) pyplot.show() |
Running the example calculates the outputs for a range of values and creates a plot of inputs versus outputs.
We can see the familiar S-shape of the Tanh activation function.
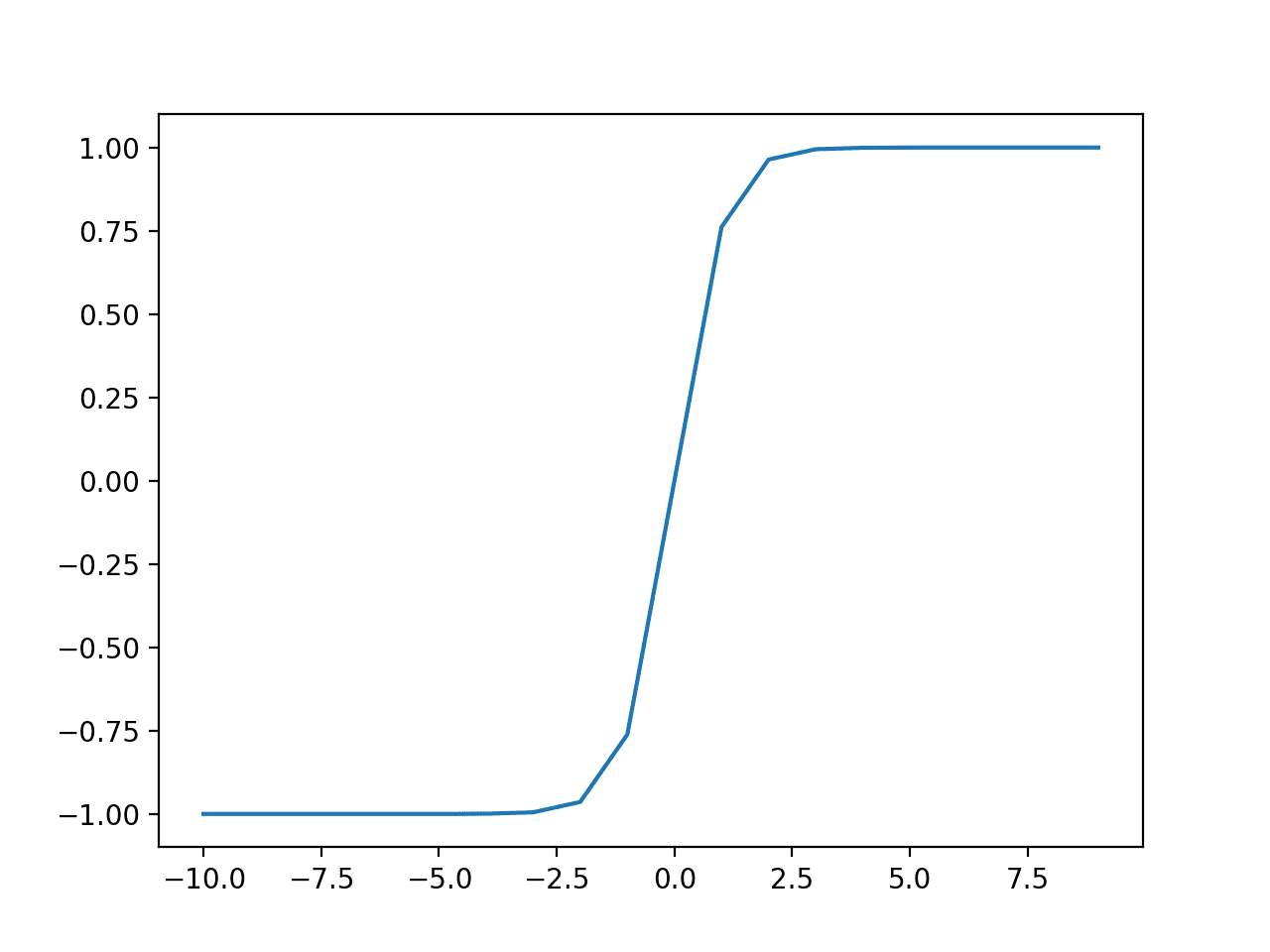
Plot of Inputs vs. Outputs for the Tanh Activation Function.
When using the TanH function for hidden layers, it is a good practice to use a “Xavier Normal” or “Xavier Uniform” weight initialization (also referred to Glorot initialization, named for Xavier Glorot) and scale input data to the range -1 to 1 (e.g. the range of the activation function) prior to training.
How to Choose a Hidden Layer Activation Function
A neural network will almost always have the same activation function in all hidden layers.
It is most unusual to vary the activation function through a network model.
Traditionally, the sigmoid activation function was the default activation function in the 1990s. Perhaps through the mid to late 1990s to 2010s, the Tanh function was the default activation function for hidden layers.
… the hyperbolic tangent activation function typically performs better than the logistic sigmoid.
— Page 195, Deep Learning, 2016.
Both the sigmoid and Tanh functions can make the model more susceptible to problems during training, via the so-called vanishing gradients problem.
You can learn more about this problem in this tutorial:
The activation function used in hidden layers is typically chosen based on the type of neural network architecture.
Modern neural network models with common architectures, such as MLP and CNN, will make use of the ReLU activation function, or extensions.
In modern neural networks, the default recommendation is to use the rectified linear unit or ReLU …
— Page 174, Deep Learning, 2016.
Recurrent networks still commonly use Tanh or sigmoid activation functions, or even both. For example, the LSTM commonly uses the Sigmoid activation for recurrent connections and the Tanh activation for output.
- Multilayer Perceptron (MLP): ReLU activation function.
- Convolutional Neural Network (CNN): ReLU activation function.
- Recurrent Neural Network: Tanh and/or Sigmoid activation function.
If you’re unsure which activation function to use for your network, try a few and compare the results.
The figure below summarizes how to choose an activation function for the hidden layers of your neural network model.
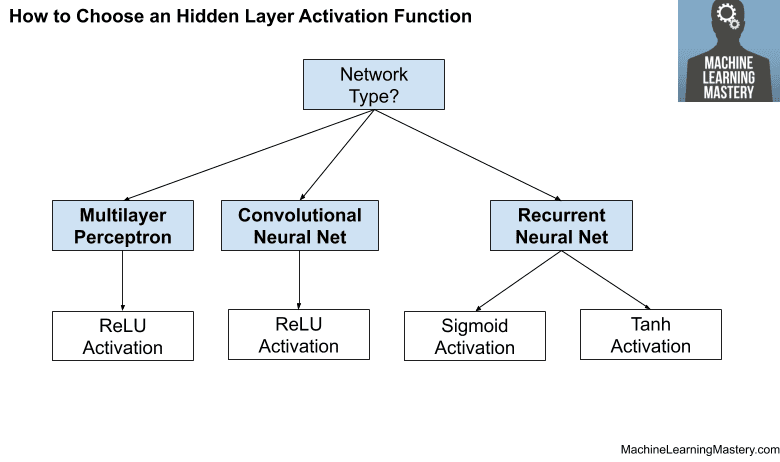
How to Choose a Hidden Layer Activation Function
Activation for Output Layers
The output layer is the layer in a neural network model that directly outputs a prediction.
All feed-forward neural network models have an output layer.
There are perhaps three activation functions you may want to consider for use in the output layer; they are:
- Linear
- Logistic (Sigmoid)
- Softmax
This is not an exhaustive list of activation functions used for output layers, but they are the most commonly used.
Let’s take a closer look at each in turn.
Linear Output Activation Function
The linear activation function is also called “identity” (multiplied by 1.0) or “no activation.”
This is because the linear activation function does not change the weighted sum of the input in any way and instead returns the value directly.
We can get an intuition for the shape of this function with the worked example below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# example plot for the linear activation function from matplotlib import pyplot # linear activation function def linear(x): return x # define input data inputs = [x for x in range(-10, 10)] # calculate outputs outputs = [linear(x) for x in inputs] # plot inputs vs outputs pyplot.plot(inputs, outputs) pyplot.show() |
Running the example calculates the outputs for a range of values and creates a plot of inputs versus outputs.
We can see a diagonal line shape where inputs are plotted against identical outputs.
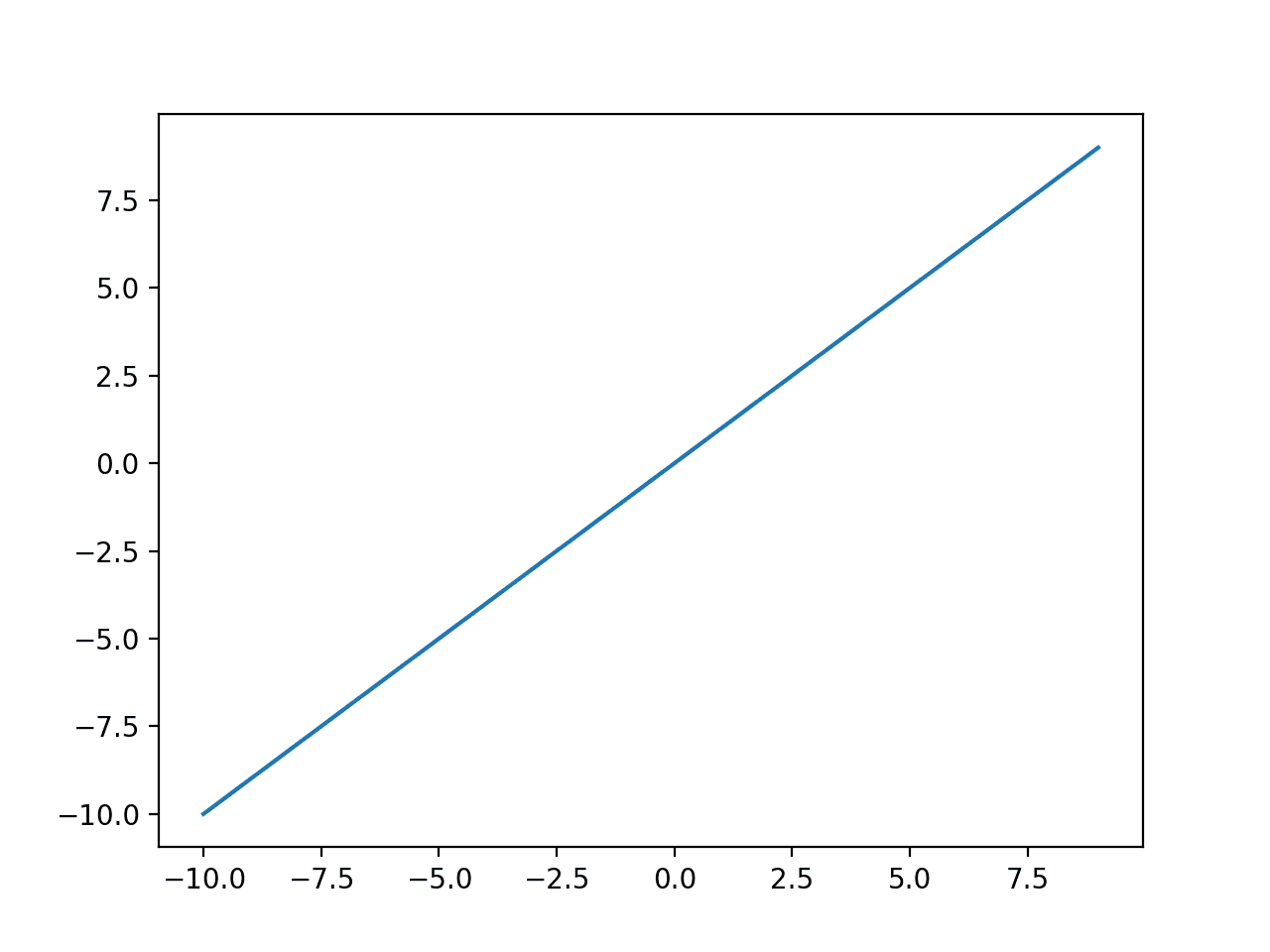
Plot of Inputs vs. Outputs for the Linear Activation Function
Target values used to train a model with a linear activation function in the output layer are typically scaled prior to modeling using normalization or standardization transforms.
Sigmoid Output Activation Function
The sigmoid of logistic activation function was described in the previous section.
Nevertheless, to add some symmetry, we can review for the shape of this function with the worked example below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# example plot for the sigmoid activation function from math import exp from matplotlib import pyplot # sigmoid activation function def sigmoid(x): return 1.0 / (1.0 + exp(-x)) # define input data inputs = [x for x in range(-10, 10)] # calculate outputs outputs = [sigmoid(x) for x in inputs] # plot inputs vs outputs pyplot.plot(inputs, outputs) pyplot.show() |
Running the example calculates the outputs for a range of values and creates a plot of inputs versus outputs.
We can see the familiar S-shape of the sigmoid activation function.

Plot of Inputs vs. Outputs for the Sigmoid Activation Function.
Target labels used to train a model with a sigmoid activation function in the output layer will have the values 0 or 1.
Softmax Output Activation Function
The softmax function outputs a vector of values that sum to 1.0 that can be interpreted as probabilities of class membership.
It is related to the argmax function that outputs a 0 for all options and 1 for the chosen option. Softmax is a “softer” version of argmax that allows a probability-like output of a winner-take-all function.
As such, the input to the function is a vector of real values and the output is a vector of the same length with values that sum to 1.0 like probabilities.
The softmax function is calculated as follows:
- e^x / sum(e^x)
Where x is a vector of outputs and e is a mathematical constant that is the base of the natural logarithm.
You can learn more about the details of the Softmax function in this tutorial:
We cannot plot the softmax function, but we can give an example of calculating it in Python.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
from numpy import exp # softmax activation function def softmax(x): return exp(x) / exp(x).sum() # define input data inputs = [1.0, 3.0, 2.0] # calculate outputs outputs = softmax(inputs) # report the probabilities print(outputs) # report the sum of the probabilities print(outputs.sum()) |
Running the example calculates the softmax output for the input vector.
We then confirm that the sum of the outputs of the softmax indeed sums to the value 1.0.
|
1 2 |
[0.09003057 0.66524096 0.24472847] 1.0 |
Target labels used to train a model with the softmax activation function in the output layer will be vectors with 1 for the target class and 0 for all other classes.
How to Choose an Output Activation Function
You must choose the activation function for your output layer based on the type of prediction problem that you are solving.
Specifically, the type of variable that is being predicted.
For example, you may divide prediction problems into two main groups, predicting a categorical variable (classification) and predicting a numerical variable (regression).
If your problem is a regression problem, you should use a linear activation function.
- Regression: One node, linear activation.
If your problem is a classification problem, then there are three main types of classification problems and each may use a different activation function.
Predicting a probability is not a regression problem; it is classification. In all cases of classification, your model will predict the probability of class membership (e.g. probability that an example belongs to each class) that you can convert to a crisp class label by rounding (for sigmoid) or argmax (for softmax).
If there are two mutually exclusive classes (binary classification), then your output layer will have one node and a sigmoid activation function should be used. If there are more than two mutually exclusive classes (multiclass classification), then your output layer will have one node per class and a softmax activation should be used. If there are two or more mutually inclusive classes (multilabel classification), then your output layer will have one node for each class and a sigmoid activation function is used.
- Binary Classification: One node, sigmoid activation.
- Multiclass Classification: One node per class, softmax activation.
- Multilabel Classification: One node per class, sigmoid activation.
The figure below summarizes how to choose an activation function for the output layer of your neural network model.
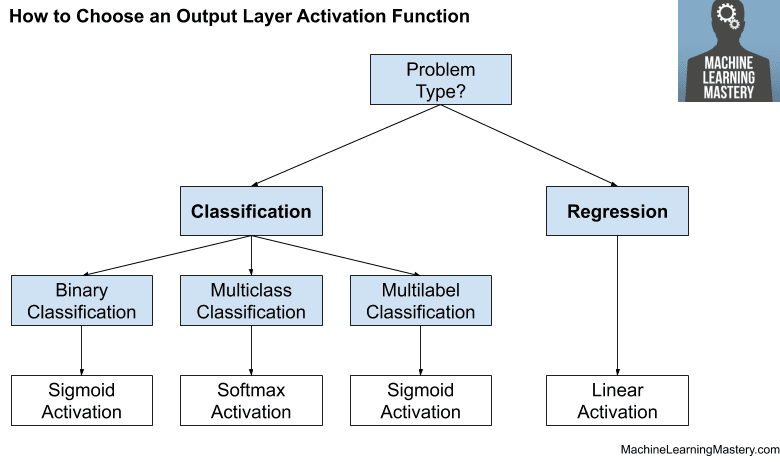
How to Choose an Output Layer Activation Function
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
- A Gentle Introduction to the Rectified Linear Unit (ReLU)
- Softmax Activation Function with Python
- 4 Types of Classification Tasks in Machine Learning
- How to Fix the Vanishing Gradients Problem Using the ReLU
Books
- Deep Learning, 2016.
- Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks, 1999.
- Neural Networks for Pattern Recognition, 1996.
- Deep Learning with Python, 2017.
Articles
Summary
In this tutorial, you discovered how to choose activation functions for neural network models.
Specifically, you learned:
- Activation functions are a key part of neural network design.
- The modern default activation function for hidden layers is the ReLU function.
- The activation function for output layers depends on the type of prediction problem.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.





Your materials in machinelearningmastery.com link are very good.
Thanks!
This was great!
Thanks!
Thank you very much )))
You’re welcome!
For softmax example, I think you forgot to include this line:
from numpy import exp
Thanks! Fixed.
math.exp shows following error:
TypeError: must be real number, not list
Fixed, thanks.
Thank You. It is beneficial.
Question: Can I build a single neural network which contains both regression and classification targets?
You’re welcome.
Yes, you would use multiple output layers/models, one loss function for each output model and prepare your training set accordingly.
Keras functional API will help:
https://machinelearningmastery.com/keras-functional-api-deep-learning/
Thanks Jason Brown, I would like to ask what textbooks would you advise someone that wants to develop the skills of building neural network from scratch to use.
Good question, these books:
https://machinelearningmastery.com/books-for-deep-learning-practitioners/
hello Jason,
I`m testing a LSTM grid_search() with precipitation dataset and that model config:
# define model
model = Sequential()
model.add(LSTM(n_nodes, activation=’relu’, input_shape=(n_input, n_features)))
model.add(Dense(n_nodes, activation=’relu’))
model.add(Dense(1, activation=’sigmoid’))
model.compile(loss=’mse’, optimizer=’adam’)
# fit model
model.fit(train_x, train_y, epochs=n_epochs, batch_size=n_batch, verbose=0)
return model
The output “model.add(Dense(1, activation=’sigmoid’))” line is correct?
About my example. LSTMs is an RNN and shouldn’t use Tanh or Sigmoid at the hidden layer activation?
Great articles as always!!!
No.
The output layer suggests a binary classification task.
The loss function suggests a regression task.
Ok. I remove the output layer because the results are all the same.
So, for a lstm model I must use the activation relu?
The activation function in the output layer must match the type of problem you are solving, see the above tutorial on how to choose the activation function.
Great article Sir.
Thanks!
Thanks ever so much. I’m greatly inspired!
You’re welcome.
Can an embedding layer be a method of normalizing or standardizing the data as input layer to the model?
Not really. Embedding is used to encode categorical vars into a distributed representation.
And once you have such a representation of the data for each category, is transformation still needed before passing to subsequent layer?
No.
Thank you Jason!
You’re welcome.
What should the output activation for Polynomial/ non linear regression?
And what if the output is multi label non linear regression?
Linear activation in both cases.
Jason, what is your opinion of recent functions like “swish” or “mish”?
I don’t know much about them. I hope to dig into them some more. ReLU works wonderfully.
Hi Jason,
very nice summary of Activation functions!
concepts pretty well schematized
thanks
Thanks!
Hello, sir
Thank you so much for making a Data Science as a piece of cake.
I’ve a question What is the difference Multilabel and Muticlasses because I see you define it as the same one node per class ?
You’re welcome!
Good question, here’s a definition of each type of classification:
https://machinelearningmastery.com/types-of-classification-in-machine-learning/
How about regression on ratio that is always between 0 and 1? Or, multiples ratios that need to be summed to one?
sigmoid for 0-1, softmax for more than output that sum to 1.
This is covered in the above tutorial, perhaps re-read?
Thanks!
You’re welcome.
Thanks! If you don’t mind, can I use you diagram images “How to Choose an….” for my blog postings? I will write the source links as well.
Yes, as long as you link to this blog post and clearly cite the source.
Thanks! 🙂
Hi Jason,
I am trying to change the activation equation of SimpleRNN layer in keras via subclassing.
so,
1. I override the call method in SimpleRNNCell class as follows:
class NotSoSimpleRNNCell(SimpleRNNCell):
def call(self, inputs, states, **kawrgs):
output, new_state = super(NotSoSimpleRNNCell, self).call(inputs, states, **kwargs)
output = output – self.activation(self.bias)
new_state = [output] if nest.is_nested(states) else output
return output, new_state
2. Then, I override the init method in SimpleRNN class as follows:
class NotSoSimpleRNN(SimpleRNN):
def __init__(self,
units,
activation=’tanh’,
use_bias=True,
kernel_initializer=’glorot_uniform’,
recurrent_initializer=’orthogonal’,
bias_initializer=’zeros’,
kernel_regularizer=None,
recurrent_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
recurrent_constraint=None,
bias_constraint=None,
dropout=0.,
recurrent_dropout=0.,
return_sequences=False,
return_state=False,
go_backwards=False,
stateful=False,
unroll=False,
**kwargs):
if ‘implementation’ in kwargs:
kwargs.pop(‘implementation’)
logging.warning(‘The
implementationargument ‘‘in
SimpleRNNhas been deprecated. ‘‘Please remove it from your layer call.’)
if ‘enable_caching_device’ in kwargs:
cell_kwargs = {‘enable_caching_device’:
kwargs.pop(‘enable_caching_device’)}
else:
cell_kwargs = {}
cell = NotSoSimpleRNNCell(
units,
activation=activation,
use_bias=use_bias,
kernel_initializer=kernel_initializer,
recurrent_initializer=recurrent_initializer,
bias_initializer=bias_initializer,
kernel_regularizer=kernel_regularizer,
recurrent_regularizer=recurrent_regularizer,
bias_regularizer=bias_regularizer,
kernel_constraint=kernel_constraint,
recurrent_constraint=recurrent_constraint,
bias_constraint=bias_constraint,
dropout=dropout,
recurrent_dropout=recurrent_dropout,
dtype=kwargs.get(‘dtype’),
trainable=kwargs.get(‘trainable’, True),
**cell_kwargs)
super(NotSoSimpleRNN, self).__init__(
cell,
return_sequences=return_sequences,
return_state=return_state,
go_backwards=go_backwards,
stateful=stateful,
unroll=unroll,
**kwargs)
3. Then, I created an object of NotSoSimpleRNN as follows:
U= Input(shape=(T,1), batch_size=1)
H1= NotSoSimpleRNN(3, activation=’tanh’, return_sequences=True, stateful=True)(U)
but I got this error:
/usr/local/lib/python3.7/dist-packages/tensorflow/python/keras/layers/recurrent.py in __call__(self, inputs, initial_state, constants, **kwargs)
654 inputs, initial_state, constants = _standardize_args(inputs,
655 initial_state,
–> 656 constants,
657 self._num_constants)
658
TypeError: _standardize_args() missing 1 required positional argument: ‘num_constants’
which is a part of the base RNN class.
————————
Q: Is this a right approach to reach my target? Why does this argument is not initialized while calling the call method of the base RNN class?
Thanks in advance for your time.
Perhaps try posting your code and error on stackoverflow.com
can I used the softmax activation function to classify binary problem?
You can, but it is not common. You should use sigmoid.
The explanation is just great! Many thanks.
You’re welcome.
Excellent article. I liked the idea of the summary as a diagram.
Good work.
Thanks!
Hi! Really great reading! I have one question on the regression part. You stated “regression, one unit, linear activation function”. Can’t I have several output units for regression? I thought that was possible..
Yes, you sure can, here’s an example:
https://machinelearningmastery.com/deep-learning-models-for-multi-output-regression/
Aha, great! Thanks. One more (last) thing: If I, just for fun, chose to have a linear activation function for the hidden layer, that means having no activation function at all if I understand it correctly?
How do I handle this in the backpropagation? Let say that I have another NN with the sigmoid function. I send g(z)=sigmoid(z) in the forward feed to the next layer. In the backprop I take the derivative of g(z), i.e. g'(z). For a linear activation function also for the hidden layer, that would be sending z forward and z’ backwards?
Thanks again!
Correct.
Backprop will handle that case just fine, no derivation function because to the activation function – just the raw error.
Hello, thanks for the very good article. I have a doubt for a while and decided to ask for some help. Hwy should we scale the data in the range of the activation output? for example you say standardize for tanh because the output ranges from -1 to 1. I have a problem with rely also.. normalize (min max) data when using relu, in part i understand because all negative inputs would become zero. but all positive inputs will output the same result, so relu becomes just a linear function right? It would be nice if you could share some references too. Thanks!
You can use a minmaxscaler object from sklearn, or write code to scale manually.
this article was great, i’m new to neural networks and this was a crystal clear tutorial for beginners!
i’m wondering, if i have a problem where my final output should be in the positive real numbers, it seems to me that i’d want a ReLU activation function. but you recommended in this tutorial not to use ReLU for the output layer. would you say this particular use case might be an exception and to try ReLU? if not, what would you recommend as the activation function?
appreciate your help!
In your particular case, it may work. Indeed depends on the problem, sometimes we may use linear activation (i.e. no activation) for the final layer.
appreciate the confirmation adrian!
It is very helpful
If you add some graphical representations for each section, that will help us to understand even more easily.
Wikipedia has it all in the table: https://en.wikipedia.org/wiki/Activation_function
I like it this machinelearningastery.cm site
if you add more concrate questions and examples that was best.
Thank you for the feedback Alemu!
I’m learning machine learning and this website is amazing to me.
I’m impressed that both the general idea behind the models and how to use them in practice are explained in such a clear way.
Thank you very much !
Thank you for the great feedback Guillaume!
You are awesome sir, Whenever I have any doubts, first I visit machinelearningmastery.com to find the article
Thank you for the feedback and support Sachin!
It is very helpful, greatly appreciated.
Thank you for the feedback and support Jannadi! We greatly appreciate it!
I am doing a PhD on AI and copyright law and use your website so often and have learnt so much! It is one of my go to websites to check anything AI.
Can I ask a very simple question. I presume an activation function is used in the trained model also – not just in the training phase?
Hi Ben…Your understanding is correct. The following resource may also prove beneficial:
https://machinelearningmastery.com/using-activation-functions-in-neural-networks/
Thank you!
You are very welcome Benjamin!