How to Configure the Learning Rate When Training Deep Learning Neural Networks

Last Updated on August 6, 2019

The weights of a neural network cannot be calculated using an analytical method. Instead, the weights must be discovered via an empirical optimization procedure called stochastic gradient descent.

The optimization problem addressed by stochastic gradient descent for neural networks is challenging and the space of solutions (sets of weights) may be comprised of many good solutions (called global optima) as well as easy to find, but low in skill solutions (called local optima).

The amount of change to the model during each step of this search process, or the step size, is called the “learning rate” and provides perhaps the most important hyperparameter to tune for your neural network in order to achieve good performance on your problem.

In this tutorial, you will discover the learning rate hyperparameter used when training deep learning neural networks.

After completing this tutorial, you will know:

• Learning rate controls how quickly or slowly a neural network model learns a problem.
• How to configure the learning rate with sensible defaults, diagnose behavior, and develop a sensitivity analysis.
• How to further improve performance with learning rate schedules, momentum, and adaptive learning rates.

Kick-start your project with my new book Better Deep Learning, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

How to Configure the Learning Rate Hyperparameter When Training Deep Learning Neural Networks
Photo by Bernd Thaller, some rights reserved.

Tutorial Overview

This tutorial is divided into six parts; they are:

1. What Is the Learning Rate?
2. Effect of Learning Rate
3. How to Configure Learning Rate
4. Add Momentum to the Learning Process
5. Use a Learning Rate Schedule
6. Adaptive Learning Rates

What Is the Learning Rate?

Deep learning neural networks are trained using the stochastic gradient descent algorithm.

Stochastic gradient descent is an optimization algorithm that estimates the error gradient for the current state of the model using examples from the training dataset, then updates the weights of the model using the back-propagation of errors algorithm, referred to as simply backpropagation.

The amount that the weights are updated during training is referred to as the step size or the “learning rate.”

Specifically, the learning rate is a configurable hyperparameter used in the training of neural networks that has a small positive value, often in the range between 0.0 and 1.0.

… learning rate, a positive scalar determining the size of the step.

— Page 86, Deep Learning, 2016.

The learning rate is often represented using the notation of the lowercase Greek letter eta (n).

During training, the backpropagation of error estimates the amount of error for which the weights of a node in the network are responsible. Instead of updating the weight with the full amount, it is scaled by the learning rate.

This means that a learning rate of 0.1, a traditionally common default value, would mean that weights in the network are updated 0.1 * (estimated weight error) or 10% of the estimated weight error each time the weights are updated.

Effect of Learning Rate

A neural network learns or approximates a function to best map inputs to outputs from examples in the training dataset.

The learning rate hyperparameter controls the rate or speed at which the model learns. Specifically, it controls the amount of apportioned error that the weights of the model are updated with each time they are updated, such as at the end of each batch of training examples.

Given a perfectly configured learning rate, the model will learn to best approximate the function given available resources (the number of layers and the number of nodes per layer) in a given number of training epochs (passes through the training data).

Generally, a large learning rate allows the model to learn faster, at the cost of arriving on a sub-optimal final set of weights. A smaller learning rate may allow the model to learn a more optimal or even globally optimal set of weights but may take significantly longer to train.

At extremes, a learning rate that is too large will result in weight updates that will be too large and the performance of the model (such as its loss on the training dataset) will oscillate over training epochs. Oscillating performance is said to be caused by weights that diverge (are divergent). A learning rate that is too small may never converge or may get stuck on a suboptimal solution.

When the learning rate is too large, gradient descent can inadvertently increase rather than decrease the training error. […] When the learning rate is too small, training is not only slower, but may become permanently stuck with a high training error.

— Page 429, Deep Learning, 2016.

In the worst case, weight updates that are too large may cause the weights to explode (i.e. result in a numerical overflow).

When using high learning rates, it is possible to encounter a positive feedback loop in which large weights induce large gradients which then induce a large update to the weights. If these updates consistently increase the size of the weights, then [the weights] rapidly moves away from the origin until numerical overflow occurs.

— Page 238, Deep Learning, 2016.

Therefore, we should not use a learning rate that is too large or too small. Nevertheless, we must configure the model in such a way that on average a “good enough” set of weights is found to approximate the mapping problem as represented by the training dataset.

How to Configure Learning Rate

It is important to find a good value for the learning rate for your model on your training dataset.

The learning rate may, in fact, be the most important hyperparameter to configure for your model.

The initial learning rate [… ] This is often the single most important hyperparameter and one should always make sure that it has been tuned […] If there is only time to optimize one hyper-parameter and one uses stochastic gradient descent, then this is the hyper-parameter that is worth tuning

— Practical recommendations for gradient-based training of deep architectures, 2012.

In fact, if there are resources to tune hyperparameters, much of this time should be dedicated to tuning the learning rate.

The learning rate is perhaps the most important hyperparameter. If you have time to tune only one hyperparameter, tune the learning rate.

— Page 429, Deep Learning, 2016.

Unfortunately, we cannot analytically calculate the optimal learning rate for a given model on a given dataset. Instead, a good (or good enough) learning rate must be discovered via trial and error.

… in general, it is not possible to calculate the best learning rate a priori.

— Page 72, Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks, 1999.

The range of values to consider for the learning rate is less than 1.0 and greater than 10^-6.

Typical values for a neural network with standardized inputs (or inputs mapped to the (0,1) interval) are less than 1 and greater than 10^−6

— Practical recommendations for gradient-based training of deep architectures, 2012.

The learning rate will interact with many other aspects of the optimization process, and the interactions may be nonlinear. Nevertheless, in general, smaller learning rates will require more training epochs. Conversely, larger learning rates will require fewer training epochs. Further, smaller batch sizes are better suited to smaller learning rates given the noisy estimate of the error gradient.

A traditional default value for the learning rate is 0.1 or 0.01, and this may represent a good starting point on your problem.

A default value of 0.01 typically works for standard multi-layer neural networks but it would be foolish to rely exclusively on this default value

— Practical recommendations for gradient-based training of deep architectures, 2012.

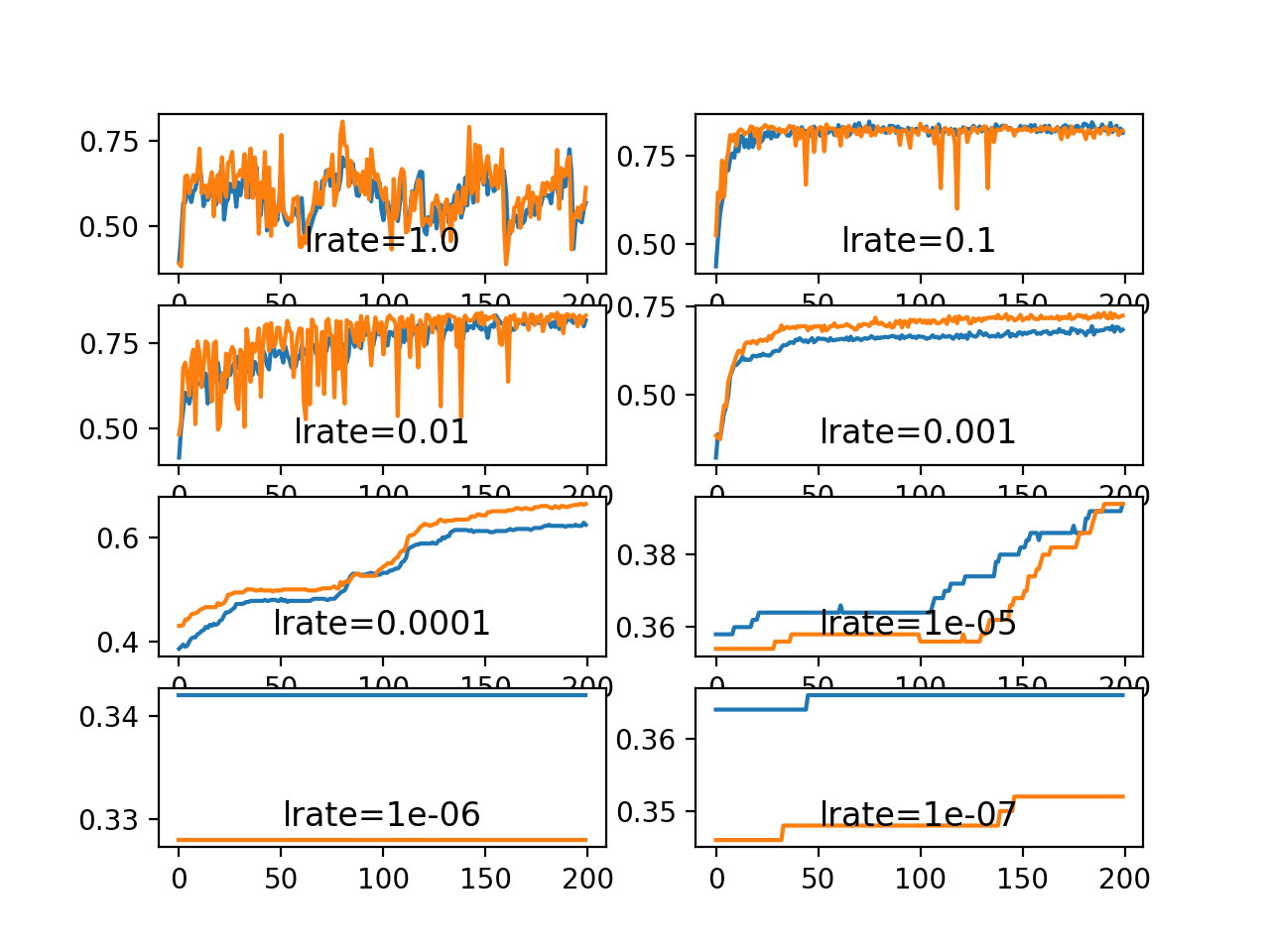
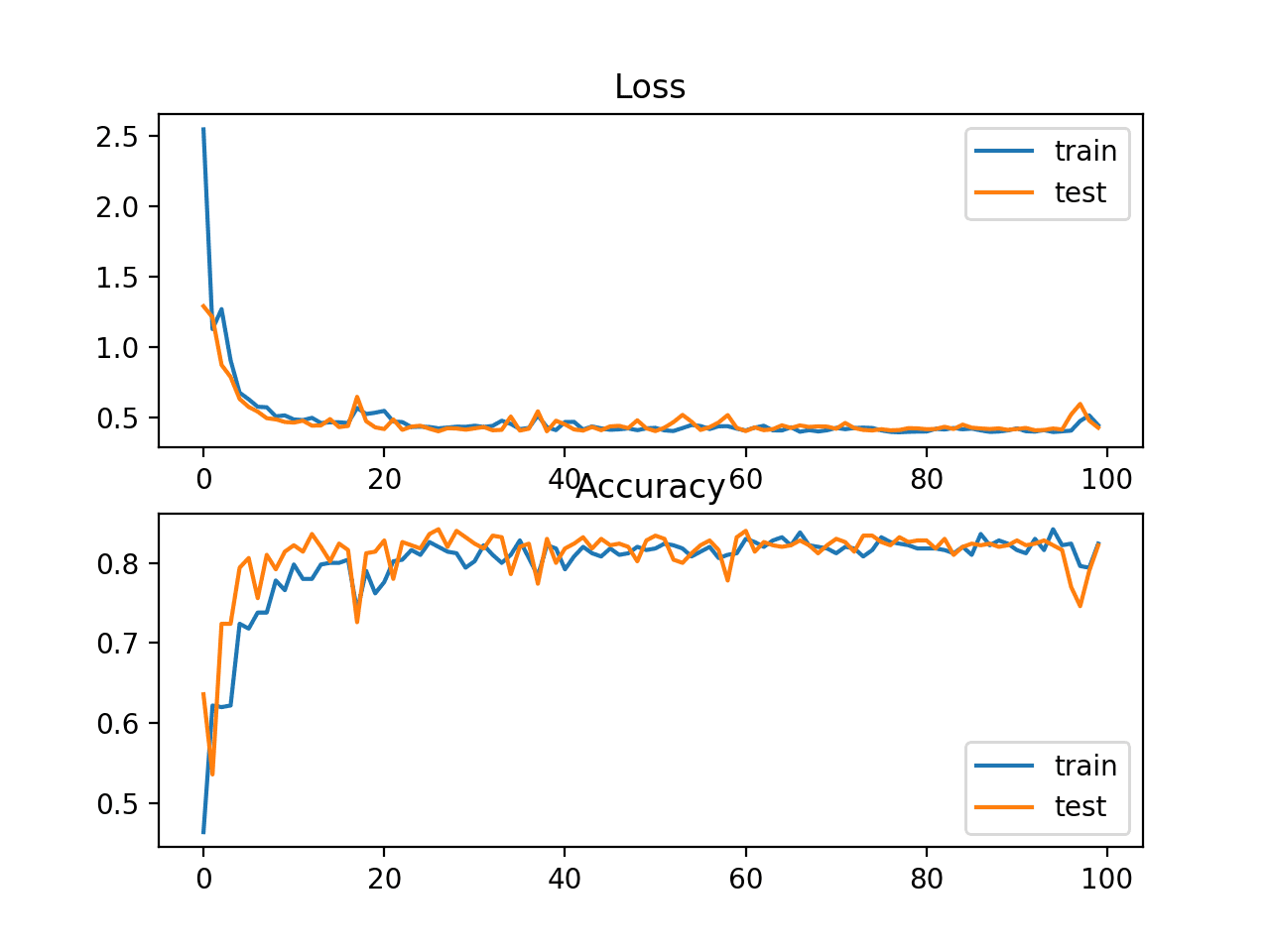
Diagnostic plots can be used to investigate how the learning rate impacts the rate of learning and learning dynamics of the model. One example is to create a line plot of loss over training epochs during training. The line plot can show many properties, such as:

• The rate of learning over training epochs, such as fast or slow.
• Whether model has learned too quickly (sharp rise and plateau) or is learning too slowly (little or no change).
• Whether the learning rate might be too large via oscillations in loss.

Configuring the learning rate is challenging and time-consuming.

The choice of the value for [the learning rate] can be fairly critical, since if it is too small the reduction in error will be very slow, while, if it is too large, divergent oscillations can result.

— Page 95, Neural Networks for Pattern Recognition, 1995.

An alternative approach is to perform a sensitivity analysis of the learning rate for the chosen model, also called a grid search. This can help to both highlight an order of magnitude where good learning rates may reside, as well as describe the relationship between learning rate and performance.

It is common to grid search learning rates on a log scale from 0.1 to 10^-5 or 10^-6.

Typically, a grid search involves picking values approximately on a logarithmic scale, e.g., a learning rate taken within the set {.1, .01, 10−3, 10−4 , 10−5}

— Page 434, Deep Learning, 2016.

When plotted, the results of such a sensitivity analysis often show a “U” shape, where loss decreases (performance improves) as the learning rate is decreased with a fixed number of training epochs to a point where loss sharply increases again because the model fails to converge.

If you need help experimenting with the learning rate for your model, see the post:

• Understand the Impact of Learning Rate on Model Performance With Deep Learning Neural Networks

Add Momentum to the Learning Process

Training a neural network can be made easier with the addition of history to the weight update.

Specifically, an exponentially weighted average of the prior updates to the weight can be included when the weights are updated. This change to stochastic gradient descent is called “momentum” and adds inertia to the update procedure, causing many past updates in one direction to continue in that direction in the future.

The momentum algorithm accumulates an exponentially decaying moving average of past gradients and continues to move in their direction.

— Page 296, Deep Learning, 2016.

Momentum can accelerate learning on those problems where the high-dimensional “weight space” that is being navigated by the optimization process has structures that mislead the gradient descent algorithm, such as flat regions or steep curvature.

The method of momentum is designed to accelerate learning, especially in the face of high curvature, small but consistent gradients, or noisy gradients.

— Page 296, Deep Learning, 2016.

The amount of inertia of past updates is controlled via the addition of a new hyperparameter, often referred to as the “momentum” or “velocity” and uses the notation of the Greek lowercase letter alpha (a).

… the momentum algorithm introduces a variable v that plays the role of velocity — it is the direction and speed at which the parameters move through parameter space. The velocity is set to an exponentially decaying average of the negative gradient.

— Page 296, Deep Learning, 2016.

It has the effect of smoothing the optimization process, slowing updates to continue in the previous direction instead of getting stuck or oscillating.

One very simple technique for dealing with the problem of widely differing eigenvalues is to add a momentum term to the gradient descent formula. This effectively adds inertia to the motion through weight space and smoothes out the oscillations

— Page 267, Neural Networks for Pattern Recognition, 1995.

Momentum is set to a value greater than 0.0 and less than one, where common values such as 0.9 and 0.99 are used in practice.

Common values of [momentum] used in practice include .5, .9, and .99.

— Page 298, Deep Learning, 2016.

Momentum does not make it easier to configure the learning rate, as the step size is independent of the momentum. Instead, momentum can improve the speed of the optimization process in concert with the step size, improving the likelihood that a better set of weights is discovered in fewer training epochs.

Use a Learning Rate Schedule

An alternative to using a fixed learning rate is to instead vary the learning rate over the training process.

The way in which the learning rate changes over time (training epochs) is referred to as the learning rate schedule or learning rate decay.

Perhaps the simplest learning rate schedule is to decrease the learning rate linearly from a large initial value to a small value. This allows large weight changes in the beginning of the learning process and small changes or fine-tuning towards the end of the learning process.

In practice, it is necessary to gradually decrease the learning rate over time, so we now denote the learning rate at iteration […] This is because the SGD gradient estimator introduces a source of noise (the random sampling of m training examples) that does not vanish even when we arrive at a minimum.

— Page 294, Deep Learning, 2016.

In fact, using a learning rate schedule may be a best practice when training neural networks. Instead of choosing a fixed learning rate hyperparameter, the configuration challenge involves choosing the initial learning rate and a learning rate schedule. It is possible that the choice of the initial learning rate is less sensitive than choosing a fixed learning rate, given the better performance that a learning rate schedule may permit.

The learning rate can be decayed to a small value close to zero. Alternately, the learning rate can be decayed over a fixed number of training epochs, then kept constant at a small value for the remaining training epochs to facilitate more time fine-tuning.

In practice, it is common to decay the learning rate linearly until iteration [tau]. After iteration [tau], it is common to leave [the learning rate] constant.

— Page 295, Deep Learning, 2016.

Adaptive Learning Rates

The performance of the model on the training dataset can be monitored by the learning algorithm and the learning rate can be adjusted in response.

This is called an adaptive learning rate.

Perhaps the simplest implementation is to make the learning rate smaller once the performance of the model plateaus, such as by decreasing the learning rate by a factor of two or an order of magnitude.

A reasonable choice of optimization algorithm is SGD with momentum with a decaying learning rate (popular decay schemes that perform better or worse on different problems include decaying linearly until reaching a fixed minimum learning rate, decaying exponentially, or decreasing the learning rate by a factor of 2-10 each time validation error plateaus).

— Page 425, Deep Learning, 2016.

Alternately, the learning rate can be increased again if performance does not improve for a fixed number of training epochs.

An adaptive learning rate method will generally outperform a model with a badly configured learning rate.

The difficulty of choosing a good learning rate a priori is one of the reasons adaptive learning rate methods are so useful and popular. A good adaptive algorithm will usually converge much faster than simple back-propagation with a poorly chosen fixed learning rate.

— Page 72, Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks, 1999.

Although no single method works best on all problems, there are three adaptive learning rate methods that have proven to be robust over many types of neural network architectures and problem types.

They are AdaGrad, RMSProp, and Adam, and all maintain and adapt learning rates for each of the weights in the model.

Perhaps the most popular is Adam, as it builds upon RMSProp and adds momentum.

At this point, a natural question is: which algorithm should one choose? Unfortunately, there is currently no consensus on this point. Currently, the most popular optimization algorithms actively in use include SGD, SGD with momentum, RMSProp, RMSProp with momentum, AdaDelta and Adam.

— Page 309, Deep Learning, 2016.

A robust strategy may be to first evaluate the performance of a model with a modern version of stochastic gradient descent with adaptive learning rates, such as Adam, and use the result as a baseline. Then, if time permits, explore whether improvements can be achieved with a carefully selected learning rate or simpler learning rate schedule.

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Post

• Understand the Impact of Learning Rate on Model Performance With Deep Learning Neural Networks

Papers

• Practical recommendations for gradient-based training of deep architectures, 2012.

Books

• Chapter 8: Optimization for Training Deep Models, Deep Learning, 2016.
• Chapter 6: Learning Rate and Momentum, Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks, 1999.
• Section 5.7: Gradient descent, Neural Networks for Pattern Recognition, 1995.

Articles

• Stochastic gradient descent, Wikipedia.
• What learning rate should be used for backprop?, Neural Network FAQ.

Summary

In this tutorial, you discovered the learning rate hyperparameter used when training deep learning neural networks.

Specifically, you learned:

• Learning rate controls how quickly or slowly a neural network model learns a problem.
• How to configure the learning rate with sensible defaults, diagnose behavior, and develop a sensitivity analysis.
• How to further improve performance with learning rate schedules, momentum, and adaptive learning rates.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

Develop Better Deep Learning Models Today!

Train Faster, Reduce Overftting, and Ensembles

...with just a few lines of python code

Discover how in my new Ebook:
Better Deep Learning

It provides self-study tutorials on topics like:
weight decay, batch normalization, dropout, model stacking and much more...

Bring better deep learning to your projects!

Skip the Academics. Just Results.

See What's Inside