Recurrent neural networks are a type of neural network where the outputs from previous time steps are fed as input to the current time step.
This creates a network graph or circuit diagram with cycles, which can make it difficult to understand how information moves through the network.
In this post, you will discover the concept of unrolling or unfolding recurrent neural networks.
After reading this post, you will know:
- The standard conception of recurrent neural networks with cyclic connections.
- The concept of unrolling of the forward pass when the network is copied for each input time step.
- The concept of unrolling of the backward pass for updating network weights during training.
Kick-start your project with my new book Long Short-Term Memory Networks With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
Unrolling Recurrent Neural Networks
Recurrent neural networks are a type of neural network where outputs from previous time steps are taken as inputs for the current time step.
We can demonstrate this with a picture.
Below we can see that the network takes both the output of the network from the previous time step as input and uses the internal state from the previous time step as a starting point for the current time step.
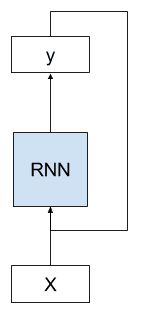
Example of an RNN with a cycle
RNNs are fit and make predictions over many time steps. We can simplify the model by unfolding or unrolling the RNN graph over the input sequence.
A useful way to visualise RNNs is to consider the update graph formed by ‘unfolding’ the network along the input sequence.
— Supervised Sequence Labelling with Recurrent Neural Networks, 2008.
Unrolling the Forward Pass
Consider the case where we have multiple time steps of input (X(t), X(t+1), …), multiple time steps of internal state (u(t), u(t+1), …), and multiple time steps of outputs (y(t), y(t+1), …).
We can unfold the above network schematic into a graph without any cycles.
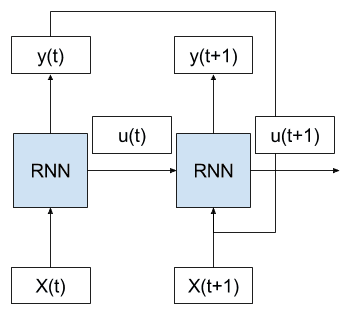
Example of Unrolled RNN on the forward pass
We can see that the cycle is removed and that the output (y(t)) and internal state (u(t)) from the previous time step are passed on to the network as inputs for processing the next time step.
Key in this conceptualization is that the network (RNN) does not change between the unfolded time steps. Specifically, the same weights are used for each time step and it is only the outputs and the internal states that differ.
In this way, it is as though the whole network (topology and weights) are copied for each time step in the input sequence.
Further, each copy of the network may be thought of as an additional layer of the same feed forward neural network.
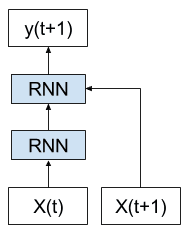
Example of Unrolled RNN with each copy of the network as a layer
RNNs, once unfolded in time, can be seen as very deep feedforward networks in which all the layers share the same weights.
— Deep learning, Nature, 2015
This is a useful conceptual tool and visualization to help in understanding what is going on in the network during the forward pass. It may or may not also be the way that the network is implemented by the deep learning library.
Unrolling the Backward Pass
The idea of network unfolding plays a bigger part in the way recurrent neural networks are implemented for the backward pass.
As is standard with [backpropagation through time] , the network is unfolded over time, so that connections arriving at layers are viewed as coming from the previous timestep.
— Framewise phoneme classification with bidirectional LSTM and other neural network architectures, 2005
Importantly, the backpropagation of error for a given time step depends on the activation of the network at the prior time step.
In this way, the backward pass requires the conceptualization of unfolding the network.
Error is propagated back to the first input time step of the sequence so that the error gradient can be calculated and the weights of the network can be updated.
Like standard backpropagation, [backpropagation through time] consists of a repeated application of the chain rule. The subtlety is that, for recurrent networks, the loss function depends on the activation of the hidden layer not only through its influence on the output layer, but also through its influence on the hidden layer at the next timestep.
— Supervised Sequence Labelling with Recurrent Neural Networks, 2008
Unfolding the recurrent network graph also introduces additional concerns. Each time step requires a new copy of the network, which in turn takes up memory, especially for larger networks with thousands or millions of weights. The memory requirements of training large recurrent networks can quickly balloon as the number of time steps climbs into the hundreds.
… it is required to unroll the RNNs by the length of the input sequence. By unrolling an RNN N times, every activations of the neurons inside the network are replicated N times, which consumes a huge amount of memory especially when the sequence is very long. This hinders a small footprint implementation of online learning or adaptation. Also, this “full unrolling” makes a parallel training with multiple sequences inefficient on shared memory models such as graphics processing units (GPUs)
— Online Sequence Training of Recurrent Neural Networks with Connectionist Temporal Classification, 2015
Further Reading
This section provides more resources on the topic if you are looking go deeper.
Papers
- Online Sequence Training of Recurrent Neural Networks with Connectionist Temporal Classification, 2015
- Framewise phoneme classification with bidirectional LSTM and other neural network architectures, 2005
- Supervised Sequence Labelling with Recurrent Neural Networks, 2008
- Deep learning, Nature, 2015
Articles
- A Gentle Introduction to Backpropagation Through Time
- Understanding LSTM Networks, 2015
- Rolling and Unrolling RNNs, 2016
- Unfolding RNNs, 2017
Summary
In this tutorial, you discovered the visualization and conceptual tool of unrolling recurrent neural networks.
Specifically, you learned:
- The standard conception of recurrent neural networks with cyclic connections.
- The concept of unrolling of the forward pass when the network is copied for each input time step.
- The concept of unrolling of the backward pass for updating network weights during training.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
Develop LSTMs for Sequence Prediction Today!
Develop Your Own LSTM models in Minutes
...with just a few lines of python code
Discover how in my new Ebook:
Long Short-Term Memory Networks with Python
It provides self-study tutorials on topics like:
CNN LSTMs, Encoder-Decoder LSTMs, generative models, data preparation, making predictions and much more...
Finally Bring LSTM Recurrent Neural Networks to
Your Sequence Predictions Projects
Skip the Academics. Just Results.
Each time step requires a new copy of the network, which in turn takes up memory, especially for larger networks with thousands or millions of weights.
I thought different steps of RNN share the same weight, so why unfolding will improve the number of weight and consumes more memory?
Besides, why unfoding makes the parallel traning inefficient on GPU? As I konw, one optimization method of RNN is unrolling it and doing a big gemm for all inputs to improve the efficiency of gemm.
This article is so helpful for me. Thanks.
I can take a good start of RNN coz of this.
Thanks.
Being fascinated with neural networks from both the points of view of solving practical problems but also in seeking understanding by analog of how the mind works, it is hard to believe that biological neural networks would explode in terms of “RAM”. While biological neural networks must be recurrent, there must be compaction, as exhibited perhaps in studies that accessing a memory changes a memory.
I would love to know more about this. I also must disclaim that I am a novice in cognition, and so if my critique seems obvious I hope it is forgivable.
Artificial neural networks are not trying to model the brain, they are a math trick that we find useful for modeling prediction problems.
Hi, what tool do you use for drawing these diagrams?
The google drawing doc tool thingo.
Hi Jason; really useful post. When unrolling a network which has multiple recurrent layers, does one unroll each instance of recurrence as a separate subgraph? Please see https://imgur.com/a/aFhCl for visual aid.
nevermind, i think i understand now :D.
Each, each layer would be unrolled separately, at least that is how I would approach it off the cuff.
Which layers are you referring to when you say, “all the layers share the same weights”. weights connecting input to RNN layer and RNN layer to output layer I presume.
Also can you please provide a visualization of internal state for RNN?
The layers in the unrolled RNN.
Thanks for the suggestion.
Also when you say, “the output (y(t)) and internal state (u(t)) from the previous time step are passed on to the network as inputs for processing the next time step.” I’m not sure if we pass previous time step’s “internal state” as input to current time step’s internal state.I think we are working “upon” the internal state of the previous time step. Please tell me if my understanding is right.
The internal state are like a local variable used by the unit across time steps.
Hi
I have a question regarding back-propagation in a RNN. While applying the chain rule from the output towards the weight matrixes and biases, is there any step in between where we calculate the partial derivative w.r.t the feature vector X? I can’t imagine this could be the case as because we can’t modify / adjust the feature vector anyway, as it’s “readonly”.
The reason I’m asking is because I saw this at the end of the following article:
https://eli.thegreenplace.net/2018/backpropagation-through-a-fully-connected-layer/
The paragraph with the title “Addendum – gradient w.r.t. x”
Could you please shed some light on this?
Thanks!
Perhaps contact the author of the article and ask what they meant?
Thanks for your answer.
Independent of that Blog post, may I ask you directly if to your knowledge a partial derivative w.r.t. to the Input feature vector may be calculated at all? If so in which kind of NN, or maybe a link to a paper or your corresponding Blog post about that etc.
I don’t know off hand sorry.
Hi
Just for the record for anyone interested in why we would calculate the derivative w.r.t the feature vector X.
In RNNs as we use the chain rule to calculate DL/DW (gradient w.r.t the weight matrices) we would indeed need to calculate the gradient w.r.t to X as we backpropagate.
More details about this can be found in a follow up blog post from the same author about RNNs:
https://eli.thegreenplace.net/2018/understanding-how-to-implement-a-character-based-rnn-language-model/
As we apply the chain rule to calculate Dy[t]/dw:
Dy[t]/dw = Dy[t]/dh[t] * dh[t]/dw
By this multiplication we need Dy[t]/dh[t] which is exactly the calculation of derivative w.r.t the input vector (here called h, the state vector of RNN instead of X).
Thanks for sharing.
What does partially unrolling a RNN during backprop means?
Does it literally mean that we are unrolling only a partial number of steps?
And the reason we are doing it is because as one of the quotes mentioned, unrolling the whole RNN might be computationally expensive?
It is unrolled in memory.
We do it to trade-off compute speed and memory usage. Also as a conceptual model for understanding what is going on in an RNN during training.
nice machine learning technique about RNN,,,,, share a simple model of RNN as you shared keras neural network before. thanks
The oldest RNN implementation in Keras is called SimpleRNN, but people usually prefer LSTM or GRU over it. We do have an example in LSTM: https://machinelearningmastery.com/define-encoder-decoder-sequence-sequence-model-neural-machine-translation-keras/
I think your content is probably the best among articles on internet. Thank you so much !
Great feedback Anurag!