Convolutional Neural Network models, or CNNs for short, can be applied to time series forecasting.
There are many types of CNN models that can be used for each specific type of time series forecasting problem.
In this tutorial, you will discover how to develop a suite of CNN models for a range of standard time series forecasting problems.
The objective of this tutorial is to provide standalone examples of each model on each type of time series problem as a template that you can copy and adapt for your specific time series forecasting problem.
After completing this tutorial, you will know:
How to develop CNN models for univariate time series forecasting.
How to develop CNN models for multivariate time series forecasting.
How to develop CNN models for multi-step time series forecasting.
This is a large and important post; you may want to bookmark it for future reference.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
How to Develop Convolutional Neural Network Models for Time Series Forecasting Photo by Bureau of Land Management, some rights reserved.
Tutorial Overview
In this tutorial, we will explore how to develop a suite of different types of CNN models for time series forecasting.
The models are demonstrated on small contrived time series problems intended to give the flavor of the type of time series problem being addressed. The chosen configuration of the models is arbitrary and not optimized for each problem; that was not the goal.
This tutorial is divided into four parts; they are:
Univariate CNN Models
Multivariate CNN Models
Multi-Step CNN Models
Multivariate Multi-Step CNN Models
Univariate CNN Models
Although traditionally developed for two-dimensional image data, CNNs can be used to model univariate time series forecasting problems.
Univariate time series are datasets comprised of a single series of observations with a temporal ordering and a model is required to learn from the series of past observations to predict the next value in the sequence.
This section is divided into two parts; they are:
Data Preparation
CNN Model
Data Preparation
Before a univariate series can be modeled, it must be prepared.
The CNN model will learn a function that maps a sequence of past observations as input to an output observation. As such, the sequence of observations must be transformed into multiple examples from which the model can learn.
Consider a given univariate sequence:
1
[10, 20, 30, 40, 50, 60, 70, 80, 90]
We can divide the sequence into multiple input/output patterns called samples, where three time steps are used as input and one time step is used as output for the one-step prediction that is being learned.
1
2
3
4
5
X, y
10, 20, 30 40
20, 30, 40 50
30, 40, 50 60
...
The split_sequence() function below implements this behavior and will split a given univariate sequence into multiple samples where each sample has a specified number of time steps and the output is a single time step.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# split a univariate sequence into samples
def split_sequence(sequence,n_steps):
X,y=list(),list()
foriinrange(len(sequence)):
# find the end of this pattern
end_ix=i+n_steps
# check if we are beyond the sequence
ifend_ix>len(sequence)-1:
break
# gather input and output parts of the pattern
seq_x,seq_y=sequence[i:end_ix],sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
returnarray(X),array(y)
We can demonstrate this function on our small contrived dataset above.
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# univariate data preparation
from numpy import array
# split a univariate sequence into samples
def split_sequence(sequence,n_steps):
X,y=list(),list()
foriinrange(len(sequence)):
# find the end of this pattern
end_ix=i+n_steps
# check if we are beyond the sequence
ifend_ix>len(sequence)-1:
break
# gather input and output parts of the pattern
seq_x,seq_y=sequence[i:end_ix],sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
returnarray(X),array(y)
# define input sequence
raw_seq=[10,20,30,40,50,60,70,80,90]
# choose a number of time steps
n_steps=3
# split into samples
X,y=split_sequence(raw_seq,n_steps)
# summarize the data
foriinrange(len(X)):
print(X[i],y[i])
Running the example splits the univariate series into six samples where each sample has three input time steps and one output time step.
1
2
3
4
5
6
[10 20 30] 40
[20 30 40] 50
[30 40 50] 60
[40 50 60] 70
[50 60 70] 80
[60 70 80] 90
Now that we know how to prepare a univariate series for modeling, let’s look at developing a CNN model that can learn the mapping of inputs to outputs.
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
CNN Model
A one-dimensional CNN is a CNN model that has a convolutional hidden layer that operates over a 1D sequence. This is followed by perhaps a second convolutional layer in some cases, such as very long input sequences, and then a pooling layer whose job it is to distill the output of the convolutional layer to the most salient elements.
The convolutional and pooling layers are followed by a dense fully connected layer that interprets the features extracted by the convolutional part of the model. A flatten layer is used between the convolutional layers and the dense layer to reduce the feature maps to a single one-dimensional vector.
We can define a 1D CNN Model for univariate time series forecasting as follows.
Key in the definition is the shape of the input; that is what the model expects as input for each sample in terms of the number of time steps and the number of features.
We are working with a univariate series, so the number of features is one, for one variable.
The number of time steps as input is the number we chose when preparing our dataset as an argument to the split_sequence() function.
The input shape for each sample is specified in the input_shape argument on the definition of the first hidden layer.
We almost always have multiple samples, therefore, the model will expect the input component of training data to have the dimensions or shape:
1
[samples, timesteps, features]
Our split_sequence() function in the previous section outputs the X with the shape [samples, timesteps], so we can easily reshape it to have an additional dimension for the one feature.
1
2
3
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features=1
X=X.reshape((X.shape[0],X.shape[1],n_features))
The CNN does not actually view the data as having time steps, instead, it is treated as a sequence over which convolutional read operations can be performed, like a one-dimensional image.
In this example, we define a convolutional layer with 64 filter maps and a kernel size of 2. This is followed by a max pooling layer and a dense layer to interpret the input feature. An output layer is specified that predicts a single numerical value.
Once the model is defined, we can fit it on the training dataset.
1
2
# fit model
model.fit(X,y,epochs=1000,verbose=0)
After the model is fit, we can use it to make a prediction.
We can predict the next value in the sequence by providing the input:
1
[70, 80, 90]
And expecting the model to predict something like:
1
[100]
The model expects the input shape to be three-dimensional with [samples, timesteps, features], therefore, we must reshape the single input sample before making the prediction.
1
2
3
4
# demonstrate prediction
x_input=array([70,80,90])
x_input=x_input.reshape((1,n_steps,n_features))
yhat=model.predict(x_input,verbose=0)
We can tie all of this together and demonstrate how to develop a 1D CNN model for univariate time series forecasting and make a single prediction.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# univariate cnn example
from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
# split a univariate sequence into samples
def split_sequence(sequence,n_steps):
X,y=list(),list()
foriinrange(len(sequence)):
# find the end of this pattern
end_ix=i+n_steps
# check if we are beyond the sequence
ifend_ix>len(sequence)-1:
break
# gather input and output parts of the pattern
seq_x,seq_y=sequence[i:end_ix],sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
returnarray(X),array(y)
# define input sequence
raw_seq=[10,20,30,40,50,60,70,80,90]
# choose a number of time steps
n_steps=3
# split into samples
X,y=split_sequence(raw_seq,n_steps)
# reshape from [samples, timesteps] into [samples, timesteps, features]
Running the example prepares the data, fits the model, and makes a prediction.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that the model predicts the next value in the sequence.
1
[[101.67965]]
Multivariate CNN Models
Multivariate time series data means data where there is more than one observation for each time step.
There are two main models that we may require with multivariate time series data; they are:
Multiple Input Series.
Multiple Parallel Series.
Let’s take a look at each in turn.
Multiple Input Series
A problem may have two or more parallel input time series and an output time series that is dependent on the input time series.
The input time series are parallel because each series has observations at the same time steps.
We can demonstrate this with a simple example of two parallel input time series where the output series is the simple addition of the input series.
Running the example prints the dataset with one row per time step and one column for each of the two input and one output parallel time series.
1
2
3
4
5
6
7
8
9
[[ 10 15 25]
[ 20 25 45]
[ 30 35 65]
[ 40 45 85]
[ 50 55 105]
[ 60 65 125]
[ 70 75 145]
[ 80 85 165]
[ 90 95 185]]
As with the univariate time series, we must structure these data into samples with input and output samples.
A 1D CNN model needs sufficient context to learn a mapping from an input sequence to an output value. CNNs can support parallel input time series as separate channels, like red, green, and blue components of an image. Therefore, we need to split the data into samples maintaining the order of observations across the two input sequences.
If we chose three input time steps, then the first sample would look as follows:
Input:
1
2
3
10, 15
20, 25
30, 35
Output:
1
65
That is, the first three time steps of each parallel series are provided as input to the model and the model associates this with the value in the output series at the third time step, in this case, 65.
We can see that, in transforming the time series into input/output samples to train the model, that we will have to discard some values from the output time series where we do not have values in the input time series at prior time steps. In turn, the choice of the size of the number of input time steps will have an important effect on how much of the training data is used.
We can define a function named split_sequences() that will take a dataset as we have defined it with rows for time steps and columns for parallel series and return input/output samples.
Running the example first prints the shape of the X and y components.
We can see that the X component has a three-dimensional structure.
The first dimension is the number of samples, in this case 7. The second dimension is the number of time steps per sample, in this case 3, the value specified to the function. Finally, the last dimension specifies the number of parallel time series or the number of variables, in this case 2 for the two parallel series.
This is the exact three-dimensional structure expected by a 1D CNN as input. The data is ready to use without further reshaping.
We can then see that the input and output for each sample is printed, showing the three time steps for each of the two input series and the associated output for each sample.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
(7, 3, 2) (7,)
[[10 15]
[20 25]
[30 35]] 65
[[20 25]
[30 35]
[40 45]] 85
[[30 35]
[40 45]
[50 55]] 105
[[40 45]
[50 55]
[60 65]] 125
[[50 55]
[60 65]
[70 75]] 145
[[60 65]
[70 75]
[80 85]] 165
[[70 75]
[80 85]
[90 95]] 185
We are now ready to fit a 1D CNN model on this data, specifying the expected number of time steps and features to expect for each input sample, in this case three and two respectively.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example prepares the data, fits the model, and makes a prediction.
1
[[206.0161]]
There is another, more elaborate way to model the problem.
Each input series can be handled by a separate CNN and the output of each of these submodels can be combined before a prediction is made for the output sequence.
We can refer to this as a multi-headed CNN model. It may offer more flexibility or better performance depending on the specifics of the problem that is being modeled. For example, it allows you to configure each sub-model differently for each input series, such as the number of filter maps and the kernel size.
Now that both input submodels have been defined, we can merge the output from each model into one long vector which can be interpreted before making a prediction for the output sequence.
The image below provides a schematic for how this model looks, including the shape of the inputs and outputs of each layer.
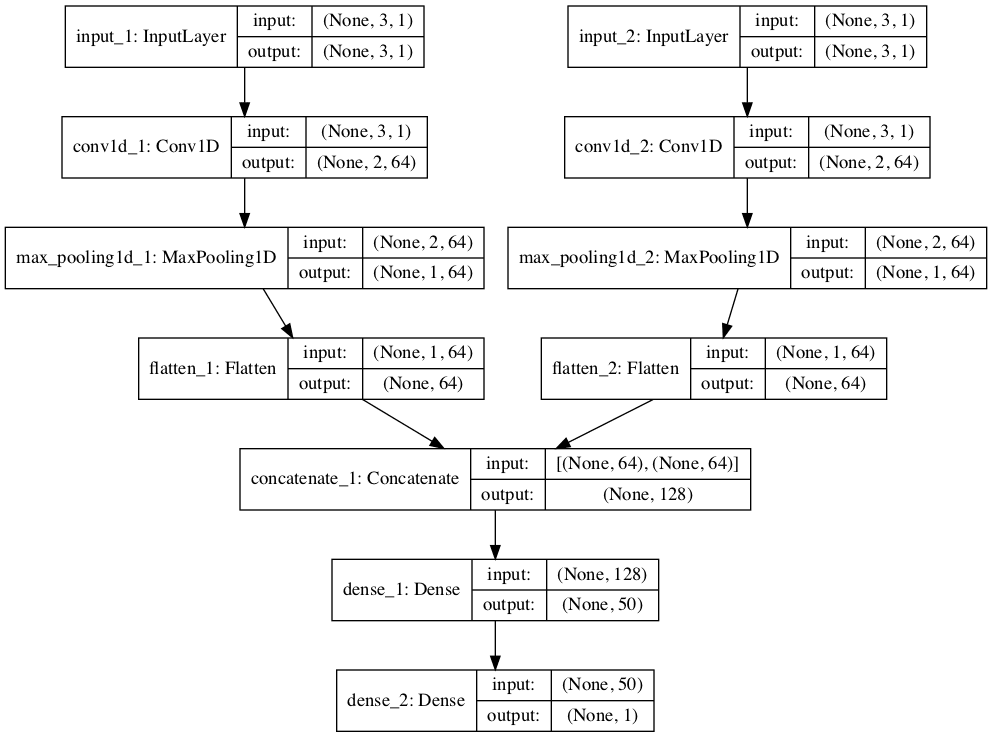
Plot of Multi-Headed 1D CNN for Multivariate Time Series Forecasting
This model requires input to be provided as a list of two elements where each element in the list contains data for one of the submodels.
In order to achieve this, we can split the 3D input data into two separate arrays of input data; that is from one array with the shape [7, 3, 2] to two 3D arrays with [7, 3, 1]
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example prepares the data, fits the model, and makes a prediction.
1
[[205.871]]
Multiple Parallel Series
An alternate time series problem is the case where there are multiple parallel time series and a value must be predicted for each.
For example, given the data from the previous section:
1
2
3
4
5
6
7
8
9
[[ 10 15 25]
[ 20 25 45]
[ 30 35 65]
[ 40 45 85]
[ 50 55 105]
[ 60 65 125]
[ 70 75 145]
[ 80 85 165]
[ 90 95 185]]
We may want to predict the value for each of the three time series for the next time step.
This might be referred to as multivariate forecasting.
Again, the data must be split into input/output samples in order to train a model.
The first sample of this dataset would be:
Input:
1
2
3
10, 15, 25
20, 25, 45
30, 35, 65
Output:
1
40, 45, 85
The split_sequences() function below will split multiple parallel time series with rows for time steps and one series per column into the required input/output shape.
Running the example first prints the shape of the prepared X and y components.
The shape of X is three-dimensional, including the number of samples (6), the number of time steps chosen per sample (3), and the number of parallel time series or features (3).
The shape of y is two-dimensional as we might expect for the number of samples (6) and the number of time variables per sample to be predicted (3).
The data is ready to use in a 1D CNN model that expects three-dimensional input and two-dimensional output shapes for the X and y components of each sample.
Then, each of the samples is printed showing the input and output components of each sample.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(6, 3, 3) (6, 3)
[[10 15 25]
[20 25 45]
[30 35 65]] [40 45 85]
[[20 25 45]
[30 35 65]
[40 45 85]] [ 50 55 105]
[[ 30 35 65]
[ 40 45 85]
[ 50 55 105]] [ 60 65 125]
[[ 40 45 85]
[ 50 55 105]
[ 60 65 125]] [ 70 75 145]
[[ 50 55 105]
[ 60 65 125]
[ 70 75 145]] [ 80 85 165]
[[ 60 65 125]
[ 70 75 145]
[ 80 85 165]] [ 90 95 185]
We are now ready to fit a 1D CNN model on this data.
In this model, the number of time steps and parallel series (features) are specified for the input layer via the input_shape argument.
The number of parallel series is also used in the specification of the number of values to predict by the model in the output layer; again, this is three.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example prepares the data, fits the model and makes a prediction.
1
[[100.11272 105.32213 205.53436]]
As with multiple input series, there is another more elaborate way to model the problem.
Each output series can be handled by a separate output CNN model.
We can refer to this as a multi-output CNN model. It may offer more flexibility or better performance depending on the specifics of the problem that is being modeled.
We can then define one output layer for each of the three series that we wish to forecast, where each output submodel will forecast a single time step.
1
2
3
4
5
6
# define output 1
output1=Dense(1)(cnn)
# define output 2
output2=Dense(1)(cnn)
# define output 3
output3=Dense(1)(cnn)
We can then tie the input and output layers together into a single model.
To make the model architecture clear, the schematic below clearly shows the three separate output layers of the model and the input and output shapes of each layer.
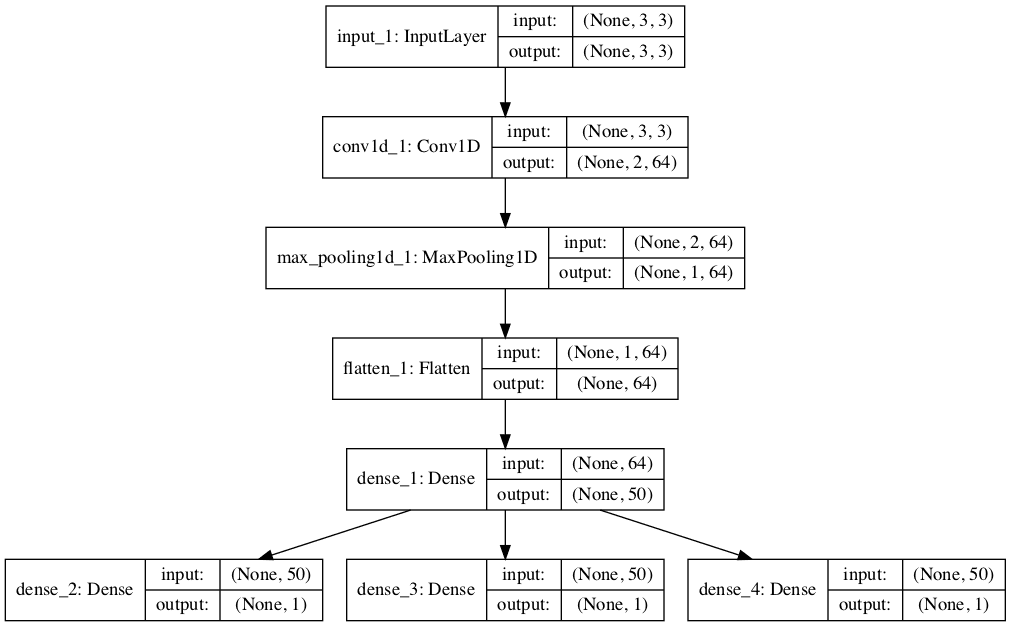
Plot of Multi-Output 1D CNN for Multivariate Time Series Forecasting
When training the model, it will require three separate output arrays per sample. We can achieve this by converting the output training data that has the shape [7, 3] to three arrays with the shape [7, 1].
1
2
3
4
# separate output
y1=y[:,0].reshape((y.shape[0],1))
y2=y[:,1].reshape((y.shape[0],1))
y3=y[:,2].reshape((y.shape[0],1))
These arrays can be provided to the model during training.
1
2
# fit model
model.fit(X,[y1,y2,y3],epochs=2000,verbose=0)
Tying all of this together, the complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# multivariate output 1d cnn example
from numpy import array
from numpy import hstack
from keras.models import Model
from keras.layers import Input
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example prepares the data, fits the model, and makes a prediction.
1
2
3
[array([[100.96118]], dtype=float32),
array([[105.502686]], dtype=float32),
array([[205.98045]], dtype=float32)]
Multi-Step CNN Models
In practice, there is little difference to the 1D CNN model in predicting a vector output that represents different output variables (as in the previous example), or a vector output that represents multiple time steps of one variable.
Nevertheless, there are subtle and important differences in the way the training data is prepared. In this section, we will demonstrate the case of developing a multi-step forecast model using a vector model.
Before we look at the specifics of the model, let’s first look at the preparation of data for multi-step forecasting.
Data Preparation
As with one-step forecasting, a time series used for multi-step time series forecasting must be split into samples with input and output components.
Both the input and output components will be comprised of multiple time steps and may or may not have the same number of steps.
For example, given the univariate time series:
1
[10, 20, 30, 40, 50, 60, 70, 80, 90]
We could use the last three time steps as input and forecast the next two time steps.
The first sample would look as follows:
Input:
1
[10, 20, 30]
Output:
1
[40, 50]
The split_sequence() function below implements this behavior and will split a given univariate time series into samples with a specified number of input and output time steps.
Running the example splits the univariate series into input and output time steps and prints the input and output components of each.
1
2
3
4
5
[10 20 30] [40 50]
[20 30 40] [50 60]
[30 40 50] [60 70]
[40 50 60] [70 80]
[50 60 70] [80 90]
Now that we know how to prepare data for multi-step forecasting, let’s look at a 1D CNN model that can learn this mapping.
Vector Output Model
The 1D CNN can output a vector directly that can be interpreted as a multi-step forecast.
This approach was seen in the previous section were one time step of each output time series was forecasted as a vector.
As with the 1D CNN models for univariate data in a prior section, the prepared samples must first be reshaped. The CNN expects data to have a three-dimensional structure of [samples, timesteps, features], and in this case, we only have one feature so the reshape is straightforward.
1
2
3
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features=1
X=X.reshape((X.shape[0],X.shape[1],n_features))
With the number of input and output steps specified in the n_steps_in and n_steps_out variables, we can define a multi-step time-series forecasting model.
The model can make a prediction for a single sample. We can predict the next two steps beyond the end of the dataset by providing the input:
1
[70, 80, 90]
We would expect the predicted output to be:
1
[100, 110]
As expected by the model, the shape of the single sample of input data when making the prediction must be [1, 3, 1] for the 1 sample, 3 time steps of the input, and the single feature.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example forecasts and prints the next two time steps in the sequence.
1
[[102.86651 115.08979]]
Multivariate Multi-Step CNN Models
In the previous sections, we have looked at univariate, multivariate, and multi-step time series forecasting.
It is possible to mix and match the different types of 1D CNN models presented so far for the different problems. This too applies to time series forecasting problems that involve multivariate and multi-step forecasting, but it may be a little more challenging.
In this section, we will explore short examples of data preparation and modeling for multivariate multi-step time series forecasting as a template to ease this challenge, specifically:
Multiple Input Multi-Step Output.
Multiple Parallel Input and Multi-Step Output.
Perhaps the biggest stumbling block is in the preparation of data, so this is where we will focus our attention.
Multiple Input Multi-Step Output
There are those multivariate time series forecasting problems where the output series is separate but dependent upon the input time series, and multiple time steps are required for the output series.
For example, consider our multivariate time series from a prior section:
1
2
3
4
5
6
7
8
9
[[ 10 15 25]
[ 20 25 45]
[ 30 35 65]
[ 40 45 85]
[ 50 55 105]
[ 60 65 125]
[ 70 75 145]
[ 80 85 165]
[ 90 95 185]]
We may use three prior time steps of each of the two input time series to predict two time steps of the output time series.
Input:
1
2
3
10, 15
20, 25
30, 35
Output:
1
2
65
85
The split_sequences() function below implements this behavior.
Running the example first prints the shape of the prepared training data.
We can see that the shape of the input portion of the samples is three-dimensional, comprised of six samples, with three time steps and two variables for the two input time series.
The output portion of the samples is two-dimensional for the six samples and the two time steps for each sample to be predicted.
The prepared samples are then printed to confirm that the data was prepared as we specified.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(6, 3, 2) (6, 2)
[[10 15]
[20 25]
[30 35]] [65 85]
[[20 25]
[30 35]
[40 45]] [ 85 105]
[[30 35]
[40 45]
[50 55]] [105 125]
[[40 45]
[50 55]
[60 65]] [125 145]
[[50 55]
[60 65]
[70 75]] [145 165]
[[60 65]
[70 75]
[80 85]] [165 185]
We can now develop a 1D CNN model for multi-step predictions.
In this case, we will demonstrate a vector output model. The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# multivariate multi-step 1d cnn example
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
Running the example fits the model and predicts the next two time steps of the output sequence beyond the dataset.
We would expect the next two steps to be [185, 205].
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
It is a challenging framing of the problem with very little data, and the arbitrarily configured version of the model gets close.
1
[[185.57011 207.77893]]
Multiple Parallel Input and Multi-Step Output
A problem with parallel time series may require the prediction of multiple time steps of each time series.
For example, consider our multivariate time series from a prior section:
1
2
3
4
5
6
7
8
9
[[ 10 15 25]
[ 20 25 45]
[ 30 35 65]
[ 40 45 85]
[ 50 55 105]
[ 60 65 125]
[ 70 75 145]
[ 80 85 165]
[ 90 95 185]]
We may use the last three time steps from each of the three time series as input to the model, and predict the next time steps of each of the three time series as output.
The first sample in the training dataset would be the following.
Input:
1
2
3
10, 15, 25
20, 25, 45
30, 35, 65
Output:
1
2
40, 45, 85
50, 55, 105
The split_sequences() function below implements this behavior.
Running the example first prints the shape of the prepared training dataset.
We can see that both the input (X) and output (Y) elements of the dataset are three dimensional for the number of samples, time steps, and variables or parallel time series respectively.
The input and output elements of each series are then printed side by side so that we can confirm that the data was prepared as we expected.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
(5, 3, 3) (5, 2, 3)
[[10 15 25]
[20 25 45]
[30 35 65]] [[ 40 45 85]
[ 50 55 105]]
[[20 25 45]
[30 35 65]
[40 45 85]] [[ 50 55 105]
[ 60 65 125]]
[[ 30 35 65]
[ 40 45 85]
[ 50 55 105]] [[ 60 65 125]
[ 70 75 145]]
[[ 40 45 85]
[ 50 55 105]
[ 60 65 125]] [[ 70 75 145]
[ 80 85 165]]
[[ 50 55 105]
[ 60 65 125]
[ 70 75 145]] [[ 80 85 165]
[ 90 95 185]]
We can now develop a 1D CNN model for this dataset.
We will use a vector-output model in this case. As such, we must flatten the three-dimensional structure of the output portion of each sample in order to train the model. This means, instead of predicting two steps for each series, the model is trained on and expected to predict a vector of six numbers directly.
1
2
3
# flatten output
n_output=y.shape[1]*y.shape[2]
y=y.reshape((y.shape[0],n_output))
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# multivariate output multi-step 1d cnn example
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
Running the example fits the model and predicts the values for each of the three time steps for the next two time steps beyond the end of the dataset.
We would expect the values for these series and time steps to be as follows:
1
2
90, 95, 185
100, 105, 205
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that the model forecast gets reasonably close to the expected values.
I got a non related question. Recently I have been developed almost exclusively in javascript (both front react and backend with node js). It has been long time i have done asny solid coding in python, hence my skillset is rusty.
Now, I wonder, how do you see the applying of programming languages for ML apps.
Tensorflow is running now both inn a browser tf.js as well on the backend with node js (just like python?). That sounds like a great thing – one language for everything. There are also courses on the topic, getting more traction https://www.udemy.com/machine-learning-with-javascript/
Is javascript enough for machine learning apps? or python should be used? Can you please elaborate?
I cannot imagine being able to convince my team that a JS solution would make more sense, unless the existing system was all JS or it as a front-end demo or something. Or maybe if the model was fit using something fast and used to make predictions in JS.
Really, you want to use the same tech stack as the rest of the existing system/enterprise.
Nice site. Just a comment. IMO, It’s a bit pretentious and weak to put the title PhD after your name (” I’m Jason Brownlee PhD…”). You don’t need to validate yourself through a useless degree. You have already earned the respect of all of us through your wonderful work. A mention of your credentials at a bio page would have sufficed. Just my two cents.
My wife has an MS in Robotics Engineering and is a Registered Professional Engineer. I have a PhD in physics from UT. I Know how hard we both worked for our credentials and I certainly would not call them useless. You earned your credentials BRAVO.
I think the best way is to test out both. It is hard to tell which works on what scenarios. But you can think in this way: CNN is memoryless and look at a window at once, but LSTM is stateful with cell state and hidden state built up as you feed in the data. Which one sounds more reasonable for your data? That might be the choice you want to explore first.
Hi Jason
Your books and posts have been very helpful in igniting my interest in machine learning. I just started learning deep learning and would like to know your approach on generating rain forecast maps given a data set with images (in gif format) of historical precipitation maps. Seeing as the sequence of past observations are images and not numbers like the examples above how would one prepare the image data.(I’m very new to deep learning)
Your site is pure gold and It is becoming my reference! You are making difference, thanks for educating for us. I became a ML engineer now because your hardwork, thanks again!
In addition, what’s your opinion on using filters in “descending order”,
I mean Input ->Conv1d(40 filters)->Dropout->Conv1d(20 filters)->Dropout->Conv1d(3 filters).
I’ve got a question regarding the input dimension while fitting the model, which in case of Conv1D is [samples, timesteps, features]. Now comparing this with the following article using MLP: https://machinelearningmastery.com/how-to-develop-multilayer-perceptron-models-for-time-series-forecasting/ the dimension becomes [samples, features]. What is the reason for this difference although both models should handel “one dimensional” input?
After some tests, I believe that I can’t predict the next N sequences since the output y is always dependent on the input x (unless I misunderstood the all concept). If so, what is your advice to predict the next N sequences?
Thanks a lot Dr. Jason. May Allah bless you , we are excited to watch CNN after implementing it to Shampoo Sales Dataset… Do you have any idea to do this.
I have a question though: could you tell me what the data structure of
X1 = X[:, :, 0].reshape(X.shape[0], X.shape[1], n_features)
X2 = X[:, :, 1].reshape(X.shape[0], X.shape[1], n_features)
in the second example of the multiple input series looks like? As an exercise I’m recreating the code using tensorflow.js and while the code is mostly easy to translate, the data structures in python – a language I’m not really familiar with in detail – often get confusing.
Most of the time you have shown a plain example of the input data, but not in this case. So it’s kind of hard for me to understand how you split the data in detail and what you feed into the two visible parts of the network.
Hello Jason,
Thank you for your wonderful tutorials. I have a question (sorry if it looks stupid as I am a beginner), if we have 2 outputs from our NN, is it possible to customize the link of certain nodes from last hidden layer to certain output nodes? e.g. if we have two output nodes and 4 nodes in last hidden layer, is it possible that we link 2 nodes from last hidden layer to a specific node in output layer and other 2 nodes in last hidden layer to the other node in the output layer. If yes, can you refer me to relevant literature? I have drawn a rough sketch here. https://imgur.com/a/w8YnRwq
Thank you very much for your response. Can you please elaborate it a little more? Do you mean by setting certain weights which affect these particular ‘connections’ as zero? and why did you say ‘after training’?
ValueError: Negative dimension size caused by subtracting 3 from 2 for ‘conv2d_25/convolution’ (op: ‘Conv2D’) with input shapes: [?,200,2,48], [3,3,48,13].
With 7 steps in and 40 steps out I get a good MAPE of about 4%.
Even though its a good error rate, my intuition is telling me that using values in the last 7 weeks to predict values for 40 weeks in the future might not be very believable by the end user of the prediction (forecast). What I mean is that the CNN is trained on patterns in those 7 weeks and then is able to predict the pattern 40 weeks in future?
I may be misinterpreting the whole definitions of the time steps in and out so any clarification from you will be greatly appreciated!
I also tried 40 steps in and 40 steps out which yields a MAPE of about 10-12%.
I think a possible reason is my time series has an upward trend with seasonal spikes every 52 weeks and so when the CNN is training it gets “confused” by the spikes which makes the rest of predictions have a higher error rate. Is there any tricks in CNNs to combat that?
Perhaps try scaling the data prior to modeling, or even removing trends prior to modeling, then inverse the transforms before calculating error and compare results.
We cannot know what the right amount of input history will be for your problem, you must discover the right amount via experimentation with a robust test harness.
Hello! I ‘ve been fighting the problem of utilizing the Conv1D for several hours now, and for the life of me, I can’t get it to work no matter what I do. Following your ‘Multivariate CNN’ code, I have a dataset of a pandas data frame of dimension (9666,10) [9 features and the 10th column my y), which I convert to numpy array before I run any further operations, and then use the split_sequences function with n_steps = 3, which gives me X of dimension (9664, 3, 9) and y of (9664,). When I run it gives me the “ValueError: Error when checking target: expected conv1d_25 to have 3 dimensions, but got array with shape (9664, 1)”.
Could you please help me out? I cannot believe it won’t work after so much effort
I was only using the very first 1DConv layer just to check if the input was correct. When I added a Flatten() and then a Dense(1) as the output layer, it worked! I did not know that using only the 1D layer would result in such a strange dimensionality error.
Another question, now that I got it to work: When I use “adam” as the optimizer it works fine, but when I switch it to ‘sgd’ it gives me ‘nan’ as the loss, starting from the very first Epoch, with the above data. What could that be?
If I have a structured data set, such as Titanic data set, is it possible to use 1D convolutional NN to train this dataset? I think it is possible, but I don’t know if it is more feasible and better performance.
oringinal X.shape = (sample, no_features)
reshape X to X.shape = (sample, no_feature, 1)
then use several 1D cnn layers to reduce the size of no_feature, finally use one or two dense layer to do classification.
I learned that if the collected data can be transfer into the 2D image data or 2D matrices, we can train them using the pre-trained models. Especially. when we only have a small dataset.
However, in this paper, their transformation is hard to understand. I can’t figure out what the model learned? What are your opinions?
Having over thousands of time-series data ( .CSV) will be used for training, for example, intra-day stock prices, I am asked to solve a problem which is to predict if a stock will rise or drop. I have no idea how to start with, says, using RNN or CNN, LSTM? or just simple classifier. Besides, I think I will use the first hour data to predict the trend.
0001.CSV: [D1,D2……, D60] (input), [Min,Max] (Output)(should I say it “y”?)
0002.CSV: [D1,D2……, D60] (input), [Min,Max] (Output)
……
3680.CSV: [D1,D2……, D60] (input), [Min,Max] (Output)
which models above is appropriate to do that? Thanks a lot
I’m confused with the two examples of the Multivariate Multi-Step CNN Models.
You said that the model “predicts the next two time-steps of the output sequence beyond the dataset”.
In the ‘Multiple Input Multi-Step Output’ : “..We would expect the next two steps to be [185, 205]” and in the ‘Multiple Parallel Input and Multi-Step Output’: ‘We would expect the values for these series and time steps to be as follows:[ 90, 95, 185 ] , [ 100, 105, 205].
My question:
In both examples the first expected output value -185 (first example) and [90,95,185] (second example) are part of the dataset (not beyond) and were in the training set, so why we need to ‘predict’ them when the model has seen them?
isn’t it only one time-step prediction of the third feature (the out-seq)?
Pardon my ignorance, but in the Multivariate CNN Models, I am struggling to understand why the model ignores the prior results of the previous time steps. Is it because CNN is borrowed from an image recognition frame work that we cannot do something like ( I am assuming here that the 2 first columns are independent variables, and the third the dependent one, and each line is 3 time steps.
Input
[ 10 15 25 ]
[ 20 25 45 ]
[ 30 35 ? ] ( not sure what encoding the missing values should take here)
Thanks for your time: Your example in the section “Multivariate CNN Models”
, shows the structure of 1 data point as :
“If we chose three input time steps, then the first sample would look as follows:”
Input:
1 10, 15
2 10, 15
3 30, 35
Output:
1 65
It seems to me that there is as much to learn, given that the third column is a linear combination of the first 2, from the item 1,2 as there is from the item 3 for that sample. As in the output are all linear combination of columns 1 and 2. But the model dismisses using all the data available ( value 25 for item 1 and value 45 for item 2
) in the model. I thought that letting the network study the linear relationship not only at item 3 but also at item 1 and 2 would improve the results. So I was asking why not using that data structure instead:
Input
10 15 25
20 25 45
30 35 ?
Output
65
instead of just
1 10, 15
2 10, 15
3 30, 35
Output:
1 65
that’s because 10+15 adds no value to getting to know the relationship 30+35=65
while knowing that 10+15=25 at item 1, might help understanding the relationship 30+35=65 for that sample? (I was thinking here in a more general time series case than in this particular example. where for example the residual of 10+15 vs 25 might mean something to the residual of 30+35 vs 65)
would it be possible to make the model able to take any input size if you make it fully convolutional, by exchanging the dense layers by a 1×1 convolution?
Then it would not be necessary to fix the input_shape which would make the model be able to do a multi step prediction of a fixed length independent from the input length.
Am I correct with this assumption? If yes why is this never addressed in your tutorials?
hi,jason.thank you for your tutorial. I want to ask you the question that how can we visualize the data after being processing by the pooling layer and a dense layer, and the shape of the processed data.
Hi Jason,
Good post (as always)!
I got a non related question. Recently I have been developed almost exclusively in javascript (both front react and backend with node js). It has been long time i have done asny solid coding in python, hence my skillset is rusty.
Now, I wonder, how do you see the applying of programming languages for ML apps.
Tensorflow is running now both inn a browser tf.js as well on the backend with node js (just like python?). That sounds like a great thing – one language for everything. There are also courses on the topic, getting more traction
https://www.udemy.com/machine-learning-with-javascript/
Is javascript enough for machine learning apps? or python should be used? Can you please elaborate?
thanks and regards
JSman
Hmmm, maybe for small apps.
I cannot imagine being able to convince my team that a JS solution would make more sense, unless the existing system was all JS or it as a front-end demo or something. Or maybe if the model was fit using something fast and used to make predictions in JS.
Really, you want to use the same tech stack as the rest of the existing system/enterprise.
Dear @Dr.Jason Brownlee,
thank you for sharing your very useful information and codes.
similar to the @JSman, i have done my work on a different platform(i mean Matlab) instead of Python language.
this is my time series prediction code that uses CNN, LSTM, and MLP Net.
please visit my code from my Mathworks account from the link below:
https://www.mathworks.com/matlabcentral/fileexchange/69506-time-series-prediction
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/can-you-read-review-or-debug-my-code/
Hi Jason,
A very high quality article for me to learn more about deep learning. It really help me a lots.Please keep sharing the knowledge. Thank you!
Cheer
Thanks, I’m glad to hear that.
Thank you so much for such an informative article, I have learnt a lot.
You’re welcome.
Nice site. Just a comment. IMO, It’s a bit pretentious and weak to put the title PhD after your name (” I’m Jason Brownlee PhD…”). You don’t need to validate yourself through a useless degree. You have already earned the respect of all of us through your wonderful work. A mention of your credentials at a bio page would have sufficed. Just my two cents.
Thanks for the feedback.
Testing showed me that “phd” splashed around helps with creditability for first time visitors.
Dr. Brownlee,
My wife has an MS in Robotics Engineering and is a Registered Professional Engineer. I have a PhD in physics from UT. I Know how hard we both worked for our credentials and I certainly would not call them useless. You earned your credentials BRAVO.
Armando
Agreed. Completing degree a degree not useless, although it may not be required to be a practitioner in a given field (e.g. applied machine learning).
How to increase the number of prediction???? Where in code plz tell
What do you mean by the number of prediction, do you mean time steps?
If so, you can start with one of the multi-step forecasting examples and adapt it for your needs.
Thanks Jason for your new clear, detailed and very well explained explanation (as always)!.
I’m glad it helped.
Hi Thanks for this wonderful article.
Please help me to understand when we can use LSTMs and CNNs for Time series forecasting?
I think the best way is to test out both. It is hard to tell which works on what scenarios. But you can think in this way: CNN is memoryless and look at a window at once, but LSTM is stateful with cell state and hidden state built up as you feed in the data. Which one sounds more reasonable for your data? That might be the choice you want to explore first.
I index an image by a low-level feature (color) as form of a digital vector can i can exploit the current topic for an image clasifier
Maybe.
Thanks Jason for a very detailed explanation of CNN, and the many ways we can approach a time forecasting problem with CNNs.
I’m happy it helped.
Hi Jason,
I have become a fan, after reading this post of yours.
I have been trying to use 1D CNNs for one of my network anomaly applications, but somehow couldn’t get them to work effectively.
This post has all that I need to get my network up and running.
Thanks.
I’m happy to hear that!
Hi Jason
Your books and posts have been very helpful in igniting my interest in machine learning. I just started learning deep learning and would like to know your approach on generating rain forecast maps given a data set with images (in gif format) of historical precipitation maps. Seeing as the sequence of past observations are images and not numbers like the examples above how would one prepare the image data.(I’m very new to deep learning)
Perhaps you can use a CNN-LSTM or ConvLSTM to read in the images?
Jason! We can apply RNN-LSTM to the structured data too, what is the edge of using CNN for multivariate timeseries prediction?
No, RNNs are for sequence prediction:
https://machinelearningmastery.com/when-to-use-mlp-cnn-and-rnn-neural-networks/
Your site is pure gold and It is becoming my reference! You are making difference, thanks for educating for us. I became a ML engineer now because your hardwork, thanks again!
Thanks, I’m glad it helps.
Awesome Jason!
I would like to know your opinion on this :
CNN architecture : Input ->Conv1d->Dropout->Conv1d . (There is no Dense Layer, as you noticed!)
Purpose : Multistep Time series Forecasting. For example, 20 “past” input -> 3 “future” output, (continuous output and input).
Use the structure that gives the best performance.
I generally recommend a Dense layer as the output layer when making predictions so that you can specify the transform and structure of the output.
Thank you for your answer!
In addition, what’s your opinion on using filters in “descending order”,
I mean Input ->Conv1d(40 filters)->Dropout->Conv1d(20 filters)->Dropout->Conv1d(3 filters).
P.S. 40,20, 3 are just random numbers.
Seems odd.
Don’t seek my permission, use the model architecture that gives the best performance.
Thanks for providing all this.
I’ve got a question regarding the input dimension while fitting the model, which in case of Conv1D is [samples, timesteps, features]. Now comparing this with the following article using MLP: https://machinelearningmastery.com/how-to-develop-multilayer-perceptron-models-for-time-series-forecasting/ the dimension becomes [samples, features]. What is the reason for this difference although both models should handel “one dimensional” input?
The CNN must read across subsequences of the input, therefore a 3D input shape is required, much like LSTMs.
With subsequence you mean the timesteps of each given feature, right?
No, for all features.
Hi Jason,
Great article!
After some tests, I believe that I can’t predict the next N sequences since the output y is always dependent on the input x (unless I misunderstood the all concept). If so, what is your advice to predict the next N sequences?
I recommend testing multiple framings of your problem and multiple techniques in order to discover what works best for your specific dataset.
Thanks a lot Dr. Jason. May Allah bless you , we are excited to watch CNN after implementing it to Shampoo Sales Dataset… Do you have any idea to do this.
Yes, you can use the CNN on univariate data, although it will very likely be outperformed by a simple linear model.
Perhaps this post will help:
https://machinelearningmastery.com/how-to-grid-search-deep-learning-models-for-time-series-forecasting/
Hi Jason,
great article, thank you!
I have a question though: could you tell me what the data structure of
X1 = X[:, :, 0].reshape(X.shape[0], X.shape[1], n_features)
X2 = X[:, :, 1].reshape(X.shape[0], X.shape[1], n_features)
in the second example of the multiple input series looks like? As an exercise I’m recreating the code using tensorflow.js and while the code is mostly easy to translate, the data structures in python – a language I’m not really familiar with in detail – often get confusing.
Most of the time you have shown a plain example of the input data, but not in this case. So it’s kind of hard for me to understand how you split the data in detail and what you feed into the two visible parts of the network.
Thanks in advance!
Tom
Hi Tom, here we are extracting the first and second features as separate 3d arrays.
A good place to get started with numpy arrays is here:
https://machinelearningmastery.com/index-slice-reshape-numpy-arrays-machine-learning-python/
Hello Jason,
Thank you for your wonderful tutorials. I have a question (sorry if it looks stupid as I am a beginner), if we have 2 outputs from our NN, is it possible to customize the link of certain nodes from last hidden layer to certain output nodes? e.g. if we have two output nodes and 4 nodes in last hidden layer, is it possible that we link 2 nodes from last hidden layer to a specific node in output layer and other 2 nodes in last hidden layer to the other node in the output layer. If yes, can you refer me to relevant literature? I have drawn a rough sketch here. https://imgur.com/a/w8YnRwq
I’m sure you can, but I don’t have an example sorry.
Perhaps try setting the weights to zero after training?
Thank you very much for your response. Can you please elaborate it a little more? Do you mean by setting certain weights which affect these particular ‘connections’ as zero? and why did you say ‘after training’?
Yes, because I don’t think you can do it other ways (e.g. disable weights). Perhaps you can find a better approach.
if we have excel file with 40000 rows and two column than how i can transform to 2D or 3D array as you have taken just 5 number sequence?
I have a number of tutorials on this, perhaps start here:
https://machinelearningmastery.com/convert-time-series-supervised-learning-problem-python/
Then here:
https://machinelearningmastery.com/faq/single-faq/how-do-i-prepare-my-data-for-an-lstm
i got this error
ValueError: Negative dimension size caused by subtracting 3 from 2 for ‘conv2d_25/convolution’ (op: ‘Conv2D’) with input shapes: [?,200,2,48], [3,3,48,13].
Sorry to hear that, maybe one of these ideas will help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
Hi,
I’m trying to implement “Multi-Step CNN Model” on a time serie so i’m using a 1D convolutional network.
I use a time sequence of 7 weeks as the number of steps in and 40 weeks as the number of weeks to predict.
Is that a bad idea?
Should the number of steps in always be greater or equal to the number of outputs?
Thanks.
I recommend testing a range of diffrent approaches in order to discover what works best for your specific dataset.
Thank you for the very fast response!
With 7 steps in and 40 steps out I get a good MAPE of about 4%.
Even though its a good error rate, my intuition is telling me that using values in the last 7 weeks to predict values for 40 weeks in the future might not be very believable by the end user of the prediction (forecast). What I mean is that the CNN is trained on patterns in those 7 weeks and then is able to predict the pattern 40 weeks in future?
I may be misinterpreting the whole definitions of the time steps in and out so any clarification from you will be greatly appreciated!
I also tried 40 steps in and 40 steps out which yields a MAPE of about 10-12%.
I think a possible reason is my time series has an upward trend with seasonal spikes every 52 weeks and so when the CNN is training it gets “confused” by the spikes which makes the rest of predictions have a higher error rate. Is there any tricks in CNNs to combat that?
Thank you for taking the time to help me!
Perhaps try scaling the data prior to modeling, or even removing trends prior to modeling, then inverse the transforms before calculating error and compare results.
More on what time steps are here (for LSTMs, but applies directly to 1D CNNs):
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
We cannot know what the right amount of input history will be for your problem, you must discover the right amount via experimentation with a robust test harness.
Thank you.
Your web site is probably one of the best online for learning ML!
Thank you!
Hello! I ‘ve been fighting the problem of utilizing the Conv1D for several hours now, and for the life of me, I can’t get it to work no matter what I do. Following your ‘Multivariate CNN’ code, I have a dataset of a pandas data frame of dimension (9666,10) [9 features and the 10th column my y), which I convert to numpy array before I run any further operations, and then use the split_sequences function with n_steps = 3, which gives me X of dimension (9664, 3, 9) and y of (9664,). When I run it gives me the “ValueError: Error when checking target: expected conv1d_25 to have 3 dimensions, but got array with shape (9664, 1)”.
Could you please help me out? I cannot believe it won’t work after so much effort
That is odd, what type of output layer do you have?
It sounds like you might have a decoder output model attached?
Firstly, thanks a lot for prompt assistance!
I was only using the very first 1DConv layer just to check if the input was correct. When I added a Flatten() and then a Dense(1) as the output layer, it worked! I did not know that using only the 1D layer would result in such a strange dimensionality error.
Another question, now that I got it to work: When I use “adam” as the optimizer it works fine, but when I switch it to ‘sgd’ it gives me ‘nan’ as the loss, starting from the very first Epoch, with the above data. What could that be?
Could be exploding gradients:
https://machinelearningmastery.com/how-to-avoid-exploding-gradients-in-neural-networks-with-gradient-clipping/
Hi Jason,
Regarding Conv1D, is there a rule of thumb for figuring out the correct number for filters and kernels?
Thanks.
Not really, see this:
https://machinelearningmastery.com/faq/single-faq/how-many-layers-and-nodes-do-i-need-in-my-neural-network
A great article again. Thank you so much.
If I have a structured data set, such as Titanic data set, is it possible to use 1D convolutional NN to train this dataset? I think it is possible, but I don’t know if it is more feasible and better performance.
oringinal X.shape = (sample, no_features)
reshape X to X.shape = (sample, no_feature, 1)
then use several 1D cnn layers to reduce the size of no_feature, finally use one or two dense layer to do classification.
Your oppions are highly appreciated
No, it would only be appropriate for sequence input. E.g. data with spatial or temporal relationship across input features.
Thank you Jason!
Hi Jason,
I just read a paper about using CNN to tabular data. Please have a look.
https://arxiv.org/pdf/1903.06246v1.pdf
What did you learn from it?
I learned that if the collected data can be transfer into the 2D image data or 2D matrices, we can train them using the pre-trained models. Especially. when we only have a small dataset.
However, in this paper, their transformation is hard to understand. I can’t figure out what the model learned? What are your opinions?
Perhaps contact the author of the paper with your question about their method?
Dear Jason,
Having over thousands of time-series data ( .CSV) will be used for training, for example, intra-day stock prices, I am asked to solve a problem which is to predict if a stock will rise or drop. I have no idea how to start with, says, using RNN or CNN, LSTM? or just simple classifier. Besides, I think I will use the first hour data to predict the trend.
0001.CSV: [D1,D2……, D60] (input), [Min,Max] (Output)(should I say it “y”?)
0002.CSV: [D1,D2……, D60] (input), [Min,Max] (Output)
……
3680.CSV: [D1,D2……, D60] (input), [Min,Max] (Output)
which models above is appropriate to do that? Thanks a lot
Perhaps you can model it across time series as a binary classification problem?
I’d encourage you to explore multiple framings of the problem and test a suite of differnt models.
This might help as a start:
https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
Thank you very much
Excuse me, your web page will be apply to my thesis for my reference. Do you have a book for discussion like this learning?
Yes, I cover it in this book:
https://machinelearningmastery.com/deep-learning-for-time-series-forecasting/
Thank you very much for another great post.
I’m confused with the two examples of the Multivariate Multi-Step CNN Models.
You said that the model “predicts the next two time-steps of the output sequence beyond the dataset”.
In the ‘Multiple Input Multi-Step Output’ : “..We would expect the next two steps to be [185, 205]” and in the ‘Multiple Parallel Input and Multi-Step Output’: ‘We would expect the values for these series and time steps to be as follows:[ 90, 95, 185 ] , [ 100, 105, 205].
My question:
In both examples the first expected output value -185 (first example) and [90,95,185] (second example) are part of the dataset (not beyond) and were in the training set, so why we need to ‘predict’ them when the model has seen them?
isn’t it only one time-step prediction of the third feature (the out-seq)?
Hi Jason
Pardon my ignorance, but in the Multivariate CNN Models, I am struggling to understand why the model ignores the prior results of the previous time steps. Is it because CNN is borrowed from an image recognition frame work that we cannot do something like ( I am assuming here that the 2 first columns are independent variables, and the third the dependent one, and each line is 3 time steps.
Input
[ 10 15 25 ]
[ 20 25 45 ]
[ 30 35 ? ] ( not sure what encoding the missing values should take here)
Output
[65]
Thanks
I’m not sure I follow, sorry. Can you elaborate, which example are you referring to exactly?
Thanks for your time: Your example in the section “Multivariate CNN Models”
, shows the structure of 1 data point as :
“If we chose three input time steps, then the first sample would look as follows:”
Input:
1 10, 15
2 10, 15
3 30, 35
Output:
1 65
It seems to me that there is as much to learn, given that the third column is a linear combination of the first 2, from the item 1,2 as there is from the item 3 for that sample. As in the output are all linear combination of columns 1 and 2. But the model dismisses using all the data available ( value 25 for item 1 and value 45 for item 2
) in the model. I thought that letting the network study the linear relationship not only at item 3 but also at item 1 and 2 would improve the results. So I was asking why not using that data structure instead:
Input
10 15 25
20 25 45
30 35 ?
Output
65
instead of just
1 10, 15
2 10, 15
3 30, 35
Output:
1 65
that’s because 10+15 adds no value to getting to know the relationship 30+35=65
while knowing that 10+15=25 at item 1, might help understanding the relationship 30+35=65 for that sample? (I was thinking here in a more general time series case than in this particular example. where for example the residual of 10+15 vs 25 might mean something to the residual of 30+35 vs 65)
Thanks
Sure, you can use any framing of the prediction problem you wish.
The idea of this post is to give you many examples or different framings that you can use as a starting point for your own problem.
Hi Jason,
would it be possible to make the model able to take any input size if you make it fully convolutional, by exchanging the dense layers by a 1×1 convolution?
Then it would not be necessary to fix the input_shape which would make the model be able to do a multi step prediction of a fixed length independent from the input length.
Am I correct with this assumption? If yes why is this never addressed in your tutorials?
Perhaps, but not with Keras – it likes to nail down all shapes and sizes so it can optimize the graph.
hi,jason.thank you for your tutorial. I want to ask you the question that how can we visualize the data after being processing by the pooling layer and a dense layer, and the shape of the processed data.