Training a neural network can become unstable given the choice of error function, learning rate, or even the scale of the target variable.
Large updates to weights during training can cause a numerical overflow or underflow often referred to as “exploding gradients.”
The problem of exploding gradients is more common with recurrent neural networks, such as LSTMs given the accumulation of gradients unrolled over hundreds of input time steps.
A common and relatively easy solution to the exploding gradients problem is to change the derivative of the error before propagating it backward through the network and using it to update the weights. Two approaches include rescaling the gradients given a chosen vector norm and clipping gradient values that exceed a preferred range. Together, these methods are referred to as “gradient clipping.”
In this tutorial, you will discover the exploding gradient problem and how to improve neural network training stability using gradient clipping.
After completing this tutorial, you will know:
- Training neural networks can become unstable, leading to a numerical overflow or underflow referred to as exploding gradients.
- The training process can be made stable by changing the error gradients either by scaling the vector norm or clipping gradient values to a range.
- How to update an MLP model for a regression predictive modeling problem with exploding gradients to have a stable training process using gradient clipping methods.
Kick-start your project with my new book Better Deep Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to Avoid Exploding Gradients in Neural Networks With Gradient Clipping
Photo by Ian Livesey, some rights reserved.
Tutorial Overview
This tutorial is divided into six parts; they are:
- Exploding Gradients and Clipping
- Gradient Clipping in Keras
- Regression Predictive Modeling Problem
- Multilayer Perceptron With Exploding Gradients
- MLP With Gradient Norm Scaling
- MLP With Gradient Value Clipping
Exploding Gradients and Clipping
Neural networks are trained using the stochastic gradient descent optimization algorithm.
This requires first the estimation of the loss on one or more training examples, then the calculation of the derivative of the loss, which is propagated backward through the network in order to update the weights. Weights are updated using a fraction of the back propagated error controlled by the learning rate.
It is possible for the updates to the weights to be so large that the weights either overflow or underflow their numerical precision. In practice, the weights can take on the value of an “NaN” or “Inf” when they overflow or underflow and for practical purposes the network will be useless from that point forward, forever predicting NaN values as signals flow through the invalid weights.
The difficulty that arises is that when the parameter gradient is very large, a gradient descent parameter update could throw the parameters very far, into a region where the objective function is larger, undoing much of the work that had been done to reach the current solution.
— Page 413, Deep Learning, 2016.
The underflow or overflow of weights is generally refers to as an instability of the network training process and is known by the name “exploding gradients” as the unstable training process causes the network to fail to train in such a way that the model is essentially useless.
In a given neural network, such as a Convolutional Neural Network or Multilayer Perceptron, this can happen due to a poor choice of configuration. Some examples include:
- Poor choice of learning rate that results in large weight updates.
- Poor choice of data preparation, allowing large differences in the target variable.
- Poor choice of loss function, allowing the calculation of large error values.
Exploding gradients is also a problem in recurrent neural networks such as the Long Short-Term Memory network given the accumulation of error gradients in the unrolled recurrent structure.
Exploding gradients can be avoided in general by careful configuration of the network model, such as choice of small learning rate, scaled target variables, and a standard loss function. Nevertheless, exploding gradients may still be an issue with recurrent networks with a large number of input time steps.
One difficulty when training LSTM with the full gradient is that the derivatives sometimes become excessively large, leading to numerical problems. To prevent this, [we] clipped the derivative of the loss with respect to the network inputs to the LSTM layers (before the sigmoid and tanh functions are applied) to lie within a predefined range.
— Generating Sequences With Recurrent Neural Networks, 2013.
A common solution to exploding gradients is to change the error derivative before propagating it backward through the network and using it to update the weights. By rescaling the error derivative, the updates to the weights will also be rescaled, dramatically decreasing the likelihood of an overflow or underflow.
There are two main methods for updating the error derivative; they are:
- Gradient Scaling.
- Gradient Clipping.
Gradient scaling involves normalizing the error gradient vector such that vector norm (magnitude) equals a defined value, such as 1.0.
… one simple mechanism to deal with a sudden increase in the norm of the gradients is to rescale them whenever they go over a threshold
— On the difficulty of training Recurrent Neural Networks, 2013.
Gradient clipping involves forcing the gradient values (element-wise) to a specific minimum or maximum value if the gradient exceeded an expected range.
Together, these methods are often simply referred to as “gradient clipping.”
When the traditional gradient descent algorithm proposes to make a very large step, the gradient clipping heuristic intervenes to reduce the step size to be small enough that it is less likely to go outside the region where the gradient indicates the direction of approximately steepest descent.
— Page 289, Deep Learning, 2016.
It is a method that only addresses the numerical stability of training deep neural network models and does not offer any general improvement in performance.
The value for the gradient vector norm or preferred range can be configured by trial and error, by using common values used in the literature or by first observing common vector norms or ranges via experimentation and then choosing a sensible value.
In our experiments we have noticed that for a given task and model size, training is not very sensitive to this [gradient norm] hyperparameter and the algorithm behaves well even for rather small thresholds.
— On the difficulty of training Recurrent Neural Networks, 2013.
It is common to use the same gradient clipping configuration for all layers in the network. Nevertheless, there are examples where a larger range of error gradients are permitted in the output layer compared to hidden layers.
The output derivatives […] were clipped in the range [−100, 100], and the LSTM derivatives were clipped in the range [−10, 10]. Clipping the output gradients proved vital for numerical stability; even so, the networks sometimes had numerical problems late on in training, after they had started overfitting on the training data.
— Generating Sequences With Recurrent Neural Networks, 2013.
Want Better Results with Deep Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Gradient Clipping in Keras
Keras supports gradient clipping on each optimization algorithm, with the same scheme applied to all layers in the model
Gradient clipping can be used with an optimization algorithm, such as stochastic gradient descent, via including an additional argument when configuring the optimization algorithm.
Two types of gradient clipping can be used: gradient norm scaling and gradient value clipping.
Gradient Norm Scaling
Gradient norm scaling involves changing the derivatives of the loss function to have a given vector norm when the L2 vector norm (sum of the squared values) of the gradient vector exceeds a threshold value.
For example, we could specify a norm of 1.0, meaning that if the vector norm for a gradient exceeds 1.0, then the values in the vector will be rescaled so that the norm of the vector equals 1.0.
This can be used in Keras by specifying the “clipnorm” argument on the optimizer; for example:
|
1 2 3 |
.... # configure sgd with gradient norm clipping opt = SGD(lr=0.01, momentum=0.9, clipnorm=1.0) |
Gradient Value Clipping
Gradient value clipping involves clipping the derivatives of the loss function to have a given value if a gradient value is less than a negative threshold or more than the positive threshold.
For example, we could specify a norm of 0.5, meaning that if a gradient value was less than -0.5, it is set to -0.5 and if it is more than 0.5, then it will be set to 0.5.
This can be used in Keras by specifying the “clipvalue” argument on the optimizer, for example:
|
1 2 3 |
... # configure sgd with gradient value clipping opt = SGD(lr=0.01, momentum=0.9, clipvalue=0.5) |
Regression Predictive Modeling Problem
A regression predictive modeling problem involves predicting a real-valued quantity.
We can use a standard regression problem generator provided by the scikit-learn library in the make_regression() function. This function will generate examples from a simple regression problem with a given number of input variables, statistical noise, and other properties.
We will use this function to define a problem that has 20 input features; 10 of the features will be meaningful and 10 will not be relevant. A total of 1,000 examples will be randomly generated. The pseudorandom number generator will be fixed to ensure that we get the same 1,000 examples each time the code is run.
|
1 2 |
# generate regression dataset X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) |
Each input variable has a Gaussian distribution, as does the target variable.
We can create plots of the target variable showing both the distribution and spread. The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# regression predictive modeling problem from sklearn.datasets import make_regression from matplotlib import pyplot # generate regression dataset X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # histogram of target variable pyplot.subplot(121) pyplot.hist(y) # boxplot of target variable pyplot.subplot(122) pyplot.boxplot(y) pyplot.show() |
Running the example creates a figure with two plots showing a histogram and a box and whisker plot of the target variable.
The histogram shows the Gaussian distribution of the target variable. The box and whisker plot shows that the range of samples varies between about -400 to 400 with a mean of about 0.0.
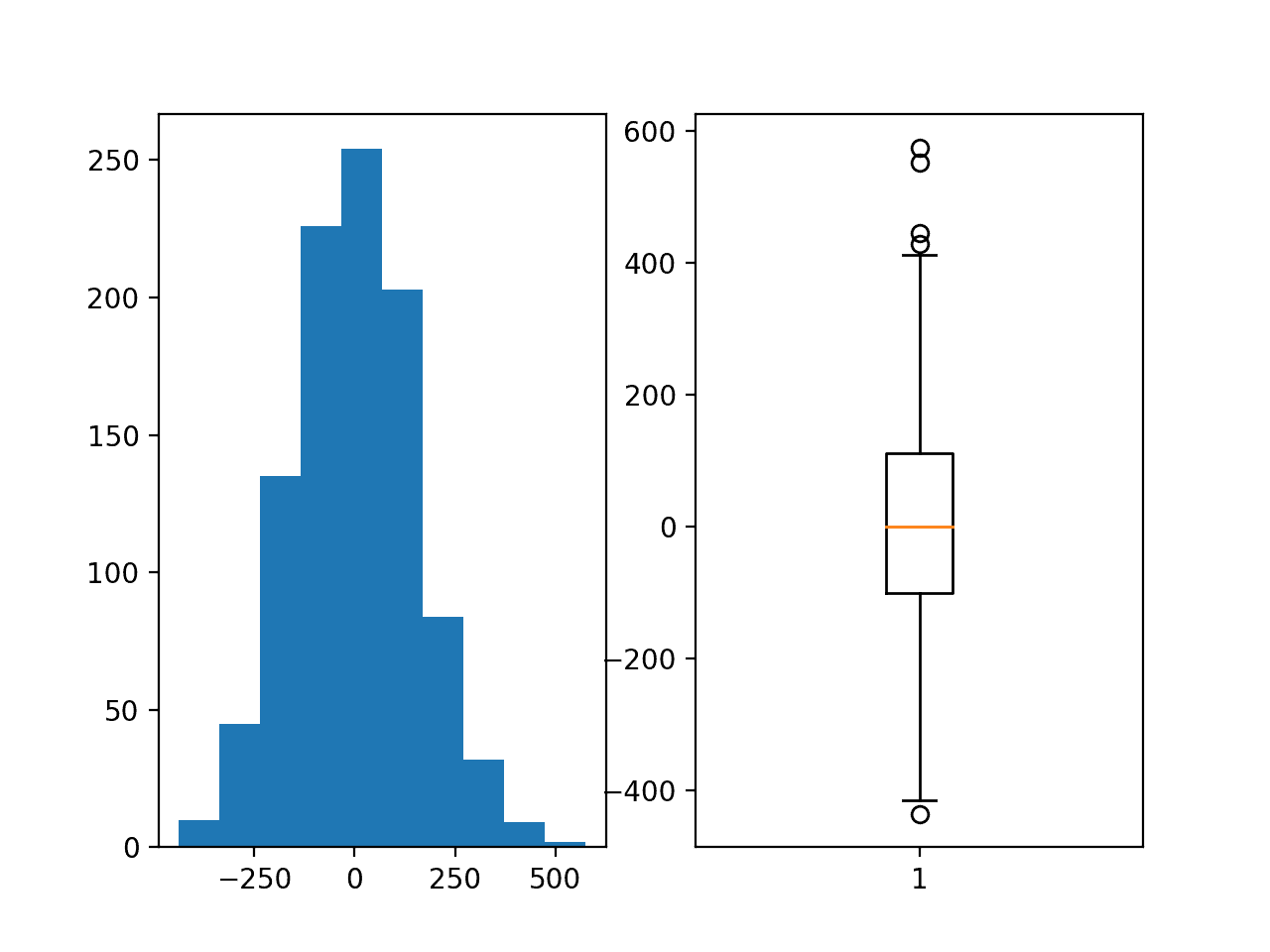
Histogram and Box and Whisker Plot of the Target Variable for the Regression Problem
Multilayer Perceptron With Exploding Gradients
We can develop a Multilayer Perceptron (MLP) model for the regression problem.
A model will be demonstrated on the raw data, without any scaling of the input or output variables. This is a good example to demonstrate exploding gradients as a model trained to predict the unscaled target variable will result in error gradients with values in the hundreds or even thousands, depending on the batch size used during training. Such large gradient values are likely to lead to unstable learning or an overflow of the weight values.
The first step is to split the data into train and test sets so that we can fit and evaluate a model. We will generate 1,000 examples from the domain and split the dataset in half, using 500 examples for train and test sets.
|
1 2 3 4 |
# split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] |
Next, we can define an MLP model.
The model will expect 20 inputs in the 20 input variables in the problem. A single hidden layer will be used with 25 nodes and a rectified linear activation function. The output layer has one node for the single target variable and a linear activation function to predict real values directly.
|
1 2 3 4 |
# define model model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) |
The mean squared error loss function will be used to optimize the model and the stochastic gradient descent optimization algorithm will be used with the sensible default configuration of a learning rate of 0.01 and a momentum of 0.9.
|
1 2 |
# compile model model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9)) |
The model will be fit for 100 training epochs and the test set will be used as a validation set, evaluated at the end of each training epoch.
The mean squared error is calculated on the train and test datasets at the end of training to get an idea of how well the model learned the problem.
|
1 2 3 |
# evaluate the model train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) |
Finally, learning curves of mean squared error on the train and test sets at the end of each training epoch are graphed using line plots, providing learning curves to get an idea of the dynamics of the model while learning the problem.
|
1 2 3 4 5 6 |
# plot loss during training pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
Tying these elements together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# mlp with unscaled data for the regression problem from sklearn.datasets import make_regression from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # generate regression dataset X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # define model model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) # compile model model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9)) # fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # evaluate the model train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_mse, test_mse)) # plot loss during training pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
Running the example fits the model and calculates the mean squared error on the train and test sets.
In this case, the model is unable to learn the problem, resulting in predictions of NaN values. The model weights exploded during training given the very large errors and in turn error gradients calculated for weight updates.
|
1 |
Train: nan, Test: nan |
This demonstrates that some intervention is required with regard to the target variable for the model to learn this problem.
A line plot of training history is created but does not show anything as the model almost immediately results in a NaN mean squared error.
A traditional solution would be to rescale the target variable using either standardization or normalization, and this approach is recommended for MLPs. Nevertheless, an alternative that we will investigate in this case will be the use of gradient clipping.
MLP With Gradient Norm Scaling
We can update the training of the model in the previous section to add gradient norm scaling.
This can be implemented by setting the “clipnorm” argument on the optimizer.
For example, the gradients can be rescaled to have a vector norm (magnitude or length) of 1.0, as follows:
|
1 2 3 |
# compile model opt = SGD(lr=0.01, momentum=0.9, clipnorm=1.0) model.compile(loss='mean_squared_error', optimizer=opt) |
The complete example with this change is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# mlp with unscaled data for the regression problem with gradient norm scaling from sklearn.datasets import make_regression from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # generate regression dataset X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # define model model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) # compile model opt = SGD(lr=0.01, momentum=0.9, clipnorm=1.0) model.compile(loss='mean_squared_error', optimizer=opt) # fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # evaluate the model train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_mse, test_mse)) # plot loss during training pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
Running the example fits the model and evaluates it on the train and test sets, printing the mean squared error.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that scaling the gradient with a vector norm of 1.0 has resulted in a stable model capable of learning the problem and converging on a solution.
|
1 |
Train: 5.082, Test: 27.433 |
A line plot is also created showing the means squared error loss on the train and test datasets over training epochs.
The plot shows how loss dropped from large values above 20,000 down to small values below 100 rapidly over 20 epochs.
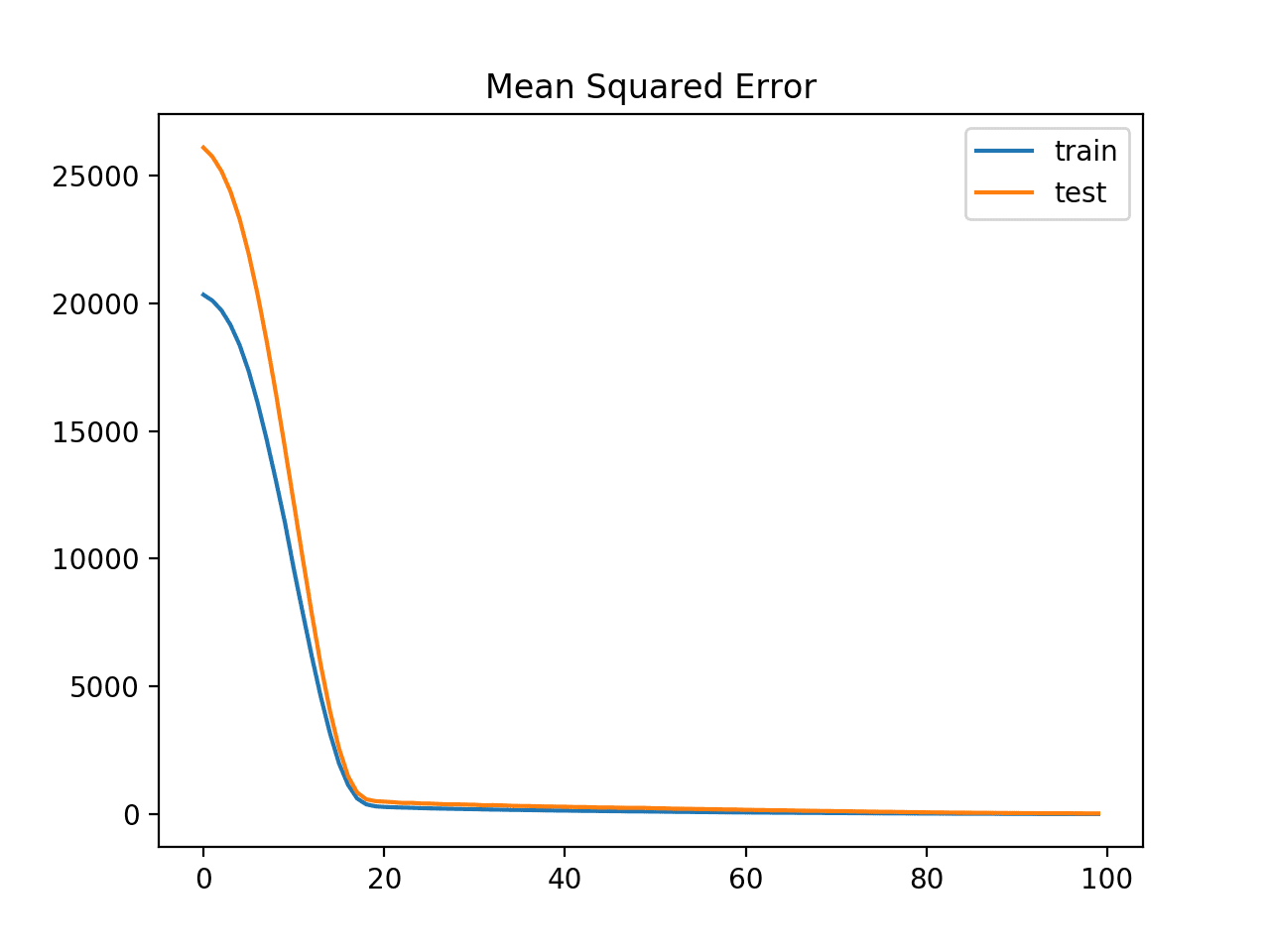
Line Plot of Mean Squared Error Loss for the Train (blue) and Test (orange) Datasets Over Training Epochs With Gradient Norm Scaling
There is nothing special about the vector norm value of 1.0, and other values could be evaluated and the performance of the resulting model compared.
MLP With Gradient Value Clipping
Another solution to the exploding gradient problem is to clip the gradient if it becomes too large or too small.
We can update the training of the MLP to use gradient clipping by adding the “clipvalue” argument to the optimization algorithm configuration. For example, the code below clips the gradient to the range [-5 to 5].
|
1 2 3 |
# compile model opt = SGD(lr=0.01, momentum=0.9, clipvalue=5.0) model.compile(loss='mean_squared_error', optimizer=opt) |
The complete example of training the MLP with gradient clipping is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# mlp with unscaled data for the regression problem with gradient clipping from sklearn.datasets import make_regression from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # generate regression dataset X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # define model model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) # compile model opt = SGD(lr=0.01, momentum=0.9, clipvalue=5.0) model.compile(loss='mean_squared_error', optimizer=opt) # fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # evaluate the model train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_mse, test_mse)) # plot loss during training pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
Running this example fits the model and evaluates it on the train and test sets, printing the mean squared error.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that in this case, the model is able to learn the problem without exploding gradients achieving an MSE of below 10 on both the train and test sets.
|
1 |
Train: 9.487, Test: 9.985 |
A line plot is also created showing the means squared error loss on the train and test datasets over training epochs.
The plot shows that the model learns the problem fast, achieving a sub-100 MSE loss within just a few training epochs.
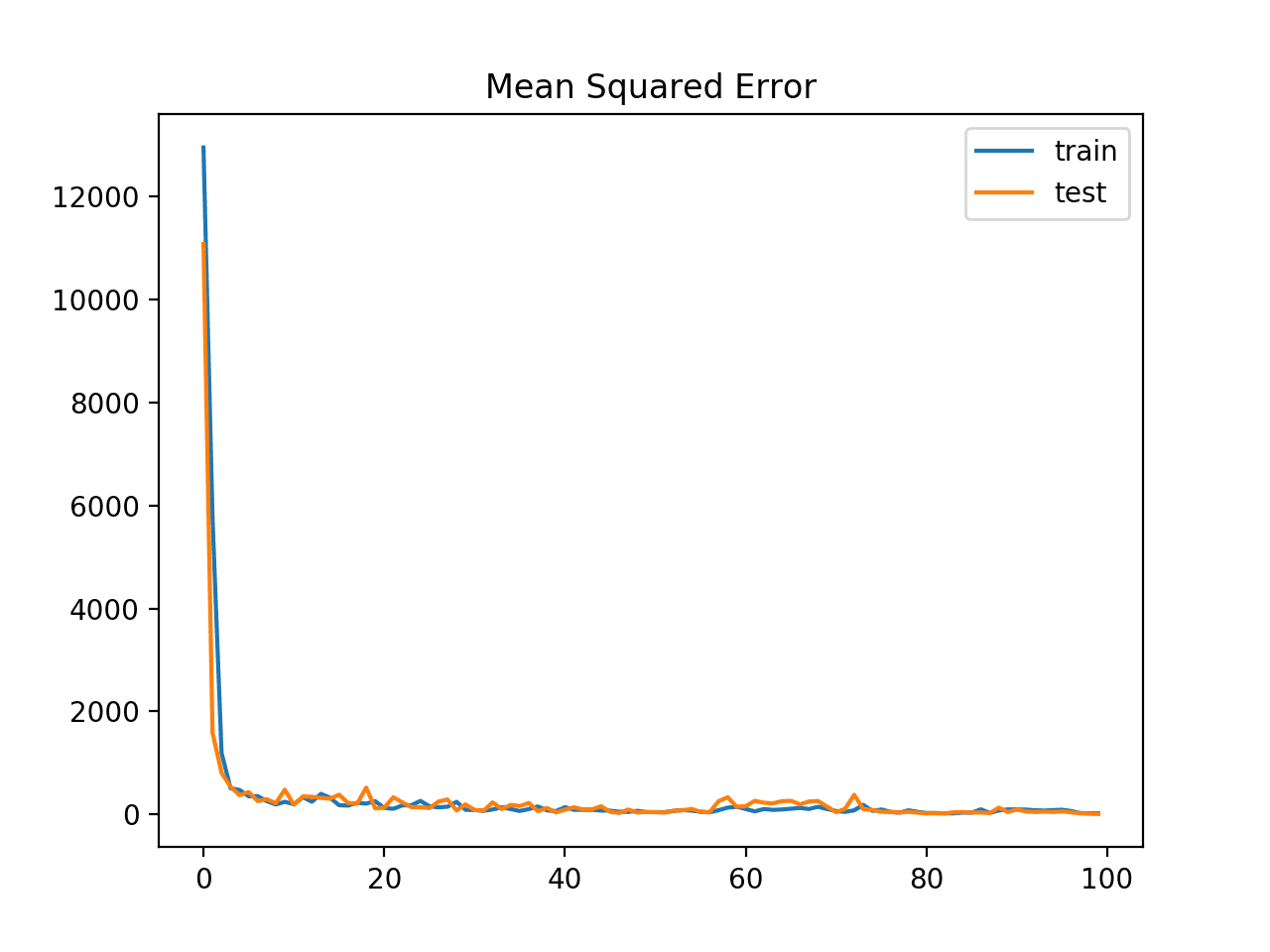
Line Plot of Mean Squared Error Loss for the Train (blue) and Test (orange) Datasets Over Training Epochs With Gradient Value Clipping
A clipped range of [-5, 5] was chosen arbitrarily; you can experiment with different sized ranges and compare performance of the speed of learning and final model performance.
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Vector Norm Values. Update the example to evaluate different gradient vector norm values and compare performance.
- Vector Clip Values. Update the example to evaluate different gradient value ranges and compare performance.
- Vector Norm and Clip. Update the example to use a combination of vector norm scaling and vector value clipping on the same training run and compare performance.
If you explore any of these extensions, I’d love to know.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Posts
Books
- Section 8.2.4 Cliffs and Exploding Gradients, Deep Learning, 2016.
- Section 10.11.1 Clipping Gradients, Deep Learning, 2016.
Papers
- On the difficulty of training Recurrent Neural Networks, 2013.
- Generating Sequences With Recurrent Neural Networks, 2013.
API
Summary
In this tutorial, you discovered the exploding gradient problem and how to improve neural network training stability using gradient clipping.
Specifically, you learned:
- Training neural networks can become unstable, leading to a numerical overflow or underflow referred to as exploding gradients.
- The training process can be made stable by changing the error gradients, either by scaling the vector norm or clipping gradient values to a range.
- How to update an MLP model for a regression predictive modeling problem with exploding gradients to have a stable training process using gradient clipping methods.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.







Very huge information available in this post.
Thanks.
This man is a true genius. I admire him and his work, contributions.
Thanks Lee. I’m glad the tutorials help.
I’m just a simple human.
Thank you for the interesting tutorial! I have two questions and will be grateful for your response:
1. Does scaling the input mean gradient scaling or clipping is not required?
2. You showed through an example that using non-scaled input can result into nan values, and applied gradient clipping to resolve the issue. Is there any other sign(s) that shows gradient clipping/scaling are required for the designed network?
You’re welcome.
It depends on your data and your model as to whether gradient scaling and clipping is required.
Yes, try it and if the results are better, keep it. Or inspect gradients during training to see if they are very large.
Hi Jason
Thank you for the tutorials! They’re really helpful.
I was wondering if there is a relation between MSE and exploding gradients. I’m trying to create a neural network, which works for small inputs/small layers but as soon as the size crosses a small threshold, the loss goes straight to NaN. I was wondering if this is normal or if something’s wrong with the network (it uses Dense, ReLU and sigmoid layers, with an MSE, and vanilla gradient descent implemented)
Thanks
Yes and no, but exploding gradients can happen with cross entropy just as easily.
jason this was an incredible post. Congratulation any many thanks. I have I question please. I built a model and I use the recurrent recoluraziton like this,
model.add(LSTM(64, return_sequences=True, recurrent_regularizer=l2(0.0015), input_shape=(timesteps, input_dim)))
model.add(Dropout(0.5))
model.add(LSTM(64, recurrent_regularizer=l2(0.0015), input_shape=(timesteps, input_dim))),
is the same as the Gradient Scaling that you talk above?
Thanks.
No, the “recurrent_regularizer” is weight decay:
https://machinelearningmastery.com/how-to-reduce-overfitting-in-deep-learning-with-weight-regularization/
Hi,
I am training a semantic segmentation CNN model for binary task with extremely imbalanced dataset. I am attempting to use the dice loss for my model but my gradients are exploding and the decoder loss is in the range of ~5000. I already applied gradient normalization but the least the loss values goes to is ~3000 something. Any suggestions on how to stabilize the training? Any help in this regard will be highly appreciated. Thanks
Perhaps ensure you are also scaling input data.
Perhaps also add some weight regularization to keep weight small.
hi jason ,
when loss value is high….Is there relationship between loss value and exploding gradient…
2) loss value is negative, what is the meaning..
Yes, this can happen.
Negative loss is odd / should not happen.
hi jason,
lstm can read the EEG signals without using feature extraction.
Generally, yes you can pass sequences of time series to an LSTM.
It is still a good idea to scale input data and perhaps make it stationary.
thank you
You’re welcome.
Hi Jason, I appreciate your posts. A comment on this one: To my understanding, the main issue with exploding gradients is you can have small regions in your space where the gradient is much larger than nearby areas, meaning that the first order Taylor approximation is only valid in a small local region. If your gradient descent algorithm enters one of these high gradient regions, then it ends up taking a large step, which overshoots local minima and doesn’t actually improve the loss function (often doing the opposite) since it moves way outside the area where the local gradient approximation was valid. This doesn’t need to involve any overflow or underflow and would also happen on a hypothetical computer with perfect precision. Please correct me if I’m mistaken!
Maybe. The tutorial is more focused on addressing exploding gradients as a failure case, rather than guessing at their cause.
Underflow is used incorrectly here. Underflow happens when numbers get too small to be represented (not minus infinity). See wikipedia.
Thank you for the feedback Mark!