Navigation

How to Develop Multilayer Perceptron Models for Time Series Forecasting

By on August 28, 2020 in Deep Learning for Time Series 133

Multilayer Perceptrons, or MLPs for short, can be applied to time series forecasting.

A challenge with using MLPs for time series forecasting is in the preparation of the data. Specifically, lag observations must be flattened into feature vectors.

In this tutorial, you will discover how to develop a suite of MLP models for a range of standard time series forecasting problems.

The objective of this tutorial is to provide standalone examples of each model on each type of time series problem as a template that you can copy and adapt for your specific time series forecasting problem.

In this tutorial, you will discover how to develop a suite of Multilayer Perceptron models for a range of standard time series forecasting problems.

After completing this tutorial, you will know:

  • How to develop MLP models for univariate time series forecasting.
  • How to develop MLP models for multivariate time series forecasting.
  • How to develop MLP models for multi-step time series forecasting.

Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

How to Develop Multilayer Perceptron Models for Time Series Forecasting

How to Develop Multilayer Perceptron Models for Time Series Forecasting
Photo by Bureau of Land Management, some rights reserved.

Tutorial Overview

This tutorial is divided into four parts; they are:

  1. Univariate MLP Models
  2. Multivariate MLP Models
  3. Multi-Step MLP Models
  4. Multivariate Multi-Step MLP Models

Univariate MLP Models

Multilayer Perceptrons, or MLPs for short, can be used to model univariate time series forecasting problems.

Univariate time series are a dataset comprised of a single series of observations with a temporal ordering and a model is required to learn from the series of past observations to predict the next value in the sequence.

This section is divided into two parts; they are:

  1. Data Preparation
  2. MLP Model

Data Preparation

Before a univariate series can be modeled, it must be prepared.

The MLP model will learn a function that maps a sequence of past observations as input to an output observation. As such, the sequence of observations must be transformed into multiple examples from which the model can learn.

Consider a given univariate sequence:

We can divide the sequence into multiple input/output patterns called samples, where three time steps are used as input and one time step is used as output for the one-step prediction that is being learned.

The split_sequence() function below implements this behavior and will split a given univariate sequence into multiple samples where each sample has a specified number of time steps and the output is a single time step.

We can demonstrate this function on our small contrived dataset above.

The complete example is listed below.

Running the example splits the univariate series into six samples where each sample has three input time steps and one output time step.

Now that we know how to prepare a univariate series for modeling, let’s look at developing an MLP model that can learn the mapping of inputs to outputs.

Need help with Deep Learning for Time Series?

Take my free 7-day email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

MLP Model

A simple MLP model has a single hidden layer of nodes, and an output layer used to make a prediction.

We can define an MLP for univariate time series forecasting as follows.

Important in the definition is the shape of the input; that is what the model expects as input for each sample in terms of the number of time steps.

The number of time steps as input is the number we chose when preparing our dataset as an argument to the split_sequence() function.

The input dimension for each sample is specified in the input_dim argument on the definition of first hidden layer. Technically, the model will view each time step as a separate feature instead of separate time steps.

We almost always have multiple samples, therefore, the model will expect the input component of training data to have the dimensions or shape:

Our split_sequence() function in the previous section outputs the X with the shape [samples, features] ready to use for modeling.

The model is fit using the efficient Adam version of stochastic gradient descent and optimized using the mean squared error, or ‘mse‘, loss function.

Once the model is defined, we can fit it on the training dataset.

After the model is fit, we can use it to make a prediction.

We can predict the next value in the sequence by providing the input:

And expecting the model to predict something like:

The model expects the input shape to be two-dimensional with [samples, features], therefore, we must reshape the single input sample before making the prediction, e.g with the shape [1, 3] for 1 sample and 3 time steps used as input features.

We can tie all of this together and demonstrate how to develop an MLP for univariate time series forecasting and make a single prediction.

Running the example prepares the data, fits the model, and makes a prediction.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the model predicts the next value in the sequence.

Multivariate MLP Models

Multivariate time series data means data where there is more than one observation for each time step.

There are two main models that we may require with multivariate time series data; they are:

  1. Multiple Input Series.
  2. Multiple Parallel Series.

Let’s take a look at each in turn.

Multiple Input Series

A problem may have two or more parallel input time series and an output time series that is dependent on the input time series.

The input time series are parallel because each series has an observation at the same time step.

We can demonstrate this with a simple example of two parallel input time series where the output series is the simple addition of the input series.

We can reshape these three arrays of data as a single dataset where each row is a time step and each column is a separate time series. This is a standard way of storing parallel time series in a CSV file.

The complete example is listed below.

Running the example prints the dataset with one row per time step and one column for each of the two input and one output parallel time series.

As with the univariate time series, we must structure these data into samples with input and output samples.

We need to split the data into samples maintaining the order of observations across the two input sequences.

If we chose three input time steps, then the first sample would look as follows:

Input:

Output:

That is, the first three time steps of each parallel series are provided as input to the model and the model associates this with the value in the output series at the third time step, in this case 65.

We can see that, in transforming the time series into input/output samples to train the model, that we will have to discard some values from the output time series where we do not have values in the input time series at prior time steps. In turn, the choice of the size of the number of input time steps will have an important effect on how much of the training data is used.

We can define a function named split_sequences() that will take a dataset as we have defined it with rows for time steps and columns for parallel series and return input/output samples.

We can test this function on our dataset using three time steps for each input time series as input.

The complete example is listed below.

Running the example first prints the shape of the X and y components.

We can see that the X component has a three-dimensional structure.

The first dimension is the number of samples, in this case 7. The second dimension is the number of time steps per sample, in this case 3, the value specified to the function. Finally, the last dimension specifies the number of parallel time series or the number of variables, in this case 2 for the two parallel series.

We can then see that the input and output for each sample is printed, showing the three time steps for each of the two input series and the associated output for each sample.

Before we can fit an MLP on this data, we must flatten the shape of the input samples.

MLPs require that the shape of the input portion of each sample is a vector. With a multivariate input, we will have multiple vectors, one for each time step.

We can flatten the temporal structure of each input sample, so that:

Becomes:

First, we can calculate the length of each input vector as the number of time steps multiplied by the number of features or time series. We can then use this vector size to reshape the input.

We can now define an MLP model for the multivariate input where the vector length is used for the input dimension argument.

When making a prediction, the model expects three time steps for two input time series.

We can predict the next value in the output series proving the input values of:

The shape of the 1 sample with 3 time steps and 2 variables would be [1, 3, 2]. We must again reshape this to be 1 sample with a vector of 6 elements or [1, 6]

We would expect the next value in the sequence to be 100 + 105 or 205.

The complete example is listed below.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

Running the example prepares the data, fits the model, and makes a prediction.

There is another more elaborate way to model the problem.

Each input series can be handled by a separate MLP and the output of each of these submodels can be combined before a prediction is made for the output sequence.

We can refer to this as a multi-headed input MLP model. It may offer more flexibility or better performance depending on the specifics of the problem that are being modeled.

This type of model can be defined in Keras using the Keras functional API.

First, we can define the first input model as an MLP with an input layer that expects vectors with n_steps features.

We can define the second input submodel in the same way.

Now that both input submodels have been defined, we can merge the output from each model into one long vector, which can be interpreted before making a prediction for the output sequence.

We can then tie the inputs and outputs together.

The image below provides a schematic for how this model looks, including the shape of the inputs and outputs of each layer.

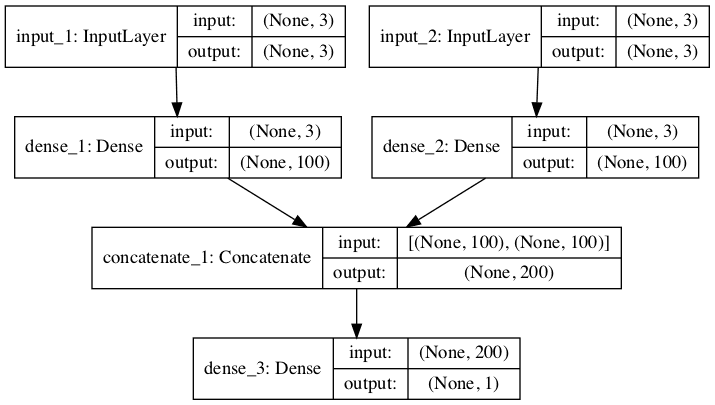
Plot of Multi-Headed MLP for Multivariate Time Series Forecasting

Plot of Multi-Headed MLP for Multivariate Time Series Forecasting

This model requires input to be provided as a list of two elements, where each element in the list contains data for one of the submodels.

In order to achieve this, we can split the 3D input data into two separate arrays of input data: that is from one array with the shape [7, 3, 2] to two 2D arrays with the shape [7, 3]

These data can then be provided in order to fit the model.

Similarly, we must prepare the data for a single sample as two separate two-dimensional arrays when making a single one-step prediction.

We can tie all of this together; the complete example is listed below.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

Running the example prepares the data, fits the model, and makes a prediction.

Multiple Parallel Series

An alternate time series problem is the case where there are multiple parallel time series and a value must be predicted for each.

For example, given the data from the previous section:

We may want to predict the value for each of the three time series for the next time step.

This might be referred to as multivariate forecasting.

Again, the data must be split into input/output samples in order to train a model.

The first sample of this dataset would be:

Input:

Output:

The split_sequences() function below will split multiple parallel time series with rows for time steps and one series per column into the required input/output shape.

We can demonstrate this on the contrived problem; the complete example is listed below.

Running the example first prints the shape of the prepared X and y components.

The shape of X is three-dimensional, including the number of samples (6), the number of time steps chosen per sample (3), and the number of parallel time series or features (3).

The shape of y is two-dimensional as we might expect for the number of samples (6) and the number of time variables per sample to be predicted (3).

Then, each of the samples is printed showing the input and output components of each sample.

We are now ready to fit an MLP model on this data.

As with the previous case of multivariate input, we must flatten the three dimensional structure of the input data samples to a two dimensional structure of [samples, features], where lag observations are treated as features by the model.

The model output will be a vector, with one element for each of the three different time series.

We can now define our model, using the flattened vector length for the input layer and the number of time series as the vector length when making a prediction.

We can predict the next value in each of the three parallel series by providing an input of three time steps for each series.

The shape of the input for making a single prediction must be 1 sample, 3 time steps and 3 features, or [1, 3, 3]. Again, we can flatten this to [1, 6] to meet the expectations of the model.

We would expect the vector output to be:

We can tie all of this together and demonstrate an MLP for multivariate output time series forecasting below.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

Running the example prepares the data, fits the model, and makes a prediction.

As with multiple input series, there is another, more elaborate way to model the problem.

Each output series can be handled by a separate output MLP model.

We can refer to this as a multi-output MLP model. It may offer more flexibility or better performance depending on the specifics of the problem that is being modeled.

This type of model can be defined in Keras using the Keras functional API.

First, we can define the input model as an MLP with an input layer that expects flattened feature vectors.

We can then define one output layer for each of the three series that we wish to forecast, where each output submodel will forecast a single time step.

We can then tie the input and output layers together into a single model.

To make the model architecture clear, the schematic below clearly shows the three separate output layers of the model and the input and output shapes of each layer.

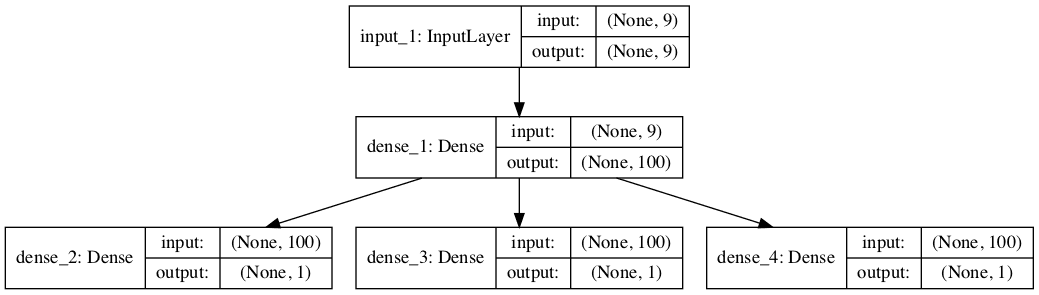
Plot of Multi-Output MLP for Multivariate Time Series Forecasting

Plot of Multi-Output MLP for Multivariate Time Series Forecasting

When training the model, it will require three separate output arrays per sample.

We can achieve this by converting the output training data that has the shape [7, 3] to three arrays with the shape [7, 1].

These arrays can be provided to the model during training.

Tying all of this together, the complete example is listed below.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

Running the example prepares the data, fits the model, and makes a prediction.

Multi-Step MLP Models

In practice, there is little difference to the MLP model in predicting a vector output that represents different output variables (as in the previous example) or a vector output that represents multiple time steps of one variable.

Nevertheless, there are subtle and important differences in the way the training data is prepared. In this section, we will demonstrate the case of developing a multi-step forecast model using a vector model.

Before we look at the specifics of the model, let’s first look at the preparation of data for multi-step forecasting.

Data Preparation

As with one-step forecasting, a time series used for multi-step time series forecasting must be split into samples with input and output components.

Both the input and output components will be comprised of multiple time steps and may or may not have the same number of steps.

For example, given the univariate time series:

We could use the last three time steps as input and forecast the next two time steps.

The first sample would look as follows:

Input:

Output:

The split_sequence() function below implements this behavior and will split a given univariate time series into samples with a specified number of input and output time steps.

We can demonstrate this function on the small contrived dataset.

The complete example is listed below.

Running the example splits the univariate series into input and output time steps and prints the input and output components of each.

Now that we know how to prepare data for multi-step forecasting, let’s look at an MLP model that can learn this mapping.

Vector Output Model

The MLP can output a vector directly that can be interpreted as a multi-step forecast.

This approach was seen in the previous section were one time step of each output time series was forecasted as a vector.

With the number of input and output steps specified in the n_steps_in and n_steps_out variables, we can define a multi-step time-series forecasting model.

The model can make a prediction for a single sample. We can predict the next two steps beyond the end of the dataset by providing the input:

We would expect the predicted output to be:

As expected by the model, the shape of the single sample of input data when making the prediction must be [1, 3] for the 1 sample and 3 time steps (features) of the input and the single feature.

Tying all of this together, the MLP for multi-step forecasting with a univariate time series is listed below.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

Running the example forecasts and prints the next two time steps in the sequence.

Multivariate Multi-Step MLP Models

In the previous sections, we have looked at univariate, multivariate, and multi-step time series forecasting.

It is possible to mix and match the different types of MLP models presented so far for the different problems. This too applies to time series forecasting problems that involve multivariate and multi-step forecasting, but it may be a little more challenging, particularly in preparing the data and defining the shape of inputs and outputs for the model.

In this section, we will look at short examples of data preparation and modeling for multivariate multi-step time series forecasting as a template to ease this challenge, specifically:

  1. Multiple Input Multi-Step Output.
  2. Multiple Parallel Input and Multi-Step Output.

Perhaps the biggest stumbling block is in the preparation of data, so this is where we will focus our attention.

Multiple Input Multi-Step Output

There are those multivariate time series forecasting problems where the output series is separate but dependent upon the input time series, and multiple time steps are required for the output series.

For example, consider our multivariate time series from a prior section:

We may use three prior time steps of each of the two input time series to predict two time steps of the output time series.

Input:

Output:

The split_sequences() function below implements this behavior.

We can demonstrate this on our contrived dataset. The complete example is listed below.

Running the example first prints the shape of the prepared training data.

We can see that the shape of the input portion of the samples is three-dimensional, comprised of six samples, with three time steps and two variables for the two input time series.

The output portion of the samples is two-dimensional for the six samples and the two time steps for each sample to be predicted.

The prepared samples are then printed to confirm that the data was prepared as we specified.

We can now develop an MLP model for multi-step predictions using a vector output.

The complete example is listed below.

Running the example fits the model and predicts the next two time steps of the output sequence beyond the dataset.

We would expect the next two steps to be [185, 205].

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

It is a challenging framing of the problem with very little data, and the arbitrarily configured version of the model gets close.

Multiple Parallel Input and Multi-Step Output

A problem with parallel time series may require the prediction of multiple time steps of each time series.

For example, consider our multivariate time series from a prior section:

We may use the last three time steps from each of the three time series as input to the model and predict the next time steps of each of the three time series as output.

The first sample in the training dataset would be the following.

Input:

Output:

The split_sequences() function below implements this behavior.

We can demonstrate this function on the small contrived dataset.

The complete example is listed below.

Running the example first prints the shape of the prepared training dataset.

We can see that both the input (X) and output (Y) elements of the dataset are three dimensional for the number of samples, time steps, and variables or parallel time series respectively.

The input and output elements of each series are then printed side by side so that we can confirm that the data was prepared as we expected.

We can now develop an MLP model to make multivariate multi-step forecasts.

In addition to flattening the shape of the input data, as we have in prior examples, we must also flatten the three-dimensional structure of the output data. This is because the MLP model is only capable of taking vector inputs and outputs.

The complete example is listed below.

Running the example fits the model and predicts the values for each of the three time steps for the next two time steps beyond the end of the dataset.

We would expect the values for these series and time steps to be as follows:

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

We can see that the model forecast gets reasonably close to the expected values.

Summary

In this tutorial, you discovered how to develop a suite of Multilayer Perceptron, or MLP, models for a range of standard time series forecasting problems.

Specifically, you learned:

  • How to develop MLP models for univariate time series forecasting.
  • How to develop MLP models for multivariate time series forecasting.
  • How to develop MLP models for multi-step time series forecasting.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

Develop Deep Learning models for Time Series Today!

Deep Learning for Time Series Forecasting

Develop Your Own Forecasting models in Minutes

...with just a few lines of python code

Discover how in my new Ebook:
Deep Learning for Time Series Forecasting

It provides self-study tutorials on topics like:
CNNs, LSTMs, Multivariate Forecasting, Multi-Step Forecasting and much more...

Finally Bring Deep Learning to your Time Series Forecasting Projects

Skip the Academics. Just Results.

See What's Inside

More On This Topic

133 Responses to How to Develop Multilayer Perceptron Models for Time Series Forecasting

  1. Avatar
    Rita November 9, 2018 at 11:48 am #

    Hello Jason,

    Really good intro to MLP Neural Networks, just wondering if you had any training or tutorials on the same thing but on R instead of Python?

    Reply
  2. Avatar
    David Montgomery November 11, 2018 at 1:33 am #

    Hi Jason

    Lovely tutorial. Is there any specific reason you do

    out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])

    over

    out_seq = in_seq1 + in_seq2 ?

    Reply
    • Avatar
      Jason Brownlee November 11, 2018 at 6:09 am #

      Thanks David!

      If they are equivalent, then not really.

      Reply
  3. Avatar
    David Heffernan November 18, 2018 at 8:13 pm #

    Great article! Well written and learned a lot. I am trying to work on my own project now but am a bit stuck trying to integrate categorical variables into this. I think I want to create a univariate multistep MLP however for each sample there are a few categorical variables. Can I turn this into a multivariate multistep problem. For example, suppose I have two separate stores (store A and store B) and the history of sales for each store over the past few years and I want to predict the next month.

    Could I generate multivariable samples as so:
    [10, A]
    [20, A]
    [30, A]
    [40, A]
    …
    [100,A]

    Reply
  4. Avatar
    Aisha November 29, 2018 at 9:27 pm #

    Hi M. Brownlee,

    How can we calculate the mean error squared, for example, to estimate this model performance?

    Usually, we decompose the base into a train and test, why is it not the case in this example?

    Reply
    • Avatar
      Jason Brownlee November 30, 2018 at 6:32 am #

      You can add ‘mse’ to the list of metrics calculated by the model.

      Or you can use the model to make predictions, then calculate the MSE directly.

      Reply
  5. Avatar
    Jiayi Liu December 1, 2018 at 8:32 am #

    Hey your blog help me a lot as I am researching using neural network to predict a specific model. I just have a question about this paper. In the beginning you have a sequence of data which you can use split sequence command, but what if I have a column/list of data, how do I split my data?
    Thank you

    Reply
  6. Avatar
    mk January 7, 2019 at 7:23 pm #

    How to transform input and output as Household Power Consumption dataset
    Multiple Input Multi-Step Output

    Input, Output
    [d01, d02, d03, d04, d05, d06, d07], [d08, d09, d10, d11, d12, d13, d14]
    [d02, d03, d04, d05, d06, d07, d08], [d09, d10, d11, d12, d13, d14, d15]
    …

    Reply
  7. Avatar
    mk January 9, 2019 at 1:32 pm #

    Multiple Parallel Input and Multi-Step Output

    The problem is the most complex, but his model is the simplest.

    model.add(Dense(100, activation=’relu’, input_dim=n_input))

    How do we understand Multiple Parallel Input.

    Reply
    • Avatar
      Jason Brownlee January 10, 2019 at 7:44 am #

      Think about it as multivariate input – multiple features, e.g. parallel time series.

      Reply
  8. Avatar
    Aisha January 10, 2019 at 3:31 am #

    Hello M. Brownlee,

    when I update my data in a txt file like this:

    with open(‘testfile.txt’) as inputfile:
    for line in inputfile:
    raw_seq.append(line.strip().split(‘,’))
    #print (raw_seq)
    …
    look_for = raw_seq[len(raw_seq)-n_steps_in:len(raw_seq)]
    x_input = array(look_for)

    , it gives me this error
    ”
    File “C:\Users\AppData\Local\Programs\Python\Python36\lib\site-packages\keras\engine\training_utils.py”, line 127, in standardize_input_data
    ‘with shape ‘ + str(data_shape))
    ValueError: Error when checking input: expected dense_1_input to have 2 dimensions, but got array with shape (6, 1, 1)
    ”

    can you inform me, please !

    Cordially

    Reply
    • Avatar
      Jason Brownlee January 10, 2019 at 7:56 am #

      Perhaps post your code and error to stackoverfolow.

      Reply
  9. Avatar
    Sarra January 10, 2019 at 8:42 pm #

    Please, how can we proceed in this case:
    Time series: [2 4 6 0 1 3 5 0 6 7 8 0], we find that after every 3 values it returns to 0.
    Logically, we must have this feature in the prediction like [2 4 6 0 1 3 5 0 6 7 8 0 V1 V2 V3 0 V’1 …]

    What should I do?

    Do I make the prediction until I get this! Or is there a parameter to define?

    Thank you to answer me

    Reply
    • Avatar
      Jason Brownlee January 11, 2019 at 7:43 am #

      Sorry, I don’t follow your question, perhaps you can elaborate on the problem that you’re having?

      Reply
  10. Avatar
    Huizi January 17, 2019 at 8:05 am #

    Great work Jason!

    I have a simple question about the final X we feed into the model. Does it matter if I change the order of column index of X?

    for example, lets say array

    X=([[10, 15, 20, 25, 30, 35],
    [20, 25, 30, 35, 40, 45],…]),

    does it matter if I change X into

    X=([[10, 20, 15, 25, 35, 30],
    [20, 30, 25, 35, 45, 40],…]),
    ???

    Reply
    • Avatar
      Jason Brownlee January 17, 2019 at 1:44 pm #

      The order of the columns must remain consistent between training and test.

      Reply
  11. Avatar
    Ahmad February 20, 2019 at 10:48 pm #

    Hi Jason . This is interesting and quite helpful. Can I apply the same to Extreme learning machine for multivariate time series data.

    Thank you

    Reply
  12. Avatar
    Hanif Han February 22, 2019 at 3:55 pm #

    Hi Jason, do you know how to split the predict result.

    [[102.572365 113.88405 ]] -> [[102.572365]] , [[113.88405 ]]

    Thanks

    Reply
  13. Avatar
    Adi March 8, 2019 at 8:57 am #

    Hi Jason,

    For univariate model, I used

    raw_seq = [10, 0, 0, 20, 0, 0, 0, 30, 0, 40, 0, 0]

    and predict = [40, 0 , 0]

    the prediction was [[-33.33]].. How to avoid negative predictions?

    Thanks!

    Reply
    • Avatar
      Jason Brownlee March 8, 2019 at 2:17 pm #

      Perhaps scale input and output prior to modeling, e.g. try normalizing the data?

      Reply
  14. Avatar
    Amel April 17, 2019 at 11:33 pm #

    After training and choosing the right model, how can we save it to use it in the future for other forecast numbers

    Reply
    • Avatar
      Jason Brownlee April 18, 2019 at 8:46 am #

      You can call:

      Reply
  15. Avatar
    Jackson April 22, 2019 at 12:55 pm #

    Hi,Jason.
    Can MLP perform multivariate time series prediction?How to achieve it?

    Reply
    • Avatar
      Jackson April 22, 2019 at 12:58 pm #

      Sorry，I read your follow-up article and my question was answered.The article is great, thanks.

      Reply
    • Avatar
      Jason Brownlee April 22, 2019 at 2:27 pm #

      Yes, I have examples in the above tutorial.

      Reply
  16. Avatar
    Michael April 23, 2019 at 5:54 am #

    Hello Jason Brownlee! I want to express my profound gratitude to you! Just by following your short crash course I’ve learnt soo much. Thank you and keep up the good work!
    I have a question : is there a way to make a trained model to predict more number of values than the number of values it was trained with?
    Using the multivariate-multi-step example, the model was trained with 3 outputs. Is there a way to tell the model instead of 3 outputs try to predict the best 5 outputs?

    Reply
  17. Avatar
    Amel April 23, 2019 at 8:31 pm #

    hello Jase,

    have you an example that you use a LSTM model.h5
    (already save in .h5)

    thank you.

    Reply
  18. Avatar
    Em April 25, 2019 at 9:18 am #

    Jason,

    I have noticed that you are shuffling your data in the .fit part. Is it a right approach, though?

    Reply
    • Avatar
      Jason Brownlee April 25, 2019 at 2:39 pm #

      Yes, the fit() function will shuffle the samples.

      Recall that the MLP is a static model. Also recall that the data separation via walk-forward validation does not introduce data leakage.

      Reply
      • Avatar
        SB August 21, 2019 at 7:32 am #

        Hi Jason,
        could you please elaborate on your comment? I don’t understand what you mean.
        What does ML being a static model have to do with the fact, that we shuffle time series data. I thought with time series we do not want to shuffle in order to preserve the time order, right? In this example couldn’t we use walk-forward validation?

        Reply
        • Avatar
          Jason Brownlee August 21, 2019 at 2:00 pm #

          The MLP is not concerned if all history is shuffled during training. MLP is static, whereas the LSTM is not, and shuffling would cause a loss of information across samples in a batch and the state that is maintained by the model.

          Also, shuffling samples is also does not effect the model evaluation strategy, as long as walk-forward validation is used to estimate model skill on out of sample examples that are in the future.

          Not sure if that helps, perhaps I miss your underlying concern?

          Reply
          • Avatar
            SB August 22, 2019 at 6:26 am #

            Hi Jason,
            Thanks for your quick reply! I was confused by “static” couldn’t you use walk-forward validation (where you’d retrain/refit the MLP after each prediction/time step in test/output data) and thus make the NN a dynamic model? Do you happen to have such an example i.e. blog post of a MLP that you (dynamically) evaluate using walk-forward validation? Thanks.

          • Avatar
            Jason Brownlee August 22, 2019 at 6:35 am #

            Yes, you can do that. That is not what I meant by static, see the note about some models having state and MLPs not having state.

  19. Avatar
    Keerti June 19, 2019 at 4:40 am #

    Hello Jason. First of all i would like to thank you for your excellent blogs.

    What if i want to take the predicted output (t) and then use it as training to predict my next output (t+1) and continue this uptil some point t+100 ?
    If yes, how could i optimise the errors if i already know and values and want to validate ?

    Thanks in advance.

    Reply
  20. Avatar
    haochen June 19, 2019 at 5:48 pm #

    Hello Jason Brownlee! In this case, the number of parameters（weigtht,bias） is larger than the number of samples. Is there an overfitting problem? The same problem exists in LSTM.

    Reply
  21. Avatar
    Ala June 24, 2019 at 3:36 am #

    I am kind of confused. You have tutorials for time series forecasting both using MLP and lstm. I though lstm due to recurrent structure is a better fit for time series problem. The input dimension is also different in lstm and we take number of features into account as a 3D tensor.
    Can you suggest me for multivariate time series with n_step=1 which method I should choose (MLP or lstm )?

    Reply
    • Avatar
      Jason Brownlee June 24, 2019 at 6:35 am #

      There is no single algorithm good/best for all problems.

      In fact, most neural nets are out-performed by linear methods for univariate time series problems.

      Reply
  22. Avatar
    Michael July 17, 2019 at 9:06 pm #

    Hello Master Brownlee, in a multiheaded MLP, the outputs of a prediction when printed is represented like so [array([[49.88555]], dtype=float32, array[[88.384747]], dtype=float32]]) ]
    please how can I make the predict to represent only value, or how can I get only the values in a script? thanks a lot in advance

    Reply
  23. Avatar
    Takis Angelides July 25, 2019 at 7:23 pm #

    Lets say we have hourly data and want to make prediction on the next 4 hours using 200 time steps in the past as features. Is there a difference between a univariate model which outputs only 1 value and we take that value pump it back into the data to predict the next value and repeat until we have 4 predictions and a univariate model which is designed/trained to predict the next 4 hours in 1 go (ie multi-step)?

    Thank you for the effort to provide free tutorials, they provide crucial help to beginners.

    A kind suggestion would be to expand more on the theory. What the community needs is good explanation on the theory without missing parts or skipping the maths and implementations of that theory in working code that can be generalized to the purpose of the reader.

    Reply
    • Avatar
      Jason Brownlee July 26, 2019 at 8:18 am #

      Yes there is a difference and the difference may or may not matter for your dataset.

      I would recommend testing both (and more) and see what works for your specific dataset.

      The theory will not help you make better predictions, there are no theories for mapping algorithms to datasets. You must use experiments.

      Reply
  24. Avatar
    Takis Angelides July 25, 2019 at 9:54 pm #

    How do you suggest we visual/plot the predictions vs the actual values in a multi step univariate model? The output for each prediction in the test set for example overlaps with the next few and the few before depending on the n_steps_out.

    Reply
    • Avatar
      Jason Brownlee July 26, 2019 at 8:24 am #

      I would recommend creating a line plot of the expected output and predicted output for the univariate series.

      Reply
  25. Avatar
    Gizo August 19, 2019 at 12:32 am #

    is it possible the above Multivariate Multi-Step MLP code to receive data from file?
    how?

    thanks.

    Reply
  26. Avatar
    Lucas Duarte August 21, 2019 at 12:50 pm #

    hey, Jason! I tryed to use your code on Anacondas. but it hasn’t worked.
    this is what it send me.

    Using TensorFlow backend.
    —————————————————————————
    ModuleNotFoundError Traceback (most recent call last)
    in
    32 from numpy import array
    33 from numpy import hstack
    —> 34 from keras.models import Sequential
    35 from keras.layers import Dense
    36

    ~\Anaconda3\lib\site-packages\keras\__init__.py in
    1 from __future__ import absolute_import
    2
    —-> 3 from . import utils
    4 from . import activations
    5 from . import applications

    ~\Anaconda3\lib\site-packages\keras\utils\__init__.py in
    4 from . import data_utils
    5 from . import io_utils
    —-> 6 from . import conv_utils
    7
    8 # Globally-importable utils.

    ~\Anaconda3\lib\site-packages\keras\utils\conv_utils.py in
    7 from six.moves import range
    8 import numpy as np
    —-> 9 from .. import backend as K
    10
    11

    ~\Anaconda3\lib\site-packages\keras\backend\__init__.py in
    87 elif _BACKEND == ‘tensorflow’:
    88 sys.stderr.write(‘Using TensorFlow backend.\n’)
    —> 89 from .tensorflow_backend import *
    90 else:
    91 # Try and load external backend.

    ~\Anaconda3\lib\site-packages\keras\backend\tensorflow_backend.py in
    3 from __future__ import print_function
    4
    —-> 5 import tensorflow as tf
    6 from tensorflow.python.framework import ops as tf_ops
    7 from tensorflow.python.training import moving_averages

    ~\Anaconda3\lib\site-packages\tensorflow\__init__.py in
    26
    27 # pylint: disable=g-bad-import-order
    —> 28 from tensorflow.python import pywrap_tensorflow # pylint: disable=unused-import
    29 from tensorflow.python.tools import module_util as _module_util
    30

    ~\Anaconda3\lib\site-packages\tensorflow\python\__init__.py in
    47 import numpy as np
    48
    —> 49 from tensorflow.python import pywrap_tensorflow
    50
    51 # Protocol buffers

    ~\Anaconda3\lib\site-packages\tensorflow\python\pywrap_tensorflow.py in
    23 import traceback
    24
    —> 25 from tensorflow.python.platform import self_check
    26
    27

    ModuleNotFoundError: No module named ‘tensorflow.python.platform’

    Reply
  27. Avatar
    Nghia September 2, 2019 at 2:31 am #

    Hi Jason and thanks for your articles, it very helpful with me.
    I tried “Multiple Parallel Series” with multivariate output mlp example, I used output submode as your example post

    Could you explain the difference between two predicted results or I was wrong?
    When
    x_input = array([[70,75,145], [80,85,165], [90,95,185]])
    yhat = model.predict(x_input, verbose=0)
    result:
    [array([[101.30953]], dtype=float32), array([[106.59332]], dtype=float32), array([[207.61252]], dtype=float32)]
    it nearly with expected

    But when
    x_input = array([[70,75,145], [80,85,165], [90,95,185], [100,105,205], [110,115,225], [120,125,245]])
    x_input = x_input.reshape((2, n_input)
    pre = model.predict(x_input, verbose=0)
    np.reshape(pre, (2,3))
    result:
    array([[101.30955, 135.60982, 106.5933 ],
    [141.29143, 207.61253, 275.84082]], dtype=float32)

    Thanks for your help

    Reply
    • Avatar
      Jason Brownlee September 2, 2019 at 5:31 am #

      You can ignore the test problems.

      The test problems are not real and are not intended to be correctly predicted every run – they are designed as the basis so that you can undertand the models and model architecture.

      Reply
      • Avatar
        Nghia September 2, 2019 at 11:58 am #

        Thanks,
        I mean, why with the same model
        Predicting the same data again gives different results
        1st and 2nd times are not the same

        x_input = array ([[70,75,145], [80,85,165], [90,95,185]])
        expect: [100, 105, 205]
        result:
        [array ([[101.30953]], dtype = float32), array ([[106.59332]], dtype = float32), array ([[207.61252]], dtype = float32)]

        when predict with 2 x_input:
        x_input = array ([[70,75,145], [80,85,165], [90,95,185], [100,105,205], [110,115,225], [120,125,245]])
        expect: [100, 105, 205], [130, 135, 265]
        result:
        array ([[101.30955, 135.60982, 106.5933],
        [141.29143, 207.61253, 275.84082]], dtype = float32)

        I think the the result of the second predictive must have the same result as the first one
        [array ([[101.30953]], dtype = float32), array ([[106.59332]], dtype = float32), array ([[207.61252]], dtype = float32)]
        but it the difference

        Reply
  28. Avatar
    Gustavo Nunes September 9, 2019 at 11:16 am #

    Thank you for the explanation, it’ll be very useful for me. If I may, I’d like to ask how can I adjust hyperparameters for MLP for time series?

    Reply
  29. Avatar
    Albi September 18, 2019 at 2:47 am #

    Hello Jason,
    As done by the other guys, I I thank you for the very interesting article.

    Anyhow I have a question. We usually divide the initial data into training and test sets in order to check the overfitting. So the two questions are:
    1) Why is it not the case in this example?
    2) How can we manage the train and test sets in such type of time-forecasting?

    Reply
  30. Avatar
    Lin September 30, 2019 at 2:39 pm #

    Thanks for the article Jason. It really helps me a lot.
    And I wonder what if the input series is in different time steps, e.g.
    input1 = [1 ,3, 5] # recorded every 2 hours
    input2 = [1, 2, 3, 4, 5, 6] # recorded every hour

    How would you design the model to receive both input1 and input2.

    Reply
  31. Avatar
    Cagli October 1, 2019 at 5:25 pm #

    Hello Jason thanks for tutorial. I have a question. I’m working time series forecasting for Epilepsy EEG dataset. I want to apply MLP my dataset. You may have probably seen it is here: http://epileptologie-bonn.de/cms/front_content.php?idcat=193&lang=3&changelang=3
    How can i apply it to MLP?
    Thx.

    Reply
  32. Avatar
    Mark October 2, 2019 at 9:09 pm #

    Hi,
    Thanks for the article, I am wondering when should you use MLP vs LSTM or RNN methods. If I have a related time series like energy consumption data from many multiple devices. Which method would you recommend and why? Which one is better in picking up seasonality? especially that you can pass seasonality to MLP multivariate model?

    Thanks in advance!

    Reply
  33. Avatar
    Ann December 7, 2019 at 12:35 am #

    Hello. in the multiple input series case. What is network exactly learning? is it learning the fact and it should sum up the last couple? or is it trying to predict next value of separate time series and then summing them up?

    I have the following problem: I want to predict inflation at next step and it is linear combination of 5 time series groups. so I want to train the model until time t with 5 time series and it to give the inflation index for t+1. Will this model work for this case?

    Reply
  34. Avatar
    jasper December 25, 2019 at 12:35 pm #

    Hi Jason,

    Is Multilayer Perceptron Models(MLP) belonging to the “deep learning” type ? I wonder that this method requires some network with cells like LSTM, CNN, RNN. Do you agree with? many thanks.

    Reply
  35. Avatar
    Arunesh Sarker March 29, 2020 at 6:00 am #

    Hello sir,
    The tutorial is really awesome. But I had a doubt. I’m using Jupyter notebook, and after implementing the univariate MLP, I implemented the multiple input of multivariate MLP. The expected answer according to this post is 205.04436, but I’m getting a value of 100.59, which was the result of my univariate MLP. Can you please tell me am I going wrong somewhere, or is it a technical issue with Jupyter notebook?
    Many thanks

    Reply
    • Avatar
      Jason Brownlee March 29, 2020 at 6:05 am #

      Thanks!

      You might need to run the example a few times given the stochastic nature of the learning algorithms.

      Reply
  36. Avatar
    João Guilherme Cotta April 26, 2020 at 3:44 am #

    Hello Jason,

    Thanks for making available such helpful tutorials.

    Do you have any material on time series predictions using a multilayer perceptron with backpropagation? I checked your other tutorial on MLP with BP but it is used for classification purposes. This tutorial on time series is also interesting but it does not use backpropagation.

    Thanks in advance.

    Reply
    • Avatar
      Jason Brownlee April 26, 2020 at 6:19 am #

      The above tutorial is EXACTLY THIS – MLPs fit via backprop for time series forecasting.

      Reply
  37. Avatar
    Dexter May 10, 2020 at 9:33 am #

    Hello Jason, many thanks for your tutorials!!! Help me a lot!!!

    In your opinion, is MLP better than LSTM for precipitation prediction, for example? Or depends on other factors?

    Thanks in advance!

    Reply