Recurrent neural networks are able to learn the temporal dependence across multiple timesteps in sequence prediction problems.
Modern recurrent neural networks like the Long Short-Term Memory, or LSTM, network are trained with a variation of the Backpropagation algorithm called Backpropagation Through Time. This algorithm has been modified further for efficiency on sequence prediction problems with very long sequences and is called Truncated Backpropagation Through Time.
An important configuration parameter when training recurrent neural networks like LSTMs using Truncated Backpropagation Through Time is deciding how many timesteps to use as input. That is, how exactly to split up your very long input sequences into subsequences in order to get the best performance.
In this post, you will discover 6 different ways you can split up very long input sequences to effectively train recurrent neural networks using Truncated Backpropagation Through Time in Python with Keras.
After reading this post, you will know:
- What Truncated Backpropagation Through Time is and how it has been implemented in the Python deep learning library Keras.
- How exactly the choice of the number of input timesteps affects learning within recurrent neural networks.
- 6 different techniques you can use to split up your very long sequence prediction problems to make best use of the Truncated Backpropagation Through Time training algorithm.
Kick-start your project with my new book Long Short-Term Memory Networks With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to Prepare Sequence Prediction for Truncated Backpropagation Through Time in Keras
Photo by Giò, some rights reserved.
Truncated Backpropagation Through Time
Backpropagation is the training algorithm used to update the weights in a neural network in order to minimize the error between the expected output and the predicted output for a given input.
For sequence prediction problems where there is an order dependence between observations, recurrent neural networks are used instead of classical feed-forward neural networks. Recurrent neural networks are trained using a variation of the Backpropagation algorithm called Backpropagation Through Time, or BPTT for short.
In effect, BPTT unrolls the recurrent neural network and propagates the error backward over the entire input sequence, one timestep at a time. The weights are then updated with the accumulated gradients.
BPTT can be slow to train recurrent neural networks on problems with very long input sequences. In addition to speed, the accumulation of gradients over so many timesteps can result in a shrinking of values to zero, or a growth of values that eventually overflow, or explode.
A modification of BPTT is to limit the number of timesteps used on the backward pass and in effect estimate the gradient used to update the weights rather than calculate it fully.
This variation is called Truncated Backpropagation Through Time, or TBPTT.
The TBPTT training algorithm has two parameters:
- k1: Defines the number of timesteps shown to the network on the forward pass.
- k2: Defines the number of timesteps to look at when estimating the gradient on the backward pass.
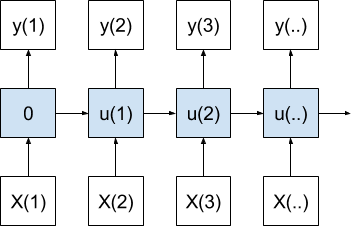
As such, we can use the notation TBPTT(k1, k2) when considering how to configure the training algorithm, where k1 = k2 = n, where n is the input sequence length for classical non-truncated BPTT.
Impact of TBPTT Configuration on the RNN Sequence Model
Modern recurrent neural networks like LSTMs can use their internal state to remember over very long input sequences. Such as over thousands of timesteps.
This means that the configuration of TBPTT does not necessarily define the memory of the network that you are optimizing with the choice of the number of timesteps. You can choose when the internal state of the network is reset separately from the regime used to update network weights.
Instead, the choice of TBPTT parameters influences how the network estimates the error gradient used to update the weights. More generally, the configuration defines the number of timesteps from which the network may be considered to model your sequence problem.
We can state this formally as something like:
|
1 |
yhat(t) = f(X(t), X(t-1), X(t-2), ... X(t-n)) |
Where yhat is the output for a specific timestep, f(…) is the relationship that the recurrent neural network is approximating, and X(t) are observations at specific timesteps.
It is conceptually similar (but quite different in practice) to the window size on Multilayer Perceptrons trained on time series problems or to the p and q parameters of linear time series models like ARIMA. The TBPTT defines the scope of the input sequence for the model during training.
Need help with LSTMs for Sequence Prediction?
Take my free 7-day email course and discover 6 different LSTM architectures (with code).
Click to sign-up and also get a free PDF Ebook version of the course.
Keras Implementation of TBPTT
The Keras deep learning library provides an implementation of TBPTT for training recurrent neural networks.
The implementation is more restricted than the general version listed above.
Specifically, the k1 and k2 values are equal to each other and fixed.
- TBPTT(k1, k2), where k1 = k2
This is realized by the fixed sized three-dimensional input required to train recurrent neural networks like the Long Short-Term Memory network, or LSTM.
The LSTM expects input data to have the dimensions: samples, timesteps, and features.
It is the second dimension of this input format, the timesteps that defines the number of timesteps used for forward and backward passes on your sequence prediction problem.
Therefore, careful choice must be given to the number of timesteps specified when preparing your input data for sequence prediction problems in Keras.
The choice of timesteps will influence both:
- The internal state accumulated during the forward pass.
- The gradient estimate used to update weights on the backward pass.
Note that by default, the internal state of the network is reset after each batch, but more explicit control over when the internal state is reset can be achieved by using a so-called stateful LSTM and calling the reset operation manually.
For more on stateful LSTMs in Keras, see the posts:
- How to Seed State for LSTMs for Time Series Forecasting in Python
- Stateful and Stateless LSTM for Time Series Forecasting with Python
- Understanding Stateful LSTM Recurrent Neural Networks in Python with Keras
Prepare Sequence Data for TBPTT in Keras
The way that you break up your sequence data will define the number of timesteps used in the forward and backward passes of BPTT.
As such, you must put careful thought into how you will prepare your training data.
This section lists 6 techniques you may consider.
1. Use Data As-Is
You may use your input sequences as-is if the number of timesteps in each sequence is modest, such as tens or a few hundred timesteps.
Practical limits have been suggested for TBPTT of about 200-to-400 timesteps.
If your sequence data is less than or equal to this range, you may reshape the sequence observations as timesteps for the input data.
For example, if you had a collection of 100 univariate sequences of 25 timesteps, this could be reshaped as 100 samples, 25 timesteps, and 1 feature or [100, 25, 1].
2. Naive Data Split
If you have long input sequences, such as thousands of timesteps, you may need to break the long input sequences into multiple contiguous subsequences.
This will require the use of a stateful LSTM in Keras so that internal state is preserved across the input of the sub-sequences and only reset at the end of a true fuller input sequence.
For example, if you had 100 input sequences of 50,000 timesteps, then each input sequence could be divided into 100 subsequences of 500 timesteps. One input sequence would become 100 samples, therefore the 100 original samples would become 10,000. The dimensionality of the input for Keras would be 10,000 samples, 500 timesteps, and 1 feature or [10000, 500, 1]. Care would be needed to preserve state across each 100 subsequences and reset the internal state after each 100 samples either explicitly or by using a batch size of 100.
A split that neatly divides the full sequence into fixed-sized subsequences is preferred. The choice of the factor of the full sequence (subsequence length) is arbitrary, hence the name “naive data split”.
The splitting of the sequence into subsequences does not take into account domain information about a suitable number of timesteps to estimate the error gradient used to update weights.
3. Domain-Specific Data Split
It can be hard to know the correct number of timesteps required to provide a useful estimate of the error gradient.
We can use the naive approach (above) to get a model quickly, but the model may be far from optimized.
Alternately, we can use domain specific information to estimate the number of timesteps that will be relevant to the model while learning the problem.
For example, if the sequence problem is a regression time series, perhaps a review of the autocorrelation and partial autocorrelation plots can inform the choice of the number of the timesteps.
If the sequence problem is a natural language processing problem, perhaps the input sequence can be divided by sentence and then padded to a fixed length, or split according to the average sentence length in the domain.
Think broadly and consider what knowledge specific to your domain that you can use to split up the sequence into meaningful chunks.
4. Systematic Data Split (e.g. grid search)
Rather than guessing at a suitable number of timesteps, you can systematically evaluate a suite of different subsequence lengths for your sequence prediction problem.
You could perform a grid search over each sub-sequence length and adopt the configuration that results in the best performing model on average.
Some notes of caution if you are considering this approach:
- Start with subsequence lengths that are a factor of the full sequence length.
- Use padding and perhaps masking if exploring subsequence lengths that are not a factor of the full sequence length.
- Consider using a slightly over-prescribed network (more memory cells and more training epochs) than is required to address the problem to help rule out network capacity as a limitation on your experiment.
- Take the average performance over multiple runs (e.g. 30) of each different configuration.
If compute resources are not a limitation, then a systematic investigation of different numbers of timesteps is recommended.
5. Lean Heavily On Internal State With TBPTT(1, 1)
You can reformulate your sequence prediction problem as having one input and one output each timestep.
For example, if you had 100 sequences of 50 timesteps, each timestep would become a new sample. The 100 samples would become 5,000. The three-dimensional input would become 5,000 samples, 1 timestep, and 1 feature, or [5000, 1, 1].
Again, this would require the internal state to be preserved across each timestep of the sequence and reset at the end of each actual sequence (50 samples).
This would put the burden of learning the sequence prediction problem on the internal state of the recurrent neural network. Depending on the type of problem, it may be more than the network can handle and the prediction problem may not be learnable.
Personal experience suggests that this formulation may work well for prediction problems that require memory over the sequence, but perform poorly when the outcome is a complex function of past observations.
6. Decouple Forward and Backward Sequence Length
The Keras deep learning library used to support a decoupled number of timesteps for the forward and backward pass of Truncated Backpropagation Through Time.
In essence, the k1 parameter could be specified by the number of timesteps on input sequences and the k2 parameter could be specified by a “truncate_gradient” argument on the LSTM layer.
This is no longer supported, but there is some desire to have this feature re-added to the library. It is unclear exactly why it was removed, although evidence suggests it was done for efficiency reasons.
You could explore this approach in Keras. Some ideas include:
- Install and use an older version of the Keras library that supports the “truncate_gradient” argument (circa 2015).
- Extend the LSTM layer implementation in Keras to support a “truncate_gradient” type behavior.
Perhaps there are third-party extensions available for Keras that support this behavior.
If you find any, let me know in the comments below.
Summary
In this post, you discovered how you can prepare your sequence prediction problem data to make effective use of the Truncated Backpropagation Through Time training algorithm in the Python deep learning library Keras.
Specifically, you learned:
- How Truncated Backpropagation Through Time works and how this is implemented in Keras.
- How to reformulate or split your data with very long input sequences in the context of TBPTT.
- How to systematically investigate different TBPTT configurations in Keras.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.







Hello Jason, thank you for the nice tutorial! Can you provide a short example on how to use TBPTT with Keras? (I haven’t found it in keras.optimizers)
You do not choose BPTT, it is the foundation for the way Keras trains all RNNs.
Does that help?
Yes, thank you very much!
Could you provide some information on the relation between the training algorithm and the optimizers and on the particular variant of BPTT (standard/truncated, online/offline)?
BPTT really talks about how to estimate the gradient for the update, e.g. the direction and magnitude when updating weights.
Optimization algorithms make use of the gradient over multiple iterations to update the weights.
Thank you very much for your clear explainations!
You’re welcome.
How to implement this In a code in keras
Many, many thanks for these tutorials!!! Just a suggestion: when creating an example though, please make it a point to not repeat the numbers. The paragraph here was confusing at first, because 100 here refers to the number of sequences, and also the number of subsequences. I guess you meant it as follows??
“For example, if you had 100 input sequences of 25,000 timesteps, then each input sequence could be divided into 50 subsequences of 500 timesteps. One input sequence would become 50 samples, therefore the 100 original samples would become 5,000. The dimensionality of the input for Keras would be 5,000 samples, 500 timesteps, and 1 feature or [5000, 500, 1]. Care would be needed to preserve state across each 50 subsequences and reset the internal state after each 50 samples either explicitly or by using a batch size of 50.” (or 100???)
Many thanks again! So nice of you to share your knowledge with the world!
Thanks, great suggestion. Maybe I need more editors!
The naive data split is kind of like the so called “box car” technique. So:
[6, 1, 7, 5, 9, 2]
would become,
[[6, 1, 7],
[5, 9, 2]]
But I’ve seen people use another (7th?) technique. The “stair step” technique.
[[6, 1, 7],
[1, 7, 5],
[7, 5, 9],
[5, 9, 2]]
So, (1) what kind of RNN’s use this “stair step” technique and (2) are there any issues with double or triple counting the gradients? For example, the input values 7 and 5 are run through the net 3 times but the 6 (and 2) are only run through once?
Thanks.
RNNs are flexible in general and can accept each framing of the problem.
The model is designed to have a long input sequence rather than multiple overlapping short input sequences. The specific impact on skill will depend on the dataset.
@Jason
Thanks a lot for the detailed tutorial.
I wanted to ask about a corner case :
Suppose I want to train a very large sequence (whose length is not known) and i want the model to go through the whole data without computing loss via BPTT (inefficiency is not an issue). In other words, k1 for forward pass is fixed (1, k1, n_inputs) but k2 is dynamic based on input.
Any suggestions how will I be able to achieve that in keras.
Perhaps some custom code.
Hi Jason,
You mention that “Care would be needed to preserve state across each 100 subsequences and reset the internal state after each 100 samples either explicitly or by using a batch size of 100.” My understanding was that each sample in a batch is processed independently, not just in keras but in all machine learning algorithms. Therefore each one of the 100 sub-sequences in a batch would be treated with its own states, so it wouldn’t work in the framework of the stateful LSTM according to me.
I wanted to have your opinion on this.
Thanks for this awesome blog by the way.
Best,
– Pierre
RNNs have state, other algorithms do not.
State is preserved by default across samples in a batch.
“For example, if you had 100 sequences of 50 timesteps, each timestep would become a new sample. The 100 samples would become 5,000. The three-dimensional input would become 5,000 samples, 1 timestep, and 1 feature, or [5000, 1, 1].”
But if I had 100 labels (consisting of 0’s and 1’s) originally i.e. (single label for single sequence), I would use the command ‘ fit(train_data, train_labels, batch_size=25) ‘. Now, after creating 5000 samples from the original 100 samples, I have to provide a single label after processing every 50 samples because every original sample has now been split into 50 samples . I should not provide the labels for each of the sample. So, how should I change my fit command now?
Assuming that ‘train_data’ has the shape (100,50,3)->(samples,timesteps,features) and train_labels has the shape(100,).
Thank you in advance Jason.
Yes, if you have 100 samples, it means you have 100 inputs and 100 outputs and you can provide them directly to your model for training.
Actually, if I wanted to ask that if I had 100 inputs and one label for each input i.e.( total 100 labels ), how should I reshape my labels when I split my 100 inputs into 5000 inputs? each of the original 100 inputs had 50 timesteps as mentioned above i.e.(“For example, if you had 100 sequences of 50 timesteps, each timestep would become a new sample”). Now, every 50 inputs correspond to one of the original 100 inputs.
You could try that as a one-to-one problem.
Also, try to model it as a seq2seq problem, e.g. 50 steps in then 50 steps out.
Hi thanks for the tutorial is really helpful!
I have to train an LSTM to fit a nonlinear dynamical model. I just have a record of a very long sequence representing the system operation, let’s say 100.000 time-steps. It is a SISO process so I have a sequence of shape [100.000, 1] for the inputs and a sequence of shape [100.000, 1] for the outputs. I split the sequences in 100 smaller sequences and split those sequences again in other 10 sequences. My data have now shape [100, 10, 100, 1] where data[0] are the first 10 smaller subsequences. I rearrange the data to have in data[0] all the first sequences of the 10 subsequences in the subsequences obtained with the first split, ending with a data shape of [10, 100, 100, 1]. (I know it’s difficult to understand, sorry). I apply a forward and backward pass to the network using data[0], I get an estimate of the state at the end of data[0] and use it to initialize the state to train using data[1] which is the ensemble of all the second subsequences of the sequences obtained with the first split. I can use the estimated state to initialize the network since there is temporal continuity in the data and in this way I’m also able to train on a batch of sequences.
In your tutorial you said that using a sequence length of 1, we are attributing all the information to the network state. This is more or less what I need since in a dynamical process the actual state is carrying all the information needed to describe it. Do you think I should change something in my training procedure?
Thanks a lot
In general, I recommend brainstorming and trying everything you can think of – you learn more about the problem and about the methods.
In your case, it might be interesting to start with a linear method and some MLP or CNNs and compare to the LSTM to confirm it is adding any value.
It might also be interesting to test a dynamic LSTM over the entire input sequence to see if it offers any benefit.
More ideas here:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
Sir, can you explain how to apply truncatedBPTT on a seq2seq model built using tensorflow.
I want to get insight about how to apply truncation on “embedded inputs” in decoder
Sorry, I don’t have an example of BPTT in tensorflow.
Hi
I used the naive data split, but I don’t really understand how to evaluate the model. The test data is still the full-length sequence. Should I split the test sequence too? I need a prediction only when it has the whole sequence. Can you point me, how to solve this?
One other question relating to the Bidirectional LSTM. Can this method be used there too? I mean if I have a sequence [1,2,3,4,5,6] and split it to [1,2,3] and [4,5,6] in the reverse order it will be [3,2,1][6,5,4] which is not what we want. Do I miss anything?
Thank you for your help and your time.
In general, I would recommend a process of walk-forward validation.
This is best understood in the context of time series:
https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
Hi Jason
If I understand correctly, there is nothing like a parameter for BPTT and TBPTT in keras.
whether it is TBPTT or BPTT only parameter that we can play around is timesteps.
That means to achieve TBPTT,
1. Design input so that there is continuity across batch.
2. make sure you don’t reset your state in next batch
Keras does BPTT for RNNs, it does not give the control needed to do TBPTT.
It is more about the length of the sequence that is fed, used to calculate error and used to perform weight updates.
Jason – thank you for all these wonderful articles. I have a question about batch size with LSTM Autoencoders.
In another article I think you also mentioned using batch size of 1 to fully exploit the capabilities of an LSTM.
I am using an LSTM autoencoder for reconstruction purposes and my time series are all under 400 timesteps (with padding, to deal with sequence length).
So, since I am NOT have the sequence span 2 samples, it seems that batch size of 1 is best for my framing, since the weights are reset after each batch, which is what I care about if I am trying to minimize reconstruction error? Am I understanding this correctly?
But like you said, this can make the learning process unstable, right? So far, I have found that using BatchNormalization tends to “stabilize” the learning process, fyi. Would this also be a place to utilize kernel and/or activity regularizers to help stabilize the learning process?
Sounds good.
Perhaps compare to other configurations to confirm your expectations.
Hi Jason,
What I conclude from the Naive Split example is that:
If we have a batch of size 100 samples and the input shape of (10000,500,1) then we will have 1 back prop. after each 500 timesteps (1 sample) and state is accumulated till the end of the batch then the state will be reset on the new batch.
Is that true? do we need to make the stateful argument=True to keep the state accumulated within a batch?
Regards,
Ramy
Typically state is reset at the end of a batch. Stateful allows you to control when the state is reset.
Thanks for your reply.
I really have confusion about how often backprop. is applied, is it every sample or a batch?
In TF documentation, the batch size states number of samples per gradient update which means 1 update/batch.
and here I understand that the update happens after the sample size (500 in the example) whatever the batch size is.
Q1: Can you please clarify this point?
If it’s 1 update/batch then what will be the benefit from batching set of subsequences? it still a backprop. through the original long sequence.
Thanks in advance for your time.
Yes, one update per batch.
Yes, the benefit is grouping sequences on problems where that makes sense.
sequences are grouped in a batch but where’s the truncation?
it’s still backprop. through one long sequence.
I mean what’s the difference between backprop. through a batch of 100 examples each of 100 timestep and backprop. through a bacth of 1 example but 10000 timestep?
In keras, k1==k2, so we don’t get to control back prop truncation compared to the forward pass (i.e. forward and backward passes are over all time steps).
Perhaps this post on unrolling will help:
https://machinelearningmastery.com/rnn-unrolling/
Thanks, Jason for your time and explanation.
so that means if we have a sequence shaped as (n,k,d),
where n: is the number of subsequences (samples),
the only way to configure the NW in Keras to implement TBPTT(k,k) is to make the batch_size=1 while keeping the NW stateful and reset the state after each epoch.
If stateless then every subsequence (sample) is treated as a separate sequence.
This case will act as a mini-batch-gradient-descent learning but with keeping cross batch statefulness.
Could you please correct me if I’m mistaken?
Yes, I believe so.
From my understanding, one of the main benefits of RNN’s and LSTM over window size Multilayer perceptron trained on time series is that in the latter, one has to specify the window size. Thus we are specifically mentioning the range over where the pattern will display. In the former, I had understood that we do not need to specify where the pattern is displayed, thus the network can see very subtle patterns.
By creating timesteps, do we limit the range wherein the network can find a pattern? This seems possible to me as the gradient in learning on a limited part of the data at a time.
However, since LSTM does store memory, this memory could affect the learning in the future, thus increasing the range wherein the network finds pattern.
So as you can see, I am not sure of the answer. I would love a response.
P.S: Great series of articles, really appreciated.
Technically you’re right but in Keras, you need to attach an input layer to the LSTM and hence you still need to provide the window size.
Hi Oliver…You are correct regarding LSTMs and the memory storage. While this is a enables this network type to learn trends and seasonality of a dataset, keep in mind that for longer forecast horizons, training may be greatly affected and in some cases without optimization, may not even converge.