Machine learning and deep learning methods are often reported to be the key solution to all predictive modeling problems.
An important recent study evaluated and compared the performance of many classical and modern machine learning and deep learning methods on a large and diverse set of more than 1,000 univariate time series forecasting problems.
The results of this study suggest that simple classical methods, such as linear methods and exponential smoothing, outperform complex and sophisticated methods, such as decision trees, Multilayer Perceptrons (MLP), and Long Short-Term Memory (LSTM) network models.
These findings highlight the requirement to both evaluate classical methods and use their results as a baseline when evaluating any machine learning and deep learning methods for time series forecasting in order demonstrate that their added complexity is adding skill to the forecast.
In this post, you will discover the important findings of this recent study evaluating and comparing the performance of a classical and modern machine learning methods on a large and diverse set of time series forecasting datasets.
After reading this post, you will know:
Classical methods like ETS and ARIMA out-perform machine learning and deep learning methods for one-step forecasting on univariate datasets.
Classical methods like Theta and ARIMA out-perform machine learning and deep learning methods for multi-step forecasting on univariate datasets.
Machine learning and deep learning methods do not yet deliver on their promise for univariate time series forecasting, and there is much work to do.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
Findings Comparing Classical and Machine Learning Methods for Time Series Forecasting Photo by Lyndon Hatherall, some rights reserved.
In this post, we will take a close look at the study by Makridakis, et al. that carefully evaluated and compared classical time series forecasting methods to the performance of modern machine learning methods.
This post is divided into seven sections; they are:
Study Motivation
Time Series Datasets
Time Series Forecasting Methods
Data Preparation
One-Step Forecasting Results
Multi-Step Forecasting Results
Outcomes
Study Motivation
The goal of the study was to clearly demonstrate the capability of a suite of different machine learning methods as compared to classical time series forecasting methods on a very large and diverse collection of univariate time series forecasting problems.
The study was a response to the increasing number of papers and claims that machine learning and deep learning methods offer superior results for time series forecasting with little objective evidence.
Literally hundreds of papers propose new ML algorithms, suggesting methodological advances and accuracy improvements. Yet, limited objective evidence is available regarding their relative performance as a standard forecasting tool.
The authors clearly lay out three issues with the flood of claims; they are:
Their conclusions are based on a few, or even a single time series, raising questions about the statistical significance of the results and their generalization.
The methods are evaluated for short-term forecasting horizons, often one-step-ahead, not considering medium and long-term ones.
No benchmarks are used to compare the accuracy of ML methods versus alternative ones.
As a response, the study includes eight classical methods and 10 machine learning methods evaluated using one-step and multiple-step forecasts across a collection of 1,045 monthly time series.
Although not definitive, the results are intended to be objective and robust.
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Time Series Datasets
The time series datasets used in the study were drawn from the time series datasets used in the M3-Competition.
The M3-Competition was the third in a series of competitions that sought to discover exactly what algorithms perform well in practice on real time series forecasting problems. The results of the competition were published in the 2000 paper titled “The M3-Competition: Results, Conclusions and Implications.”
The datasets used in the competition were drawn from a wide range of industries and had a range of different time intervals, from hourly to annual.
The 3003 series of the M3-Competition were selected on a quota basis to include various types of time series data (micro, industry, macro, etc.) and different time intervals between successive observations (yearly, quarterly, etc.).
The table below, taken from the paper, provides a summary of the 3,003 datasets used in the competition.
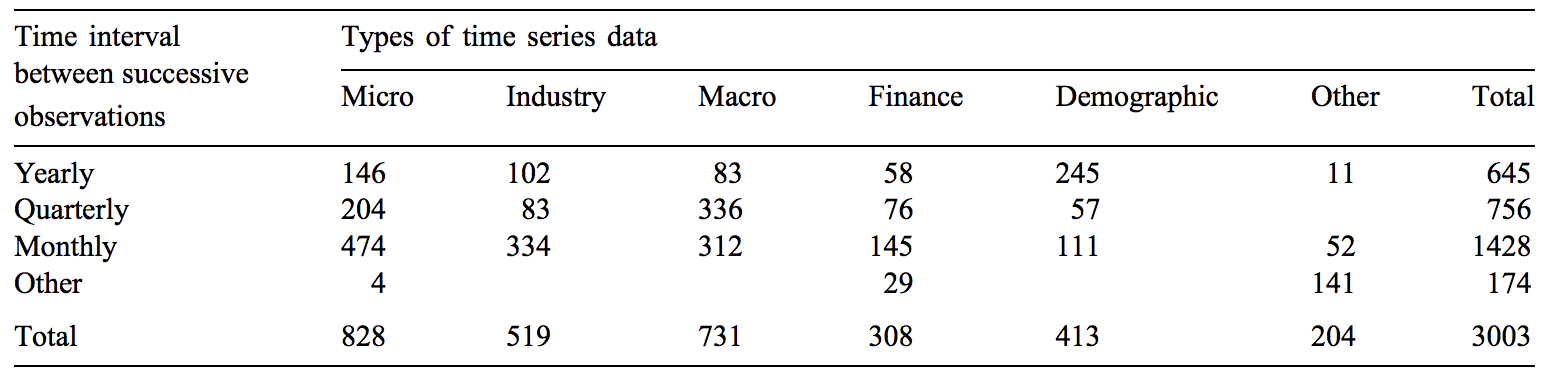
Table of Datasets, Industry and Time Interval Used in the M3-Competition Taken from “The M3-Competition: Results, Conclusions and Implications.”
The finding of the competition was that simpler time series forecasting methods outperform more sophisticated methods, including neural network models.
This study, the previous two M-Competitions and many other empirical studies have proven, beyond the slightest doubt, that elaborate theoretical constructs or more sophisticated methods do not necessarily improve post-sample forecasting accuracy, over simple methods, although they can better fit a statistical model to the available historical data.
The more recent study that we are reviewing in this post that evaluate machine learning methods selected a subset of 1,045 time series with a monthly interval from those used in the M3 competition.
… evaluate such performance across multiple forecasting horizons using a large subset of 1045 monthly time series used in the M3 Competition.
In that paper, each time series was adjusted using a power transform, deseasonalized and detrended.
[…] before computing the 18 forecasts, they preprocessed the series in order to achieve stationarity in their mean and variance. This was done using the log transformation, then deseasonalization and finally scaling, while first differences were also considered for removing the component of trend.
Inspired by these operations, variations of five different data transforms were applied for an MLP for one-step forecasting and their results were compared. The five transforms were:
Original data.
Box-Cox Power Transform.
Deseasonalizing the data.
Detrending the data.
All three transforms (power, deseasonalize, detrend).
Generally, it was found that the best approach was to apply a power transform and deseasonalize the data, and perhaps detrend the series as well.
The best combination according to sMAPE is number 7 (Box-Cox transformation, deseasonalization) while the best one according to MASE is number 10 (Box-Cox transformation, deseasonalization and detrending)
All models were evaluated using one-step time series forecasting.
Specifically, the last 18 time steps were used as a test set, and models were fit on all remaining observations. A separate one-step forecast was made for each of the 18 observations in the test set, presumably using a walk-forward validation method where true observations were used as input in order to make each forecast.
The forecasting model was developed using the first n – 18 observations, where n is the length of the series. Then, 18 forecasts were produced and their accuracy was evaluated compared to the actual values not used in developing the forecasting model.
A surprising result was that RNNs and LSTMs were found to perform poorly.
It should be noted that RNN is among the less accurate ML methods, demonstrating that research progress does not necessarily guarantee improvements in forecasting performance. This conclusion also applies in the performance of LSTM, another popular and more advanced ML method, which does not enhance forecasting accuracy too.
Comparing the performance of all methods, it was found that the machine learning methods were all out-performed by simple classical methods, where ETS and ARIMA models performed the best overall.
This finding confirms the results from previous similar studies and competitions.
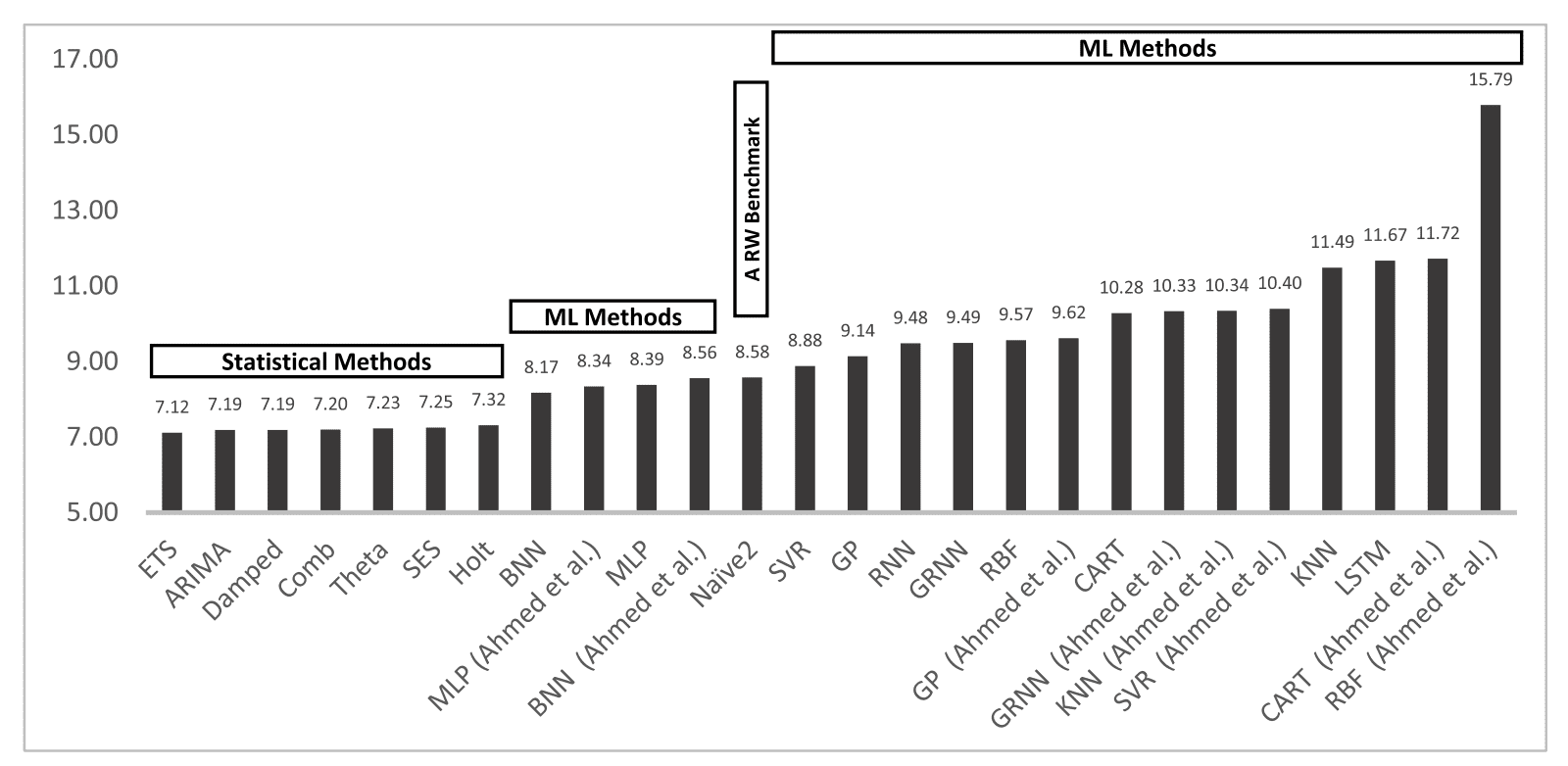
Bar Chart Comparing Model Performance (sMAPE) for One-Step Forecasts Taken from “Statistical and Machine Learning forecasting methods: Concerns and ways forward.”
Multi-Step Forecasting Results
Multi-step forecasting involves predicting multiple steps ahead of the last known observation.
Three approaches to multi-step forecasting were evaluated for the machine learning methods; they were:
Iterative forecasting
Direct forecasting
Multi-neural network forecasting
The classical methods were found to outperform the machine learning methods again.
In this case, methods such as Theta, ARIMA, and a combination of exponential smoothing (Comb) were found to achieve the best performance.
In brief, statistical models seem to generally outperform ML methods across all forecasting horizons, with Theta, Comb and ARIMA being the dominant ones among the competitors according to both error metrics examined.
The study provides important supporting evidence that classical methods may dominate univariate time series forecasting, at least on the types of forecasting problems evaluated.
The study demonstrates the worse performance and the increase in computational cost of machine learning and deep learning methods for univariate time series forecasting for both one-step and multi-step forecasts.
These findings strongly encourage the use of classical methods, such as ETS, ARIMA, and others as a first step before more elaborate methods are explored, and requires that the results from these simpler methods be used as a baseline in performance that more elaborate methods must clear in order to justify their usage.
It also highlights the need to not just consider the careful use of data preparation methods, but to actively test multiple different combinations of data preparation schemes for a given problem in order to discover what works best, even in the case of classical methods.
Machine learning and deep learning methods may still achieve better performance on specific univariate time series problems and should be evaluated.
The study does not look at more complex time series problems, such as those datasets with:
Complex irregular temporal structures.
Missing observations
Heavy noise.
Complex interrelationships between multiple variates.
The study concludes with an honest puzzlement at why machine learning methods perform so poorly in practice, given their impressive performance in other areas of artificial intelligence.
The most interesting question and greatest challenge is to find the reasons for their poor performance with the objective of improving their accuracy and exploiting their huge potential. AI learning algorithms have revolutionized a wide range of applications in diverse fields and there is no reason that the same cannot be achieved with the ML methods in forecasting. Thus, we must find how to be applied to improve their ability to forecast more accurately.
Comments are made by the authors regarding LSTMs and RNNs, that are generally believed to be the deep learning approach for sequence prediction problems in general, and in this case their clearly poor performance in practice.
[…] one would expect RNN and LSTM, which are more advanced types of NNs, to be far more accurate than the ARIMA and the rest of the statistical methods utilized.
They comment that LSTMs appear to be more suited at fitting or overfitting the training dataset rather than forecasting it.
Another interesting example could be the case of LSTM that compared to simpler NNs like RNN and MLP, report better model fitting but worse forecasting accuracy
There is work to do and machine learning methods and deep learning methods hold the promise of better learning time series data than classical statistical methods, and even doing so directly on the raw observations via automatic feature learning.
Given their ability to learn, ML methods should do better than simple benchmarks, like exponential smoothing. Accepting the problem is the first step in devising workable solutions and we hope that those in the field of AI and ML will accept the empirical findings and work to improve the forecasting accuracy of their methods.
In this post, you discovered the important findings of a recent study evaluating and comparing the performance of classical and modern machine learning methods on a large and diverse set of time series forecasting datasets.
Specifically, you learned:
Classical methods like ETS and ARIMA out-perform machine learning and deep learning methods for one-step forecasting on univariate datasets.
Classical methods like Theta and ARIMA out-perform machine learning and deep learning methods for multi-step forecasting on univariate datasets.
Machine learning and deep learning methods do not yet deliver on their promise for univariate time series forecasting and there is much work to do.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
Develop Deep Learning models for Time Series Today!
Thanks for posting this. I recently started going through a course on Time Series forecasting and this just confirms my need to understand the more basic and standard statistical methods before I look at deep-learning techniques.
Cool, like this write up. One question, it seems like it was all just univariate models am I right? Would be really curious to see something similar but using multivariate data and models.
Very informatinve thanks Jason. Confirmed what I’ve always assumed that more variables are probably required to give deep learning an upper hand in TS prediction.
I’m surprised that you don’t know of any comparative studies involving the latter?
Maybe this was stated in the readings, but it seems like for each time series, no work was done on feature selection / feature engineering, i.e. the inputs to both the traditional models and the ML models consisted solely of the time series’ own historical values?
The benchmarking has been done for various models with just time series as one of the input component and typical output as predictive component is that correct, if so whats the value plotted on the right side, and why is it mentioned as the basic statistic methods to be compartively better, can you throw some light on it
I’m don’t know much about time series analysis, but after you remove the trend and seasonality, aren’t you left with noise?
If this is true, it’s no wonder the large non-linear models are over-fitting the training set, and getting poor performance on the test sample. Basically, there is no signal for the model to fit to.
Yeah, I guess there would have to be some signal there. I should take a look at some of the time series in their dataset. I couldn’t find any images in their paper.
I’ve seen some stock market series with the trend and seasonality removed, and that just looks like noise to me. Maybe there is some time-dependence, in that one point is likely to be close to the previous point. That would explain why the moving-average type methods work well for predicting the next one or two points.
It seems that deep learning methods can’t learn effectively seasonality and trend, concerning simple methods. I am saying simple because Bengio has published a new method N-BEATS with a clever, I would say, architecture, that is superior to state space RNN without using any statistical concept.
Dear Dr Jason,
I have been going through “Deep Learning For Time Series Forecasting”. So far I am up to page 102. I have also gone through your other time series book.
At this point in my readings, under the “DL for TS forecasting” in developing a univariate forecast, you never had to specify the model for the simple examples. Compared to ‘classical’ time series forecasting, one has to specify whether it is AR, MA, ARIMA, SARIMA etc.
Could I come to the conclusion that despite classical univariate time series using AR, MA, ARIMA that using DL methods one does not have to think or concern about using AR, MA, ARIMA? Note I am up to p102 (pdf document) of the DL book.
For univariate problems, classical methods dominate. In some cases, methods like MLP and CNN can learn a reasonable model without the same data preparation, but a well configured classical model would almost certainly out perform it. Not always of course, just on most problems of interest.
This is good post for me.When i run my code .It loads to slow. I wait for it around 30 min but it does not occur the resullt.
# prepare the models to evaluate
Thanks for your sharing! As a begininger, I want to ask what is ‘univariate time series’ and how can you generate it or how can you judge whether it is a univariate time series or not?
Is there any python code ready to use to compare the performance of a classical time series model like SARIMAX with ML models? Maybe one of your books have it?
We shine this spotlight on the Multivariate Time Series,which is currently focused on by most people.More and more people regard LSTM as part of the model and claim to have achieved accurate results.There are many hybrid model,so LSTM is still play import role in Multivariate Time Series. Multivariate Time Series are more fit in reality.
Is there results from Comparing Classical and Machine Learning Methods for Multivariate Time Series Forecasting?
This is a very interesting post. Yes, I can see how especially in the univariate case the classical models would dominate. I think this idea of “classical” really means that those models make stronger assumptions about the data, such as the autocorrelation and decay of shocks–normally that $/rho$ parameter. So if the assumptions hold, then the classical models will learn faster. Seems like for DL or ML models, these have to actually learn the autocorrelation structure from the data, and this would take a longer number of epochs and require more data.
I think you are right on the money when you say that the model needs to match the data. Trying to use a high powered DL tool on a dataset that is too small just leads to lots of bad predictions.
Dear Jason,
I have fit a pretty ok neural networking model with a MAPE of 2,5% on my electrical demand forecast. Currently I am trying to compare it to an ARIMA model however I am having some trouble. My data is taken every half hour for almost a year so there are 16464 observations. My NN model has no problem using this data however at the moment my ARIMA(48,1,0) model doesn’t get past model.fit(disp=0), the program just keeps running until I keyboard interrupt. I am unsure whether my code is wrong(I don’t think it is), the data I am using is too large, etc.
In general is the runtime of an ARIMA model longer than that of training a NN?
Thanks.
For deseasonalization, we deseasonalize -> predict -> reseasonalize the prediction to get the real prediction value.
Do you have any post on how to re-apply the seasonality to the prediction value? Or if you could point to an example in one of your two time series books?
Using seasonal difference for deseasonalization and then inverse transform the prediction does not work so well. I suggest you to use STL decomposition and then train your model on the seasonal adjusted data. Now you have to make two predictions, one for the seasonal adjusted data using your trained model and one for the seasonal component using the seasonal naive method. Then you add those two predictions.
One concern with Makridakis paper, is that the research is biased towards using very small datasets as it is mentioned here https://arxiv.org/abs/1909.13316.
Do you know of a similar research to Makridakis’s (comparing many methods) that is based on large datasets? E.g. Few years of hourly time series, like air quality data.
I forgot to add that I am looking for a research that specifically includes NN (The Cerqueira et al paper you linked is very interesting, but doesn’t include NN).
Can’t we get the good results using the Machine Learning methods (ensembling methods) by preparing the dataset according to the lag and forecasting recursively or any other type of forecasting technique? If not, please point me to the resource why not?
I hope you are well. Thank you very much for all your posts they are very helpful.
I am currently working on an empirical analysis where I am applying both Arima and RBF Neural Net.
I have done a lot of research and it is really unclear to me whether I should make the data stationary before applying the neural net? some papers say that weak stationarity is the assumption under a NN but i have seen papers applying RBF NN on non stationary time series.
I could just go ahead and make everything stationary but maybe it is interesting to apply the RBF on both stationary and non stationary data. Any thoughts?
Try making the data stationary, fit the model then compare the results to a model fit on the raw data. Use the approach that results in the best performance.
Do you agree with the fact that stationarity in NN is not well discussed in the literature?
Do you also agree with the fact that weak stationarity is an assumption in NN? I have never been taught that when i went to NN class thats why i am a bit sceptical
A quick question on time series data prediction. My application is to predict human’s motion based the his current and past motion. Is it possible for me to do the prediction in real time with any of the machine learning method you introduced? I need the prediction in real time to control a robot to move in the space(I use the prediction to overcome the time dely).
I’ve been exploring exponential, HMM and LSTM. But haven’t made the prediction in real time. I am confused on which one to use. Can you please recommend?
1. What is the best metric for time series data ?
2. On what occasions do we make the series stationary ?? Is it for applying machine learning algorithms ? How do we interpret the predicted value in that case ?
3. For cross validation of time series , what would be the best way to do ?
a. Is it better to vary the train and test dates keeping the fixed length of train window and test window . OR b. keep incrementing train window , with a fixed test window OR c. Vary both the train window and test window ??
Thanks for your reply Jason.
Any references on how to interpret the predictions , after making the series stationary ?
Also , yes, I was referring to walk-forward validation. With in that method, whether to keep a fixed observations or sliding window format ?? Do we evaluate both these methods? Or depends on the case?
Hi, I just wondered was predicting in the M£ competition data is it price? and is one model to predict all the series of 3003 models are trained for each series?
Thanks, Jason for your supportive post and continuous advice.
I am doing research on Short, Medium, and Long Range Time Serious Rainfall Forecasting So have you a valuable post regarding this please link it to me.
Firstly thank you so much for putting up this content, really informative !
Suppose I’ve to forecast the sales for 100 stores for a retail chain, conventional methods like ARIMA (Auto Arima) will take a really long time to finish training.
In this kind of scenarios, I’ve found Machine learning models to give better accuracy and faster training.
What are your thoughts on using conventional time series models when data scale is large ?
Hi Jason! I am struggling to choose between using a ML model or time-series.
I have been working with Real World data, I have a dataset with info about 10million users, collected over a span of varying duration (5 to 20 years).
-Most features are constant (family history, smoker (y/n)…), but,
-I have some time-dependant features (e.g., weight, blood test values,…),
-(Also, these features were collected at different time points, i.e., for some users, we have semestral info, for others, we have 2 measures in 15 years)
-So far I have been predicting my target considering my features are static (by averaging values, or using the most recent one) using XGBoost Classifier or other classifiers.
-Could I try to use a time series for this case? Or just stick to ML Classifiers and try to incorporate the progression of values in another way?
There’s a cost in detrending and desasonalizing a time series. Therefore, a modern method like LSTM may be more useful if doesn’t demand these transformations in order to obtain convenient forecasting results.
Great feedback Hilton! Excellent point regarding LSTMs! It may prove helpful to establish a baseline of performance by utilizing classical algorithms such as ARIMA and then compare with deep learning methods such as CNN and LSTM. You may even find that classical methods outperform deep learning methods depending upon the data.
I was just wondering if there has been progress or any improvements at all on the ML and DL’s predictive abilities in forecasting? Do the classical methods like ARIMA still outperform those complex ones?
Thanks for posting this. I recently started going through a course on Time Series forecasting and this just confirms my need to understand the more basic and standard statistical methods before I look at deep-learning techniques.
You can get started with the basics here:
https://machinelearningmastery.com/start-here/#timeseries
Cool, like this write up. One question, it seems like it was all just univariate models am I right? Would be really curious to see something similar but using multivariate data and models.
Yes, just univariate data/models.
I agree, I similar study for multivariate datasets would be fascinating!
Very informatinve thanks Jason. Confirmed what I’ve always assumed that more variables are probably required to give deep learning an upper hand in TS prediction.
I’m surprised that you don’t know of any comparative studies involving the latter?
Agreed!
Such studies may exist, but I have not come across them, at least not at this level of robustness.
Appreciate the insightful article!
Maybe this was stated in the readings, but it seems like for each time series, no work was done on feature selection / feature engineering, i.e. the inputs to both the traditional models and the ML models consisted solely of the time series’ own historical values?
Could you confirm if this is true?
All of the data was univariate, only one feature to select.
Is your comment confirming what Terrence said or is it saying that with univariate data there’s ever only one feature to select? I thought you could do feature engineering with univariate data to create more than one feature. https://machinelearningmastery.com/basic-feature-engineering-time-series-data-python/
Univariate data has one variable.
You can engineer new features if you want.
Thanks for the clarification!
You’re welcome.
Thanks for this. Juicy!
Have you a ‘go to’ reference for survey of issues and methods for (quoting you)
Complex irregular temporal structures.
Missing observations
Heavy noise.
Complex interrelationships between multiple variates.
?
Thank you again …would gladly repay your effort with a coffee or drink any time you’re in the DMV.
Thanks!
Not at this stage.
The benchmarking has been done for various models with just time series as one of the input component and typical output as predictive component is that correct, if so whats the value plotted on the right side, and why is it mentioned as the basic statistic methods to be compartively better, can you throw some light on it
“Right side”?
I don’t follow, can you elaborate please?
I’m don’t know much about time series analysis, but after you remove the trend and seasonality, aren’t you left with noise?
If this is true, it’s no wonder the large non-linear models are over-fitting the training set, and getting poor performance on the test sample. Basically, there is no signal for the model to fit to.
Does this make sense?
Great question!
If you are left with noise, there there is nothing to predict.
The idea is that you are left with a time-dependent signal (that is not trend or seasonality) and noise.
Yeah, I guess there would have to be some signal there. I should take a look at some of the time series in their dataset. I couldn’t find any images in their paper.
I’ve seen some stock market series with the trend and seasonality removed, and that just looks like noise to me. Maybe there is some time-dependence, in that one point is likely to be close to the previous point. That would explain why the moving-average type methods work well for predicting the next one or two points.
Stock prices are just noise, called a random walk:
https://machinelearningmastery.com/gentle-introduction-random-walk-times-series-forecasting-python/
The best you can do is using a persistence model.
Interestingly, a ML-statistical approach won the recent M4 forecasting competition.
The combination was exponential smoothing and RNN. More information is here
https://eng.uber.com/m4-forecasting-competition/
https://www.sciencedirect.com/science/article/pii/S0169207018300785
Yes, it’s an interesting result. I hope to reproduce it myself soon.
According to this link
https://github.com/uber/pyro/issues/1287
The author is working on open-sourcing his model
Spyros told me the code for the method is open source here:
https://github.com/M4Competition/M4-methods/tree/master/118%20-%20slaweks17
It seems that deep learning methods can’t learn effectively seasonality and trend, concerning simple methods. I am saying simple because Bengio has published a new method N-BEATS with a clever, I would say, architecture, that is superior to state space RNN without using any statistical concept.
They can in some cases, LSTMs are particularly poor though.
Dear Dr Jason,
I have been going through “Deep Learning For Time Series Forecasting”. So far I am up to page 102. I have also gone through your other time series book.
At this point in my readings, under the “DL for TS forecasting” in developing a univariate forecast, you never had to specify the model for the simple examples. Compared to ‘classical’ time series forecasting, one has to specify whether it is AR, MA, ARIMA, SARIMA etc.
Could I come to the conclusion that despite classical univariate time series using AR, MA, ARIMA that using DL methods one does not have to think or concern about using AR, MA, ARIMA? Note I am up to p102 (pdf document) of the DL book.
Thank you,
Anthony of Sydney
Hmmm.
For univariate problems, classical methods dominate. In some cases, methods like MLP and CNN can learn a reasonable model without the same data preparation, but a well configured classical model would almost certainly out perform it. Not always of course, just on most problems of interest.
This is good post for me.When i run my code .It loads to slow. I wait for it around 30 min but it does not occur the resullt.
# prepare the models to evaluate
Defined 10 models
Traceback (most recent call last):
Perhaps try running with less data?
The shape of my dataset is 6200 . Have any method do time series air quality ?
I recommend testing a suite of methods in order to discover what works best for your specific dataset.
the shape of my dataset is (6200,22 ), i try to use 1:-328 for training data but not have result
Thanks for your sharing! As a begininger, I want to ask what is ‘univariate time series’ and how can you generate it or how can you judge whether it is a univariate time series or not?
A univariate time series is a single variable observed over time.
A good place to get started with time series is here:
https://machinelearningmastery.com/start-here/#timeseries
Is there any python code ready to use to compare the performance of a classical time series model like SARIMAX with ML models? Maybe one of your books have it?
There are examples in the deep learning for time series book for evaluating each model type separately, you can then compare the results yourself.
We shine this spotlight on the Multivariate Time Series,which is currently focused on by most people.More and more people regard LSTM as part of the model and claim to have achieved accurate results.There are many hybrid model,so LSTM is still play import role in Multivariate Time Series. Multivariate Time Series are more fit in reality.
Is there results from Comparing Classical and Machine Learning Methods for Multivariate Time Series Forecasting?
Not on this level, hopefully we see a similar study on the topic soon.
This is a very interesting post. Yes, I can see how especially in the univariate case the classical models would dominate. I think this idea of “classical” really means that those models make stronger assumptions about the data, such as the autocorrelation and decay of shocks–normally that $/rho$ parameter. So if the assumptions hold, then the classical models will learn faster. Seems like for DL or ML models, these have to actually learn the autocorrelation structure from the data, and this would take a longer number of epochs and require more data.
I think you are right on the money when you say that the model needs to match the data. Trying to use a high powered DL tool on a dataset that is too small just leads to lots of bad predictions.
Thanks, I agree and very well put!
Having more knowledge of your data allows you to build assumptions into your model (or choose models with those assumptions) and in turn do well.
Dear Jason,
I have fit a pretty ok neural networking model with a MAPE of 2,5% on my electrical demand forecast. Currently I am trying to compare it to an ARIMA model however I am having some trouble. My data is taken every half hour for almost a year so there are 16464 observations. My NN model has no problem using this data however at the moment my ARIMA(48,1,0) model doesn’t get past model.fit(disp=0), the program just keeps running until I keyboard interrupt. I am unsure whether my code is wrong(I don’t think it is), the data I am using is too large, etc.
In general is the runtime of an ARIMA model longer than that of training a NN?
Thanks.
Perhaps try a simpler AR or a more advanced SARIMA?
Perhaps try a linear regression model directly?
i faced same problem.
try using lesser seasonality value in ARIMA. it would solve the problem.
Thanks for sharing.
Hello Jason,
Great work! Is there any python package for Theta method?
Thanks.
I’m not sure off-hand. I don’t recall seeing one.
Thank you for your post!
For deseasonalization, we deseasonalize -> predict -> reseasonalize the prediction to get the real prediction value.
Do you have any post on how to re-apply the seasonality to the prediction value? Or if you could point to an example in one of your two time series books?
Thanks!
Correct.
Yes, see this:
https://machinelearningmastery.com/machine-learning-data-transforms-for-time-series-forecasting/
Using seasonal difference for deseasonalization and then inverse transform the prediction does not work so well. I suggest you to use STL decomposition and then train your model on the seasonal adjusted data. Now you have to make two predictions, one for the seasonal adjusted data using your trained model and one for the seasonal component using the seasonal naive method. Then you add those two predictions.
I disagree in general, seasonal differencing can be very effective. Data dependent.
Try many transforms and compare result – this is unbeatable advice.
One concern with Makridakis paper, is that the research is biased towards using very small datasets as it is mentioned here https://arxiv.org/abs/1909.13316.
Agreed. But the univariate datasets are representative of what most devs/beginners use with LSTMs.
Do you know of a similar research to Makridakis’s (comparing many methods) that is based on large datasets? E.g. Few years of hourly time series, like air quality data.
Thanks
I forgot to add that I am looking for a research that specifically includes NN (The Cerqueira et al paper you linked is very interesting, but doesn’t include NN).
Not off hand.
Hello Brownlee,
Can’t we get the good results using the Machine Learning methods (ensembling methods) by preparing the dataset according to the lag and forecasting recursively or any other type of forecasting technique? If not, please point me to the resource why not?
Perhaps, depends on the specifics of your data and your chosen model.
For univariate data, a good linear model will crush almost every other method. E.g. a good SARIMA or ETS.
Why? Unknowable. All we have is a ton of evidence from empirical studies.
Dear Jason,
I hope you are well. Thank you very much for all your posts they are very helpful.
I am currently working on an empirical analysis where I am applying both Arima and RBF Neural Net.
I have done a lot of research and it is really unclear to me whether I should make the data stationary before applying the neural net? some papers say that weak stationarity is the assumption under a NN but i have seen papers applying RBF NN on non stationary time series.
I could just go ahead and make everything stationary but maybe it is interesting to apply the RBF on both stationary and non stationary data. Any thoughts?
Thank you a lot
https://www.researchgate.net/publication/5384895_Trend_Time-Series_Modeling_and_Forecasting_With_Neural_Networks
Try making the data stationary, fit the model then compare the results to a model fit on the raw data. Use the approach that results in the best performance.
thank you Jason. I ll go ahead and do that.
Do you agree with the fact that stationarity in NN is not well discussed in the literature?
Do you also agree with the fact that weak stationarity is an assumption in NN? I have never been taught that when i went to NN class thats why i am a bit sceptical
Thank you very much Sir!
Sure.
Yes.
Remain skeptical of all results. The models are trying to fool you. Worse, you’re trying to fool yourself.
Hey Jason Brownlee,
Prophet is recently developed by Facebook for time series forecasting.
Is it a Machine Learning time series Or classical time series?
Machine learning.
Hi Jason,
A quick question on time series data prediction. My application is to predict human’s motion based the his current and past motion. Is it possible for me to do the prediction in real time with any of the machine learning method you introduced? I need the prediction in real time to control a robot to move in the space(I use the prediction to overcome the time dely).
I’ve been exploring exponential, HMM and LSTM. But haven’t made the prediction in real time. I am confused on which one to use. Can you please recommend?
Yes, this may help:
https://machinelearningmastery.com/how-to-develop-rnn-models-for-human-activity-recognition-time-series-classification/
ETS?
ARIMA?
Etc, Etc,
Nothing worse than learning a new subject when you have stop every miute and go and look up an acronym!
Agreed.
ETS: Error, Trend, and Seasonality
https://machinelearningmastery.com/how-to-grid-search-triple-exponential-smoothing-for-time-series-forecasting-in-python/
ARIMA: autoregressive integrated moving average
https://machinelearningmastery.com/arima-for-time-series-forecasting-with-python/
Hey Jason .
Kindly help with the following clarifications:
1. What is the best metric for time series data ?
2. On what occasions do we make the series stationary ?? Is it for applying machine learning algorithms ? How do we interpret the predicted value in that case ?
3. For cross validation of time series , what would be the best way to do ?
a. Is it better to vary the train and test dates keeping the fixed length of train window and test window . OR b. keep incrementing train window , with a fixed test window OR c. Vary both the train window and test window ??
Thanks so much!
Vidya
Thanks !
You must choose a metric that best captures the goals of your project.
It is generally a good practice to make a time series stationary.
Cross validation is invalid for time series, you must use walk-forward validation.
Thanks for your reply Jason.
Any references on how to interpret the predictions , after making the series stationary ?
Also , yes, I was referring to walk-forward validation. With in that method, whether to keep a fixed observations or sliding window format ?? Do we evaluate both these methods? Or depends on the case?
Thanks!
It must be a sliding window, not sure how you can achieve walk forward validation with a fixed input.
Hi, I just wondered was predicting in the M£ competition data is it price? and is one model to predict all the series of 3003 models are trained for each series?
Yes, a given algorithm is applied to each series.
Thanks, Jason for your supportive post and continuous advice.
I am doing research on Short, Medium, and Long Range Time Serious Rainfall Forecasting So have you a valuable post regarding this please link it to me.
Perhaps you can adapt the tutorials here for your dataset:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
Hi Jason,
Firstly thank you so much for putting up this content, really informative !
Suppose I’ve to forecast the sales for 100 stores for a retail chain, conventional methods like ARIMA (Auto Arima) will take a really long time to finish training.
In this kind of scenarios, I’ve found Machine learning models to give better accuracy and faster training.
What are your thoughts on using conventional time series models when data scale is large ?
You’re welcome.
Good question, this will give you some ideas:
https://machinelearningmastery.com/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites
Hi Jason! I am struggling to choose between using a ML model or time-series.
I have been working with Real World data, I have a dataset with info about 10million users, collected over a span of varying duration (5 to 20 years).
-Most features are constant (family history, smoker (y/n)…), but,
-I have some time-dependant features (e.g., weight, blood test values,…),
-(Also, these features were collected at different time points, i.e., for some users, we have semestral info, for others, we have 2 measures in 15 years)
-So far I have been predicting my target considering my features are static (by averaging values, or using the most recent one) using XGBoost Classifier or other classifiers.
-Could I try to use a time series for this case? Or just stick to ML Classifiers and try to incorporate the progression of values in another way?
Perhaps try both and discover what works well or best for your problem.
Hi Jason, can one use nueral network (MLP) in SPSS to forcast time series data?
Sorry, I don’t know about SPSS.
Thanks for your great work, Jason !
There’s a cost in detrending and desasonalizing a time series. Therefore, a modern method like LSTM may be more useful if doesn’t demand these transformations in order to obtain convenient forecasting results.
Great feedback Hilton! Excellent point regarding LSTMs! It may prove helpful to establish a baseline of performance by utilizing classical algorithms such as ARIMA and then compare with deep learning methods such as CNN and LSTM. You may even find that classical methods outperform deep learning methods depending upon the data.
Hi Jason,
I was just wondering if there has been progress or any improvements at all on the ML and DL’s predictive abilities in forecasting? Do the classical methods like ARIMA still outperform those complex ones?
Thanks in advance,
J
Hi Johnson…For most time series forecasting tasks, we recommend deep learning models:
https://machinelearningmastery.com/start-here/#deep_learning_time_series