Basic Feature Engineering With Time Series Data in Python

Time Series data must be re-framed as a supervised learning dataset before we can start using machine learning algorithms.

There is no concept of input and output features in time series. Instead, we must choose the variable to be predicted and use feature engineering to construct all of the inputs that will be used to make predictions for future time steps.

In this tutorial, you will discover how to perform feature engineering on time series data with Python to model your time series problem with machine learning algorithms.

After completing this tutorial, you will know:

• The rationale and goals of feature engineering time series data.
• How to develop basic date-time based input features.
• How to develop more sophisticated lag and sliding window summary statistics features.

Kick-start your project with my new book Time Series Forecasting With Python, including step-by-step tutorials and the Python source code files for all examples.

Let’s dive in.

• Updated Jun/2017: Fixed a typo in the expanding window code example.
• Updated Apr/2019: Updated the link to dataset.
• Updated Aug/2019: Updated data loading to use new API.
• Updated Sep/2019: Fixed bug in data loading.

Basic Feature Engineering With Time Series Data in Python
Photo by José Morcillo Valenciano, some rights reserved.

Feature Engineering for Time Series

A time series dataset must be transformed to be modeled as a supervised learning problem.

That is something that looks like:

To something that looks like:

So that we can train a supervised learning algorithm.

Input variables are also called features in the field of machine learning, and the task before us is to create or invent new input features from our time series dataset. Ideally, we only want input features that best help the learning methods model the relationship between the inputs (X) and the outputs (y) that we would like to predict.

In this tutorial, we will look at three classes of features that we can create from our time series dataset:

1. Date Time Features: these are components of the time step itself for each observation.
2. Lag Features: these are values at prior time steps.
3. Window Features: these are a summary of values over a fixed window of prior time steps.

Before we dive into methods for creating input features from our time series data, let’s first review the goal of feature engineering.

Goal of Feature Engineering

The goal of feature engineering is to provide strong and ideally simple relationships between new input features and the output feature for the supervised learning algorithm to model.

In effect, we are are moving complexity.

Complexity exists in the relationships between the input and output data. In the case of time series, there is no concept of input and output variables; we must invent these too and frame the supervised learning problem from scratch.

We may lean on the capability of sophisticated models to decipher the complexity of the problem. We can make the job for these models easier (and even use simpler models) if we can better expose the inherent relationship between inputs and outputs in the data.

The difficulty is that we do not know the underlying inherent functional relationship between inputs and outputs that we’re trying to expose. If we did know, we probably would not need machine learning.

Instead, the only feedback we have is the performance of models developed on the supervised learning datasets or “views” of the problem we create. In effect, the best default strategy is to use all the knowledge available to create many good datasets from your time series dataset and use model performance (and other project requirements) to help determine what good features and good views of your problem happen to be.

For clarity, we will focus on a univariate (one variable) time series dataset in the examples, but these methods are just as applicable to multivariate time series problems. Next, let’s take a look at the dataset we will use in this tutorial.

Minimum Daily Temperatures Dataset

In this post, we will use the Minimum Daily Temperatures dataset.

This dataset describes the minimum daily temperatures over 10 years (1981-1990) in Melbourne, Australia.

The units are in degrees Celsius and there are 3,650 observations. The source of the data is credited as the Australian Bureau of Meteorology.

• Download the dataset.

Below is a sample of the first 5 rows of data, including the header row.

Below is a plot of the entire dataset.

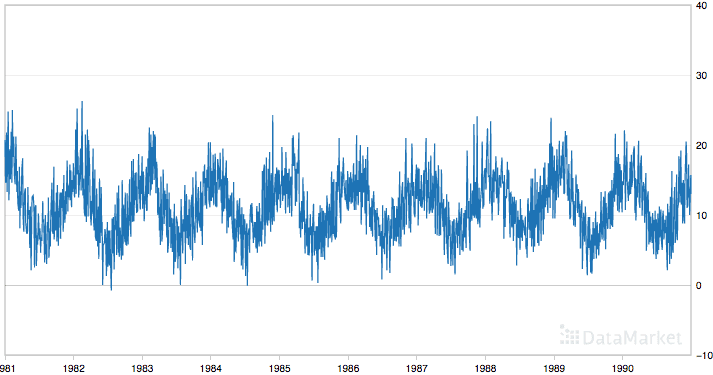
Minimum Daily Temperatures

The dataset shows an increasing trend and possibly some seasonal components.

• Download the dataset.

Date Time Features

Let’s start with some of the simplest features that we can use.

These are features from the date/time of each observation. In fact, these can start off simply and head off into quite complex domain-specific areas.

Two features that we can start with are the integer month and day for each observation. We can imagine that supervised learning algorithms may be able to use these inputs to help tease out time-of-year or time-of-month type seasonality information.

The supervised learning problem we are proposing is to predict the daily minimum temperature given the month and day, as follows:

We can do this using Pandas. First, the time series is loaded as a Pandas Series. We then create a new Pandas DataFrame for the transformed dataset.

Next, each column is added one at a time where month and day information is extracted from the time-stamp information for each observation in the series.

Below is the Python code to do this.

Running this example prints the first 5 rows of the transformed dataset.

Using just the month and day information alone to predict temperature is not sophisticated and will likely result in a poor model. Nevertheless, this information coupled with additional engineered features may ultimately result in a better model.

You may enumerate all the properties of a time-stamp and consider what might be useful for your problem, such as:

• Minutes elapsed for the day.
• Hour of day.
• Business hours or not.
• Weekend or not.
• Season of the year.
• Business quarter of the year.
• Daylight savings or not.
• Public holiday or not.
• Leap year or not.

From these examples, you can see that you’re not restricted to the raw integer values. You can use binary flag features as well, like whether or not the observation was recorded on a public holiday.

In the case of the minimum temperature dataset, maybe the season would be more relevant. It is creating domain-specific features like this that are more likely to add value to your model.

Date-time based features are a good start, but it is often a lot more useful to include the values at previous time steps. These are called lagged values and we will look at adding these features in the next section.

Lag Features

Lag features are the classical way that time series forecasting problems are transformed into supervised learning problems.

The simplest approach is to predict the value at the next time (t+1) given the value at the previous time (t-1). The supervised learning problem with shifted values looks as follows:

The Pandas library provides the shift() function to help create these shifted or lag features from a time series dataset. Shifting the dataset by 1 creates the t-1 column, adding a NaN (unknown) value for the first row. The time series dataset without a shift represents the t+1.

Let’s make this concrete with an example. The first 3 values of the temperature dataset are 20.7, 17.9, and 18.8. The shifted and unshifted lists of temperatures for the first 3 observations are therefore:

We can concatenate the shifted columns together into a new DataFrame using the concat() function along the column axis (axis=1).

Putting this all together, below is an example of creating a lag feature for our daily temperature dataset. The values are extracted from the loaded series and a shifted and unshifted list of these values is created. Each column is also named in the DataFrame for clarity.

Running the example prints the first 5 rows of the new dataset with the lagged feature.

You can see that we would have to discard the first row to use the dataset to train a supervised learning model, as it does not contain enough data to work with.

The addition of lag features is called the sliding window method, in this case with a window width of 1. It is as though we are sliding our focus along the time series for each observation with an interest in only what is within the window width.

We can expand the window width and include more lagged features. For example, below is the above case modified to include the last 3 observed values to predict the value at the next time step.

Running this example prints the first 5 rows of the new lagged dataset.

Again, you can see that we must discard the first few rows that do not have enough data to train a supervised model.

A difficulty with the sliding window approach is how large to make the window for your problem.

Perhaps a good starting point is to perform a sensitivity analysis and try a suite of different window widths to in turn create a suite of different “views” of your dataset and see which results in better performing models. There will be a point of diminishing returns.

Additionally, why stop with a linear window? Perhaps you need a lag value from last week, last month, and last year. Again, this comes down to the specific domain.

In the case of the temperature dataset, a lag value from the same day in the previous year or previous few years may be useful.

We can do more with a window than include the raw values. In the next section, we’ll look at including features that summarize statistics across the window.

Rolling Window Statistics

A step beyond adding raw lagged values is to add a summary of the values at previous time steps.

We can calculate summary statistics across the values in the sliding window and include these as features in our dataset. Perhaps the most useful is the mean of the previous few values, also called the rolling mean.

For example, we can calculate the mean of the previous two values and use that to predict the next value. For the temperature data, we would have to wait 3 time steps before we had 2 values to take the average of before we could use that value to predict a 3rd value.

For example:

Pandas provides a rolling() function that creates a new data structure with the window of values at each time step. We can then perform statistical functions on the window of values collected for each time step, such as calculating the mean.

First, the series must be shifted. Then the rolling dataset can be created and the mean values calculated on each window of two values.

Here are the values in the first three rolling windows:

This suggests that we will not have usable data until the 3rd row.

Finally, as in the previous section, we can use the concat() function to construct a new dataset with just our new columns.

The example below demonstrates how to do this with Pandas with a window size of 2.

Running the example prints the first 5 rows of the new dataset. We can see that the first two rows are not useful.

• The first NaN was created by the shift of the series.
• The second because NaN cannot be used to calculate a mean value.
• Finally, the third row shows the expected value of 19.30 (the mean of 20.7 and 17.9) used to predict the 3rd value in the series of 18.8.

There are more statistics we can calculate and even different mathematical ways of calculating the definition of the “window.”

Below is another example that shows a window width of 3 and a dataset comprised of more summary statistics, specifically the minimum, mean, and maximum value in the window.

You can see in the code that we are explicitly specifying the sliding window width as a named variable. This lets us use it both in calculating the correct shift of the series and in specifying the width of the window to the rolling() function.

In this case, the window width of 3 means we must shift the series forward by 2 time steps. This makes the first two rows NaN. Next, we need to calculate the window statistics with 3 values per window. It takes 3 rows before we even have enough data from the series in the window to start calculating statistics. The values in the first 5 windows are as follows:

This suggests that we would not expect usable data until at least the 5th row (array index 4)

Running the code prints the first 5 rows of the new dataset.

We can spot check the correctness of the values on the 5th row (array index 4). We can see that indeed 17.9 is the minimum and 20.7 is the maximum of values in the window of [20.7, 17.9, 18.8].

Expanding Window Statistics

Another type of window that may be useful includes all previous data in the series.

This is called an expanding window and can help with keeping track of the bounds of observable data. Like the rolling() function on DataFrame, Pandas provides an expanding() function that collects sets of all prior values for each time step.

These lists of prior numbers can be summarized and included as new features. For example, below are the lists of numbers in the expanding window for the first 5 time steps of the series:

Again, you can see that we must shift the series one-time step to ensure that the output value we wish to predict is excluded from these window values. Therefore the input windows look as follows:

Thankfully, the statistical calculations exclude the NaN values in the expanding window, meaning no further modification is required.

Below is an example of calculating the minimum, mean, and maximum values of the expanding window on the daily temperature dataset.

Running the example prints the first 5 rows of the dataset.

Spot checking the expanding minimum, mean, and maximum values shows the example having the intended effect.

Summary

In this tutorial, you discovered how to use feature engineering to transform a time series dataset into a supervised learning dataset for machine learning.

Specifically, you learned:

• The importance and goals of feature engineering time series data.
• How to develop date-time and lag-based features.
• How to develop sliding and expanding window summary statistic features.

Do you know of more feature engineering methods for time series?
Let me know in the comments below.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

Want to Develop Time Series Forecasts with Python?

Develop Your Own Forecasts in Minutes

...with just a few lines of python code

Discover how in my new Ebook:
Introduction to Time Series Forecasting With Python

It covers self-study tutorials and end-to-end projects on topics like: Loading data, visualization, modeling, algorithm tuning, and much more...

Finally Bring Time Series Forecasting to
Your Own Projects

Skip the Academics. Just Results.

See What's Inside