How to Create an ARIMA Model for Time Series Forecasting in Python

By Jason Brownlee on November 18, 2023 in Time Series 834

A popular and widely used statistical method for time series forecasting is the ARIMA model.

ARIMA stands for AutoRegressive Integrated Moving Average and represents a cornerstone in time series forecasting. It is a statistical method that has gained immense popularity due to its efficacy in handling various standard temporal structures present in time series data.

In this tutorial, you will discover how to develop an ARIMA model for time series forecasting in Python.

After completing this tutorial, you will know:

About the ARIMA model the parameters used and assumptions made by the model.
How to fit an ARIMA model to data and use it to make forecasts.
How to configure the ARIMA model on your time series problem.

Kick-start your project with my new book Time Series Forecasting With Python, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

Updated Apr/2019: Updated the link to dataset.
Updated Sep/2019: Updated examples to use latest API.
Updated Dec/2020: Updated examples to use latest API.
Updated Nov/2023: #####

Autoregressive Integrated Moving Average Model

The ARIMA (AutoRegressive Integrated Moving Average) model stands as a statistical powerhouse for analyzing and forecasting time series data.

It explicitly caters to a suite of standard structures in time series data, and as such provides a simple yet powerful method for making skillful time series forecasts.

ARIMA is an acronym that stands for AutoRegressive Integrated Moving Average. It is a generalization of the simpler AutoRegressive Moving Average and adds the notion of integration.

Let’s decode the essence of ARIMA:

AR (Autoregression): This emphasizes the dependent relationship between an observation and its preceding or ‘lagged’ observations.
I (Integrated): To achieve a stationary time series, one that doesn’t exhibit trend or seasonality, differencing is applied. It typically involves subtracting an observation from its preceding observation.
MA (Moving Average): This component zeroes in on the relationship between an observation and the residual error from a moving average model based on lagged observations.

Each of these components is explicitly specified in the model as a parameter. A standard notation is used for ARIMA(p,d,q) where the parameters are substituted with integer values to quickly indicate the specific ARIMA model being used.

The parameters of the ARIMA model are defined as follows:

p: The lag order, representing the number of lag observations incorporated in the model.
d: Degree of differencing, denoting the number of times raw observations undergo differencing.
q: Order of moving average, indicating the size of the moving average window.

A linear regression model is constructed including the specified number and type of terms, and the data is prepared by a degree of differencing to make it stationary, i.e. to remove trend and seasonal structures that negatively affect the regression model.

Interestingly, any of these parameters can be set to 0. Such configurations enable the ARIMA model to mimic the functions of simpler models like ARMA, AR, I, or MA.

Adopting an ARIMA model for a time series assumes that the underlying process that generated the observations is an ARIMA process. This may seem obvious but helps to motivate the need to confirm the assumptions of the model in the raw observations and the residual errors of forecasts from the model.

Next, let’s take a look at how we can use the ARIMA model in Python. We will start with loading a simple univariate time series.

Stop learning Time Series Forecasting the slow way!

Take my free 7-day email course and discover how to get started (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Shampoo Sales Dataset

The Shampoo Sales dataset provides a snapshot of monthly shampoo sales spanning three years, resulting in 36 observations. Each observation is a sales count. The genesis of this dataset is attributed to Makridakis, Wheelwright, and Hyndman (1998).

Getting Started:

Download the dataset
Save it to your current working directory with the filename “shampoo-sales.csv”.

Loading and Visualizing the Dataset:

Below is an example of loading the Shampoo Sales dataset with Pandas with a custom function to parse the date-time field. The dataset is baselined in an arbitrary year, in this case 1900.

from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot

def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
print(series.head())
series.plot()
pyplot.show()

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

print(series.head())

series.plot()

pyplot.show()

When executed, this code snippet will display the initial five dataset entries:

Month
1901-01-01 266.0
1901-02-01 145.9
1901-03-01 183.1
1901-04-01 119.3
1901-05-01 180.3
Name: Sales, dtype: float64

Month

1901-01-01 266.0

1901-02-01 145.9

1901-03-01 183.1

1901-04-01 119.3

1901-05-01 180.3

Name: Sales, dtype: float64

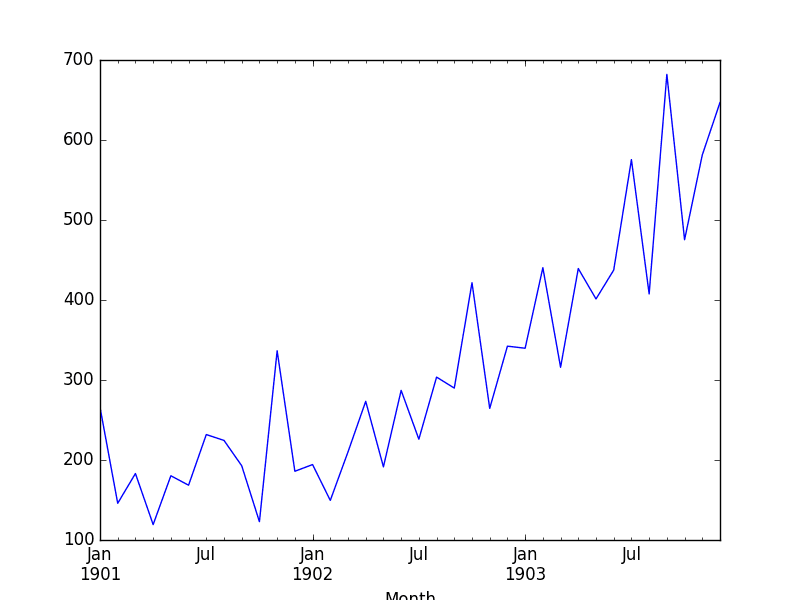
Shampoo Sales Dataset Plot

The data is also plotted as a time series with the month along the x-axis and sales figures on the y-axis.

We can see that the Shampoo Sales dataset has a clear trend. This suggests that the time series is not stationary and will require differencing to make it stationary, at least a difference order of 1.

Pandas offers a built-in capability to plot autocorrelations. The following example showcases the autocorrelation for an extensive set of time series lags:

from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot

def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
autocorrelation_plot(series)
pyplot.show()

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

from pandas.plotting import autocorrelation_plot

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

autocorrelation_plot(series)

pyplot.show()

Running the example, we can see that there is a positive correlation with the first 10-to-12 lags that is perhaps significant for the first 5 lags.

This provides a hint: initiating the AR parameter of our model with a value of 5 could be a beneficial starting point.

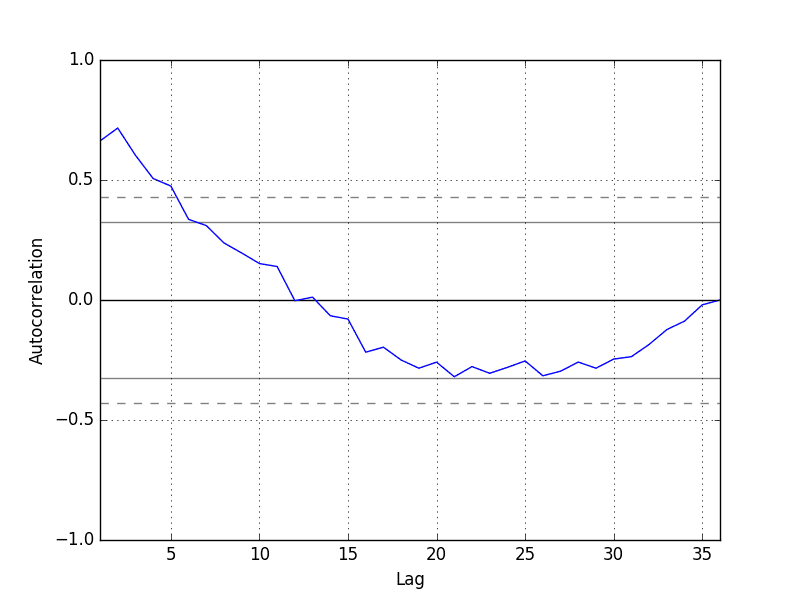
Autocorrelation Plot of Shampoo Sales Data

ARIMA with Python

The statsmodels library stands as a vital tool for those looking to harness the power of ARIMA for time series forecasting in Python.

Building an ARIMA Model: A Step-by-Step Guide:

Model Definition: Initialize the ARIMA model by invoking ARIMA() and specifying the p, d, and q parameters.
Model Training: Train the model on your dataset using the fit() method.
Making Predictions: Generate forecasts by utilizing the predict() function and designating the desired time index or indices.

Let’s start with something simple. We will fit an ARIMA model to the entire Shampoo Sales dataset and review the residual errors.

We’ll employ the ARIMA(5,1,0) configuration:

5 lags for autoregression (AR)
1st order differencing (I)
No moving average term (MA)

# fit an ARIMA model and plot residual errors
from pandas import datetime
from pandas import read_csv
from pandas import DataFrame
from statsmodels.tsa.arima.model import ARIMA
from matplotlib import pyplot
# load dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)
series.index = series.index.to_period('M')
# fit model
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit()
# summary of fit model
print(model_fit.summary())
# line plot of residuals
residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
# density plot of residuals
residuals.plot(kind='kde')
pyplot.show()
# summary stats of residuals
print(residuals.describe())

# fit an ARIMA model and plot residual errors

from pandas import datetime

from pandas import read_csv

from pandas import DataFrame

from statsmodels.tsa.arima.model import ARIMA

from matplotlib import pyplot

# load dataset

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)

series.index = series.index.to_period('M')

# fit model

model = ARIMA(series, order=(5,1,0))

model_fit = model.fit()

# summary of fit model

print(model_fit.summary())

# line plot of residuals

residuals = DataFrame(model_fit.resid)

residuals.plot()

pyplot.show()

# density plot of residuals

residuals.plot(kind='kde')

pyplot.show()

# summary stats of residuals

print(residuals.describe())

Running the example prints a summary of the fit model. This summarizes the coefficient values used as well as the skill of the fit on the on the in-sample observations.

                               SARIMAX Results
==============================================================================
Dep. Variable:                  Sales   No. Observations:                   36
Model:                 ARIMA(5, 1, 0)   Log Likelihood                -198.485
Date:                Thu, 10 Dec 2020   AIC                            408.969
Time:                        09:15:01   BIC                            418.301
Sample:                    01-31-1901   HQIC                           412.191
                         - 12-31-1903
Covariance Type:                  opg
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1         -0.9014      0.247     -3.647      0.000      -1.386      -0.417
ar.L2         -0.2284      0.268     -0.851      0.395      -0.754       0.298
ar.L3          0.0747      0.291      0.256      0.798      -0.497       0.646
ar.L4          0.2519      0.340      0.742      0.458      -0.414       0.918
ar.L5          0.3344      0.210      1.593      0.111      -0.077       0.746
sigma2      4728.9608   1316.021      3.593      0.000    2149.607    7308.314
===================================================================================
Ljung-Box (L1) (Q):                   0.61   Jarque-Bera (JB):                 0.96
Prob(Q):                              0.44   Prob(JB):                         0.62
Heteroskedasticity (H):               1.07   Skew:                             0.28
Prob(H) (two-sided):                  0.90   Kurtosis:                         2.41
===================================================================================

SARIMAX Results

==============================================================================

Dep. Variable: Sales No. Observations: 36

Model: ARIMA(5, 1, 0) Log Likelihood -198.485

Date: Thu, 10 Dec 2020 AIC 408.969

Time: 09:15:01 BIC 418.301

Sample: 01-31-1901 HQIC 412.191

- 12-31-1903

Covariance Type: opg

==============================================================================

coef std err z P>|z| [0.025 0.975]

------------------------------------------------------------------------------

ar.L1 -0.9014 0.247 -3.647 0.000 -1.386 -0.417

ar.L2 -0.2284 0.268 -0.851 0.395 -0.754 0.298

ar.L3 0.0747 0.291 0.256 0.798 -0.497 0.646

ar.L4 0.2519 0.340 0.742 0.458 -0.414 0.918

ar.L5 0.3344 0.210 1.593 0.111 -0.077 0.746

sigma2 4728.9608 1316.021 3.593 0.000 2149.607 7308.314

===================================================================================

Ljung-Box (L1) (Q): 0.61 Jarque-Bera (JB): 0.96

Prob(Q): 0.44 Prob(JB): 0.62

Heteroskedasticity (H): 1.07 Skew: 0.28

Prob(H) (two-sided): 0.90 Kurtosis: 2.41

===================================================================================

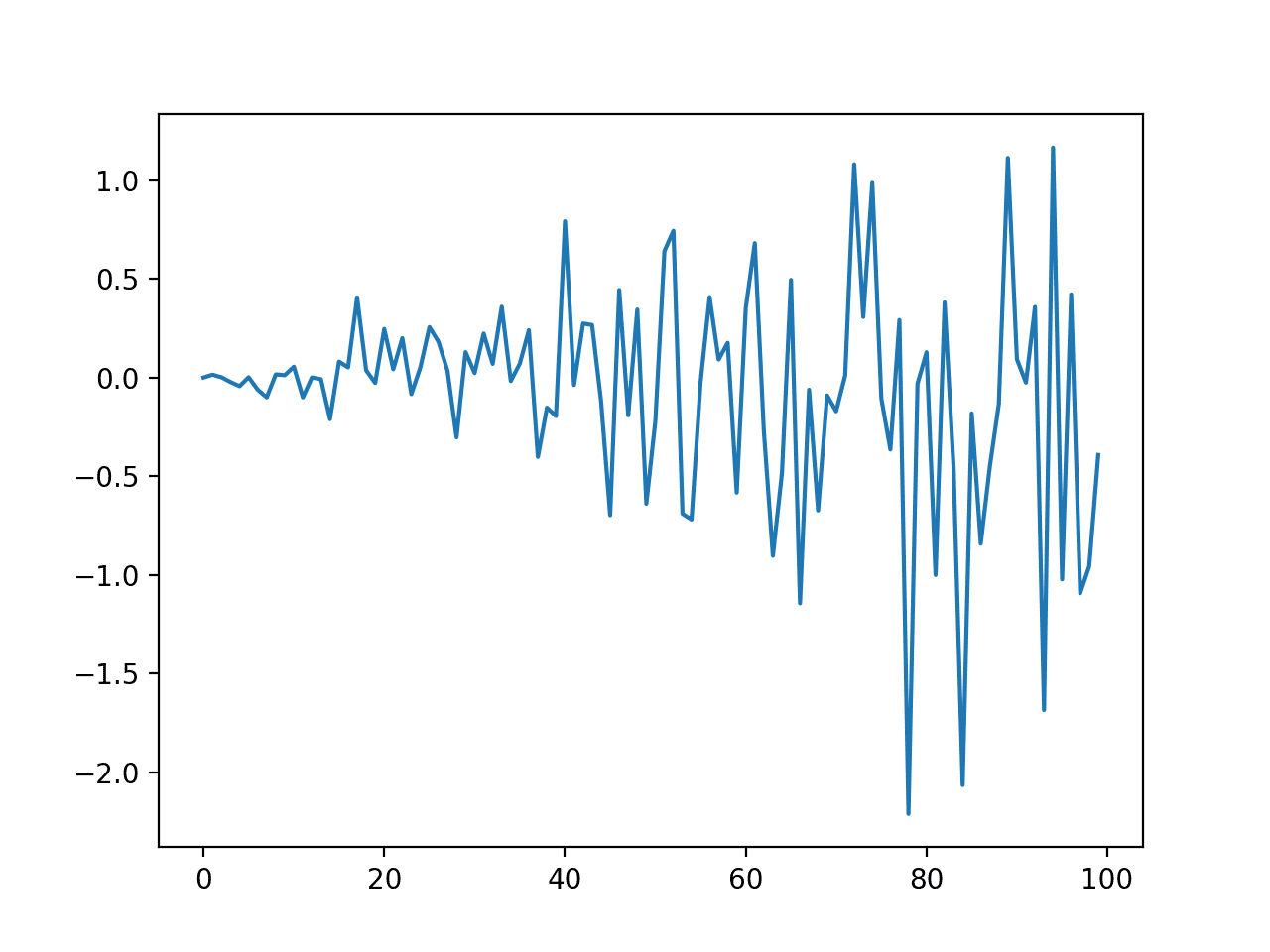
First, we get a line plot of the residual errors, suggesting that there may still be some trend information not captured by the model.

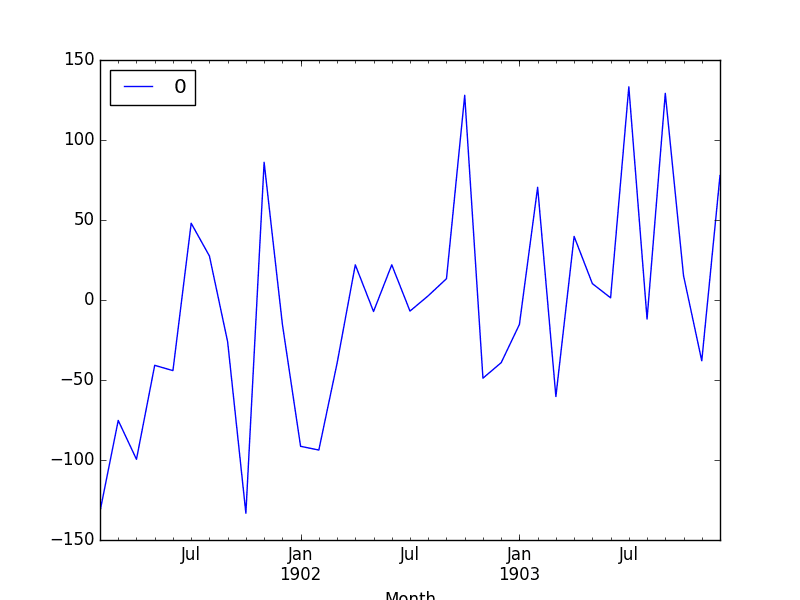
ARMA Fit Residual Error Line Plot

Next, we get a density plot of the residual error values, suggesting the errors are Gaussian, but may not be centred on zero.

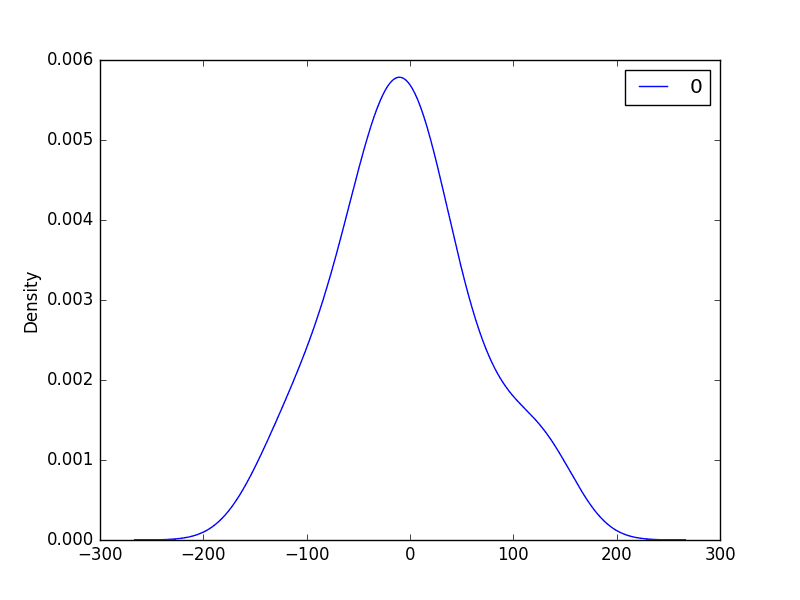
ARMA Fit Residual Error Density Plot

The distribution of the residual errors is displayed. The results show that indeed there is a bias in the prediction (a non-zero mean in the residuals).

count   36.000000
mean    21.936144
std     80.774430
min   -122.292030
25%    -35.040859
50%     13.147219
75%     68.848286
max    266.000000

count 36.000000

mean 21.936144

std 80.774430

min -122.292030

25% -35.040859

50% 13.147219

75% 68.848286

max 266.000000

Note, that although we used the entire dataset for time series analysis, ideally we would perform this analysis on just the training dataset when developing a predictive model.

Next, let’s look at how we can use the ARIMA model to make forecasts.

Rolling Forecast ARIMA Model

The ARIMA model can be used to forecast future time steps.

The ARIMA model is adept at forecasting future time points. In a rolling forecast, the model is often retrained as new data becomes available, allowing for more accurate and adaptive predictions.

We can use the predict() function on the ARIMAResults object to make predictions. It accepts the index of the time steps to make predictions as arguments. These indexes are relative to the start of the training dataset used to make predictions.

How to Forecast with ARIMA:

Use the predict() function on the ARIMAResults object. This function requires the index of the time steps for which predictions are needed.
To revert any differencing and return predictions in the original scale, set the typ argument to ‘levels’.
For a simpler one-step forecast, employ the forecast() function.

We can split the training dataset into train and test sets, use the train set to fit the model and generate a prediction for each element on the test set.

A rolling forecast is required given the dependence on observations in prior time steps for differencing and the AR model. A crude way to perform this rolling forecast is to re-create the ARIMA model after each new observation is received.

# evaluate an ARIMA model using a walk-forward validation
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error
from math import sqrt
# load dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)
series.index = series.index.to_period('M')
# split into train and test sets
X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
# walk-forward validation
for t in range(len(test)):
	model = ARIMA(history, order=(5,1,0))
	model_fit = model.fit()
	output = model_fit.forecast()
	yhat = output[0]
	predictions.append(yhat)
	obs = test[t]
	history.append(obs)
	print('predicted=%f, expected=%f' % (yhat, obs))
# evaluate forecasts
rmse = sqrt(mean_squared_error(test, predictions))
print('Test RMSE: %.3f' % rmse)
# plot forecasts against actual outcomes
pyplot.plot(test)
pyplot.plot(predictions, color='red')
pyplot.show()

# evaluate an ARIMA model using a walk-forward validation

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

from statsmodels.tsa.arima.model import ARIMA

from sklearn.metrics import mean_squared_error

from math import sqrt

# load dataset

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)

series.index = series.index.to_period('M')

# split into train and test sets

X = series.values

size = int(len(X) * 0.66)

train, test = X[0:size], X[size:len(X)]

history = [x for x in train]

predictions = list()

# walk-forward validation

for t in range(len(test)):

model = ARIMA(history, order=(5,1,0))

model_fit = model.fit()

output = model_fit.forecast()

yhat = output[0]

predictions.append(yhat)

obs = test[t]

history.append(obs)

print('predicted=%f, expected=%f' % (yhat, obs))

# evaluate forecasts

rmse = sqrt(mean_squared_error(test, predictions))

print('Test RMSE: %.3f' % rmse)

# plot forecasts against actual outcomes

pyplot.plot(test)

pyplot.plot(predictions, color='red')

pyplot.show()

We manually keep track of all observations in a list called history that is seeded with the training data and to which new observations are appended each iteration.

Putting this all together, below is an example of a rolling forecast with the ARIMA model in Python.

Running the example prints the prediction and expected value each iteration.

We can also calculate a final root mean squared error score (RMSE) for the predictions, providing a point of comparison for other ARIMA configurations.

predicted=343.272180, expected=342.300000
predicted=293.329674, expected=339.700000
predicted=368.668956, expected=440.400000
predicted=335.044741, expected=315.900000
predicted=363.220221, expected=439.300000
predicted=357.645324, expected=401.300000
predicted=443.047835, expected=437.400000
predicted=378.365674, expected=575.500000
predicted=459.415021, expected=407.600000
predicted=526.890876, expected=682.000000
predicted=457.231275, expected=475.300000
predicted=672.914944, expected=581.300000
predicted=531.541449, expected=646.900000
Test RMSE: 89.021

predicted=343.272180, expected=342.300000

predicted=293.329674, expected=339.700000

predicted=368.668956, expected=440.400000

predicted=335.044741, expected=315.900000

predicted=363.220221, expected=439.300000

predicted=357.645324, expected=401.300000

predicted=443.047835, expected=437.400000

predicted=378.365674, expected=575.500000

predicted=459.415021, expected=407.600000

predicted=526.890876, expected=682.000000

predicted=457.231275, expected=475.300000

predicted=672.914944, expected=581.300000

predicted=531.541449, expected=646.900000

Test RMSE: 89.021

A line plot is created showing the expected values (blue) compared to the rolling forecast predictions (red). We can see the values show some trend and are in the correct scale.

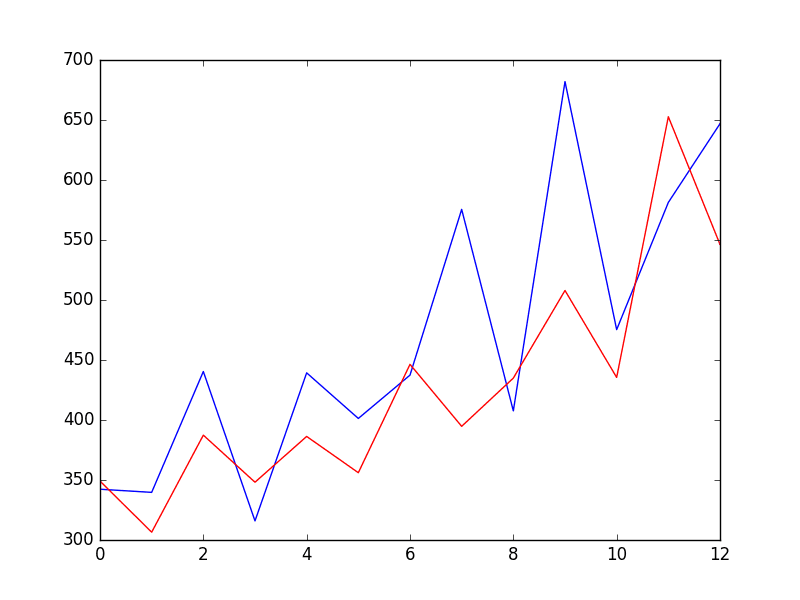
ARIMA Rolling Forecast Line Plot

The model could use further tuning of the p, d, and maybe even the q parameters.

Configuring an ARIMA Model

ARIMA is often configured using the classical Box-Jenkins Methodology. This process employs a meticulous blend of time series analysis and diagnostics to pinpoint the most fitting parameters for the ARIMA model.

The Box-Jenkins Methodology: A Three-Step Process:

Model Identification: Begin with visual tools like plots and leverage summary statistics. These aids help recognize trends, seasonality, and autoregressive elements. The goal here is to gauge the extent of differencing required and to determine the optimal lag size.
Parameter Estimation: This step involves a fitting procedure tailored to derive the coefficients integral to the regression model.
Model Checking: Armed with plots and statistical tests delve into the residual errors. This analysis illuminates the temporal structure that the model might have missed.

The process is repeated until either a desirable level of fit is achieved on the in-sample or out-of-sample observations (e.g. training or test datasets).

The process was described in the classic 1970 textbook on the topic titled Time Series Analysis: Forecasting and Control by George Box and Gwilym Jenkins. An updated 5th edition is now available if you are interested in going deeper into this type of model and methodology.

Given that the model can be fit efficiently on modest-sized time series datasets, grid searching parameters of the model can be a valuable approach.

For an example of how to grid search the hyperparameters of the ARIMA model, see the tutorial:

How to Grid Search ARIMA Model Hyperparameters with Python

Summary

In this tutorial, you discovered how to develop an ARIMA model for time series forecasting in Python.

Specifically, you learned:

ARIMA Model Overview: Uncovered the foundational aspects of the ARIMA model, its configuration nuances, and the key assumptions it operates on.
Quick Time Series Analysis: Explored a swift yet comprehensive analysis of time series data using the ARIMA model.
Out-of-Sample Forecasting with ARIMA: Delved into harnessing the ARIMA model for making predictions beyond the sample data.

Do you have any questions about ARIMA, or about this tutorial?

Ask your questions in the comments below and I will do my best to answer.

834 Responses to How to Create an ARIMA Model for Time Series Forecasting in Python

SalemAmeen January 9, 2017 at 7:22 am #

Many thank

Reply
- Jason Brownlee January 9, 2017 at 7:53 am #
  
  You’re welcome.
  
  Reply
  - Hugo Santillan April 10, 2019 at 1:52 pm #
    
    Hi Jason! Great tutorial.
    Just a reeal quick question ..how can I fit and run the last code for multiple varialbles?..the dataset that looks like this:
    
    Date,CO,NO2,O3,PM10,SO2,Temperature
    2016-01-01 00:00:00,0.615,0.01966,0.00761,49.92,0.00055,18.1
    
    Reply
    - Jason Brownlee April 11, 2019 at 6:26 am #
      
      You can model the target variable alone.
      
      Alternately you can provide the other variables as exog variables, such as SARIMAX.
      https://machinelearningmastery.com/time-series-forecasting-methods-in-python-cheat-sheet/
      
      Finally, you could use a neural network:
      https://machinelearningmastery.com/start-here/#deep_learning_time_series
      
      Reply
      - Andre February 2, 2020 at 10:38 am #
        
        Hey,
        
        Nice article, it helped me a lot.
        I have a question as to how to make predictions in a scenario where you are attempting to make new predictions not included in the dataset.
        For each item in the test set, after a prediction is made, the correct data point, taken from test, is added to the history.
        How can I make predictions when I don’t have a test set to extract the right data points from?
      - Jason Brownlee February 3, 2020 at 5:43 am #
        
        Good question, see this tutorial:
        https://machinelearningmastery.com/make-sample-forecasts-arima-python/
      - Ashwin August 26, 2021 at 11:52 pm #
        
        Hi Jason,
        
        can we apply this for stock or crypto? Can you try develop a code on tradingview platform?
      - Adrian Tam August 27, 2021 at 6:10 am #
        
        Why not! But caution: doing ARIMA on stock market usually not providing good enough result to invest in it.
  - joseph November 5, 2019 at 8:22 pm #
    
    have a question am doing a project concerning data analytics insights for retail company sales case study certain supermarket in my area and am proposing to use ARIMA can it be appropriate and how can i apply it
    
    Reply
    - Jason Brownlee November 6, 2019 at 6:32 am #
      
      Perhaps start by modeling one product?
      
      Reply
  - Jagan January 22, 2020 at 8:18 pm #
    
    Hi Jason! Great Tutorial!!
    
    I have a usecase of timeseries forecasting where I have to predict sales of different products out of the electronics store. There are around 300 types of different products. And I have to predict the sales on the next day for each of the product based on previous one year data. But not every product is being sold each day.
    
    My guess is I have to create a tsa for each product. but the data quality for each product is low as not each product is being sold each day. And my use case is that I have to predict sales of each product.
    
    Any way I can use time series on whole data without using tsa on each product individually?
    
    Reply
    - Jason Brownlee January 23, 2020 at 6:29 am #
      
      Good question, I have some suggestions here (replace “sites” with “products”):
      https://machinelearningmastery.com/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites
      
      Reply
      - Grace October 25, 2022 at 6:13 pm #
        
        If I want to predict on New values out of the data set how should I do
      - James Carmichael October 26, 2022 at 7:23 am #
        
        Hi Grace…The following discussion may be of interest:
        
        https://stats.stackexchange.com/questions/223457/predict-from-estimated-arima-model-with-new-data
  - Abhishek December 3, 2020 at 11:58 pm #
    
    Hi I am trying to understand data set related to daily return of a stock. I calculated autocorrelation and partial autocorrelation function as a function of lag. I am observing
    that ACF lies within two standard error limits. But I find PACF to be large value at few non-zero lags, one and two. I want to ask you is this behaviour strange ? ACF zero and PACF large and non-zero. If this behaviour not strange, then how does one arrive at the correct order of ARIMA model for this data.
    
    Reply
    - Jason Brownlee December 4, 2020 at 6:43 am #
      
      Stock prices are not predictable:
      https://machinelearningmastery.com/faq/single-faq/can-you-help-me-with-machine-learning-for-finance-or-the-stock-market
      
      Reply
  - Razi December 18, 2021 at 12:17 am #
    
    hi. great tutorial.
    what’s your advice for finding correlation between two data sets.
    I have two csv file, one showing amount of money spent on advertising and one showing amount of sale. and I wanna find out effect of advertisement on sale and forecasting future sale with different amount of advertisement. I know one way is finding correlation with panda like:
    sales_df[‘colx’].corr(spend_df[‘coly’])
    but I wanna know is there a better way?
    
    Reply
    - Adrian Tam December 19, 2021 at 1:45 pm #
      
      It is better if you take the lag of spending into consideration. Advertising affects future sales, not the sales at the time of advertising.
      
      Reply
    - James Carmichael December 21, 2021 at 11:35 am #
      
      Hi Razi…Review the following and let me know if you have any further questions.
      
      https://machinelearningmastery.com/how-to-use-correlation-to-understand-the-relationship-between-variables/
      
      Reply
- Chris May 18, 2019 at 12:20 pm #
  
  Hi Jason! Great tutorial.
  
  I got a question that needs your kind help.
  
  For some reason, I need to calculate residuals of a fitted ARMA-GARCH model manually, but found that the calculated residuals are different of those directly from the R package such rugarh. I put the estimated parameters back to the model and use the training data to back out the residuals. How to get the staring residuals at t=0, t=-1 etc. Should I treat the fitted ARMA-GARCH just as an fitted ARMA model? In that case why we need to fit an ARMA-GARCH model to the training data.
  
  Reply
  - Jason Brownlee May 19, 2019 at 7:59 am #
    
    Sorry, I’m not familiar wit the “rugarh” package or how it functions.
    
    Reply
- A. Sharma August 1, 2019 at 6:51 am #
  
  Hi Jason,
  Could you do a GaussianProcess example with the same data. And compare the two- those two methods seem to be applicable to similar problems- I would love to see your insights.
  
  Reply
  - Jason Brownlee August 1, 2019 at 6:57 am #
    
    Thanks for the great suggestion. I hope to cover Gaussian Processes in the future.
    
    Reply
    - a Sharma August 1, 2019 at 10:47 am #
      
      Thanks. If you also did a comparative study of the two, that would be great- I realize that might be out of the regular, thought I’d still ask. Also can I sign up for email notification?
      
      Reply
      - Jason Brownlee August 1, 2019 at 2:12 pm #
        
        Thanks.
        
        You can sign-up for notification about all new tutorials here:
        https://machinelearningmastery.com/newsletter/
    - estudent February 18, 2021 at 5:37 pm #
      
      Hi, appreciate your great explanations, awesome! I wonder how will you load a statistics feature-engineered time series dataset/dataframe into ARIMA? Would appreciate if you have example or article. Thanks!
      
      Reply
      - Jason Brownlee February 19, 2021 at 5:57 am #
        
        Perhaps as exog variables?
        
        Perhaps try an alternate ml model instead?
- Ahmed hesham March 16, 2020 at 7:52 pm #
  
  Hello,
  I have climate change data for the past 8 years and I need to do a regression model using climate as a factor so I need at least climate data for 30 years which I can’t find online. Is it possible to get the previous 22 years climate change using ARIMA based on the last 8 years data.
  Thank you
  
  Reply
  - Jason Brownlee March 17, 2020 at 8:13 am #
    
    No, that would be way too much data. ARIMA is for small datasets – or at least the python implementation cannot handle much data.
    
    Perhaps explore using a linear regression or other ML methods as a first step.
    
    Reply
    - Muhammad Ali November 9, 2020 at 11:57 pm #
      
      ARIMA model can be used for any number of observations, yes its performance is more better if one used it for short-term forecasting.
      
      Reply
      - Jason Brownlee November 10, 2020 at 6:44 am #
        
        Generally, yes.
Blessing Ojeme January 9, 2017 at 1:20 pm #

Much appreciated, Jason. Keep them coming, please.

Reply
- Jason Brownlee January 10, 2017 at 8:55 am #
  
  Sure thing! I’m glad you’re finding them useful.
  
  What else would you like to see?
  
  Reply
  - Utkarsh July 22, 2017 at 10:31 pm #
    
    Hi Jason ,can you suggest how one can solve time series problem if the target variable is categorical having around 500 categories.
    
    Thanks
    
    Reply
    - Jason Brownlee July 23, 2017 at 6:24 am #
      
      That is a lot of categories.
      
      Perhaps moving to a neural network type model with a lot of capacity. You may also require a vast amount of data to learn this problem.
      
      Reply
      - Sreekar March 25, 2021 at 6:52 pm #
        
        Hi Jason and Utkarsh,
        
        I am also working on a similar dataset which is univariate with a timestamp and a categorical value (around 150 distinct categories). Can we use an ARIMA model for this task?
      - Jason Brownlee March 26, 2021 at 6:22 am #
        
        Not sure if ARIMA supports categorical exog variables.
        
        Perhaps check the documentation?
        Perhaps encode the categorical variable and try modeling anyway?
        Perhaps try an alternate model?
  - Yash July 25, 2018 at 8:01 pm #
    
    What if there are multiple columns in dataset. For example: Instead of only 1 items like the shampoo, there could be a column with item numbers ranging from 1 – 20 and a column with number of stores and finally a column with respective sales?
    
    Reply
    - Jason Brownlee July 26, 2018 at 7:40 am #
      
      If you have parallel input time series, you can use the other variables as exogenous variables. If you want to predict all variables, you can use VAR.
      
      If you want to support multiple series generally as input, you can use ML methods, this will help as a start:
      https://machinelearningmastery.com/convert-time-series-supervised-learning-problem-python/
      
      Reply
  - Aflal May 13, 2020 at 7:35 am #
    
    OMG. Searching for weeks, never found an article like this one. Thank a lot.
    I need your advice please,
    I need to predict Retail sales data with variables like weather, sales Discount’, holiday etc.
    
    Which is the best model is to use? And why?
    How can decide the best fit model?
    (Can I use SARIMAX for this?)
    
    Love from Sri Lanka
    
    Sorry for bad English
    
    Reply
    - Jason Brownlee May 13, 2020 at 7:45 am #
      
      You’re welcome.
      
      Perhaps test a few diffrent models and discover what works best for your dataset.
      
      Reply
      - Aflal May 16, 2020 at 6:10 am #
        
        But I’m your suggestion tour pointed out, we can’t use arimax for multivariate forecasting.
        What is your suggestion??
        
        Any link I could follow to find a solution
        Thanks again
      - Jason Brownlee May 16, 2020 at 6:26 am #
        
        Perhaps try some of the techniques listed here:
        https://machinelearningmastery.com/start-here/#deep_learning_time_series
- Somayeh November 27, 2017 at 2:43 am #
  
  Hi Jason,
  Recently I am working on time series prediction, but my research is a little bit complicated for me to understand how to fix a time series models to predict future values of multi targets.
  Recently I read your post in multi-step and multivariate time series prediction with LSTM. But my problem have a series input values for every time (for each second we have recorded more than 500 samples). We have 22 inputs and 3 targets. All the data has been collected during 600 seconds and then predict 3 targets for 600 next seconds. Please help me how can solve this problem?
  It is noticed we have trend and seasonality pulses for targets during the time.
  
  Reply
  - morteza February 19, 2018 at 2:58 am #
    
    do you find a solution to this problem?
    
    Reply
Chow Xixi January 9, 2017 at 6:00 pm #

good,Has been paid close attention to your blog.

Reply
- Jason Brownlee January 10, 2017 at 8:55 am #
  
  Thanks!
  
  Reply
Kevin January 17, 2017 at 12:58 am #

Gives me loads of errors:

Traceback (most recent call last):
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 2276, in converter
date_parser(*date_cols), errors=’ignore’)
File “/Users/kevinoost/PycharmProjects/ARIMA/main.py”, line 6, in parser
return datetime.strptime(‘190’+x, ‘%Y-%m’)
TypeError: strptime() argument 1 must be str, not numpy.ndarray

During handling of the above exception, another exception occurred:

Traceback (most recent call last):
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 2285, in converter
dayfirst=dayfirst),
File “pandas/src/inference.pyx”, line 841, in pandas.lib.try_parse_dates (pandas/lib.c:57884)
File “pandas/src/inference.pyx”, line 838, in pandas.lib.try_parse_dates (pandas/lib.c:57802)
File “/Users/kevinoost/PycharmProjects/ARIMA/main.py”, line 6, in parser
return datetime.strptime(‘190’+x, ‘%Y-%m’)
File “/Users/kevinoost/anaconda/lib/python3.5/_strptime.py”, line 510, in _strptime_datetime
tt, fraction = _strptime(data_string, format)
File “/Users/kevinoost/anaconda/lib/python3.5/_strptime.py”, line 343, in _strptime
(data_string, format))
ValueError: time data ‘190Sales of shampoo over a three year period’ does not match format ‘%Y-%m’

During handling of the above exception, another exception occurred:

Traceback (most recent call last):
File “/Users/kevinoost/PycharmProjects/ARIMA/main.py”, line 8, in
series = read_csv(‘shampoo-sales.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 562, in parser_f
return _read(filepath_or_buffer, kwds)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 325, in _read
return parser.read()
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 815, in read
ret = self._engine.read(nrows)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 1387, in read
index, names = self._make_index(data, alldata, names)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 1030, in _make_index
index = self._agg_index(index)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 1111, in _agg_index
arr = self._date_conv(arr)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/parsers.py”, line 2288, in converter
return generic_parser(date_parser, *date_cols)
File “/Users/kevinoost/anaconda/lib/python3.5/site-packages/pandas/io/date_converters.py”, line 38, in generic_parser
results[i] = parse_func(*args)
File “/Users/kevinoost/PycharmProjects/ARIMA/main.py”, line 6, in parser
return datetime.strptime(‘190’+x, ‘%Y-%m’)
File “/Users/kevinoost/anaconda/lib/python3.5/_strptime.py”, line 510, in _strptime_datetime
tt, fraction = _strptime(data_string, format)
File “/Users/kevinoost/anaconda/lib/python3.5/_strptime.py”, line 343, in _strptime
(data_string, format))
ValueError: time data ‘190Sales of shampoo over a three year period’ does not match format ‘%Y-%m’

Process finished with exit code 1

Help would be much appreciated.

Reply
- Jason Brownlee January 17, 2017 at 7:39 am #
  
  It looks like there might be an issue with your data file.
  
  Open the csv in a text editor and confirm the header line looks sensible.
  
  Also confirm that you have no extra data at the end of the file. Sometimes the datamarket files download with footer data that you need to delete.
  
  Reply
  - Joseph Brown March 7, 2018 at 8:35 am #
    
    Hi Jason,
    
    I’m getting this same error. I checked the data and looks fine. I not sure what else to do, still learning. Please help.
    
    Data
    
    “Month”;”Sales of shampoo over a three year period”
    “1-01”;266.0
    “1-02”;145.9
    “1-03”;183.1
    “1-04”;119.3
    “1-05”;180.3
    “1-06”;168.5
    “1-07”;231.8
    “1-08”;224.5
    “1-09”;192.8
    “1-10”;122.9
    “1-11”;336.5
    “1-12”;185.9
    “2-01”;194.3
    “2-02”;149.5
    “2-03”;210.1
    “2-04”;273.3
    “2-05”;191.4
    “2-06”;287.0
    “2-07”;226.0
    “2-08”;303.6
    “2-09”;289.9
    “2-10”;421.6
    “2-11”;264.5
    “2-12”;342.3
    “3-01”;339.7
    “3-02”;440.4
    “3-03”;315.9
    “3-04”;439.3
    “3-05”;401.3
    “3-06”;437.4
    “3-07”;575.5
    “3-08”;407.6
    “3-09”;682.0
    “3-10”;475.3
    “3-11”;581.3
    “3-12”;646.9
    
    Reply
    - Jason Brownlee March 7, 2018 at 3:02 pm #
      
      The data you have pasted is separated by semicolons, not commas as expected.
      
      Reply
- Al January 21, 2018 at 8:56 pm #
  
  Hi Kevin,
  the last line of the data set, at least in the current version that you can download, is the text line “Sales of shampoo over a three year period”. The parser barfs on this because it is not in the specified format for the data lines. Try using the “nrows” parameter in read_csv.
  
  series = read_csv(‘~/Downloads/shampoo-sales.csv’, header=0, nrows=36, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
  
  worked for me.
  
  Reply
  - Jason Brownlee January 22, 2018 at 4:43 am #
    
    Great tip!
    
    Reply
  - Serail April 7, 2018 at 4:13 pm #
    
    Thanks for your excellent tip
    
    Reply
  - Alex November 25, 2018 at 8:56 pm #
    
    Thanks, had the same problem, worked!
    
    Reply
NGUYEN Quang Anh January 19, 2017 at 6:28 pm #

Let say I have a time series data with many attribute. For example a row will have (speed, fuel, tire_pressure), how could we made a model out of this ? the value of each column may affect each other, so we cannot do forecasting on solely 1 column. I google a lot but all the example I’ve found so far only work on time series of 1 attribute.

Reply
- Jason Brownlee January 20, 2017 at 10:19 am #
  
  This is called multivariate time series forecasting. Linear models like ARIMA were not designed for this type of problem.
  
  generally, you can use the lag-based representation of each feature and then apply a standard machine learning algorithm.
  
  I hope to have some tutorials on this soon.
  
  Reply
  - rchesak May 30, 2017 at 12:37 pm #
    
    Wanted to check in on this, do you have any tutorials on multivariate time series forecasting?
    
    Also, when you say standard machine learning algorithm, would a random forest model work?
    
    Thanks!
    
    Reply
    - rchesak May 30, 2017 at 12:52 pm #
      
      Update: the statsmodels.tsa.arima_model.ARIMA() function documentation says it takes the optional parameter exog, which is described in the documentation as ‘an optional array of exogenous variables’. This sounds like multivariate analysis to me, would you agree?
      
      I am trying to predict number of cases of a mosquito-borne disease, over time, given weather data. So I believe the ARIMA model should work for this, correct?
      
      Thank you!
      
      Reply
      - Jason Brownlee June 2, 2017 at 12:32 pm #
        
        I have not experimented with this argument.
    - Jason Brownlee June 2, 2017 at 12:32 pm #
      
      No multivariate examples at this stage.
      
      Yes, any supervised learning method.
      
      Reply
  - XiongCat October 4, 2023 at 10:54 pm #
    
    Can tensorflow do the job with multiple attributes.
    
    Reply
    - James Carmichael October 5, 2023 at 9:54 am #
      
      Hi XiongCat…You may find the following of interest:
      
      https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/
      
      Reply
- Muyi Ibidun February 7, 2017 at 9:36 am #
  
  Hello Ng,
  
  Your problem fits what VAR (Vector Autoregression) models is designed for. See the following links for more information. I hope this helps your work.
  
  https://en.wikipedia.org/wiki/Vector_autoregression
  http://statsmodels.sourceforge.net/devel/vector_ar.html
  
  Reply
Kelvid January 20, 2017 at 11:55 am #

Hi, would you have a example for the seasonal ARIMA post? I have installed latest statsmodels module, but there is an error of import the SARIMAX. Do help if you manage to figure it out. Thanks.

Reply
- Jason Brownlee January 21, 2017 at 10:23 am #
  
  Hi Kelvid, I don’t have one at the moment. I ‘ll prepare an example of SARIMAX and post it soon.
  
  Reply
Muhammad Arsalan January 29, 2017 at 10:13 pm #

It is so informative..thankyou

Reply
- Jason Brownlee February 1, 2017 at 10:16 am #
  
  I’m glad to hear that Muhammad.
  
  Reply
Sebastian January 31, 2017 at 3:33 am #

Great post Jason!

I have a couple of questions:

– Just to be sure. model_fit.forecast() is single step ahead forecasts and model_fit.predict() is for multiple step ahead forecasts?

– I am working with a series that seems at least quite similar to the shampoo series (by inspection). When I use predict on the training data, I get this zig-zag pattern in the prediction as well. But for the test data, the prediction is much smoother and seems to saturate at some level. Would you expect this? If not, what could be wrong?

Reply
- Jason Brownlee February 1, 2017 at 10:28 am #
  
  Hi Sebastian,
  
  Yes, forecast() is for one step forecasts. You can do one step forecasts with predict() also, but it is more work.
  
  I would not expect prediction beyond a few time steps to be very accurate, if that is your question?
  
  Reply
  - Sebastian February 3, 2017 at 9:25 am #
    
    Thanks for the reply!
    
    Concerning the second question. Yes, you are right the prediction is not very accurate. But moreover, the predicted time series has a totally different frequency content. As I said, it is smooth and not zig-zaggy as the original data. Is this normal or am I doing something wrong. I also tried the multiple step prediction (model_fit.predict()) on the training data and then the forecast seem to have more or less the same frequency content (more zig-zaggy) as the data I am trying to predict.
    
    Reply
    - Jason Brownlee February 3, 2017 at 10:22 am #
      
      Hi Sebastian, I see.
      
      In the case of predicting on the training dataset, the model has access to real observations. For example, if you predict the next 5 obs somewhere in the training dataset, it will use obs(t+4) to predict t+5 rather than prediction(t+4).
      
      In the case of predicting beyond the end of the model data, it does not have obs to make predictions (unless you provide them), it only has access to the predictions it made for prior time steps. The result is the errors compound and things go off the rails fast (flat forecast).
      
      Does that make sense/help?
      
      Reply
      - Sebastian February 3, 2017 at 6:34 pm #
        
        That helped!
        
        Thanks!
      - Jason Brownlee February 4, 2017 at 10:00 am #
        
        Glad to hear it Sebastian.
      - satya May 22, 2017 at 9:19 pm #
        
        Hi Jason,
        
        suppose my training set is 1949 to 1961. Can I get the data for 1970 with using Forecast or Predict function
        
        Thanks
        Satya
      - Jason Brownlee May 23, 2017 at 7:51 am #
        
        Yes, you would have to predict 10 years worth of data though. The predictions after 10 years would likely have a lot of error.
      - Ani July 6, 2018 at 1:22 am #
        
        Hi Jason,
        
        Continuing on this note, how far ahead can you forecast using something like ARIMA or AR or GARCH in Python? I’m guessing most of these utilize some sort of Kalman filter forecasting mechanism?
        
        To give you a sense of my data, given between 60k and 80k data points, how far ahead in terms of number of predictions can we make reliably? Similar to Sebastian, I have pretty jagged predictions in-sample, but essentially as soon as the valid/test area begins, I have no semblance of that behavior and instead just get a pretty flat curve. Let me know what you think. Thanks!
      - Jason Brownlee July 6, 2018 at 6:43 am #
        
        The skill of AR+GARH (or either) really depends on the choice of model parameters and on the specifics of the problem.
        
        Perhaps you can try grid searching different parameters?
        Perhaps you can review ACF/PACF plots for your data that may suggest better parameters?
        Perhaps you can try non-linear methods?
        Perhaps your problem is truly challenging/not predictable?
        
        I hope that helps as a start.
  - Iván Moreno September 15, 2021 at 9:28 am #
    
    Dear Jason,
    
    One question. I need to perform in-sample one-step forecast using a ARMA model without re-train it. How can I start?
    
    Best regards.
    
    Reply
    - Adrian Tam September 16, 2021 at 12:34 am #
      
      You should look for get_prediction() function, see https://www.statsmodels.org/stable/generated/statsmodels.tsa.arima.model.ARIMAResults.html
      
      Reply
Elliot January 31, 2017 at 10:07 am #

So this is building a model and then checking it off of the given data right?

-How can I predict what would come next after the last data point? Am I misunderstanding the code?

Reply
- Jason Brownlee February 1, 2017 at 10:34 am #
  
  Hi Elliot,
  
  You can predict the next data point at the end of the data by training on all of the available data then calling model.forecast().
  
  I have a post on how to make predictions here:
  https://machinelearningmastery.com/make-predictions-time-series-forecasting-python/
  
  Does that help?
  
  Reply
  - Elliot February 1, 2017 at 11:44 am #
    
    I tried the model.forecast at the end of the program.
    
    “AttributeError: ‘ARIMA’ object has no attribute ‘forecast'”
    
    Also on your article: https://machinelearningmastery.com/make-predictions-time-series-forecasting-python/
    
    In step 3, when it says “Prediction: 46.755211”, is that meaning after it fit the model on the dataset, it uses the model to predict what would happen next from the dataset, right?
    
    Reply
    - Jason Brownlee February 2, 2017 at 1:58 pm #
      
      Hi Elliot, the forecast() function is on the ARIMAResults object. You can learn more about it here:
      http://statsmodels.sourceforge.net/stable/generated/statsmodels.tsa.arima_model.ARIMAResults.forecast.html
      
      Reply
Muyi Ibidun February 7, 2017 at 9:38 am #

Thanks Jason for this post!

It was really useful. And your blogs are becoming a must read for me because of the applicable and piecemeal nature of your tutorials.

Keep up the good work!

Reply
- Jason Brownlee February 7, 2017 at 10:25 am #
  
  You’re welcome, I’m glad to hear that.
  
  Reply
Kalin Stoyanov February 8, 2017 at 9:30 pm #

Hi,
This is not the first post on ARIMA, but it is the best so far. Thank you.

Reply
- Jason Brownlee February 9, 2017 at 7:24 am #
  
  I’m glad to hear you say that Kalin.
  
  Reply
James Zhang February 10, 2017 at 7:42 pm #

Hey Jason,

thank you very much for the post, very good written! I have a question: so I used your approach to build the model, but when I try to forecast the data that are out of sample, I commented out the obs = test[t] and change history.append(obs) to history.append(yhat), and I got a flat prediction… so what could be the reason? and how do you actually do the out-of-sample predictions based on the model fitted on train dataset? Thank you very much!

Reply
- Jason Brownlee February 11, 2017 at 5:00 am #
  
  Hi james,
  
  Each loop in the rolling forecast shows you how to make a one-step out of sample forecast.
  
  Train your ARIMA on all available data and call forecast().
  
  If you want to perform a multi-step forecast, indeed, you will need to treat prior forecasts as “observations” and use them for subsequent forecasts. You can do this automatically using the predict() function. Depending on the problem, this approach is often not skillful (e.g. a flat forecast).
  
  Does that help?
  
  Reply
  - James February 16, 2017 at 2:03 am #
    
    Hi Jason,
    
    thank you for you reply! so what could be the reason a flat forecast occurs and how to avoid it?
    
    Reply
    - Jason Brownlee February 16, 2017 at 11:09 am #
      
      Hi James,
      
      The model may not have enough information to make a good forecast.
      
      Consider exploring alternate methods that can perform multi-step forecasts in one step – like neural nets or recurrent neural nets.
      
      Reply
      - James February 16, 2017 at 7:41 pm #
        
        Hi Jason,
        
        thanks a lot for your information! still need to learn a lot from people like you! 😀 nice day!
      - Jason Brownlee February 17, 2017 at 9:53 am #
        
        I’m here to help James!
Supriya February 16, 2017 at 1:27 am #

when i calculate train and test error , train rmse is greater than test rmse.. why is it so?

Reply
- Jason Brownlee February 16, 2017 at 11:08 am #
  
  I see this happen sometimes Supriya.
  
  It suggests the model may not be well suited for the data.
  
  Reply
Matias T February 18, 2017 at 12:04 am #

Hello Jason, thanks for this amazing post.
I was wondering how does the “size” work here. For example lets say i want to forecast only 30 days ahead. I keep getting problems with the degrees of freedom.
Could you please explain this to me.

Thanks

Reply
- Jason Brownlee February 18, 2017 at 8:40 am #
  
  Hi Matias, the “size” in the example is used to split the data into train/test sets for model evaluation using walk forward validation.
  
  You can set this any way you like or evaluate your model different ways.
  
  To forecast 30 days ahead, you are going to need a robust model and enough historic data to evaluate this model effectively.
  
  Reply
  - Matias R February 21, 2017 at 6:39 am #
    
    I get it. Thanks Jason.
    
    I was thinking, in this particular example, ¿will the prediction change if we keep adding data?
    
    Reply
    - Jason Brownlee February 21, 2017 at 9:41 am #
      
      Great question Matias.
      
      The amount of history is one variable to test with your model.
      
      Design experiments to test if having more or less history improves performance.
      
      Reply
ubald kuijpers February 24, 2017 at 10:05 pm #

Dear Jason,

Thank you for explaining the ARIMA model in such clear detail.
It helped me to make my own model to get numerical forrcasts and store it in a database.
So nice that we live in an era where knowledge is de-mystified .

Reply
- Jason Brownlee February 25, 2017 at 5:55 am #
  
  I’m glad to here it!
  
  Reply
Jacques Sauve February 25, 2017 at 6:41 am #

Hi Jason. Very good work!
It would be great to see how forecasting models can be used to detect anomalies in time series. thanks.

Reply
- Jason Brownlee February 26, 2017 at 5:26 am #
  
  Great suggestion, thanks Jacques.
  
  Reply
Mehran March 1, 2017 at 12:56 am #

Hi there. Many thanks. I think you need to change the way you parse the datetime to:

datetime.strptime(’19’+x, ‘%Y-%b’)

Many thanks

Reply
- Jason Brownlee March 1, 2017 at 8:41 am #
  
  Are you sure?
  
  See this list of abbreviations:
  https://docs.python.org/3/library/datetime.html#strftime-and-strptime-behavior
  
  The “%m” refers to “Month as a zero-padded decimal number.” which is exactly what we have here.
  
  See a sample of the raw data file:
  
  "Month","Sales" "1-01",266.0 "1-02",145.9 "1-03",183.1 "1-04",119.3 "1-05",180.3
  
  1
  2
  3
  4
  5
  6
  
  "Month","Sales"
  "1-01",266.0
  "1-02",145.9
  "1-03",183.1
  "1-04",119.3
  "1-05",180.3
  
  The “%b” refers to “Month as locale’s abbreviated name.” which we do not have here.
  
  Reply
Niirkshith March 6, 2017 at 4:49 pm #

Hi Jason,
Lucky i found this at the begining of my project.. Its a great start point and enriching.
Keep it coming :).
This can also be used for non linear time series as well?

Thanks,
niri

Reply
- Jason Brownlee March 7, 2017 at 9:31 am #
  
  Glad to hear it Niirkshith.
  
  Try and see.
  
  Reply

Anthony of Sydney March 8, 2017 at 9:00 am #

Dear Dr Jason,

In the above example of the rolling forecast, you used the rmse of the predicted and the actual value.

Another way of getting the residuals of the model is to get the std devs of the residuals of the fitted model

model = modelling.ARIMA(data, (ar,diff,ma)); #ar, diff and ma are the model params    
model_fit = model.fit()
residuals = pd.DataFrame(model_fit.resid)
#calculate the std dev of the residuals, we use numpy's std dev function
print("the std dev of the residuals = %f" % np.std(residuals))
residuals.plot()

model = modelling.ARIMA(data, (ar,diff,ma)); #ar, diff and ma are the model params

model_fit = model.fit()

residuals = pd.DataFrame(model_fit.resid)

#calculate the std dev of the residuals, we use numpy's std dev function

print("the std dev of the residuals = %f" % np.std(residuals))

residuals.plot()

Question, is the std dev of the residuals the same as the root_mean_squared(actual, predicted)?
Thank you
Anthony of Sydney NSW

what is the difference between measuring the std deviation of the residuals of a fitted model and the rmse of the rolling forecast will

Jason Brownlee March 8, 2017 at 9:50 am #

No, they are not the same.

See this post on performance measures:
https://machinelearningmastery.com/time-series-forecasting-performance-measures-with-python/

The RMSE is like the average residual error, but not quite because of the square and square root that makes the result positive.

Reply

Niirkshith March 10, 2017 at 1:28 pm #

Hi Jason,
Great writeup, had a query, when u have a seasonal data and do seasonal differencing. i.e for exy(t)=y(t)-y(t-12) for yearly data. What will be the value of d in ARIMA(p,d,q).

Reply
- Niirkshith March 10, 2017 at 1:29 pm #
  
  typo, ex y(t)=y(t)-y(t-12) for monthly data not yearly
  
  Reply
- Jason Brownlee March 11, 2017 at 7:56 am #
  
  Great question Niirkshith.
  
  ARIMA will not do seasonal differencing (there is a version that will called SARIMA). The d value on ARIMA will be unrelated to the seasonal differencing and will assume the input data is already seasonally adjusted.
  
  Reply
Niirkshith March 13, 2017 at 1:09 pm #

Thanks for getting back.

Reply
ivan March 19, 2017 at 5:17 am #

Hi, Jason

thanks for this example. My question how is chosen the parameter q ?
best Ivan

Reply
- Jason Brownlee March 19, 2017 at 9:11 am #
  
  You can use ACF and PACF plots to help choose the values for p and q.
  
  See this post:
  https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  Reply
Narbukra March 30, 2017 at 4:21 am #

Hi Jason, I am wondering if you did a similar tutorial on multi-variate time series forecasting?

Reply
- Jason Brownlee March 30, 2017 at 8:57 am #
  
  Not yet, I am working on some.
  
  Reply
  - Nirikshith May 12, 2017 at 1:02 pm #
    
    Hi Jason,
    any updates on the same
    
    Reply
  - Shruti June 8, 2018 at 6:54 pm #
    
    Hi Jason,
    Nice post.
    
    Can you please suggest how should I resolve this error: LinAlgError: SVD did not converge
    
    I have a univariate time series.
    
    Reply
    - Jason Brownlee June 9, 2018 at 6:48 am #
      
      Sounds like the data is not a good fit for the method, it may have all zeros or some other quirk.
      
      Reply

David March 30, 2017 at 8:53 am #

Hi Jason,

Thanks for the great post! It was very helpful. I’m currently trying to forecast with the ARIMA model using order (4, 1, 5) and I’m getting an error message “The computed initial MA coefficients are not invertible. You should induce invertibility, choose a different model order, or you can pass your own start_params.” The model works when fitting, but seems to error out when I move to model_fit = model.fit(disp=0). The forecast works well when using your parameters of (0, 1, 5) and I used ACF and PACF plots to find my initial p and q parameters. Any ideas on the cause/fix for the error? Any tips would be much appreciated.

mostafa kotb October 17, 2017 at 4:52 am #

i have the same problem as yours, i use ARIMA with order (5,1,2) and i have been searching for a solution, but still couldn’t find it.

Vit January 30, 2019 at 9:13 pm #

Hi, I have exactly the same problem. Have you already found any solution to that?

Thank you for any information,
Vit

Jason Brownlee January 31, 2019 at 5:32 am #

Perhaps try a different model configuration?

Long August 8, 2020 at 12:06 pm #

Sorry, it is difficult for (3,1,3) as well.
It worked for prediction for the first step of the test data, but gave out the error on the second prediction step.

My code is as follow:

train_size = 0.66
series = shampoo_data["Sales"].values
train, test = series[:int(series.size * train_size)], series[int(series.size * train_size):]
predictions = []
true_values = []
history = [x for x in train]
for t in range(test.size):
    model = ARIMA(history, order=(0,1,3))
    model_fit = model.fit(disp=0)
    forecast_results = model_fit.forecast(steps=1, alpha=0.05)
    pred = forecast_results[0][0]
    std_error = forecast_results[1][0]
    ci = forecast_results[2][0]
    obs = test[t]
#     import pdb; pdb.set_trace()
    print("Predicted: %.3f +- %.3f (CI: %.3f, %.3f), Expected: %.3f " % (pred, std_error, ci[0], ci[1], obs))
    predictions.append(pred)
    true_values.append(obs)
    history.append(obs)
rmse = mean_squared_error(true_values, predictions, squared=False)
mse = mean_squared_error(true_values, predictions)
print("RMSE: %.3f" % rmse)
print("MSE: %.3f" % mse)
fig = plt.figure(figsize=(20,10))
months = shampoo_data["Month"].values[int(series.size * train_size):] 
plt.plot(months, test, label="true_values")
plt.plot(months, predictions, color="red", label="predictions")
plt.legend()
plt.show()

train_size = 0.66

series = shampoo_data["Sales"].values

train, test = series[:int(series.size * train_size)], series[int(series.size * train_size):]

predictions = []

true_values = []

history = [x for x in train]

for t in range(test.size):

model = ARIMA(history, order=(0,1,3))

model_fit = model.fit(disp=0)

forecast_results = model_fit.forecast(steps=1, alpha=0.05)

pred = forecast_results[0][0]

std_error = forecast_results[1][0]

ci = forecast_results[2][0]

obs = test[t]

# import pdb; pdb.set_trace()

print("Predicted: %.3f +- %.3f (CI: %.3f, %.3f), Expected: %.3f " % (pred, std_error, ci[0], ci[1], obs))

predictions.append(pred)

true_values.append(obs)

history.append(obs)

rmse = mean_squared_error(true_values, predictions, squared=False)

mse = mean_squared_error(true_values, predictions)

print("RMSE: %.3f" % rmse)

print("MSE: %.3f" % mse)

fig = plt.figure(figsize=(20,10))

months = shampoo_data["Month"].values[int(series.size * train_size):]

plt.plot(months, test, label="true_values")

plt.plot(months, predictions, color="red", label="predictions")

plt.legend()

plt.show()

tom reilly April 27, 2017 at 6:39 am #

It’s a great blog that you have, but the PACF determines the AR order not the ACF.

Reply
- Jason Brownlee April 27, 2017 at 8:49 am #
  
  Thanks Tom.
  
  I believe ACF and PACF both inform values for q and p:
  https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  Reply
Evgeniy May 2, 2017 at 1:22 am #

Good afternoon!
Is there an analog to the function auto.arima in the package for python from the package of the language R.
For automatic selection of ARIMA parameters?
Thank you!

Reply
- Jason Brownlee May 2, 2017 at 6:00 am #
  
  Yes, you can grid search yourself, see how here:
  https://machinelearningmastery.com/grid-search-arima-hyperparameters-with-python/
  
  Reply
timer May 18, 2017 at 7:23 pm #

Hi. Great one. Suppose I have multiple airlines data number of passengers for two years recorded on daily basis. Now I want to predict for each airline number of possible passangers on next few months. How can I fit these time series models. Separate model for each airline or one single model?

Reply
- Jason Brownlee May 19, 2017 at 8:16 am #
  
  Try both approaches and double down on what works best.
  
  Reply
  - Kashif May 26, 2017 at 2:06 am #
    
    Hi Jason, if in my dataset, my first column is date (YYYYMMDD) and second column is time (hhmmss) and third column is value at given date and time. So could I use ARIMA model for forecasting such type of time series ?
    
    Reply
    - Jason Brownlee June 2, 2017 at 11:47 am #
      
      Yes, use a custom parse function to combine the date and time into one index column.
      
      Reply
- Ashwini March 26, 2020 at 5:39 pm #
  
  I have very similar data set. So how to train arima/sarima single model with above kind of data, i.e.. multiple data points at each timestep?
  
  Reply
  - Jason Brownlee March 27, 2020 at 6:04 am #
    
    I’m not sure these models can support data of that type.
    
    Perhaps start here:
    https://machinelearningmastery.com/start-here/#deep_learning_time_series
    
    Reply
Kashif May 25, 2017 at 6:30 pm #

Hi Sir, Do you have tutorial about vector auto regression model (for multi-variate time series forecasting?)

Reply
- Jason Brownlee June 2, 2017 at 11:42 am #
  
  Not at the moment.
  
  Reply
Ebrahim Aly May 30, 2017 at 5:03 am #

Thanks a lot, Dr. Jason. This tutorial explained a lot. But I tried to run it on an oil prices data set from Bp and I get the following error:

SVD did not converge

I used (p,d,q) = (5, 1, 0)

Would you please help me on solving or at least understanding this error?

Reply
- Jason Brownlee June 2, 2017 at 12:29 pm #
  
  Perhaps consider rescaling your input data and explore other configurations?
  
  Reply
Alex June 9, 2017 at 8:01 am #

Hi Jason,
I have a general question about ARIMA model in the case of multiple Time Series:
suppose you have not only one time series but many (i.e. the power generated per hour at 1000 different wind farms). So you have a dataset of 1000 time series of N points each and you want to predict the next N+M points for each of the time series.
Analyzing each time series separately with the ARIMA could be a waste. Maybe there are similarities in the time evolution of these 1000 different patterns which could help my predictions. What approach would you suggest in this case?

Reply
- Jason Brownlee June 10, 2017 at 8:11 am #
  
  You could not use ARIMA.
  
  For linear models, you could use vector autoregressions (VAR).
  
  For nonlinear methods, I’d recommend a neural network.
  
  I hope that helps as a start.
  
  Reply
Donato June 13, 2017 at 10:23 pm #

Hi Jeson, it’s possible to training the ARIMA with more files? Thanks!

Reply
- Jason Brownlee June 14, 2017 at 8:45 am #
  
  Do you mean multiple series?
  
  See VAR:
  http://www.statsmodels.org/dev/vector_ar.html
  
  Reply
TaeWoo Kim June 23, 2017 at 3:22 am #

“First, we get a line plot of the residual errors, suggesting that there may still be some trend information not captured by the model.”

So are you looking for a smooth flat line in the curve?

Reply
- Jason Brownlee June 23, 2017 at 6:47 am #
  
  No, the upward trend that appears to exist in the plot of residuals.
  
  Reply
Ukesh June 24, 2017 at 12:37 am #

At the end of the code, when I tried to print the predictions, it printed as the array, how do I convert it to the data points???

print(predictions)

[array([ 309.59070719]), array([ 388.64159699]), array([ 348.77807261]), array([ 383.60202178]), array([ 360.99214813]), array([ 449.34210105]), array([ 395.44928401]), array([ 434.86484106]), array([ 512.30201612]), array([ 428.59722583]), array([ 625.99359188]), array([ 543.53887362])]

Reply
Ukesh June 24, 2017 at 12:53 am #

Never mind.. I figured it out…

forecasts = numpy.array(predictions)

[[ 309.59070719]
[ 388.64159699]
[ 348.77807261]
[ 383.60202178]
[ 360.99214813]
[ 449.34210105]
[ 395.44928401]
[ 434.86484106]
[ 512.30201612]
[ 428.59722583]
[ 625.99359188]
[ 543.53887362]]

Keep up the good work Jason.. Your blogs are extremely helpful and easy to follow.. Loads of appreciation..

Reply
- Jason Brownlee June 24, 2017 at 8:03 am #
  
  Glad to hear it.
  
  Reply
Vincent June 29, 2017 at 6:53 pm #

Hi Jason and thank you for this post, its really helpful!

I have one question regarding ARIMA computation time.

I’m working on a dataset of 10K samples, and I’ve tried rolling and “non rolling” (where coefficients are only estimated once or at least not every new sample) forecasting with ARIMA :
– rolling forecast produces good results but takes a big amount of time (I’m working with an old computer, around 3/6h depending on the ARMA model);
– “non rolling” doesn’t forecast well at all.

Re-estimating the coefficients for each new sample is the only possibility for proper ARIMA forecasting?

Thanks for your help!

Reply
- Jason Brownlee June 30, 2017 at 8:11 am #
  
  I would focus on the approach that gives the best results on your problem and is robust. Don’t get caught up on “proper”.
  
  Reply
Kashif July 12, 2017 at 11:29 pm #

Dear Respected Sir, I have tried to use ARIMA model for my dataset, some samples of my dataset are following,
YYYYMMDD hhmmss Duration
20100916 130748 18
20100916 131131 99
20100916 131324 214
20100916 131735 72
20100916 135342 37
20100916 144059 250
20100916 150148 87
20100916 150339 0
20100916 150401 180
20100916 154652 248
20100916 183403 0
20100916 210148 0
20100917 71222 179
20100917 73320 0
20100917 81718 25
20100917 93715 15
But when I used ARIMA model for such type of dataset, the prediction was very bad and test MSE was very high as well, My dataset has irregular pattern and autocorrelation is also very low. so could ARIMA model be used for such type of dataset ? or I have to do some modification in my dataset for using ARIMA model?
Looking forward.
Thanks

Reply
- Jason Brownlee July 13, 2017 at 9:56 am #
  
  Perhaps try data transforms?
  Perhaps try other algorithms?
  Perhaps try gathering more data.
  
  Here are more ideas:
  https://machinelearningmastery.com/machine-learning-performance-improvement-cheat-sheet/
  
  Reply
Vaibhav Agarwal July 14, 2017 at 6:53 am #

Hi Jason,

def parser(x):
return datetime.strptime(‘190’+x, ‘%Y-%m’)
series = read_csv(‘/home/administrator/Downloads/shampoo.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
print(series.head())

for these lines of code, I’m getting the following error

ValueError: time data ‘190Sales of shampoo over a three year period’ does not match format ‘%Y-%m’

Please help.

Thanks

Reply
- Jason Brownlee July 14, 2017 at 8:37 am #
  
  Check that you have deleted the footer in the raw data file.
  
  Reply
Kushal July 14, 2017 at 6:53 pm #

Hi Jason

Does ARIMA have any limitations for size of the sample. I have a dataset with 18k rows of data, ARIMA just doesn’t complete.

Thanks

Kushal

Reply
- Jason Brownlee July 15, 2017 at 9:41 am #
  
  Yes, it does not work well with lots of data (linalg methods under the covers blow up) and it can take forever as you see.
  
  You could fit the model using gradient descent, but not with statsmodels, you may need to code it yourself.
  
  Reply
Olivia July 18, 2017 at 4:51 am #

Love this. The code is very straightforward and the explanations are nice.
I would like to see a HMM model on here. I have been struggling with a few different packages (pomegranate and hmmlearn) for some time now. would like to see what you can do with it! (particularly a stock market example)

Reply
- Jason Brownlee July 18, 2017 at 8:48 am #
  
  Thanks Olivia, I hope to cover HMMs in the future.
  
  Reply
Ben July 19, 2017 at 11:27 am #

Good evening,
In what I am doing, I have a training set and a test set. In the training set, I am fitting an ARIMA model, let’s say ARIMA(0,1,1) to the training set. What I want to do is use this model and apply it to the test set to get the residuals.
So far I have:
model = ARIMA(data,order = (0,1,1))
model_fit = model.fit(disp=0)
res = model_fit.resid
This gives me the residuals for the training set. So I want to apply the ARIMA model in ‘model’ to the test data.
Is there a function to do this?
Thank you

Reply
- Jason Brownlee July 19, 2017 at 4:09 pm #
  
  Hi Ben,
  
  You could use your fit model to make a prediction for the test dataset then compare the predictions vs the real values to calculate the residual errors.
  
  Reply
  - Ben July 19, 2017 at 11:04 pm #
    
    Could you give me an example of the syntax? I understand that idea, but when I would try the results were very poor.
    
    Reply
    - Jason Brownlee July 20, 2017 at 6:20 am #
      
      I provide a suite of examples, please search the blog for ARIMA or start here:
      https://machinelearningmastery.com/start-here/#timeseries
      
      Reply
Shaun July 27, 2017 at 9:29 am #

Hi Jason,

In your example, you append the real data set to the history list- aren’t you supposed to append the prediction?

history.append(obs), where obs is test[t].

in a real example, you don’t have access to the real “future” data. if you were to continue your example with dates beyond the data given in the csv, the results are poor. Can you elaborate?

Reply
- Jason Brownlee July 28, 2017 at 8:25 am #
  
  We are doing walk-forward validation.
  
  In this case, we are assuming that the real ob is made available after the prediction is made and before the next prediction is required.
  
  Reply
Jai July 31, 2017 at 3:59 pm #

Hi,

How i do fix following error ?

—————————————————————————
ImportError Traceback (most recent call last)
in ()
6 #fix deprecated – end
7 from pandas import DataFrame
—-> 8 from statsmodels.tsa.arima_model import ARIMA
9
10 def parser(x):

ImportError: No module named ‘statsmodels’

i have already install the statsmodels module.

(py_env) E:\WinPython-64bit-3.5.3.1Qt5_2\virtual_env\scikit-learn>pip3 install –
-upgrade “E:\WinPython\packages\statsmodels-0.8.0-cp35-cp35m-win_amd64.whl”
Processing e:\winpython\packages\statsmodels-0.8.0-cp35-cp35m-win_amd64.whl
Installing collected packages: statsmodels
Successfully installed statsmodels-0.8.0

http://www.lfd.uci.edu/~gohlke/pythonlibs/

Reply
- Jai July 31, 2017 at 5:25 pm #
  
  problem fixed,
  
  from statsmodels.tsa.arima_model import ARIMA
  #this must come after statsmodels.tsa.arima_model, not before
  from matplotlib import pyplot
  
  Reply
  - Jason Brownlee August 1, 2017 at 7:52 am #
    
    Glad to hear it.
    
    Reply
- Jason Brownlee August 1, 2017 at 7:50 am #
  
  It looks like statsmodels was not installed correctly or is not available in your current environment.
  
  You installed using pip3, are you running a python3 env to run the code?
  
  Reply
  - Jai August 1, 2017 at 4:18 pm #
    
    interestingly, under your Rolling Forecast ARIMA Model explanation, matplotlib was above statsmodels.
    
    from matplotlib import pyplot
    from statsmodels.tsa.arima_model import ARIMA
    
    i am using jupyter notebook from WinPython-64bit-3.5.3.1Qt5 to run your examples. i keep getting ImportError: No module named ‘statsmodels’ if i declare import this way in ARIMA with Python explanation
    
    from matplotlib import pyplot
    from pandas import DataFrame
    from statsmodels.tsa.arima_model import ARIMA
    
    Reply
    - Jai August 1, 2017 at 4:21 pm #
      
      i think it could be i need to restart the virtual environment to let the environment recognize it, today i re-test the following declarations it is ok.
      
      from matplotlib import pyplot
      from pandas import DataFrame
      from statsmodels.tsa.arima_model import ARIMA
      
      thanks for the replies. case close
      
      Reply
      - Jason Brownlee August 2, 2017 at 7:46 am #
        
        Glad to hear it.
    - Jason Brownlee August 2, 2017 at 7:46 am #
      
      You will need to install statsmodels.
      
      Reply
Fathi July 31, 2017 at 5:44 pm #

Great explanation
can anyone help me to write code in R about forecasting such as (50,52,50,55,57) i need to forecasting the next 3 hour, kindly help me to write code using R with ARIMA and SARIMA Model
thanks in advance

Reply
- Jason Brownlee August 1, 2017 at 7:55 am #
  
  I have a good list of books to help you with ARIMA in R here:
  https://machinelearningmastery.com/books-on-time-series-forecasting-with-r/
  
  Reply
Fathi August 9, 2017 at 10:49 pm #

Dear :sir
i hope all of you fine
could any help me to analysis my data I will pay for him
if u can help me plz contact me fathi_nias@yahoo.com
thanks

Reply
- Jason Brownlee August 10, 2017 at 6:57 am #
  
  Consider hiring someone on upwork.com
  
  Reply
Quentin August 11, 2017 at 10:37 pm #

Can the ACF be shown using bars so you can look to see where it drops off when estimating order of MA model? Or have you done a tutorial on interpreting ACF/PACF plots please elsewhere?

Reply
- Jason Brownlee August 12, 2017 at 6:50 am #
  
  Yes, consider using the blog search. Here it is:
  https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  Reply
Amritanshu August 18, 2017 at 8:20 pm #

Hi Jason

I am getting the error when trying to run the code:

from matplotlib import pyplot
from pandas import DataFrame
from pandas.core import datetools
from pandas import read_csv
from statsmodels.tsa.arima_model import ARIMA

series = read_csv(‘sales-of-shampoo-over-a-three-year.csv’, header=0, parse_dates=[0], index_col=0)
# fit model
model = ARIMA(series, order=(0, 0, 0))
model_fit = model.fit(disp=0)
print(model_fit.summary())
# plot residual errors
residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
residuals.plot(kind=’kde’)
pyplot.show()
print(residuals.describe())

Error Mesg on Console :

C:\Python36\python.exe C:/Users/aamrit/Desktop/untitled1/am.py
C:/Users/aamrit/Desktop/untitled1/am.py:3: FutureWarning: The pandas.core.datetools module is deprecated and will be removed in a future version. Please use the pandas.tseries module instead.
from pandas.core import datetools
Traceback (most recent call last):
File “C:\Python36\lib\site-packages\pandas\core\tools\datetimes.py”, line 444, in _convert_listlike
values, tz = tslib.datetime_to_datetime64(arg)
File “pandas\_libs\tslib.pyx”, line 1810, in pandas._libs.tslib.datetime_to_datetime64 (pandas\_libs\tslib.c:33275)
TypeError: Unrecognized value type:

During handling of the above exception, another exception occurred:

Traceback (most recent call last):
File “C:\Python36\lib\site-packages\statsmodels\tsa\base\tsa_model.py”, line 56, in _init_dates
dates = to_datetime(dates)
File “C:\Python36\lib\site-packages\pandas\core\tools\datetimes.py”, line 514, in to_datetime
result = _convert_listlike(arg, box, format, name=arg.name)
File “C:\Python36\lib\site-packages\pandas\core\tools\datetimes.py”, line 447, in _convert_listlike
raise e
File “C:\Python36\lib\site-packages\pandas\core\tools\datetimes.py”, line 435, in _convert_listlike
require_iso8601=require_iso8601
File “pandas\_libs\tslib.pyx”, line 2355, in pandas._libs.tslib.array_to_datetime (pandas\_libs\tslib.c:46617)
File “pandas\_libs\tslib.pyx”, line 2538, in pandas._libs.tslib.array_to_datetime (pandas\_libs\tslib.c:45511)
File “pandas\_libs\tslib.pyx”, line 2506, in pandas._libs.tslib.array_to_datetime (pandas\_libs\tslib.c:44978)
File “pandas\_libs\tslib.pyx”, line 2500, in pandas._libs.tslib.array_to_datetime (pandas\_libs\tslib.c:44859)
File “pandas\_libs\tslib.pyx”, line 1517, in pandas._libs.tslib.convert_to_tsobject (pandas\_libs\tslib.c:28598)
File “pandas\_libs\tslib.pyx”, line 1774, in pandas._libs.tslib._check_dts_bounds (pandas\_libs\tslib.c:32752)
pandas._libs.tslib.OutOfBoundsDatetime: Out of bounds nanosecond timestamp: 1-01-01 00:00:00

During handling of the above exception, another exception occurred:

Traceback (most recent call last):
File “C:/Users/aamrit/Desktop/untitled1/am.py”, line 9, in
model = ARIMA(series, order=(0, 0, 0))
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 997, in __new__
return ARMA(endog, (p, q), exog, dates, freq, missing)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 452, in __init__
super(ARMA, self).__init__(endog, exog, dates, freq, missing=missing)
File “C:\Python36\lib\site-packages\statsmodels\tsa\base\tsa_model.py”, line 44, in __init__
self._init_dates(dates, freq)
File “C:\Python36\lib\site-packages\statsmodels\tsa\base\tsa_model.py”, line 58, in _init_dates
raise ValueError(“Given a pandas object and the index does ”
ValueError: Given a pandas object and the index does not contain dates

Process finished with exit code 1

Reply
- Jason Brownlee August 19, 2017 at 6:17 am #
  
  Ensure you have removed the footer data from the CSV data file.
  
  Reply
Amritanshu August 18, 2017 at 11:44 pm #

Hi Jason

Please help me to resolve the error

I am getting error :

Traceback (most recent call last):
File “C:/Users/aamrit/Desktop/untitled1/am.py”, line 10, in
model_fit = model.fit(disp=0)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 1151, in fit
callback, start_ar_lags, **kwargs)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 956, in fit
start_ar_lags)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 578, in _fit_start_params
start_params = self._fit_start_params_hr(order, start_ar_lags)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 508, in _fit_start_params_hr
endog -= np.dot(exog, ols_params).squeeze()
TypeError: Cannot cast ufunc subtract output from dtype(‘float64’) to dtype(‘int64’) with casting rule ‘same_kind’

Code :

import pandas as pd
import numpy as np
import matplotlib.pylab as plt
from datetime import datetime
from statsmodels.tsa.arima_model import ARIMA

data = pd.read_csv(‘AirPassengers.csv’, header=0, parse_dates=[0], index_col=0)
model = ARIMA(data, order=(1,1,0),exog=None, dates=None, freq=None, missing=’none’)
model_fit = model.fit(disp=0)
print(model_fit.summary())

Reply
- Jason Brownlee August 19, 2017 at 6:21 am #
  
  Sorry, I have not seen this error before, consider posting to stack overflow.
  
  Reply
- kyci November 27, 2017 at 6:16 pm #
  
  It is a bug in statsmodels. You should convert the integer values in ‘data’ to float first (e.g., by using np.float()).
  
  Reply
  - Jason Brownlee November 28, 2017 at 8:36 am #
    
    Great tip.
    
    Reply
    - Vicente Queiroz March 30, 2018 at 8:43 pm #
      
      @kyci is correct as you can check in https://github.com/statsmodels/statsmodels/issues/3504.
      I was following this tutorial for my dataset, and what fixed my problem was just converting to float, like this:
      X = series.values
      X = X.astype(‘float32’)
      
      Reply
- Anup May 18, 2018 at 11:04 pm #
  
  How can I add multiple EXOG variales in the model?
  
  Reply
Amritanshu August 29, 2017 at 8:00 pm #

Jason, I am able to implement the model but the results are very vague for the predicted….

how to find the exact values for p,d and q ?

Reply
- Jason Brownlee August 30, 2017 at 6:14 am #
  
  My best advice is to use a grid search for those parameters:
  https://machinelearningmastery.com/grid-search-arima-hyperparameters-with-python/
  
  Reply
  - Amritanshu August 30, 2017 at 8:13 pm #
    
    Thanks a lot Jason…. if value of d=0 then we should not bother about using differncing methods ?
    
    Reply
    - Jason Brownlee August 31, 2017 at 6:18 am #
      
      It depends.
      
      The d only does a 1-step difference. You may still want to perform a seasonal difference.
      
      Reply
Amritanshu August 31, 2017 at 5:21 pm #

Jason, Can I get a link to understand it in a better way ? I am a bit confused on this.

Reply
- Jason Brownlee September 1, 2017 at 6:43 am #
  
  You can get started with time series here:
  https://machinelearningmastery.com/start-here/#timeseries
  
  Reply
Amritanshu September 5, 2017 at 11:22 pm #

Hi Jason

I am trying to predict values for the future. I am facing issue.

My data is till 31st July and I want to have prediction of 20 days…..

My Date format in excel file for the model is 4/22/17 –MM-DD-YY

output = model_fit.predict(start=’2017-01-08′,end=’2017-20-08′)

Error :

Traceback (most recent call last):
File “C:/untitled1/prediction_new.py”, line 31, in
output = model_fit.predict(start=’2017-01-08′,end=’2017-20-08′)
File “C:\Python36\lib\site-packages\statsmodels\base\wrapper.py”, line 95, in wrapper
obj = data.wrap_output(func(results, *args, **kwargs), how)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 1492, in predict
return self.model.predict(self.params, start, end, exog, dynamic)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 733, in predict
start = self._get_predict_start(start, dynamic)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 668, in _get_predict_start
method)
File “C:\Python36\lib\site-packages\statsmodels\tsa\arima_model.py”, line 375, in _validate
start = _index_date(start, dates)
File “C:\Python36\lib\site-packages\statsmodels\tsa\base\datetools.py”, line 52, in _index_date
date = dates.get_loc(date)
AttributeError: ‘NoneType’ object has no attribute ‘get_loc’

Can you please help ?

Reply
- Jason Brownlee September 7, 2017 at 12:45 pm #
  
  Sorry, I’m not sure about the cause of this error. Perhaps try predicting one day and go from there?
  
  Reply
  - Amritanshu September 20, 2017 at 10:20 pm #
    
    Not working … can you please help ?
    
    Reply
Kashif September 6, 2017 at 8:11 pm #

Hi Sir
Please help me to resolve this error
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot

def parser(x):
return datetime.strptime(‘190’+x, ‘%Y-%m’)

series = read_csv(‘E:/data/csv/shampoo-sales.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
print(series.head())
series.plot()
pyplot.show()

ERROR is
runfile(‘C:/Users/kashi/Desktop/prog/Date_time.py’, wdir=’C:/Users/kashi/Desktop/prog’)
Traceback (most recent call last):

File “”, line 1, in
runfile(‘C:/Users/kashi/Desktop/prog/Date_time.py’, wdir=’C:/Users/kashi/Desktop/prog’)

File “C:\Users\kashi\Anaconda3\lib\site-packages\spyder\utils\site\sitecustomize.py”, line 866, in runfile
execfile(filename, namespace)

File “C:\Users\kashi\Anaconda3\lib\site-packages\spyder\utils\site\sitecustomize.py”, line 102, in execfile
exec(compile(f.read(), filename, ‘exec’), namespace)

File “C:/Users/kashi/Desktop/prog/Date_time.py”, line 10, in
series = read_csv(‘E:/data/csv/shampoo-sales.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 562, in parser_f
return _read(filepath_or_buffer, kwds)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 325, in _read
return parser.read()

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 815, in read
ret = self._engine.read(nrows)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1387, in read
index, names = self._make_index(data, alldata, names)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1030, in _make_index
index = self._agg_index(index)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1111, in _agg_index
arr = self._date_conv(arr)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 2288, in converter
return generic_parser(date_parser, *date_cols)

File “C:\Users\kashi\Anaconda3\lib\site-packages\pandas\io\date_converters.py”, line 38, in generic_parser
results[i] = parse_func(*args)

File “C:/Users/kashi/Desktop/prog/Date_time.py”, line 8, in parser
return datetime.strptime(‘190’+x, ‘%Y-%m’)

File “C:\Users\kashi\Anaconda3\lib\_strptime.py”, line 510, in _strptime_datetime
tt, fraction = _strptime(data_string, format)

File “C:\Users\kashi\Anaconda3\lib\_strptime.py”, line 343, in _strptime
(data_string, format))

ValueError: time data ‘1901-Jan’ does not match format ‘%Y-%m’

I have already removed the footer note from the dataset and I also open dataset in text editor. But I couldn’t remove this error. But when I comment ”date_parser=parser” my code runs but doesn’t show years,
How to resolve it?
Thanks

Reply
- Jason Brownlee September 7, 2017 at 12:53 pm #
  
  Perhaps %m should be %b?
  
  Reply
Alec September 21, 2017 at 6:41 pm #

Getting this problem:

File “/shampoo.py”, line 6, in parser
return datetime.strptime(‘190’+x, ‘%Y-%m’)
TypeError: ufunc ‘add’ did not contain a loop with signature matching types dtype(‘<U32') dtype('<U32') dtype('<U32')

I've tried '%Y-%b' but that only gives me the "does not match format" error.

Any ideas?

/ Thanks

Reply
- Jason Brownlee September 22, 2017 at 5:35 am #
  
  Hi Alex, sorry to hear that.
  
  Confirm that you downloaded the CSV version of the dataset and that you have deleted the footer information from the file.
  
  Reply
  - Alec September 22, 2017 at 5:41 pm #
    
    Hey,
    
    I got it to work right after I wrote the post…
    
    The header in the .csv was written as “Month,””Sales” and that caused the error, so I just changed it to “month”, “sales” and it worked.
    
    Thanks for putting in the effort to follow up on posts!
    
    Reply
    - Jason Brownlee September 23, 2017 at 5:36 am #
      
      Glad to hear that Alec!
      
      Reply
Teja October 6, 2017 at 8:15 am #

Hey,
I’ve two years monthly data of different products and their sales at different stores. How can I perform Time series forecasting on each product at each location?

Thanks in advance.

Reply
- Jason Brownlee October 6, 2017 at 11:04 am #
  
  You could explore modeling products separately, stores separately, and try models that combine the data. See what works best.
  
  Reply
Shud October 23, 2017 at 7:47 pm #

Hey Jason,

You mentioned that since the residuals doesn’t have mean = 0, there is a bias. I have same situation. But the spread of the residuals is in the order of 10^5. So i thought it is okay to have non-zero mean. Your thoughts please?

Reply
- Shud October 23, 2017 at 8:20 pm #
  
  Btw my mean is ~400
  
  Reply
zhifeng November 4, 2017 at 1:17 am #

For those who came with an error of ValueError: time data ‘1901-Jan’ does not match format ‘%Y-%m’

please replace the month column with following:

Month
1-1
1-2
1-3
1-4
1-5
1-6
1-7
1-8
1-9
1-10
1-11
1-12
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
2-10
2-11
2-12
3-1
3-2
3-3
3-4
3-5
3-6
3-7
3-8
3-9
3-10
3-11
3-12

Reply
cuongquyet November 10, 2017 at 9:59 pm #

Dear Jason,

Firstly, I would like to thanks about your sharing

Secondly, I have a small question about ARIMA with Python. I have about 700 variables need to be forecasted with ARIMA model. How Python supports this issuse Jason

For example, I have data of total orders in a country, and it will be contributte to each districts
So I need to forecast for each districts (about 700 districts)

Thanks you so much

Reply
- Jason Brownlee November 11, 2017 at 9:22 am #
  
  Generally, ARIMA only supports univariate time series, you may need to use another method.
  
  That is a lot of variables, perhaps you could explore a multilayer perceptron model?
  
  Reply
volity November 13, 2017 at 10:11 pm #

The result of model_fit.forecast() is like (array([ 242.03176448]), array([ 91.37721802]), array([[ 62.93570815, 421.12782081]])). The first number is yhat, can you explain what the other number means in the result? thank you!

Reply
- Jason Brownlee November 14, 2017 at 10:13 am #
  
  It may be the confidence interval:
  https://machinelearningmastery.com/time-series-forecast-uncertainty-using-confidence-intervals-python/
  
  Reply
Chetan November 14, 2017 at 10:32 am #

Great blogpost Jason!
Had a follow up question on the same topic.
Is it possible to do the forecast with the ARIMA model at a higher frequency than the training dataset?
For instance, let’s say the training dataset is sampled at 15min interval and after building the model, can I forecast at 1second level intervals?
If not directly as is, any ideas on what approaches can be taken? One approach I am entertaining is creating a Kernel Density Estimator and sampling it to create higher frequency samples on top of the forecasts.
Thanks, much appreciate your help!

Reply
- Jason Brownlee November 15, 2017 at 9:44 am #
  
  Hmm, it might not be the best tool. You might need something like a neural net so that you can design a one-to-many mapping function for data points over time.
  
  Reply
Monsoon November 18, 2017 at 3:23 am #

Hi Jason,

Your tutorial was really helpful to understand the concept of solving time series forecasting problem. But I have small doubt regarding the steps you followed at the very end. I’m pasting your code down below-

X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
for t in range(len(test)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test[t]
history.append(obs)
print(‘predicted=%f, expected=%f’ % (yhat, obs))
error = mean_squared_error(test, predictions)

Note:1) here in the above for each iteration you’re adding the elements from the “test” and the forecasted value because in real forecasting we don’t have future data to include in test, isn’t it? Or is it that your’re trying to explain something and I’m not getting it.

2) Second doubt, aren’t you suppose to perform “reverse difference” for that you have used first order differencing in the model?

Kindly, please clear my doubt

Note: I have also went through one of your other tutorial where you have forecasted the average daily temperature in Australia.

https://machinelearningmastery.com/make-sample-forecasts-arima-python/

here the steps you followed were convincing, also you have performed “inverse difference” step to scale the prediction to original scale.
I have followed the steps from the one above but I m unable to forecast correctly.

Reply
- Jason Brownlee November 18, 2017 at 10:23 am #
  
  In this case, we are assuming the real observation is available after prediction. This is often the case, but perhaps over days, weeks, months, etc.
  
  The differencing and reverse differencing were performed by the ARIMA model itself.
  
  Reply
Somayeh November 28, 2017 at 12:39 am #

Hi Jason,
Recently I am working on time series prediction, but my research is a little bit complicated for me to understand how to fix a time series models to predict future values of multi targets.
Recently I read your post in multi-step and multivariate time series prediction with LSTM. But my problem have a series input values for every time (for each second we have recorded more than 500 samples). We have 22 inputs and 3 targets. All the data has been collected during 600 seconds and then predict 3 targets for 600 next seconds. Please help me how can solve this problem?
It is noticed we have trend and seasonality pulses for targets during the time.

Reply
- Jason Brownlee November 28, 2017 at 8:37 am #
  
  Perhaps here would be a good place to start:
  https://machinelearningmastery.com/start-here/#timeseries
  
  Reply
Desmond December 7, 2017 at 6:04 pm #

Hey just a quick check with you regarding the prediction part. I need to do some forecast of future profit based on the data from past profit. Let’s say I got the data for the past 3 years, and then I wanted to perform a forecast on the next 12 months in next year. Does the model above applicable in this case?

Thanks!

Reply
- Jason Brownlee December 8, 2017 at 5:36 am #
  
  This post will help you make predictions that are out of sample:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
  - Desmond December 9, 2017 at 7:52 pm #
    
    Hey Jason thanks so much for the clarification! But just to clarify, when I run the example above, my inputs are the past records for the past 3 years grouped by month. Then, how the code actually plot out the forecasted graph is basically takes in those input and plot, am I right? So, can I assumed that the graph that plotted out is meant for the prediction of next year?
    
    Reply
    - Jason Brownlee December 10, 2017 at 5:24 am #
      
      I don’t follow, sorry. You can plot anything you wish.
      
      Reply
      - Desmond December 10, 2017 at 2:29 pm #
        
        Sorry but what does the expected and predicted means actually?
      - Jason Brownlee December 11, 2017 at 5:21 am #
        
        The expected value is the real observation from your dataset. The predicted value is the value predicted by your model.
      - Desmond December 10, 2017 at 4:25 pm #
        
        Also, why the prediction has 13 points (start from 0 to 12) when each year only have 12 months? Looking forward to hear from you soon and thanks!
      - Jason Brownlee December 11, 2017 at 5:23 am #
        
        I arbitrarily chose to make predictions for 33% of the data which turned out to be 13 months.
        
        You’re right, it would have been clearer if I only predicted the final year.
      - Desmond December 11, 2017 at 4:12 pm #
        
        Hey Jason, thanks so much for the replies! But just to check with you, which line of the code should I modify so that it will only predict for the next 12 months instead of 13?
        
        Also, just to be sure, if I were to predict for the profit for next year, the value that I should take should be the predicted rather than expected, am I right?
        
        Thanks!!
      - Jason Brownlee December 11, 2017 at 4:55 pm #
        
        Sorry, I cannot prepare a code example for you, the URLs I have provided show you exactly what to do.
      - Desmond December 11, 2017 at 6:24 pm #
        
        Hey Jason, thanks so much but I am still confused as I am new to data analytic. The model above aims to make a prediction on what you already have or trying to forecast on what you do not have?
        
        Also, may I check with you on how it works? Because I downloaded the sample dataset and the dataset contains the values of past 3 years grouped by months. So, can I assume the prediction takes all the values from past years into account in order to calculate for the prediction value? Or it simply takes the most recent one and calculate for the prediction?
        
        Thanks!
Desmond December 11, 2017 at 4:17 pm #

Hey Jason, I am so sorry for the spams. But just a quick check with you again, let’s say I have some zero value for the profit, will it break the forecast function? Or the forecast function must take in all non-zero value. Because sometimes I am getting “numpy.linalg.linalg.LinAlgError: SVD did not converge” error message and I not sure if it is the zero values that is causing the problem. 🙂

Reply
- Jason Brownlee December 11, 2017 at 4:56 pm #
  
  Good question, it might depend on the model.
  
  Perhaps spot check some values and see how the model behaves?
  
  Reply
  - Desmond December 11, 2017 at 8:33 pm #
    
    May I know what kind of situation will cause the error above? Is it because of drastic up and down from 3 different dataset?
    
    Reply
Sushil Namdeo Raut December 13, 2017 at 10:26 am #

Hi Jason,
Thanks for this post. I am getting following error while running the very first code:

ValueError: time data ‘1901-Jan’ does not match format ‘%Y-%m’

Reply
- Jason Brownlee December 13, 2017 at 4:13 pm #
  
  Ensure your data is in CSV format and that the footer was removed.
  
  Reply
Denise December 13, 2017 at 7:07 pm #

Hi Jason, thanks so much for the share! The tutorial was good! However, when I am using my own data set, I am getting the same error message as one of the guy above. The error message is ‘numpy.linalg.linalg.LinAlgError: SVD did not converge’.

I tried to crack my head out trying to observe the data sets that caused the error message but I could not figure out anything. I tried with 0 value and very very very drastic drop or increase in the data, some seems okay but at some point, some data set will just fail and return the error message.

May I know what kind of data or condition will trigger the error above so I can take extra precaution when preparing the data?

Reply
- Jason Brownlee December 14, 2017 at 5:36 am #
  
  Perhaps try manually differencing the data first?
  
  Perhaps there are a lot of 0 values in your data that the model does not like?
  
  Reply
  - Denise December 14, 2017 at 2:38 pm #
    
    I tried with multiple set of data without a single zero. I realized a problem but I not sure if my observation is correct as I am still trying to figure out how the code above works, for that part I might need your enlightenment.
    
    Let’s say the data is 1000, 100, 10000 respectively to first, second and third year. This kind of data will throw out the error message above. So can I assume that, as long as there is a big drastic drop/increase in the data set, in this case from 100 to 10000, this kind of condition will execute with error?
    
    Reply
    - Jason Brownlee December 14, 2017 at 4:46 pm #
      
      Sorry Denise, I’m not sure I follow.
      
      Reply
- anand February 27, 2018 at 4:40 am #
  
  Hey Denise, i got the same issue. did you get any solution for this problem??
  
  Reply
Kelly December 17, 2017 at 8:00 am #

Hi Jason,

Thank you for the tutorial, it’s great! I have a question about stationarity and differencing. If time series is non stationary but is made stationary with simple differencing, are you required to have d=1 in your selected model? Can I choose a Model with no differencing for this data if it gives me a better root mean square error and there is no evidence of autocorrelation?

Reply
- Jason Brownlee December 17, 2017 at 8:57 am #
  
  Yes, you can let the ARIMA difference or perform it yourself.
  
  But ARIMA will do it automatically for you which might be easier.
  
  Reply
Satyajit Pattnaik December 20, 2017 at 10:53 pm #

@Jason, This article has helped me a lot for the training set predictions which i had managed to do earlier too, but could you help me with the future forecasting, let say your date data is till 10th November, 2017 and i want to predict the values for the next one week or next 3 days..

If we get help for this, that would be amazing 🙂

Reply
- Jason Brownlee December 21, 2017 at 5:26 am #
  
  See this post on how to make predictions:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Satyajit Pattnaik December 21, 2017 at 2:23 am #

@Jason,

For future predictions, let say i have data till 10th November, and based on your analysis as shown above, can you help me with the future predictions for a week or so, need an idea of how to predict future data..

Reply
- Jason Brownlee December 21, 2017 at 5:27 am #
  
  Yes, see this post:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Shariq Suhail December 27, 2017 at 4:29 pm #

Great post Jason!
I have a question:

– We need to ensure that the residuals of our model are uncorrelated and normally distributed with zero mean.
What if the residuals are not normally distributed?

It would be very grateful if you could explain how to approach in such scenario.

Thanks
Shariq

Reply
- Jason Brownlee December 28, 2017 at 5:18 am #
  
  It may mean that you could improve your model with some data transform, perhaps something like a boxcox?
  
  Reply
Namrata Nayak December 28, 2017 at 5:12 pm #

@Jason, What if we don’t want Rolling forecast, which means, my forecast should only be based on the training data, and it should predict the test data..

I am using the below code:

X = ts.values
size = int(len(X) * 0.75)
train, test = X[0:size], X[size:len(X)]
model = ARIMA(train, order=(4, 1, 2))
results_AR = model.fit(disp=0)
preds=results_AR.predict(size+1,size+16)
pyplot.plot(test[0:17])
pyplot.plot(preds, color=’red’)
pyplot.show()

This prediction is giving me really bad results, need urgent help on this.

Reply
- Jason Brownlee December 29, 2017 at 5:19 am #
  
  This is called a multi-step forecast and it is very challenging. You may need a different model.
  
  More here:
  https://machinelearningmastery.com/multi-step-time-series-forecasting/
  
  Reply
Vadim Pliner December 29, 2017 at 3:17 am #

Hi Jason, I have two questions.
1. Let’s say I want to estimate an AR model like this: x(t)=a*x(t-2) + e. If I use ARIMA(2,0,0), it will add the term x(t-1) as well, which I don’t want. In SAS I would use p=(2) on the estimate statement of proc arima rather than p=2.
2. How do I incorporate covariates? For example, a simple model like this: x(t)=a*x(t-2) + b*f(t) + e, where f(t) e.g. is 1 if it’s the month of January and 0 otherwise.
Thanks.

Reply
- Jason Brownlee December 29, 2017 at 5:24 am #
  
  Re the first question, it’s good. I don’t know how to do this with statsmodels off the cuff, some google searchers are needed.
  
  Re multivariates, you may need to use ARIMAX or SARIMAX or similar method.
  
  Reply
Fawad January 3, 2018 at 6:16 pm #

Hi,

I am getting the following error when loading the series dataframe in python
“ValueError: time data ‘190Sales of shampoo over a three year period’ does not match format ‘%Y-%m'”

Ive just copy pasted the code from this website but its not working. Any suggestions? Im using Sypder

Reply
- Jason Brownlee January 4, 2018 at 8:08 am #
  
  Ensure you remove the footer from the data file.
  
  Reply
Jelly January 9, 2018 at 1:58 pm #

Hi, may I know what are the yhat, obs and error variable are for? As for the error, is it better with greater value or the other way around? Thanks!

Reply
- Jason Brownlee January 9, 2018 at 3:19 pm #
  
  yhat are the predictions. obs are the observations or the actual real data.
  
  Reply
  - Jelly January 9, 2018 at 4:11 pm #
    
    Thanks! Then what about the MSE? Is it the greater the better or the other way around?
    
    Reply
    - Jason Brownlee January 10, 2018 at 5:20 am #
      
      A smaller error is better.
      
      Reply
Satyajit Pattnaik January 17, 2018 at 10:13 pm #

Could you please have a blog on Anomaly detection using timeseries data, may be from the above example itself.

Reply
- Jason Brownlee January 18, 2018 at 10:09 am #
  
  Thanks for the suggestion.
  
  Reply
Omar Irbaihat January 23, 2018 at 1:51 am #

hey sir , thanks for that , Is ARIMA good for predictions of currencies exchange rate or not ?

Reply
- Jason Brownlee January 23, 2018 at 8:05 am #
  
  I don’t know about currency exchange problems sorry. Try it and see.
  
  Reply
Chintan January 25, 2018 at 7:20 am #

Hello,
Is it possible to predict hourly temperature for upcoming 5 years based on hourly temperature data of last 5 years ?
I am trying this out with ARIMA model, its giving me vrey bad output ( attenuating curve ).

Reply
- Jason Brownlee January 25, 2018 at 9:10 am #
  
  You could model that, but I expect the skill to be very poor. The further in the future you want to predict, the worse the skill.
  
  Reply
Jing February 2, 2018 at 9:24 am #

if the time series corresponds to brownian motion time series generated with different Hurst value (let’s say H1 = 0.6 and H2 = 0.7), is this model a good fit to classify if it is H1 or H2?

Reply
Rajan R G February 12, 2018 at 1:25 am #

Hi Jason,

I have followed all of your posts related to Time Series to do my first data science project. I have done the parameter optimization also. The same code is working in my laptop but when i ran in Kaggle it shows “The computed initial AR coefficients are not stationary
You should induce stationarity, choose a different model order, or you can
pass your own start_params”. The python version is same in my environment and in Kaggle. Is this common?

Reply
- Jason Brownlee February 12, 2018 at 8:30 am #
  
  Sorry, I don’t know about “running code in kaggle”.
  
  Reply
  - Sofia May 22, 2019 at 7:59 pm #
    
    I get the same error when I run the code in my local PC. Not for every p and q though, but for higher values.
    
    Reply
    - Jason Brownlee May 23, 2019 at 6:00 am #
      
      Perhaps try using a “d” term to make the data stationary.
      
      Reply
Deepu Raj March 10, 2018 at 6:53 pm #

Hello, may I know what is the purpose for these two lines?

size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]

Thanks!

Reply
- Deepu Raj March 10, 2018 at 7:05 pm #
  
  Also, just to double confirm with you on my understanding, basically what the algorithm does is, take in all input in csv and fit into model, perform a forecast, append the forecast value into the model, then go thru the for loop again to recreate a new ARIMA model, forecast then append new forecast value, then go thru the for loop again?
  
  In addition, the next row prediction is always depends on the past prediction values?
  
  Reply
  - Jason Brownlee March 11, 2018 at 6:23 am #
    
    Yes, I believe so. Note, this is just one framing of the problem.
    
    Reply
- Jason Brownlee March 11, 2018 at 6:21 am #
  
  To split the dataset into train and test sets.
  
  Reply
  - Deepu Raj March 11, 2018 at 7:38 pm #
    
    Is there a specific reason for you to multiply with 0.66? Thanks!
    
    Reply
    - Jason Brownlee March 12, 2018 at 6:28 am #
      
      No reason, just an arbitrarily chosen 66%/37% split of the data.
      
      Reply
James Neligan March 13, 2018 at 6:56 am #

I need to forecasting the next x hour. How can i do this?

Reply
- Jason Brownlee March 13, 2018 at 3:03 pm #
  
  This post might help:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Ajay March 15, 2018 at 2:28 am #

Thanks Jason for making it simple. I run the program but getting error
1st error :
TypeError: Cannot cast ufunc subtract output from dtype(‘float64’) to dtype(‘int64’) with casting rule ‘same_kind’

After changing code , i got 2nd error
model = ARIMA(series.astype(float), order=(5,1,0))

I m getting following error
LinAlgError: SVD did not converge

Reply
- Jason Brownlee March 15, 2018 at 6:32 am #
  
  Looks like the data might have some issues. Perhaps calculate some summary stats, visualizations and look at the raw data to see if there is anything obvious.
  
  Reply
  - Ajay Verma March 16, 2018 at 2:16 am #
    
    Thanks Jason for the quick response. Now i tried for Sampoo dataset, getting following error :
    ValueError: time data ‘1901-Jan’ does not match format ‘%d-%m’
    
    Code :
    def parser(x): return datetime.strptime(‘190’+x, ‘%d-%m’)
    
    series = read_csv(‘shampoo-sales.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
    print(series.head())
    series.plot()
    pyplot.show()
    
    Reply
    - Jason Brownlee March 16, 2018 at 6:21 am #
      
      Perhaps your data contains the footer. Here is a clean version of the data ready to go:
      https://raw.githubusercontent.com/jbrownlee/Datasets/master/shampoo.csv
      
      Reply

Satyajit Pattnaik March 19, 2018 at 7:28 pm #

When we use a recursive model for ARIMA, let say like saw in one of your examples:

for t in range(len(test)):
    try:
        model = ARIMA(history, order=(4,0,2))
        model_fit = model.fit(disp=0)
        output = model_fit.forecast()
        yhat = output[0]
        predictions.append(yhat)
        obs = test[t]
        history.append(obs)
    except (ValueError, LinAlgError):
        pass
    print('predicted=%f, expected=%f' % (yhat, obs))

for t in range(len(test)):

try:

model = ARIMA(history, order=(4,0,2))

model_fit = model.fit(disp=0)

output = model_fit.forecast()

yhat = output[0]

predictions.append(yhat)

obs = test[t]

history.append(obs)

except (ValueError, LinAlgError):

pass

print('predicted=%f, expected=%f' % (yhat, obs))

Why my final test vs predicted graph is coming as if, the predictions are following the test values, it’s like if test is following a pattern, predictions is following similar pattern, hence ultimately our ARIMA predictions isn’t working properly, i hope you got my point.

For example: if test[0] keeps increasing till test[5] and decreases, then prediction[1] keeps increasing till predictions[5] and decreases..

Jason Brownlee March 20, 2018 at 6:14 am #

It suggests the model is not skilful and is acting like a persistence model.

It may also be possible that persistence is the best that can be achieved on your problem.

Reply
- Satyajit Pattnaik March 21, 2018 at 5:46 pm #
  
  Does that mean, ARIMA isn’t giving good results for my problem?
  
  What are different ways of solving this problem by ARIMA, can differencing or Log approach be a good solution?
  
  Reply
  - Jason Brownlee March 22, 2018 at 6:19 am #
    
    You can use ACF/PACF plots to help choose ARIMA parameters, or you can grid search ARIMA parametres on your test set.
    
    Reply

Mihir Ranade March 21, 2018 at 12:28 am #

Hello! Thank you for this great tutorial. It’d be a great help if you guide me through one of my problems.

I want to implement a machine learning model to predict(forecast) points scored by each player in the upcoming game week.

Say I have values for a player (Lukaku) for 28 game weeks and I train my model based on some selected features for those 28 weeks. How do I predict the outcome of the 29th week?

I am trying to predict total points to be scored by every player for the coming game week.
So basically what should be the input to my model for 29th game week? Since the game assigns points as per live football games happening during the week, I wont have any input data for 29th week.

Thank you 🙂

Reply
- Jason Brownlee March 21, 2018 at 6:37 am #
  
  I would recommend looking into rating systems:
  https://en.wikipedia.org/wiki/Elo_rating_system
  
  Reply
Raphael March 30, 2018 at 2:20 am #

Hi Jason,
Great tutorial once again!

I have a question on your Rolling Forecast ARIMA model.

When your are appending obs (test(t)) on each step to history, aren’t we getting data leakage?
The test set is supposed to be unseen data, right? Or are you using the test set as a validation set?

Reply
- Jason Brownlee March 30, 2018 at 6:42 am #
  
  In this case no, we are assuming the real observation is available at the end of each iteration.
  
  You can change the assumptions and therefore the test setup if you like.
  
  Reply
  - Raphael April 2, 2018 at 6:09 am #
    
    oh I see, i misunderstood this assumption, sorry. But how can I predict multiple steps? I used the predict() method from ARIMA model but the results were weird.
    
    Reply
    - Jason Brownlee April 2, 2018 at 2:44 pm #
      
      Yes, you can use the predict() function. Performance may be poor as predicting multiple steps into the future is very challenging.
      
      Reply
Ftima April 2, 2018 at 6:57 pm #

Hi,

In case we try to introduce more than one input, then how can fit the model and make prediction?

Thanks

Reply
- Jason Brownlee April 3, 2018 at 6:32 am #
  
  We don’t fit one point, we fit a series of points.
  
  Reply
Hsiang April 9, 2018 at 9:35 am #

Hi Jason,

Very nice introduction! Thank you very much for always bringing us excellent ML knowledge.

Can you further explain why you chose (p,d,q) = (5,1,0)? Or you did gird search (which you show in other blogs) using training/test sets to find minimum msg appears at (5,1,0)? Did you know any good reference for diagnostic plots for the hyper-parameters grid searching?

Meanwhile, I am interested in both time-series book and LSTM book. If I purchased both, any further deal?

Reply
- Jason Brownlee April 10, 2018 at 6:09 am #
  
  I recommend using both a PACF/ACF interpretation and grid searching approaches. I have tutorials on both.
  
  Sorry, I cannot create custom bundles of books, you can see the full catalog here:
  https://machinelearningmastery.com/products
  
  Reply
  - Hsiang April 12, 2018 at 6:05 pm #
    
    Hi Jason,
    
    Thank you for your answer. I have purchased time series book.
    I still have few more questions on ARIMA model:
    
    (1) The shampoo sale data obviously shows non-stationary; strictly speaking, we should transform data until it becomes stationary data by taking logarithm and differencing (Box-Cox transformation), and then apply to ARIMA model. Is it correct?
    
    (2) Does the time series data with first-order differencing on ARIMA (p,0,q) give the similar results to the time series data without differencing on ARIMA(p,1,q)? i.e. d = 1 in ARIMA(p,d,q)
    equivalently process data with first-order difference?
    
    (3) In this example, we chose ARIMA (5,1,0) and p=5 came from the autocorrelation plot. However, what I read from the book https://www.otexts.org/fpp/8/5 said to judge value of p, we should check PACF plot, instead ACF. Are there any things I missed or misunderstood?
    
    Reply
    - Jason Brownlee April 13, 2018 at 6:36 am #
      
      The shampoo data is non stationary and should be differenced, this can happen before modeling or as part of the ARIMA.
      
      No, 0 and 1 for d mean no differencing and first order differencing respectively.
      
      Yes, you can check ACF and PACF for configuring the p and q variables, see this post:
      https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
      
      Reply
Marco April 11, 2018 at 6:06 am #

Hi Jason,
In your code you use :

yhat=output[0]

So you take the first element of output, what are the other elements of output represent?
Thank you

Reply
- Jason Brownlee April 11, 2018 at 6:42 am #
  
  You can see all of the returned elements here:
  http://www.statsmodels.org/dev/generated/statsmodels.tsa.arima_model.ARMAResults.forecast.html
  
  Reply
  - Ugur August 6, 2021 at 6:08 pm #
    
    I am also trying to figure out what the other elements of output represent but Jason the link you provided does not work. Could you provide a fresh link?
    
    Reply
    - Jason Brownlee August 7, 2021 at 5:38 am #
      
      See here:
      https://www.statsmodels.org/stable/generated/statsmodels.tsa.arima_model.ARMAResults.forecast.html#statsmodels.tsa.arima_model.ARMAResults.forecast
      
      Reply
Mutasem April 22, 2018 at 12:48 pm #

Thank you for your efforts … i have question
i’m using the following code as mentioned above
def parser(x):
return datetime.strptime(‘190’ +x, ‘%Y-%m’)

but the error appears :

ValueError: time data ‘1902-Jan’ does not match format ‘%Y-%m’

could you please help me ….

Reply
- Jason Brownlee April 23, 2018 at 6:13 am #
  
  It looks like you downloaded the dataset in a different format.
  
  You can get the correct dataset here:
  https://raw.githubusercontent.com/jbrownlee/Datasets/master/shampoo.csv
  
  Reply
Harshil April 24, 2018 at 8:26 pm #

Hey Jason,
Best article I have ever seen. Currently I am working on data driven time series forecasting with PYTHON by ARIMA model. I have data of appliance energy which depends on 26 variables over period of 4 months. My question is how can I use 26 variables to forecast the future value?

Reply
- Jason Brownlee April 25, 2018 at 6:19 am #
  
  Thanks.
  
  Sorry, I don’t have an example of ARIMA with multiple input variables.
  
  Reply
Harshil April 26, 2018 at 5:33 pm #

Hello Jason,
Thanks for your reply.

Can I solve my problem with ARIMA model?

Reply
- Jason Brownlee April 27, 2018 at 6:02 am #
  
  Perhaps a variant that supports multiple series.
  
  Reply
Muhammad May 8, 2018 at 10:42 am #

Hey Jason, I am new to data analytics. From the chart, may I know how you determined it is stationary or non-stationary as well as how do you see whether it has a lagged value?

Thanks!

Reply
- Jason Brownlee May 8, 2018 at 2:53 pm #
  
  Yes, you can learn more about ACF and PACF and their interpretation here:
  https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  Reply
Sven May 20, 2018 at 8:40 am #

Hello Jason,

can Autoregression model be used for forecasting stock price ?

Reply
- Jason Brownlee May 21, 2018 at 6:23 am #
  
  Yes, but it will likely do worse than a persistence model.
  
  Learn more here:
  https://machinelearningmastery.com/gentle-introduction-random-walk-times-series-forecasting-python/
  
  Reply
Randal Michnovicz May 30, 2018 at 7:21 am #

Hello! I think you may have made a mistake in the following paragraph.

“If we used 100 observations in the training dataset to fit the model, then the index of the next time step for making a prediction would be specified to the prediction function as start=101, end=101. This would return an array with one element containing the prediction.”

Since python is zero-indexed, the index of the next time step for making a prediction should be 100, I think.

Reply
- Jason Brownlee May 30, 2018 at 3:06 pm #
  
  Not in this case. Try it and see.
  
  Reply
Franky Philip June 7, 2018 at 2:19 am #

Hello Jason!
I’m stuck at this error when i execute these lines of code:

from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot

def parser(x):
return datetime.strptime(‘190’+x, ‘%Y-%m’)

series = read_csv(‘shampoo_time_series.csv’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
print(series.head())
series.plot()
pyplot.show().

Error:-
time data ‘19001-Jan’ does not match format ‘%Y-%m’

Reply
- Jason Brownlee June 7, 2018 at 6:33 am #
  
  Perhaps you downloaded a different version of the dataset. Here is a direct link:
  https://raw.githubusercontent.com/jbrownlee/Datasets/master/shampoo.csv
  
  Does that help?
  
  Reply
bakhouche June 13, 2018 at 6:40 pm #

hi dear,
can ask you please what is the meaning of the arrow that cant be copied, thank you.

Reply
- Jason Brownlee June 14, 2018 at 5:59 am #
  
  Sorry, what arrow?
  
  Reply
Arsim June 17, 2018 at 8:24 am #

Hi Jason,
great tutorial, as always! Thank you very much for providing your excellent knowledge to the vast community! You really helped me to get a better understanding of this ARIMA type of models.

Do you plan to make a tutorial on nonlinear time-series models such as SETAR? Would be great, because I could not really find anything in this region.

Reply
- Jason Brownlee June 18, 2018 at 6:36 am #
  
  Thanks for the suggestion.
  
  I do hope to cover more methods for nonlinear time series in the future.
  
  Reply
Saloni Patil June 21, 2018 at 6:59 pm #

Hi Jason
I tried the code with my data. ACF, PACF plots aren’t showing me any significant correlations. Is there anything by which I can still try the forecast? What should be one’s steps on encounter of such data?

Reply
- Jason Brownlee June 22, 2018 at 6:04 am #
  
  Perhaps try a grid search on ARIMA parameters and see what comes up?
  
  Reply
ezgi June 22, 2018 at 10:29 pm #

Hi Jason,

Is it possible to make a forecast with xgboost for a time series data with categorical variables?

Reply
- Jason Brownlee June 23, 2018 at 6:18 am #
  
  Yes.
  
  Reply
dnyanada June 26, 2018 at 3:48 am #

Hello Jason, I have been following your articles and it has been very helpful.
I am running the same code above and get following error:

ValueError Traceback (most recent call last)
in ()
7 pred=list()
8 for i in range(len(test)):
—-> 9 model=ARIMA(history,order=(5,1,0))
10 model_fit=model.fit(disp=0)
11 output=model_fit.forecast()

~\AppData\Local\Continuum\anaconda3\lib\site-packages\statsmodels\tsa\arima_model.py in __new__(cls, endog, order, exog, dates, freq, missing)
998 else:
999 mod = super(ARIMA, cls).__new__(cls)
-> 1000 mod.__init__(endog, order, exog, dates, freq, missing)
1001 return mod
1002

~\AppData\Local\Continuum\anaconda3\lib\site-packages\statsmodels\tsa\arima_model.py in __init__(self, endog, order, exog, dates, freq, missing)
1013 # in the predict method
1014 raise ValueError(“d > 2 is not supported”)
-> 1015 super(ARIMA, self).__init__(endog, (p, q), exog, dates, freq, missing)
1016 self.k_diff = d
1017 self._first_unintegrate = unintegrate_levels(self.endog[:d], d)

~\AppData\Local\Continuum\anaconda3\lib\site-packages\statsmodels\tsa\arima_model.py in __init__(self, endog, order, exog, dates, freq, missing)
452 super(ARMA, self).__init__(endog, exog, dates, freq, missing=missing)
453 exog = self.data.exog # get it after it’s gone through processing
–> 454 _check_estimable(len(self.endog), sum(order))
455 self.k_ar = k_ar = order[0]
456 self.k_ma = k_ma = order[1]

~\AppData\Local\Continuum\anaconda3\lib\site-packages\statsmodels\tsa\arima_model.py in _check_estimable(nobs, n_params)
438 def _check_estimable(nobs, n_params):
439 if nobs 440 raise ValueError(“Insufficient degrees of freedom to estimate”)
441
442

ValueError: Insufficient degrees of freedom to estimate

the code used
from sklearn.metrics import mean_squared_error
size = int(len(df) * 0.66)
train,test=df[0:size],df[size:len(df)]
print(train.shape)
print(test.shape)
history=[x for x in train]
pred=list()
for i in range(len(test)):
model=ARIMA(history,order=(5,1,0))
model_fit=model.fit(disp=0)
output=model_fit.forecast()
yhat=output[0]
pred.append(yhat)
obs=test[i]
history.append(obs)
print(‘predicted = %f,expected = %f’,(yhat,obs))
error=mean_squared_error(test,pred)
print(‘Test MSE: %.3f’ % error)

plt.plot(test)
plt.plot(pred,color=’red’)
plt.show()

On;ly change I have made in code is date index. I have done something like this for dates
dt=pd.date_range(“2015-01-01”, “2017-12-1″, freq=”MS”)

Can you explain what is wrong?

also,
I was under impression that you use auto_corr function to determine Q parameter in ARIMA model. then in your code when you call ARIMA why have you used (5,1,0) assuming it is (p,d,q)? i thought it was suppose to be (0,1,5)?

Reply
- Jason Brownlee June 26, 2018 at 6:45 am #
  
  I have more on the ACF/PACF plots and how to interpret them here:
  https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  Reply
Dnyanada Arjunwadkar June 26, 2018 at 9:28 am #

Hello Jason, I posted a problem earlier today that I have successfully resolved. thanks for your help.

Reply
- Jason Brownlee June 26, 2018 at 2:26 pm #
  
  Glad to hear it.
  
  Reply
Dnyanada Arjunwadkar June 27, 2018 at 4:13 am #

Hello Jason,

Thanks for the helpful article.
My question is :
“A rolling forecast is required given the dependence on observations in prior time steps for differencing and the AR model.”

can you please elaborate?
How do we decide when to use Rolling forecast and when not to use rolling forecast?
what are the factors do you consider?

Thanks

Reply
- Jason Brownlee June 27, 2018 at 8:22 am #
  
  I believe I mean a walk-forward validation. More here:
  https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
  
  Reply
mithril July 5, 2018 at 1:30 am #

Hello,

My company is supermaket , which have 30 stores and over 2000 products. My boss want me to predict each product sale number in next 7 days.

I think below features would affect sales count much

1. a day is festival
2. a day is weekend
3. a day’s weather
4. a day is coupon day

But I don’t know how to embed above features with ARIMA model.
And also our data is from 2017-12 to now, there is no history season data。

Could you please give me a some advice?

Thank you.

Reply
- Jason Brownlee July 5, 2018 at 7:57 am #
  
  They could be exogenous binary variables that the statsmodels ARIMA does support.
  
  Reply
Paola July 22, 2018 at 8:13 am #

Great article! But I have a question. I have a daily time series, and I am following the steps from the time series forecasting book. How do I obtain the acf and pacf visually (for the Manually Congured ARIMA)? because I will have more than 1000 lag values (as my dataset is for many years), and after this I will need to search for the hyperparameters. I will really appreciate the help

Reply
- Jason Brownlee July 23, 2018 at 6:00 am #
  
  An ARIMA might not be appropriate for 1000 lags.
  
  Reply
Luisa July 22, 2018 at 8:15 am #

Great

Reply
- Jason Brownlee July 23, 2018 at 6:00 am #
  
  Thanks.
  
  Reply
Ivan July 22, 2018 at 11:56 pm #

thank you very much, Jason.

However. I have some problem. Whenever I adopt your code for forcasting when no validation data is available,
for t in range(93): model = ARIMA(history, order=(5,1,0)) model_fit = model.fit(disp=0) output = model_fit.forecast() yhat = output[0] predictions.append(yhat) history.append(yhat) print('predicted=%f' % (yhat))
my series converge to a constant number after a certain number of iterations, which is not right. What is the mistake?

Reply
- Jason Brownlee July 23, 2018 at 6:12 am #
  
  You can fit a final model and make a prediction by calling forecast().
  
  Here’s an example:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Siddharth August 3, 2018 at 3:52 pm #

Hi Jason,

Your articles are great to read as they give just the right amount of background and detail and are practical oriented. Please continue writing.

I have a question though, being not from the statistical background, i am having difficulty in interpreting the output that is displayed after the summary of the fit model under the heading of “ARIMA model results”. This summarizes the coefficient values used as well as the skill of the fit on the on the in-sample observations.

Can you please provide some explanation on their attributes and how the information assists us in the interpretation of the results

Reply
- Jason Brownlee August 4, 2018 at 5:59 am #
  
  Thanks.
  
  Perhaps focus on the skill of the model and using the forecast of the model?
  
  Reply
Anna August 5, 2018 at 8:57 am #

Hi Jason,
Thanks a lot for this awesome tutorial.

I am training on a dataset where I have to predict Traffic and Revenue during a campaign (weeks 53,54,55) driven by this marketing campaigns. I think I can only use data preceding the campaigns (weeks 1 to 52) even though I have the numbers for campaign and post campaign.

I have a file as follows:

week// campaign-period // TV-traffic // Revenue Trafiic
1 //pre-campaign // 108567 // 184196,63
2 //pre-campaign // 99358 // 166628,38
…
53 // Campaign // 135058 //240163,25
54 // Campaign // 129275 //238369,88
…
56 // post-campaign //94062 // 141284,88
…
62 // post-campaign // 86695 // 130153,38

It seems like a statistical problem and I don’t know whether ARIMA is suitable for this use case (very few data, only 52 values to predict the following one). Do you think I can give it a shot with ARIMA or do you think there are other models that could be more suitable for such a use case please?

Thanks a lot for your help.

Reply
- Jason Brownlee August 6, 2018 at 6:23 am #
  
  Perhaps list out 10 or more different framings of the problem, then try fitting models to a few to see what works best?
  
  Reply
  - Anna August 12, 2018 at 4:31 am #
    
    Hi Jason,
    Thanks a lot for this awesome tutorial.
    
    I am training on a dataset where I have to predict Traffic and Revenue during a campaign (weeks 53,54,55) driven by this marketing campaigns. I think I can only use data preceding the campaigns (weeks 1 to 52) even though I have the numbers for campaign and post campaign.
    
    I have a file as follows:
    
    week// campaign-period // TV-traffic // Revenue Trafiic
    1 //pre-campaign // 108567 // 184196,63
    2 //pre-campaign // 99358 // 166628,38
    …
    53 // Campaign // 135058 //240163,25
    54 // Campaign // 129275 //238369,88
    …
    56 // post-campaign //94062 // 141284,88
    …
    62 // post-campaign // 86695 // 130153,38
    
    It seems like a statistical problem and I don’t know whether ARIMA is suitable for this use case (very few data, only 52 values to predict the following one). Do you think I can give it a shot with ARIMA or do you think there are other models that could be more suitable for such a use case please?
    
    Thanks a lot for your help.
    
    Thank you for your help
    
    Reply
    - Jason Brownlee August 12, 2018 at 6:36 am #
      
      Perhaps try it and see how you go?
      
      Reply
Nii Anyetei August 7, 2018 at 5:46 am #

Hi Jason, the constant updates are great and very helpful. I need a bit of help with my work. Im trying to forecast solid waste generation in using ANN. But I’m finding challenges with data and modeling my problem. If you could at least get me a headway that can help me produce something in 2weeks I will be grateful. I want to consider variables such as already generated solid waste, population, income levels, educational levels, etc. I hope to hear from you soon.

Reply
- Jason Brownlee August 7, 2018 at 6:35 am #
  
  This is a good place to start for deep learning:
  https://machinelearningmastery.com/start-here/#deeplearning
  
  Reply
Wen Ge August 8, 2018 at 7:32 pm #

Many thanks Jason, it’s really helpful!

Just one question, my data set contains some sales value = 0, would that affect the performance of ARIMA model? if there will be issues, anyway I can deal with the zero values in my data set? Thanks in advance for your advice!

Reply
- Jason Brownlee August 9, 2018 at 7:36 am #
  
  It can deal with zero values.
  
  Reply
Brian Stephans August 15, 2018 at 1:55 am #

Hello Jason,

Any idea why I am having issues with datetime?

This is the error that I have received

Traceback (most recent call last):
File “/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/pandas/io/parsers.py”, line 3021, in converter
date_parser(*date_cols), errors=’ignore’)
File “/Users/Brian/PycharmProjects/MachineLearningMasteryTimeSeries1/ARIMA.py”, line 9, in parser
return datetime.strptime(‘190’ + x, ‘%Y-%m’)
TypeError: strptime() argument 1 must be str, not numpy.ndarray

During handling of the above exception, another exception occurred:

Thank You
Brian

Reply
- Jason Brownlee August 15, 2018 at 6:07 am #
  
  Perhaps your data file, try this one instead:
  https://raw.githubusercontent.com/jbrownlee/Datasets/master/shampoo.csv
  
  Reply
Anton Petrov August 17, 2018 at 1:32 am #

The formating of csv seems different for everyone who downloads it, here’s the format that is used by Jason (just copy pasted this into a shampoo-sales.csv file and save)

– thanks to the person above for the tip

1-1,266
1-2,145.9
1-3,183.1
1-4,119.3
1-5,180.3
1-6,168.5
1-7,231.8
1-8,224.5
1-9,192.8
1-10,122.9
1-11,336.5
1-12,185.9
2-1,194.3
2-2,149.5
2-3,210.1
2-4,273.3
2-5,191.4
2-6,287
2-7,226
2-8,303.6
2-9,289.9
2-10,421.6
2-11,264.5
2-12,342.3
3-1,339.7
3-2,440.4
3-3,315.9
3-4,439.3
3-5,401.3
3-6,437.4
3-7,575.5
3-8,407.6
3-9,682
3-10,475.3
3-11,581.3
3-12,646.9

Reply
- Jason Brownlee August 17, 2018 at 6:31 am #
  
  It is also available on my github:
  https://github.com/jbrownlee/Datasets
  
  Reply
SA August 17, 2018 at 8:08 am #

Hello Jason

I’m trying to divide time series dataset into several dataset and select the best one as preprocessing dataset.I would like to use RMSE to evaluate each subset.In other word to select the window size and frame size before I do the training . Please let me know if you have any article on rows selection not column selection

Reply
- Jason Brownlee August 17, 2018 at 2:04 pm #
  
  Yes, this post will help tune the parameters of ARIMA that will include tuning the size of the window for each aspect of the ARIMA model:
  https://machinelearningmastery.com/grid-search-arima-hyperparameters-with-python/
  
  Reply
SA August 18, 2018 at 8:07 am #

Hello Jason

Many thanks for your reply. I have tried the code on the following data set and got “Best ARIMANone MSE=inf”

date price
0 20160227 427.1
1 20161118 750.9
2 20160613 690.9
3 20160808 588.7
4 20170206 1047.3

RangeIndex: 657 entries, 0 to 656
Data columns (total 2 columns):
date 657 non-null int64
price 657 non-null float64
dtypes: float64(1), int64(1)
memory usage: 10.3 KB

Reply
SA August 18, 2018 at 8:16 am #

Hello Jason

Just to clarify my previous question that i have 700 rows of date and price and I would like select the best 70(window size) rows for prediction and decide on the frame size , frame step and extent of prediction.

Reply
- Jason Brownlee August 19, 2018 at 6:14 am #
  
  Sounds great, let me know how you go!
  
  Reply
  - SA August 19, 2018 at 7:11 am #
    
    Hi Jason
    
    Please let me know if you have an article help on specifying frame size , frame step and extent of prediction as data pre-processing step using RMSE and SEP.
    
    Reply
    - Jason Brownlee August 20, 2018 at 6:30 am #
      
      I do, the grid search of the ARIMA algorithm I linked to above does that.
      
      Perhaps try working through it first?
      
      Reply
      - SA August 21, 2018 at 6:41 am #
        
        Thanks Jason. Your post in Grid search is great. I have already applied the Grid Search and got best Arima model .
        
        Now I want to use the result and train the window in LSTM
        
        RIMA(1, 0, 0) MSE=39.723
        ARIMA(1, 0, 1) MSE=39.735
        ARIMA(1, 1, 0) MSE=36.148
        ARIMA(3, 0, 0) MSE=39.749
        ARIMA(3, 1, 0) MSE=36.141
        ARIMA(3, 1, 1) MSE=36.131
        ARIMA(6, 0, 0) MSE=39.806
        ARIMA(6, 1, 0) MSE=36.134
        ARIMA(6, 1, 1) MSE=36.128
        Best ARIMA(6, 1, 1) MSE=36.128
      - Jason Brownlee August 21, 2018 at 2:13 pm #
        
        An LSTM is a very different algorithm. Perhaps difference the series and use at least 6 time steps as input?
      - SA August 22, 2018 at 7:29 am #
        
        I have 5 years of time series data .Will 6 time steps (6 days) be enough as window size.I want to get the best optimal window as input to LSTM !
        
        Appreciate your feedback.
      - Jason Brownlee August 22, 2018 at 1:51 pm #
        
        Test many different sized subsequence lengths and see what works best.
      - SA August 23, 2018 at 7:13 am #
        
        Can I use Gridsearch for the testing purpose to specify the window size for LSTM?And if yes what would be the paramerters equal to 60/90/120 days ?
      - Jason Brownlee August 23, 2018 at 8:04 am #
        
        I would recommend running the grid search yourself with a for-loop.
        
        Try time periods that might make sense for your problem.
      - SA August 24, 2018 at 8:06 am #
        
        So I did the for-loop and manage to get different windows.
        Now to calculate the RMSE do I need to do linear regiression prediction for each window in order to calculate the RMSE or is there any other way around?
      - Jason Brownlee August 24, 2018 at 9:16 am #
        
        I would expect that you would fit a model for different sized windows and compare the RMSE of the models. The models could be anything you wish, try a few diffrent approaches even.
      - SA August 25, 2018 at 7:38 am #
        
        I got the following as example for two window size 360 days and 180 days
        For 360 days
        Window start after 0 days with windwo size 360 and step 100 have RMSE 734.1743876097737
        Window start after 100 days with windwo size 360 and step 100 have RMSE 369.94549420288877
        Window start after 200 days with windwo size 360 and step 100 have RMSE 105.70778076287142
        For 180 days
        
        Window start after 0 days with windwo size 180 and step 90 have RMSE 653.9070358902835
        Window start after 90 days with windwo size 180 and step 90 have RMSE 326.7832188924093
        Window start after 180 days with windwo size 180 and step 90 have RMSE 135.01118940666115
        Window start after 270 days with windwo size 180 and step 90 have RMSE 38.422587695965746
        Window start after 360 days with windwo size 180 and step 90 have RMSE 60.73374764651785
        Window start after 450 days with windwo size 180 and step 90 have RMSE 52.386817309349176
      - Jason Brownlee August 26, 2018 at 6:19 am #
        
        Well done!
      - SA August 26, 2018 at 7:04 am #
        
        Thanks Jason
        Appreciate your support.
        Your posts are really great and well organized.
        I’m excited to ready your publications 🙂
      - Jason Brownlee August 27, 2018 at 6:10 am #
        
        Thanks for your support!
Waldo August 18, 2018 at 9:36 pm #

Hi Jason! Here client and time series forecaster!
When forecasting, I very often get this error:

LinAlgError: SVD did not converge

Any ideas how to solve this in general?

Thanks!

Reply
- Jason Brownlee August 19, 2018 at 6:20 am #
  
  This is common.
  
  Sounds like the linear algebra library used to solve the linear regression equation for a given configuration failed.
  
  Try other configurations?
  Try fitting a linear regression model manually to the lag obs?
  Try normalizing the data beforehand?
  
  Let me know how you go.
  
  Reply
Renato August 23, 2018 at 9:51 am #

Hey Jason, what model i can use to equipment fault detection and prediction? So have some variables that correlate with others and i need to identification which are. See you soon.

Reply
- Jason Brownlee August 23, 2018 at 1:54 pm #
  
  Try a suite of methods in order to discover what works best for your specific problem.
  
  Reply
Romain September 2, 2018 at 7:20 pm #

Hello Jason,

There is something that I struggle to understand, it would awesome if you could give me a hand.

In ARIMA models, the optimization fits the MA and AR parameters. Which can be summed up as parameters of linear combination of previous terms for the AR and previous errors for the MA. A quick math formula could be :

X_t – a_1 X_t-1 … – a_p X_t-p … = e_t + b_1 e_t-1 + … + b_q e_t-q

When the fit method is used, it takes the train values of the signal to fit the parameters (a and b)

When the forecast method is used, it forecast the next value of the signal using the fitted model and the train values

When the predict method is used, it forecast the next values of the signal from start to stop.

Let’s say I fit a model on n steps in the train set. Now I want to make predictions. I can predict step n+1. Now I am days n+1 and I have the exact signal value. I would like to actualize the model to predict n+2.

In the rolling forecast part of your code, you fit again the model with the expanded train set (up to n+1). But in that case the model parameters are changed. It’s not the same model anymore.

Is it possible to train one model and then actualize the signal values (the x and e) without changing the parameters (a and b)?

It seems to me that it is important to keep one unique model and evaluate it against different time steps instead of training n different models for each new time steps we get.

I hope I was clear enough. I miss probably a key to understand the problem.

Thanks
Romain

Reply
- Jason Brownlee September 3, 2018 at 6:15 am #
  
  The model will use the prediction as the input to predict t+2.
  
  Reply
Matthew Orehek September 7, 2018 at 7:28 am #

Hi Jason – Very helpful post here, thanks for sharing. I’m curious why parameter ‘p’ should be equal to the number of significant lags from the auto correlation plot? Just was wondering if you could give any more context to this part of the problem. Thanks.

Reply
- Jason Brownlee September 7, 2018 at 8:11 am #
  
  Generally, we want to know how may lag observations have a measurable relationship with the next step so that the model can work on using them effectively.
  
  Reply
Christopher September 12, 2018 at 12:44 pm #

I used your code to forecast daily temperature (it has a lag of 365). The forecast is always a day behind, i.e. learning history cannot accurately forecast next day’s temperature. I’ve played with the params with AIC.

Reply
- Jason Brownlee September 12, 2018 at 2:39 pm #
  
  Perhaps try alternate configurations?
  Perhaps try alternate algorithms?
  Perhaps try additional transforms to the data?
  
  This might help:
  https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
  
  Reply
Anuradha Chaurasia September 16, 2018 at 11:23 pm #

How to use ARIMA model in SPSS with few sample as 6 years data and according to this data for how many years we can forecast the future.

Reply
- Jason Brownlee September 17, 2018 at 6:31 am #
  
  Sorry, I don’t have examples of SPSS.
  
  Reply
Qianqian September 18, 2018 at 1:25 am #

Hi Jason,

Thanks for sharing! Very helpful post.
Recently I am writing the methodology of ARIMA, but I can not find any reference (for example, some ARIMA formulas contain constant but some don’t have ). So could you please give me some reference (or ARIMA formula information) of “statsmodels.tsa.arima_model import ARIMA” used in Python?

Thank you in advance.

Reply
- Jason Brownlee September 18, 2018 at 6:20 am #
  
  The best textbook on ARIMA is:
  https://amzn.to/2MD9lKw
  
  Reply
- Pranab May 26, 2020 at 12:50 pm #
  
  Hi Qianqian,
  Prof. Hyndman’s textbook: https://otexts.com/fpp2/arima.html
  Hope this helps.
  
  Reply
Milind Mahajani September 20, 2018 at 12:44 am #

If one has a time series where the time steps are not uniform, what should be done while fitting a model such as ARIMA? I have price data for a commodity for about 4 years. The prices are available only for days that a purchase was made. This is often, but not always, every day. So sometimes purchases are made after 2, 3 or even more days and the prices are therefore available only for those days I need to forecast the price for the next week.

Thanks for any advice on this.

Reply
- Jason Brownlee September 20, 2018 at 8:01 am #
  
  Perhaps try modeling anyway?
  Perhaps try an alternative model?
  Perhaps try imputing the missing values?
  
  Reply
  - Milind Mahajani September 20, 2018 at 8:27 pm #
    
    Thank you, Dr Jason!
    
    Reply
Kruthika Vishwanath September 25, 2018 at 6:55 am #

Hi Jason,

Thanks for this post.

I am working on finding an anomaly using arima. Will I be able to find from the difference in actual & predicted value shown above ?

Thanks,
Kruthika

Reply
- Jason Brownlee September 25, 2018 at 2:43 pm #
  
  Sorry, I don’t have examples of using ARIMA for anomaly detection.
  
  Reply
Bhadri September 29, 2018 at 6:20 pm #

Hi Jason,

I have couple of questions.

1. is it necessary that we need to have always uni variate data set to predict for time series using ARIMA? What if i have couple of features that i want to pass along with the date time?

2. is it also necessary that we have a non-stationary data to use time series for modelling? what if the data is already stationary? can i still do the modelling using time series?

Thanks
Bhadri

Reply
- Jason Brownlee September 30, 2018 at 6:02 am #
  
  ARIMA can support exogenous variables, this is called ARIMAX.
  
  If the data is already stationary, you can begin modeling without transforms.
  
  Reply
  - Bhadri September 30, 2018 at 3:13 pm #
    
    Thanks Jason!! do u have any examples related to ARIMAX or point me to some articles..
    
    Reply
    - Jason Brownlee October 1, 2018 at 6:24 am #
      
      Yes, there are examples here:
      https://machinelearningmastery.com/time-series-forecasting-methods-in-python-cheat-sheet/
      
      Reply
awa October 17, 2018 at 4:36 pm #

Hello sir,
This is a great article. But sir I have couple of questions?
1. Assume that if we have three inputs and one output with time period. Then how do we predict the next future value according to the past values to next time period using ARIMA model? (if we need to predict value next time interval period is 120min)
as a example

6:00:00 63 0 0 63
7:00:00 63 0 2 104
8:00:00 104 11 0 93
9:00:00 93 0 50 177

2. To predict value should I have to do time forecast according to the data that I mentioned earlier?

Reply
- Jason Brownlee October 18, 2018 at 6:25 am #
  
  You could treat the other inputs as exogenous variables and use ARIMAX, or you could use another method like a machine learning algorithm or neural network that supports multivariate inputs.
  
  Reply
Mohammad October 31, 2018 at 3:07 pm #

This is a great post, thank you very much.

I’m new in this field, and I look for simple introduction to ARIMA models in general then an article about multivariate ARIMA.

Could you please help me.

Reply
- Jason Brownlee November 1, 2018 at 6:01 am #
  
  Thanks.
  
  I don’t think I have an example of a multivariate ARIMA, maybe ARIMAX/SARIMAX would be useful as a start:
  https://machinelearningmastery.com/time-series-forecasting-methods-in-python-cheat-sheet/
  
  Reply
Ramy November 2, 2018 at 10:07 pm #

Hey Jason,

I was wondering if you are aware of any auto arima functions to fine tune p,d,q parameters. I am aware that R has an auto.arima function to fine tune those parameters but was wondering if you’re familiar with any Python library.

Reply
- Jason Brownlee November 3, 2018 at 7:06 am #
  
  Yes, I wrote one in Python here:
  https://machinelearningmastery.com/how-to-grid-search-sarima-model-hyperparameters-for-time-series-forecasting-in-python/
  
  Reply
Sheldon November 6, 2018 at 1:11 pm #

Hi Jaosn.

Thanks a lot for the great tutorial!

Have followed your post : “How to Grid Search ARIMA Model Hyperparameters with Python” to fine tune the p,q and d value. Have come across the below point in the post.

“The first is to ensure the input data are floating point values (as opposed to integers or strings), as this can cause the ARIMA procedure to fail.”

My initial data is in the below format. Month and #Sales

2014-11 4504794
2014-12 7656479
2015-01 9340428
2015-02 7229578
2015-03 7092866
2015-04 14514074
2015-05 9995460
2015-06 8593406
2015-07 8774430
2015-08 8448562

I applied a log transofrmation on the above data set to convert the numbers to flot as below:-

dateparse = lambda dates: pd.datetime.strptime(dates, ‘%Y-%m’)
salessataparsed = pd.read_csv(‘sales.csv’, parse_dates=[‘Month’], index_col=’Month’,date_parser=dateparse)
salessataparsed.head()
ts_log = np.log(salessataparsed[‘#Sales’])

Below is the ts_log.head() output.

2014-11-01 15.320654
2014-12-01 15.851037
2015-01-01 16.049873
2015-02-01 15.793691
2015-03-01 15.774600
2015-04-01 16.490560
2015-05-01 16.117632
2015-06-01 15.966517

With this log value, applied the grid search approach to decide the best value of p,q and d.
Howver, I got Best ARIMA(0, 1, 0) MSE=0.023. Looks good ? is it acceptable? Wondering if p=0 and q=0 is acceptable. Please confirm.

Next, I have 37 Observations from Nov 2014 to 31-Dec-2017. I want to do future predictions for 2018, 2019 etc.How to do this?

Also, do you have any Youtube videos explaining each of the steps in grid approach, how to make future forecatsts available ? It would be great if you can share the Youtube link. 🙂

Once again thanks a lot for the article and your help!

Reply
- Jason Brownlee November 6, 2018 at 2:21 pm #
  
  You can discover if your model is skillful by comparing its performance to a naive model:
  https://machinelearningmastery.com/faq/single-faq/how-to-know-if-a-model-has-good-performance
  
  Perhaps try standardizing or normalizing the data as well.
  
  I don’t make videos, only text-based tutorials, sorry.
  
  I show how to use an ARIMA model to make forecasts here:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
  - Sheldon November 6, 2018 at 5:33 pm #
    
    Great ! Thanks a ton Jason.
    
    Kindly confirm if the p,q value is 0 is an acceptable scenario.
    
    Perhaps try standardizing or normalizing the data as well : I am not sure how to proceed with this?
    It would be great if you can share related article if you have any. 🙂
    
    For now, I am going to implement the future forecasting using the above link with this ARIMA(0,1,0) and will check how it behaves. 🙂
    
    Reply
    - Jason Brownlee November 7, 2018 at 6:00 am #
      
      See this post:
      https://machinelearningmastery.com/machine-learning-data-transforms-for-time-series-forecasting/
      
      Reply
Michelle November 13, 2018 at 1:08 am #

Hi Jason, thanks for the tutorial i am new to the world of predictive analysis but i have a project to predict when a customer is likely to make next purchase. I have dataset which include historical transactions and amount.

Will this tutorial help me or is there any suggestion on material/resource i can use.

Could you please advice

Reply
- Jason Brownlee November 13, 2018 at 5:48 am #
  
  I recommend following this process:
  https://machinelearningmastery.com/start-here/#process
  
  Reply
Ayub November 28, 2018 at 3:44 am #

Hi Jason,

Used your epic tutorial to forecast bookings.
I used the whole of 2017 as my data set and after applying everything in your post the predicted graph seems to be one day off i.e. prediction graph looks spot on with each data point very close to the what it should be, the only thing is is that it’s a day late…is this normal? Is there something within the code that causes something like this?

Thanks

Reply
- Jason Brownlee November 28, 2018 at 7:46 am #
  
  This is a common problem, I explain more here:
  https://machinelearningmastery.com/faq/single-faq/why-is-my-forecasted-time-series-right-behind-the-actual-time-series
  
  Reply
Kris November 29, 2018 at 9:09 pm #

Hi, i have had a question for a while, now this might be silly but I can’t figure out whats wrong here…

So I have a timeseries data and when i used order=(0,1,0) that is, differencing is 1 then i get a timeseries that is ahead of time by one.
example:
input: 10, 12, 11, 15
output: 8, 9.9, 12.02, 11.3, 14.9

Now if I shift the resulting series by one timeperiod, it’ll match quite well.

Also, similar output can be seen is (0,2,1) that is, differencing is 2 and MA is 1.

Could someone explain why is this happening and what am i missing here.
[numbers in example are representative not actual]

Reply
- Jason Brownlee November 30, 2018 at 6:30 am #
  
  It suggest that the model is using the input as the output, this is called a persistence model:
  https://machinelearningmastery.com/faq/single-faq/why-is-my-forecasted-time-series-right-behind-the-actual-time-series
  
  Reply
  - Kris December 3, 2018 at 6:29 am #
    
    Thanks Jason, I went through the link and it helps me see a clear picture which should have been obvious to notice but i missed it.
    
    If you please, could also share some thoughts on…
    
    – My model uses order(0,1,0). i.e. differencing is 1. Do such model makes sense for a practical scenario where we are trying to predict inventory requirement for a part(based on past consumption) that may fail in coming future(where failing of a part is totally a random act of nature).
    
    – Also, (0,2,1) and (0,1,0) gives very similar results. Is this expected in some sense. Is there any concept that i am missing here.
    
    Thanks a lot again, for your help.
    
    Reply
    - Jason Brownlee December 3, 2018 at 6:55 am #
      
      I generally recommend using the model that gives the best performance and is the simplest.
      
      Reply
Dhananjai Sharma December 4, 2018 at 8:08 pm #

Hello Jason!

Thank you for the tutorial. It’s a good start to implementing an ARIMA model in Python. I have a question: You have used the actual data samples to update your training dataset after each prediction as given in “history.append(obs)”. Now let’s take a real life example when you don’t have any further actual data and you use your predictions only to update your training dataset which looks like “history.append(yhat)”. What will happen in this case? I am working on air quality prediction and in my case, the former scenario keeps the seasonal pattern in the test set but the latter does not show any seasonal pattern at all. Please let me know what’s your take on this.

Regards,
Dhananjai
—

Reply
- Jason Brownlee December 5, 2018 at 6:15 am #
  
  You can re-fit the model using predictions as obs and/or predictions as inputs for subsequent predictions (recursive).
  
  Perhaps evaluate a few approaches on your dataset and see how it impacts model performance.
  
  Reply
Beshoy Akram December 8, 2018 at 3:19 am #

Hi Jason ,
Thank you for the tutorial.
I have two questions :
first : why you set moving average “q” Parameter by 0 ?
second : why you set Lag value To 5 not 7 for example?
Thanks.

Reply
- Jason Brownlee December 8, 2018 at 7:12 am #
  
  They are an arbitrary configuration.
  
  Perhaps try other configurations and compare results.
  
  Reply
ben December 10, 2018 at 6:31 pm #

Thank you for your great tutorial.

I know that the third output from model_fit.forecast() consists of the confidence interval. But how can I plot the confidence interval on the whole range automatically?

Thanks

Reply
- Jason Brownlee December 11, 2018 at 7:40 am #
  
  I believe this tutorial will help:
  https://machinelearningmastery.com/time-series-forecast-uncertainty-using-confidence-intervals-python/
  
  Reply
Glenn Dalida December 11, 2018 at 2:06 am #

What’s the difference of predicted and expected? Sorry I’m a just a novice.

Reply
- Jason Brownlee December 11, 2018 at 7:48 am #
  
  “Predicted” is what is output by the model.
  
  “Expected” or “actual” are the true observations.
  
  Reply
Ronald December 23, 2018 at 2:17 am #

Hey Jason,

Amazing blog, subscribed and loving it. I had a question about how you would send the output of the model to a data table in CSV?

Ramy

Reply
- Jason Brownlee December 23, 2018 at 6:07 am #
  
  You can save a Numpy array as a csv directly:
  https://docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.savetxt.html
  
  Reply
Benny Late December 23, 2018 at 6:01 am #

Hi Jason, man I love this blog.

I’m running this with a separate data set. I’ve shaped my dataset, but when I run the error line, I’m getting this:
ValueError: Found array with dim 3. Estimator expected <= 2.

What are you thoughts?

Thanks,
Benny

Shaping:
X_train = np.reshape(X_train, (len(X_train), 1, X_train.shape[1]))
X_test = np.reshape(X_test, (len(X_test), 1, X_test.shape[1]))

Code:
history = [x for x in X_train]
predictions = list()
for t in range(len(X_test)):
model = ARIMA(history, order=(10,0,3))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = X_test[t]
history.append(obs)
print('predicted=%f, expected=%f' % (yhat, obs))

error = mean_squared_error(X_test, predictions)
print('Test MSE: %.3f' % error)

Reply
- Jason Brownlee December 23, 2018 at 6:10 am #
  
  You’re data has too many dimensions. It should be 2D, but you have given it 3D data, perhaps change it to 2d!
  
  Reply
  - Benny Late December 23, 2018 at 6:16 am #
    
    Oh. I thought that’s what I did with reshaping. Whoops =)
    
    I’ll hunt up some code. Thank you.
    
    Reply
Walid December 24, 2018 at 7:12 pm #

Hi Jason,
Thanks for this great work!
If you allow me, I have a question: how was the confidence interval calculated in the above example? I know its equation, but I do not know what are the values to be used for (sigma) and (number of samples).
Thank you once more.

Reply
- Jason Brownlee December 25, 2018 at 7:20 am #
  
  You can review the statsmodels source code to see exactly how it was calculated. The API documentation may also be helpful.
  
  Reply
Saravana Ayyappa January 1, 2019 at 6:44 am #

Thanks a lot Jason!
I am preparing a time series model for my capstone project, i have around 500 items and the p,d,q value is different for each item, how can i deploy this as a tool? do i have to create model each time for different items?

Thanks in advance.

Reply
- Jason Brownlee January 1, 2019 at 11:12 am #
  
  Perhaps model each series separately?
  
  Reply
Avd January 10, 2019 at 6:02 pm #

How many minimum data points do we require for creating accurate prediction using ARIMA model. We are predicting future cut-off values of colleges using previous records, how many years of records would we need to predict just the cutoff value of next year.

Reply
- Jason Brownlee January 11, 2019 at 7:41 am #
  
  I recommend testing with different amounts of history on your specific dataset and discover the right amount of data for modeling.
  
  Reply
Renu Kalra January 16, 2019 at 10:58 pm #

If I am not wrong, ACF plot is used to get MA value for ARIMA. But here, you have taken AR value as 5 using ACF plot?

Reply
Nauman Naeem January 22, 2019 at 1:07 am #

Hi Jason Brownlee!
I have been following your blog since some time and the concepts and code snippets here often come handy.
I’m totally new to time series analysis and have read some posts (mostly yours), a few lectures and of course questions from stackoverflow.
What confuses me is, to make a series stationary we difference it, double differencing in case seasonality and trend both are present in the series. Now while performing ARIMA, the parameter ‘I’ depicts what? Number of times we have performed differencing or lag value we chose for differencing (for the removal of seasonality).
For example, let say there is a dataset of monthly average temperatures of a place (possibly affected by global warming). Now there is seasonality (lag value of 12) and a global upward trend too.
before performing ARIMA I need to make the series stationary, right?
To do that I Difference twice like this:
differenced = series – series.shift(1) # to remove trend
double_differenced = differenced – differenced.shift(12) # to remove seasonality.
Now what should be passed as ‘I’ to ARIMA?
2? As we did double(2) differencing
or
1 or 12 as that’s the value we used for shifting.

Also if you’re kind enough, can you elaborate more how *exactly* did you decide the value of ‘p’ and ‘q’ from acf and pacf plots.
Or link me to some post if you have already explained that in layman terms somewhere else!

Extremely thankful for your time and effort!

Reply
- Jason Brownlee January 22, 2019 at 6:25 am #
  
  It might be better to let the ARIMA model perform the differencing rather than do it manually.
  
  And, if you have seasonality, you can use SARIMA to difference the trend and seasonality for you.
  
  If you difference manually, you don’t need the model to do it again.
  
  Reply
jaideep January 29, 2019 at 9:54 am #

The computed initial MA coefficients are not invertible
You should induce invertibility, choose a different model order, or you can
pass your own start_params.

How do I fix this error? Best ARIMA params are (4,1,3)

Reply
- Jason Brownlee January 29, 2019 at 11:41 am #
  
  Perhaps try a different configuration or try to prepare the data before modeling.
  
  Reply
SKN January 30, 2019 at 1:21 am #

Do we have a similar function in python like we have auto.arima in R?

Reply
- Jason Brownlee January 30, 2019 at 8:14 am #
  
  I wrote one here:
  https://machinelearningmastery.com/how-to-grid-search-sarima-model-hyperparameters-for-time-series-forecasting-in-python/
  
  And another here:
  https://machinelearningmastery.com/grid-search-arima-hyperparameters-with-python/
  
  Reply
SKN January 31, 2019 at 12:19 am #

Thank you very much, your blogs really come in handy for a beginner in python. when I run the ARIMA forecasting using above codes, getting some format error. I have tried to use Shampoo sales data too. below is the error note,

File “”, line 1, in
runfile(‘C:/Users/43819008/untitled2.py’, wdir=’C:/Users/43819008′)

File “C:\ProgramData\Anaconda3\lib\site-packages\spyder\utils\site\sitecustomize.py”, line 880, in runfile
execfile(filename, namespace)

ValueError: time data ‘19019-01-2019’ does not match format ‘%Y-%m’

I have tried all the format in excel and saved as CSV. but nothing helped me. hope you can help me.

Reply
- Jason Brownlee January 31, 2019 at 5:34 am #
  
  Looks like an issue loading the data.
  
  You could try removing the date column and changing the load function call to not use the custom function?
  
  Reply
Abid Mehmood February 14, 2019 at 11:24 pm #

Hello Everyone , I want to implement ARIMA model but this error is not leaving me.

from . import kalman_loglike
ImportError: cannot import name ‘kalman_loglike’

Reply
- Jason Brownlee February 15, 2019 at 8:06 am #
  
  Looks like you’re trying to import a module that does not exist or is not installed.
  
  Reply
  - Abid Mehmood February 16, 2019 at 10:44 pm #
    
    I got that.
    Thank you very very much ,
    
    Reply
Barry A. February 21, 2019 at 3:37 am #

Hi Jason, I recently came accross your blog and really like the things I have learned in a short period of time. Machine learning and AI are still relatively new to me, but I try to catch up with your information. As the ARIMA Model comes from the statistics field and predicts from past data, could it be used as the basis of a machine learning algorithm? For example: if you would create a system that would update the predictions as soon as the data of a new month arrives, can it be called a machine learning algorithm? Or are there better standarized machine learning solutions to make sales predictions?

Reply
- Jason Brownlee February 21, 2019 at 8:16 am #
  
  Sure.
  
  Yes, ARIMA is a great place to start.
  
  Reply
Fredrick Ughimi February 25, 2019 at 7:55 am #

Hello AI,

>>the last line of the data set, at least in the current version that you can download, is the text line “Sales of shampoo over a three year period”. The parser barfs on this because it is not in the specified format for the data lines. Try using the “nrows” parameter in read_csv.

series = read_csv(‘~/Downloads/shampoo-sales.csv’, header=0, nrows=36, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

worked for me.

Thank you for posting this. I was having the same issue. This solved it.

Thanks Jason for another great tutorial.

Reply
- Jason Brownlee February 25, 2019 at 2:09 pm #
  
  Thanks, I’m glad it helped.
  
  Reply
Mo March 1, 2019 at 6:27 am #

Jason,

thank you it was very helpful in many different ways. I just want to know how you predict and how far you can predict in the future.

Reply
- Jason Brownlee March 1, 2019 at 2:18 pm #
  
  Thanks, good question. This post will show you how to predict:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
JY March 6, 2019 at 6:33 pm #

Hi Jason,

Thanks for your write-up. I’ve tried all the suggestions here but still getting these two errors.

in parser(x)
5 def parser(x):
—-> 6 return datetime.strptime(‘190’+x, ‘%Y-%m’)
7

TypeError: strptime() argument 1 must be str, not numpy.ndarray

ValueError: time data ‘1901-Jan’ does not match format ‘%Y-%m

I removed the footer, tried with your csv file , tried with nrows but nothing worked. Please give me your valuable feedback.Thanks.

Reply
- Jason Brownlee March 7, 2019 at 6:44 am #
  
  Perhaps confirm that you downloaded the dataset in the correct format?
  
  Reply
Charlie March 16, 2019 at 1:36 am #

i use R to get the p,q but it does work in the statsmodel’s arima model which always raise SVD did not converge even i set the p,q very small

Reply
- Jason Brownlee March 16, 2019 at 7:57 am #
  
  Hmm, maybe the R version is preparing the data automatically before modelling in some way?
  
  Reply
cryptoripple March 20, 2019 at 10:56 pm #

how can I get future forecast value with arima?

Reply
- Jason Brownlee March 21, 2019 at 8:15 am #
  
  See this tutorial:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
AJIT MUNJULURU March 28, 2019 at 3:42 am #

Hi Jason,

Your materials on Time Series have been extremely useful. I want to clarify a basic question on Model results. For an ARMA(3,0) , the statsmodel prints the output as
coef P>Z

const c 0.00
ar.L1 x1 0.003
ar.L2 x2 0.10
ar.L3 x3 0.0001

And the Data is:

Actual Daily Traffic Predicted Traffic
Jan7 100
Jan8 95
Jan9 85
Jan10 105

If I want to convert the output to a linear equation will the Predicted Traffic for Jan10 be :Pred= c+ x1*85 + 0*x2 + x3*100 ?? Appreciate your thoughts

Reply
- Jason Brownlee March 28, 2019 at 8:22 am #
  
  Great question, I have an example of making a manual prediction here:
  https://machinelearningmastery.com/make-manual-predictions-arima-models-python/
  
  Reply
  - AJIT MUNJULURU March 29, 2019 at 7:12 am #
    
    Thank you very much Jason. That post was very helpful. Putting the options no constant has given me the exact result for prediction. i.e., dot product of coefficients and the lagged values.
    
    Reply
    - Jason Brownlee March 29, 2019 at 8:49 am #
      
      Glad it hear it.
      
      Reply
Jay March 30, 2019 at 8:35 am #

i am newbie and trying to learn time series. getting following error, please help.

series = read_csv(‘sales.csv’, delimiter=’,’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
Traceback (most recent call last):

File “”, line 1, in
series = read_csv(‘sales.csv’, delimiter=’,’, header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 678, in parser_f
return _read(filepath_or_buffer, kwds)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 446, in _read
data = parser.read(nrows)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1036, in read
ret = self._engine.read(nrows)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1922, in read
index, names = self._make_index(data, alldata, names)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1426, in _make_index
index = self._agg_index(index)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 1504, in _agg_index
arr = self._date_conv(arr)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\parsers.py”, line 3033, in converter
return generic_parser(date_parser, *date_cols)

File “E:\ProgramData\Anaconda3\lib\site-packages\pandas\io\date_converters.py”, line 39, in generic_parser
results[i] = parse_func(*args)

File “”, line 2, in parser
return datetime.strptime(‘190’+x, ‘%Y-%m’)

File “E:\ProgramData\Anaconda3\lib\_strptime.py”, line 565, in _strptime_datetime
tt, fraction = _strptime(data_string, format)

File “E:\ProgramData\Anaconda3\lib\_strptime.py”, line 362, in _strptime
(data_string, format))

ValueError: time data ‘1901-Jan’ does not match format ‘%Y-%m’

Reply
- Jason Brownlee March 31, 2019 at 9:22 am #
  
  Looks like you need to download the data with numeric date format, or change the data parsing string.
  
  Reply
  - Jay April 6, 2019 at 6:56 am #
    
    Thanks, it is resolved, i have to download another file.
    
    Reply
    - Jason Brownlee April 7, 2019 at 5:22 am #
      
      Glad to hear that.
      
      Reply
Joker Ho March 31, 2019 at 6:46 pm #

Hi Jason!
I have a compile error: insufficient degree of freedom to estimate, when finishing my program on ARIMA in Python. Could you tell me what leads to this error? Cuz I found little answer in other solution website like stack overflow.
Hoping to hear from you!
Thank you, Jason!

Reply
- Jason Brownlee April 1, 2019 at 7:48 am #
  
  Perhaps your data requires further preparation – it can happen if you have lots of zero values or observations with the same value.
  
  Reply
Nick V April 9, 2019 at 11:38 am #

Hi, Jason.
Thanks for the writeup. When running your code with a small dataset (60-ish values) it runs without a hitch, but when I run it with an identically-formatted, much larger database (~1200 values) it throws this error:
“TypeError: must be str, not list”
Any idea why this is? Thanks in advance.

Reply
- Jason Brownlee April 9, 2019 at 2:41 pm #
  
  Perhaps confirm that you have loaded your data correctly, as a floating point values?
  
  Reply
Orsola April 14, 2019 at 8:20 am #

Hi Jason,
Do you know how predict from estimated ARIMA model with new data, preserving the parameters just fitted in the previus model?
I’m trying to accomplish in python something similar to R:

# Refit the old model with newData
new_model <- Arima(as.ts(Data), model = old_model)

Reply
- Jason Brownlee April 15, 2019 at 7:48 am #
  
  Yes, you can use the forecast() or predict() functions.
  
  More here:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Naveksha Sood April 22, 2019 at 5:53 pm #

Jason, great tutorial! I follow your blogs and book regularly and they help me a lot!
However I have some conceptual doubts that I hope you can help me with.

1. If you don’t do a rolling forecast and only use the predict function, it gives us various predicted values (number of predicted values are equal to length of training data). How are the predictions made in this case? Does it use the previous predicted values to make next predictions?

2. When I validate a neural network made of one or more LSTM layers, I pass actual test data to the predict function and hence it uses that data to make predictions, so is walk forward validation/ rolling forecast redundant there?

Reply
- Jason Brownlee April 23, 2019 at 7:53 am #
  
  Good question, ideally you want to fit the ARIMA model on all available data – up to the point of prediction.
  
  So, in a walk-forward validation you might want to re-fit the ARIMA each iteration.
  
  Reply
Karl April 24, 2019 at 1:46 am #

Hi Jason, thank you so much for all your tutorials. They have been of great help to me.

I had a question about the ARIMA model in statsmodels. If I want to select certain lags for the parameter p instead of all lags up until p how would I to do it ? I have not seen functionality for this in statsmodels, I wondered if you knew.

Whenever you find the time. Kind regards Karl

Reply
- Jason Brownlee April 24, 2019 at 8:06 am #
  
  You might have to write a custom implementation I’m afraid.
  
  Reply
Naveksha Sood April 25, 2019 at 3:28 pm #

Yes, I totally understand why we use walk forward validation, but I see a major drawback of it i.e it works great with shorter time series, however when you have a longer time series and multiple variables, it takes a really really long time to re-fit a SARIMAX model and get the predictions.
That’s why what I intended to ask in the second point is, if instead of a SARIMA model, I use an LSTM model, do I still need to do walk forward validation, since it already uses the actual values up to the point of prediction.

Reply
- Jason Brownlee April 26, 2019 at 8:23 am #
  
  Yes. But you may not have to refit the model each step. I often do not.
  
  Reply
Yarong April 26, 2019 at 6:51 am #

Hi Jason, thanks for the great post. My time series problem is kind of different. The data lag I have is large and inconsistent. For example, I want to know for the order I received 6 pm today, how many hours we will use to fulfill this order. We might not know the fulfillment time for order received at 5 pm, 4 pm, or not even yesterday since they might not be fulfilled yet. We have no access to the future data in real life, do you have any suggestion on this? Thank you so much.

Reply
- Jason Brownlee April 26, 2019 at 8:40 am #
  
  That sounds like a great problem.
  
  I recommend using this framework to help think about different ways you can frame the problem for prediction:
  https://machinelearningmastery.com/how-to-define-your-machine-learning-problem/
  
  Reply
Naveksha Sood April 26, 2019 at 8:03 pm #

Ok, Have you covered it in any of your articles? Can you refer me to it?

Reply
- Luis Zarate May 4, 2019 at 8:30 am #
  
  Hi Jason. Thank You very much for teach how ti make Forecast. Butaca i have a doubt, in this example only we have 12 prediction for 12 observations (or expected values).
  
  Un this case, i would like yo know. What is the prediction to the short future.
  
  Thank so much.
  
  Atte. Luis
  
  Reply
  - Jason Brownlee May 5, 2019 at 6:19 am #
    
    Perhaps this post will help:
    https://machinelearningmastery.com/make-sample-forecasts-arima-python/
    
    Reply
Mitchyuuu May 8, 2019 at 12:39 pm #

Hi! Thank You for your teach.I have a problem when I use the ARIMA to build a model for the multivariate data,but appear some error”TypeError:must be str,not list”at”model=ARIMA(history,order=(5,1,0))”.The history data is a list of 500*2.

Reply
- Jason Brownlee May 8, 2019 at 2:12 pm #
  
  Sounds like you might not have loaded the dataset correctly.
  
  Perhaps confirm it was loaded as real values, not strings.
  
  Reply
me May 8, 2019 at 9:03 pm #

Hi can you please show us some plots ,spcific to ARIMA ?
thank you

Reply
- Jason Brownlee May 9, 2019 at 6:41 am #
  
  Like what exactly?
  
  Reply
Anindya Sankar Chattopadhyay May 12, 2019 at 7:31 pm #

Hi Jason:

Thanks for this tutorial.

Just wondering how was a value of 0 was decided for q? For that don’t you need the PACF plot?

Any help will be much appreciated.

Regards,
Anindya

Reply
- Jason Brownlee May 13, 2019 at 6:45 am #
  
  I may have configured the model in this tutorial based on a trial and error.
  
  Reply
Abhishek Mishra May 13, 2019 at 1:44 pm #

Hey man, great tutorial. I just wanted to ask you how does residual error or its graph fit into time series analysis, I mean i am not able to understand the importance of residual error, what does it show. I am still in the learning phase.

Reply
- Jason Brownlee May 13, 2019 at 2:34 pm #
  
  Thanks, we expect the residual error to be random – if there is a pattern to it, it means our model is missing something important.
  
  Reply
Greg Houston May 14, 2019 at 9:19 am #

Hi Jason,

I’m considering buying your book. Will the code examples be up to date seeing as it is now 2019? Also, what success have you had forecasting several time series, lets say 30, with the same model. Would you suggest more of an ensemble approach?

Reply
- gregory houston May 14, 2019 at 9:23 am #
  
  Oh, is any other reading material you would suggest? We did not cover time series in my masters program, so I’m a newbie.
  
  Reply
  - Jason Brownlee May 14, 2019 at 2:28 pm #
    
    Yes, you can get started with the basics here:
    https://machinelearningmastery.com/start-here/#timeseries
    
    Advanced topics here:
    https://machinelearningmastery.com/start-here/#deep_learning_time_series
    
    Reply
- Jason Brownlee May 14, 2019 at 2:28 pm #
  
  Yes, I update the books frequently. After purchasing, you can email me any time to get the latest version.
  
  Hmm, 30 is not a large number, it might be best developing a separate model for each and compare the results to any model that tries to learn across the series.
  
  Reply
mbelahcen May 22, 2019 at 8:01 pm #

Hello Jason,

I still don’t understand why the forecast is one step ahead of the actual value. Why is this behavior expected, If for instance my model predicts very well the timeseries but with a lag, does this mean that my model is good or I should go on tuning to take off the lag?
In the case of the lag, the line print(‘predicted=%f, expected=%f’ % (yhat, obs)) isn’t it also lagged and not representative of the actual comparison?

Thanks

Reply
- Jason Brownlee May 23, 2019 at 6:00 am #
  
  I think you are describing a persistence forecast, this might help:
  https://machinelearningmastery.com/faq/single-faq/why-is-my-forecasted-time-series-right-behind-the-actual-time-series
  
  Reply
Bankole Akinuli May 29, 2019 at 6:52 pm #

Dear Prof. Kindly help to write the equation for ARIMA (0,0,0); (0,1,0); (1, 0,1), VARMA (1,1), and ARMA (5,4)
Thanks

Reply
- Jason Brownlee May 30, 2019 at 8:59 am #
  
  I cannot write equations for you, this would be trivial though, start with the ARIMA equation and add the terms you need.
  
  Perhaps get a good textbook on the topic.
  
  Reply
Bankole Akinuli May 31, 2019 at 11:22 am #

I appreciate your view and advice, sir. Please, suggest relevant textbook on ARIMA and how or where i can get one. Warmest regards.

Reply
- Jason Brownlee May 31, 2019 at 2:44 pm #
  
  Here are some suggestions:
  https://machinelearningmastery.com/books-on-time-series-forecasting-with-r/
  
  Reply
Mithlesh Patel June 3, 2019 at 8:46 pm #

Thanks Jason for overview of ARIMA model with example,
In below code, are you creating model again and fitting in each pass of for loop ?
In other algorithms we generally create model and fit model once and later use same to predict values from test dataset.

for t in range(len(test)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)

Reply
- Jason Brownlee June 4, 2019 at 7:51 am #
  
  Yes, this is called walk forward validation and it is the preferred way for evaluating time series models.
  
  You can learn more here:
  https://machinelearningmastery.com/backtest-machine-learning-models-time-series-forecasting/
  
  Reply
mickael June 4, 2019 at 3:17 am #

Hi,

Great post, and blog in general!

I have a question regarding the practical use of ARIMA. Is it possible to use it (after fitting on some dataset), to test the prediction from any new input data, just like any regression algorithm ?
For instance, I have one year of temperature data on which I fit my model, using the last 7 points (say 1 point per day) for autoregression. Then, to use the model in production, I want to simply store the last 7 days and use them to predict the next one. (Without the need to fit my model again and again each day)

Many thanks,

Mickaël

Reply
- Jason Brownlee June 4, 2019 at 7:57 am #
  
  Yes, here is an example:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Dav June 8, 2019 at 2:35 am #

Hi

I am new to Auto Regression and Python. Great articles, I am finding them very helpful.

My question is around how much historical time series is enough to stand a chance of getting a good prediction? For example, if I have two years worth of data (adjusted to remove trends and seasonality) then does it really make a difference if I use all of it in a training set or use latest use latest subset e.g last 50 days (assuming lags would be less than 10?)?

Also, how should I think about accounting for seasonality. I understand I would need to remove it from the time series in order to get a reasonable prediction. Should I then have an overlay on top of predicted values to impalement the impact of seasonality?

Thanks
Dav

Reply
- Jason Brownlee June 8, 2019 at 7:03 am #
  
  It depends on the dataset, try different amounts of history to see how sensitive your model is to dataset size.
  
  You can remove seasonality or let the model remove it for you in the case of SARIMA. Any structure removed must be added to predictions, it is easier to let the model do it for you perhaps.
  
  Reply
Dav June 10, 2019 at 6:23 pm #

got it, thanks

Reply
baktr_ June 15, 2019 at 8:19 pm #

Hi Jason, thanks for your blog, i’m newbie, i have a question: model ARIMA is machine learning?

Reply
- Jason Brownlee June 16, 2019 at 7:12 am #
  
  It was developed in statistics and borrowed in machine learning.
  
  The intent makes it machine learning, more here:
  https://machinelearningmastery.com/faq/single-faq/how-are-statistics-and-machine-learning-related
  
  Reply
Adi June 28, 2019 at 11:58 pm #

Hi Jason,

Thank you for this. What are some good strategies to handle zeros (zero demand) in your time series. I know consecutive zeros can be a problem for AR algorithms (false collinearity) and for Triple exponential multiplicative version.. Is there any useful resource you can point to? Something like a normalizing/ denormalizing?
Also, if I have a lot of time series to forecast for, where I cannot really visualize each of them, what are some indicators that will be helpful to describe the time series and the path to follow?

Thanks

Reply
- Jason Brownlee June 29, 2019 at 6:56 am #
  
  Good question – it is probably going to be domain specific how to best handle it.
  
  Test many things.
  
  Try small random values?
  Try impute with mean value?
  Try alternate methods, like neural nets?
  …
  
  Reply
staph July 3, 2019 at 6:23 pm #

Hi Jason how long does it take to fit a model, code is taking ages at the fit line

model_fit = model.fit(disp=0)

Reply
- Jason Brownlee July 4, 2019 at 7:42 am #
  
  It really depends on the size of the dataset.
  
  Reply
sundus July 7, 2019 at 5:23 am #

much appreciated..

Reply
- Jason Brownlee July 7, 2019 at 7:55 am #
  
  You’re welcome.
  
  Reply
Niloofar July 11, 2019 at 7:19 pm #

Hi, thanks Mr.Brownlee for your great posts. I had a question, can ARIMA model be used to forecast NA values in a dataset? I mean can it handle missing values?

Reply
- Jason Brownlee July 12, 2019 at 8:34 am #
  
  No.
  
  More on missing values here:
  https://machinelearningmastery.com/handle-missing-timesteps-sequence-prediction-problems-python/
  
  Reply
Hugo Pire July 20, 2019 at 7:06 am #

Hello Jason and thank you for your great posts

I am trying to fit an ARIMA model to an company invoices timeseries. It has a timestamp (not regulary spaced) and a value that can be negative or positive – with a large interval.

Do I have to interpolate in order to have regular intervals? If I use a naive solution, as group by day, I get a lot of zero values.

Could you help me?

Reply
- Jason Brownlee July 20, 2019 at 10:59 am #
  
  I have some suggestions here:
  https://machinelearningmastery.com/faq/single-faq/how-do-i-handle-discontiguous-time-series-data
  
  Reply
Toraskar August 5, 2019 at 5:38 pm #

Hello Jason and thank you for your posts
can you please make same project for stock price prediction using Arima model??

Reply
- Jason Brownlee August 6, 2019 at 6:30 am #
  
  Sorry, I choose not to give examples for the stock market. I believe it is not predictable and a waste of time.
  
  Reply
Amin Nasri August 6, 2019 at 1:45 am #

Hi,

How can I specify which lags the model uses, for instance, a two degree AR model with 1 and 24 as lags?

Thanks in advance for your reply.

Reply
- Jason Brownlee August 6, 2019 at 6:41 am #
  
  It will use all lags in between.
  
  To use otherwise, you may have to develop your own implementation.
  
  Reply
Nir August 6, 2019 at 3:36 pm #

Hi Jason,
Thanks for writing such a detailed tutorial.
In your text, you mentioned that “A crude way to perform this rolling forecast is to re-create the ARIMA model after each new observation is received.” Is there another way to do so without retraining the model? Is there a way just to update the inputs (and not the parameters?
After our first prediction, we get the true value and the prediction error we now use the new information to predict the next step (without retraining)?

Thanks!

Reply
- Jason Brownlee August 7, 2019 at 7:41 am #
  
  Yes, you can forecast for the future interval directly without updating the model, e.g. model.forecast() or model.predict()
  
  Is that what you mean?
  
  Reply
  - Nir August 20, 2019 at 9:08 am #
    
    Hi Jason,
    
    Thanks for the rapid reply, and sorry for not being clear.
    If I understood it right, model.forecast() will forecast one step at a time.
    I’ve 4 months’ worth of data sampled every 1 min. I’d like to test how well it predicts the next minute (or 10 minutes). If my training dataset ends at time t, after predicting t+1, the true value will be available and can help to predict t+2. I see 3 options to do so:
    1. Use model.predict() for 2 samples, but then I don’t use the new information.
    2. As in your example, retrain the model every timestamp – I’d like to avoid this as I’m considering running this in real-time and don’t want to retrain at every sample. I don’t think the model parameters have changed.
    3. Update the model input without retraining the model. Meaning, update the time series samples by adding new observation but without updating the model parameters
    
    Thanks,
    Nir
    
    Reply
    - Jason Brownlee August 20, 2019 at 2:10 pm #
      
      Not quite.
      
      You can use forecast() and specify the number of steps required.
      
      You can use predict() to specify an interval of dates or time steps.
      
      See this post:
      https://machinelearningmastery.com/make-sample-forecasts-arima-python/
      
      Yes, perhaps try with and without refitting the model, and try refitting every hour, day, week and compare.
      
      Reply
Amin Nasri August 6, 2019 at 6:59 pm #

Thanks for your response. In Matlab, you can choose specific lags.

When I am trying to use all the lags in between it takes forever to make a model.

Reply
- Jason Brownlee August 7, 2019 at 7:45 am #
  
  Yes, the statsmodel implementation could use some improvement.
  
  Reply
Marcel August 14, 2019 at 9:20 pm #

Hey Jason, I’m currently doing my thesis on forecasting electricity load and am also using the ARIMA from statsmodels.
You mentioned, that the reestimation you are doing for forecasting is a crude way of doing this as you compute a new ARIMA for every step. What would be a nicer way to do this? Maybe with fitting the model on the training data and after each forecasting step appending the real value to the data and then forecasting the next step (without having to fit the model again)? I couldn’t figure out yet how to do this, might this work with the initialize() function of the ARIMAResults class?
Btw, thanks a lot for this excellent tutorial, it’s really well explained!

Reply
- Jason Brownlee August 15, 2019 at 8:07 am #
  
  Ideally fitting the model only when needed would be the best approach, e.g. testing when a refit is required.
  
  A fit model can forecast any future period, e.g. see forecast() and predict().
  
  Reply
Rittick Sinha Roy August 18, 2019 at 12:53 am #

Hey Jason I’m doing a project on crime prediction and wanted to use ARIMA model could you help me in understanding what kind of factors would predict the trend

Reply
- Jason Brownlee August 18, 2019 at 6:47 am #
  
  If you are using an ARIMA, it will remove the trend via differencing. Perhaps try different d values.
  
  Or, perhaps try a grid search of different model parameters;
  https://machinelearningmastery.com/grid-search-arima-hyperparameters-with-python/
  
  Reply
Asieh August 28, 2019 at 5:24 am #

Hi Jason,

What made you choose 5 lags for this dataset? In other words, what is the threshold we should choose for autocorrelation? Is it above 0.5? What about negative correlation? So in this example, the absolute value of the negative correlation is <0.5. How would we choose the number of lags (p) if it was say -0.52?

Thanks,
Asieh

Reply
- Jason Brownlee August 28, 2019 at 6:43 am #
  
  Perhaps test a range of values and see what works best for your specific dataset.
  
  Reply
Dongchan Christopher Kim September 7, 2019 at 5:34 pm #

Loving the post! It definitely helps me grab of ARIMA. I needed to find a technique forecasting sales of an object where the growth path jumps up and down drastically. And this was the point I needed to have some smoothing ways for the projection rather than stochastic process. Not to mention, the code is simple and efficient well enough. Thank you very much.

Reply
- Jason Brownlee September 8, 2019 at 5:15 am #
  
  Thanks, I’m happy that it heled!
  
  Reply
mark patzelt September 11, 2019 at 5:35 pm #

Hello Jason. I am new to Series Forecasting in Python. I would like to dig into it and learn how to forecast time series. I have recreated your ARIMA sample with my own data and it worked. I have a unix time series and would need to forecast the next 5 future values. I have not fully grasped the concept of predicted/expected and how I can get these future values. Did I misunderstand the model? I will buy your ebook, but maybe your response will help me proceed fast.

Reply
- Jason Brownlee September 12, 2019 at 5:15 am #
  
  Perhaps this post will help:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
  - mark patzelt September 12, 2019 at 6:42 pm #
    
    One more question: I am using a time series with a frequency of 1 minute. The series is correctly setting a DateTimeIndex in col 0 and there seem to be no values missing. When I call ARIMA I get this message: “ValueWarning: No frequency information was provided, so inferred frequency T will be used. % freq, ValueWarning)”. None of you examples are based in 1 minute frequencies. Is it not possible to work with 1 minute time series with ARIMA?
    
    Reply
    - Jason Brownlee September 13, 2019 at 5:40 am #
      
      Good question, I don’t have an example, but I can’t see that the ARIMA model will care about the frequency as long as it is consistent.
      
      Reply
      - mark patzelt September 13, 2019 at 4:07 pm #
        
        All sorted. I am using the unix time stamps and its working. I am almost through with your book and have already included the ARIMA model in my project. I have implemented the grid search and have generated the best order combination. I would assume that the order combination is the key to making the best possible forecast, right (considering that the dataset has been prepared and is suitable for modeling)?
      - Jason Brownlee September 14, 2019 at 6:12 am #
        
        Correct. Test different orders and see what works well/best for your specific dataset.
mark patzelt September 12, 2019 at 4:34 pm #

Thank you for the link. This will defenitly help. I am half way through your book on Time Series Forecasting and will get there too, I guess. Your book is well written, hands on. Ta

Reply
- Jason Brownlee September 13, 2019 at 5:38 am #
  
  Thanks Mark.
  
  Reply
Brian McaAdams October 3, 2019 at 6:37 am #

Hey Jason,

Interested if you know what type of correlation pandas.plotting.autocorrelation_plot is using. I get a different result with this data set using pandas.Series.autocorr over 35 lags than I do from autocorrelation_plot.

This is a copy paste of the autocorrelation_plot code to retrieve the data:

from pandas.compat import lmap
series = shampoo_df.Sales

n = len(series)
data = np.asarray(series)
mean = np.mean(data)
c0 = np.sum((data – mean) ** 2) / float(n)

def r(h):
return ((data[:n – h] – mean) *
(data[h:] – mean)).sum() / float(n) / c0

x = np.arange(n) + 1
y = lmap(r, x)

There isn’t any information I can find about why they wouldn’t be using pearson’s r. This almost looks like it could be it, but it isn’t. And mathematically float(n) cancels out in the equation above, which is odd that it wasn’t caught.

Anyway, if you could shed any light on why pandas.Series.autocorr is different than pandas.plotting.autocorrelation_plot that would be very helpful!

Reply
- Jason Brownlee October 3, 2019 at 6:55 am #
  
  I believe it is simple linear correlation, i.e. pearsons.
  
  Minor differences in implementation can cause differences in result, e.g. rounding errors, choice of math libs, etc.
  
  Reply
Karan Sehgal November 4, 2019 at 12:54 am #

Hi Jason,

1) ARIMA model works on three parameters – Auto-regression, Differencing and Moving average. So does the ARIMA model makes three separate columns like – one for AR, another for Differencing and and other for Moving average separately or it does only one column and does all the above operations on the same column only (AR, I, MA) ?

2) If ARIMA makes separate columns like (AR, I and MA) for forecasting, then should we also do the same thing to forecast time series using supervised machine learning or we can create only one column with all the operation (AR, I and MA) done on that column only.

Thanks.

Reply
- Jason Brownlee November 4, 2019 at 6:47 am #
  
  It does not create different columns, it creates “transformed inputs” to a linear model that is fit.
  
  Reply
  - Karan Sehgal November 4, 2019 at 1:39 pm #
    
    so there are different columns for transformed inputs created or only one column ?
    
    Reply
    - Jason Brownlee November 5, 2019 at 6:43 am #
      
      I don’t follow your question, sorry. Perhaps you can elaborate?
      
      Reply
      - Karan Sehgal November 6, 2019 at 2:10 am #
        
        I mean to say if in ARIMA model our values for (p,d,q) is (2,1,2) then it will create variables – two variables for Auto Regression i.e for Lag 1 & Lag 2 and two variables for Moving Average i.e MA1 and MA2 and all the variables created i.e AR1, AR2, MA1 and MA2 will be differenced one time as value of d is 1.
        
        do we need to difference the value for y variable also ?
      - Jason Brownlee November 6, 2019 at 6:42 am #
        
        From memory, yes I believe so. Perhaps confirm.
Karan Sehgal November 6, 2019 at 5:00 am #

Why ACF and PACF plots applied on stationary Series only ?

Reply
- Jason Brownlee November 6, 2019 at 6:47 am #
  
  To help you see the signal that the model will learn, and not get distracted by trend/seasonality which get in the way.
  
  Reply
Karan Sehgal November 6, 2019 at 5:07 am #

to make the series stationary, we deseasonalize the series by dividing it with seasonal index and difference it for detrending it. Now the same stationary series need to be used for both x and y variables (Dependent and independent variables) and if so then we have to reverse the above process to get the original data.

I am following the below approach to make the series stationary. Is this the right approach ?
The process of deseasonalizing – dividing it with seasonal index and detrending by differencing x(t) – x(t-1)

Reply
- Jason Brownlee November 6, 2019 at 6:48 am #
  
  Correct.
  
  Examples here:
  https://machinelearningmastery.com/remove-trends-seasonality-difference-transform-python/
  
  Reply
Karan Sehgal November 6, 2019 at 6:36 am #

Why we require a stationary data series for time series forecasting ?

Reply
- Jason Brownlee November 6, 2019 at 6:49 am #
  
  To learn the signal in the data.
  
  Reply
Paul November 8, 2019 at 6:03 pm #

Hi Jason,

It seems that the most of methods discribed in this tutorial are meant for testing on the data we already have. How about multi step prediction? Is there any simple way to extend some of the methods to perform multi step forecast? Thanks in advance.

Reply
- Jason Brownlee November 9, 2019 at 6:11 am #
  
  Call model.forecast()
  
  Here is an example:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Ahmed November 20, 2019 at 4:30 am #

Hi, Jason,
What is the reason here by multipling the length with 0.66?
(size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]

Reply
- Jason Brownlee November 20, 2019 at 6:22 am #
  
  To split the data into train and test sets.
  
  Reply
Alexander Dautzenberg November 24, 2019 at 2:51 am #

Hi Jason,

for my bachelors thesis I need to generate “Sample months of solar radiation”. The problems is as follows: Ive got ten years of historic hourly solar radiation. Its in a DataFrame where every column represents an hour of a day and every row is one day (so starting with the first of january of the first year and ending with the 31st of january of the last year). Now I need to feed my data into a SARIMA Model for each month of the year so that I can use it to generate a fictive month of solar radiation. I want to generate 1000 years and they should each be a bit different, have some kind of a random component to them.

Do you have any idea how to do this?

If I just feed it the DataFrame as is, it returns the “Invalid value for design matrix. Requires a 2- or 3-dimensional array, got 1 dimensions” error.

If I flatten the DataFrame (.values.flatten()), I think it doesnt “see” the seasonality and returns an array as long as the input data when the predict() method is called

Reply
- Jason Brownlee November 24, 2019 at 9:22 am #
  
  This might help you think about the data:
  https://machinelearningmastery.com/time-series-forecasting-supervised-learning/
  
  An ARIMA/SARIMA/etc model expects one sequence of observations. It will transform the data into a supervised learning problem for you.
  
  Does that help?
  
  Reply
Matt November 29, 2019 at 3:06 pm #

In your example you re-fit the model every timestep to do a rolling forecast. This is horrendously inefficient of course–how can this be avoided? Can’t the model be applied to a window of the test set data, and a prediction of next step generated, without re-training it?

Reply
- Jason Brownlee November 29, 2019 at 6:18 pm #
  
  Yes, you could fit the model once and use it each evaluation, but the risk is it does not use the most recent obs in the selection of coefficients.
  
  Reply
  - Matt December 2, 2019 at 4:38 am #
    
    Thanks a lot for your reply. How do you do that? I just want to run inference with an ARIMA the same way I would with e.g. RNN–train it up, then feed it arbitrary subsequences from a test dataset and generate the predicted next item in each case. As obvious as a use case as this is, I haven’t been able to see how to effectively do this. The predict method, for example, doesn’t seem to take in the current subsequence, which seems bizarre. I must not be understanding something, but what?
    
    Reply
    - Jason Brownlee December 2, 2019 at 6:10 am #
      
      You can fit the model once on the training dataset and make predictions by calling predict() and specifying the interval in the future (beyond the end of the training set) to predict.
      
      Predict will take any future contiguous sequence of steps to predict.
      
      Also this might help:
      https://machinelearningmastery.com/make-sample-forecasts-arima-python/
      
      Reply
      - Matt December 2, 2019 at 12:29 pm #
        
        Thanks for the link to your other tutorial, that also was very helpful. But it seems to confirm that Python’s ARIMA can only predict just the few samples after the data set! Using that example, let’s suppose I want to predict days 8-14 past the end of the training set–at this point I’d want to take the real data from days 1-7 into account. But apparently I’d have to retrain the model, with the training data now extended to include these days 1-7. This makes no sense to me, I would have thought that an ARIMA model, once all its coefficients are determined, could be applied to any arbritrary sequence. A (7,0,1) model should need just the prior seven days to make a prediction right? *Any* prior 7 days. Help.
      - Jason Brownlee December 2, 2019 at 1:55 pm #
        
        Nice.
        
        Yes, I show how to pull the coefficients out of the model and use them manually, if that is any help:
        https://machinelearningmastery.com/make-manual-predictions-arima-models-python/
        
        I did it to help show how the model works, but you could adapt it for a production system that makes predictions on demand if you like.
      - Matt December 2, 2019 at 3:48 pm #
        
        Wow you have a tutorial for everything! Awesome. Thanks a lot. Btw a few years back I recommended your computer vision book to someone at work (on the strength of what I’d seen in the tutorials), who in fact went and bought it from you. Glad now more than ever that I did.
        
        Anyway I’m surprised that what I want here isn’t more of a standard use case. But the idea of course is that to get a good sense of how well the model does, and compare with other models, then I need to generate lots of short-term predictions from a test set, and do so efficiently.
        
        Suggestion–put a link to this tutorial in the original ARIMA blogpost that launched this thread.
      - Jason Brownlee December 3, 2019 at 4:47 am #
        
        Thanks!
        
        Appreciate the suggestion.
Khan December 3, 2019 at 1:08 am #

How we can use ARIMA with multiple input variables?

Reply
- Jason Brownlee December 3, 2019 at 4:53 am #
  
  It is called VARIMA, see this:
  https://machinelearningmastery.com/time-series-forecasting-methods-in-python-cheat-sheet/
  
  Reply
Ef December 14, 2019 at 10:50 pm #

How we can remove AutoCorrelation of our data?

Reply
- Jason Brownlee December 15, 2019 at 6:05 am #
  
  Differencing can remove trends, seasonal differencing can remove seasonality.
  
  Reply
Shubh December 20, 2019 at 6:07 pm #

PLS HELP!
I have a datetime stamp column and the Power consumed against it. I used ARIMA to forecast Load consumption using:
results_ARIMA = results_AR.forecast(steps=24)

I’m getting the result as:
(array([2.29239839, 2.26938029, 2.25877423, 2.25559929, 2.25846445,
2.26670267, 2.27794598, 2.28892255, 2.29774307, 2.30384135,
2.30707076, 2.30747149, 2.30555066, 2.30218792, 2.29826336,
2.29444756, 2.29121391, 2.28885976, 2.28748131, 2.28698461,
2.28715699, 2.28774348, 2.28849448, 2.2891958 ]),
array([0.02200684, 0.05321806, 0.08660913, 0.11822268, 0.14836925,
0.17610274, 0.19985402, 0.21907622, 0.23444159, 0.24686324,
0.2570923 , 0.26579143, 0.2735913 , 0.28101168, 0.28840908,
0.29599757, 0.30388675, 0.31209504, 0.32055845, 0.32915964,
0.33776759, 0.34626676, 0.35457151, 0.36263193]),
array([[2.24926578, 2.335531 ],
[2.16507481, 2.37368577],
[2.08902345, 2.428525 ],
[2.02388709, 2.48731149],
[1.96766606, 2.54926284],
[1.92154764, 2.6118577 ],
[1.8862393 , 2.66965266],
[1.85954104, 2.71830405],
[1.838246 , 2.75724014],
[1.81999828, 2.78768442],
[1.80317912, 2.81096241],
[1.78652986, 2.82841311],
[1.76932157, 2.84177976],
[1.75141515, 2.85296069],
[1.73299196, 2.86353476],
[1.71430298, 2.87459214],
[1.69560682, 2.88682099],
[1.67716473, 2.90055479],
[1.6591983 , 2.91576432],
[1.64184358, 2.93212565],
[1.62514468, 2.94916929],
[1.6090731 , 2.96641385],
[1.59354709, 2.98344188],
[1.57845029, 2.99994131]]))

Why is that in that format? I only want a single column of predicted values.

Reply
- shubh December 20, 2019 at 9:20 pm #
  
  I figured it out. It was showing the arrays of values, upper limit and lower limit. Just used results_ARIMA = results_AR.forecast(steps=24).[0]
  
  Reply
  - Jason Brownlee December 21, 2019 at 7:11 am #
    
    Yes, correct! Well done.
    
    Reply
- Jason Brownlee December 21, 2019 at 7:08 am #
  
  I believe it returns point forecasts and a prediction interval.
  
  This tutorial will help:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
Mauro Júnior December 26, 2019 at 6:35 am #

Hello Jason Brwnlee! Congratulations on the article, it is very well explained and easy to understand! I know this is not the purpose of this publication, but I would like to share with you my lines of code, which I adapted from yours, trying to develop the study, but using AutoArima. I have not been very successful at forecasting and am unable to find what is missing so I can reproduce this study with AutoArima. Can you help me?

X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
for t in range(len(test)):
model = auto_arima(train, trace = True, error_action=’ignore’, surpress_warnings=True)
model_fit = model.fit(train)
output = model_fit.predict(n_periods=len(teste + 7))
yhat = output[0]
predictions.append(yhat)
obs = test[t]
history.append(obs)
print(‘predicted=%f, expected=%f’ % (yhat, obs))
error = mean_squared_error(test, predictions)
print(‘Test MSE: %.3f’ % error)
#plot
pyplot.plot(test)
pyplot.plot(predictions, color=’red’)
pyplot.show()

Reply
- Jason Brownlee December 26, 2019 at 7:43 am #
  
  Thanks.
  
  Perhaps this will help with making a prediction:
  https://machinelearningmastery.com/make-sample-forecasts-arima-python/
  
  Reply
clare antony January 2, 2020 at 9:11 pm #

Can i able to predict the job’s waiting time , i took a dataset from grid5000 and i feel really hard to handle the correlation of the dataset , Can you able to give any suggestion

Navigation

How to Create an ARIMA Model for Time Series Forecasting in Python

Autoregressive Integrated Moving Average Model

Stop learning Time Series Forecasting the slow way!

Shampoo Sales Dataset

ARIMA with Python

Rolling Forecast ARIMA Model

Configuring an ARIMA Model

Summary

Want to Develop Time Series Forecasts with Python?

Develop Your Own Forecasts in Minutes

Finally Bring Time Series Forecasting to
Your Own Projects

More On This Topic

834 Responses to How to Create an ARIMA Model for Time Series Forecasting in Python

Navigation

Autoregressive Integrated Moving Average Model

Stop learning Time Series Forecasting the slow way!

Shampoo Sales Dataset

ARIMA with Python

Rolling Forecast ARIMA Model

Configuring an ARIMA Model

Summary

Want to Develop Time Series Forecasts with Python?

Develop Your Own Forecasts in Minutes

Finally Bring Time Series Forecasting to Your Own Projects

More On This Topic

834 Responses to How to Create an ARIMA Model for Time Series Forecasting in Python

Finally Bring Time Series Forecasting to
Your Own Projects