Hypothesis Test for Comparing Machine Learning Algorithms

By Jason Brownlee on September 1, 2020 in Statistics 43

Machine learning models are chosen based on their mean performance, often calculated using k-fold cross-validation.

The algorithm with the best mean performance is expected to be better than those algorithms with worse mean performance. But what if the difference in the mean performance is caused by a statistical fluke?

The solution is to use a statistical hypothesis test to evaluate whether the difference in the mean performance between any two algorithms is real or not.

In this tutorial, you will discover how to use statistical hypothesis tests for comparing machine learning algorithms.

After completing this tutorial, you will know:

Performing model selection based on the mean model performance can be misleading.
The five repeats of two-fold cross-validation with a modified Student’s t-Test is a good practice for comparing machine learning algorithms.
How to use the MLxtend machine learning to compare algorithms using a statistical hypothesis test.

Kick-start your project with my new book Statistics for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

Hypothesis Test for Comparing Machine Learning Algorithms
Photo by Frank Shepherd, some rights reserved.

Tutorial Overview

This tutorial is divided into three parts; they are:

Hypothesis Test for Comparing Algorithms
5×2 Procedure With MLxtend
Comparing Classifier Algorithms

Hypothesis Test for Comparing Algorithms

Model selection involves evaluating a suite of different machine learning algorithms or modeling pipelines and comparing them based on their performance.

The model or modeling pipeline that achieves the best performance according to your performance metric is then selected as your final model that you can then use to start making predictions on new data.

This applies to regression and classification predictive modeling tasks with classical machine learning algorithms and deep learning. It’s always the same process.

The problem is, how do you know the difference between two models is real and not just a statistical fluke?

This problem can be addressed using a statistical hypothesis test.

One approach is to evaluate each model on the same k-fold cross-validation split of the data (e.g. using the same random number seed to split the data in each case) and calculate a score for each split. This would give a sample of 10 scores for 10-fold cross-validation. The scores can then be compared using a paired statistical hypothesis test because the same treatment (rows of data) was used for each algorithm to come up with each score. The Paired Student’s t-Test could be used.

A problem with using the Paired Student’s t-Test, in this case, is that each evaluation of the model is not independent. This is because the same rows of data are used to train the data multiple times — actually, each time, except for the time a row of data is used in the hold-out test fold. This lack of independence in the evaluation means that the Paired Student’s t-Test is optimistically biased.

This statistical test can be adjusted to take the lack of independence into account. Additionally, the number of folds and repeats of the procedure can be configured to achieve a good sampling of model performance that generalizes well to a wide range of problems and algorithms. Specifically two-fold cross-validation with five repeats, so-called 5×2-fold cross-validation.

This approach was proposed by Thomas Dietterich in his 1998 paper titled “Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms.”

For more on this topic, see the tutorial:

Statistical Significance Tests for Comparing Machine Learning Algorithms

Thankfully, we don’t need to implement this procedure ourselves.

5×2 Procedure With MLxtend

The MLxtend library by Sebastian Raschka provides an implementation via the paired_ttest_5x2cv() function.

First, you must install the mlxtend library, for example:

sudo pip install mlxtend

1	sudo pip install mlxtend

To use the evaluation, you must first load your dataset, then define the two models that you wish to compare.

...
# load data
X, y = ....
# define models
model1 = ...
model2 = ...

...

# load data

X, y = ....

# define models

model1 = ...

model2 = ...

You can then call the paired_ttest_5x2cv() function and pass in your data and models and it will report the t-statistic value and the p-value as to whether the difference in the performance of the two algorithms is significant or not.

...
# compare algorithms
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y)

...

# compare algorithms

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y)

The p-value must be interpreted using an alpha value, which is the significance level that you are willing to accept.

If the p-value is less or equal to the chosen alpha, we reject the null hypothesis that the models have the same mean performance, which means the difference is probably real. If the p-value is greater than alpha, we fail to reject the null hypothesis that the models have the same mean performance and any observed difference in the mean accuracies is probability a statistical fluke.

The smaller the alpha value, the better, and a common value is 5 percent (0.05).

...
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

...

# interpret the result

if p <= 0.05:

print('Difference between mean performance is probably real')

else:

print('Algorithms probably have the same performance')

Now that we are familiar with the way to use a hypothesis test to compare algorithms, let’s look at some examples.

Comparing Classifier Algorithms

In this section, let’s compare the performance of two machine learning algorithms on a binary classification task, then check if the observed difference is statistically significant or not.

First, we can use the make_classification() function to create a synthetic dataset with 1,000 samples and 20 input variables.

The example below creates the dataset and summarizes its shape.

# create classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# summarize the dataset
print(X.shape, y.shape)

# create classification dataset

from sklearn.datasets import make_classification

# define dataset

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# summarize the dataset

print(X.shape, y.shape)

Running the example creates the dataset and summarizes the number of rows and columns, confirming our expectations.

We can use this data as the basis for comparing two algorithms.

(1000, 10) (1000,)

1	(1000, 10) (1000,)

We will compare the performance of two linear algorithms on this dataset. Specifically, a logistic regression algorithm and a linear discriminant analysis (LDA) algorithm.

The procedure I like is to use repeated stratified k-fold cross-validation with 10 folds and three repeats. We will use this procedure to evaluate each algorithm and return and report the mean classification accuracy.

The complete example is listed below.

# compare logistic regression and lda for binary classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from matplotlib import pyplot
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# evaluate model 1
model1 = LogisticRegression()
cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)
print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))
# evaluate model 2
model2 = LinearDiscriminantAnalysis()
cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)
print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))
# plot the results
pyplot.boxplot([scores1, scores2], labels=['LR', 'LDA'], showmeans=True)
pyplot.show()

# compare logistic regression and lda for binary classification

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from matplotlib import pyplot

# define dataset

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# evaluate model 1

model1 = LogisticRegression()

cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)

print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))

# evaluate model 2

model2 = LinearDiscriminantAnalysis()

cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)

print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))

# plot the results

pyplot.boxplot([scores1, scores2], labels=['LR', 'LDA'], showmeans=True)

pyplot.show()

Running the example first reports the mean classification accuracy for each algorithm.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

In this case, the results suggest that LDA has better performance if we just look at the mean scores: 89.2 percent for logistic regression and 89.3 percent for LDA.

LogisticRegression Mean Accuracy: 0.892 (0.036)
LinearDiscriminantAnalysis Mean Accuracy: 0.893 (0.033)

1 2	LogisticRegression Mean Accuracy: 0.892 (0.036) LinearDiscriminantAnalysis Mean Accuracy: 0.893 (0.033)

A box and whisker plot is also created summarizing the distribution of accuracy scores.

This plot would support my decision in choosing LDA over LR.

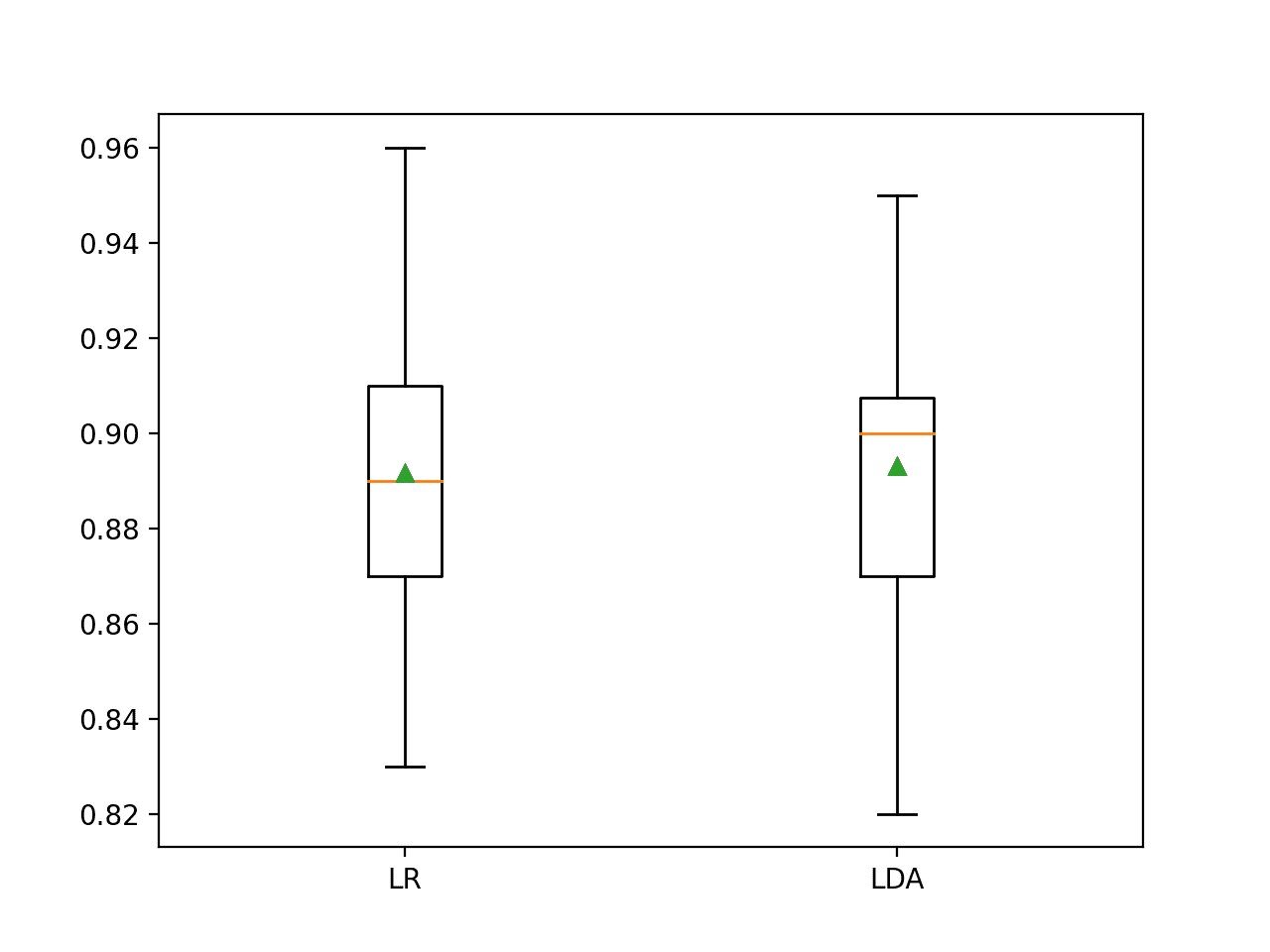
Box and Whisker Plot of Classification Accuracy Scores for Two Algorithms

Now we can use a hypothesis test to see if the observed results are statistically significant.

First, we will use the 5×2 procedure to evaluate the algorithms and calculate a p-value and test statistic value.

...
# check if difference between algorithms is real
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)
# summarize
print('P-value: %.3f, t-Statistic: %.3f' % (p, t))

...

# check if difference between algorithms is real

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)

# summarize

print('P-value: %.3f, t-Statistic: %.3f' % (p, t))

We can then interpret the p-value using an alpha of 5 percent.

...
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

...

# interpret the result

if p <= 0.05:

print('Difference between mean performance is probably real')

else:

print('Algorithms probably have the same performance')

Tying this together, the complete example is listed below.

# use 5x2 statistical hypothesis testing procedure to compare two machine learning algorithms
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from mlxtend.evaluate import paired_ttest_5x2cv
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# evaluate model 1
model1 = LogisticRegression()
cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)
print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))
# evaluate model 2
model2 = LinearDiscriminantAnalysis()
cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)
print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))
# check if difference between algorithms is real
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)
# summarize
print('P-value: %.3f, t-Statistic: %.3f' % (p, t))
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

# use 5x2 statistical hypothesis testing procedure to compare two machine learning algorithms

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from mlxtend.evaluate import paired_ttest_5x2cv

# define dataset

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# evaluate model 1

model1 = LogisticRegression()

cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)

print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))

# evaluate model 2

model2 = LinearDiscriminantAnalysis()

cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)

print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))

# check if difference between algorithms is real

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)

# summarize

print('P-value: %.3f, t-Statistic: %.3f' % (p, t))

# interpret the result

if p <= 0.05:

print('Difference between mean performance is probably real')

else:

print('Algorithms probably have the same performance')

Running the example, we first evaluate the algorithms before, then report on the result of the statistical hypothesis test.

In this case, we can see that the p-value is about 0.3, which is much larger than 0.05. This leads us to fail to reject the null hypothesis, suggesting that any observed difference between the algorithms is probably not real.

We could just as easily choose logistic regression or LDA and both would perform about the same on average.

This highlights that performing model selection based only on the mean performance may not be sufficient.

LogisticRegression Mean Accuracy: 0.892 (0.036)
LinearDiscriminantAnalysis Mean Accuracy: 0.893 (0.033)
P-value: 0.328, t-Statistic: 1.085
Algorithms probably have the same performance

LogisticRegression Mean Accuracy: 0.892 (0.036)

LinearDiscriminantAnalysis Mean Accuracy: 0.893 (0.033)

P-value: 0.328, t-Statistic: 1.085

Algorithms probably have the same performance

Recall that we are reporting performance using a different procedure (3×10 CV) than the procedure used to estimate the performance in the statistical test (5×2 CV). Perhaps results would be different if we looked at scores using five repeats of two-fold cross-validation?

The example below is updated to report classification accuracy for each algorithm using 5×2 CV.

# use 5x2 statistical hypothesis testing procedure to compare two machine learning algorithms
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from mlxtend.evaluate import paired_ttest_5x2cv
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# evaluate model 1
model1 = LogisticRegression()
cv1 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)
scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)
print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))
# evaluate model 2
model2 = LinearDiscriminantAnalysis()
cv2 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)
scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)
print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))
# check if difference between algorithms is real
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)
# summarize
print('P-value: %.3f, t-Statistic: %.3f' % (p, t))
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

# use 5x2 statistical hypothesis testing procedure to compare two machine learning algorithms

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from mlxtend.evaluate import paired_ttest_5x2cv

# define dataset

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# evaluate model 1

model1 = LogisticRegression()

cv1 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)

scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)

print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))

# evaluate model 2

model2 = LinearDiscriminantAnalysis()

cv2 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)

scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)

print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))

# check if difference between algorithms is real

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)

# summarize

print('P-value: %.3f, t-Statistic: %.3f' % (p, t))

# interpret the result

if p <= 0.05:

print('Difference between mean performance is probably real')

else:

print('Algorithms probably have the same performance')

Running the example reports the mean accuracy for both algorithms and the results of the statistical test.

In this case, we can see that the difference in the mean performance for the two algorithms is even larger, 89.4 percent vs. 89.0 percent in favor of logistic regression instead of LDA as we saw with 3×10 CV.

LogisticRegression Mean Accuracy: 0.894 (0.012)
LinearDiscriminantAnalysis Mean Accuracy: 0.890 (0.013)
P-value: 0.328, t-Statistic: 1.085
Algorithms probably have the same performance

LogisticRegression Mean Accuracy: 0.894 (0.012)

LinearDiscriminantAnalysis Mean Accuracy: 0.890 (0.013)

P-value: 0.328, t-Statistic: 1.085

Algorithms probably have the same performance

Summary

In this tutorial, you discovered how to use statistical hypothesis tests for comparing machine learning algorithms.

Specifically, you learned:

Performing model selection based on the mean model performance can be misleading.
The five repeats of two-fold cross-validation with a modified Student’s t-Test is a good practice for comparing machine learning algorithms.
How to use the MLxtend machine learning to compare algorithms using a statistical hypothesis test.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

43 Responses to Hypothesis Test for Comparing Machine Learning Algorithms

Peter August 21, 2020 at 6:38 am #

Thanks for the post!!

Another possible option would be the bayesian approach through BEST

https://best.readthedocs.io/en/latest/

Reply
- Jason Brownlee August 21, 2020 at 6:45 am #
  
  Thanks for sharing!
  
  Reply
Dipti August 22, 2020 at 11:26 pm #

Really it was good….for those who have not proper knowledge can easily understand. I m Associate professor in Statistics in one of the reputed Science college.

Reply
- Jason Brownlee August 23, 2020 at 6:25 am #
  
  Thanks!
  
  Reply

Anthony The Koala August 23, 2020 at 1:47 pm #

Dear Dr Jason,
I have extended the above accuracy with the models used at https://machinelearningmastery.com/calculate-the-bias-variance-trade-off/#comment-550512. That is I have made pairwise combinations of the models from that site and this site and produced the following results.

This contained statistically significant and not significant comparisons

comparing  LogisticRegression()  with  KNeighborsClassifier()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
P-value: 0.131, t-Statistic: -1.802
not statistically significant

------------------------------
comparing  LogisticRegression()  with  DecisionTreeClassifier()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.035)
P-value: 0.004, t-Statistic: 5.098
statistically significant

------------------------------
comparing  LogisticRegression()  with  SVC()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.003, t-Statistic: -5.318
statistically significant

------------------------------
comparing  LogisticRegression()  with  GaussianNB()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.368, t-Statistic: 0.988
not statistically significant

------------------------------
comparing  LogisticRegression()  with  LinearDiscriminantAnalysis()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.328, t-Statistic: 1.085
not statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  DecisionTreeClassifier()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
DecisionTreeClassifier() Mean Accuracy: 0.832 (0.033)
P-value: 0.007, t-Statistic: 4.420
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  SVC()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.028, t-Statistic: -3.062
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  GaussianNB()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.211, t-Statistic: 1.434
not statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  LinearDiscriminantAnalysis()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.136, t-Statistic: 1.777
not statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  SVC()
DecisionTreeClassifier() Mean Accuracy: 0.829 (0.040)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.002, t-Statistic: -5.782
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  GaussianNB()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.036)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.041, t-Statistic: -2.732
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  LinearDiscriminantAnalysis()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.034)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.002, t-Statistic: -6.124
statistically significant

------------------------------
comparing  SVC()  with  GaussianNB()
SVC() Mean Accuracy: 0.952 (0.021)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.018, t-Statistic: 3.467
statistically significant

------------------------------
comparing  SVC()  with  LinearDiscriminantAnalysis()
SVC() Mean Accuracy: 0.952 (0.021)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.003, t-Statistic: 5.191
statistically significant

------------------------------
comparing  GaussianNB()  with  LinearDiscriminantAnalysis()
GaussianNB() Mean Accuracy: 0.866 (0.039)<p
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.450, t-Statistic: -0.819
not statistically significant

------------------------------

100

101

102

103

104

105

comparing LogisticRegression() with KNeighborsClassifier()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

P-value: 0.131, t-Statistic: -1.802

not statistically significant

------------------------------

comparing LogisticRegression() with DecisionTreeClassifier()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

DecisionTreeClassifier() Mean Accuracy: 0.831 (0.035)

P-value: 0.004, t-Statistic: 5.098

statistically significant

------------------------------

comparing LogisticRegression() with SVC()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

SVC() Mean Accuracy: 0.952 (0.021)

P-value: 0.003, t-Statistic: -5.318

statistically significant

------------------------------

comparing LogisticRegression() with GaussianNB()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

GaussianNB() Mean Accuracy: 0.866 (0.039)

P-value: 0.368, t-Statistic: 0.988

not statistically significant

------------------------------

comparing LogisticRegression() with LinearDiscriminantAnalysis()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.328, t-Statistic: 1.085

not statistically significant

------------------------------

comparing KNeighborsClassifier() with DecisionTreeClassifier()

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

DecisionTreeClassifier() Mean Accuracy: 0.832 (0.033)

P-value: 0.007, t-Statistic: 4.420

statistically significant

------------------------------

comparing KNeighborsClassifier() with SVC()

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

SVC() Mean Accuracy: 0.952 (0.021)

P-value: 0.028, t-Statistic: -3.062

statistically significant

------------------------------

comparing KNeighborsClassifier() with GaussianNB()

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

GaussianNB() Mean Accuracy: 0.866 (0.039)

P-value: 0.211, t-Statistic: 1.434

not statistically significant

------------------------------

comparing KNeighborsClassifier() with LinearDiscriminantAnalysis()

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.136, t-Statistic: 1.777

not statistically significant

------------------------------

comparing DecisionTreeClassifier() with SVC()

DecisionTreeClassifier() Mean Accuracy: 0.829 (0.040)

SVC() Mean Accuracy: 0.952 (0.021)

P-value: 0.002, t-Statistic: -5.782

statistically significant

------------------------------

comparing DecisionTreeClassifier() with GaussianNB()

DecisionTreeClassifier() Mean Accuracy: 0.831 (0.036)

GaussianNB() Mean Accuracy: 0.866 (0.039)

P-value: 0.041, t-Statistic: -2.732

statistically significant

------------------------------

comparing DecisionTreeClassifier() with LinearDiscriminantAnalysis()

DecisionTreeClassifier() Mean Accuracy: 0.831 (0.034)

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.002, t-Statistic: -6.124

statistically significant

------------------------------

comparing SVC() with GaussianNB()

SVC() Mean Accuracy: 0.952 (0.021)

GaussianNB() Mean Accuracy: 0.866 (0.039)

P-value: 0.018, t-Statistic: 3.467

statistically significant

------------------------------

comparing SVC() with LinearDiscriminantAnalysis()

SVC() Mean Accuracy: 0.952 (0.021)

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.003, t-Statistic: 5.191

statistically significant

------------------------------

comparing GaussianNB() with LinearDiscriminantAnalysis()

GaussianNB() Mean Accuracy: 0.866 (0.039)<p

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.450, t-Statistic: -0.819

not statistically significant

------------------------------

The statistically significant models were:

comparing  LogisticRegression()  with  DecisionTreeClassifier()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.035)
P-value: 0.004, t-Statistic: 5.098
statistically significant

------------------------------
comparing  LogisticRegression()  with  SVC()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.003, t-Statistic: -5.318
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  DecisionTreeClassifier()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
DecisionTreeClassifier() Mean Accuracy: 0.832 (0.033)
P-value: 0.007, t-Statistic: 4.420
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  SVC()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.028, t-Statistic: -3.062
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  SVC()
DecisionTreeClassifier() Mean Accuracy: 0.829 (0.040)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.002, t-Statistic: -5.782
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  GaussianNB()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.036)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.041, t-Statistic: -2.732
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  LinearDiscriminantAnalysis()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.034)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.002, t-Statistic: -6.124
statistically significant

------------------------------
comparing  SVC()  with  GaussianNB()
SVC() Mean Accuracy: 0.952 (0.021)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.018, t-Statistic: 3.467
statistically significant

------------------------------
comparing  SVC()  with  LinearDiscriminantAnalysis()
SVC() Mean Accuracy: 0.952 (0.021)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.003, t-Statistic: 5.191
statistically significant

comparing LogisticRegression() with DecisionTreeClassifier()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

DecisionTreeClassifier() Mean Accuracy: 0.831 (0.035)

P-value: 0.004, t-Statistic: 5.098

statistically significant

------------------------------

comparing LogisticRegression() with SVC()

LogisticRegression() Mean Accuracy: 0.892 (0.034)

SVC() Mean Accuracy: 0.952 (0.021)

P-value: 0.003, t-Statistic: -5.318

statistically significant

------------------------------

comparing KNeighborsClassifier() with DecisionTreeClassifier()

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

DecisionTreeClassifier() Mean Accuracy: 0.832 (0.033)

P-value: 0.007, t-Statistic: 4.420

statistically significant

------------------------------

comparing KNeighborsClassifier() with SVC()

KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)

SVC() Mean Accuracy: 0.952 (0.021)

P-value: 0.028, t-Statistic: -3.062

statistically significant

------------------------------

comparing DecisionTreeClassifier() with SVC()

DecisionTreeClassifier() Mean Accuracy: 0.829 (0.040)

SVC() Mean Accuracy: 0.952 (0.021)

P-value: 0.002, t-Statistic: -5.782

statistically significant

------------------------------

comparing DecisionTreeClassifier() with GaussianNB()

DecisionTreeClassifier() Mean Accuracy: 0.831 (0.036)

GaussianNB() Mean Accuracy: 0.866 (0.039)

P-value: 0.041, t-Statistic: -2.732

statistically significant

------------------------------

comparing DecisionTreeClassifier() with LinearDiscriminantAnalysis()

DecisionTreeClassifier() Mean Accuracy: 0.831 (0.034)

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.002, t-Statistic: -6.124

statistically significant

------------------------------

comparing SVC() with GaussianNB()

SVC() Mean Accuracy: 0.952 (0.021)

GaussianNB() Mean Accuracy: 0.866 (0.039)

P-value: 0.018, t-Statistic: 3.467

statistically significant

------------------------------

comparing SVC() with LinearDiscriminantAnalysis()

SVC() Mean Accuracy: 0.952 (0.021)

LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)

P-value: 0.003, t-Statistic: 5.191

statistically significant

Conclusion:
Out of the statistically significant models SVC had the highest accuracy of 0.952 compared to LDA of 0.894. The p-value is 0.003

Thank you,
Anthony of Sydney

Anthony The Koala August 23, 2020 at 1:57 pm #

Dear Dr Jason,
apologies, I forgot to consider the comparison of SVC and KNeighborsClassifier with average values of 0.952 and 0.942 respectively and significant with p-value of 0.028.

Further conclusion:
Though there was little difference in accuracy between SVC and KNeighborsClassifier, it appears for the particular dataset consisting of X and y, SVC is likely to be the most suitable method for accuracy.

So if one is to made predictions for a given dataset X, y , SVC is likely to be model of choice.

Thank you,
Anthony of Sydney

Reply
- Jason Brownlee August 24, 2020 at 6:15 am #
  
  Nice, thanks for sharing.
  
  Reply

Jason Brownlee August 24, 2020 at 6:13 am #

Nice work!

A good way to present pair-wise hypothesis tests is in a matrix with algorithms along both axis and significant true/false in each cell of the matrix.

Anthony The Koala August 24, 2020 at 12:22 pm #

Dear Dr Jason,
Thank you for your reply.
When you say that a “…good way to present pair wise hypothesis testing in a matrix…” could you elaborate please. Do you mean pair-wise boxplots, with a scatter matrix pairs?

Is there a scatter_matrix that enables one to switch from a scatter plot to a pairwise comparison of boxplots?

Thank you,
Anthony of Sydney

Jason Brownlee August 24, 2020 at 1:55 pm #

No, not a plot, a matrix or table with true/false values indicating whether there is a significant difference between each pair of algorithms or not.

One can then review the actual mean values for each algorithm that has significant results and ignore the rest.

A list of pairs can also be used.

Anthony The Koala August 24, 2020 at 2:21 pm #

Dear Dr Jason,
Thank you for that.
Do you mean a table such as this:

Model Combination Pair.      Model1  score1 std1  Model2 score2 std1  sig/no diff
LDA()  SVC()                       LDA       0.894   0.03  SVC     0.952  0.021 sig
...........................
...........................
DTC() LDA()                        DTC      0.831   0.03  LDA      0.894 0.031 sig

Model Combination Pair. Model1 score1 std1 Model2 score2 std1 sig/no diff

LDA() SVC() LDA 0.894 0.03 SVC 0.952 0.021 sig

...........................

DTC() LDA() DTC 0.831 0.03 LDA 0.894 0.031 sig

Please advise.
Thank you,
Anthony of Sydney

Jason Brownlee August 25, 2020 at 6:34 am #

I don’t think so. It was something I did way back in my phd days.
Anthony The Koala August 24, 2020 at 2:24 pm #

Dear Dr Jason,
Please widen the above ‘table’ it shows

Model, Combination Pair, model1, score1,std1, model2, score2,std2, sig/not sig

1

Model, Combination Pair, model1, score1,std1, model2, score2,std2, sig/not sig

Thank you,
Anthony of Sydney

Anthony The Koala August 24, 2020 at 4:05 pm #

Dear Dr Jason,
A modification to the program, produced this list:

model pairs, model1, mean, std, model2, mean, std, sig/not sig
lr & cart,     lr, 0.89, 0.03,  cart, 0.83, 0.03,   sig
lr & svm,     lr, 0.89, 0.03,  svm, 0.95, 0.02,   sig
knn & cart,     knn, 0.94, 0.02,  cart, 0.83, 0.03,   sig
knn & svm,     knn, 0.94, 0.02,  svm, 0.95, 0.02,   sig
cart & svm,     cart, 0.83, 0.03,  svm, 0.95, 0.02,   sig
cart & bayes,     cart, 0.83, 0.04,  bayes, 0.87, 0.04,   sig
cart & lda,     cart, 0.83, 0.04,  lda, 0.89, 0.03,   sig
svm & bayes,     svm, 0.95, 0.02,  bayes, 0.87, 0.04,   sig
svm & lda,     svm, 0.95, 0.02,  lda, 0.89, 0.03,   sig

model pairs, model1, mean, std, model2, mean, std, sig/not sig

lr & cart, lr, 0.89, 0.03, cart, 0.83, 0.03, sig

lr & svm, lr, 0.89, 0.03, svm, 0.95, 0.02, sig

knn & cart, knn, 0.94, 0.02, cart, 0.83, 0.03, sig

knn & svm, knn, 0.94, 0.02, svm, 0.95, 0.02, sig

cart & svm, cart, 0.83, 0.03, svm, 0.95, 0.02, sig

cart & bayes, cart, 0.83, 0.04, bayes, 0.87, 0.04, sig

cart & lda, cart, 0.83, 0.04, lda, 0.89, 0.03, sig

svm & bayes, svm, 0.95, 0.02, bayes, 0.87, 0.04, sig

svm & lda, svm, 0.95, 0.02, lda, 0.89, 0.03, sig

Do you mean something like the above?
If so is there a way to display text in a nice way = the text aligns nicely.

Thank you,
Anthony of Sydney

Jason Brownlee August 25, 2020 at 6:38 am #

Nice work!

Anthony The Koala August 24, 2020 at 7:00 pm #

Dear Dr Jason,
This is a text-graphic of the output using the package ‘prettyable’ from https://pypi.org/project/PrettyTable/

pip install prettytable --upgrade

1	pip install prettytable --upgrade

Some code to demonstrate implementation:

from prettytable import PrettyTable
................
................
#values of the *_values determined elsewhere................
x = PrettyTable()
column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)
x.add_column(column_names[1],model_values)
x.add_column(column_names[2],mean1_values)
x.add_column(column_names[3],std1_values)
x.add_column(column_names[4],model_values)
x.add_column(column_names[5],mean2_values)
x.add_column(column_names[6],std2_values)
x.add_column(column_names[7],sig_values)
print(x)

from prettytable import PrettyTable

................

#values of the *_values determined elsewhere................

x = PrettyTable()

column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)

x.add_column(column_names[1],model_values)

x.add_column(column_names[2],mean1_values)

x.add_column(column_names[3],std1_values)

x.add_column(column_names[4],model_values)

x.add_column(column_names[5],mean2_values)

x.add_column(column_names[6],std2_values)

x.add_column(column_names[7],sig_values)

print(x)

Output – expand the width of the page by hovering your mouse over the top of this output to view complete viewing.

+--------------+--------+-------+-------+--------+-------+-------+-------------+
| model pairs  | model1 | mean1 |  std  | model2 |  mean |  std  | sig/not sig |
+--------------+--------+-------+-------+--------+-------+-------+-------------+
|  lr & cart   |   lr   | 0.892 | 0.034 |  cart  | 0.828 | 0.037 |     sig     |
|   lr & svm   |   lr   | 0.892 | 0.034 |  svm   | 0.952 | 0.021 |     sig     |
|  knn & cart  |  knn   | 0.942 | 0.022 |  cart  | 0.832 | 0.039 |     sig     |
|  knn & svm   |  knn   | 0.942 | 0.022 |  svm   | 0.952 | 0.021 |     sig     |
|  cart & svm  |  cart  | 0.830 | 0.033 |  svm   | 0.952 | 0.021 |     sig     |
| cart & bayes |  cart  | 0.832 | 0.038 | bayes  | 0.866 | 0.039 |     sig     |
|  cart & lda  |  cart  | 0.830 | 0.039 |  lda   | 0.894 | 0.031 |     sig     |
| svm & bayes  |  svm   | 0.952 | 0.021 | bayes  | 0.866 | 0.039 |     sig     |
|  svm & lda   |  svm   | 0.952 | 0.021 |  lda   | 0.894 | 0.031 |     sig     |
+--------------+--------+-------+-------+--------+-------+-------+-------------+

+--------------+--------+-------+-------+--------+-------+-------+-------------+

+--------------+--------+-------+-------+--------+-------+-------+-------------+

| lr & cart | lr | 0.892 | 0.034 | cart | 0.828 | 0.037 | sig |

| lr & svm | lr | 0.892 | 0.034 | svm | 0.952 | 0.021 | sig |

| knn & cart | knn | 0.942 | 0.022 | cart | 0.832 | 0.039 | sig |

| knn & svm | knn | 0.942 | 0.022 | svm | 0.952 | 0.021 | sig |

| cart & svm | cart | 0.830 | 0.033 | svm | 0.952 | 0.021 | sig |

| cart & bayes | cart | 0.832 | 0.038 | bayes | 0.866 | 0.039 | sig |

| cart & lda | cart | 0.830 | 0.039 | lda | 0.894 | 0.031 | sig |

| svm & bayes | svm | 0.952 | 0.021 | bayes | 0.866 | 0.039 | sig |

| svm & lda | svm | 0.952 | 0.021 | lda | 0.894 | 0.031 | sig |

+--------------+--------+-------+-------+--------+-------+-------+-------------+

Thank you,

Anthony of Sydney

Jason Brownlee August 25, 2020 at 6:40 am #

Very cool.

Weka does this too I think and adds a * to the mean that is larger – to make the table easier to scan.

Anthony The Koala August 25, 2020 at 12:31 am #

Dear Dr Jason,
The above was an ascii text table. The following two are graphical implementations using plotly and matplotlib

#This is the graphical implementation of the table using plotly and matplotlib

#column names and labels calculated earlier.
column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean2", "std", "sig/not sig"]
columns = [models,model1,mean1,std1,model2,mean2,std2,sig]

#Graphical implementation using plotly
import plotly.graph_objects as go
fig = go.Figure(data=[go.Table(header=dict(values=column_names), cells=dict(values=columns))])
fig.show()

#Graphical implementation using matplotlib 
from matplotlib import pyplot
fig = pyplot.figure()
ax = fig.add_subplot(111)
ax.axis('off')
the_table = ax.table(cellText= array(columns).T,colLabels=column_names,loc='center')
pyplot.show()

#This is the graphical implementation of the table using plotly and matplotlib

#column names and labels calculated earlier.

column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean2", "std", "sig/not sig"]

columns = [models,model1,mean1,std1,model2,mean2,std2,sig]

#Graphical implementation using plotly

import plotly.graph_objects as go

fig = go.Figure(data=[go.Table(header=dict(values=column_names), cells=dict(values=columns))])

fig.show()

#Graphical implementation using matplotlib

from matplotlib import pyplot

fig = pyplot.figure()

ax = fig.add_subplot(111)

ax.axis('off')

the_table = ax.table(cellText= array(columns).T,colLabels=column_names,loc='center')

pyplot.show()

Thank you,
Anthony of Sydney

Jason Brownlee August 25, 2020 at 6:42 am #

Nice!

Anthony The Koala August 25, 2020 at 2:03 pm #

Dear Dr Jason,
You mentioned “….Weka does this too I think and adds a * to the mean that is larger – to make the table easier to scan.>

I spent an extra two minutes to modify the code in python.

        #mean1 and mean2 are numeric that is converted to a string.
        #asterisk is added to string whether mean1 > mean2 and vice versa
	temp_mean1 = "%.3f"%mean1 
	temp_mean2 = "%.3f"%mean2
	if mean1 > mean2:
		temp_mean1 = temp_mean1 + "*"
	else:	
		temp_mean2 = temp_mean2 + "*"

#mean1 and mean2 are numeric that is converted to a string.

#asterisk is added to string whether mean1 > mean2 and vice versa

temp_mean1 = "%.3f"%mean1

temp_mean2 = "%.3f"%mean2

if mean1 > mean2:

temp_mean1 = temp_mean1 + "*"

else:

temp_mean2 = temp_mean2 + "*"

Here is the result:

+--------------+--------+--------+-------+--------+--------+-------+-------------+
| model pairs  | model1 | mean1  |  std  | model2 | mean2  |  std  | sig/not sig |
+--------------+--------+--------+-------+--------+--------+-------+-------------+
|  lr & cart   |   lr   | 0.892* | 0.034 |  cart  | 0.831  | 0.039 |     sig     |
|   lr & svm   |   lr   | 0.892  | 0.034 |  svm   | 0.952* | 0.021 |     sig     |
|  knn & cart  |  knn   | 0.942* | 0.022 |  cart  | 0.831  | 0.039 |     sig     |
|  knn & svm   |  knn   | 0.942  | 0.022 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & svm  |  cart  | 0.832  | 0.036 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & lda  |  cart  | 0.830  | 0.036 |  lda   | 0.894* | 0.031 |     sig     |
| svm & bayes  |  svm   | 0.952* | 0.021 | bayes  | 0.866  | 0.039 |     sig     |
|  svm & lda   |  svm   | 0.952* | 0.021 |  lda   | 0.894  | 0.031 |     sig     |
+--------------+--------+--------+-------+--------+--------+-------+-------------+

+--------------+--------+--------+-------+--------+--------+-------+-------------+

+--------------+--------+--------+-------+--------+--------+-------+-------------+

| lr & cart | lr | 0.892* | 0.034 | cart | 0.831 | 0.039 | sig |

| lr & svm | lr | 0.892 | 0.034 | svm | 0.952* | 0.021 | sig |

| knn & cart | knn | 0.942* | 0.022 | cart | 0.831 | 0.039 | sig |

| knn & svm | knn | 0.942 | 0.022 | svm | 0.952* | 0.021 | sig |

| cart & svm | cart | 0.832 | 0.036 | svm | 0.952* | 0.021 | sig |

| cart & lda | cart | 0.830 | 0.036 | lda | 0.894* | 0.031 | sig |

| svm & bayes | svm | 0.952* | 0.021 | bayes | 0.866 | 0.039 | sig |

| svm & lda | svm | 0.952* | 0.021 | lda | 0.894 | 0.031 | sig |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

Thank you,
Anthony of Sydney

Jason Brownlee August 26, 2020 at 6:43 am #

This is really great stuff Anthony!

Anthony The Koala August 28, 2020 at 2:40 am #

Dear Dr Jason,
The table above used the package prettytable.
Unfortunately you cannot add a header using prettytable package.
If you want to add a header like the table below:

+--------------------------------------------------------------------------------+
|                    Pairwise comparison of scores for models                    |
+--------------+--------+--------+-------+--------+--------+-------+-------------+
| model pairs  | model1 | mean1  |  std  | model2 | mean2  |  std  | sig/not sig |
+--------------+--------+--------+-------+--------+--------+-------+-------------+
|  lr & cart   |   lr   | 0.892* | 0.034 |  cart  | 0.834  | 0.037 |     sig     |
|   lr & svm   |   lr   | 0.892  | 0.034 |  svm   | 0.952* | 0.021 |     sig     |
|  knn & cart  |  knn   | 0.942* | 0.022 |  cart  | 0.832  | 0.034 |     sig     |
|  knn & svm   |  knn   | 0.942  | 0.022 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & svm  |  cart  | 0.830  | 0.035 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & lda  |  cart  | 0.831  | 0.032 |  lda   | 0.894* | 0.031 |     sig     |
| svm & bayes  |  svm   | 0.952* | 0.021 | bayes  | 0.866  | 0.039 |     sig     |
|  svm & lda   |  svm   | 0.952* | 0.021 |  lda   | 0.894  | 0.031 |     sig     |
+--------------+--------+--------+-------+--------+--------+-------+-------------+

+--------------------------------------------------------------------------------+

| Pairwise comparison of scores for models |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

+--------------+--------+--------+-------+--------+--------+-------+-------------+

| lr & cart | lr | 0.892* | 0.034 | cart | 0.834 | 0.037 | sig |

| lr & svm | lr | 0.892 | 0.034 | svm | 0.952* | 0.021 | sig |

| knn & cart | knn | 0.942* | 0.022 | cart | 0.832 | 0.034 | sig |

| knn & svm | knn | 0.942 | 0.022 | svm | 0.952* | 0.021 | sig |

| cart & svm | cart | 0.830 | 0.035 | svm | 0.952* | 0.021 | sig |

| cart & lda | cart | 0.831 | 0.032 | lda | 0.894* | 0.031 | sig |

| svm & bayes | svm | 0.952* | 0.021 | bayes | 0.866 | 0.039 | sig |

| svm & lda | svm | 0.952* | 0.021 | lda | 0.894 | 0.031 | sig |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

Use the pytable package. First you uninstall prettytable then install pytable.

rem in your dos window

pip uninstall prettytable

pip uninstall ptable --upgrade

rem in your dos window

pip uninstall prettytable

pip uninstall ptable --upgrade

In your python program you import the ptable package as importing prettytable.

In this example, you add another line

x.title = "Pairwise comparison of scores for models"

1	x.title = "Pairwise comparison of scores for models"

Here is the code:

from prettytable import PrettyTable
x = PrettyTable()
column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)
x.title = "Pairwise comparison of scores for models  "
x.add_column(column_names[1],model_values)
x.add_column(column_names[2],mean1_values)
x.add_column(column_names[3],std1_values)
x.add_column(column_names[4],model_values)
x.add_column(column_names[5],mean2_values)
x.add_column(column_names[6],std2_values)
x.add_column(column_names[7],sig_values)
print(x)

from prettytable import PrettyTable

x = PrettyTable()

column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)

x.title = "Pairwise comparison of scores for models "

x.add_column(column_names[1],model_values)

x.add_column(column_names[2],mean1_values)

x.add_column(column_names[3],std1_values)

x.add_column(column_names[4],model_values)

x.add_column(column_names[5],mean2_values)

x.add_column(column_names[6],std2_values)

x.add_column(column_names[7],sig_values)

print(x)

Thank you,
Anthony of Sydney

Jason Brownlee August 28, 2020 at 6:53 am #

Nice work.

Anthony The Koala August 28, 2020 at 11:03 pm #

Dear Dr Jason,
From my enhancements to your tutorial on comparing the scores of models, I have shown how one can make a table of the significant relationships between one model versus another model.

This tutorial showed the boxplots of the scores when comparing models.

Without showing the code in its entirety, I go to the essentials of plotting data of boxplots using matplotlib, matplotlib and seaborn which uses matplotlib. Note I did not accidentally write matplotlib twice. There are two methods.

I will relate this to the tutorial.

It is assumed that the packages have been declared at the top of the program.

This is presented as a ‘conceptual’ method but without the accoutrements

First matplotlib where subplots is instantiated with number of rows and number of columns

#This is matplotlib using rows and cols method
fig, ax = pyplot.subplots(vert,horiz)
fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')
fig.tight_layout()
index_limit = len(data from an array containing model1 and model2 )
counter = 0; #Use this to access an array containing model1 and model2 data. and other arrays such as whether the relationship between the two models is sig or not sig
for i in range(vert):
	for j in range(horiz):
           ............
           ............
          model1_scores = data from an array containing model1 and model2 [counter];#conceptual
          model2_scores = data from an array containing model1 and model2 [counter];#conceptual
          ax[i,j].boxplot([model1_scores,model2_scores],showmeans=True)
          .........
         ..........
         counter +=1;# for use in accessing other arrays su
         if counter  == index_limit:
              ax[i,j+1].set_axis_off(); #ensure that you don't have an empty graph
              break

#This is matplotlib using rows and cols method

fig, ax = pyplot.subplots(vert,horiz)

fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')

fig.tight_layout()

index_limit = len(data from an array containing model1 and model2 )

counter = 0; #Use this to access an array containing model1 and model2 data. and other arrays such as whether the relationship between the two models is sig or not sig

for i in range(vert):

for j in range(horiz):

............

model1_scores = data from an array containing model1 and model2 [counter];#conceptual

model2_scores = data from an array containing model1 and model2 [counter];#conceptual

ax[i,j].boxplot([model1_scores,model2_scores],showmeans=True)

.........

..........

counter +=1;# for use in accessing other arrays su

if counter == index_limit:

ax[i,j+1].set_axis_off(); #ensure that you don't have an empty graph

break

This uses matplotlib : compare the difference between instantiation of subplots in this and the previous example

fig = pyplot.figure()
fig.subplots_adjust(hspace=0.7,wspace = 0.3)
fig.tight_layout()
fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')
counter = 0; #Use this to access an array containing model1 and model2 data. and other arrays such as whether the relationship between the two models is sig or not sig
for item in data from an array containing model1 and model2 :
	ax = fig.add_subplot(int(vert),int(horiz),int(item[0]+1))
	
        model1_scores = data from an array containing model1 and model2 [counter];#conceptual
       model2_scores = data from an array containing model1 and model2 [counter];#conceptual

       ax.boxplot([model1_scores,model2_scores],showmeans=True)
       counter += 1; #the counter in this instance may be used to get other arrays associated with model1 and model2

fig = pyplot.figure()

fig.subplots_adjust(hspace=0.7,wspace = 0.3)

fig.tight_layout()

fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')

counter = 0; #Use this to access an array containing model1 and model2 data. and other arrays such as whether the relationship between the two models is sig or not sig

for item in data from an array containing model1 and model2 :

ax = fig.add_subplot(int(vert),int(horiz),int(item[0]+1))

model1_scores = data from an array containing model1 and model2 [counter];#conceptual

model2_scores = data from an array containing model1 and model2 [counter];#conceptual

ax.boxplot([model1_scores,model2_scores],showmeans=True)

counter += 1; #the counter in this instance may be used to get other arrays associated with model1 and model2

This example uses seaborn and matplotlib.

A boxplot in seaborn requires (i) a DataFrame, and (ii) restructing the two variables model1 and model2 into one array The boxplot in seaborn does IS NOT

 import seaborn as sns
#This shows difference between matplotlib's boxplot using variables model1 and model2
pyplot.boxplot([model1, model2], showmeans=True)
#This won't display properly - you'll get len(model1) boxplots!
sns.boxplot([model1,model2],showmeans=True)

import seaborn as sns

#This shows difference between matplotlib's boxplot using variables model1 and model2

pyplot.boxplot([model1, model2], showmeans=True)

#This won't display properly - you'll get len(model1) boxplots!

sns.boxplot([model1,model2],showmeans=True)

What is required in seaborn’s boxplot is to have two variables, the categorical variable identifying model1 and model2, and another array consisting of the stacking of model1 and models’ values.

The generation of the separate categorical and values arrays are performed automatically using pandas’ melt and DataFrame function.

import seaborn as sns
from pandas import DataFrame
from pandas import melt
#This is matplotlib using rows and cols method
fig, ax = pyplot.subplots(vert,horiz)
fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')
fig.tight_layout()
index_limit = len(data from an array containing model1 and model2 )
counter = 0; #Use this to access an array containing model1 and model2 data.
for i in range(vert):
	for j in range(horiz):
           ............
           ............
          model1_scores = data from an array containing model1 and model2 [counter];#conceptual
          model2_scores = data from an array containing model1 and model2 [counter];#conceptual

         labels = (str(type(list_of_models[0]).__name__) , str(type(list_of_models[1]).__name__))
         model1_scores = data from an array containing model1 and model2  
	 model1_scores = data from an array containing model1 and model2 
        #sns requires all data to be in a DataFrame
        temp_array = array([x1,x2]).T    
        # The column names will show the paritcular model pair's names, eg LDA and SVC
        tempdf = DataFrame(temp_array,columns=array(labels))
        # This next procedure generates two columns
        # one column containing the hidden array of labels and the other model1 and model2
        tempdf = melt(tempdf)
        # By DEFAULT tempdf has two columns of data, named 'variable' and 'value'
        # Let's rename the labels, 'models' for the x axis and 'scores' for the y axis
	templabel = ['models','scores']
	tempdf.columns = templabel
     	ax[i,j].set_ylabel("scores",fontsize=8)
       # I choose not to display xlabel as the tick labels are self-explanatory
       ax[i,j].set_xlabel("")
       sns.boxplot(x=tempdf.columns[0],y=tempdf.columns[1], data=tempdf, width=0.2, showmeans=True, color='white' ,ax=ax[i,j])
	.........
         ..........
         counter +=1
         if counter  == index_limit:
              ax[i,j+1].set_axis_off(); #ensure that you don't have an empty graph
              break

import seaborn as sns

from pandas import DataFrame

from pandas import melt

#This is matplotlib using rows and cols method

fig, ax = pyplot.subplots(vert,horiz)

fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')

fig.tight_layout()

index_limit = len(data from an array containing model1 and model2 )

counter = 0; #Use this to access an array containing model1 and model2 data.

for i in range(vert):

for j in range(horiz):

............

model1_scores = data from an array containing model1 and model2 [counter];#conceptual

model2_scores = data from an array containing model1 and model2 [counter];#conceptual

labels = (str(type(list_of_models[0]).__name__) , str(type(list_of_models[1]).__name__))

model1_scores = data from an array containing model1 and model2

#sns requires all data to be in a DataFrame

temp_array = array([x1,x2]).T

# The column names will show the paritcular model pair's names, eg LDA and SVC

tempdf = DataFrame(temp_array,columns=array(labels))

# This next procedure generates two columns

# one column containing the hidden array of labels and the other model1 and model2

tempdf = melt(tempdf)

# By DEFAULT tempdf has two columns of data, named 'variable' and 'value'

# Let's rename the labels, 'models' for the x axis and 'scores' for the y axis

templabel = ['models','scores']

tempdf.columns = templabel

ax[i,j].set_ylabel("scores",fontsize=8)

# I choose not to display xlabel as the tick labels are self-explanatory

ax[i,j].set_xlabel("")

sns.boxplot(x=tempdf.columns[0],y=tempdf.columns[1], data=tempdf, width=0.2, showmeans=True, color='white' ,ax=ax[i,j])

.........

..........

counter +=1

if counter == index_limit:

ax[i,j+1].set_axis_off(); #ensure that you don't have an empty graph

break

A bonus.
You can use a DataFrame in conjunction with the melt method to generate an array of categorical variable associated with the other ‘array’ of data.

The categorical variable’s is derived when intializing the DataFrame.

df = DataFrame([model1_scores, model2_scores],columns = labels, .....)
#df has the labels for the columns
df = melt(df) ; # df generates one column of categories based on the value of labels (of the columns)
df.columns = ['category', 'scores']
category = df.values[:,0]
values = df.values[:,1]

df = DataFrame([model1_scores, model2_scores],columns = labels, .....)

#df has the labels for the columns

df = melt(df) ; # df generates one column of categories based on the value of labels (of the columns)

df.columns = ['category', 'scores']

category = df.values[:,0]

values = df.values[:,1]

Thank you,
Anthony of Sydney

Jason Brownlee August 29, 2020 at 8:01 am #

Nice work, thanks for sharing!

Reply

Aaron Yeardley September 23, 2020 at 8:39 pm #

Hi Jason,
This is a very interesting post which will help me with my PhD work a lot so thank you.
I am just wondering what your advice would be if you wanted to test multiple machine learning algorithms on multiple data sets.

I was thinking I could test each data set using cross-validation and then get a table of results for each machine learning algorithm to conduct a hypothesis test. An example below shows a table presenting the standardised RMSE for various machine learning algorithms:

Dataset | GP1 | GP2 | ANN | Linear Regression
Ishigami | 0.21 | 0.16 | 0.19 | 0.32
Sobol | blah | blah | blah | blah
….
….

and so on.

So in this case. Would there be a recommended hypothesis test to compare the regression techniques? Any literature you would recommend to investigate this further? And what are your thoughts on this sort of analysis?

My issue is that most of the literature I am finding is comparing two machine learning techniques as the best for just one dataset. Whereas I am wanting to find an overall better technique for numerous datasets.

Thanks,
Aaron

Reply
- Jason Brownlee September 24, 2020 at 6:13 am #
  
  Perhaps pair-wise tests between all cases.
  
  Reply
- Sadegh August 17, 2022 at 10:02 pm #
  
  Hi Aaron, I hope you’ll find your answer till now, however I would share a really great Book that essentially is in the depth of this field, that is : Evaluating Learning Algorithms A Classification Perspective By “NATHALIE JAPKOWICZ, University of Ottawa” and “MOHAK SHAH, McGill University”.
  I hope this reference help you and others out with these problems.
  
  Reply
Kasia March 11, 2021 at 7:51 pm #

Anyone has an idea how to calculate power of such a test? 🙂

Reply
- Jason Brownlee March 12, 2021 at 4:54 am #
  
  Perhaps the references in this tutorial will help:
  https://machinelearningmastery.com/statistical-power-and-power-analysis-in-python/
  
  Reply
Laura May 7, 2021 at 3:44 am #

Hi Jason,

Thanks for the article! It is indeed very helpful!

May I ask what method would you suggest when using large datasets? Cross-validation would be very time-consuming, so maybe there is something else out there that I could consider?

Thanks,
Laura

Reply
- Jason Brownlee May 7, 2021 at 6:30 am #
  
  For very large datasets, perhaps a train/test split and a mcnemars test:
  https://machinelearningmastery.com/mcnemars-test-for-machine-learning/
  
  Reply
  - Silvia August 8, 2022 at 2:38 am #
    
    Is there a recommended test when the model has been trained k (let’s say 5) times on the same train/test split (it is a benchmark). So not exactly cross validation (no variability in the data split) but multiple runs due to the model own stoochasticity.
    
    Reply
vvv July 2, 2021 at 1:52 am #

when I make this test, should I do preprocessing the data before it, or not necessary

Reply
- Jason Brownlee July 2, 2021 at 5:21 am #
  
  No need.
  
  Reply
ds July 12, 2021 at 7:36 am #

if i compare ML and DL classifiers, cross val score in DL how is wittren?

Reply
- Jason Brownlee July 13, 2021 at 5:13 am #
  
  Perhaps you can use a standard test harness like cross-validation:
  https://machinelearningmastery.com/repeated-k-fold-cross-validation-with-python/
  
  Reply
Shruti January 5, 2022 at 3:10 am #

Hi, I came across this paper and it seems to be very close to your article. I don’t know if it was plagiarised but wanted to bring it to your notice.

https://www.spu.edu.iq/kjar/index.php/kjar/article/view/630/333

Reply
- James Carmichael January 5, 2022 at 6:54 am #
  
  Thank you for the feedback, Shruti!
  
  Reply
Michael February 26, 2022 at 10:07 pm #

Hello Jason. Just 1 quick question. Why do you define cv and cv2? Doesn’t this mean that the 2 models will be trained and evaluated in different splits of data? Would it be wrong if you just used 1 cv?

Reply
- Gabriel Leite March 23, 2022 at 8:37 am #
  
  I only used 1 too
  
  Reply
carol March 8, 2023 at 9:05 am #

Hello Jason, Thank you for your great post. I have a question for comparing two deep learning models such as u-net and attention u-net. Is it possible to fix the dataset (add 10% of data for test and the rest for training), and train the two models using a set of the same hyperparameters on the fix dataset. Then, using hypothesis testing on the obtained results?

Reply
- James Carmichael March 8, 2023 at 9:17 am #
  
  Hi Carol…You are very welcome! Certainly your understanding is correct! You may also want to try the various models on new data and compare the root mean square error of each.
  
  https://machinelearningmastery.com/regression-metrics-for-machine-learning/
  
  Other ideas are presented here:
  
  https://machinelearningmastery.com/evaluate-performance-deep-learning-models-keras/
  
  Reply

Navigation

Hypothesis Test for Comparing Machine Learning Algorithms

Tutorial Overview

Hypothesis Test for Comparing Algorithms

5×2 Procedure With MLxtend

Comparing Classifier Algorithms

Further Reading

Tutorials

Papers

APIs

Summary

Get a Handle on Statistics for Machine Learning!

Develop a working understanding of statistics

Discover how to Transform Data into Knowledge

More On This Topic

43 Responses to Hypothesis Test for Comparing Machine Learning Algorithms

Leave a Reply Click here to cancel reply.