Optimization is a big part of machine learning. Almost every machine learning algorithm has an optimization algorithm at it’s core.
In this post you will discover a simple optimization algorithm that you can use with any machine learning algorithm. It is easy to understand and easy to implement. After reading this post you will know:
- What is gradient descent?
- How can gradient descent be used in algorithms like linear regression?
- How can gradient descent scale to very large datasets?
- What are some tips for getting the most from gradient descent?
Kick-start your project with my new book Master Machine Learning Algorithms, including step-by-step tutorials and the Excel Spreadsheet files for all examples.
Let’s get started.

Gradient Descent For Machine Learning
Photo by Grand Canyon National Park, some rights reserved.
Gradient Descent
Gradient descent is an optimization algorithm used to find the values of parameters (coefficients) of a function (f) that minimizes a cost function (cost).
Gradient descent is best used when the parameters cannot be calculated analytically (e.g. using linear algebra) and must be searched for by an optimization algorithm.
Intuition for Gradient Descent
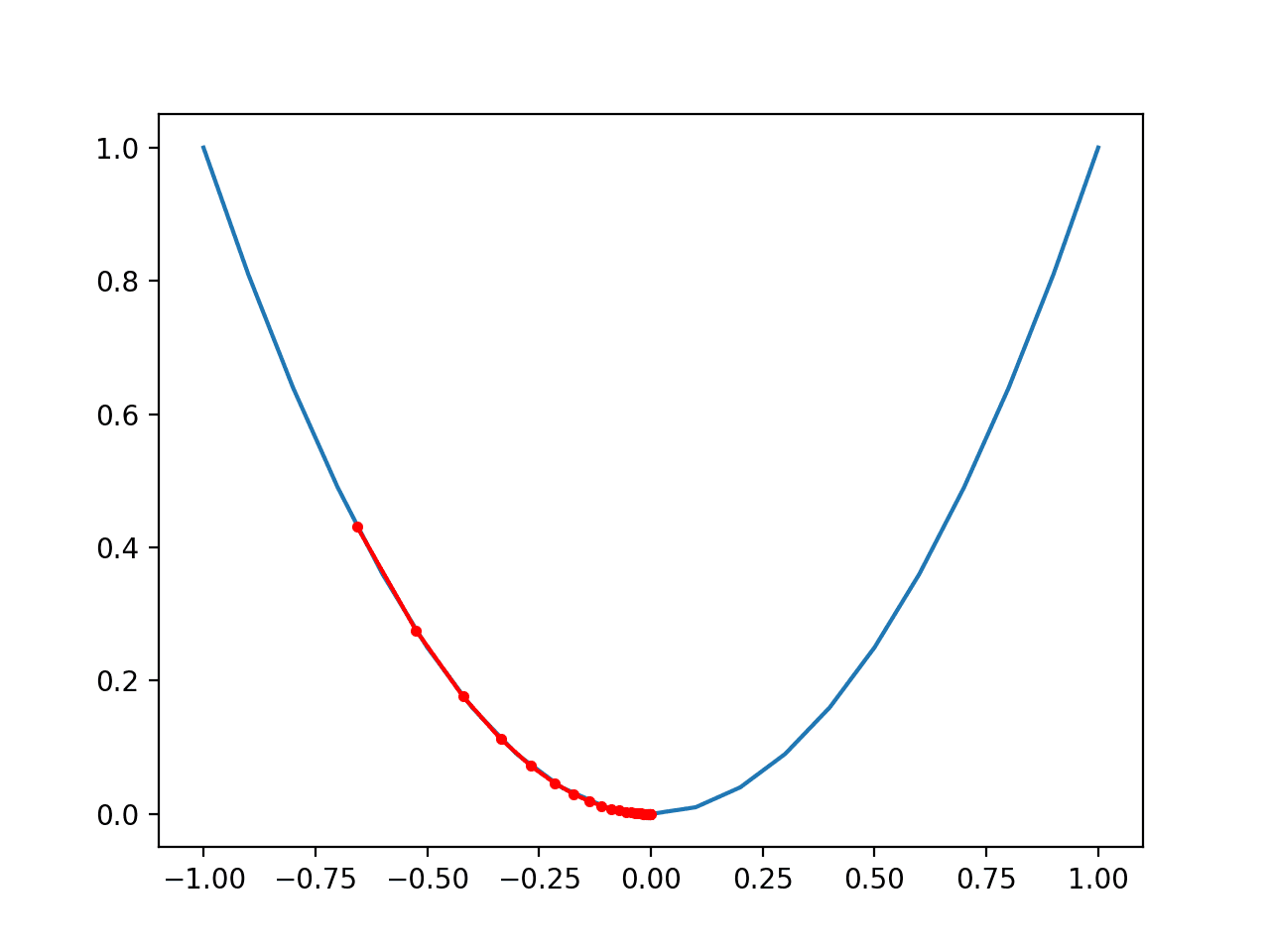
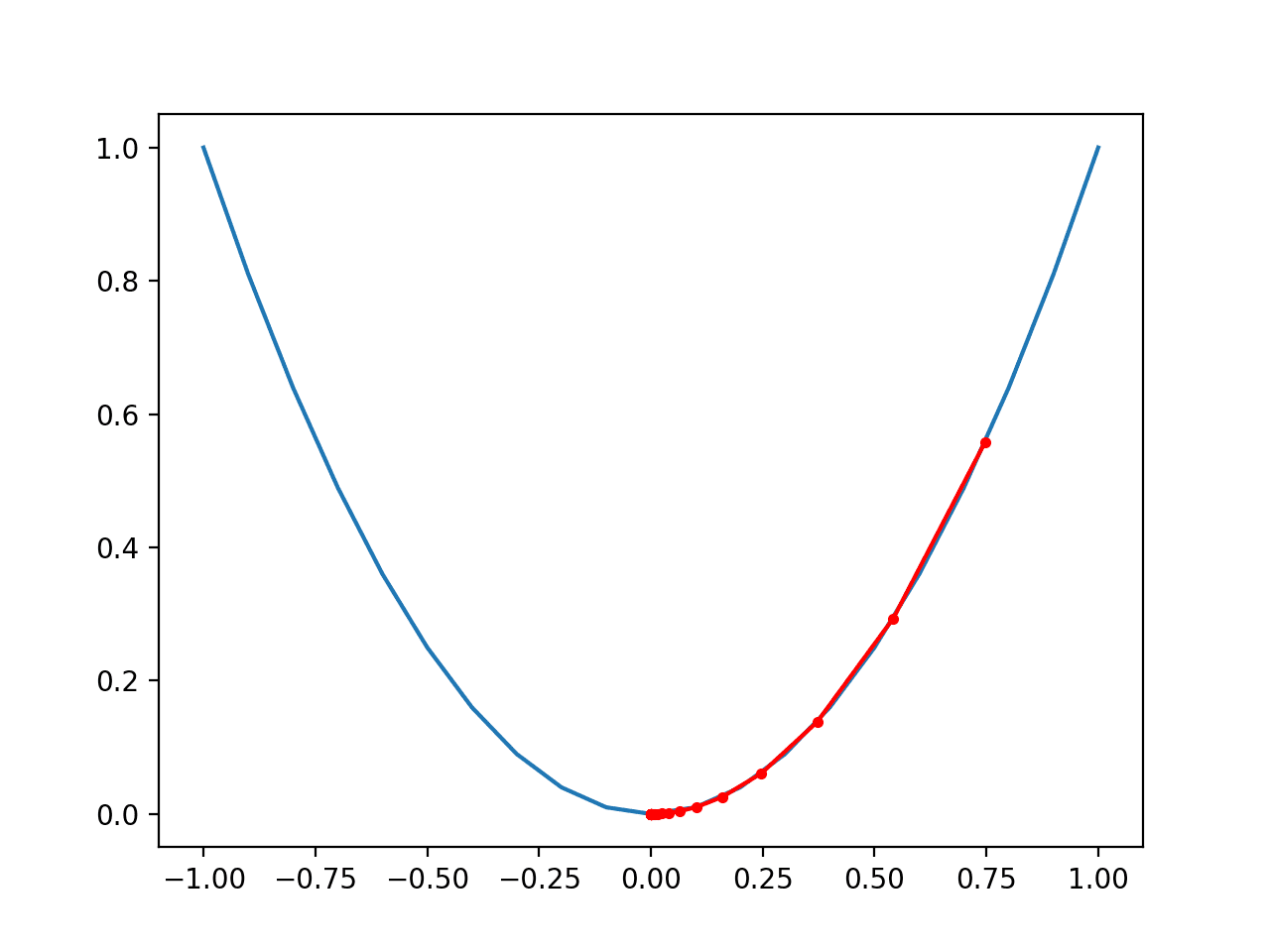
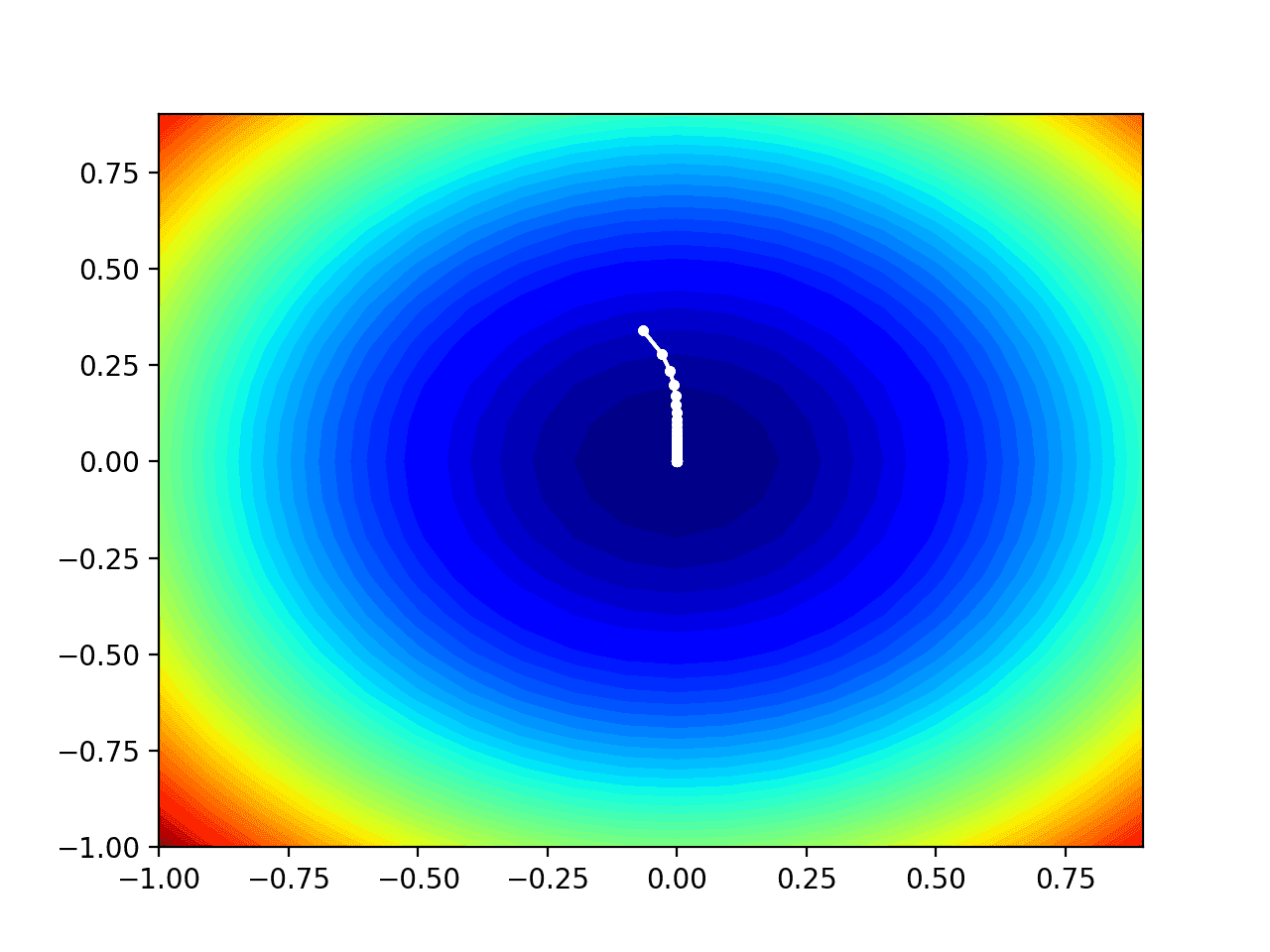
Think of a large bowl like what you would eat cereal out of or store fruit in. This bowl is a plot of the cost function (f).

Large Bowl
Photo by William Warby, some rights reserved.
A random position on the surface of the bowl is the cost of the current values of the coefficients (cost).
The bottom of the bowl is the cost of the best set of coefficients, the minimum of the function.
The goal is to continue to try different values for the coefficients, evaluate their cost and select new coefficients that have a slightly better (lower) cost.
Repeating this process enough times will lead to the bottom of the bowl and you will know the values of the coefficients that result in the minimum cost.
Get your FREE Algorithms Mind Map
Sample of the handy machine learning algorithms mind map.
I've created a handy mind map of 60+ algorithms organized by type.
Download it, print it and use it.
Also get exclusive access to the machine learning algorithms email mini-course.
Gradient Descent Procedure
The procedure starts off with initial values for the coefficient or coefficients for the function. These could be 0.0 or a small random value.
coefficient = 0.0
The cost of the coefficients is evaluated by plugging them into the function and calculating the cost.
cost = f(coefficient)
or
cost = evaluate(f(coefficient))
The derivative of the cost is calculated. The derivative is a concept from calculus and refers to the slope of the function at a given point. We need to know the slope so that we know the direction (sign) to move the coefficient values in order to get a lower cost on the next iteration.
delta = derivative(cost)
Now that we know from the derivative which direction is downhill, we can now update the coefficient values. A learning rate parameter (alpha) must be specified that controls how much the coefficients can change on each update.
coefficient = coefficient – (alpha * delta)
This process is repeated until the cost of the coefficients (cost) is 0.0 or close enough to zero to be good enough.
You can see how simple gradient descent is. It does require you to know the gradient of your cost function or the function you are optimizing, but besides that, it’s very straightforward. Next we will see how we can use this in machine learning algorithms.
Batch Gradient Descent for Machine Learning
The goal of all supervised machine learning algorithms is to best estimate a target function (f) that maps input data (X) onto output variables (Y). This describes all classification and regression problems.
Some machine learning algorithms have coefficients that characterize the algorithms estimate for the target function (f). Different algorithms have different representations and different coefficients, but many of them require a process of optimization to find the set of coefficients that result in the best estimate of the target function.
Common examples of algorithms with coefficients that can be optimized using gradient descent are Linear Regression and Logistic Regression.
The evaluation of how close a fit a machine learning model estimates the target function can be calculated a number of different ways, often specific to the machine learning algorithm. The cost function involves evaluating the coefficients in the machine learning model by calculating a prediction for the model for each training instance in the dataset and comparing the predictions to the actual output values and calculating a sum or average error (such as the Sum of Squared Residuals or SSR in the case of linear regression).
From the cost function a derivative can be calculated for each coefficient so that it can be updated using exactly the update equation described above.
The cost is calculated for a machine learning algorithm over the entire training dataset for each iteration of the gradient descent algorithm. One iteration of the algorithm is called one batch and this form of gradient descent is referred to as batch gradient descent.
Batch gradient descent is the most common form of gradient descent described in machine learning.
Stochastic Gradient Descent for Machine Learning
Gradient descent can be slow to run on very large datasets.
Because one iteration of the gradient descent algorithm requires a prediction for each instance in the training dataset, it can take a long time when you have many millions of instances.
In situations when you have large amounts of data, you can use a variation of gradient descent called stochastic gradient descent.
In this variation, the gradient descent procedure described above is run but the update to the coefficients is performed for each training instance, rather than at the end of the batch of instances.
The first step of the procedure requires that the order of the training dataset is randomized. This is to mix up the order that updates are made to the coefficients. Because the coefficients are updated after every training instance, the updates will be noisy jumping all over the place, and so will the corresponding cost function. By mixing up the order for the updates to the coefficients, it harnesses this random walk and avoids it getting distracted or stuck.
The update procedure for the coefficients is the same as that above, except the cost is not summed over all training patterns, but instead calculated for one training pattern.
The learning can be much faster with stochastic gradient descent for very large training datasets and often you only need a small number of passes through the dataset to reach a good or good enough set of coefficients, e.g. 1-to-10 passes through the dataset.
Tips for Gradient Descent
This section lists some tips and tricks for getting the most out of the gradient descent algorithm for machine learning.
- Plot Cost versus Time: Collect and plot the cost values calculated by the algorithm each iteration. The expectation for a well performing gradient descent run is a decrease in cost each iteration. If it does not decrease, try reducing your learning rate.
- Learning Rate: The learning rate value is a small real value such as 0.1, 0.001 or 0.0001. Try different values for your problem and see which works best.
- Rescale Inputs: The algorithm will reach the minimum cost faster if the shape of the cost function is not skewed and distorted. You can achieved this by rescaling all of the input variables (X) to the same range, such as [0, 1] or [-1, 1].
- Few Passes: Stochastic gradient descent often does not need more than 1-to-10 passes through the training dataset to converge on good or good enough coefficients.
- Plot Mean Cost: The updates for each training dataset instance can result in a noisy plot of cost over time when using stochastic gradient descent. Taking the average over 10, 100, or 1000 updates can give you a better idea of the learning trend for the algorithm.
Summary
In this post you discovered gradient descent for machine learning. You learned that:
- Optimization is a big part of machine learning.
- Gradient descent is a simple optimization procedure that you can use with many machine learning algorithms.
- Batch gradient descent refers to calculating the derivative from all training data before calculating an update.
- Stochastic gradient descent refers to calculating the derivative from each training data instance and calculating the update immediately.
Do you have any questions about gradient descent for machine learning or this post? Leave a comment and ask your question and I will do my best to answer it.




Thanks for all your work, Jason.
It’s very helpful
You’re welcome Victor
Sir ,can u please write a blog by comparing different optimization algorithms (GD,SGD,ADAM….) by taking a dataset with code .
Thanks for the suggestion.
It is the best and simplest explaination I have ever read.
Keep it up.
Thanks Sara.
Yes …the concept has been explained in sach a simple way
Beautifully Explained ! Thank you very much
You’re welcome Aravind, I’m glad it was useful.
Hey Jason,
Can you explain what do you mean by update?
Hi Krishna, I mean change the coefficients that are being optimized.
Hi Brownlee,
Thanks for sharing the topic . your explanation is easy and crystal clear .
I’m glad you found it useful.
Simple and elegant to grasp. Thanks Jason
Thanks.
The post mentions “The first step of the procedure requires that the order of the training dataset is randomized”. When does this need to be done? At the start of each epoch or before running the entire operation?
I’ve tried both but cannot see any noticeable difference looking simply at the plot.
Thanks
Hi Carmen, generally, it is a good idea to randomize prior to each epoch. The changes after each update can start to cancel each other out if sample order is not changed, resulting in worse performance.
I also have another question.
I’ve been going through the tutorial for linear regression and it seems to me that alpha and the number of epochs are what you’d call tuning parameters, is that right? Meaning we need to try different values to see which ones yield the best prediction (on the training dataset, at least).
Using the number of epochs as an example, I’ve created a loop to sequentially try 4, 5, 6… 100 epochs and for each epoch setting I’ve saved the RMSE value obtained and then plotted RMSE as a function of epoch setting chosen. This also allowed me to identify the epoch setting that yields the lowest RMSE on the training dataset at least.
Would you say that this is a generic way in which 1) we can get a feel for how tuning parameters affect prediction accuracy in a model and 2) identify the best combination of tuning parameters?
Thanks
Yep, nice approach.
Generally I like to try broad brush numbers of epochs (10, 100, 1000 on a log scale) and zoom in from there.
Searching blocks of pre-defined parameters is called grid searching, a topic I write a bit about on the blog.
Sorry, me again 🙂
On the topic of alpha, the learning parameter. Is there a benefit to setting this to a really small value? I’ve tried several and it looks like the number of epochs must be that much greater in order to obtain a very small RMSE. So the tradeoff seems to be — it takes longer. But what is the real benefit to being a “slow learner”? Intuitively, it feels like it should reduce variance but I’m not sure I’m right. Does number of observations in the training dataset affect how this value should be set?
Thanks
Great question. The number of epochs and learning rate are linked.
Small alpha needs more training, and the reverse.
You will see this pattern in algorithm after algorithm, the amount of update and how long to learn.
The Explanation is useful
Thanks jason
I’m glad you liked it zerious95, thanks.
hi jason could you give an example of how to use this method on some data set? just to see the whole process in action
Sure Dapo, see this tutorial:
https://machinelearningmastery.com/linear-regression-tutorial-using-gradient-descent-for-machine-learning/
Thank you for your article it is very useful for new ones but I still have a question. What should I do if my coordinate is on the top of the wavy function, it would be easier to show in the pic but I cannot paste it, so imagine a sin function and its waves . I mean derivative at this point equals zero and this point is the maximum so gradient descent probably won`t work here.
Jason,
Really great and simple explanation. Been reading up on Gradient Descent, and this by far made the most sense. I’ve read that partial derivatives is used in Gradient Descent. It’s been a while since I took calculus, and I feel like a need a refresh. Do you think taking a Calculus 1 course would be the best bet? Or should I just read up on partial derivatives or derivatives? Any suggestions for resources, or what type of Calculus course to focus on would be appreciated. Thanks
Hi Andy,
If you plan on doing research on new gradient descent methods or implementing gradient descent yourself for operational use, then getting familiar with the “why” of the algorithm is a good idea.
If you want to use it and deliver results, I would suggest it might not be the best use of your time.
Hi Json,
Nice explanation about gradient decent and it is great help for pple like us,novis to the machine learning.
My question is how we find derivative in a multi dimension situation.
Eg:
f(x1,x2) = x1^2 + x2^3+7
In kind of this situation what woud be the derivative subject?
Is it df(x1,x2)/x1 or df(x1,x2)/dx2. Or would it be a partial differential approach.
Thank you
Yes, when ever the function has more than one independent variables such as x_1, x_2 etc, then we use the concept of partial derivatives.
For updating the coefficients, you will find partial derivative of f w.r.t x_1 keeping x_2 as constant and next par der w.r.t x_2 keeping x_1 as constant and so on
Thanks a Lot Sir! Your effort is really appreciable!
Thanks, I’m glad you found the post useful.
Dear Mr. Jason sir,
Can I have a list of algorithms which perform gradient descent or gradient optimization, something like the L-BFGS algorithms or the Conjugate gradient?
Also, sir, I am doing pattern recognition using an autoencoder model on Brani maps, and I am using the L-BFGS for gradient descent/optimization. Can you suggest me some better algorithms for this purpose??
Thanks a lot sir
Sorry, I do not have a list.
Take a look at any modern neural net library for a good list, for example, here is the list in Keras:
https://keras.io/optimizers/
Adam is excellent:
https://machinelearningmastery.com/adam-optimization-algorithm-for-deep-learning/
Just excellent explanation…brilliant …..explained in such a simple way that a layman can easily understand…
Thanks.
Thanks very much, a very good and comprehensive explanation
Thanks.
Jason,your teaching efforts are to be considered commendable.
However, students should not be encouraged to avoid the math behind ML. Rather, they should be advised to embrace its study with enthusiasm. Any non-mathematicized study of such matters will produce a crippled and wanting knowledge of the subject.
Thanks for your thoughts Andrea.
Hello Jason,
Firstly, I want to say that this post is awesome for everyone looking for information about optimization algorithms like gradient descent and others.
Secondly, I have a query regarding minimizing the cost function of linear regression using gradient descent :
In the documentation of scikit learn at this link scikit-learn.org/stable/modules/linear_model.html
I saw a statement mentioning that,
LinearRegression fits a linear model with coefficients w = (w_1, …, w_p) to minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation. Mathematically it solves a problem of the form:
\underset{w}{min\,} {|| X w – y||_2}^2
So, my question is that if I use LinearRegression class of sklearn.Linear Model package for minimizing the cost function(i.e., residual sum of squares), how does this class minimizes it and obtain the model coefficients(i.e., theta0, theta1)
that minimizes this cost function? What do you think which optimization algorithm does LinearRegression class uses to minimize the cost function and obtain model coefficients?
Can I use SGDRegressor class of sklearn library to minimize the cost function and obtain the model coefficients(i.e., theta0, theta1) that minimizes this cost function using optimization algorithm like stochastic gradient descent?
Please help…….
sklearn and other libraries do not use gradient descent, instead linear algebra methods are often used. You can do this when all data can easily fit into memory.
We use linear regression here to demo gradient descent because it is an easy algorithm to understand. We might not use this algorithm to fit a linear regression if all data can fit into memory and we can use linalg methods instead.
Hi Jason
Excellent article I can say at least what I have gone through about Gradient descent.
Thank you so much for a nice article.
I hope “SGDRegressor” from “sklearn” using this cost function to calculate the best coefficients of linear quadratic equation while LinearRegressor using normal equation to solve the same.
However, here I doubt how will we start with initial set of coefficients in SGD so that we will start converging towards best ?
SGD does not guarantee the best coefficients, only good enough coefficients.
You can try and run the process many times and take the best across all runs.
Thank you Jason for your answer, could you please let me know what is the best way to start with some random coefficients?
Small random numbers in the range 0-1
Why we change delta w on gradient decent?
What is convergence?
Why we done gradient decent in convergence?
When gradient decent not working as convergence?why we need appropriate learning rate?
can i create an ai using python and implement it into xcode and android studio and use it to create an ai app.
Is there a way to create an os that is an ai? if so how to do it
Sorry, I don’t know about xcode or android studio, I cannot give you good advice.
Hi Jason,
Thank you for your explanation of gradient descent. I have a question regarding stochastic gradient descent.
For this explanation:
“The update procedure for the coefficients is the same as that above, except the cost is not summed over all training patterns, but instead calculated for one training pattern.”
Regarding this, I am just confused that how the cost is calculated for one training pattern? Isnt that for batch gradient descent?
Thank You
The difference is that the gradient is estimated from one sample rather than a batch of samples and therefore is more noisy.
can you refer any article to learn implementation of this algorithm in python?
Yes, see here:
https://machinelearningmastery.com/implement-linear-regression-stochastic-gradient-descent-scratch-python/
Hey Jason,
Great explanation, One question though. I am particularly new to calculus but how does the sign of slope tell us in which direction to move.
I mean if the slope is negative we decrease the values of coefficients and vice versa?
Or it depends on each curve/function.
Yes, it is as simple as that. Moving left or right on the number line.
now how does all these calculus of gradients apply in natural language processing text classification text summarisation ?
Gradient descent is the same regardless of the general problem being solved by the network.
Thanks a lot for all your explanations, Jason. It has been very helpful for me.
Any chance to get examples of how to apply Gradient Descent and Stochastic Gradient Descent using Artificial Neural Network model with R (Caret) and Python (Sklearn) by using cross-validation and tuning the parameters?
Sure, start here:
https://machinelearningmastery.com/start-here/#deeplearning
Superb. Very useful article and it makes it clear and simple to understand about gradient descent for machine learning.
Thanks.
Superb Explanation. I am a big fan of your Machine Learning pages.
Thanks.
really good explanation of the topic and could understand thoroughly. Look forward to reading more topics based on machine learning. One comment on the making it more interesting – try adding examples and visuals.
Thanks for the suggestion.
It was very helpful .Thanks jason
I’m happy to hear that!
Informative page, thanks Sir.
Thanks.
Neat & clean clarification. Thanks for sharing.
Thanks.
Hi Jason, you have done a great work. Thanks very much. Hope you dont mind if I contact you for help on my future work on machine learning. I am a Mathematician working on algorithms for optimization problems. Regards
I’m here to help, if I can.
Phenomenal post! Thanks for getting this information out there.
Excited to see how applied machine learning can improve lives.
Thanks Ben.
That was nice and simple explanation sir, Thank you. But where I can learn the implementation of this algorithm?
Thanks.
You can implement it in Python here:
https://machinelearningmastery.com/linear-regression-tutorial-using-gradient-descent-for-machine-learning/
Thank you very very much for the post… As you have mentioned the ebook above, it is little expensive. But if you could offer it at a lesser price that would be great, as I am a student right now.
No problem, you can contact me here and I can send you a student discount:
https://machinelearningmastery.com/contact/
Firstly, I want to say sorry If my Question is not up to the standard here. I’m really a beginner in this field.
thank you for this sharing. Is is an interesting topic. But, I have some questions regarding Gradient Descent in Multilayer Perceptron. Hope that you can answer that.
First, Let say that we take IRIS dataset and train it using MLP and set the epochs to 10.
In your artilces, Stochastic Gradient Descent update the cost(coefficients) for every sample in the dataset. So, for every iteration, what is the last cost function for every class? Let say for class 1 IRIS got 50 samples, so is it the sample cost with the lowest RSS will be the last cost values for that iteration or the last sample cost?
For Batch Gradient Descent, you mention that the cost is calculated for a machine learning algorithm over the entire training dataset for each iteration. How this can be done in MLP? Can you explain further on this part? How the last Coefficients for every class was determine and update. And what is the Final Coefficients values for every classes?
We would use cross entropy as the loss function for a classification task, learn what cross entropy is here:
https://machinelearningmastery.com/cross-entropy-for-machine-learning/
For calculating the loss or error, we can either sum or average across all the samples in the batch or in the whole dataset.
The coefficients or weights are updated iteratively until we decide to stop training.
Hi Jason,
I enjoy your tutorials and learn a lot always. The optimization is to minimize the cost function. How do we define a cost function for unsupervised learning? Can we optimize unsupervised ML algorithms and how?
Thanks,
Sophia
Yes, typically the objective function is some framing of the separation between groups.
Perhaps start here:
https://machinelearningmastery.com/clustering-algorithms-with-python/
Hi Jason,
ML optimization is a process. I think the first step of optimization is to define the cost/loss function and the measure/evaluation method. I think the data preparation, e.g. feature engineering, hyperparameter tuning, model tuning, e.g. ensemble of models should be part of optimization.
Do you have an article regarding ML optimization in general?
Thanks,
Sophia
I hope to write a book on the topic soon.
Hi Jason,
very nice conceptual tutorial on Stochastic Gradient Descent (SGD)
Correct me if i am wrong. I will define SGD as :
” In our exploration of the search space where live the weights that define the mapping function, for every model (that live in another model space), between inputs (X) and output (Y), …the SGD is the way to minimize a certain cost or loss function – that establish a criterium of searching e.g. the error between actual and estimated outputs- is performing via gradient (mathematical derivatives that express the sensitivity of the cost function to the contribution of each of those referred weights of the model multiply by the learning rate step), …and the SDG receive the name of ” stochastic” because the weights updated of the model is performed on every dataset batch (partially chosen randomly -and even shuffled-), … Instead of doing the weights update for the whole dataset.
So finally there is “stochasticity” because the algorithm is performed a little bit different (chosen batch) every time is running…”
regards,
JG
Thanks.
Maybe. The stochastic nature is because we are approximating the gradient of the objective function because we don’t have access to the true objective function or the true gradient.
Great ! thks
You’re welcome.
Hello, I just want to ask that can gradient descent apply to every algorithm (e.g. random forest, SVM)? Is gradient descent an algorithm itself (no need for a linear regression algorithm with it)? If gradient descent is so helpful, why everyone isn’t using it in their linear regression model? And why people don’t use gradient descent on other algorithms too? It is really necessary to apply it to every algorithm?
I am studying gradient descent and now I am onto the coding part. Which I am pretty confused by how to really apply it into my code: where should I apply it in my code? How to use gradient descent with an algorithm to predict something? There are some other optimization algorithms too, so should I used these different optimization algorithm instead of gradient descent?
No, only those algorithms that have coefficients that can be incrementally.
Even if it can be applied, there is probably an optimization algorithm that is more efficient, e.g. it can be used for linear regression and logistic regression but would be inefficient.
OK, thanks a lot!
You’re welcome.
Hi sir, gradient descent is used for regression problem only and grid and randomserach cv is also optimization algorithm which is only used for classification.
Or we can use gradient, grid and random search for all algorithm.
Thanks for this…. ❤️
Gradient descent can be used for any optimization problem you want, it may or may not be the most appropriate method for the problem.
Cant download your mind mapping sir. kindly look into it
Sorry to hear that, you can email me here and ask for a copy directly:
https://machinelearningmastery.com/contact/
Hi Jason,
There is a contradictory post w.r.t the differences between stochastic gradient descent and batch gradient descent. In this post the lines goes like this,
***
Gradient descent can be slow to run on very large datasets.
Because one iteration of the gradient descent algorithm requires a prediction for each instance in the training dataset, it can take a long time when you have many millions of instances.
In situations when you have large amounts of data, you can use a variation of gradient descent called stochastic gradient descent.
***
But in your other post (link below), it states otherwise.
***
Downsides of stochastic gradient descent:
Updating the model so frequently is more computationally expensive than other configurations of gradient descent, taking significantly longer to train models on large datasets.
***
https://machinelearningmastery.com/gentle-introduction-mini-batch-gradient-descent-configure-batch-size/
Can you please let me know which one to follow?
Stochastic gradient descent is always slower than batch.
Hi dear Sir,
I have oil well drilling data and I want to exploratory it using machine learning.
Please can you help me to do that !!??
Best regards
Thanks for asking.
Sorry, I cannot help you with your project.
I’m eager to help, but I don’t have the capacity to get involved in your project at the level you need or at a level to do a good job.
I’m sure you can understand my position, as I get many of requests to help with projects each day.
Nevertheless, I am happy to answer any specific questions you have about machine learning.
Hi Jason,
I believe that gradient descent helps us estimate parameters that minimize the cost function and are close enough to the best model. Then those parameters can be changed according to how the model overfits or underfits the data. Kindly confirm if this notion is correct and if not advise accordingly.
Best Regards.
How Gradient Descent is different from Stochastic Gradient Descent? Describe in either words.
Hi Qamar…You may find the following of interest:
https://machinelearningmastery.com/difference-between-backpropagation-and-stochastic-gradient-descent/
why it is called Schoastic Gradient method?
Hi Allabaksh…The following resource may be of interest:
https://machinelearningmastery.com/stochastic-in-machine-learning/
Thanks. It helped me build some intuition about the gradient descent.
You are very welcome ling! We appreciate your support and feedback.
Damn this is the best explanation! Thanks a lot!
You are very welcome unknownAI!