The cause of poor performance in machine learning is either overfitting or underfitting the data.
In this post, you will discover the concept of generalization in machine learning and the problems of overfitting and underfitting that go along with it.
Kick-start your project with my new book Master Machine Learning Algorithms, including step-by-step tutorials and the Excel Spreadsheet files for all examples.
Let’s get started.

Overfitting and Underfitting With Machine Learning Algorithms
Photo by Ian Carroll, some rights reserved.
Approximate a Target Function in Machine Learning
Supervised machine learning is best understood as approximating a target function (f) that maps input variables (X) to an output variable (Y).
Y = f(X)
This characterization describes the range of classification and prediction problems and the machine algorithms that can be used to address them.
An important consideration in learning the target function from the training data is how well the model generalizes to new data. Generalization is important because the data we collect is only a sample, it is incomplete and noisy.
Get your FREE Algorithms Mind Map
Sample of the handy machine learning algorithms mind map.
I've created a handy mind map of 60+ algorithms organized by type.
Download it, print it and use it.
Also get exclusive access to the machine learning algorithms email mini-course.
Generalization in Machine Learning
In machine learning we describe the learning of the target function from training data as inductive learning.
Induction refers to learning general concepts from specific examples which is exactly the problem that supervised machine learning problems aim to solve. This is different from deduction that is the other way around and seeks to learn specific concepts from general rules.
Generalization refers to how well the concepts learned by a machine learning model apply to specific examples not seen by the model when it was learning.
The goal of a good machine learning model is to generalize well from the training data to any data from the problem domain. This allows us to make predictions in the future on data the model has never seen.
There is a terminology used in machine learning when we talk about how well a machine learning model learns and generalizes to new data, namely overfitting and underfitting.
Overfitting and underfitting are the two biggest causes for poor performance of machine learning algorithms.
Statistical Fit
In statistics, a fit refers to how well you approximate a target function.
This is good terminology to use in machine learning, because supervised machine learning algorithms seek to approximate the unknown underlying mapping function for the output variables given the input variables.
Statistics often describe the goodness of fit which refers to measures used to estimate how well the approximation of the function matches the target function.
Some of these methods are useful in machine learning (e.g. calculating the residual errors), but some of these techniques assume we know the form of the target function we are approximating, which is not the case in machine learning.
If we knew the form of the target function, we would use it directly to make predictions, rather than trying to learn an approximation from samples of noisy training data.
Overfitting in Machine Learning
Overfitting refers to a model that models the training data too well.
Overfitting happens when a model learns the detail and noise in the training data to the extent that it negatively impacts the performance of the model on new data. This means that the noise or random fluctuations in the training data is picked up and learned as concepts by the model. The problem is that these concepts do not apply to new data and negatively impact the models ability to generalize.
Overfitting is more likely with nonparametric and nonlinear models that have more flexibility when learning a target function. As such, many nonparametric machine learning algorithms also include parameters or techniques to limit and constrain how much detail the model learns.
For example, decision trees are a nonparametric machine learning algorithm that is very flexible and is subject to overfitting training data. This problem can be addressed by pruning a tree after it has learned in order to remove some of the detail it has picked up.
Underfitting in Machine Learning
Underfitting refers to a model that can neither model the training data nor generalize to new data.
An underfit machine learning model is not a suitable model and will be obvious as it will have poor performance on the training data.
Underfitting is often not discussed as it is easy to detect given a good performance metric. The remedy is to move on and try alternate machine learning algorithms. Nevertheless, it does provide a good contrast to the problem of overfitting.
A Good Fit in Machine Learning
Ideally, you want to select a model at the sweet spot between underfitting and overfitting.
This is the goal, but is very difficult to do in practice.
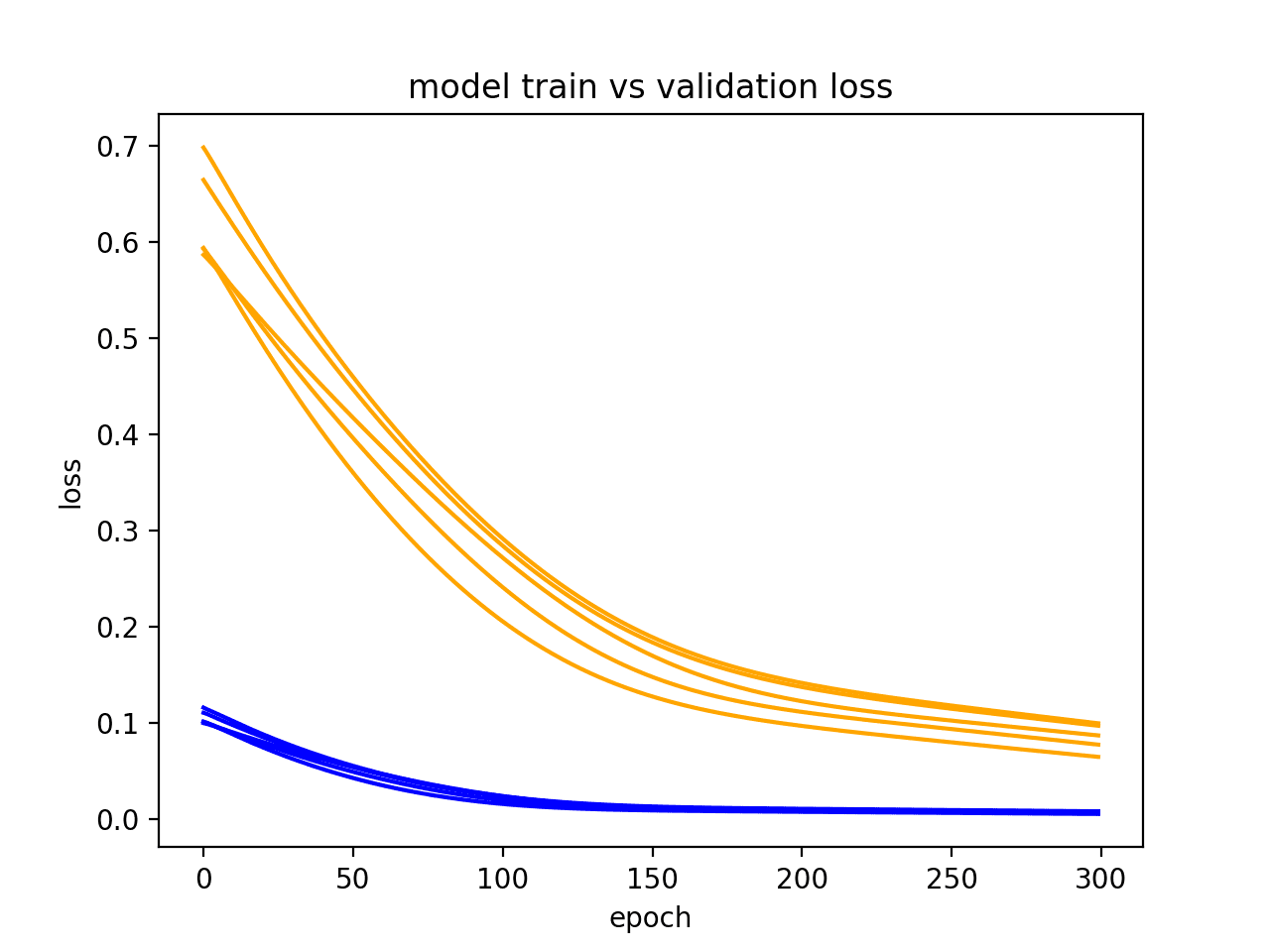
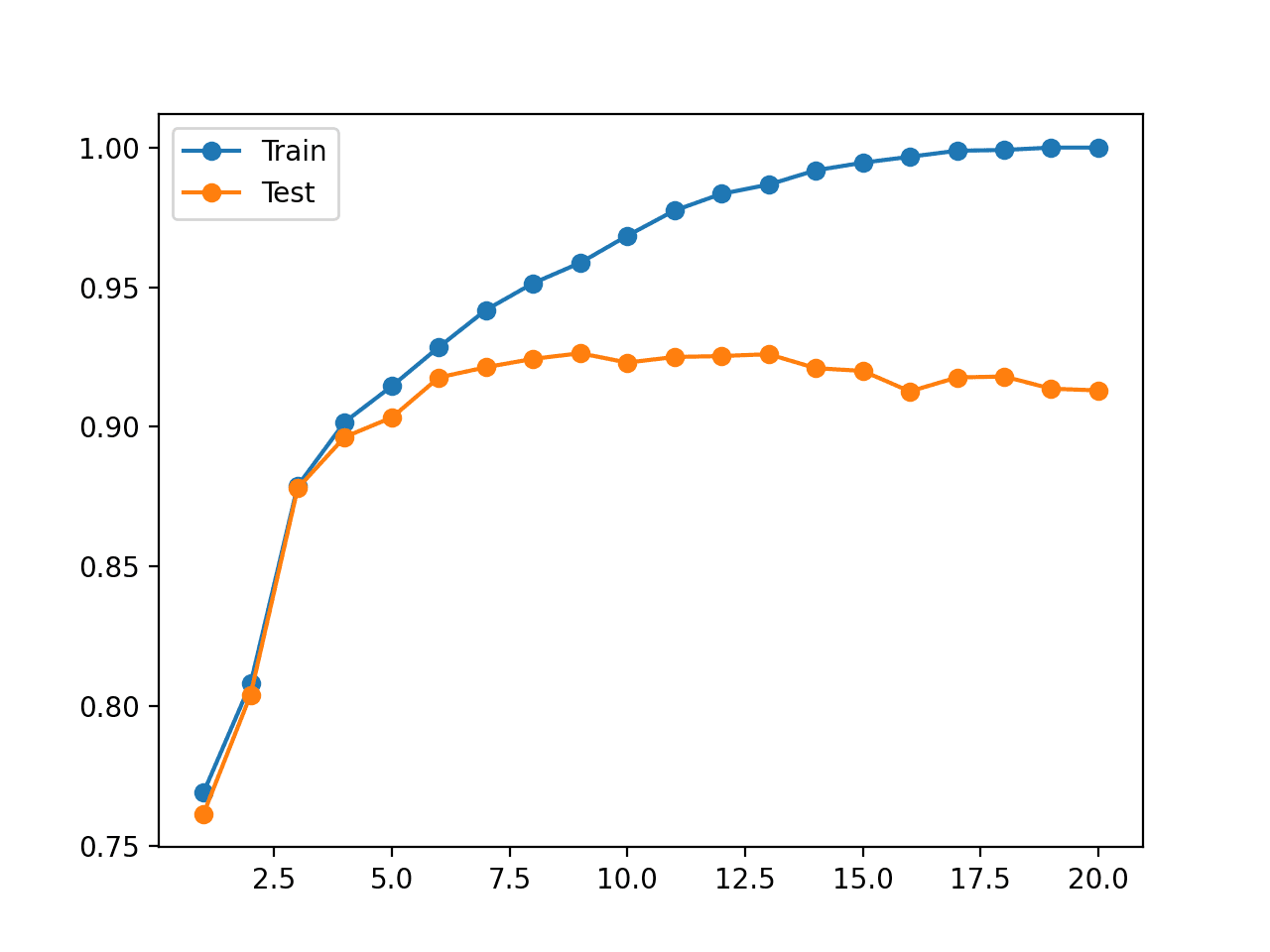
To understand this goal, we can look at the performance of a machine learning algorithm over time as it is learning a training data. We can plot both the skill on the training data and the skill on a test dataset we have held back from the training process.
Over time, as the algorithm learns, the error for the model on the training data goes down and so does the error on the test dataset. If we train for too long, the performance on the training dataset may continue to decrease because the model is overfitting and learning the irrelevant detail and noise in the training dataset. At the same time the error for the test set starts to rise again as the model’s ability to generalize decreases.
The sweet spot is the point just before the error on the test dataset starts to increase where the model has good skill on both the training dataset and the unseen test dataset.
You can perform this experiment with your favorite machine learning algorithms. This is often not useful technique in practice, because by choosing the stopping point for training using the skill on the test dataset it means that the testset is no longer “unseen” or a standalone objective measure. Some knowledge (a lot of useful knowledge) about that data has leaked into the training procedure.
There are two additional techniques you can use to help find the sweet spot in practice: resampling methods and a validation dataset.
How To Limit Overfitting
Both overfitting and underfitting can lead to poor model performance. But by far the most common problem in applied machine learning is overfitting.
Overfitting is such a problem because the evaluation of machine learning algorithms on training data is different from the evaluation we actually care the most about, namely how well the algorithm performs on unseen data.
There are two important techniques that you can use when evaluating machine learning algorithms to limit overfitting:
- Use a resampling technique to estimate model accuracy.
- Hold back a validation dataset.
The most popular resampling technique is k-fold cross validation. It allows you to train and test your model k-times on different subsets of training data and build up an estimate of the performance of a machine learning model on unseen data.
A validation dataset is simply a subset of your training data that you hold back from your machine learning algorithms until the very end of your project. After you have selected and tuned your machine learning algorithms on your training dataset you can evaluate the learned models on the validation dataset to get a final objective idea of how the models might perform on unseen data.
Using cross validation is a gold standard in applied machine learning for estimating model accuracy on unseen data. If you have the data, using a validation dataset is also an excellent practice.
Further Reading
This section lists some recommended resources if you are looking to learn more about generalization, overfitting and underfitting in machine learning.
- Generalization on Wikipedia
- Overfitting on Wikipedia
- Inductive Reasoning on Wikipedia
- Problem of Induction on Wikipedia
- Goodness of Fit on Wikipedia
- What is an intuitive explanation of overfitting? on Quora
- How to Reduce Overfitting in Deep Learning Neural Networks
Summary
In this post, you discovered that machine learning is solving problems by the method of induction.
You learned that generalization is a description of how well the concepts learned by a model apply to new data. Finally, you learned about the terminology of generalization in machine learning of overfitting and underfitting:
- Overfitting: Good performance on the training data, poor generliazation to other data.
- Underfitting: Poor performance on the training data and poor generalization to other data
Do you have any questions about overfitting, underfitting or this post? Leave a comment and ask your question and I will do my best to answer it.






Loving the website Jason! We are currently looking at building a platform to connect data scientists and the like to companies http://www.kortx.co.uk
Hi Jason,
Are resampling and hold-out (the two options for limiting overfitting) mutually exclusive, or do they often get used together? Would using both render one of the techniques redundant?
Thanks
Hi Gary,
Typically you want to pick one method to estimate the performance of your algorithm. Generally, k-fold cross validation is the recommended method. Using two such approaches in conjunction does not really make sense, at least to me off the cuff.
Thank you Jason for these article,
I applied you recipe quite successfully! Nevertheless, I remarked that cross validation does not prevent from overfitting.
Depending on data and algorithm, it can be very easy to get low error rate using cross validation but overfitting.
Did use saw that already ?
This is the reason why I’m using two steps :
1. compare means of train set score with test set score to check I do not overfit to much, and adjust algorithm parameters
2. compute cross validation to get the general performance using previous parameters.
Am I wrong while doing this procedure ?
Many Thanks!
I agree Bruno, CV is a technique to reduce overfitting, but must be employed carefully (e.g. no of folds).
The human is biased, so you also limit the number of human-in-the-loop iterations, because we will encourage the method to overfit, even with CV. Therefore it is also a good idea to hold back a validation dataset that is only evaluated once for final model selection.
You procedure looks fine, consider adding a validation dataset for use after CV.
please tell me how to make a model overfit and then how to regularize that model to remove the overfitting problem
Overfit by training too long, regularize with L2, early stopping or dropout.
Jason, I can’t figure out how to use the validation set
Do you use it to check for performance agreement/no overfiting with CV score ?
Which score (and error) do you use as model performance : the one computed from the validation set or the one from the CV ?
Thank a lot
Hi Bruno,
I would suggest using the CV to estimate the skill of a model.
I would further suggest that the validation dataset can be used as a smoke test. For example, the error should be within 2-3 standard deviations of the mean error estimate of the CV, e.g. “reasonable”.
Finally, once you pick a model, you can go ahead and train it on all your training data and start using it to make predictions.
I hope that helps.
Hi Jason,
‘got it!
Many thanks for your clear answers and your time.
You’re welcome Bruno.
Hi Jason,
I was wondering why cant we use a validation dataset and then find the sweet spot by comparing our model with the training set and validation dataset, what are the disadvantages of using this procedure?
Hi Lijo,
It’s hard. Your approach may work fine, but on some problems it may lead to overfitting. Experiment and see.
The knowledge of how well the model does on the held out (invisible) validation set is being fed back into model selection, influencing the training process.
my constant value is around 111.832 , is that called overfitting? I’m doing a logistic regression to predict malware detection with data traffic 5000 records, i did feature selection technique in rapid miner extracting 7 features out of 56 and do the statistical logistic regression in SPSS . three, significant feature selected out of 7, At last, I need to draw threshold graph where cut off is 80% from the probability value. like I said, my constant is high and performance 97%. please advise.
Hi Wan,
Overfitting refers to learning the training dataset set so well that it costs you performance on new unseen data. That the model cannot generalize as well to new examples.
You can evaluate this my evaluating your model on new data, or using resampling techniques like k-fold cross validation to estimate the performance on new data.
Does that help?
Great explanation, as always. If you feel like correcting a small typo:
“Underfitting refers to a model that can neither model the training data **not** generalize to new data.” (I’m not a native English speaker but think it should be “nor”).
Thanks John, I fixed a few typos including the one you pointed out.
Hi Jason,
Great tutorial regarding overfitting…
Thanks a lot
Thanks Saqib, I’m glad to hear that.
Is the solution to a XOR problem a overfit?
It cannot be solved with 2 units, and one output?
Perhaps underfit – as in under-provisioned to be able to solve it. Or even ill-suited.
Hi Jason, great article!
So just to confirm, cross-validation doesn’t actually prevent overfitting, it’s just used to give you an idea of how well your model would perform on unseen data, and then you can modify the parameters to improve its performance? I.E. It’s just an evaluation technique
Hope you reply in time as I got an exam on this! Cheers
Correct!
How do you solve underfitting?
More data or more training.
Hello,
In both OF and UF has poor performance on generalization. So, what is the solution to have a rich generalization ?
Thank you.
Careful tuning of your model 🙂
There’s no silver bullet.
What if my k-nearest neighbor classifier cause overfitting while making predictive model? How can i reduce overfitting in this case or more specifically, in classification problems? As wecan use regularization(ridge, lasso, elastic net) in case of regression problems to reduce overfitting, so can i use regularization in classification problems as well. Please help…..
Reduce the k value to reduce overfitting.
Thanks. I will check how it works and then i will get back to you with my results.
Good luck!
Hi Jason, Thanks for the wonderful article I have a small doubt..
Do We perform cross validation with in subsets of training data or we do between training and test data..
Cross validation creates train/test sets multiple times to allow us to build and evaluate multiple models when making predictions on unseen data.
But those train/test datasets will be from training only
Not “training” but “available data”.
Hi Jason,
Your explanation of this is amazing and it truly helped me a lot. But I just have one question regarding the two important techniques we can use to limit overfitting.
My question is that as the popular resampling technique to use is k-fold validation, what is the difference between this and bootstrapping?
Looking forward to your answer,
Thank You
Bootstrapping draws random samples with replacement from a dataset whereas k-fold cross-valiation splits a dataset into non-overlapping subsets.
Hi jason,
Thanks for another great article!!
Is it a good idea if a split data into 3 parts (training set, test set & validation set)? I will use the validation set only at the end of the project and use the test set sometimes to check whether the cross-validation accuracy matches the accuracy for the test set.
How can I find out that the model I get after cross-validation is not overfitting? By immediately applying the model to the test set( not the final validation set)? I don’t want to wait until the end of the project to find out that my model is overfitting 🙂
thanks
We can estimate the skill of the model with cross-validation, and confirm it with a held back test dataset.
These are only estimates, we cannot know for sure whether we have over/underfit, but we work had to best robust estimates of model skill.
How can I determine the no of folds i.e. k in K-fold cross-validation to avoid overfitting in the cross-validated model? Is there any rule of thumbs e.g. the ratio between the number of observations and K?
Thanks
The number of samples in a fold should be representative of the broader dataset, if possible.
Hi DR Jason,
This is very good post. I have a question, if I have the following scores: accuracy on training 98%, accuracy on test 95% that means that I have overfitting problem in my model? or there a range of difference I have to consider that the is overfitting? I used K Fold CV and I am getting difference in scores of training and test.
Best regards.
That is a good skill. I would stop there and start using the model.
No need to post 100 times, I deleted the duplicates. All comments are moderated and will appear after I moderate them.
Thank you DR. Jason,
I apologize for the duplicates. I detected typing errors after send the question that is why I sent duplicated I was trying to correct. Next time I will make sure the text is well written before send.
Maybe I misunderstood about overfitting because I understood that both the training and test accuracy must be equal or the test accuracy must be greater than the training accuracy. Because if the training accuracy is greater than test accuracy then the model has overfitted the training data.
That made me confuse because when I train my model some times I get training accuracy of 95% and and test accuracy of 85% and so on depending on the shuffle and that differences make uncomfortable and without confidence that my model has learned enough. And I try to modify my programming code thinking that my code is not well written I and I never stop doing that until I find equal scores.
Just to make sure If I find 95% of accuracy on training and 85% of accuracy on test I can’t be worried too? and I can use my model too? I understood the above answer but I need to make sure because I have two weeks now thinking my model is overfitting and trying to correct my code. And trying to find if there is an acceptable range of difference between accuracies to decide if the model has overfitted or no.
Best regards.
Skill will never be identical on training and test, it is an ideal.
Analysis of the learning curves can help to understand what might be going on. Sometimes nothing is going on – your model was fit and is good.
Understood,
Thank you.
Best Regards
Hi,
Thanks for a great post. I was just wondering if you have a academic source for
“Overfitting is more likely with nonparametric models….”? Writing my thesis so would have to refer to something published
Would you also agree that parametric models have a higher chance of underfitting the data as they put constraints on the target function?
Thanks,
Michael
Not offhand, Perhaps try some searches on google scholar and google books.
Any good intro text on ml will say something similar.
Hi
I have Two datasets i.e. S1 and S2 in my project. When I used 10-fold on S1, I get accuracy 92.34%, but I have also show results on S2 as testing(Independent) dataset. When I train my model on S1 and test on S2, I get results 74%, while existing methods accuracy is 86.43% on 10-fold and 80.65% on Independent test. How can I resolve my problem
Great question, I answer it here:
https://machinelearningmastery.com/the-model-performance-mismatch-problem/
Hi DR Jason,
Is there any reason to be worried when the training accuracy is less than the test accuracy?
I am working on a Naive Bayes from scratch and I am getting 91.7% of accuracy on training set and 98.5% of accuracy on test set, and my doubt is if this results a acceptable because a I see the difference of scores is very high.
Best regards.
Perhaps the test set is too small or not representative of the dataset?
Perhaps but I have 70 observations in training set and 394 observation on test set. And on data preparation I made my data binary 0 and 1 using a threshold. I am not using Naive Bayes for Gaussian distributed data, I am using Naive Bayes for categorical data.
Perhaps a more training data is required.
What about when the performance on the validation dataset is better than the training dataset?
is that good? if yes, is there a limit to which it is good?
I have seen this sometimes myself. I don’t understand it.
I do have some notes here as well:
https://machinelearningmastery.com/faq/single-faq/what-if-model-skill-on-the-test-dataset-is-better-than-the-training-dataset
Hi Jason,
I am facing a very typical problem in my lstm seq-2-seq model which is overfitting.
My target sequence is massively imbalanced which one class and since the problem is classifying the tokens in a sequence into different classes (NER) I cannot resample the sequence (it makes the same problem).
Do you have any idea on how can I overcome this problem?
Thanks!
Good question.
Perhaps you can explore data augmentation to generate new samples as an alternative to oversampling?
Perhaps try alternative or modified loss functions to fit the model?
Perhaps try penalization?
Perhaps try smaller model or less training?
Perhaps check the literature for similar problems and see what was tried?
Thanks a lot Jason for the great suggestions. I will try them and inform you if I get any results.
Some questions, I would like to start with data augmentation, changing the loss function and penalization. (each one separately and then combining maybe)
Could you please give me some links on these three if you have already any post on them or if you know any other usefull posts?
Have searched a lot on changing the weights on loss function but haven’t found any good source.
I don’t have much material on augmentation sorry.
Hi, I have a model which at the moment of training has a loss validation smaller than loss training, is this model good? I use 10 Stratified K- Fold Cross Validation
Hi Afandi…My recommendation in this case would be to establish a baseline of performance and compare your algorithms:
https://machinelearningmastery.com/hypothesis-test-for-comparing-machine-learning-algorithms/
Hello Sir.
I wanted to ask you whether or not generalization had some drawbacks? and when exactly do we go for it? Does it depend on the size of the data-set?
Yes, it is less specific. It solves the average case, at the cost of specific cases.
Hi there Jason!
You helped me a lot with all of your articles and I’d love to express my gratitude.
A problem, however, that I’m not getting quite my thumb on, is, which method might be suited to estimate the goodness of fit, that you mentioned here, for nonlinear predictions produced by NNs to compare different projections made.
R² is proves just useful for linear models, I’m not quite sure about the Chi² (e.g.,how to choose degrees of freedom, alpha for the p-value and how to dertimine the crit. – and if this meaningful at all for comperation between different nonlinar models) and the AIC/BIC need the number of params used – a thing which you can get from your keras produced models, but e.g. not from the MLPRegressor of SKlearn. And then, which kind of param and weight is actually used by the model is by the nature of NNs totally opaque, so I’m doubting that AIC/BIC is of much value.
What is your experience for the goodness of fit?
Greets and lots of thanks in advance,
Tobias
Sorry, it really depends on the distribution of data and the goals of the project.
Great question though. Hmm, it might make a good blog post.
Well in this case, the time series data has a main bulk but also lots of outliers. The models shall reflect distribution by drawing a regression on the test data and detecting the key turning points. Overfitted, the model will end up quite ragged, covering though lots of data points and producing thus a higher R² – so actually in my case R² is more of an indicator for an overfitted NN.
I am facing a problem wherein if I run my program for 1st,2nd and 3rd times,which has a train test split and the mlp has 64 neurons/hidden layer with 2 such layers, 2 classes in output layer and dropout(0.5) after the 1st hidden layer, I am getting ok results.
When I run it 4th time, I get an underfitting model (probably due to dropout) (difference between validation accuracy and training accuracy being 10-15%)
When I run 5th time, I getting overfitting model(difference between validation accuracy and training accuracy being 5-10%)
Is there problem with my dataset or is my model parameters not correctly tuned?
How can I rectify this problem?
This is a common issue that I explain here:
https://machinelearningmastery.com/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
also Ihave taken test size 0.3
You are the best !!!
Thanks.
hi jason, could you please describe , how to decide which supervised machine learning algorithm to use for which kind of data..Like multiclass classification, binary classification and regression and etc.. also how to prepare the raw data into best quality of data so that we can get very good accuracy..please keep in mind i am very new to machine learning..
That is the job of applied machine learning, and there are no right answers. You must discover what works best for your specific dataset, and what data prep leads to a stable model.
I explain more here:
https://machinelearningmastery.com/faq/single-faq/what-algorithm-config-should-i-use
Hi Jason Browniee,
First of all thank you for taking time to answer the questions of almost everyone who has posted one. I appreciate your patience.
I am having a very hard time selecting a good non parametric learning algorithm. I have a train set and a test set. The test set is put aside for now. I then train the model and use GridSearchCV which selects the best hyper-parameters after doing cross-validation. Now, I always see (on the data that I have) that an overfit model (Model that has very low MSE on the train test compared to the Mean MSE from cross validations ) performs very well on the test set compared to a properly fit model. This makes me lean towards a overfit model.I have shuffled my train set 5 times and trained the overfit and under-fit models but i still find the overfit model as a winner. Please advise how I can improve my selection process.
Perhaps try regularizing your chosen model to reduce the overfitting effect?
I have more suggestions here:
https://machinelearningmastery.com/introduction-to-regularization-to-reduce-overfitting-and-improve-generalization-error/
HI Jason,
Thanks for you earlier response.
I am comparing two models, an XGBoostRegressor and and ANN(Reported in some literature). Both are trained and tested on the same dataset.
XGB parameters are choose based on 5 fold cross validation-just FYI
RMSE on train set XGB is 0.021 < RMSE on train set ANN is 0.0348
RMSE on the test set XGB is 0.0331 < ANN is 0.0337
Learning curve look good (I could not find a way to send it to you) Validation curve tapers nicely
and ends at 0.04 RMSE and the Training curve picks up slowly and stabilizes at 0.02 RMSE. There is a gap between these two but not very wide.
Question-1:
Can I outright say that XGB model is better than ANN or do I need to consider anything else ?
Question-2:
Isnt the performance on the test set enough to prove that my XGB model generalizes well or do I need to pull any other statistics?
Well done and great questions!
You can comment on the evidence you have collected, but in empirical investigation (or science broadly) nothing is ever final.
Agreed! But can I say my model is better than the ANN though? ANN results were published in a research paper as the best so far comaperd to many empirically established regression equations. So can I claim incremental victory given the slight advantage of my XGB model? This is an engineering problem not any sort of kagel competition. Thanks in advance!
If the model was evaluated under identical conditions, you can make that claim.
This is often hard to do as publications rarely give sufficient detail to reproduce a result or sufficiently compare.
Ok! Thank you.
If my model seen the test set for many times .is there any possibility that my model can overfit to the test set
Yes, it is you that would be performing the overfitting, trying to optimize the model cfg to the test set.
I think that this is best definition of overfitting:
The overfitting is simply the direct consequence of considering the statistical parameters, and therefore the results obtained, as a useful information without checking that them was not obtained in a random way. Therefore, in order to estimate the presence of overfitting we have to use the algorithm on a database equivalent to the real one but with randomly generated values, repeating this operation many times we can estimate the probability of obtaining equal or better results in a random way. If this probability is high, we are most likely in an overfitting situation. For example, the probability that a fourth-degree polynomial has a correlation of 1 with 5 random points on a plane is 100%, so this correlation is useless and we are in an overfitting situation.
Very nice Andrea, thanks for sharing.
thank you Jason
if you are interested about this topic I wrote a paradox.
The paradox is based on the consideration that the value of a statistical datum does not represent a useful information, but becomes a useful information only when it is possible to proof that it was not obtained in a random way.
here the link on ssrn
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3416559
Thanks for sharing.
Hey Jason,
I have a small doubt. I have trained a model on a dataset with hardly 1500 images with ResNet50 and achieved a very good accuracy and it overfits(>=95%). And i used the same dataset for validation. But to my surprise, the accuracy on the Validation was very bad(<=0.05%). Why is that?!
See the tutorials here to diagnose and improve model performance:
https://machinelearningmastery.com/start-here/#better
Hey Jason
I am comparing performance of Decision tree, Random forest, Rotation forest on Iris dataset.
I am getting score 100 for training set and 92-94 for test. Can we call this a case of overfitting? If yes, how can we avoid this?
Probably not, it is probably a good fit.
What is the criteria in terms of R2 score or any quantitative score to call a model an underfit or overfit model?
Hi Adhya…you may find the following of interest:
https://machinelearningmastery.com/overfitting-machine-learning-models/
So where do we draw the boundary? Is there a range of score difference for training and testing around which we can say that the model probably a good fit and not overfitting.
It’s relative, perhaps read this tutorial:
https://machinelearningmastery.com/learning-curves-for-diagnosing-machine-learning-model-performance/
Very useful Jason.
Thanks for such a clear explanation
You’re welcome, I’m happy to hear that!
I am generating medical image patches through gan, and using xception model as discriminator. Discriminator accuracy, loss and Generator loss can be seen through link (https://send.firefox.com/download/af6c5c5f7852f511/#LCdCpRKOuKquO0h0i6lWOw)
1. Why Discriminator loss and accuracy converge that fast, is this good or bad?
2. Generator loss is fluctuating so much and loss is too-high but it reduced through epochs, what that mean?
3. Generated Image is not that accurate, but discriminator accuracy is high, What can be the reason for that?
Jason can you kindly answer these questions.
Thanks.
Sorry, I don’t have the capacity to download an review your results.
Generally, GANs do not converge:
https://machinelearningmastery.com/faq/single-faq/why-is-my-gan-not-converging
The suggestions here may help you tune your GAN:
https://machinelearningmastery.com/how-to-train-stable-generative-adversarial-networks/
Hi Jason,
Very informative post. Thanks for that.
I have a classification model that needs to go into production. I think it needs to be tested on a validation set derived from past customer data that the model has never seen. This will give us the performance metrics that is indicative of the performance in production.
If we do k-fold with the data (not including the validation data), each of these folds will only test a model trained on 80% data. Every fold will test a different model on a different 80% of the data we hold. None of them will test the final model that will go into production that was trained using 100% of the data. So my conclusion is that hold-out validation will prodvide the better estimate of the model in production.
Is my reasoning correct?
Appreciate your response on this.
Yes, but it gives a reasonable estimate of the modeling pipeline when making predictions on data not used in prediction. From this you can choose a model and describe expected performance.
Hi Jason, i am currently revising for an exam and practising using exam questions. I am however stuck on the question that i have posted below. I am wanting to ask what do you believe the answer would be?
Which of the following actions can reduce overfitting in a machine learning model? (Select all that apply)
1. increasing the number of parameters in the model
2. reducing the number of parameters in the model
3. increasing the learning rate
4. reducing the learning rate
5. increasing the size of the dataset
6. reducing the size of the dataset
2
thank you, i would like to ask would increasing the dataset also help?
Perhaps try it and see.
Hello Jason, your explanation very clearly. but still i can’t imagine or understand how overfitting happen in naive bayes. please, can you explain it to me.
thanks.
Perhaps this will help:
https://machinelearningmastery.com/overfitting-machine-learning-models/
Compare and contrast Naïve Bayes, Logistic regression and decision tree. Which of these algorithms is prone to overfitting and underfitting?
I don’t think the idea of overfitting makes sense or is relevant when choosing a model based on predictive skill.
It is a diagnostic tool when investigating the performance of a model.
See this tutorial:
https://machinelearningmastery.com/overfitting-machine-learning-models/
is feature selection is important to avoid overfiting or underfiting?
Perhaps. Feature selection is to provide more important input to train the model. Speaking from information theory perspective, you try to give more signal and less noise to the model. This will surely help if you did it correctly.
Hi Jason,
Thank you for all of your insightful posts, they’re great!
I was trying to download the ‘Get your FREE Algorithms Mind Map’ repeatedly and it was nowhere in to be found in the mail (checked the spam and everything). could this be fixed somehow or is there another place i can find that map? it looks too good to miss out on 🙂
Thanks
Hi Rachel…Please refer to the following mini-course and follow the link provided within it.
https://machinelearningmastery.com/machine-learning-algorithms-mini-course/
Regards,
Hello James,
What about if the training accuracy is less than validation or test accuracy? It is underfitting, am I right?
Hi Muhammad…This is possibly the case. More detail can be found here:
https://machinelearningmastery.com/overfitting-machine-learning-models/