Supervised machine learning algorithms can best be understood through the lens of the bias-variance trade-off.
In this post, you will discover the Bias-Variance Trade-Off and how to use it to better understand machine learning algorithms and get better performance on your data.
Kick-start your project with my new book Master Machine Learning Algorithms, including step-by-step tutorials and the Excel Spreadsheet files for all examples.
Let’s get started.
- Update Oct/2019: Removed discussion of parametric/nonparametric models (thanks Alex).

Gentle Introduction to the Bias-Variance Trade-Off in Machine Learning
Photo by Matt Biddulph, some rights reserved.
Overview of Bias and Variance
In supervised machine learning an algorithm learns a model from training data.
The goal of any supervised machine learning algorithm is to best estimate the mapping function (f) for the output variable (Y) given the input data (X). The mapping function is often called the target function because it is the function that a given supervised machine learning algorithm aims to approximate.
The prediction error for any machine learning algorithm can be broken down into three parts:
- Bias Error
- Variance Error
- Irreducible Error
The irreducible error cannot be reduced regardless of what algorithm is used. It is the error introduced from the chosen framing of the problem and may be caused by factors like unknown variables that influence the mapping of the input variables to the output variable.
In this post, we will focus on the two parts we can influence with our machine learning algorithms. The bias error and the variance error.
Get your FREE Algorithms Mind Map
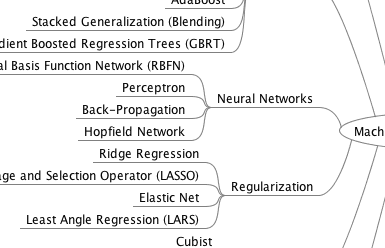
Sample of the handy machine learning algorithms mind map.
I've created a handy mind map of 60+ algorithms organized by type.
Download it, print it and use it.
Also get exclusive access to the machine learning algorithms email mini-course.
Bias Error
Bias are the simplifying assumptions made by a model to make the target function easier to learn.
Generally, linear algorithms have a high bias making them fast to learn and easier to understand but generally less flexible. In turn, they have lower predictive performance on complex problems that fail to meet the simplifying assumptions of the algorithms bias.
- Low Bias: Suggests less assumptions about the form of the target function.
- High-Bias: Suggests more assumptions about the form of the target function.
Examples of low-bias machine learning algorithms include: Decision Trees, k-Nearest Neighbors and Support Vector Machines.
Examples of high-bias machine learning algorithms include: Linear Regression, Linear Discriminant Analysis and Logistic Regression.
Variance Error
Variance is the amount that the estimate of the target function will change if different training data was used.
The target function is estimated from the training data by a machine learning algorithm, so we should expect the algorithm to have some variance. Ideally, it should not change too much from one training dataset to the next, meaning that the algorithm is good at picking out the hidden underlying mapping between the inputs and the output variables.
Machine learning algorithms that have a high variance are strongly influenced by the specifics of the training data. This means that the specifics of the training have influences the number and types of parameters used to characterize the mapping function.
- Low Variance: Suggests small changes to the estimate of the target function with changes to the training dataset.
- High Variance: Suggests large changes to the estimate of the target function with changes to the training dataset.
Generally, nonlinear machine learning algorithms that have a lot of flexibility have a high variance. For example, decision trees have a high variance, that is even higher if the trees are not pruned before use.
Examples of low-variance machine learning algorithms include: Linear Regression, Linear Discriminant Analysis and Logistic Regression.
Examples of high-variance machine learning algorithms include: Decision Trees, k-Nearest Neighbors and Support Vector Machines.
Bias-Variance Trade-Off
The goal of any supervised machine learning algorithm is to achieve low bias and low variance. In turn the algorithm should achieve good prediction performance.
You can see a general trend in the examples above:
- Linear machine learning algorithms often have a high bias but a low variance.
- Nonlinear machine learning algorithms often have a low bias but a high variance.
The parameterization of machine learning algorithms is often a battle to balance out bias and variance.
Below are two examples of configuring the bias-variance trade-off for specific algorithms:
- The k-nearest neighbors algorithm has low bias and high variance, but the trade-off can be changed by increasing the value of k which increases the number of neighbors that contribute t the prediction and in turn increases the bias of the model.
- The support vector machine algorithm has low bias and high variance, but the trade-off can be changed by increasing the C parameter that influences the number of violations of the margin allowed in the training data which increases the bias but decreases the variance.
There is no escaping the relationship between bias and variance in machine learning.
- Increasing the bias will decrease the variance.
- Increasing the variance will decrease the bias.
There is a trade-off at play between these two concerns and the algorithms you choose and the way you choose to configure them are finding different balances in this trade-off for your problem
In reality, we cannot calculate the real bias and variance error terms because we do not know the actual underlying target function. Nevertheless, as a framework, bias and variance provide the tools to understand the behavior of machine learning algorithms in the pursuit of predictive performance.
Further Reading
This section lists some recommend resources if you are looking to learn more about bias, variance and the bias-variance trade-off.
- Bias-variance tradeoff on Wikipedia
- Understanding the Bias-Variance Tradeoff
- Inductive Bias on Wikipedia
Summary
In this post, you discovered bias, variance and the bias-variance trade-off for machine learning algorithms.
You now know that:
- Bias is the simplifying assumptions made by the model to make the target function easier to approximate.
- Variance is the amount that the estimate of the target function will change given different training data.
- Trade-off is tension between the error introduced by the bias and the variance.
Do you have any questions about bias, variance or the bias-variance trade-off. Leave a comment and ask your question and I will do my best to answer.






I have just read a nice and delicate blogpost about bias-variance tradeoff. Looking forward to learn more Machine Learning Algorithms in a simpler fashion.
Model which overfits more likely to have high or low ____
Bias pr varience
bias
overfitting
——————-
bias>>low
variance>>high
High variance
high variance
for overfitting models
low biased and high variance
Hi, I want to check bias-variance tradeoff for iris dataset.. Is anyone knows how to find it>?????????
please tell the solution…
Hi, I required to find using r programming functions.. please reply…
There is a typo i guess…. High bias means more assumptions for the target function. Eg: Linear regression.
But in the article it is specified as opposite,
” High-Bias: Suggests less assumptions about the form of the target function. “
Thanks, fixed.
Hi, less assumptions probably mean less complex model, so I guess high-bias may suggest less complex model and less assumptions.
A high bias assumes a strong assumption or strong restrictions on the model.
I agree with Fei Du
Fei Du and Massi are wrong. A simpler model is one with more assumptions. This is how a generalized linear model becomes linear when we remove non-linear terms. Less complex and fewer assumptions are opposite in this case. A linear model is a special case of a polynomial and thus puts more restrictions on the model.
Model complexity is a sticky concept, there are many ways to measure it (e.g. freedom, capacity, parameters, etc).
A high bias model can be complex or simple, complexity is a different axis of consideration.
This is perfect explanation. Thanks for your efforts.
Thank you.
Very simple explanation. thanks.
I’m glad it helped Sam.
Good explanation, Thank you!
I’m glad it helped.
Nice work!!! I have one query if we decrease the variance then we observe the bias increases and vice versa, but is the rate of fall and rise of these parameters is same or constant or it is dependent of specific algorithms used. Can we tune a model based on bias-variance trade off?
They are tied together.
Yes, one must tune the trade-off on a specific problem to get the right level of generalization required.
while designing any model which must be considered to minimize first bias or variance so as to get a better model ?
Perhaps start with something really high bias and slowly move toward higher variance?
Is there any limit or a scale to know the errors are minimum or maximum in bias and variance?
No, it is problem/metrics/algorithm specific.
Thank you
What are some the measures for understanding bias and variance in our model? How can we quantify bias-variance trade-off? Thanks.
Good question, it may be possible for specific algorithms, such as in knn increasing k from 1 to n (number of patterns) and plotting model skill in a test set.
hello
I guess this post is too old , but still I am giving a try may be if you can answer my question it would be helpful for me
What role exactly Bias and variance could play on the result for training data
what is actually means by the trade-off between variance and bias
how it could effect the approach overall
Thanks
It is an abstract idea to help understand how machine learning algorithms work in general. The tension that exists between prior knowledge/bias and learning from data/variance.
Hello, I am still a little confused about this. Please help me out by reading the following situation.
Suppose there are 5 parties standing in election and we want to make prediction beforehand about who will win. We choose 5 people from a community and ask them separately, the name of the party for which they are going to vote. Suppose all 5 of them chooses all 5 different parties. If we treat each person as a machine learning model, their answer as training data and make predictions accordingly then for all 5 models, we will end up predicting 5 different outputs. This makes it a high variance case because results are varying and high bias because we chose only a particular type of people (all are from a particular community). Next if we choose 1000 people for poll and there are suppose 200 people for each party. Now if we treat all 1000 people as model, we will have 200 predictions for each party. We can call it a low bias because we chose a larger group now and hence they are more representative of their population but this is still high variance, right? Because there are still equally varied results. Lastly, if 700 of those people chose one party (and that party actually wins) and rest 300 are distributed in other parties, is this what we call low variance? What will we call it if that party loses?
Also let me know if I made any incorrect remarks.
Thanks.
There would be some variance, but why high variance? If they are from the same geographical region, watch the same news, then the bias may be high but the variance low.
Also, if there are only 2 choices, e.g. binary, then things like bias and variance don’t mean much. Perhaps you want an example such as guessing the number of coins in a jar?
A question on this statement. You are saying if there are only two choices, then bias and variance don’t mean much. Do you mean two choices as in the outputs? The reason I’m asking is for various sentiment analysis ideas, wherein you have two choices (outputs): 0 or 1. Basically “does not predict” or “does predict.”
But it would seem that in such binary situations, bias could creep in. Such as in data that uses movie reviews, wherein a bias may creep in if the word “bad” was previously only used in clearly negative reviews. But then a new review comes in that says “Wanted to see this movie really bad. Not disappointed.” Here the use of “bad” is not in a negative context, but might be subject to bias.
Am I just totally missing the point of your comment?
Yes, I suppose.The reason I am saying it a high variance is because high variance is the spread of predictions by different models from target output. And in this case out of 1000 only 200 will be on target and rest 800 varied. But probably I am getting it all wrong, I will think about it some more. Thanks for the quick reply.
Is there a situation when there is high variance and high bias
No really, recall the terms are balanced.
High bias will reduce the variance.
High variance will reduce the bias.
Is this bias concept different than the bias added into neural network model y=mx + b(bias of 1)?
Yes, different concepts. The bias in a model is a specific manipulation of the model, the bias in the tradeoff is an abstract concept regarding model behavior.
Does the variance here correspond to the RMSE ?
No, but perhaps the variance in RMSE when the model is trained on different samples of training data (e.g. variance in skill given initial conditions).
Hi Jason,
Your explanation is clear and concise. A nice thing about you is you make complex math heavy topics simple and easier to understand.
Thanks.
Hi Jason,
Is my understanding correct regarding the bias?
Bias is when we assume certain things about the training data (it’s shape for example) and we choose a model accordingly. But, then we get predictions far away from the exptected values and we realise that we did a mistake in certain assumptions of our training data?
Sounds good.
Hi Jason,
This post is clear and easy to understand. I have one question regarding your statement about how SVM manages variance issue. As you said in this article, through increasing penalty parameter C, SVM could decrease its variance.
From my perspective, C is the penalty parameter, and it is different from the regularization lambda, through decreasing C, we could narrow the margin, and the learner could go a little underfitting, which would decrease the variance.
Look forward to hearing from you!
Best,
Yongtao
Not sure, I need to think about it.
Perhaps run some experiments to confirm your framing.
just wanna check if my comment is submitted
Comments are moderated, learn more here:
https://machinelearningmastery.com/faq/single-faq/where-is-my-blog-comment
Dear @Jason Brownlee : Thanks alot for another nice and easy tutorial.
So from the description can i say, that Linear algorithms (Linear/Logistic Regression & LDA) will only under-fit and never face over-fitting problem, because you said that these algorithms have high bias and low variance and vice-versa for non-linear problems (decision tree, KNN, SVM)
A high bias algorithm can still overfit.
Hi Jason,
I am struggling to calculate the bias/discrimination of the ‘Adult Dataset’, downloaded from the UCI machine learning repository. Do you know how to calculate the discrimination using a matrix? Thanks in advance.
Sorry, I don’t have a tutorial on that dataset, maybe this process will help:
https://machinelearningmastery.com/start-here/#process
I have one question though : For a model total error is calculated as
Total error = (Bias)^2 + Variance + Irreducible error
Why do we take (Bias)^2 for the calculation, why not just Bias ?
If bias is the variance then the units are squared units. It is a notation for the units.
Hi Jason,
Thank you very much for your post. It helped me understanding variance and Bias in model.
How do we identify the bias and variance when we apply Random Forest or Logistic regression? I mean what type of graph should I perform to check it? What is x-axis and what is Y-axis?
Thank you for your help on this.
Sandeep
Generally, we don’t. It is a concept to help understand the model behavior.
Feedback : Few images would have helped a lot
Thanks for the suggestion.
What would you like to see images of exactly?
your page dont have any mathematical bias.
please improve …
Thanks for the suggestion.
what are the methods to calculate bias and variance in training data set
It is a theoretical concept for understanding the challenge of predictive modeling.
Hi Jason,
You are really awesome and your blogs and tutorials have really helped me a lot through my journey in this field. I would be grateful if you can clarify a doubt that a got reading through this blog. You mention how increasing C parameter in SVM would lead to an increase in the Bias and decrease in the variance. This is what is not absolutely clear to me.
I will try to present my understanding to explain why I am confused and would love it if you can correct/clarify my understanding.
I believe the C parameter suggests how much we want to avoid misclassifying each training example. Therefore, a large C value will force the optimization to choose a smaller margin. A smaller margin would then lead to overfitting, resulting in a Low bias and a high variance.
Based on this understanding of the C parameter that I have, I am finding it hard to understand when you suggest that increasing the C parameter would lead to an increase in the Bias and decrease in the variance. I am sure I must be missing something and therefore I would love it if you can provide me with the missing pieces and help me understand this well.
Thanks again. Hoping to hear from you soon,
Ishan
Thanks.
No, larger C is more bias – more constraint – more overfitting – more prior.
Does that help?
How is KNN a parametric model? It doesn’t assume any prior on the data? Or you mean parametric in the sense of fixed number of parameters?
Thanks. I probably meant non-linear. I will update it.
UPDATED. Thanks again.
How bias and variance will effect on Number of hidden neurons in a neural network?
More nodes is probably a larger bias, lower variance.
Could you please clarify this answer? My understanding was that more nodes -> more model flexibility / fewer model assumptions about target function -> higher dependence of parameters on training data -> higher variance, lower bias. Could you point out the flaw in my reasoning?
Yes, that is about right.
Great post, very simplistic yet informative. Thanks 🙂
Thanks.
I am trying to fit a linear model on a non-linear function. For Example I have chosen x^3+x^2-5 as my non-linear function and I am fitting linear regression model. I have created ensembles of different sizes let say 10,20,30,……100. So my graph is against the ensemble size. So the bias is decreasing and variance is increasing as the ensemble size is increasing. What can I interpret from this about the function which I took.
Perhaps a linear model is inappropriate for your quadratic function?
In machine learning data are statistically independent mean that ..??
A) Higher Variance B) High correlation C) Low correlation D) Lower Bias
Not sure those concepts are connected directly are they?
overfitting underfitting, and bias-variance trade-off Are these two the same concept or is there any difference between them.
No, they are different concepts.
Increasing Training points (input data) reduces variance without any effect on bias.
So how is the below relationship valid :
Increasing the bias will decrease the variance.
Increasing the variance will decrease the bias.
Not sure I agree with your premise.
Yes, it is easy to decrease one by increasing the other, but this is not the only dynamic.
in K-fold validation , increasing k does it increase error estimates variance or decrease model variance. Why do we say LOOCV has high variance and not better than k-fold
I don’t agree with your statement.
Also, generally LOOCV has lower variance than higher k values.
“Generally, nonlinear machine learning algorithms that have a lot of flexibility have a high variance. For example, decision trees have a high variance, that is even higher if the trees are not pruned before use.”
This is mentioned in the 3rd section. Isnt is supposed to be that a algorithm that has less flexibility will have high variance because any model which has adapted well to a training set will perform bad on another set(overfitting basically) so in turn will have less flexibility.
An algorithm with less flexibility will have a high bias and a low variance.
Simple and great explanation. Thank you for such a nice article. Your posts are very detailed and informative.
You’re very welcome!
Thank you for article
Hi Jason,
would you say the following statement is true: Regularization decreases variance at the cost of introducing bias?
Regularization allows to learn a pattern from a training data set that is too small or noisy for the intended model. So I apply regularization, to decrease the fit of the model to the training data (higher bias) but I aim to gain higher generalizablity by not overfitting (lower variance, i.e. the model is more hesitant to follow patterns that might just be noise)
Correct.
Hi Jason, thank you so much for this article. One thing that is not clear to me is the fact that Bias decrease as Variance increase.
I came up with an example in my head and I would love to hear your opinion about it:
If for example my data came from Y = f(X) + e where f : x^2, I choose to model it by using polynomial regression and now I have to choose the degree of the polynomials K.
In my mind I think that a even value of K, will better fit my data because a polynomial of even degree has the same concavity of a quadratic function and so the behavior at the extreme is the same (I dont know if its the right term concavity, what I mean is that the behavior for x-> +inf and x->-inf is the same for even polynomials), and so I think they better fit my original function f(x) = x^2.
If my example is correct, in my mind I think that a polynomial of degree K=4 will have less Bias than a polynomial of degree K =3 , while having more complexity and (I think) more Variance
Not really. Because K=4 is a superset of K=3. You may end up finding Ax^4+Bx^3+Cx^2+Dx+E with the A very close to zero.
Ok Adrian I think now I got it thanks to your comment: what we mean by increasing complexity of the model is by adding more parameters to the previous version of our model (in my example, increasing the degree of the polynomial, i.e. adding more term to our polynomial function), in this way we always create a super model that contain all the previous one. In this way the Bias can only decrease as we add more term to the model, since we always “have” the previous version of the models incorporated in the new model (in my example, we have as possibilities all the polynomials with degree lower than K).
Thank you so much Adrian
You’re welcomed.
One quick clarification question. Does the bias in this context mean: (a) For a prediction model and a training dataset, the mean of the prediction errors (where we allow the positives and negatives to cancel out, of course) over all samples in the data (b) The mean over the mean errors of the prediction model produced in (a) with many different training datasets, or both?
I believe the analogy applies to variance as well (Correct me if I am wrong)
‘Variance is the amount that the estimate of the target function will change if different training data was used.’ In the given statement, what does ‘different training set’ mean ? Can the different training sets have different features or is it just a different set of rows from the previously(originally) selected features.
Hi Saumya…A different training set could be either of the scenarios you mentioned and in fact it would be beneficial if training were done on such a variation.
There are three cases:
1. Overfitting
Training loss- near 0 for every set of train test split
Test loss- high variance for different train test split
Bias- is usually tied with training loss-, if training loss is less then it is a case of low bias as per the definition of bias. So in overfitting bias is low
Variance- high
2. Underfitting
Training loss- high for every set of train test split
Test loss- high for every set of train test split
Bias- high
Variance- low because test loss is high for different set
3. Balance fit
Training loss- low for every set of train test split
Test loss- low for every set of train test split
Bias- low
Variance- low because test loss is low for different set
So from above discussion it seems that bias and variance not quite opposite to each other but they are related to somewhat due to training and test data relationship.
Great feedback Surender!
for svm c is inversely proportional to the strength of regularization.
Discuss bias-variance tradeoffs in (i) Centroid-based classifier, (ii) kNN
classifier, and (iii) SVM classifier in terms of the nature of class separation
boundaries and the data points in the training set that can effect them.
Hi Sam…You may find the following of interest:
https://monkeylearn.com/blog/what-is-a-classifier/
Discuss bias-variance tradeoffs in (i) Centroid-based classifier, (ii) kNN
classifier, and (iii) SVM classifier in terms of the nature of class separation
boundaries and the data points in the training set that can effect them.
please answer this question?
H james,
This might be a stupid question but it’s struck the back of my mind for so long, so here goes. Does the variance in bias-variance trade-off and variance in statistics (which measures variability from the average or mean ) are different? Greatly appreciate your help.
Hi Akash…They are indeed connected. The following resource is great way to understand the connection between machine learning and statistics:
https://machinelearningmastery.com/statistics_for_machine_learning/
thankyou
You are very welcome vivek!
Hi, I wonder why is the bias error called so? I assume that is because the algorithm makes an assumption about the target function and that leads the algorithm to be biased in the simplified target function.
Hi Dimitrije…The following resource may be of interset to you:
https://www.baeldung.com/cs/machine-learning-biases
Hi James, thank you!