Long Short-Term Memory (LSTM) is a type of recurrent neural network that can learn the order dependence between items in a sequence.
LSTMs have the promise of being able to learn the context required to make predictions in time series forecasting problems, rather than having this context pre-specified and fixed.
Given the promise, there is some doubt as to whether LSTMs are appropriate for time series forecasting.
In this post, we will look at the application of LSTMs to time series forecasting by some of the leading developers of the technique.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
On the Suitability of Long Short-Term Memory Networks for Time Series Forecasting Photo by becosky, some rights reserved.
LSTM for Time Series Forecasting
We will take a closer look at a paper that seeks to explore the suitability of LSTMs for time series forecasting.
They start off by commenting that univariate time series forecasting problems are actually simpler than the types of problems traditionally used to demonstrate the capabilities of LSTMs.
Time series benchmark problems found in the literature … are often conceptually simpler than many tasks already solved by LSTM. They often do not require RNNs at all, because all relevant information about the next event is conveyed by a few recent events contained within a small time window.
The paper focuses on the application of LSTMs to two complex time series forecasting problems and contrasting the results of LSTMs to other types of neural networks.
The focus of the study are two classical time series problems:
Mackey-Glass Series
This is a contrived time series calculated from a differential equation.
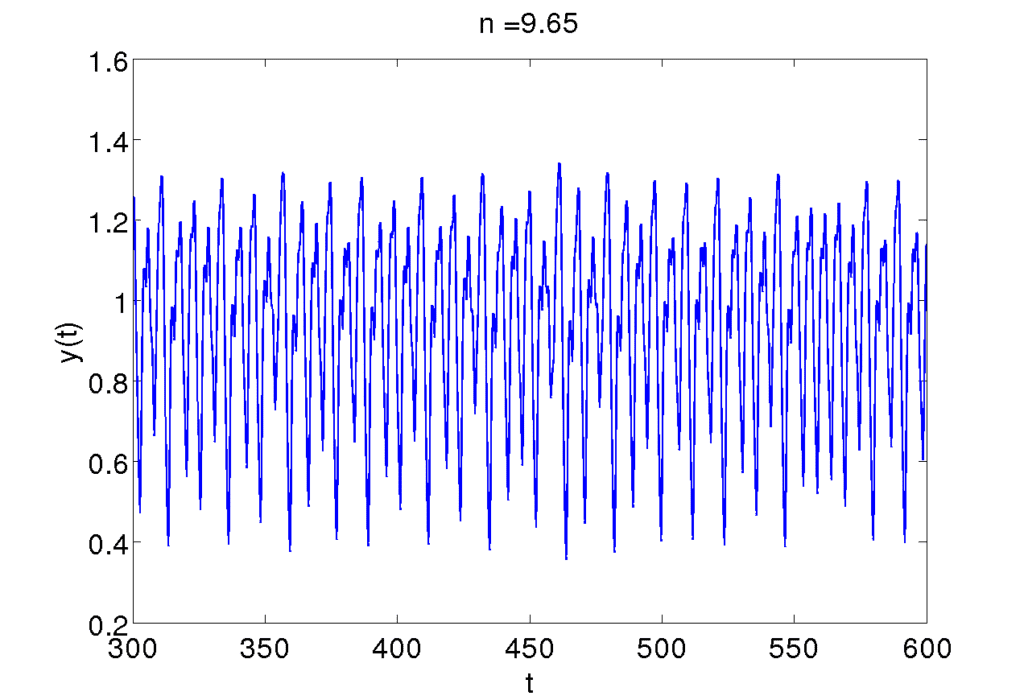
Plot of the Mackey-Glass Series, Taken from Schoarpedia
This is a series taken from a from a contest at the Santa Fe Institute.
Set A is defined as:
A clean physics laboratory experiment. 1,000 points of the fluctuations in a far-infrared laser, approximately described by three coupled nonlinear ordinary differential equations.
Example of Chaotic Laser Data (Set A), Taken from The Future of Time Series
Some of the more salient comments were in response to the poor results of the LSTMs on the Mackey-Glass Series problem.
First, they comment that increasing the learning capacity of the network did not help:
Increasing the number of memory blocks did not significantly improve the results.
This may have required a further increase in the number of training epochs. It is also possible that a stack of LSTMs may have improved results.
They comment that in order to do well on the Mackey-Glass Series, the LSTM is required to remember recent past observations, whereas the MLP is given this data explicitly.
The results for the AR-LSTM approach are clearly worse than the results for the time window approaches, for example with MLPs. The AR-LSTM network does not have access to the past as part of its input … [for the LSTM to do well] required remembering one or two events from the past, then using this information before over-writing the same memory cells.
They comment that in general, this poses more of a challenge for LSTMs and RNNs than it does for MLPs.
Assuming that any dynamic model needs all inputs from t-tau …, we note that the AR-RNN has to store all inputs from t-tau to t and overwrite them at the adequate time. This requires the implementation of a circular buffer, a structure quite difficult for an RNN to simulate.
Again, I can’t help but think that a much larger hidden layer (more memory units) and a much deeper network (stacked LSTMs) would be better suited to learn multiple past observations.
They later conclude the paper and discuss that based on the results, LSTMs may not be suited to AR type formulations of time series forecasting, at least when the lagged observations are close to the time being forecasted.
This is a fair conclusion given the LSTMs performance compared to MLPs on the tested univariate problems.
A time window based MLP outperformed the LSTM pure-AR approach on certain time series prediction benchmarks solvable by looking at a few recent inputs only. Thus LSTM’s special strength, namely, to learn to remember single events for very long, unknown time periods, was not necessary here.
LSTM learned to tune into the fundamental oscillation of each series but was unable to accurately follow the signal.
They do highlight the LSTMs ability to learn oscillation behavior (e.g. cycles or seasonality).
Our results suggest to use LSTM only on tasks where traditional time window-based approaches must fail.
LSTM’s ability to track slow oscillations in the chaotic signal may be applicable to cognitive domains such as rhythm detection in speech and music.
This is interesting, but perhaps not as useful, as such patterns are often explicitly removed wherever possible prior to forecasting. Nevertheless, it may highlight the possibility of LSTMs learning to forecast in the context of a non-stationary series.
Final Word
So, what does all of this mean?
Taken at face value, we may conclude that LSTMs are unsuitable for AR-based univariate time series forecasting. That we should turn first to MLPs with a fixed window and only to LSTMs if MLPs cannot achieve a good result.
This sounds fair.
I would argue a few points that should be considered before we write-off LSTMs for time series forecasting:
Consider more sophisticated data preparation, such as at least scaling and stationarity. If a cycle or trend is obvious, then it should be removed so that the model can focus on the underlying signal. That being said, the capability of LSTMs to perform well on non-stationary data as well or better than other methods is intriguing, but I would expect would be commensurate with an increase in required network capacity and training.
Consider the use of both larger models and hierarchical models (stacked LSTMs) to automatically learn (or “remember”) a larger temporal dependence. Larger models can learn more.
Consider fitting the model for much longer, e.g. thousands or hundreds of thousands of epochs, whilst making use of regularization techniques. LSTMs take a long time to learn complex dependencies.
I won’t point out that we can move beyond AR based models; it’s obvious, and AR models are a nice clean proving ground for LSTMs to consider and take on classical statistical methods like ARIMA and well performing neural nets like window MLPs.
I believe there’s great promise and opportunity for LSTMs applied to the problem of time series forecasting.
Do you agree?
Let me know in the comments below.
Develop Deep Learning models for Time Series Today!
Thank you for this informative article. While I have not trained any LSTM RNNs on my time series data, I’ve found that plain jane feed forward DNNs that are feature engineered correctly and use sliding window CV predicts OOS as expected. Essentially, it is not necessary for my data to have to mess with LSTMs at all. And my features aren’t all iid…
I suppose this illustrates the versatility of DNNs.
I agree that along with MLP’s , LSTM’s have an advantage over more classical statistical approaches like ARIMA : they can fit non-linear functions and moreover , you do not need to specify the type of non-linearity . There also lies the danger : regularisation is absolutely crucial to avoid overfitting .
I still hold on to my position that a lot of very interesting time series will never be cracked by any approach that only looks at past data points to forecast the next : prices are set where demand meets supply and both supply and demand care nothing about yesterday’s price .
I found that for the problem I’m working on (forecasting streamflow based on hydrometric station water level measurements), to my surprise, first differencing of the signal prior to LSTM worsened the results. Overall, I find that I can’t improve over a persistence model with LSTM or an MLP using a moving window. Not sure what to try next… (same problem with ARIMA)
@Jay: I just started to work on a similar problem in the hydrometric field. Would please contact me through our company website at https://www.sobos.at
LSTMs are much newer/younger to solve /simpler/ AR problems – most industries have already been studying and improving custom models applied on such tasks for decades. I believe RNNs shine for multivariate time series forecasts, that have been simply too difficult to model until now. Similarly with MLPs and multivariate time series models where the different features can have different forecasting powers(ie the sentiment of twitter posts can have influence for a day or two, while ny times articles could have a much longer lasting influence).
what do you mean by seasonal adjustment?if i have monthly and annually seasonality?i have taken monthly size for taking care of monthly effect.For annual part if i take it then how to merge both approaches and get a single output?
Hi Ph.D Jason,
I have multivariate time series with unevenly spaced observations. Can I use LSTM for the time series data like that. Need I transform my data into equally spaced time series data?
Thank you
Here is a paper on successful use of lstm models for time series prediction:
“We deploy LSTM networks for predicting out-of-sample directional movements for the
constituent stocks of the S&P 500 from 1992 until 2015. With daily returns of 0.46 percent and
a Sharpe Ratio of 5.8 prior to transaction costs, we find LSTM networks to outperform memory
free classification methods, i.e., a random forest (RAF), a deep neural net (DNN), and a logistic
regression classifier (LOG).”
I’ve got a question about stationarity: let’s say I’ve made seasonal & trend adjustment for my time series input, scaled it and then passed this data to some NN model (e.g., LSTM or windowed-MLP), how do I add seasonal & trend components to the final answer?
I have numerous (m), multivariate time-series (and they are of different lengths). My goal is to be able to forecast multiple-steps for a new time-series based on the previous m time-series. Can you suggest how I should approach the problem?
Hello,
Thank you so much for your posts. I wonder if I can ask you a couple of questions..
I
have seen many tutorial trying to forecast the next value given the previous value. What if I want to predict the numbers of syntax errors that a person commits while writing a word in english?
The word is a sequence of character and can have various lenght. The prediction is an integer value from zero to the length of the word. But can be set to a max lenght limit, i guess.
Would be an good example for lstm?
I believe that a combination of certain characters makes the word more difficult to spell, therefore if the network can remember the order of the character would perform better? So in this case Lstm is preferable than MLP?
If so, should i use a regression lstm and not a classification Lstm?
Perhaps you could output the same sequence with corrections?
Perhaps you could output each error detected as it is detected?
Perhaps you could output the index of errors detected?
…
This is specific to the problem you want to solve, you will need to use trial and error with different framings of the problem in order to discover what works well.
many thanks for the many and varied tutorials that you have provided here.
I am a little confused as what exactly is meant by “windowed MLP”: is this achieved by incorporating previous observations into the current observation, as described e.g. here.
Hi Jasan! Your site has been the No.1 portal for me to help myself dive into DL scene! Much obliged for disclosing such huge amount of engineering or practical usages of DL and Keras! I’m a post graduate and doing Electricity Disaggregation stuffs(Disaggregate the mixed electricity power consumption time-series data of several appliance into the respective appliance-wise power data). I’m taking some techniques from your time-series prediction tutorials, like using some time distributed cnn layers and lstm layers. I’m just starting off and knowing not much of sophisticated DL network combining patterns. Would you please share some of your suggestions or opinions on my project? Should I borrow some knowledge or use cases of NLP scene? Thank you again.
I have seen great results with CNNs and CNN-LSTMs for time series problems. If focus on these areas in my new book “deep learning for time series forecasting”.
Thanks for this great post. Suppose we are given a noisy signal x of length 100. We also know that every 10 timesteps the signal is not contaminated by noise, i.e x(1), x(10), x(20),…,x(100) are all clean datapoint that we wish to preserve. Our goal now is to denoise the input signal while promoting the output of LSTM to produce the same value as in the input every 10 steps. Is there a way to do something like that?
Hello Jason,
After getting my results from comparing MLPs and LSTMs on a data, I came to the conclusion that MLPs are much more efficient than LSTMs, when using constant number of lags (let’s say 7 days before) to predict 4 days ahead. Would You create a tutorial on using LSTMs with dynamic lag time?
Thanks.
Is it possible that LSTM fail to predict over a certain threshold for a dataset? I am working on a time series dataset, and I have varied number of time steps in each sample and the network complexity, but no matter what I do, the accuracy does not increase. The RMSE is stuck between a range of (+0.1,-0.1)
Perhaps first evaluate a naive method, then linear methods, MLPs, etc. to determine if the LSTM is skillful. It is possible that a new architecture, new data prep or perhaps new model is required.
Jason ! Thanks so much for being a mentor to so many ! I’ve bought your book ” Deep learning for time series”…really great !!
Onto my question…?
I’m very unsure what LSTMs prefer…do LSTMs prefer a windowed lagged time-series input, like windowed MLP’s ? or is there some other better strategy ?
I’m predicting solar power output (y) for the next 6 hours in advance. I’m using a sliding window approach (with multivariate input – temp. irradiance, wind speed) but i’m not getting close to Feed Forward MLP results…
So, I’m thinking a windowed approach might be totally wrong ?? I’ve played with multiple lagged window sizes. Yet, the FFNN prevails with simply 6hour lagged window…Basically do LSTMs prefer some sort of dynamically expanding input window or in your experience anything else other than fixed lagged sliding windows ?
(Data set: 400,000 data points, 4 years, 5min resolution – so very large)
hey Jason, Love your work man. It’s accelerated my progress by 10X. I couldn’t figure out why the LSTMs were doing a poor job with my AR data sets. It was great to find this article–prior to that I thought I was screwing up my code with the LSTM.
Eventually I found that (as mentioned above) after transforming to stationarity and seasonally adjusting as well I was able to get great results with a traditional Unobserved Components Model applied to the transformed data.
Hi Jason. I was wondering if I can only use a vanilla LSTM to do feature extraction.
For example, I have time series data such as bicycle routes and I want to use a many2one LSTM to output a feature vector at the last time step. This feature vector will be combined with other features and fed into a DNN. Will this approach work?
Hi Jason,
Thank you for all of your tutorial, I am a big fan of your work.
I am wondering if you have any advice regarding predicting Random walk data such as Wind speed.
I have been trying several algorithms, AR, ARMA, ARIMA, SARIMA, ANN, KNN, ANN. and all resulted in previous time step is the best predictor. it is a tough task to guess the next value relying only on historical data.
Thanks in advance
Hi Jason,
I find your posts extremely useful!
Thank you so much.
I tried to use LSTM to predict a time-series the way you posted but my challenge is when I fit the model to training data once and use for prediction the future t + x my result is not much different than fitting to initial training data and then re-fitting (updating) the model with new test data, one at a time.
I’d expect the algorithm to learn from new test points and adjust its predictions to fit the data better but I don’t see much difference.
I suspected the issue is that LSTM is only predicting the differenced, scaled “stationarized” data and does not learn about it’s non-stationary component which causes the gap between the final predictions and the actual data.
So to fix this, I removed the differencing step in data preparation and the reverse differencing in the final step and expected that since LSTM can work well for non-stationary data, I should see reasonable output but in this case the predictions have a large gap with the actual test data!
I had a problem with univariate time series that had a lot of randomness and was non-stationary, but I implemented a stacked LSTM with one layer and it performs good. I just wander how LSTM are capable of forecasting to more than one future lag, if we want to have 10 or 20 lags prediction in the future. SARIMAX model is capable of achieving so, but with expectedly poorly results in contrast to one-lag prediction.
Forgot to mention, big fan of your simple, didactic step by step approach. This approach could be manifested only by people with deep and full understanding of the problems.
Jason,
Do you have any recommendations/posts to example implementations of LSTM for time series prediction?
Yes, many posts. Please use the search feature.
Hi Jason, would it be appropriate to fit LSTM when there are somewhere between 240-260 data points?
Perhaps, try it and see.
Thank you for this informative article. While I have not trained any LSTM RNNs on my time series data, I’ve found that plain jane feed forward DNNs that are feature engineered correctly and use sliding window CV predicts OOS as expected. Essentially, it is not necessary for my data to have to mess with LSTMs at all. And my features aren’t all iid…
I suppose this illustrates the versatility of DNNs.
I generally agree Phillip.
MLPs with a window do very well on small time series forecasting problems.
hi,
but how do you define a “small” time series forecasting problem?
Perhaps hundreds to thousands of observations, perhaps one variate.
I agree that along with MLP’s , LSTM’s have an advantage over more classical statistical approaches like ARIMA : they can fit non-linear functions and moreover , you do not need to specify the type of non-linearity . There also lies the danger : regularisation is absolutely crucial to avoid overfitting .
I still hold on to my position that a lot of very interesting time series will never be cracked by any approach that only looks at past data points to forecast the next : prices are set where demand meets supply and both supply and demand care nothing about yesterday’s price .
Great points Gerrit.
I found that for the problem I’m working on (forecasting streamflow based on hydrometric station water level measurements), to my surprise, first differencing of the signal prior to LSTM worsened the results. Overall, I find that I can’t improve over a persistence model with LSTM or an MLP using a moving window. Not sure what to try next… (same problem with ARIMA)
Interesting finding.
This general list of things to try may give you some ideas:
https://machinelearningmastery.com/machine-learning-performance-improvement-cheat-sheet/
Thanks! I’ve covered all of the items on the list with the exception of using more data and reframing of the problem.
Just received more data, so that’s the first to try.
Great!
@Jay: I just started to work on a similar problem in the hydrometric field. Would please contact me through our company website at https://www.sobos.at
Great discussion,
LSTMs are much newer/younger to solve /simpler/ AR problems – most industries have already been studying and improving custom models applied on such tasks for decades. I believe RNNs shine for multivariate time series forecasts, that have been simply too difficult to model until now. Similarly with MLPs and multivariate time series models where the different features can have different forecasting powers(ie the sentiment of twitter posts can have influence for a day or two, while ny times articles could have a much longer lasting influence).
You may be right Atanas.
Why use data hungry algorithm like lstm when similar results can be obtained using a machine learning or time series methods?
Great question, the hope is that LSTMs can do things other methods cannot:
https://machinelearningmastery.com/promise-recurrent-neural-networks-time-series-forecasting/
If this is not the case on your problem, it is the wrong tool for the job.
how to work on many to one time series using LSTM?Any link with example code
See here:
https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/
how to work on multiple seasonality data with lstm?
Perhaps try seasonal adjusting the data prior to modeling.
so can i use many to one here?or say differing time steps?
Try it and see.
what do you mean by seasonal adjustment?if i have monthly and annually seasonality?i have taken monthly size for taking care of monthly effect.For annual part if i take it then how to merge both approaches and get a single output?
Seasonal adjustment means modeling and removing the seasonal element from the data.
Here’s how:
https://machinelearningmastery.com/time-series-seasonality-with-python/
I am not able to grab the concept of batches in lstm.please guide me
After n samples in the batch, the model weights are updated. One epoch is comprised of 1 or more batches based on the configured batch size.
Hi Ph.D Jason,
I have multivariate time series with unevenly spaced observations. Can I use LSTM for the time series data like that. Need I transform my data into equally spaced time series data?
Thank you
Perhaps try as-is and resampled and compare model performance.
Here is a paper on successful use of lstm models for time series prediction:
“We deploy LSTM networks for predicting out-of-sample directional movements for the
constituent stocks of the S&P 500 from 1992 until 2015. With daily returns of 0.46 percent and
a Sharpe Ratio of 5.8 prior to transaction costs, we find LSTM networks to outperform memory
free classification methods, i.e., a random forest (RAF), a deep neural net (DNN), and a logistic
regression classifier (LOG).”
https://www.econstor.eu/bitstream/10419/157808/1/886576210.pdf
Thanks for sharing Chris.
I think to comsider a problem as time series the data should have same interval of time.Iam not sure about it
Time series must have observations over time, a time dependence to the obs.
The paper referenced in this article is from 2001, could the arguments be dated?
Perhaps.
I have not seen any good results for a straight LSTM on time series and many personal experiments have confirmed these findings.
MLPs, even linear models will kill an LSTM on time series forecasting.
I’ve got a question about stationarity: let’s say I’ve made seasonal & trend adjustment for my time series input, scaled it and then passed this data to some NN model (e.g., LSTM or windowed-MLP), how do I add seasonal & trend components to the final answer?
I tried to google it but found nothing.
Thanks!
If you use differencing, then invert the differencing on the prediction.
I have a few examples on the blog.
Hi Jason,
I have numerous (m), multivariate time-series (and they are of different lengths). My goal is to be able to forecast multiple-steps for a new time-series based on the previous m time-series. Can you suggest how I should approach the problem?
Thanks!
Try a suite of different algorithms and see what works best for your specific dataset.
Really nice article, thank you!
Thanks.
Hello,
Thank you so much for your posts. I wonder if I can ask you a couple of questions..
I
have seen many tutorial trying to forecast the next value given the previous value. What if I want to predict the numbers of syntax errors that a person commits while writing a word in english?
The word is a sequence of character and can have various lenght. The prediction is an integer value from zero to the length of the word. But can be set to a max lenght limit, i guess.
Would be an good example for lstm?
I believe that a combination of certain characters makes the word more difficult to spell, therefore if the network can remember the order of the character would perform better? So in this case Lstm is preferable than MLP?
If so, should i use a regression lstm and not a classification Lstm?
Do you cover this things on your book?
Thank you!!!!!
Guido
Explore many framings of the problem.
Perhaps you could output the same sequence with corrections?
Perhaps you could output each error detected as it is detected?
Perhaps you could output the index of errors detected?
…
This is specific to the problem you want to solve, you will need to use trial and error with different framings of the problem in order to discover what works well.
Is it possible to apply LSTM for multiple seasonality
You can try, perhaps try an CNN first, then a CNN-LSTM. A straight LSTM often performs poorly on time series problems.
Hallo Jason,
many thanks for the many and varied tutorials that you have provided here.
I am a little confused as what exactly is meant by “windowed MLP”: is this achieved by incorporating previous observations into the current observation, as described e.g. here.
https://machinelearningmastery.com/time-series-forecasting-supervised-learning/
or are you referring to something else?
Thanks, Andrew
Correct. Window means a fixed set of lag observations used as input.
Hi Jasan! Your site has been the No.1 portal for me to help myself dive into DL scene! Much obliged for disclosing such huge amount of engineering or practical usages of DL and Keras! I’m a post graduate and doing Electricity Disaggregation stuffs(Disaggregate the mixed electricity power consumption time-series data of several appliance into the respective appliance-wise power data). I’m taking some techniques from your time-series prediction tutorials, like using some time distributed cnn layers and lstm layers. I’m just starting off and knowing not much of sophisticated DL network combining patterns. Would you please share some of your suggestions or opinions on my project? Should I borrow some knowledge or use cases of NLP scene? Thank you again.
I have seen great results with CNNs and CNN-LSTMs for time series problems. If focus on these areas in my new book “deep learning for time series forecasting”.
send me link sir it is downloadable or not
i need this book
[email protected]
Sure, you can start here:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
An autoregression (AR) approach was used to model these problems.
Is there any other way to deal with these problem except AR?
Yes, but you must get creative. E.g. model residuals, direct models, etc.
Thanks for this great post. Suppose we are given a noisy signal x of length 100. We also know that every 10 timesteps the signal is not contaminated by noise, i.e x(1), x(10), x(20),…,x(100) are all clean datapoint that we wish to preserve. Our goal now is to denoise the input signal while promoting the output of LSTM to produce the same value as in the input every 10 steps. Is there a way to do something like that?
Yes, you can fit a model, e.g. an autoencoder on how to denoise the signal. Perhaps start here:
https://machinelearningmastery.com/lstm-autoencoders/
Hello Jason,
After getting my results from comparing MLPs and LSTMs on a data, I came to the conclusion that MLPs are much more efficient than LSTMs, when using constant number of lags (let’s say 7 days before) to predict 4 days ahead. Would You create a tutorial on using LSTMs with dynamic lag time?
Thanks.
Thanks for the suggestion.
Almost all of my LSTM examples vectorize variable length input with zero padding.
Hi Jason,
Is it possible that LSTM fail to predict over a certain threshold for a dataset? I am working on a time series dataset, and I have varied number of time steps in each sample and the network complexity, but no matter what I do, the accuracy does not increase. The RMSE is stuck between a range of (+0.1,-0.1)
Perhaps first evaluate a naive method, then linear methods, MLPs, etc. to determine if the LSTM is skillful. It is possible that a new architecture, new data prep or perhaps new model is required.
Thanks a lot. I will try your suggestions.
Let me know how you go.
Jason ! Thanks so much for being a mentor to so many ! I’ve bought your book ” Deep learning for time series”…really great !!
Onto my question…?
I’m very unsure what LSTMs prefer…do LSTMs prefer a windowed lagged time-series input, like windowed MLP’s ? or is there some other better strategy ?
I’m predicting solar power output (y) for the next 6 hours in advance. I’m using a sliding window approach (with multivariate input – temp. irradiance, wind speed) but i’m not getting close to Feed Forward MLP results…
So, I’m thinking a windowed approach might be totally wrong ?? I’ve played with multiple lagged window sizes. Yet, the FFNN prevails with simply 6hour lagged window…Basically do LSTMs prefer some sort of dynamically expanding input window or in your experience anything else other than fixed lagged sliding windows ?
(Data set: 400,000 data points, 4 years, 5min resolution – so very large)
Any reply will be fantastic !!
Thanks for your support!
LSTMs take time steps as input, which you can think of as a window. But they process it step by step, not all at once like an MLP.
LSTMs are pretty poor at time series generally. Also, they can be hard to tune. Try many different configs and keep an eye on the learning curve.
This might help:
https://machinelearningmastery.com/start-here/#deep_learning_time_series
hey Jason, Love your work man. It’s accelerated my progress by 10X. I couldn’t figure out why the LSTMs were doing a poor job with my AR data sets. It was great to find this article–prior to that I thought I was screwing up my code with the LSTM.
Eventually I found that (as mentioned above) after transforming to stationarity and seasonally adjusting as well I was able to get great results with a traditional Unobserved Components Model applied to the transformed data.
Thanks!
Well done.
Hey, Jason. Thanks for your detailed tutorial.
Where could I find a reference on MLPs with a window?
Thank you!
This will show you how:
https://machinelearningmastery.com/how-to-develop-multilayer-perceptron-models-for-time-series-forecasting/
Thank you very much!
You’re welcome.
Hi Jason. I was wondering if I can only use a vanilla LSTM to do feature extraction.
For example, I have time series data such as bicycle routes and I want to use a many2one LSTM to output a feature vector at the last time step. This feature vector will be combined with other features and fed into a DNN. Will this approach work?
Thank you.
Perhaps try it and see.
Many thanks!
Hi Jason,
Thank you for all of your tutorial, I am a big fan of your work.
I am wondering if you have any advice regarding predicting Random walk data such as Wind speed.
I have been trying several algorithms, AR, ARMA, ARIMA, SARIMA, ANN, KNN, ANN. and all resulted in previous time step is the best predictor. it is a tough task to guess the next value relying only on historical data.
Thanks in advance
The best we can do for a random walk is use a persistence model.
Hi Dr. Jason
When implementing the LSTM algorithm, should structural risk be verified?
Thanks in advance for help.
What is “structural risk”?
Structural risk is the instability of the classification method with the new test data.
Sounds like you are describing model variance.
It is a good thing to quantify, and an easy thing to correct for using an ensemble of final models.
But in my point of view the LSTM problem is the vanishing gradient problem, not the structural risk problem. What is your opinion?.
Neural networks are a stochastic learning problem, they all suffer variance in the final model. You can learn more here:
https://machinelearningmastery.com/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
This is very diffrent from vanishing gradients:
https://machinelearningmastery.com/how-to-fix-vanishing-gradients-using-the-rectified-linear-activation-function/
Thank you very much
You’re welcome.
Hi Jason,
I find your posts extremely useful!
Thank you so much.
I tried to use LSTM to predict a time-series the way you posted but my challenge is when I fit the model to training data once and use for prediction the future t + x my result is not much different than fitting to initial training data and then re-fitting (updating) the model with new test data, one at a time.
I’d expect the algorithm to learn from new test points and adjust its predictions to fit the data better but I don’t see much difference.
I suspected the issue is that LSTM is only predicting the differenced, scaled “stationarized” data and does not learn about it’s non-stationary component which causes the gap between the final predictions and the actual data.
So to fix this, I removed the differencing step in data preparation and the reverse differencing in the final step and expected that since LSTM can work well for non-stationary data, I should see reasonable output but in this case the predictions have a large gap with the actual test data!
Nice work!
I had a problem with univariate time series that had a lot of randomness and was non-stationary, but I implemented a stacked LSTM with one layer and it performs good. I just wander how LSTM are capable of forecasting to more than one future lag, if we want to have 10 or 20 lags prediction in the future. SARIMAX model is capable of achieving so, but with expectedly poorly results in contrast to one-lag prediction.
Well done!
Yes, it is called multi-step forecasting, this can help:
https://machinelearningmastery.com/faq/single-faq/how-do-you-use-lstms-for-multi-step-time-series-forecasting
Forgot to mention, big fan of your simple, didactic step by step approach. This approach could be manifested only by people with deep and full understanding of the problems.
Thanks!