Classification predictive modeling involves predicting a class label for examples, although some problems require the prediction of a probability of class membership.
For these problems, the crisp class labels are not required, and instead, the likelihood that each example belonging to each class is required and later interpreted. As such, small relative probabilities can carry a lot of meaning and specialized metrics are required to quantify the predicted probabilities.
In this tutorial, you will discover metrics for evaluating probabilistic predictions for imbalanced classification.
After completing this tutorial, you will know:
- Probability predictions are required for some classification predictive modeling problems.
- Log loss quantifies the average difference between predicted and expected probability distributions.
- Brier score quantifies the average difference between predicted and expected probabilities.
Kick-start your project with my new book Imbalanced Classification with Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

A Gentle Introduction to Probability Metrics for Imbalanced Classification
Photo by a4gpa, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Probability Metrics
- Log Loss for Imbalanced Classification
- Brier Score for Imbalanced Classification
Probability Metrics
Classification predictive modeling involves predicting a class label for an example.
On some problems, a crisp class label is not required, and instead a probability of class membership is preferred. The probability summarizes the likelihood (or uncertainty) of an example belonging to each class label. Probabilities are more nuanced and can be interpreted by a human operator or a system in decision making.
Probability metrics are those specifically designed to quantify the skill of a classifier model using the predicted probabilities instead of crisp class labels. They are typically scores that provide a single value that can be used to compare different models based on how well the predicted probabilities match the expected class probabilities.
In practice, a dataset will not have target probabilities. Instead, it will have class labels.
For example, a two-class (binary) classification problem will have the class labels 0 for the negative case and 1 for the positive case. When an example has the class label 0, then the probability of the class labels 0 and 1 will be 1 and 0 respectively. When an example has the class label 1, then the probability of class labels 0 and 1 will be 0 and 1 respectively.
- Example with Class=0: P(class=0) = 1, P(class=1) = 0
- Example with Class=1: P(class=0) = 0, P(class=1) = 1
We can see how this would scale to three classes or more; for example:
- Example with Class=0: P(class=0) = 1, P(class=1) = 0, P(class=2) = 0
- Example with Class=1: P(class=0) = 0, P(class=1) = 1, P(class=2) = 0
- Example with Class=2: P(class=0) = 0, P(class=1) = 0, P(class=2) = 1
In the case of binary classification problems, this representation can be simplified to just focus on the positive class.
That is, we only require the probability of an example belonging to class 1 to represent the probabilities for binary classification (the so-called Bernoulli distribution); for example:
- Example with Class=0: P(class=1) = 0
- Example with Class=1: P(class=1) = 1
Probability metrics will summarize how well the predicted distribution of class membership matches the known class probability distribution.
This focus on predicted probabilities may mean that the crisp class labels predicted by a model are ignored. This focus may mean that a model that predicts probabilities may appear to have terrible performance when evaluated according to its crisp class labels, such as using accuracy or a similar score. This is because although the predicted probabilities may show skill, they must be interpreted with an appropriate threshold prior to being converted into crisp class labels.
Additionally, the focus on predicted probabilities may also require that the probabilities predicted by some nonlinear models to be calibrated prior to being used or evaluated. Some models will learn calibrated probabilities as part of the training process (e.g. logistic regression), but many will not and will require calibration (e.g. support vector machines, decision trees, and neural networks).
A given probability metric is typically calculated for each example, then averaged across all examples in the training dataset.
There are two popular metrics for evaluating predicted probabilities; they are:
- Log Loss
- Brier Score
Let’s take a closer look at each in turn.
Want to Get Started With Imbalance Classification?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Log Loss for Imbalanced Classification
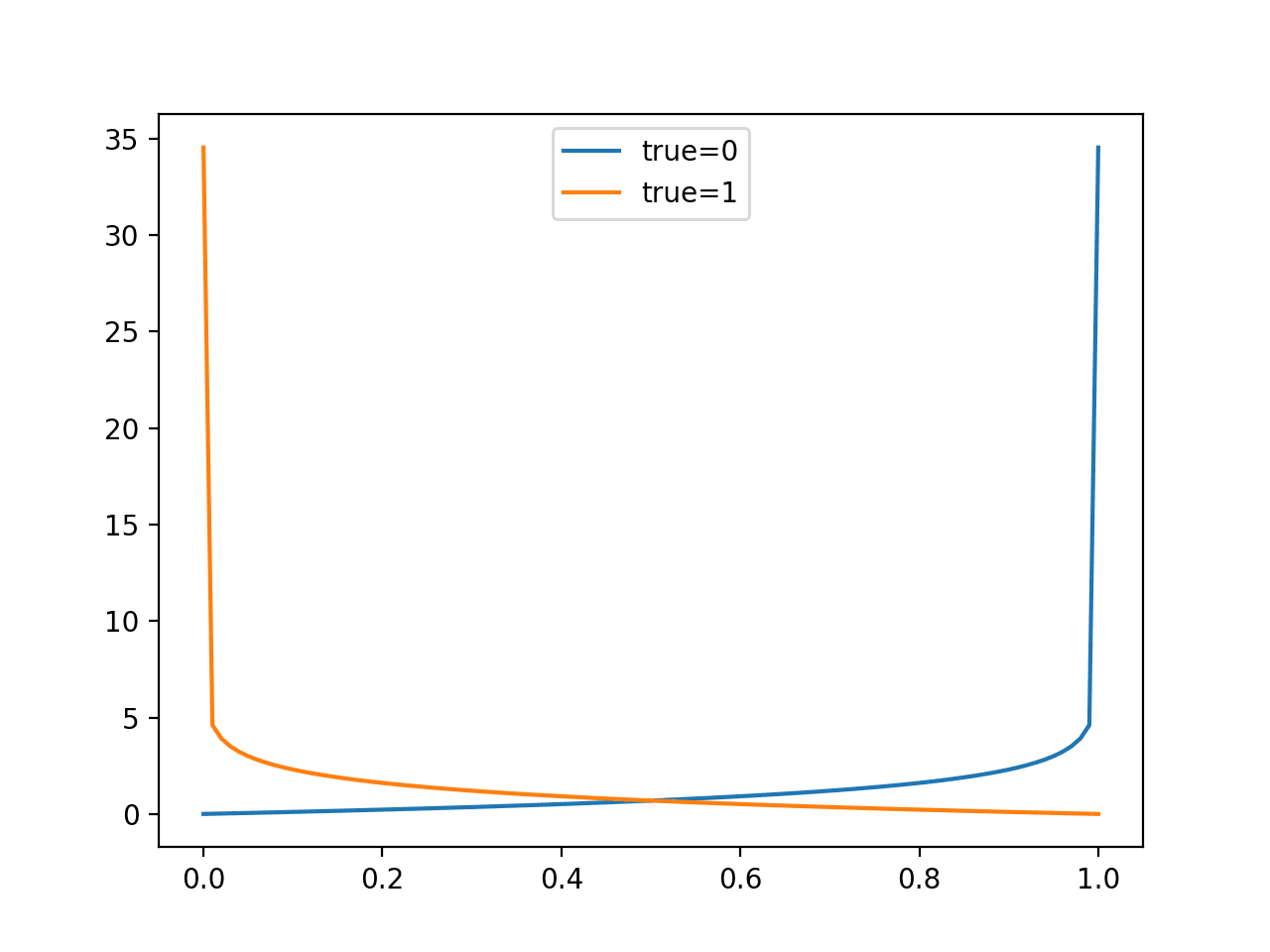
Logarithmic loss or log loss for short is a loss function known for training the logistic regression classification algorithm.
The log loss function calculates the negative log likelihood for probability predictions made by the binary classification model. Most notably, this is logistic regression, but this function can be used by other models, such as neural networks, and is known by other names, such as cross-entropy.
Generally, the log loss can be calculated using the expected probabilities for each class and the natural logarithm of the predicted probabilities for each class; for example:
- LogLoss = -(P(class=0) * log(P(class=0)) + (P(class=1)) * log(P(class=1)))
The best possible log loss is 0.0, and values are positive to infinite for progressively worse scores.
If you are just predicting the probability for the positive class, then the log loss function can be calculated for one binary classification prediction (yhat) compared to the expected probability (y) as follows:
- LogLoss = -((1 – y) * log(1 – yhat) + y * log(yhat))
For example, if the expected probability was 1.0 and the model predicted 0.8, the log loss would be:
- LogLoss = -((1 – y) * log(1 – yhat) + y * log(yhat))
- LogLoss = -((1 – 1.0) * log(1 – 0.8) + 1.0 * log(0.8))
- LogLoss = -(-0.0 + -0.223)
- LogLoss = 0.223
This calculation can be scaled up for multiple classes by adding additional terms; for example:
- LogLoss = -( sum c in C y_c * log(yhat_c))
This generalization is also known as cross-entropy and calculates the number of bits (if log base-2 is used) or nats (if log base-e is used) by which two probability distributions differ.
Specifically, it builds upon the idea of entropy from information theory and calculates the average number of bits required to represent or transmit an event from one distribution compared to the other distribution.
… the cross entropy is the average number of bits needed to encode data coming from a source with distribution p when we use model q …
— Page 57, Machine Learning: A Probabilistic Perspective, 2012.
The intuition for this definition comes if we consider a target or underlying probability distribution P and an approximation of the target distribution Q, then the cross-entropy of Q from P is the number of additional bits to represent an event using Q instead of P.
We will stick with log loss for now, as it is the term most commonly used when using this calculation as an evaluation metric for classifier models.
When calculating the log loss for a set of predictions compared to a set of expected probabilities in a test dataset, the average of the log loss across all samples is calculated and reported; for example:
- AverageLogLoss = 1/N * sum i in N -((1 – y) * log(1 – yhat) + y * log(yhat))
The average log loss for a set of predictions on a training dataset is often simply referred to as the log loss.
We can demonstrate calculating log loss with a worked example.
First, let’s define a synthetic binary classification dataset. We will use the make_classification() function to create 1,000 examples, with 99%/1% split for the two classes. The complete example of creating and summarizing the dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# create an imbalanced dataset from numpy import unique from sklearn.datasets import make_classification # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=[0.99], flip_y=0, random_state=1) # summarize dataset classes = unique(y) total = len(y) for c in classes: n_examples = len(y[y==c]) percent = n_examples / total * 100 print('> Class=%d : %d/%d (%.1f%%)' % (c, n_examples, total, percent)) |
Running the example creates the dataset and reports the distribution of examples in each class.
|
1 2 |
> Class=0 : 990/1000 (99.0%) > Class=1 : 10/1000 (1.0%) |
Next, we will develop an intuition for naive predictions of probabilities.
A naive prediction strategy would be to predict certainty for the majority class, or P(class=0) = 1. An alternative strategy would be to predict the minority class, or P(class=1) = 1.
Log loss can be calculated using the log_loss() scikit-learn function. It takes the probability for each class as input and returns the average log loss. Specifically, each example must have a prediction with one probability per class, meaning a prediction for one example for a binary classification problem must have a probability for class 0 and class 1.
Therefore, predicting certain probabilities for class 0 for all examples would be implemented as follows:
|
1 2 3 4 5 |
... # no skill prediction 0 probabilities = [[1, 0] for _ in range(len(testy))] avg_logloss = log_loss(testy, probabilities) print('P(class0=1): Log Loss=%.3f' % (avg_logloss)) |
We can do the same thing for P(class1)=1.
These two strategies are expected to perform terribly.
A better naive strategy would be to predict the class distribution for each example. For example, because our dataset has a 99%/1% class distribution for the majority and minority classes, this distribution can be “predicted” for each example to give a baseline for probability predictions.
|
1 2 3 4 5 |
... # baseline probabilities probabilities = [[0.99, 0.01] for _ in range(len(testy))] avg_logloss = log_loss(testy, probabilities) print('Baseline: Log Loss=%.3f' % (avg_logloss)) |
Finally, we can also calculate the log loss for perfectly predicted probabilities by taking the target values for the test set as predictions.
|
1 2 3 4 |
... # perfect probabilities avg_logloss = log_loss(testy, testy) print('Perfect: Log Loss=%.3f' % (avg_logloss)) |
Tying this all together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# log loss for naive probability predictions. from numpy import mean from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import log_loss # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=[0.99], flip_y=0, random_state=1) # split into train/test sets with same class ratio trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y) # no skill prediction 0 probabilities = [[1, 0] for _ in range(len(testy))] avg_logloss = log_loss(testy, probabilities) print('P(class0=1): Log Loss=%.3f' % (avg_logloss)) # no skill prediction 1 probabilities = [[0, 1] for _ in range(len(testy))] avg_logloss = log_loss(testy, probabilities) print('P(class1=1): Log Loss=%.3f' % (avg_logloss)) # baseline probabilities probabilities = [[0.99, 0.01] for _ in range(len(testy))] avg_logloss = log_loss(testy, probabilities) print('Baseline: Log Loss=%.3f' % (avg_logloss)) # perfect probabilities avg_logloss = log_loss(testy, testy) print('Perfect: Log Loss=%.3f' % (avg_logloss)) |
Running the example reports the log loss for each naive strategy.
As expected, predicting certainty for each class label is punished with large log loss scores, with the case of being certain for the minority class in all cases resulting in a much larger score.
We can see that predicting the distribution of examples in the dataset as the baseline results in a better score than either of the other naive measures. This baseline represents the no skill classifier and log loss scores below this strategy represent a model that has some skill.
Finally, we can see that a log loss for perfectly predicted probabilities is 0.0, indicating no difference between actual and predicted probability distributions.
|
1 2 3 4 |
P(class0=1): Log Loss=0.345 P(class1=1): Log Loss=34.193 Baseline: Log Loss=0.056 Perfect: Log Loss=0.000 |
Now that we are familiar with log loss, let’s take a look at the Brier score.
Brier Score for Imbalanced Classification
The Brier score, named for Glenn Brier, calculates the mean squared error between predicted probabilities and the expected values.
The score summarizes the magnitude of the error in the probability forecasts and is designed for binary classification problems. It is focused on evaluating the probabilities for the positive class. Nevertheless, it can be adapted for problems with multiple classes.
As such, it is an appropriate probabilistic metric for imbalanced classification problems.
The evaluation of probabilistic scores is generally performed by means of the Brier Score. The basic idea is to compute the mean squared error (MSE) between predicted probability scores and the true class indicator, where the positive class is coded as 1, and negative class 0.
— Page 57, Learning from Imbalanced Data Sets, 2018.
The error score is always between 0.0 and 1.0, where a model with perfect skill has a score of 0.0.
The Brier score can be calculated for positive predicted probabilities (yhat) compared to the expected probabilities (y) as follows:
- BrierScore = 1/N * Sum i to N (yhat_i – y_i)^2
For example, if a predicted positive class probability is 0.8 and the expected probability is 1.0, then the Brier score is calculated as:
- BrierScore = (yhat_i – y_i)^2
- BrierScore = (0.8 – 1.0)^2
- BrierScore = 0.04
We can demonstrate calculating Brier score with a worked example using the same dataset and naive predictive models as were used in the previous section.
The Brier score can be calculated using the brier_score_loss() scikit-learn function. It takes the probabilities for the positive class only, and returns an average score.
As in the previous section, we can evaluate naive strategies of predicting the certainty for each class label. In this case, as the score only considered the probability for the positive class, this will involve predicting 0.0 for P(class=1)=0 and 1.0 for P(class=1)=1. For example:
|
1 2 3 4 5 6 7 8 9 |
... # no skill prediction 0 probabilities = [0.0 for _ in range(len(testy))] avg_brier = brier_score_loss(testy, probabilities) print('P(class1=0): Brier Score=%.4f' % (avg_brier)) # no skill prediction 1 probabilities = [1.0 for _ in range(len(testy))] avg_brier = brier_score_loss(testy, probabilities) print('P(class1=1): Brier Score=%.4f' % (avg_brier)) |
We can also test the no skill classifier that predicts the ratio of positive examples in the dataset, which in this case is 1 percent or 0.01.
|
1 2 3 4 5 |
... # baseline probabilities probabilities = [0.01 for _ in range(len(testy))] avg_brier = brier_score_loss(testy, probabilities) print('Baseline: Brier Score=%.4f' % (avg_brier)) |
Finally, we can also confirm the Brier score for perfectly predicted probabilities.
|
1 2 3 4 |
... # perfect probabilities avg_brier = brier_score_loss(testy, testy) print('Perfect: Brier Score=%.4f' % (avg_brier)) |
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# brier score for naive probability predictions. from numpy import mean from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import brier_score_loss # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=[0.99], flip_y=0, random_state=1) # split into train/test sets with same class ratio trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y) # no skill prediction 0 probabilities = [0.0 for _ in range(len(testy))] avg_brier = brier_score_loss(testy, probabilities) print('P(class1=0): Brier Score=%.4f' % (avg_brier)) # no skill prediction 1 probabilities = [1.0 for _ in range(len(testy))] avg_brier = brier_score_loss(testy, probabilities) print('P(class1=1): Brier Score=%.4f' % (avg_brier)) # baseline probabilities probabilities = [0.01 for _ in range(len(testy))] avg_brier = brier_score_loss(testy, probabilities) print('Baseline: Brier Score=%.4f' % (avg_brier)) # perfect probabilities avg_brier = brier_score_loss(testy, testy) print('Perfect: Brier Score=%.4f' % (avg_brier)) |
Running the example, we can see the scores for the naive models and the baseline no skill classifier.
As we might expect, we can see that predicting a 0.0 for all examples results in a low score, as the mean squared error between all 0.0 predictions and mostly 0 classes in the test set results in a small value. Conversely, the error between 1.0 predictions and mostly 0 class values results in a larger error score.
Importantly, we can see that the default no skill classifier results in a lower score than predicting all 0.0 values. Again, this represents the baseline score, below which models will demonstrate skill.
|
1 2 3 4 |
P(class1=0): Brier Score=0.0100 P(class1=1): Brier Score=0.9900 Baseline: Brier Score=0.0099 Perfect: Brier Score=0.0000 |
The Brier scores can become very small and the focus will be on fractions well below the decimal point. For example, the difference in the above example between Baseline and Perfect scores is slight at four decimal places.
A common practice is to transform the score using a reference score, such as the no skill classifier. This is called a Brier Skill Score, or BSS, and is calculated as follows:
- BrierSkillScore = 1 – (BrierScore / BrierScore_ref)
We can see that if the reference score was evaluated, it would result in a BSS of 0.0. This represents a no skill prediction. Values below this will be negative and represent worse than no skill. Values above 0.0 represent skillful predictions with a perfect prediction value of 1.0.
We can demonstrate this by developing a function to calculate the Brier skill score listed below.
|
1 2 3 4 5 6 |
# calculate the brier skill score def brier_skill_score(y, yhat, brier_ref): # calculate the brier score bs = brier_score_loss(y, yhat) # calculate skill score return 1.0 - (bs / brier_ref) |
We can then calculate the BSS for each of the naive forecasts, as well as for a perfect prediction.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# brier skill score for naive probability predictions. from numpy import mean from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import brier_score_loss # calculate the brier skill score def brier_skill_score(y, yhat, brier_ref): # calculate the brier score bs = brier_score_loss(y, yhat) # calculate skill score return 1.0 - (bs / brier_ref) # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=[0.99], flip_y=0, random_state=1) # split into train/test sets with same class ratio trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2, stratify=y) # calculate reference probabilities = [0.01 for _ in range(len(testy))] brier_ref = brier_score_loss(testy, probabilities) print('Reference: Brier Score=%.4f' % (brier_ref)) # no skill prediction 0 probabilities = [0.0 for _ in range(len(testy))] bss = brier_skill_score(testy, probabilities, brier_ref) print('P(class1=0): BSS=%.4f' % (bss)) # no skill prediction 1 probabilities = [1.0 for _ in range(len(testy))] bss = brier_skill_score(testy, probabilities, brier_ref) print('P(class1=1): BSS=%.4f' % (bss)) # baseline probabilities probabilities = [0.01 for _ in range(len(testy))] bss = brier_skill_score(testy, probabilities, brier_ref) print('Baseline: BSS=%.4f' % (bss)) # perfect probabilities bss = brier_skill_score(testy, testy, brier_ref) print('Perfect: BSS=%.4f' % (bss)) |
Running the example first calculates the reference Brier score used in the BSS calculation.
We can then see that predicting certainty scores for each class results in a negative BSS score, indicating that they are worse than no skill. Finally, we can see that evaluating the reference forecast itself results in 0.0, indicating no skill and evaluating the true values as predictions results in a perfect score of 1.0.
As such, the Brier Skill Score is a best practice for evaluating probability predictions and is widely used where probability classification prediction are evaluated routinely, such as in weather forecasts (e.g. rain or not).
|
1 2 3 4 5 |
Reference: Brier Score=0.0099 P(class1=0): BSS=-0.0101 P(class1=1): BSS=-99.0000 Baseline: BSS=0.0000 Perfect: BSS=1.0000 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
- A Gentle Introduction to Probability Scoring Methods in Python
- A Gentle Introduction to Cross-Entropy for Machine Learning
- A Gentle Introduction to Logistic Regression With Maximum Likelihood Estimation
Books
- Chapter 8 Assessment Metrics For Imbalanced Learning, Imbalanced Learning: Foundations, Algorithms, and Applications, 2013.
- Chapter 3 Performance Measures, Learning from Imbalanced Data Sets, 2018.
API
- sklearn.datasets.make_classification API.
- sklearn.metrics.log_loss API.
- sklearn.metrics.brier_score_loss API.
Articles
- Brier score, Wikipedia.
- Cross entropy, Wikipedia.
- Joint Working Group on Forecast Verification Research
Summary
In this tutorial, you discovered metrics for evaluating probabilistic predictions for imbalanced classification.
Specifically, you learned:
- Probability predictions are required for some classification predictive modeling problems.
- Log loss quantifies the average difference between predicted and expected probability distributions.
- Brier score quantifies the average difference between predicted and expected probabilities.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.





Hello Jason,
I have a problem. I have a hundred observations for training. Features are related to workers. y values are city names. In the future I have to predict the city name where to move workers given a new input. It seems a classification problem. Right? First question is how to encode city names? Then is better to use Keras or Sklearn? In case of Sklearn which agorithm? And finally how to decode the y value? Thanks
Marco
Yes. Classification.
Perhaps use a label encoder for city names.
Test a suite of algorithms:
https://machinelearningmastery.com/faq/single-faq/what-algorithm-config-should-i-use
Hello Jason,
Is it possibile to use also one-hot encoding for encoding cities? What is the differences between one hot and label encoding. When to use them?
Thanks,
Marco
Yes, good question. See this:
https://machinelearningmastery.com/how-to-prepare-categorical-data-for-deep-learning-in-python/
Hello Jason,
I’m trying XGBClassifier using IRIS dataset.
1) Is it machine learning algorithm o deep learning algortihm?
2) When I encode IRIS y using labelEncoder(), why I don’t need to normalize it? (more in general do I have to normalize y?)
3) IRIS X_train values are > 1, do I need to normalize them?
Thanks,
Marco
XGBoost is machine learning, not deep learning.
Encoded labels are integers. No need to normalize the class labels.
Generally, you don’t need to normalzie inputs for tree algorithms, like xgboost.
Hi Jason,
So, if we use tree algorithms, like xgboost, we dont need to do any data transformation such as normalization or standardization?
Yes, typically this is the case.
Hello Jason,
it seems that XGBClassifier is great algorithm. I tried it with the churn dataset.
I also built a Keras MLP (with 100 epochs).
XGBClassifier is MUCH faster and are MORE accurate than the Keras one.
1. So is it possible that a macchine learning algorithm is better than a deep learning?
2. You said “Generally, you don’t need to normalzie inputs for tree algorithms, like xgboost”
it is a great news what are the other two?
3. Does XGBClassifier work for linear regression as well. Do you have any example?
Thanks,
Marco
Yes, each dataset is different and you must use controlled experiments to discover what works best for each dataset.
There is no “best” algorithm for all problems.
XGBoost can be used for regression. I may have an example on the blog, try searching.
Question number 2 – ‘tree algorithms, like xgboost, …, what are the other two?’..
make my day 🙂
Could you please in simple terms explain why one should favour Brier Skill Score to Log Loss? What is the benefit of using it compared to Log Loss?
Thanks
Log loss is great for comparing distributions.
Brier score, specifically Brier Skill Score is great for presenting scores that are relative to a baseline.
Hello Jason,
one more question about XGBoost.
I’ve seen also scikit-learn has a two versions of gradient boosting (ensemble.GradientBoostingClassifier / ensemble.ensemble.HistGradientBoostingClassifier and ensemble.GradientBoostingRegressor / ensemble.HistGradientBoostingRegressor).
What are differences with XGBoost functions? what I have to use? Are they faster?
Can I replace XGBoost functions (XGBClassifier and XGBRegressor) with then without major changes?
Thanks
Excellent question!
GBM in sklearn is the standard algorithm.
Hist-based-GBM in sklearn is experimental and is a faster version of the algorithm based on lightgbm by microsoft.
xgboost is an efficient implementation of GBM and is way faster than the sklearn implementation.
Generally, speed improvements in xgboost, lightgbm and catboost often also lead to model skill improvements also.
Hello Jason,
a I have a couple of question. The parameters inside the function are called hyperpaametrers? Or what are the hyperpaametrers in scikit-learn functions?
GradientBoostingClassifier(loss=’deviance’, learning_rate=0.1, n_estimators=100, subsample=1.0, criterion=’friedman_mse’, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False, presort=’deprecated’, validation_fraction=0.1, n_iter_no_change=None, tol=0.0001, ccp_alpha=0.0)[source]¶
The second question is about sklearn.model_selection.GridSearchCV (I’d like to use it with XGBClassifier and XGBRegressor).
Can it be used for cross validation? Do you have an example?
Thanks,
Marco
Hyperparameters are provided as arguments to an algorithm class when defining it.
Yes you can grid search xgboost using scikit-learn.
Yes, there is an example here:
https://machinelearningmastery.com/xgboost-python-mini-course/
Greatly explained, Thanks 🙂
Thanks!
Hello Jason,
I’ve seen that among ensemble methods there are AdaBoostClassifier and AdaBoostRegressor.
What are differences between AdaBoostClassifier vs. GradientBoostingClassifier and AdaBoostRegressor vs. GradientBoostingRegressor.
When is better to use Ada functions?
Thanks,
Marco
They are completely different algorithms, e.g. adaboost vs gradient boosting machines.
Adaboost is the first boosting algorithm:
https://machinelearningmastery.com/boosting-and-adaboost-for-machine-learning/
Gradient boosting is a clever extension of the idea:
https://machinelearningmastery.com/gentle-introduction-gradient-boosting-algorithm-machine-learning/
Hello Jason,
one more question is how to navigate the scikit-learn map (https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html).
It is clear to me the flow until Ensemble Classifier (i.e in case of classification yes -> SVC -> not working -> text data -> no -> KNeighbors Classifier -> not working -> then Ensemble Classifiers). Then how to choose the right flow within Ensemble Classifiers?
Is there somewhere any overall picture or map to help to choose the right ensemble classifier (or ensemble regressor in case of regression?).
Thanks,
Marco
I recommend this process:
https://machinelearningmastery.com/start-here/#process
Hi Jason, actually I have a dataset with 7 types of defect. Right now I have done with classifying all the type of defect which is only one output here. But do you have an idea on how to know the percentage of the defect will have?This means I have to make it multiple input which is first:
1. the type of defect
2. The percentage of the defect chances.
Thanks,
Nini
Correction:
This means I have to do multiple output which is is first:
1. the type of defect
2. The percentage of the defect chances.
Thanks,
Nini
No, a model can predict the probability for each class directly. E.g. an LDA, logistic regression, naive bayes, and many more.
Yes, you can use a model that predicts a class membership probability. Or a model that predicts a probability like score and use model calibration.
Is that means the multiclass for imbalance classification cannot be used to find the percentage of the defect type?:(
No, it does not mean that.
Hello,
You said that a classifier model such as xgboost can predict the probability directly. Do you have an example on this?
Another question is, I tried to use rusboost as an algo of choice to my current dataset (tested in matlab). I looked that python also has it (https://imbalanced-learn.readthedocs.io/en/stable/generated/imblearn.ensemble.RUSBoostClassifier.html)
Is this rusboost as part of the scikit-learn?
XGBoost can predict a probability, but it is not native. You must calibrate the probability predicted a tree model.
You can predict probabilities for classification by calling model.predict_proba(), see examples here:
https://machinelearningmastery.com/make-predictions-scikit-learn/
I don’t know about ruboost, but I believe the imbalanced learn models are compatible with the sklearn framework.
Thanks Jason!
You are awesome.
By the way, how do I know if all of the answers here are not replied by ML-powered ChatBot 🙂
cheers
You’re very welcome.
I’m not aware of a bot good enough for that 🙂
Hi Jason,
can you point to which tutorial about the probability calibration?
Anyway, any tutorial on autoML? Also, are you planning also to give tutorial on H2O also?
Probability calibration:
https://machinelearningmastery.com/probability-calibration-for-imbalanced-classification/
Yes, I have a ton of tutorials on automl written and scheduled – all open source libs. They will appear on the blog some time in the next few months.
hi jason,
i am using brier score for my grid search, this is passed as ‘neg_brier_score’, however, since my problem is unbalanced how can I pass a ‘brier skill’ metric?
You may have to define the function manually then specify it to the grid search.
Hi sir,
How to find the class probability of a Binary classification using random forest.
Call model.predict_proba() to get probabilities.
You may want to look into calibrating the probabilities before using them:
https://machinelearningmastery.com/calibrated-classification-model-in-scikit-learn/
Dear Jason,
you mention that Brier Score “is focused on evaluating the probabilities for the positive class.” and that “This makes it [Brier Score] more preferable than log loss, which is focused on the entire probability distribution”
However the sklearn implementation considers all classes, positives and negatives.
As such it can be influenced by unbalanced dataset as much as logloss is.
Do you any comment on this?
check for instance this snippet:
import numpy as np
from sklearn.metrics import brier_score_loss
y_true = np.array([0, 1, 1, 0])
y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
y_prob = np.array([0.1, 0.9, 0.8, 0.3])
assert brier_score_loss(y_true, y_prob) == sum((y_true - y_prob)**2) / len(y_prob)
Sorry, I don’t follow.
What does “However the sklearn implementation considers all classes, positives and negatives.” mean?
Classes are represented as positive integers, starting at zero.
Hi Jason,
The article describes comparing the predicted probabilities to the true/expected probabilities. In the example, the true/expected probabilities are explicitly known and defined as 99/1.
In practice the true probability is unknown (if it were known, what would be the point in building the model in the first place?)
In this case how do you go about assessing performance of a model whose purpose is to predict probabilities?
Hi Rahul…It is always recommended that predictive models be validated.
Hi! I’m new to ML and I was starting a new project. I have a list of ads and I would like to sort them based on the probability of conversion so that there’s a higher chance for the first ad to be clicked. The dataset has features like day of week, hour, region, device type, etc.
I have an imbalanced dataset with very low converting samples. When I run the f1 score, I get 0. I understand the model is not being able to predict conversions.
However, can I still use the value in sklearn predict_proba to compare the different ads and sort them using that value? does this make any sense?
Hi Fernando…Perhaps you could try the value as you suggested to determine the effect?
Hi,
I’m a bit confused about the expected probabilities: In the method described in the blog post, we get an predicted probability for each example from our ML method and we calculate the log loss or the Brier Score for each example. For this, we need the expected probability for each example. Since we have labels, we know the ground truth, and we could calculate expected probabilities for groups of examples using a frequentist approach, but how would one determine expected probabilities for single examples (besides the estimation of 100% and 0% if the label or this single event is correct or not, which not really meaningful)?
Hi Simon…Please clarify your question so that we may better assist you.
Hi James,
thanks for the reply. I think I figured it out myself. I was refering to the following fomular:
BrierScore = 1/N * Sum i to N (yhat_i – y_i)^2
y_i could only be 0 or 1 if we look at single events which somehow confused me. I expected to use something like a frequentist probability for a group of comparable events and in fact this is used in the “reliability” term of the 3-component decomposition of the Brier score. Seeing this 3-component decomposition of the score solved the blockage in my head
Hi Simon…Yes! You are correct in your understanding!