Time Series Forecast Study with Python: Monthly Sales of French Champagne

Last Updated on May 18, 2020

Time series forecasting is a process, and the only way to get good forecasts is to practice this process.

In this tutorial, you will discover how to forecast the monthly sales of French champagne with Python.

Working through this tutorial will provide you with a framework for the steps and the tools for working through your own time series forecasting problems.

After completing this tutorial, you will know:

• How to confirm your Python environment and carefully define a time series forecasting problem.
• How to create a test harness for evaluating models, develop a baseline forecast, and better understand your problem with the tools of time series analysis.
• How to develop an autoregressive integrated moving average model, save it to file, and later load it to make predictions for new time steps.

Kick-start your project with my new book Time Series Forecasting With Python, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

• Update Mar/2017: Fixed a typo in the code example in the “Review Residual Errors” section where the wrong model was run.
• Updated Apr/2019: Updated the link to dataset.
• Updated Aug/2019: Updated data loading and date grouping to use new API.
• Updated Feb/2020: Updated to_csv() to remove warnings.
• Updated Feb/2020: Fixed data preparation and loading.
• Update May/2020: Fixed small typo when making a prediction.

Time Series Forecast Study with Python – Monthly Sales of French Champagne
Photo by Basheer Tome, some rights reserved.

Overview

In this tutorial, we will work through a time series forecasting project from end-to-end, from downloading the dataset and defining the problem to training a final model and making predictions.

This project is not exhaustive, but shows how you can get good results quickly by working through a time series forecasting problem systematically.

The steps of this project that we will through are as follows.

1. Environment.
2. Problem Description.
3. Test Harness.
4. Persistence.
5. Data Analysis.
6. ARIMA Models.
7. Model Validation.

This will provide a template for working through a time series prediction problem that you can use on your own dataset.

1. Environment

This tutorial assumes an installed and working SciPy environment and dependencies, including:

• SciPy
• NumPy
• Matplotlib
• Pandas
• scikit-learn
• statsmodels

If you need help installing Python and the SciPy environment on your workstation, consider the Anaconda distribution that manages much of it for you.

This script will help you check your installed versions of these libraries.

The results on my workstation used to write this tutorial are as follows:

2. Problem Description

The problem is to predict the number of monthly sales of champagne for the Perrin Freres label (named for a region in France).

The dataset provides the number of monthly sales of champagne from January 1964 to September 1972, or just under 10 years of data.

The values are a count of millions of sales and there are 105 observations.

The dataset is credited to Makridakis and Wheelwright, 1989.

• Download the dataset.

Download the dataset as a CSV file and place it in your current working directory with the filename “champagne.csv“.

3. Test Harness

We must develop a test harness to investigate the data and evaluate candidate models.

This involves two steps:

1. Defining a Validation Dataset.
2. Developing a Method for Model Evaluation.

3.1 Validation Dataset

The dataset is not current. This means that we cannot easily collect updated data to validate the model.

Therefore we will pretend that it is September 1971 and withhold the last one year of data from analysis and model selection.

This final year of data will be used to validate the final model.

The code below will load the dataset as a Pandas Series and split into two, one for model development (dataset.csv) and the other for validation (validation.csv).

Running the example creates two files and prints the number of observations in each.

The specific contents of these files are:

• dataset.csv: Observations from January 1964 to September 1971 (93 observations)
• validation.csv: Observations from October 1971 to September 1972 (12 observations)

The validation dataset is about 11% of the original dataset.

Note that the saved datasets do not have a header line, therefore we do not need to cater for this when working with these files later.

3.2. Model Evaluation

Model evaluation will only be performed on the data in dataset.csv prepared in the previous section.

Model evaluation involves two elements:

1. Performance Measure.
2. Test Strategy.

3.2.1 Performance Measure

The observations are a count of champagne sales in millions of units.

We will evaluate the performance of predictions using the root mean squared error (RMSE). This will give more weight to predictions that are grossly wrong and will have the same units as the original data.

Any transforms to the data must be reversed before the RMSE is calculated and reported to make the performance between different methods directly comparable.

We can calculate the RMSE using the helper function from the scikit-learn library mean_squared_error() that calculates the mean squared error between a list of expected values (the test set) and the list of predictions. We can then take the square root of this value to give us an RMSE score.

For example:

3.2.2 Test Strategy

Candidate models will be evaluated using walk-forward validation.

This is because a rolling-forecast type model is required from the problem definition. This is where one-step forecasts are needed given all available data.

The walk-forward validation will work as follows:

• The first 50% of the dataset will be held back to train the model.
• The remaining 50% of the dataset will be iterated and test the model.
• For each step in the test dataset:
  • A model will be trained.
  • A one-step prediction made and the prediction stored for later evaluation.
  • The actual observation from the test dataset will be added to the training dataset for the next iteration.
• The predictions made during the iteration of the test dataset will be evaluated and an RMSE score reported.

Given the small size of the data, we will allow a model to be re-trained given all available data prior to each prediction.

We can write the code for the test harness using simple NumPy and Python code.

Firstly, we can split the dataset into train and test sets directly. We’re careful to always convert a loaded dataset to float32 in case the loaded data still has some String or Integer data types.

Next, we can iterate over the time steps in the test dataset. The train dataset is stored in a Python list as we need to easily append a new observation each iteration and NumPy array concatenation feels like overkill.

The prediction made by the model is called yhat for convention, as the outcome or observation is referred to as y and yhat (a ‘y‘ with a mark above) is the mathematical notation for the prediction of the y variable.

The prediction and observation are printed each observation for a sanity check prediction in case there are issues with the model.

4. Persistence

The first step before getting bogged down in data analysis and modeling is to establish a baseline of performance.

This will provide both a template for evaluating models using the proposed test harness and a performance measure by which all more elaborate predictive models can be compared.

The baseline prediction for time series forecasting is called the naive forecast, or persistence.

This is where the observation from the previous time step is used as the prediction for the observation at the next time step.

We can plug this directly into the test harness defined in the previous section.

The complete code listing is provided below.

Running the test harness prints the prediction and observation for each iteration of the test dataset.

The example ends by printing the RMSE for the model.

In this case, we can see that the persistence model achieved an RMSE of 3186.501. This means that on average, the model was wrong by about 3,186 million sales for each prediction made.

We now have a baseline prediction method and performance; now we can start digging into our data.

5. Data Analysis

We can use summary statistics and plots of the data to quickly learn more about the structure of the prediction problem.

In this section, we will look at the data from five perspectives:

1. Summary Statistics.
2. Line Plot.
3. Seasonal Line Plots
4. Density Plots.
5. Box and Whisker Plot.

5.1 Summary Statistics

Summary statistics provide a quick look at the limits of observed values. It can help to get a quick idea of what we are working with.

The example below calculates and prints summary statistics for the time series.

Running the example provides a number of summary statistics to review.

Some observations from these statistics include:

• The number of observations (count) matches our expectation, meaning we are handling the data correctly.
• The mean is about 4,641, which we might consider our level in this series.
• The standard deviation (average spread from the mean) is relatively large at 2,486 sales.
• The percentiles along with the standard deviation do suggest a large spread to the data.

5.2 Line Plot

A line plot of a time series can provide a lot of insight into the problem.

The example below creates and shows a line plot of the dataset.

Run the example and review the plot. Note any obvious temporal structures in the series.

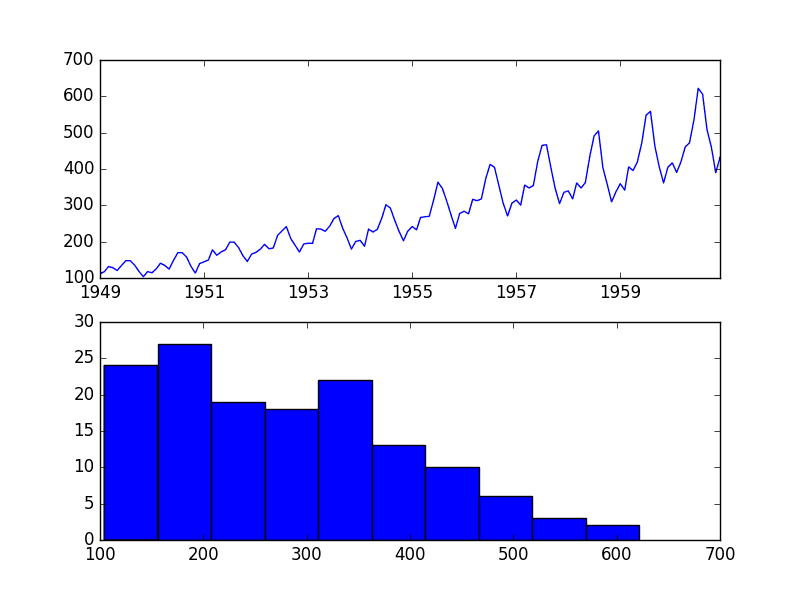
Some observations from the plot include:

• There may be an increasing trend of sales over time.
• There appears to be systematic seasonality to the sales for each year.
• The seasonal signal appears to be growing over time, suggesting a multiplicative relationship (increasing change).
• There do not appear to be any obvious outliers.
• The seasonality suggests that the series is almost certainly non-stationary.

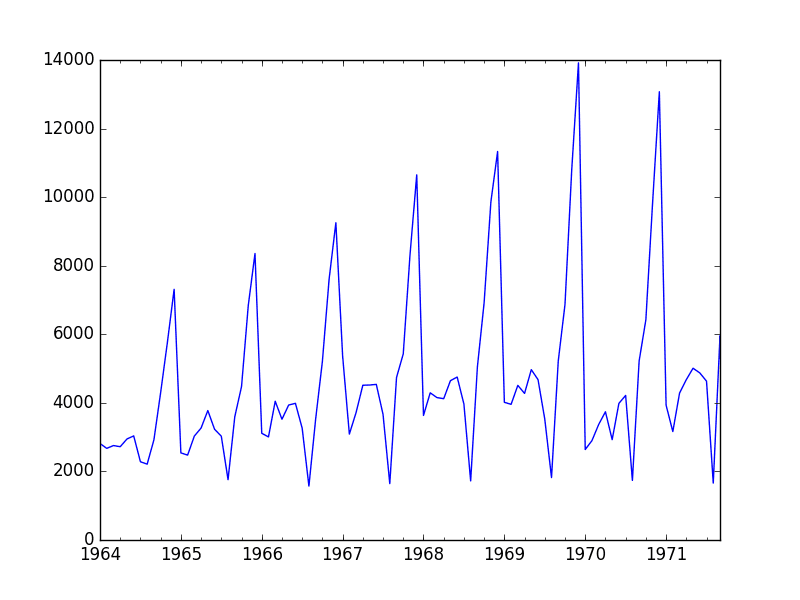
Champagne Sales Line Plot

There may be benefit in explicitly modeling the seasonal component and removing it. You may also explore using differencing with one or two levels in order to make the series stationary.

The increasing trend or growth in the seasonal component may suggest the use of a log or other power transform.

5.3 Seasonal Line Plots

We can confirm the assumption that the seasonality is a yearly cycle by eyeballing line plots of the dataset by year.

The example below takes the 7 full years of data as separate groups and creates one line plot for each. The line plots are aligned vertically to help spot any year-to-year pattern.

Running the example creates the stack of 7 line plots.

We can clearly see a dip each August and a rise from each August to December. This pattern appears the same each year, although at different levels.

This will help with any explicitly season-based modeling later.

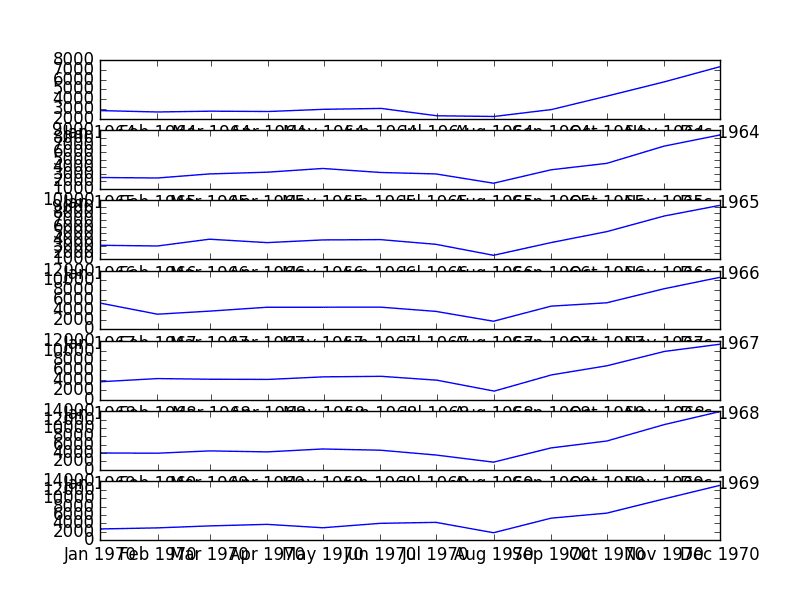
Seasonal Per Year Line Plots

It might have been easier if all season line plots were added to the one graph to help contrast the data for each year.

5.4 Density Plot

Reviewing plots of the density of observations can provide further insight into the structure of the data.

The example below creates a histogram and density plot of the observations without any temporal structure.

Run the example and review the plots.

Some observations from the plots include:

• The distribution is not Gaussian.
• The shape has a long right tail and may suggest an exponential distribution

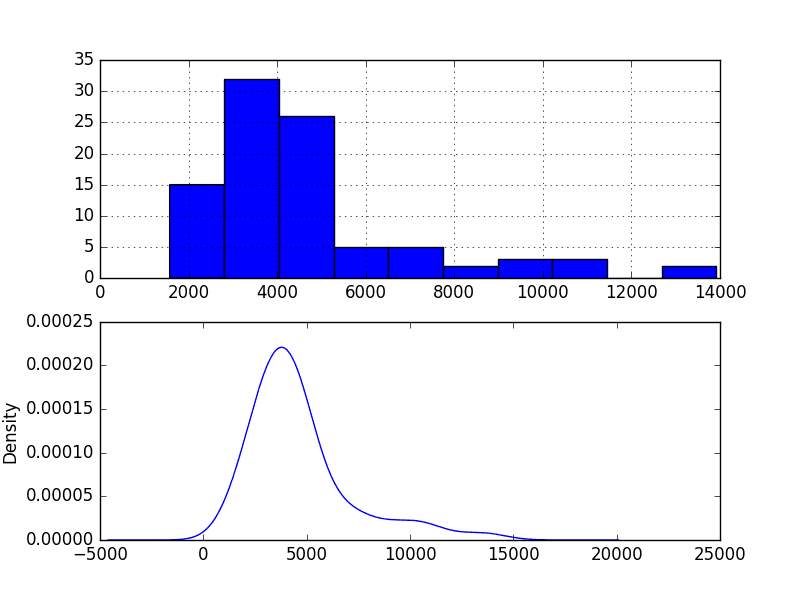
This lends more support to exploring some power transforms of the data prior to modeling.

5.5 Box and Whisker Plots

We can group the monthly data by year and get an idea of the spread of observations for each year and how this may be changing.

We do expect to see some trend (increasing mean or median), but it may be interesting to see how the rest of the distribution may be changing.

The example below groups the observations by year and creates one box and whisker plot for each year of observations. The last year (1971) only contains 9 months and may not be a useful comparison with the 12 months of observations for other years. Therefore, only data between 1964 and 1970 was plotted.

Running the example creates 7 box and whisker plots side-by-side, one for each of the 7 years of selected data.

Some observations from reviewing the plots include:

• The median values for each year (red line) may show an increasing trend.
• The spread or middle 50% of the data (blue boxes) does appear reasonably stable.
• There are outliers each year (black crosses); these may be the tops or bottoms of the seasonal cycle.
• The last year, 1970, does look different from the trend in prior years

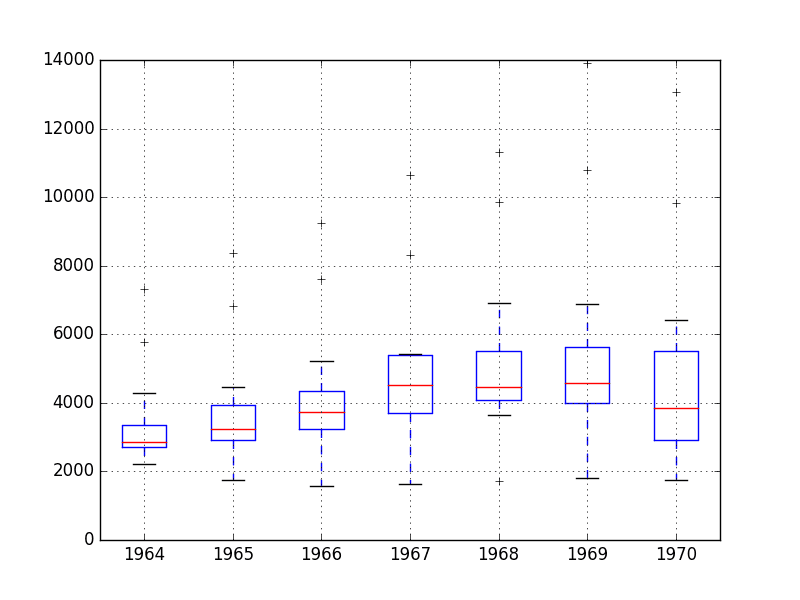
Champagne Sales Box and Whisker Plots

The observations suggest perhaps some growth trend over the years and outliers that may be a part of the seasonal cycle.

This yearly view of the data is an interesting avenue and could be pursued further by looking at summary statistics from year-to-year and changes in summary stats from year-to-year.

6. ARIMA Models

In this section, we will develop Autoregressive Integrated Moving Average, or ARIMA, models for the problem.

We will approach modeling by both manual and automatic configuration of the ARIMA model. This will be followed by a third step of investigating the residual errors of the chosen model.

As such, this section is broken down into 3 steps:

1. Manually Configure the ARIMA.
2. Automatically Configure the ARIMA.
3. Review Residual Errors.

6.1 Manually Configured ARIMA

The ARIMA(p,d,q) model requires three parameters and is traditionally configured manually.

Analysis of the time series data assumes that we are working with a stationary time series.

The time series is almost certainly non-stationary. We can make it stationary this by first differencing the series and using a statistical test to confirm that the result is stationary.

The seasonality in the series is seemingly year-to-year. Seasonal data can be differenced by subtracting the observation from the same time in the previous cycle, in this case the same month in the previous year. This does mean that we will lose the first year of observations as there is no prior year to difference with.

The example below creates a deseasonalized version of the series and saves it to file stationary.csv.

Running the example outputs the result of a statistical significance test of whether the differenced series is stationary. Specifically, the augmented Dickey-Fuller test.

The results show that the test statistic value -7.134898 is smaller than the critical value at 1% of -3.515. This suggests that we can reject the null hypothesis with a significance level of less than 1% (i.e. a low probability that the result is a statistical fluke).

Rejecting the null hypothesis means that the process has no unit root, and in turn that the time series is stationary or does not have time-dependent structure.

For reference, the seasonal difference operation can be inverted by adding the observation for the same month the year before. This is needed in the case that predictions are made by a model fit on seasonally differenced data. The function to invert the seasonal difference operation is listed below for completeness.

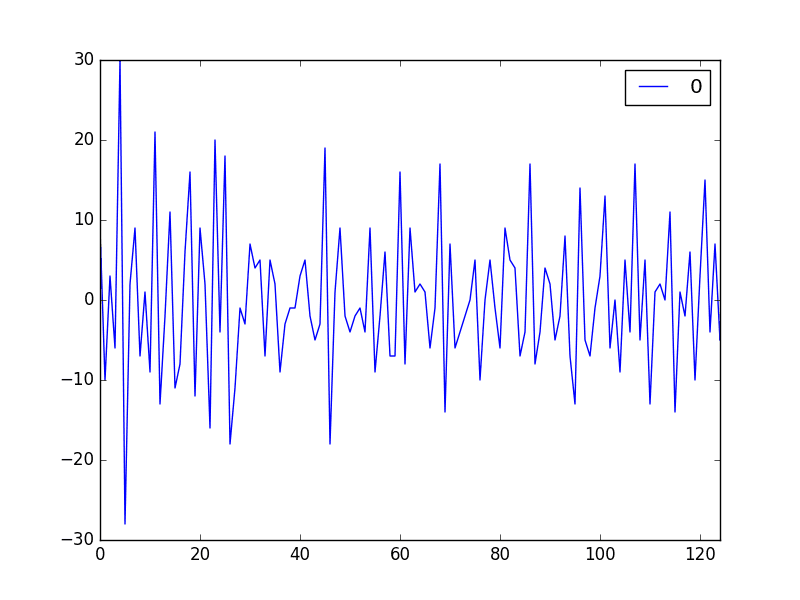
A plot of the differenced dataset is also created.

The plot does not show any obvious seasonality or trend, suggesting the seasonally differenced dataset is a good starting point for modeling.

We will use this dataset as an input to the ARIMA model. It also suggests that no further differencing may be required, and that the d parameter may be set to 0.

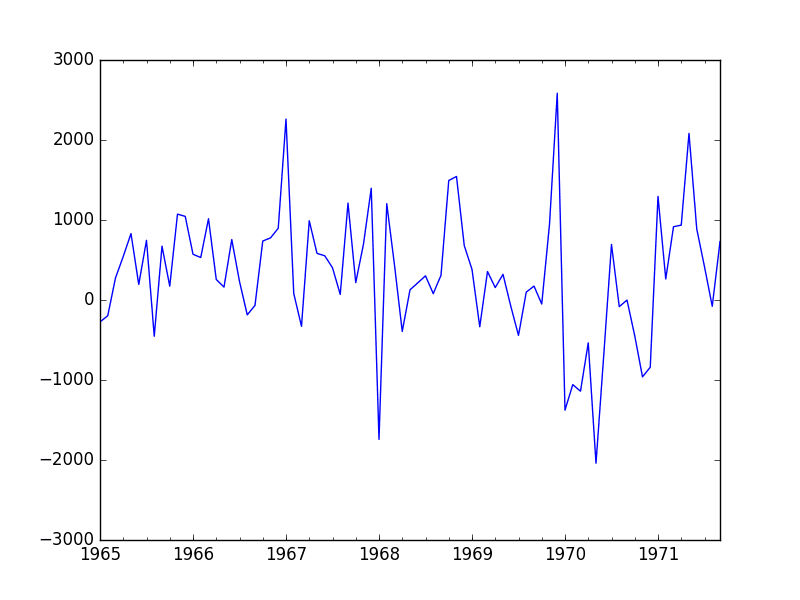
Seasonal Differenced Champagne Sales Line Plot

The next first step is to select the lag values for the Autoregression (AR) and Moving Average (MA) parameters, p and q respectively.

We can do this by reviewing Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) plots.

Note, we are now using the seasonally differenced stationary.csv as our dataset.

The example below creates ACF and PACF plots for the series.

Run the example and review the plots for insights into how to set the p and q variables for the ARIMA model.

Below are some observations from the plots.

• The ACF shows a significant lag for 1 month.
• The PACF shows a significant lag for 1 month, with perhaps some significant lag at 12 and 13 months.
• Both the ACF and PACF show a drop-off at the same point, perhaps suggesting a mix of AR and MA.

A good starting point for the p and q values is also 1.

The PACF plot also suggests that there is still some seasonality present in the differenced data.

We may consider a better model of seasonality, such as modeling it directly and explicitly removing it from the model rather than seasonal differencing.

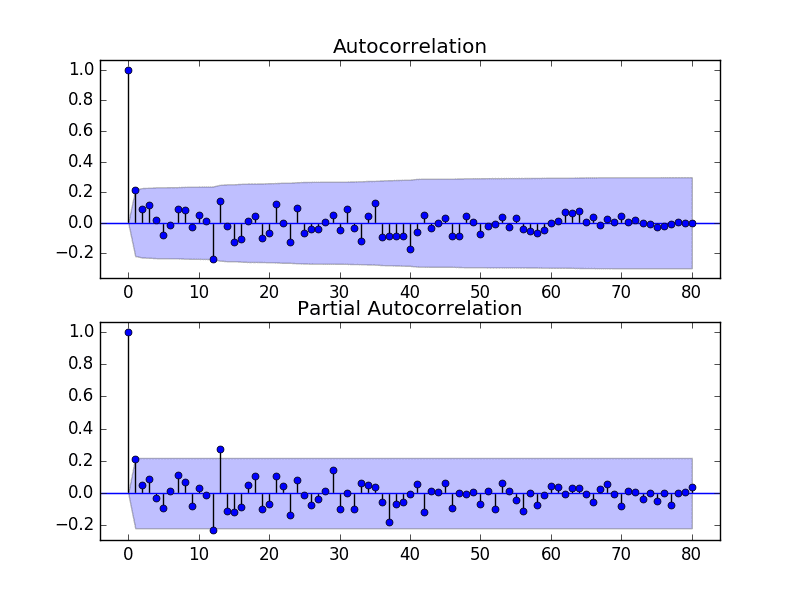
ACF and PACF Plots of Seasonally Differenced Champagne Sales

This quick analysis suggests an ARIMA(1,0,1) on the stationary data may be a good starting point.

The historic observations will be seasonally differenced prior to the fitting of each ARIMA model. The differencing will be inverted for all predictions made to make them directly comparable to the expected observation in the original sale count units.

Experimentation shows that this configuration of ARIMA does not converge and results in errors by the underlying library. Further experimentation showed that adding one level of differencing to the stationary data made the model more stable. The model can be extended to ARIMA(1,1,1).

We will also disable the automatic addition of a trend constant from the model by setting the ‘trend‘ argument to ‘nc‘ for no constant in the call to fit(). From experimentation, I find that this can result in better forecast performance on some problems.

The example below demonstrates the performance of this ARIMA model on the test harness.

Note, you may see a warning message from the underlying linear algebra library; this can be ignored for now.

Running this example results in an RMSE of 956.942, which is dramatically better than the persistence RMSE of 3186.501.

This is a great start, but we may be able to get improved results with a better configured ARIMA model.

6.2 Grid Search ARIMA Hyperparameters

The ACF and PACF plots suggest that an ARIMA(1,0,1) or similar may be the best that we can do.

To confirm this analysis, we can grid search a suite of ARIMA hyperparameters and check that no models result in better out of sample RMSE performance.

In this section, we will search values of p, d, and q for combinations (skipping those that fail to converge), and find the combination that results in the best performance on the test set. We will use a grid search to explore all combinations in a subset of integer values.

Specifically, we will search all combinations of the following parameters:

• p: 0 to 6.
• d: 0 to 2.
• q: 0 to 6.

This is (7 * 3 * 7), or 147, potential runs of the test harness and will take some time to execute.

It may be interesting to evaluate MA models with a lag of 12 or 13 as were noticed as potentially interesting from reviewing the ACF and PACF plots. Experimentation suggested that these models may not be stable, resulting in errors in the underlying mathematical libraries.

The complete worked example with the grid search version of the test harness is listed below.

Running the example runs through all combinations and reports the results on those that converge without error. The example takes a little over 2 minutes to run on modern hardware.

The results show that the best configuration discovered was ARIMA(0, 0, 1) with an RMSE of 939.464, slightly lower than the manually configured ARIMA from the previous section. This difference may or may not be statistically significant.

We will select this ARIMA(0, 0, 1) model going forward.

6.3 Review Residual Errors

A good final check of a model is to review residual forecast errors.

Ideally, the distribution of residual errors should be a Gaussian with a zero mean.

We can check this by using summary statistics and plots to investigate the residual errors from the ARIMA(0, 0, 1) model. The example below calculates and summarizes the residual forecast errors.

Running the example first describes the distribution of the residuals.

We can see that the distribution has a right shift and that the mean is non-zero at 165.904728.

This is perhaps a sign that the predictions are biased.

The distribution of residual errors is also plotted.

The graphs suggest a Gaussian-like distribution with a bumpy left tail, providing further evidence that perhaps a power transform might be worth exploring.

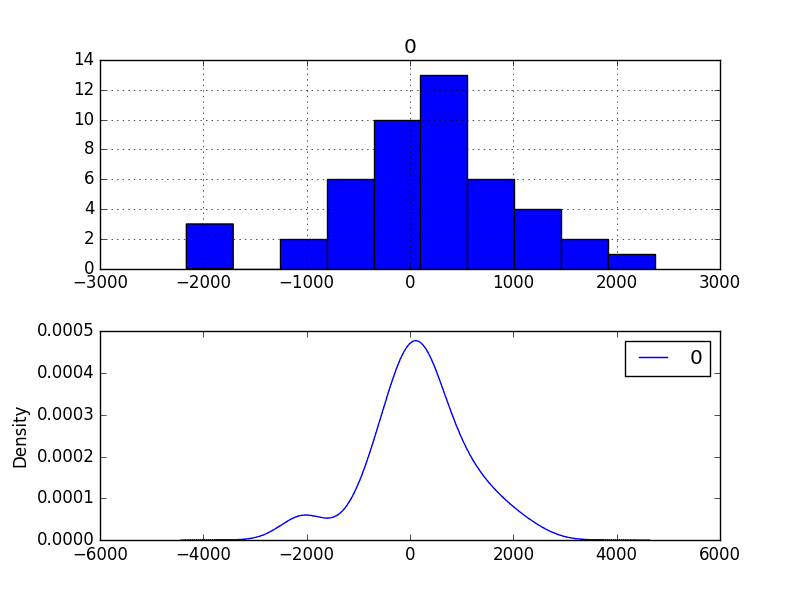
Residual Forecast Error Density Plots

We could use this information to bias-correct predictions by adding the mean residual error of 165.904728 to each forecast made.

The example below performs this bias correlation.

The performance of the predictions is improved very slightly from 939.464 to 924.699, which may or may not be significant.

The summary of the forecast residual errors shows that the mean was indeed moved to a value very close to zero.

Finally, density plots of the residual error do show a small shift towards zero.

It is debatable whether this bias correction is worth it, but we will use it for now.

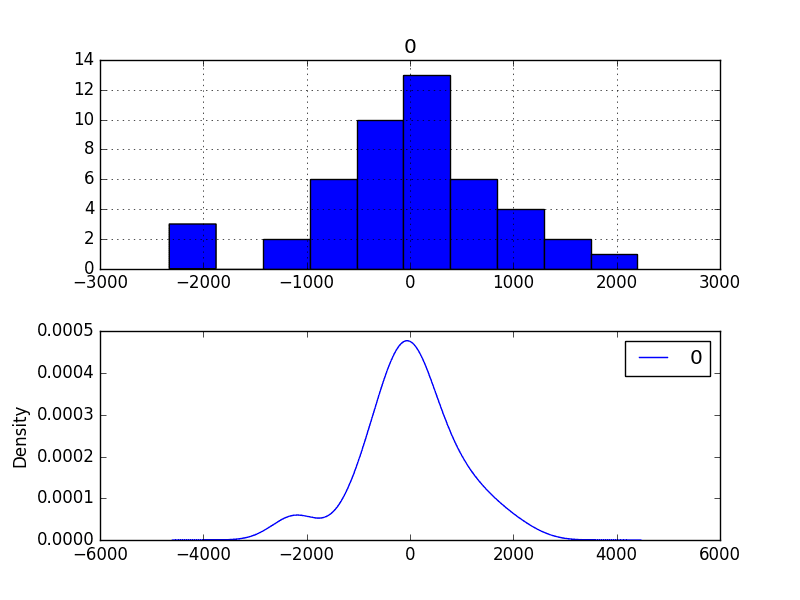
Bias-Corrected Residual Forecast Error Density Plots

It is also a good idea to check the time series of the residual errors for any type of autocorrelation. If present, it would suggest that the model has more opportunity to model the temporal structure in the data.

The example below re-calculates the residual errors and creates ACF and PACF plots to check for any significant autocorrelation.

The results suggest that what little autocorrelation is present in the time series has been captured by the model.

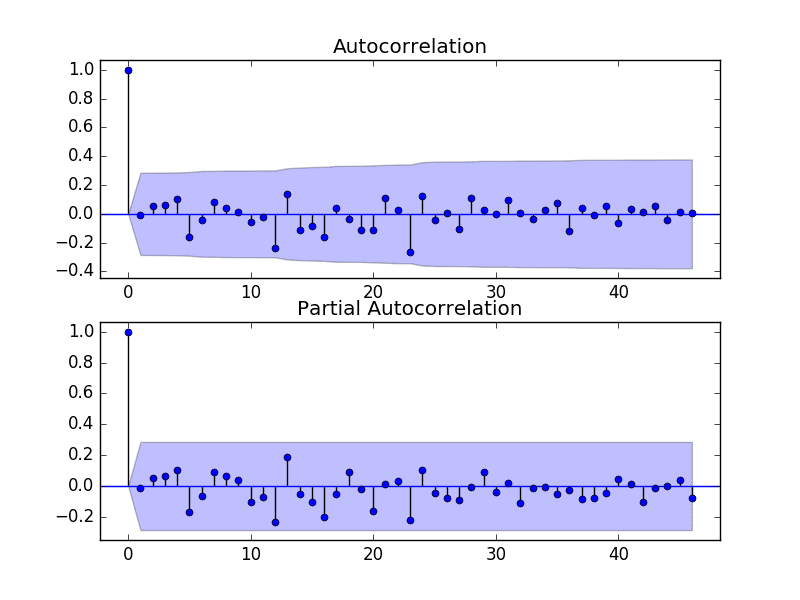
Residual Forecast Error ACF and PACF Plots

7. Model Validation

After models have been developed and a final model selected, it must be validated and finalized.

Validation is an optional part of the process, but one that provides a ‘last check’ to ensure we have not fooled or misled ourselves.

This section includes the following steps:

1. Finalize Model: Train and save the final model.
2. Make Prediction: Load the finalized model and make a prediction.
3. Validate Model: Load and validate the final model.

7.1 Finalize Model

Finalizing the model involves fitting an ARIMA model on the entire dataset, in this case on a transformed version of the entire dataset.

Once fit, the model can be saved to file for later use.

The example below trains an ARIMA(0,0,1) model on the dataset and saves the whole fit object and the bias to file.

There is a bug in the current stable version of the statsmodels library (v0.6.1) that results in an error when you try to load a saved ARIMA model from file. The error reported is:

This bug also seems present in the 0.8 release candidate 1 of statsmodels when I tested it. For more details, see Zae Myung Kim‘s discussion and fix in this GitHub issue.

We can work around this with a monkey patch that adds a __getnewargs__() instance function to the ARIMA class before saving.

The example below saves the fit model to file in the correct state so that it can be loaded successfully later.

Running the example creates two local files:

• model.pkl This is the ARIMAResult object from the call to ARIMA.fit(). This includes the coefficients and all other internal data returned when fitting the model.
• model_bias.npy This is the bias value stored as a one-row, one-column NumPy array.

7.2 Make Prediction

A natural case may be to load the model and make a single forecast.

This is relatively straightforward and involves restoring the saved model and the bias and calling the forecast() method. To invert the seasonal differencing, the historical data must also be loaded.

The example below loads the model, makes a prediction for the next time step, and prints the prediction.

Running the example prints the prediction of about 6794.

If we peek inside validation.csv, we can see that the value on the first row for the next time period is 6981.

The prediction is in the right ballpark.

7.3 Validate Model

We can load the model and use it in a pretend operational manner.

In the test harness section, we saved the final 12 months of the original dataset in a separate file to validate the final model.

We can load this validation.csv file now and use it see how well our model really is on “unseen” data.

There are two ways we might proceed:

• Load the model and use it to forecast the next 12 months. The forecast beyond the first one or two months will quickly start to degrade in skill.
• Load the model and use it in a rolling-forecast manner, updating the transform and model for each time step. This is the preferred method as it is how one would use this model in practice as it would achieve the best performance.

As with model evaluation in previous sections, we will make predictions in a rolling-forecast manner. This means that we will step over lead times in the validation dataset and take the observations as an update to the history.

Running the example prints each prediction and expected value for the time steps in the validation dataset.

The final RMSE for the validation period is predicted at 361.110 million sales.

This is much better than the expectation of an error of a little more than 924 million sales per month.

A plot of the predictions compared to the validation dataset is also provided.

At this scale on the plot, the 12 months of forecast sales figures look fantastic.

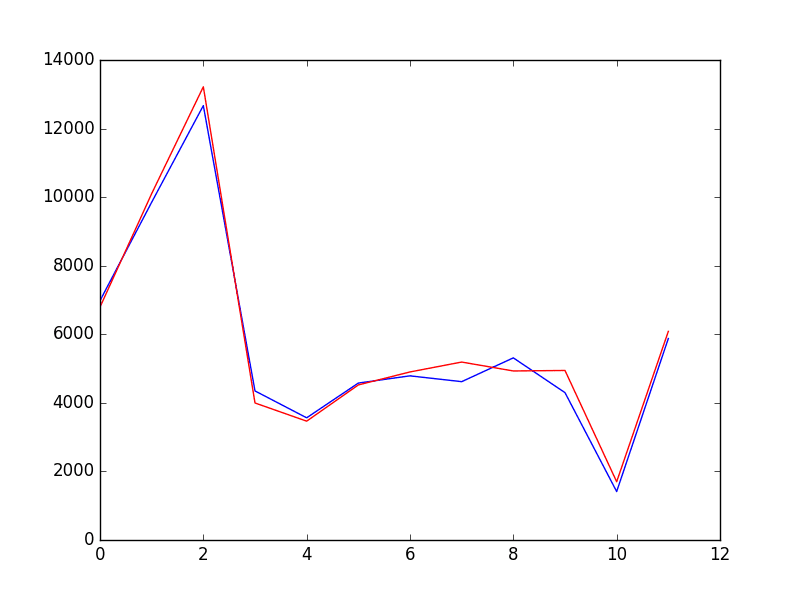
Forecast for Champagne Sales Validation Dataset

Summary

In this tutorial, you discovered the steps and the tools for a time series forecasting project with Python.

We have covered a lot of ground in this tutorial; specifically:

• How to develop a test harness with a performance measure and evaluation method and how to quickly develop a baseline forecast and skill.
• How to use time series analysis to raise ideas for how to best model the forecast problem.
• How to develop an ARIMA model, save it, and later load it to make predictions on new data.

How did you do? Do you have any questions about this tutorial?
Ask your questions in the comments below and I will do my best to answer.

Want to Develop Time Series Forecasts with Python?

Develop Your Own Forecasts in Minutes

...with just a few lines of python code

Discover how in my new Ebook:
Introduction to Time Series Forecasting With Python

It covers self-study tutorials and end-to-end projects on topics like: Loading data, visualization, modeling, algorithm tuning, and much more...

Finally Bring Time Series Forecasting to
Your Own Projects

Skip the Academics. Just Results.

See What's Inside