What metrics can you use to evaluate your machine learning algorithms?
In this post you will discover how you can evaluate your machine learning algorithms in R using a number of standard evaluation metrics.
Kick-start your project with my new book Machine Learning Mastery With R, including step-by-step tutorials and the R source code files for all examples.
Let’s get started.
Machine Learning Evaluation Metrics in R Photo by Roland Tanglao, some rights reserved.
Model Evaluation Metrics in R
There are many different metrics that you can use to evaluate your machine learning algorithms in R.
When you use caret to evaluate your models, the default metrics used are accuracy for classification problems and RMSE for regression. But caret supports a range of other popular evaluation metrics.
In the next section you will step through each of the evaluation metrics provided by caret. Each example provides a complete case study that you can copy-and-paste into your project and adapt to your problem.
Note that this post does assume you are already know how to interpret these other metrics. Don’t fret if they are new to you, I’ve provided some links for further reading where you can learn more.
Need more Help with R for Machine Learning?
Take my free 14-day email course and discover how to use R on your project (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Metrics To Evaluate Machine Learning Algorithms
In this section you will discover how you can evaluate machine learning algorithms using a number of different common evaluation metrics.
Specifically, this section will show you how to use the following evaluation metrics with the caret package in R:
Accuracy and Kappa
RMSE and R^2
ROC (AUC, Sensitivity and Specificity)
LogLoss
Accuracy and Kappa
These are the default metrics used to evaluate algorithms on binary and multi-class classification datasets in caret.
Accuracy is the percentage of correctly classifies instances out of all instances. It is more useful on a binary classification than multi-class classification problems because it can be less clear exactly how the accuracy breaks down across those classes (e.g. you need to go deeper with a confusion matrix). Learn more about Accuracy here.
Kappa or Cohen’s Kappa is like classification accuracy, except that it is normalized at the baseline of random chance on your dataset. It is a more useful measure to use on problems that have an imbalance in the classes (e.g. 70-30 split for classes 0 and 1 and you can achieve 70% accuracy by predicting all instances are for class 0). Learn more about Kappa here.
In the example below the Pima Indians diabetes dataset is used. It has a class break down of 65% to 35% for negative and positive outcomes.
Running this example, we can see tables of Accuracy and Kappa for each machine learning algorithm evaluated. This includes the mean values (left) and the standard deviations (marked as SD) for each metric, taken over the population of cross validation folds and trials.
You can see that the accuracy of the model is approximately 76% which is 11 percentage points above the baseline accuracy of 65% which is not really that impressive. The Kappa the other hand shows approximately 46% which is more interesting.
1
2
3
4
5
6
7
8
9
10
11
12
13
Generalized Linear Model
768 samples
8 predictor
2 classes: 'neg', 'pos'
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 614, 614, 615, 615, 614
Resampling results
Accuracy Kappa Accuracy SD Kappa SD
0.7695442 0.4656824 0.02692468 0.0616666
RMSE and R^2
These are the default metrics used to evaluate algorithms on regression datasets in caret.
RMSE or Root Mean Squared Error is the average deviation of the predictions from the observations. It is useful to get a gross idea of how well (or not) an algorithm is doing, in the units of the output variable. Learn more about RMSE here.
R^2 spoken as R Squared or also called the coefficient of determination provides a “goodness of fit” measure for the predictions to the observations. This is a value between 0 and 1 for no-fit and perfect fit respectively. Learn more about R^2 here.
In this example the longly economic dataset is used. The output variable is a “number employed”. It is not clear whether this is an actual count (e.g. in millions) or a percentage.
Running this example, we can see tables of RMSE and R Squared for each machine learning algorithm evaluated. Again, you can see the mean and standard deviations of both metrics are provided.
You can see that the RMSE was 0.38 in the units of Employed (whatever those units are). Whereas, the R Square value shows a good fit for the data with a value very close to 1 (0.988).
1
2
3
4
5
6
7
8
9
10
11
12
Linear Regression
16 samples
6 predictor
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 12, 12, 14, 13, 13
Resampling results
RMSE Rsquared RMSE SD Rsquared SD
0.3868618 0.9883114 0.1025042 0.01581824
Area Under ROC Curve
ROC metrics are only suitable for binary classification problems (e.g. two classes).
To calculate ROC information, you must change the summaryFunction in your trainControl to be twoClassSummary. This will calculate the Area Under ROC Curve (AUROC) also called just Area Under curve (AUC), sensitivity and specificity.
ROC is actually the area under the ROC curve or AUC. The AUC represents a models ability to discriminate between positive and negative classes. An area of 1.0 represents a model that made all predicts perfectly. An area of 0.5 represents a model as good as random. Learn more about ROC here.
ROC can be broken down into sensitivity and specificity. A binary classification problem is really a trade-off between sensitivity and specificity.
Sensitivity is the true positive rate also called the recall. It is the number instances from the positive (first) class that actually predicted correctly.
Specificity is also called the true negative rate. Is the number of instances from the negative class (second) class that were actually predicted correctly. Learn more about sensitivity and specificity here.
Here, you can see the “good” but not “excellent” AUC score of 0.833. The first level is taken as the positive class, in this case “neg” (no onset of diabetes).
Logarithmic Loss or LogLoss is used to evaluate binary classification but it is more common for multi-class classification algorithms. Specifically, it evaluates the probabilities estimated by the algorithms. Learn more about log loss here.
In this case we see logloss calculated for the iris flower multi-class classification problem.
Logloss is minimized and we can see the optimal CART model had a cp of 0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
CART
150 samples
4 predictor
3 classes: 'setosa', 'versicolor', 'virginica'
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 120, 120, 120, 120, 120
Resampling results across tuning parameters:
cp logLoss logLoss SD
0.00 0.4105613 0.6491893
0.44 0.6840517 0.4963032
0.50 1.0986123 0.0000000
logLoss was used to select the optimal model using the smallest value.
The final value used for the model was cp = 0.
Summary
In this post you discovered different metrics that you can use to evaluate the performance of your machine learning algorithms in R using caret. Specifically:
Accuracy and Kappa
RMSE and R^2
ROC (AUC, Sensitivity and Specificity)
LogLoss
You can use the recipes in this post you evaluate machine learning algorithms on your current or next machine learning project.
Next Step
Work through the example in this post.
Open your R interactive environment.
Type of copy-paste the sample code above.
Take your time and understand what is going on, use R help to read-up on functions.
Do you have any questions? Leave a comment and I will do my best.
For an imbalanced binary classification, how logical will it be if I use “Accuracy” as metric in training and find AUC score using ROCR package? Or I must use “ROC” as metric for computing AUC score?
Thank you for the good article.
Can RMSE be used to compare accuracy of difference models created by different algorithms (Polynomial Regression, SVR, Decision Tree or Random Forest)
Thank you…
Thanks for this article and your site. Running the Logarithmic Loss example with R 3.5, I got a different and sub-optimal result, claiming cp = 0.44 gives a minimal logLoss of 0.390. I got a correct result when number is increased to 10 instead of 5. Moreover, I didn’t get the SD column. Is there a trick to get them?
The reason is because you are estimating the skill of the model when making predictions on data unseen during training. New data. This is how you intend to use the model in practice.
Hi Jason! Thank you very much for your post!
In a regression problem, I want to fit a model focusing on low values, instead of high values.
In some papers that discuss metrics of evaluation models, such as “DAWSON et al (2007). HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts”, they explain that “RMSE” better fits the high values (because compared values are squared) and “Rsquared” use to seek for better shape of the values, and the values are also squared.
Then what do you suggest to set in “metrics”, if my intention is to better model the low values, applying caret-train-metrics? Because of this worry, RMSE and Rsquared do not seem adequate to apply.
Thanks again!
many thanks for your helpful tutorials.
I followed “Your First Machine Learning Project in R Step-By-Step” and then looked into this article.
I have some questions:
– do these metrics (in particular RMSE and R^2, ROC and log loss) follow the same logic of training the model and then testing it on the validation data set? or this is true only for accuracy and K?
– what does log loss do? in which sense log loss estimate the probabilities of the model?
– how do I get cut-off scores for ROC?
I want to compare adjusted r-squared of SVR, RF, ANN, MLR on new data (test data after generating predictions). I know caret has a function for R-squared and RMSE, but I can’t find any functions for ADJUSTED r-squared in R…Please help
I have one question when using the traincontrol. When i am using the below code snippet to run GBM model. I am getting the accuracy of around 86% for best tune model. But when i run on the entire train dataset it is around 98%. Why there is such a gap between the train and cross validation error.
I will be obliged. Looking forward for your reply.
Thank you for the reply Jason.
In this case, should I be checking Test accuracy Vs Cross validation accuracy of best tune model or Test Accuracy Vs Training accuracy to say whether the model is an overfit?
Correct me if I am wrong but in the case of GBM, parameters are chosen from expand.grid and a model is generated and with respect to that model accuracy is calculated?
Is there a way I can have the Validation accuracy to be calculated at each tree depth in caret R?
Thank you for your great post like always! You mentioned that Logarithmic Loss is good for multi-class classification problem. I want to ask if the multi-class are also imbalanced, is Logarithmic Loss also proper? For imbalanced multi-class dataset for classification, what metric you would suggest to use? Thank you!
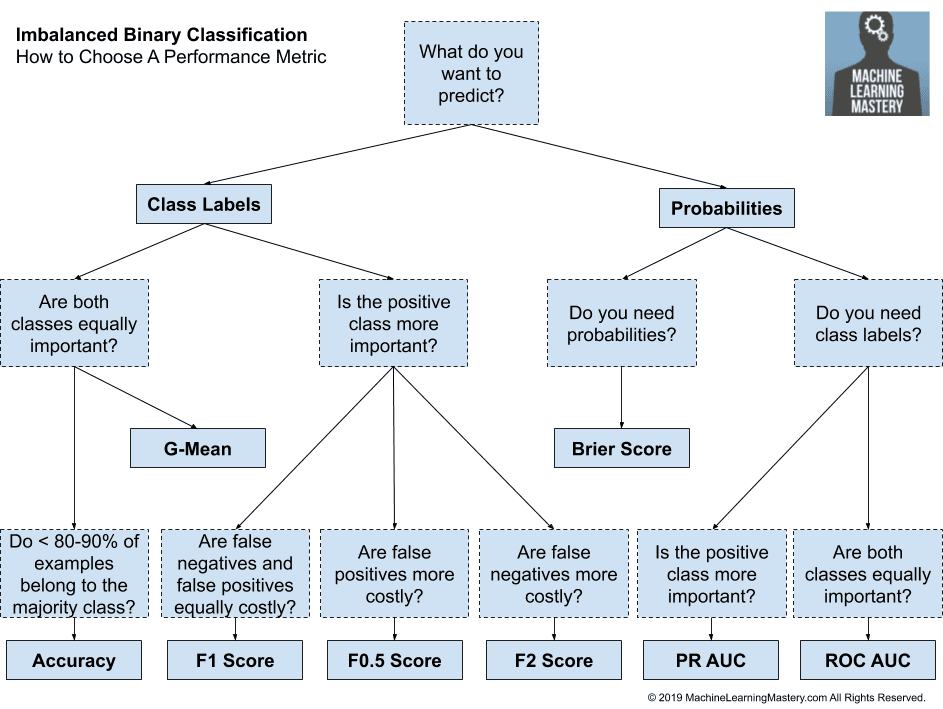
For an imbalanced binary classification, how logical will it be if I use “Accuracy” as metric in training and find AUC score using ROCR package? Or I must use “ROC” as metric for computing AUC score?
Thank you for the good article.
Can RMSE be used to compare accuracy of difference models created by different algorithms (Polynomial Regression, SVR, Decision Tree or Random Forest)
Thank you…
Hi John,
Not accuracy, but error. Yes, it can be used to compare the error of different algorithms on regression problems, not classification problems.
Hi Jason, thanks for the article. Do you know what is the relative error that used in the rpart to find the best CP?
Not offhand, is it mentioned in the ?rpart documentation
how number of wolves select feature in wolf search algorithm
I don’t know about that algorithms sorry.
Thanks for this article and your site. Running the Logarithmic Loss example with R 3.5, I got a different and sub-optimal result, claiming cp = 0.44 gives a minimal logLoss of 0.390. I got a correct result when number is increased to 10 instead of 5. Moreover, I didn’t get the SD column. Is there a trick to get them?
Perhaps the API has changed since I wrote the post?
Say I have 80% / 20% train and test data split.
Would one calculate RMSE and RSquared on the test data? Or does one calculate RMSE on test and RSquared on the train data?
Thank you
On the test data.
The reason is because you are estimating the skill of the model when making predictions on data unseen during training. New data. This is how you intend to use the model in practice.
Hi Jason! Thank you very much for your post!
In a regression problem, I want to fit a model focusing on low values, instead of high values.
In some papers that discuss metrics of evaluation models, such as “DAWSON et al (2007). HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts”, they explain that “RMSE” better fits the high values (because compared values are squared) and “Rsquared” use to seek for better shape of the values, and the values are also squared.
Then what do you suggest to set in “metrics”, if my intention is to better model the low values, applying caret-train-metrics? Because of this worry, RMSE and Rsquared do not seem adequate to apply.
Thanks again!
Perhaps try a few metrics and see what tracks with your intuitions or requirements?
Dear Dr Brownlee
many thanks for your helpful tutorials.
I followed “Your First Machine Learning Project in R Step-By-Step” and then looked into this article.
I have some questions:
– do these metrics (in particular RMSE and R^2, ROC and log loss) follow the same logic of training the model and then testing it on the validation data set? or this is true only for accuracy and K?
– what does log loss do? in which sense log loss estimate the probabilities of the model?
– how do I get cut-off scores for ROC?
Many Thanks
Most can be used to fit and evaluate a model.
You can learn more about log loss here:
https://machinelearningmastery.com/how-to-score-probability-predictions-in-python/
You can learn more about ROC here:
https://machinelearningmastery.com/roc-curves-and-precision-recall-curves-for-classification-in-python/
HI Jason,
I want to compare adjusted r-squared of SVR, RF, ANN, MLR on new data (test data after generating predictions). I know caret has a function for R-squared and RMSE, but I can’t find any functions for ADJUSTED r-squared in R…Please help
I’m no sure off the cuff sorry, perhaps try cross validated or the r user group?
Hi Jason,
Thank you for the great article.
I have one question when using the traincontrol. When i am using the below code snippet to run GBM model. I am getting the accuracy of around 86% for best tune model. But when i run on the entire train dataset it is around 98%. Why there is such a gap between the train and cross validation error.
I will be obliged. Looking forward for your reply.
gbmGrid <- expand.grid(
n.trees = (1:30)*50,
shrinkage=c(0.05,0.1,0.2,0.3),n.minobsinnode = c(10,15, 12),interaction.depth=c(4,5,6,8,9))
trainControl <- trainControl(method = "repeatedcv",
number = 3,
repeats = 3,
classProbs = T,
savePredictions = "all",
allowParallel = T)
modelFit <- train(
dv ~ . , data = train,
method = "gbm",
trControl = trainControl,
metric = "AUC",
preProcess = c("scale", "center"),
tuneGrid = gbmGrid,
bag.fraction=0.5
)
Perhaps your dataset is too small?
Yes, it is. But the model selection process shouldn’t select overfit model? Is this overfitted model?
You can tell if a model is overfit by comparing performance on a train set vs a test set.
Thank you for the reply Jason.
In this case, should I be checking Test accuracy Vs Cross validation accuracy of best tune model or Test Accuracy Vs Training accuracy to say whether the model is an overfit?
That is one approach.
If the model learns iteratively, and most do, then you can use learning curves for a single run:
https://machinelearningmastery.com/learning-curves-for-diagnosing-machine-learning-model-performance/
Correct me if I am wrong but in the case of GBM, parameters are chosen from expand.grid and a model is generated and with respect to that model accuracy is calculated?
Is there a way I can have the Validation accuracy to be calculated at each tree depth in caret R?
Perhaps you can vary the tree depth parameter on the model?
Hi Jason,
Thank you for your great post like always! You mentioned that Logarithmic Loss is good for multi-class classification problem. I want to ask if the multi-class are also imbalanced, is Logarithmic Loss also proper? For imbalanced multi-class dataset for classification, what metric you would suggest to use? Thank you!
Categorical cross entropy is the loss for multi-class classification or multinomial loss.
Perhaps start here:
https://machinelearningmastery.com/cross-entropy-for-machine-learning/