Generative Adversarial Networks, or GANs, are an architecture for training generative models, such as deep convolutional neural networks for generating images.
Although GAN models are capable of generating new random plausible examples for a given dataset, there is no way to control the types of images that are generated other than trying to figure out the complex relationship between the latent space input to the generator and the generated images.
The conditional generative adversarial network, or cGAN for short, is a type of GAN that involves the conditional generation of images by a generator model. Image generation can be conditional on a class label, if available, allowing the targeted generated of images of a given type.
In this tutorial, you will discover how to develop a conditional generative adversarial network for the targeted generation of items of clothing.
After completing this tutorial, you will know:
- The limitations of generating random samples with a GAN that can be overcome with a conditional generative adversarial network.
- How to develop and evaluate an unconditional generative adversarial network for generating photos of items of clothing.
- How to develop and evaluate a conditional generative adversarial network for generating photos of items of clothing.
Kick-start your project with my new book Generative Adversarial Networks with Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to Develop a Conditional Generative Adversarial Network From Scratch
Photo by Big Cypress National Preserve, some rights reserved
Tutorial Overview
This tutorial is divided into five parts; they are:
- Conditional Generative Adversarial Networks
- Fashion-MNIST Clothing Photograph Dataset
- Unconditional GAN for Fashion-MNIST
- Conditional GAN for Fashion-MNIST
- Conditional Clothing Generation
Conditional Generative Adversarial Networks
A generative adversarial network, or GAN for short, is an architecture for training deep learning-based generative models.
The architecture is comprised of a generator and a discriminator model. The generator model is responsible for generating new plausible examples that ideally are indistinguishable from real examples in the dataset. The discriminator model is responsible for classifying a given image as either real (drawn from the dataset) or fake (generated).
The models are trained together in a zero-sum or adversarial manner, such that improvements in the discriminator come at the cost of a reduced capability of the generator, and vice versa.
GANs are effective at image synthesis, that is, generating new examples of images for a target dataset. Some datasets have additional information, such as a class label, and it is desirable to make use of this information.
For example, the MNIST handwritten digit dataset has class labels of the corresponding integers, the CIFAR-10 small object photograph dataset has class labels for the corresponding objects in the photographs, and the Fashion-MNIST clothing dataset has class labels for the corresponding items of clothing.
There are two motivations for making use of the class label information in a GAN model.
- Improve the GAN.
- Targeted Image Generation.
Additional information that is correlated with the input images, such as class labels, can be used to improve the GAN. This improvement may come in the form of more stable training, faster training, and/or generated images that have better quality.
Class labels can also be used for the deliberate or targeted generation of images of a given type.
A limitation of a GAN model is that it may generate a random image from the domain. There is a relationship between points in the latent space to the generated images, but this relationship is complex and hard to map.
Alternately, a GAN can be trained in such a way that both the generator and the discriminator models are conditioned on the class label. This means that when the trained generator model is used as a standalone model to generate images in the domain, images of a given type, or class label, can be generated.
Generative adversarial nets can be extended to a conditional model if both the generator and discriminator are conditioned on some extra information y. […] We can perform the conditioning by feeding y into the both the discriminator and generator as additional input layer.
— Conditional Generative Adversarial Nets, 2014.
For example, in the case of MNIST, specific handwritten digits can be generated, such as the number 9; in the case of CIFAR-10, specific object photographs can be generated such as ‘frogs‘; and in the case of the Fashion MNIST dataset, specific items of clothing can be generated, such as ‘dress.’
This type of model is called a Conditional Generative Adversarial Network, CGAN or cGAN for short.
The cGAN was first described by Mehdi Mirza and Simon Osindero in their 2014 paper titled “Conditional Generative Adversarial Nets.” In the paper, the authors motivate the approach based on the desire to direct the image generation process of the generator model.
… by conditioning the model on additional information it is possible to direct the data generation process. Such conditioning could be based on class labels
— Conditional Generative Adversarial Nets, 2014.
Their approach is demonstrated in the MNIST handwritten digit dataset where the class labels are one hot encoded and concatenated with the input to both the generator and discriminator models.
The image below provides a summary of the model architecture.
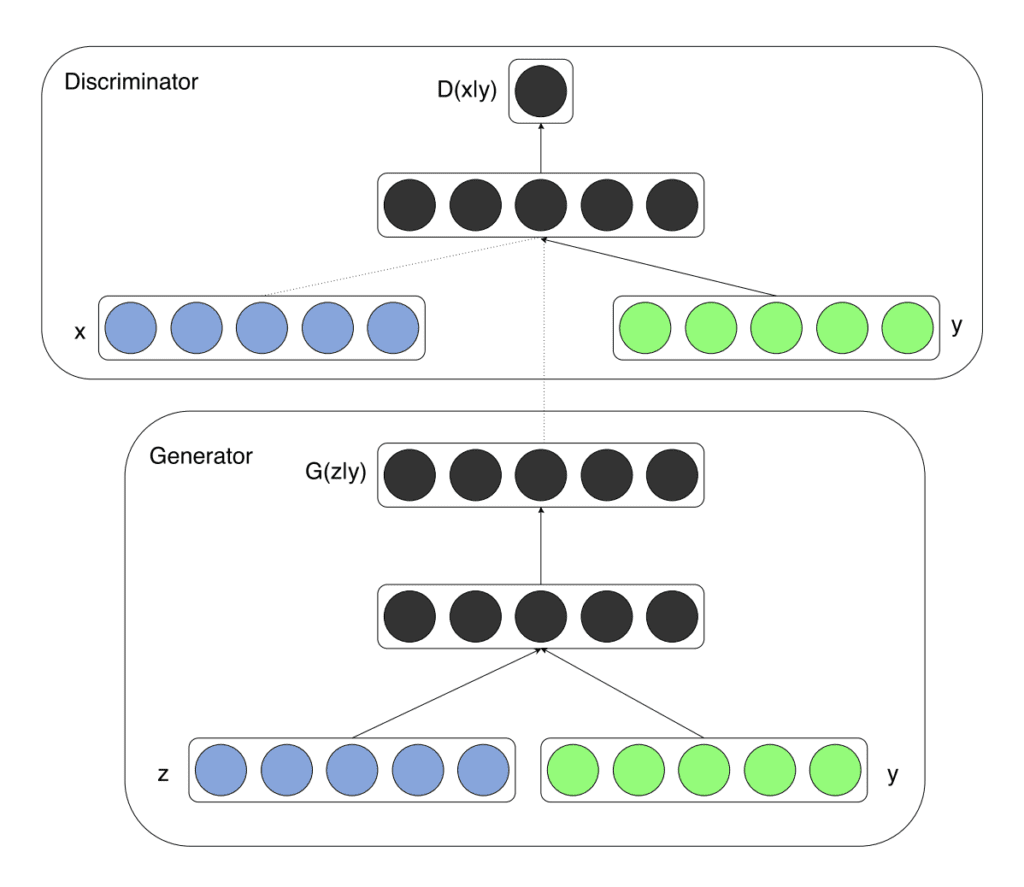
Example of a Conditional Generator and a Conditional Discriminator in a Conditional Generative Adversarial Network.
Taken from Conditional Generative Adversarial Nets, 2014.
There have been many advancements in the design and training of GAN models, most notably the deep convolutional GAN, or DCGAN for short, that outlines the model configuration and training procedures that reliably result in the stable training of GAN models for a wide variety of problems. The conditional training of the DCGAN-based models may be referred to as CDCGAN or cDCGAN for short.
There are many ways to encode and incorporate the class labels into the discriminator and generator models. A best practice involves using an embedding layer followed by a fully connected layer with a linear activation that scales the embedding to the size of the image before concatenating it in the model as an additional channel or feature map.
A version of this recommendation was described in the 2015 paper titled “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks.”
… we also explore a class conditional version of the model, where a vector c encodes the label. This is integrated into Gk & Dk by passing it through a linear layer whose output is reshaped into a single plane feature map which is then concatenated with the 1st layer maps.
— Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks, 2015.
This recommendation was later added to the ‘GAN Hacks‘ list of heuristic recommendations when designing and training GAN models, summarized as:
16: Discrete variables in Conditional GANs
– Use an Embedding layer
– Add as additional channels to images
– Keep embedding dimensionality low and upsample to match image channel size
Although GANs can be conditioned on the class label, so-called class-conditional GANs, they can also be conditioned on other inputs, such as an image, in the case where a GAN is used for image-to-image translation tasks.
In this tutorial, we will develop a GAN, specifically a DCGAN, then update it to use class labels in a cGAN, specifically a cDCGAN model architecture.
Want to Develop GANs from Scratch?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Fashion-MNIST Clothing Photograph Dataset
The Fashion-MNIST dataset is proposed as a more challenging replacement dataset for the MNIST dataset.
It is a dataset comprised of 60,000 small square 28×28 pixel grayscale images of items of 10 types of clothing, such as shoes, t-shirts, dresses, and more.
Keras provides access to the Fashion-MNIST dataset via the fashion_mnist.load_dataset() function. It returns two tuples, one with the input and output elements for the standard training dataset, and another with the input and output elements for the standard test dataset.
The example below loads the dataset and summarizes the shape of the loaded dataset.
Note: the first time you load the dataset, Keras will automatically download a compressed version of the images and save them under your home directory in ~/.keras/datasets/. The download is fast as the dataset is only about 25 megabytes in its compressed form.
|
1 2 3 4 5 6 7 |
# example of loading the fashion_mnist dataset from keras.datasets.fashion_mnist import load_data # load the images into memory (trainX, trainy), (testX, testy) = load_data() # summarize the shape of the dataset print('Train', trainX.shape, trainy.shape) print('Test', testX.shape, testy.shape) |
Running the example loads the dataset and prints the shape of the input and output components of the train and test splits of images.
We can see that there are 60K examples in the training set and 10K in the test set and that each image is a square of 28 by 28 pixels.
|
1 2 |
Train (60000, 28, 28) (60000,) Test (10000, 28, 28) (10000,) |
The images are grayscale with a black background (0 pixel value) and the items of clothing are in white ( pixel values near 255). This means if the images were plotted, they would be mostly black with a white item of clothing in the middle.
We can plot some of the images from the training dataset using the matplotlib library with the imshow() function and specify the color map via the ‘cmap‘ argument as ‘gray‘ to show the pixel values correctly.
|
1 2 |
# plot raw pixel data pyplot.imshow(trainX[i], cmap='gray') |
Alternately, the images are easier to review when we reverse the colors and plot the background as white and the clothing in black.
They are easier to view as most of the image is now white with the area of interest in black. This can be achieved using a reverse grayscale color map, as follows:
|
1 2 |
# plot raw pixel data pyplot.imshow(trainX[i], cmap='gray_r') |
The example below plots the first 100 images from the training dataset in a 10 by 10 square.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# example of loading the fashion_mnist dataset from keras.datasets.fashion_mnist import load_data from matplotlib import pyplot # load the images into memory (trainX, trainy), (testX, testy) = load_data() # plot images from the training dataset for i in range(100): # define subplot pyplot.subplot(10, 10, 1 + i) # turn off axis pyplot.axis('off') # plot raw pixel data pyplot.imshow(trainX[i], cmap='gray_r') pyplot.show() |
Running the example creates a figure with a plot of 100 images from the MNIST training dataset, arranged in a 10×10 square.

Plot of the First 100 Items of Clothing From the Fashion MNIST Dataset.
We will use the images in the training dataset as the basis for training a Generative Adversarial Network.
Specifically, the generator model will learn how to generate new plausible items of clothing using a discriminator that will try to distinguish between real images from the Fashion MNIST training dataset and new images output by the generator model.
This is a relatively simple problem that does not require a sophisticated generator or discriminator model, although it does require the generation of a grayscale output image.
Unconditional GAN for Fashion-MNIST
In this section, we will develop an unconditional GAN for the Fashion-MNIST dataset.
The first step is to define the models.
The discriminator model takes as input one 28×28 grayscale image and outputs a binary prediction as to whether the image is real (class=1) or fake (class=0). It is implemented as a modest convolutional neural network using best practices for GAN design such as using the LeakyReLU activation function with a slope of 0.2, using a 2×2 stride to downsample, and the adam version of stochastic gradient descent with a learning rate of 0.0002 and a momentum of 0.5
The define_discriminator() function below implements this, defining and compiling the discriminator model and returning it. The input shape of the image is parameterized as a default function argument in case you want to re-use the function for your own image data later.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# define the standalone discriminator model def define_discriminator(in_shape=(28,28,1)): model = Sequential() # downsample model.add(Conv2D(128, (3,3), strides=(2,2), padding='same', input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # downsample model.add(Conv2D(128, (3,3), strides=(2,2), padding='same')) model.add(LeakyReLU(alpha=0.2)) # classifier model.add(Flatten()) model.add(Dropout(0.4)) model.add(Dense(1, activation='sigmoid')) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model |
The generator model takes as input a point in the latent space and outputs a single 28×28 grayscale image. This is achieved by using a fully connected layer to interpret the point in the latent space and provide sufficient activations that can be reshaped into many copies (in this case 128) of a low-resolution version of the output image (e.g. 7×7). This is then upsampled twice, doubling the size and quadrupling the area of the activations each time using transpose convolutional layers. The model uses best practices such as the LeakyReLU activation, a kernel size that is a factor of the stride size, and a hyperbolic tangent (tanh) activation function in the output layer.
The define_generator() function below defines the generator model, but intentionally does not compile it as it is not trained directly, then returns the model. The size of the latent space is parameterized as a function argument.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# define the standalone generator model def define_generator(latent_dim): model = Sequential() # foundation for 7x7 image n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # upsample to 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')) model.add(LeakyReLU(alpha=0.2)) # upsample to 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')) model.add(LeakyReLU(alpha=0.2)) # generate model.add(Conv2D(1, (7,7), activation='tanh', padding='same')) return model |
Next, a GAN model can be defined that combines both the generator model and the discriminator model into one larger model. This larger model will be used to train the model weights in the generator, using the output and error calculated by the discriminator model. The discriminator model is trained separately, and as such, the model weights are marked as not trainable in this larger GAN model to ensure that only the weights of the generator model are updated. This change to the trainability of the discriminator weights only has an effect when training the combined GAN model, not when training the discriminator standalone.
This larger GAN model takes as input a point in the latent space, uses the generator model to generate an image which is fed as input to the discriminator model, then is output or classified as real or fake.
The define_gan() function below implements this, taking the already-defined generator and discriminator models as input.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# define the combined generator and discriminator model, for updating the generator def define_gan(generator, discriminator): # make weights in the discriminator not trainable discriminator.trainable = False # connect them model = Sequential() # add generator model.add(generator) # add the discriminator model.add(discriminator) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model |
Now that we have defined the GAN model, we need to train it. But, before we can train the model, we require input data.
The first step is to load and prepare the Fashion MNIST dataset. We only require the images in the training dataset. The images are black and white, therefore we must add an additional channel dimension to transform them to be three dimensional, as expected by the convolutional layers of our models. Finally, the pixel values must be scaled to the range [-1,1] to match the output of the generator model.
The load_real_samples() function below implements this, returning the loaded and scaled Fashion MNIST training dataset ready for modeling.
|
1 2 3 4 5 6 7 8 9 10 11 |
# load fashion mnist images def load_real_samples(): # load dataset (trainX, _), (_, _) = load_data() # expand to 3d, e.g. add channels X = expand_dims(trainX, axis=-1) # convert from ints to floats X = X.astype('float32') # scale from [0,255] to [-1,1] X = (X - 127.5) / 127.5 return X |
We will require one batch (or a half) batch of real images from the dataset each update to the GAN model. A simple way to achieve this is to select a random sample of images from the dataset each time.
The generate_real_samples() function below implements this, taking the prepared dataset as an argument, selecting and returning a random sample of Fashion MNIST images and their corresponding class label for the discriminator, specifically class=1, indicating that they are real images.
|
1 2 3 4 5 6 7 8 9 |
# select real samples def generate_real_samples(dataset, n_samples): # choose random instances ix = randint(0, dataset.shape[0], n_samples) # select images X = dataset[ix] # generate class labels y = ones((n_samples, 1)) return X, y |
Next, we need inputs for the generator model. These are random points from the latent space, specifically Gaussian distributed random variables.
The generate_latent_points() function implements this, taking the size of the latent space as an argument and the number of points required and returning them as a batch of input samples for the generator model.
|
1 2 3 4 5 6 7 |
# generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network x_input = x_input.reshape(n_samples, latent_dim) return x_input |
Next, we need to use the points in the latent space as input to the generator in order to generate new images.
The generate_fake_samples() function below implements this, taking the generator model and size of the latent space as arguments, then generating points in the latent space and using them as input to the generator model. The function returns the generated images and their corresponding class label for the discriminator model, specifically class=0 to indicate they are fake or generated.
|
1 2 3 4 5 6 7 8 9 |
# use the generator to generate n fake examples, with class labels def generate_fake_samples(generator, latent_dim, n_samples): # generate points in latent space x_input = generate_latent_points(latent_dim, n_samples) # predict outputs X = generator.predict(x_input) # create class labels y = zeros((n_samples, 1)) return X, y |
We are now ready to fit the GAN models.
The model is fit for 100 training epochs, which is arbitrary, as the model begins generating plausible items of clothing after perhaps 20 epochs. A batch size of 128 samples is used, and each training epoch involves 60,000/128, or about 468 batches of real and fake samples and updates to the model.
First, the discriminator model is updated for a half batch of real samples, then a half batch of fake samples, together forming one batch of weight updates. The generator is then updated via the composite gan model. Importantly, the class label is set to 1 or real for the fake samples. This has the effect of updating the generator toward getting better at generating real samples on the next batch.
The train() function below implements this, taking the defined models, dataset, and size of the latent dimension as arguments and parameterizing the number of epochs and batch size with default arguments. The generator model is saved at the end of training.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# train the generator and discriminator def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=100, n_batch=128): bat_per_epo = int(dataset.shape[0] / n_batch) half_batch = int(n_batch / 2) # manually enumerate epochs for i in range(n_epochs): # enumerate batches over the training set for j in range(bat_per_epo): # get randomly selected 'real' samples X_real, y_real = generate_real_samples(dataset, half_batch) # update discriminator model weights d_loss1, _ = d_model.train_on_batch(X_real, y_real) # generate 'fake' examples X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # update discriminator model weights d_loss2, _ = d_model.train_on_batch(X_fake, y_fake) # prepare points in latent space as input for the generator X_gan = generate_latent_points(latent_dim, n_batch) # create inverted labels for the fake samples y_gan = ones((n_batch, 1)) # update the generator via the discriminator's error g_loss = gan_model.train_on_batch(X_gan, y_gan) # summarize loss on this batch print('>%d, %d/%d, d1=%.3f, d2=%.3f g=%.3f' % (i+1, j+1, bat_per_epo, d_loss1, d_loss2, g_loss)) # save the generator model g_model.save('generator.h5') |
We can then define the size of the latent space, define all three models, and train them on the loaded fashion MNIST dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# size of the latent space latent_dim = 100 # create the discriminator discriminator = define_discriminator() # create the generator generator = define_generator(latent_dim) # create the gan gan_model = define_gan(generator, discriminator) # load image data dataset = load_real_samples() # train model train(generator, discriminator, gan_model, dataset, latent_dim) |
Tying all of this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 |
# example of training an unconditional gan on the fashion mnist dataset from numpy import expand_dims from numpy import zeros from numpy import ones from numpy.random import randn from numpy.random import randint from keras.datasets.fashion_mnist import load_data from keras.optimizers import Adam from keras.models import Sequential from keras.layers import Dense from keras.layers import Reshape from keras.layers import Flatten from keras.layers import Conv2D from keras.layers import Conv2DTranspose from keras.layers import LeakyReLU from keras.layers import Dropout # define the standalone discriminator model def define_discriminator(in_shape=(28,28,1)): model = Sequential() # downsample model.add(Conv2D(128, (3,3), strides=(2,2), padding='same', input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # downsample model.add(Conv2D(128, (3,3), strides=(2,2), padding='same')) model.add(LeakyReLU(alpha=0.2)) # classifier model.add(Flatten()) model.add(Dropout(0.4)) model.add(Dense(1, activation='sigmoid')) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model # define the standalone generator model def define_generator(latent_dim): model = Sequential() # foundation for 7x7 image n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # upsample to 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')) model.add(LeakyReLU(alpha=0.2)) # upsample to 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')) model.add(LeakyReLU(alpha=0.2)) # generate model.add(Conv2D(1, (7,7), activation='tanh', padding='same')) return model # define the combined generator and discriminator model, for updating the generator def define_gan(generator, discriminator): # make weights in the discriminator not trainable discriminator.trainable = False # connect them model = Sequential() # add generator model.add(generator) # add the discriminator model.add(discriminator) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model # load fashion mnist images def load_real_samples(): # load dataset (trainX, _), (_, _) = load_data() # expand to 3d, e.g. add channels X = expand_dims(trainX, axis=-1) # convert from ints to floats X = X.astype('float32') # scale from [0,255] to [-1,1] X = (X - 127.5) / 127.5 return X # select real samples def generate_real_samples(dataset, n_samples): # choose random instances ix = randint(0, dataset.shape[0], n_samples) # select images X = dataset[ix] # generate class labels y = ones((n_samples, 1)) return X, y # generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network x_input = x_input.reshape(n_samples, latent_dim) return x_input # use the generator to generate n fake examples, with class labels def generate_fake_samples(generator, latent_dim, n_samples): # generate points in latent space x_input = generate_latent_points(latent_dim, n_samples) # predict outputs X = generator.predict(x_input) # create class labels y = zeros((n_samples, 1)) return X, y # train the generator and discriminator def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=100, n_batch=128): bat_per_epo = int(dataset.shape[0] / n_batch) half_batch = int(n_batch / 2) # manually enumerate epochs for i in range(n_epochs): # enumerate batches over the training set for j in range(bat_per_epo): # get randomly selected 'real' samples X_real, y_real = generate_real_samples(dataset, half_batch) # update discriminator model weights d_loss1, _ = d_model.train_on_batch(X_real, y_real) # generate 'fake' examples X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # update discriminator model weights d_loss2, _ = d_model.train_on_batch(X_fake, y_fake) # prepare points in latent space as input for the generator X_gan = generate_latent_points(latent_dim, n_batch) # create inverted labels for the fake samples y_gan = ones((n_batch, 1)) # update the generator via the discriminator's error g_loss = gan_model.train_on_batch(X_gan, y_gan) # summarize loss on this batch print('>%d, %d/%d, d1=%.3f, d2=%.3f g=%.3f' % (i+1, j+1, bat_per_epo, d_loss1, d_loss2, g_loss)) # save the generator model g_model.save('generator.h5') # size of the latent space latent_dim = 100 # create the discriminator discriminator = define_discriminator() # create the generator generator = define_generator(latent_dim) # create the gan gan_model = define_gan(generator, discriminator) # load image data dataset = load_real_samples() # train model train(generator, discriminator, gan_model, dataset, latent_dim) |
Running the example may take a long time on modest hardware.
I recommend running the example on GPU hardware. If you need help, you can get started quickly by using an AWS EC2 instance to train the model. See the tutorial:
The loss for the discriminator on real and fake samples, as well as the loss for the generator, is reported after each batch.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, the discriminator and generator loss both sit around values of about 0.6 to 0.7 over the course of training.
|
1 2 3 4 5 6 |
... >100, 464/468, d1=0.681, d2=0.685 g=0.693 >100, 465/468, d1=0.691, d2=0.700 g=0.703 >100, 466/468, d1=0.691, d2=0.703 g=0.706 >100, 467/468, d1=0.698, d2=0.699 g=0.699 >100, 468/468, d1=0.699, d2=0.695 g=0.708 |
At the end of training, the generator model will be saved to file with the filename ‘generator.h5‘.
This model can be loaded and used to generate new random but plausible samples from the fashion MNIST dataset.
The example below loads the saved model and generates 100 random items of clothing.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# example of loading the generator model and generating images from keras.models import load_model from numpy.random import randn from matplotlib import pyplot # generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network x_input = x_input.reshape(n_samples, latent_dim) return x_input # create and save a plot of generated images (reversed grayscale) def show_plot(examples, n): # plot images for i in range(n * n): # define subplot pyplot.subplot(n, n, 1 + i) # turn off axis pyplot.axis('off') # plot raw pixel data pyplot.imshow(examples[i, :, :, 0], cmap='gray_r') pyplot.show() # load model model = load_model('generator.h5') # generate images latent_points = generate_latent_points(100, 100) # generate images X = model.predict(latent_points) # plot the result show_plot(X, 10) |
Running the example creates a plot of 100 randomly generated items of clothing arranged into a 10×10 grid.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see an assortment of clothing items such as shoes, sweaters, and pants. Most items look quite plausible and could have come from the fashion MNIST dataset. They are not perfect, however, as there are some sweaters with a single sleeve and shoes that look like a mess.

Example of 100 Generated items of Clothing using an Unconditional GAN.
Conditional GAN for Fashion-MNIST
In this section, we will develop a conditional GAN for the Fashion-MNIST dataset by updating the unconditional GAN developed in the previous section.
The best way to design models in Keras to have multiple inputs is by using the Functional API, as opposed to the Sequential API used in the previous section. We will use the functional API to re-implement the discriminator, generator, and the composite model.
Starting with the discriminator model, a new second input is defined that takes an integer for the class label of the image. This has the effect of making the input image conditional on the provided class label.
The class label is then passed through an Embedding layer with the size of 50. This means that each of the 10 classes for the Fashion MNIST dataset (0 through 9) will map to a different 50-element vector representation that will be learned by the discriminator model.
The output of the embedding is then passed to a fully connected layer with a linear activation. Importantly, the fully connected layer has enough activations that can be reshaped into one channel of a 28×28 image. The activations are reshaped into single 28×28 activation map and concatenated with the input image. This has the effect of looking like a two-channel input image to the next convolutional layer.
The define_discriminator() below implements this update to the discriminator model. The parameterized shape of the input image is also used after the embedding layer to define the number of activations for the fully connected layer to reshape its output. The number of classes in the problem is also parameterized in the function and set.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# define the standalone discriminator model def define_discriminator(in_shape=(28,28,1), n_classes=10): # label input in_label = Input(shape=(1,)) # embedding for categorical input li = Embedding(n_classes, 50)(in_label) # scale up to image dimensions with linear activation n_nodes = in_shape[0] * in_shape[1] li = Dense(n_nodes)(li) # reshape to additional channel li = Reshape((in_shape[0], in_shape[1], 1))(li) # image input in_image = Input(shape=in_shape) # concat label as a channel merge = Concatenate()([in_image, li]) # downsample fe = Conv2D(128, (3,3), strides=(2,2), padding='same')(merge) fe = LeakyReLU(alpha=0.2)(fe) # downsample fe = Conv2D(128, (3,3), strides=(2,2), padding='same')(fe) fe = LeakyReLU(alpha=0.2)(fe) # flatten feature maps fe = Flatten()(fe) # dropout fe = Dropout(0.4)(fe) # output out_layer = Dense(1, activation='sigmoid')(fe) # define model model = Model([in_image, in_label], out_layer) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model |
In order to make the architecture clear, below is a plot of the discriminator model.
The plot shows the two inputs: first the class label that passes through the embedding (left) and the image (right), and their concatenation into a two-channel 28×28 image or feature map (middle). The rest of the model is the same as the discriminator designed in the previous section.
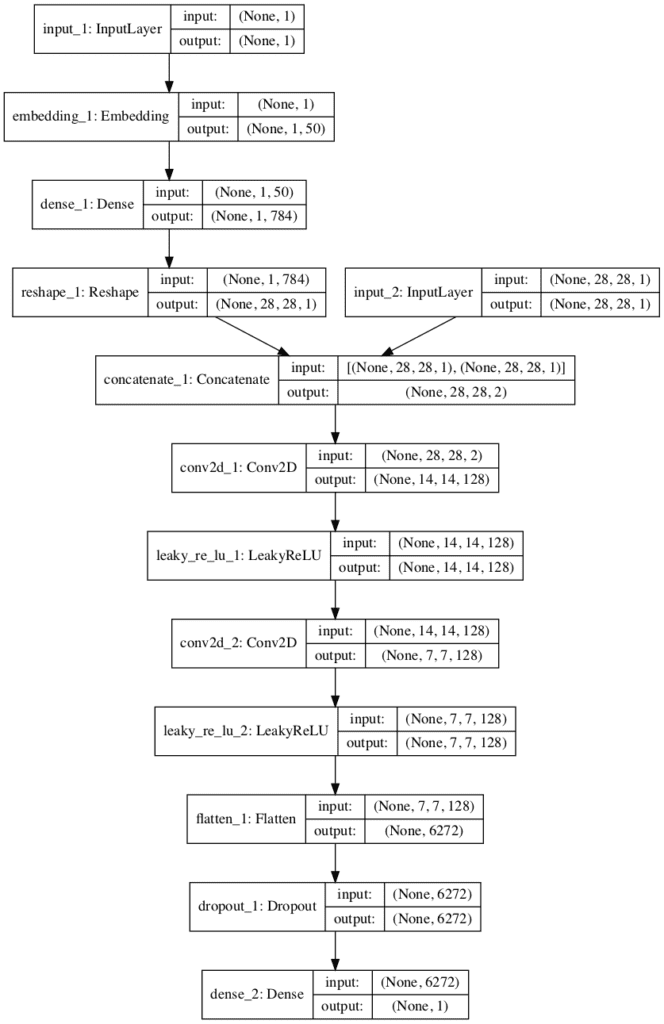
Plot of the Discriminator Model in the Conditional Generative Adversarial Network
Next, the generator model must be updated to take the class label. This has the effect of making the point in the latent space conditional on the provided class label.
As in the discriminator, the class label is passed through an embedding layer to map it to a unique 50-element vector and is then passed through a fully connected layer with a linear activation before being resized. In this case, the activations of the fully connected layer are resized into a single 7×7 feature map. This is to match the 7×7 feature map activations of the unconditional generator model. The new 7×7 feature map is added as one more channel to the existing 128, resulting in 129 feature maps that are then upsampled as in the prior model.
The define_generator() function below implements this, again parameterizing the number of classes as we did with the discriminator model.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# define the standalone generator model def define_generator(latent_dim, n_classes=10): # label input in_label = Input(shape=(1,)) # embedding for categorical input li = Embedding(n_classes, 50)(in_label) # linear multiplication n_nodes = 7 * 7 li = Dense(n_nodes)(li) # reshape to additional channel li = Reshape((7, 7, 1))(li) # image generator input in_lat = Input(shape=(latent_dim,)) # foundation for 7x7 image n_nodes = 128 * 7 * 7 gen = Dense(n_nodes)(in_lat) gen = LeakyReLU(alpha=0.2)(gen) gen = Reshape((7, 7, 128))(gen) # merge image gen and label input merge = Concatenate()([gen, li]) # upsample to 14x14 gen = Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')(merge) gen = LeakyReLU(alpha=0.2)(gen) # upsample to 28x28 gen = Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')(gen) gen = LeakyReLU(alpha=0.2)(gen) # output out_layer = Conv2D(1, (7,7), activation='tanh', padding='same')(gen) # define model model = Model([in_lat, in_label], out_layer) return model |
To help understand the new model architecture, the image below provides a plot of the new conditional generator model.
In this case, you can see the 100-element point in latent space as input and subsequent resizing (left) and the new class label input and embedding layer (right), then the concatenation of the two sets of feature maps (center). The remainder of the model is the same as the unconditional case.
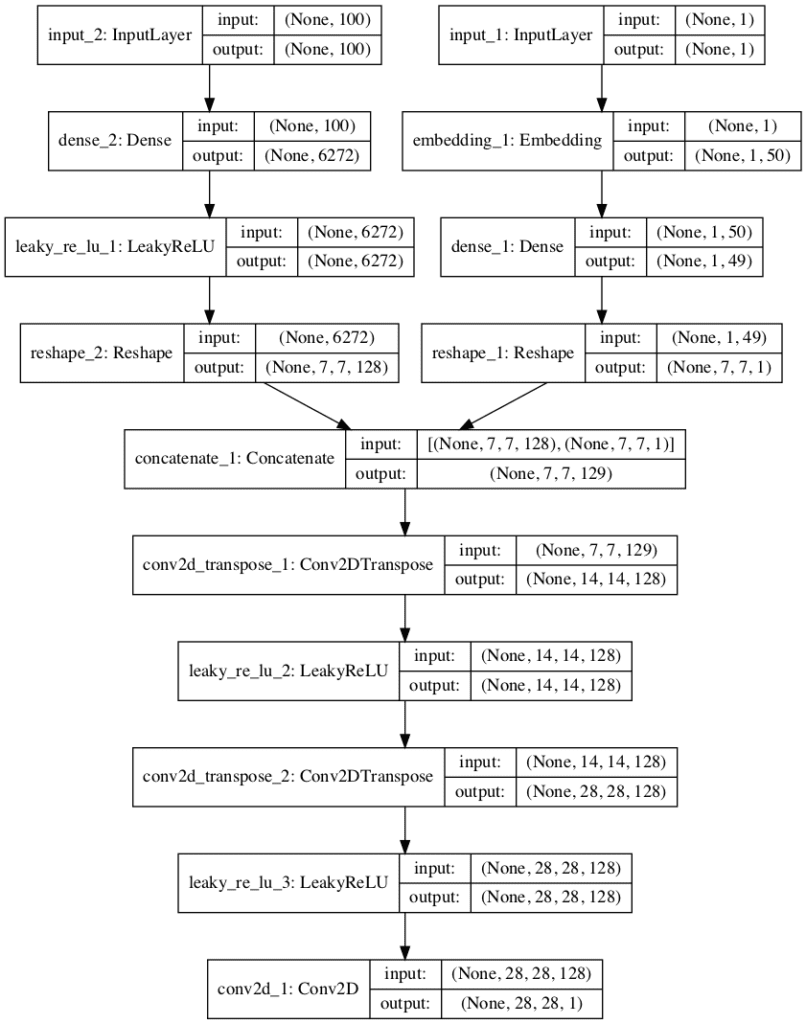
Plot of the Generator Model in the Conditional Generative Adversarial Network
Finally, the composite GAN model requires updating.
The new GAN model will take a point in latent space as input and a class label and generate a prediction of whether input was real or fake, as before.
Using the functional API to design the model, it is important that we explicitly connect the image generated output from the generator as well as the class label input, both as input to the discriminator model. This allows the same class label input to flow down into the generator and down into the discriminator.
The define_gan() function below implements the conditional version of the GAN.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# define the combined generator and discriminator model, for updating the generator def define_gan(g_model, d_model): # make weights in the discriminator not trainable d_model.trainable = False # get noise and label inputs from generator model gen_noise, gen_label = g_model.input # get image output from the generator model gen_output = g_model.output # connect image output and label input from generator as inputs to discriminator gan_output = d_model([gen_output, gen_label]) # define gan model as taking noise and label and outputting a classification model = Model([gen_noise, gen_label], gan_output) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model |
The plot below summarizes the composite GAN model.
Importantly, it shows the generator model in full with the point in latent space and class label as input, and the connection of the output of the generator and the same class label as input to the discriminator model (last box at the bottom of the plot) and the output of a single class label classification of real or fake.
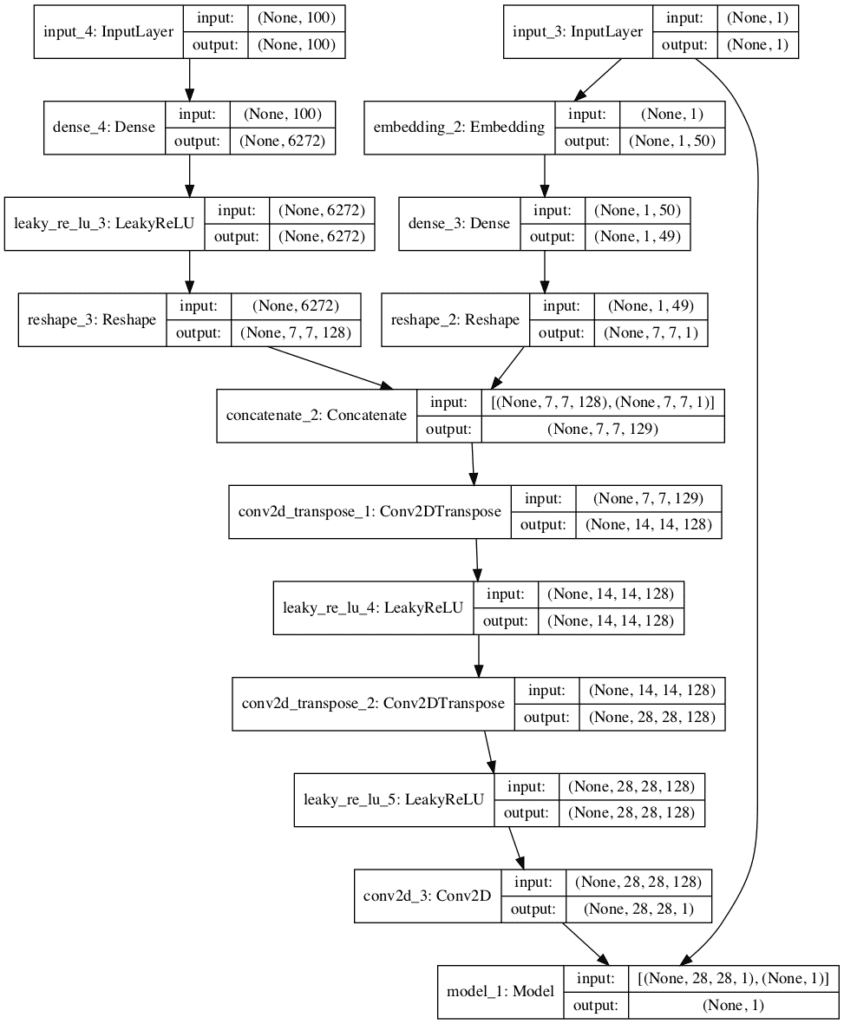
Plot of the Composite Generator and Discriminator Model in the Conditional Generative Adversarial Network
The hard part of the conversion from unconditional to conditional GAN is done, namely the definition and configuration of the model architecture.
Next, all that remains is to update the training process to also use class labels.
First, the load_real_samples() and generate_real_samples() functions for loading the dataset and selecting a batch of samples respectively must be updated to make use of the real class labels from the training dataset. Importantly, the generate_real_samples() function now returns images, clothing labels, and the class label for the discriminator (class=1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# load fashion mnist images def load_real_samples(): # load dataset (trainX, trainy), (_, _) = load_data() # expand to 3d, e.g. add channels X = expand_dims(trainX, axis=-1) # convert from ints to floats X = X.astype('float32') # scale from [0,255] to [-1,1] X = (X - 127.5) / 127.5 return [X, trainy] # select real samples def generate_real_samples(dataset, n_samples): # split into images and labels images, labels = dataset # choose random instances ix = randint(0, images.shape[0], n_samples) # select images and labels X, labels = images[ix], labels[ix] # generate class labels y = ones((n_samples, 1)) return [X, labels], y |
Next, the generate_latent_points() function must be updated to also generate an array of randomly selected integer class labels to go along with the randomly selected points in the latent space.
Then the generate_fake_samples() function must be updated to use these randomly generated class labels as input to the generator model when generating new fake images.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples, n_classes=10): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network z_input = x_input.reshape(n_samples, latent_dim) # generate labels labels = randint(0, n_classes, n_samples) return [z_input, labels] # use the generator to generate n fake examples, with class labels def generate_fake_samples(generator, latent_dim, n_samples): # generate points in latent space z_input, labels_input = generate_latent_points(latent_dim, n_samples) # predict outputs images = generator.predict([z_input, labels_input]) # create class labels y = zeros((n_samples, 1)) return [images, labels_input], y |
Finally, the train() function must be updated to retrieve and use the class labels in the calls to updating the discriminator and generator models.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# train the generator and discriminator def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=100, n_batch=128): bat_per_epo = int(dataset[0].shape[0] / n_batch) half_batch = int(n_batch / 2) # manually enumerate epochs for i in range(n_epochs): # enumerate batches over the training set for j in range(bat_per_epo): # get randomly selected 'real' samples [X_real, labels_real], y_real = generate_real_samples(dataset, half_batch) # update discriminator model weights d_loss1, _ = d_model.train_on_batch([X_real, labels_real], y_real) # generate 'fake' examples [X_fake, labels], y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # update discriminator model weights d_loss2, _ = d_model.train_on_batch([X_fake, labels], y_fake) # prepare points in latent space as input for the generator [z_input, labels_input] = generate_latent_points(latent_dim, n_batch) # create inverted labels for the fake samples y_gan = ones((n_batch, 1)) # update the generator via the discriminator's error g_loss = gan_model.train_on_batch([z_input, labels_input], y_gan) # summarize loss on this batch print('>%d, %d/%d, d1=%.3f, d2=%.3f g=%.3f' % (i+1, j+1, bat_per_epo, d_loss1, d_loss2, g_loss)) # save the generator model g_model.save('cgan_generator.h5') |
Tying all of this together, the complete example of a conditional deep convolutional generative adversarial network for the Fashion MNIST dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 |
# example of training an conditional gan on the fashion mnist dataset from numpy import expand_dims from numpy import zeros from numpy import ones from numpy.random import randn from numpy.random import randint from keras.datasets.fashion_mnist import load_data from keras.optimizers import Adam from keras.models import Model from keras.layers import Input from keras.layers import Dense from keras.layers import Reshape from keras.layers import Flatten from keras.layers import Conv2D from keras.layers import Conv2DTranspose from keras.layers import LeakyReLU from keras.layers import Dropout from keras.layers import Embedding from keras.layers import Concatenate # define the standalone discriminator model def define_discriminator(in_shape=(28,28,1), n_classes=10): # label input in_label = Input(shape=(1,)) # embedding for categorical input li = Embedding(n_classes, 50)(in_label) # scale up to image dimensions with linear activation n_nodes = in_shape[0] * in_shape[1] li = Dense(n_nodes)(li) # reshape to additional channel li = Reshape((in_shape[0], in_shape[1], 1))(li) # image input in_image = Input(shape=in_shape) # concat label as a channel merge = Concatenate()([in_image, li]) # downsample fe = Conv2D(128, (3,3), strides=(2,2), padding='same')(merge) fe = LeakyReLU(alpha=0.2)(fe) # downsample fe = Conv2D(128, (3,3), strides=(2,2), padding='same')(fe) fe = LeakyReLU(alpha=0.2)(fe) # flatten feature maps fe = Flatten()(fe) # dropout fe = Dropout(0.4)(fe) # output out_layer = Dense(1, activation='sigmoid')(fe) # define model model = Model([in_image, in_label], out_layer) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model # define the standalone generator model def define_generator(latent_dim, n_classes=10): # label input in_label = Input(shape=(1,)) # embedding for categorical input li = Embedding(n_classes, 50)(in_label) # linear multiplication n_nodes = 7 * 7 li = Dense(n_nodes)(li) # reshape to additional channel li = Reshape((7, 7, 1))(li) # image generator input in_lat = Input(shape=(latent_dim,)) # foundation for 7x7 image n_nodes = 128 * 7 * 7 gen = Dense(n_nodes)(in_lat) gen = LeakyReLU(alpha=0.2)(gen) gen = Reshape((7, 7, 128))(gen) # merge image gen and label input merge = Concatenate()([gen, li]) # upsample to 14x14 gen = Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')(merge) gen = LeakyReLU(alpha=0.2)(gen) # upsample to 28x28 gen = Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')(gen) gen = LeakyReLU(alpha=0.2)(gen) # output out_layer = Conv2D(1, (7,7), activation='tanh', padding='same')(gen) # define model model = Model([in_lat, in_label], out_layer) return model # define the combined generator and discriminator model, for updating the generator def define_gan(g_model, d_model): # make weights in the discriminator not trainable d_model.trainable = False # get noise and label inputs from generator model gen_noise, gen_label = g_model.input # get image output from the generator model gen_output = g_model.output # connect image output and label input from generator as inputs to discriminator gan_output = d_model([gen_output, gen_label]) # define gan model as taking noise and label and outputting a classification model = Model([gen_noise, gen_label], gan_output) # compile model opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model # load fashion mnist images def load_real_samples(): # load dataset (trainX, trainy), (_, _) = load_data() # expand to 3d, e.g. add channels X = expand_dims(trainX, axis=-1) # convert from ints to floats X = X.astype('float32') # scale from [0,255] to [-1,1] X = (X - 127.5) / 127.5 return [X, trainy] # # select real samples def generate_real_samples(dataset, n_samples): # split into images and labels images, labels = dataset # choose random instances ix = randint(0, images.shape[0], n_samples) # select images and labels X, labels = images[ix], labels[ix] # generate class labels y = ones((n_samples, 1)) return [X, labels], y # generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples, n_classes=10): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network z_input = x_input.reshape(n_samples, latent_dim) # generate labels labels = randint(0, n_classes, n_samples) return [z_input, labels] # use the generator to generate n fake examples, with class labels def generate_fake_samples(generator, latent_dim, n_samples): # generate points in latent space z_input, labels_input = generate_latent_points(latent_dim, n_samples) # predict outputs images = generator.predict([z_input, labels_input]) # create class labels y = zeros((n_samples, 1)) return [images, labels_input], y # train the generator and discriminator def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=100, n_batch=128): bat_per_epo = int(dataset[0].shape[0] / n_batch) half_batch = int(n_batch / 2) # manually enumerate epochs for i in range(n_epochs): # enumerate batches over the training set for j in range(bat_per_epo): # get randomly selected 'real' samples [X_real, labels_real], y_real = generate_real_samples(dataset, half_batch) # update discriminator model weights d_loss1, _ = d_model.train_on_batch([X_real, labels_real], y_real) # generate 'fake' examples [X_fake, labels], y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # update discriminator model weights d_loss2, _ = d_model.train_on_batch([X_fake, labels], y_fake) # prepare points in latent space as input for the generator [z_input, labels_input] = generate_latent_points(latent_dim, n_batch) # create inverted labels for the fake samples y_gan = ones((n_batch, 1)) # update the generator via the discriminator's error g_loss = gan_model.train_on_batch([z_input, labels_input], y_gan) # summarize loss on this batch print('>%d, %d/%d, d1=%.3f, d2=%.3f g=%.3f' % (i+1, j+1, bat_per_epo, d_loss1, d_loss2, g_loss)) # save the generator model g_model.save('cgan_generator.h5') # size of the latent space latent_dim = 100 # create the discriminator d_model = define_discriminator() # create the generator g_model = define_generator(latent_dim) # create the gan gan_model = define_gan(g_model, d_model) # load image data dataset = load_real_samples() # train model train(g_model, d_model, gan_model, dataset, latent_dim) |
Running the example may take some time, and GPU hardware is recommended, but not required.
At the end of the run, the model is saved to the file with name ‘cgan_generator.h5‘.
Conditional Clothing Generation
In this section, we will use the trained generator model to conditionally generate new photos of items of clothing.
We can update our code example for generating new images with the model to now generate images conditional on the class label. We can generate 10 examples for each class label in columns.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# example of loading the generator model and generating images from numpy import asarray from numpy.random import randn from numpy.random import randint from keras.models import load_model from matplotlib import pyplot # generate points in latent space as input for the generator def generate_latent_points(latent_dim, n_samples, n_classes=10): # generate points in the latent space x_input = randn(latent_dim * n_samples) # reshape into a batch of inputs for the network z_input = x_input.reshape(n_samples, latent_dim) # generate labels labels = randint(0, n_classes, n_samples) return [z_input, labels] # create and save a plot of generated images def save_plot(examples, n): # plot images for i in range(n * n): # define subplot pyplot.subplot(n, n, 1 + i) # turn off axis pyplot.axis('off') # plot raw pixel data pyplot.imshow(examples[i, :, :, 0], cmap='gray_r') pyplot.show() # load model model = load_model('cgan_generator.h5') # generate images latent_points, labels = generate_latent_points(100, 100) # specify labels labels = asarray([x for _ in range(10) for x in range(10)]) # generate images X = model.predict([latent_points, labels]) # scale from [-1,1] to [0,1] X = (X + 1) / 2.0 # plot the result save_plot(X, 10) |
Running the example loads the saved conditional GAN model and uses it to generate 100 items of clothing.
The clothing is organized in columns. From left to right, they are “t-shirt“, ‘trouser‘, ‘pullover‘, ‘dress‘, ‘coat‘, ‘sandal‘, ‘shirt‘, ‘sneaker‘, ‘bag‘, and ‘ankle boot‘.
We can see not only are the randomly generated items of clothing plausible, but they also match their expected category.

Example of 100 Generated items of Clothing using a Conditional GAN.
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Latent Space Size. Experiment by varying the size of the latent space and review the impact on the quality of generated images.
- Embedding Size. Experiment by varying the size of the class label embedding, making it smaller or larger, and review the impact on the quality of generated images.
- Alternate Architecture. Update the model architecture to concatenate the class label elsewhere in the generator and/or discriminator model, perhaps with different dimensionality, and review the impact on the quality of generated images.
If you explore any of these extensions, I’d love to know.
Post your findings in the comments below.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Posts
- Chapter 20. Deep Generative Models, Deep Learning, 2016.
- Chapter 8. Generative Deep Learning, Deep Learning with Python, 2017.
Papers
- Generative Adversarial Networks, 2014.
- Tutorial: Generative Adversarial Networks, NIPS, 2016.
- Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, 2015
- Conditional Generative Adversarial Nets, 2014.
- Image-To-Image Translation With Conditional Adversarial Networks, 2017.
- Conditional Generative Adversarial Nets For Convolutional Face Generation, 2015.
API
- Keras Datasets API.
- Keras Sequential Model API
- Keras Convolutional Layers API
- How can I “freeze” Keras layers?
- MatplotLib API
- NumPy Random sampling (numpy.random) API
- NumPy Array manipulation routines
Articles
- How to Train a GAN? Tips and tricks to make GANs work
- Fashion-MNIST Project, GitHub.
- Training a Conditional DC-GAN on CIFAR-10 (code), 2018.
- GAN: From Zero to Hero Part 2 Conditional Generation by GAN, 2018.
- Keras-GAN Project. Keras implementations of Generative Adversarial Networks, GitHub.
- Conditional Deep Convolutional GAN (CDCGAN) – Keras Implementation, GitHub.
Summary
In this tutorial, you discovered how to develop a conditional generative adversarial network for the targeted generation of items of clothing.
Specifically, you learned:
- The limitations of generating random samples with a GAN that can be overcome with a conditional generative adversarial network.
- How to develop and evaluate an unconditional generative adversarial network for generating photos of items of clothing.
- How to develop and evaluate a conditional generative adversarial network for generating photos of items of clothing.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.







cool ty.
Thanks Keith.
This is fantastic. Thanks for disseminating great knowledge.
What if I wanted to train the discriminator as well, as we are only training generator in the current model. Please correct me if I am wrong.
Help me understand how many samples it requires to train a generator, for it to generate new samples that resembles original distribution. Is there any constraint on minimum number of input samples for gans.
Thanks
Shravan
No, both the generator and discriminator are trained at the same time.
There is great work with the semi-supervised GAN on training a classifier with very few real samples.
Nice blog.
Do you have any blog on deployment of pytorch or tensorflow based gan model on Android?
I am desperately in need of it.
No, sorry.
Hi Jason , But you are setting the discriminator weights trainable as False
# make weights in the discriminator not trainable
d_model.trainable = False
I don’t understand it now .
Only in the context of the composite model.
To learn more about freezing weights in different contexts, see:
– How can I freeze layers and do fine-tuning?
https://keras.io/getting_started/faq/
A ton of great blog posts! I’m really excited for your book on GAN’s. I think bugged you about writing one a couple years ago! – A fan of your books.
Thanks! And thanks for bugging me Ken!
I’m really excited about it.
Ken
Request you to put the title of the book here please
Regards
Partha
Ken is referring to my upcoming book on GANs.
The title will be “Generative Adversarial Networks with Python”.
It should be available in a week or two.
I didn’t understand that how the generator will produce good results while training composite unconscious GAN by passing ones as output label, shouldn’t it be zeros?
In the unconditional GAN training.
The unconditional GAN is trained.
Perhaps I don’t understand your question?
It is crazy stuff.
Basically, we are training the generator to fool the discriminator, and in this case, the generator is conditional on the specific class label. The discriminator causes the discriminator to associate specific generated images with class labels.
If this is all new to you, perhaps start here:
https://machinelearningmastery.com/what-are-generative-adversarial-networks-gans/
Hello sir ,
I really appreciate your work .I have a question,I want to work with this technique but as an input I have an Image and then I feed it to the generator to have another image and then feed it to the descriminator but the problem is all tutorials are starting from a random input .
Do you have any blog or code you can help me with
It sounds like you might be interested in image to image translation.
This will help:
https://machinelearningmastery.com/a-gentle-introduction-to-pix2pix-generative-adversarial-network/
Great article, thank you! I have two questions.
First, you use an embedding layer on the labels in both the discriminator and generator. I don’t see what the embedding is doing for you. With just 10 labels, why is a 50-dimensional vector any more useful than a normal one-hot vector (after all, the ten one-hot vectors are orthonormal, so they’re as distinct as can be). So what is the algorithmic motivation for having an embedding layer?
Second, why then follow that with a dense layer? Again, the one-hot label vectors seem to be all we need, but here we’ve already turned them into 50-dimensional vectors. What necessary job is the dense layer accomplishing?
Thank you!
Great questions.
The embedding layer provides a projection of the class label, a distributed representation that can be used to condition the image generation and classification.
The distributed representation can be scaled up and inserted nicely into the model as a filter map like structure.
There are other ways of getting the class label into the model, but this approach is reported to be more effective. Why? That’s a hard question and might be intractable right now. Most of the GAN finding are empirical.
Try the alternate of just a one hot encoded vector concat with the z for G and a secondary input for D and compare results.
Hi Jason,
Thank you for this very useful and detailed. Do you have any references that explain the embedding idea more thoroughly, or can you offer any more intuition? I understand why you might use an embedding for words/sentences as there is an idea of semantic similarity there, but not following why in a dataset like this (or simple MNIST) an embedding layer makes sense. Is it effectively just a way of reshaping the one-hot? Thanks!
An embedding is an alternate to one hot encoding for categorical data.
It is popular for words, but can be used for any categorical or ordinal data.
In unconditional GAN codes, why discriminator model weights can be updated separately for exclusive real and fake sample ?
# update discriminator model weights
d_loss1, _ = d_model.train_on_batch(X_real, y_real)
# update discriminator model weights
d_loss2, _ = d_model.train_on_batch(X_fake, y_fake)
Basically discriminator is binary classification. If all samples are real (=1) or faked(=0) exclusively , the binary classification is unable to be converged. Why not combined X_real and X_fake together and then input the sample into discriminator which will classify real and faked sample, e.g.
d_loss, _ = d_model.train_on_batch([X_real, X_fake], [y_real, y_fake] )
You can, but it has been reported that separate batch updates keep the D model stable with respect to the performance of the generator (e.g. it does not get better – faster).
More here:
https://machinelearningmastery.com/how-to-code-generative-adversarial-network-hacks/
Thanks for the very useful tutorial!
I always get these kind of warnings:
“W0829 11:18:47.925395 14568 training.py:2197] Discrepancy between trainable weights and collected trainable weights, did you set
model.trainablewithout callingmodel.compileafter ?”Does it mean I did something different, or is this something you see as well. The model runs, so does it matter?
You can safely ignore that warning – we are abusing Keras a little 🙂
Hi Janson, very nice tutorial< I was stuck somewhere when running your code:
we define "define_discriminator(in_shape=(28,28,1))" with shape (28,28,1), and then we call it to do
"d_model.train_on_batch(X_real, y_real)", where the sample size is 64 (error message as follows):
ValueError: Error when checking model input: the list of Numpy arrays that you are passing to your model is not the size the model expected. Expected to see 1 array(s), but instead got the following list of 64 arrays: [, , …
I am new to deep learning so do not know how to fix it..
Sorry, I found out I made a mistake when I tried to copy your code< Ignore my question please.
No problem!
Sorry to hear that, I have some suggestions here that might help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
How is the discriminator model instance ‘d_model’ trained in the training loop, when the same instance is set to trainable=False in the ‘define_GAN’ method?
Setting trainable=False only effects the generator, it does not effect the discriminator.
See this:
https://keras.io/getting-started/faq/#how-can-i-freeze-keras-layers
Thank you very much! This is a clearly written, nicely structured and most inspiring tutorial. I love all the detailed explainations as well as the attached code. Excellent!
Thanks!
Thank you Jason! This is a really good tutorial. I went on to do some further experiments and I am facing some issues. I am trying to implement a cSAGAN with spectral normalization and for some reason, the discriminator throws up an error ‘NoneType’ object has no attribute ‘_inbound_nodes’.
This has been bothering me because the same attention layer worked well with an unconditioned SAGAN which works using Keras Sequential(). The problem is arising only when attention is added to this functional Keras model.
I need some insight from you on what could be wrong.
Not sure I can help you with your custom code, sorry. Perhaps try posting to stackoverflow?
I managed to figure it out eventually! It was a really silly mistake on my part. However I would still like to thank you again for this post which was the founding base for my project. You are doing a wonderful job!
Happy to hear that, well done!
Hi,
Does using an Embedding layer segment the latent space for each class? What I mean is can you use this method to get the generator to produce, for instance, a t-shirt+shoe combination?
Yes! Probably.
Hi, Jason
Do you think it is possible to train Conditional GAN with more than 1 condition? For example, I want to train a painter, which color the input picture, conditioned by non-color input picture and color label
Yes. I think infogan has multiple conditions.
Yes, sounds like a little image to image translation and a little conditional gan. Give it a try! Let me know how you go.
I’m currently following MC-GAN paper, but Info GAN look interesting as well. Definitely, gonna try it later
Very cool. Eager to hear how you go.
An awesome article Jason! Thank you for your effort.
You’re welcome.
As always, some beautiful work Brownlee. I realize this will be no surprise to you but you can run an almost identical cgan against the mnist (number) dataset by changing the following lines:
1. replace:
from tensorflow.keras.datasets.fashion_mnist import load_data
with:
from tensorflow.keras.datasets.mnist import load_data
Note: I personally use the tensorflow version of keras
2. replace all instances of:
opt = Adam(lr=0.0002, beta_1=0.5)
with:
opt = Adam(lr=0.0001, beta_1=0.5) # learning rate just needs to be slowed down
The reason I mention this (almost obvious) fact is for me, cgan produces better and more interesting results than a simple gan. Other people’s tutorials give some code and then with a wave of the hands suggest that, “it’s apparent something recognizable as numbers are being produced”.
In particular I appreciated your explanations for the Keras functional API approach.
What I do wish is there was some easy way to graphically illustrate the equivalent of first and second derivative estimates in order to better “see” why some attempts fail and other succeed. I realize that an approximation to an approximation is difficult to visualize but something along those lines would be great since single number measures tell me almost nothing diagnostic about what’s going on internally. For instance, (for illustration purposes only), it might be doing well with noses and chins but doing a poor job with eyes and ears. I’m sure there are many searching for better ways to have more science and less art in these weight estimations. I’m sure you have some great insights on this.
Again, beautiful work and thank you for your great explanations.
Thanks for your feedback and kind words.
Evaluating GANs remains challenging, some of the metrics here might give you ideas:
https://machinelearningmastery.com/how-to-evaluate-generative-adversarial-networks/
Thanks for your reply and pointing me to your tutorial. You may consider me to be a mathematical barbarian after you see some of the things I’ve attempted but my interest is in “what works”. If there are useful observations to make, I’m sure you’ll do a much more elegant job than I can. My observations are based on a limited number of experiments – I am amazed at how much you accomplish every month.
Simply for interest sake, I have a set of learning rates and betas which consistently produce good results for both the MNIST and the FASHION_MNIST dataset for me. I realize learning rates and betas are not the bleeding edge of GANS research but I am surprised the narrow range over which there is convergence:
define_discriminator opt as:
opt = Adam(lr=0.0008, beta_1=0.1)
define_gan opt as:
opt = Adam(lr=0.0006, beta_1=0.05)
I read your outline about measuring the goodness of results for gans. The tutorial is interesting but it seems to me you make your best point where you indicate that d1 and d2 ought to be about 0.6 while g ought to have values around 0.8. My general limited experience is, if I can keep my values for d1, d2 and g within reasonable bounds of those values, then I am soon going to have convergence. And if I am going to have convergence, then I need to first obtain good estimates of learning rate and momentum.
In keeping with this, you make the point in your tutorial about exploration of latent space that you may have to restart the analysis if the values of loss go out of bounds. In keeping with this view, I attempted the following which I’ve added to the training function of your tutorial on exploring latent space. Substantially, it saves a recent copy of the models where the values of loss are under 1.0 and recovers the models when the losses go out of an arbitrary bound and “tries again”. Surprisingly, it does seem to carry on from where it left off and it does appear to prevent having to restart the whole analysis.
I'm also attempting to understand what is the "maximum clarity" possible with respect to images generated. As in any statistical analysis, knowing the "maximum" is critical to understanding how far we've gotten or might theoretically go. While I recognize the mathematical usefulness of using normally distributed numbers to represent latent space, it doesn't appear to be important in practice – uniform between -3.0 and 3.0 (platykurtic) works as well as normal. I've found the following works quite well:
It's not terribly clever but it demonstrates, I think, that the points in the latent space do not have to be random spaced but different and spread out, and there may be some benefit in insuring that the latent space is uniformly covered as illustrated in the code and that the latent space does not have to be Gaussian. I haven't determined, for myself, whether or not this is the case in practice over a wide range of problems – you would obviously know better.
Finally, for the exploration of latent space, my GPU doesn't appear to have enough memory to use n_batch = 128 so I'm using n_batch = 64.
If I'm doing anything really dumb, feel free to let me know. 🙂
Very impressive, thanks for sharing!
You should consider writing up your findings more fully in a blog post.
I apologize for putting so much in the comment section of your site. Your work is amazingly good and a person realizes this only after trying out different approaches and searching for better material on the Internet. My plan is, as you suggest, to put something up as a blog post once I resolve a couple of issues.
But yes, I did do and report something really dumb in my last comment which I’d like to correct… I copied the address rather than using the ‘copy’ module and creating a backup. And, of course, I can only do this easily with the generator and the gan function. The compiled discriminator continues to work in the background gradually improving on its ability to tell the difference between real and fake, while in front the generator model jiggers its way to creating better fakes. In some ways this is how humans learn – the “slow” discriminator gradually improves over time, and the generator catches up.
By “backing up” the generator and gan models, I’m able to give every analysis many “second chances” at converging (not going out of bounds). In the interest of forcing convergence (irrespective of how really good the final model is) I used the following code:
I will put up a blog post and make many references to your great work once I better understand the limits.
Thanks for sharing.
GANs can be used for non-image data?
Yes, but they are not as effective as specialized generative models, at least from what I have seen.
your model fails while running it with mnist dataset but it works perfectly fine with fashion_mnist dataset I can not understand what is going wrong. Both d1_loss and d2_loss becomes 0.00 and gan_loss skyrockets could you give a hint in what’s going wrong here
If you change the dataset, you may need to tune the model to the change.
can you told me how to do that ? kindly
i build both model manually and bigger then this still both loss goes to zero
and i used mnist digit data
i don’t know what i’m missing !!!!kindly help with this
Yes, this is a big topic, perhaps start here:
https://machinelearningmastery.com/start-here/#gans
Hello Jason, i got some problem with EMNIST dataset.
Could you please explain basicly how to apply our model with 26 class or another datasets ? I’m new to this field and I didn’t understand anything from the link. I do not know what to do…
I implement your code for my dataset but d1_loss and d2_loss converges to 0 and also gan_loss goes up to 10.
With 26 classes, did you tried a 26-bit one-hot encoding?
Hey thank you Jason. Very impreesive article.
I’m wondering if CGAN can be used in a regression problem. Since among many GAN, only CGAN have the y label. But I’m not sure how to apply it to non-image problem. For example, I want to generate some synthetic data. I have some real data points of y,x. y = f(x1,x2,x3,x4). y is a non-linear function of x1~x4. I have few hundreds of [x1,x2, x3, x4, y] data. However, I want to have more data since the real data is hard to obtain. So basically I want to generate x1_fake, x2_fake, x3_fake, x4_fake, and y_fake where y_fake is still the same non-linear function of x1_fake~x4_fake, i.e., y_fake = f(x1_fake, x2_fake, x3_fake, x4_fake). Is it possible to generate such synthetic dataset using CGAN?
Thanks.
Yes, you could condition on a numerical variable. A different loss function and activation function would be need. I recommend experimenting.
I tunned the learning rate,batch size, epochs of the model but no use
Perhaps try some of the suggestions here:
https://machinelearningmastery.com/how-to-code-generative-adversarial-network-hacks/
Jason, have patience for this beginner question.
I’m having trouble understanding some of the syntax when you implement your cGANs
In both define_discriminator() and define_generator(), you have paired parenthesis:
examples:
define_discriminator()
line 6: li = Embedding(n_classes, 50)(in_label)
line 9: li = Dense(n_nodes)(li)
define_generator()
line 16: gen = Dense(n_nodes)(in_lat)
line 17: gen = LeakyReLU(alpha=0.2)(gen)
What is the meaning of the extra (in_label), (li), (in_lat), (gen) on the end of each of these lines?
You did not need this in your GANs code.
This is the functional API, perhaps start here:
https://machinelearningmastery.com/keras-functional-api-deep-learning/
Hi Jason!
As usual, a great explanation!
How would you modify the GAN to create n discrete values, i.e. categories, with different classes. Let’s say: n_class1=10, n_class2=15,n_class=18?
Any first thoughts or examples?
Thanks in advance,
Tobias
Thanks.
It would be a much better idea to use a bayesian model instead. This is just a demonstration for how GANs work and a bad example of a generative model for tabular data.
Please guide me how can i modify this code to use it for celebA data set. can i implement the same as that is RGB and there are various labels for a single picture.
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/can-you-change-the-code-in-the-tutorial-to-___
Hi Jason!
Very nice explanation! Thank you!
I just wonder if there is any pre-trained CGAN or GAN model out there so we can directly use as transfer learning? Specifically, I am interested in Celebra face data.
Thanks again,
Joel
Thanks!
Pre-trained, perhaps – I don’t have any sorry.
Thank you Jason, very clear and really useful for a beginner like me.
I have a question about the implementation of the training part.
why should you use half batch for generating real and fake samples but use full_batch (n_batch) in preparing latent point for the input to the generator.
X_real, y_real = generate_real_samples(dataset, half_batch)
X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch)
X_gan = generate_latent_points(latent_dim, n_batch)
Thanks.
This is a common heuristic when training GANs, you can learn more here:
https://machinelearningmastery.com/how-to-train-stable-generative-adversarial-networks/
Thank you for your quick response. I checked the link you gave me, I didn’t find information about using half-batch and n-batch. Would you please explain a bit here.
From that post:
Thank you very much for your help, Jason.
You’re welcome.
it is functional api that can be used to create branches in your model
in sequential model you can’t do that
Agreed.
Hi Jason!
Very Nice explanation . Helped me a lot in clarifying my doubts.
But I have a request – Can U make same kind Of Explanation for “Context Encoder : Feature learning by Inpainting” .
Thanks!!
Thanks!
Great suggestion.
Thanks for the Tutorial, I’ve been working my way through all the GAN tutorials you provided, it has been super helpful!
I tried training this conditional GAN on different data sets and it worked well. Now I’m trying to train it on a data set with a different number of classes (3 and 5). I changed the n_classes in every method as well as the label generation after the training and loading of the network of course. However, I get an IndexError and have been unable to solve it. Could you quickly suggest which changes need to be made to change the number of classes in the data set?
Cheers!
Thanks, I’m happy to hear that.
Sorry to hear that you’re having trouble adapting the example.
Perhaps confirm that the number of nodes in the output layer matches the number of classes in the target variable and that the target variable was appropriately one hot encoded.
Hi Jason, Thanks for the Tutorial ! I have a question below:
If each label represents the length, width and height of the product, how to not only put the label but also put the length, width and height into the model? Because I want to see the changes of different length, width and height on the model generation results. Thanks!
Interesting idea, you might want to explore using an infogan and have a parameter for each element.
Thank you. I’ll read your infogan article.
(https://machinelearningmastery.com/how-to-develop-an-information-maximizing-generative-adversarial-network-infogan-in-keras/)
At present, the model I want to generate is supervised learning, but using InfoGAN should be unsupervised model. Maybe I still use CGAN to generate and control the results?
I recommend using the techniques you think are the most appropriate to your project.
For example, I input geometric features x, y, z of various products, then output the process parameters of the product. ex: INPUT (x,y,z) and OUTPUT (temp,pressure,speed),
Is it possible for the model to predict the process parameters of the product when the geometric characteristics x, y, z of the new product are input?
It depends on the data, but yes, this is what supervised learning is designed to achieve.
Perhaps this framework will help:
https://machinelearningmastery.com/how-to-define-your-machine-learning-problem/
Hi, Jason,
I have question about the labels in conditional GAN. Instead of several categories, like integers from 0 to 9, can the labels be generated by continuous Uniform distribution(0,1)? So there will be hundreds of labels inputted to the generator or discriminator.
Do you think it is reasonable or doable? Thank you very much!
I don’t see why not.
What changes do I have to make to be able to train with 3 channel images? I changed the input_shape to (dim, dim, 3) but I still get the error: ValueError: Input 0 of layer conv2d is incompatible with the layer: expected axis -1 of input shape to have value 4 but received input with shape [None, dim, dim, 2]
Perhaps start with this model and adapt it to be conditional:
https://machinelearningmastery.com/how-to-develop-a-generative-adversarial-network-for-a-cifar-10-small-object-photographs-from-scratch/
I had to change the Embedding layer’s dimensions for the conditional Gan otherwise tf complained that it could not reshape (32,1,50) to (32,7,7).
I changed the 50 to 49 as li = Embedding(n_classes,49)(in_label).
Am I missing something or it was a typo?
That is odd, sorry to hear that.
Did you copy all other code examples as-is without modification?
Are your libraries up to date?
Do these tips help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
No since I haven’t purchased the book, I don’t have the code. I did find the problem though, and I was silly to ask the question! It was obvious that I had missed adding a Dense layer before Reshaping in the generator!
Thanks for your prompt reply.
I’m happy to hear that you solved your problem!
Hi Jason,
great post (again).
How would the conditional DCGAN would change if instead of label (condition) input, I have a facial landmark image of some dimension (e.g. a grayscale of 28,28) ? The generator, in this case, should generate an image that corresponds to the landmark image, and so is the discriminator should “judge” the image according to the landmark condition.
Specifically I’m struggling to understand what should be in the in_label and li in the define_discriminator method. thanks
Not dramatically, perhaps just adjustments to the model for the new input shape.
Hello,
Thanks a lot for this tutorial! I really needed this.
Only one question, what are the changes needed in the generator and the discriminator if I am using a custom dataset, with dimensions (64,64,3) not (28,28,1)?
This is really bugging me, I know it’s simple but I think I might be overseeing something.
Thanks for your help.
Change the expected input shape for the discriminator and perhaps add more layers to support the larger images.
Add more layers to the generator to ensure the output shape matches the expected size.
How many layers and what types – you will have to discover the answer via trial and error.
Thanks, will have a look into this.
One more thing, my dataset is loaded as a tf batch dataset (using keras image dataset from directory). How can adjust the code to train this instead of the MNIST fashion?
Sorry, I don’t know about “tf batch dataset”.
Hello,
Thanks for the detailed blogs! I am trying to improve a classifier that was trained on a small imbalance dataset, and I am considering using CGAN to extend my dataset and making it a balanced one, but here comes the question: Can I use the whole dataset (train, validation and test) to train my CGAN and then use the generated images to extend and balance my classifier? or should I use the training set only? I am a little bit confused if using the whole dataset is completely fine since the generated images will be from a different distribution. I couldn’t find any answer for my confusion, so what do you think?
I am confused because in that case, my classifier will be validated and tested on generated images that were trained on these datasets to be generated.
You apply it only to your training data
No, I think it would be valid to only the training dataset to train the GAN as part of your experiment.
In regard of your nice post below,
https://machinelearningmastery.com/generative-adversarial-network-loss-functions/
My question is that is lower g_loss better?
Because I think your code and explanations imply following statement
“In practice, this is also implemented as a binary classification problem, like the discriminator. Instead of maximizing the loss, we can flip the labels for real and fake images and minimize the cross-entropy.”
I am trying to use Bayesian Optimization method on this cDCGAN above, and I got lost deciding to define the evaluation function to look for bigger g_loss or smaller g_loss (on average).
I have done 500 epoch on this code above, but could not find g_loss is going down or up.
Thank you for the post by the way. Great work!
In general, for GANs, no:
https://machinelearningmastery.com/faq/single-faq/why-is-my-gan-not-converging
Hi Jason thanks for this.
Quick question, does the embedding work with floating point numbers? I dont’ want to only have ints for input here, I want a float too, is that possible?
Thanks you.
Embedding layers in general? Yes.
Hi Jason,
I’ve been following your blogs, posts and newsletters for the past few years!
Do you have any advice on how to apply GANs for document generation?
Thanks in advance.
Thanks!
I would recommend “language models” for document generation, not GANs:
https://machinelearningmastery.com/?s=language+models&post_type=post&submit=Search
Hi Jason,
My question is naive, but would appreciate if you answer it.
Assume that I have 1D data and want to have only dense layers in both models. Here is the code for my disc model definition:
def define_discriminator(in_shape=(10,1), n_classes=8):
# label input
in_label = Input(shape=(1,))
li = Embedding(n_classes, 50)(in_label)
n_nodes = in_shape[0]
li = Dense(n_nodes)(li)
# reshape to additional channel
li = Reshape((n_nodes, 1))(li)
in_data = Input(shape=in_shape)
# concat label as a channel
merge = Concatenate()([in_data, li])
hidden1 = Dense(64, activation=’relu’)(merge)
hidden2 = Dense(64, activation=’relu’)(hidden1)
# output
out_layer = Dense(1, activation=’sigmoid’)(hidden2)
# define model
model = Model([in_data, in_label], out_layer)
# compile model
opt = Adam(lr=0.0002, beta_1=0.5)
model.compile(loss=’binary_crossentropy’, optimizer=opt, metrics=[‘accuracy’])
return model
The problem is that when I use d_model.predict(), the output has 3 dimensions instead of 2. In fact, the shape should be (64, 1), but it is (64, 10, 1) where 10 is the input dimension. Please let me know what I am missing here.
Perhaps review a plot or summary of the model to confirm it was constructed the way you intended.
How do I apply cGAN to augment images with multi-labels?
Good question. I have not explored this, perhaps use a little trial and error to see what works well.
Let me know how you go.
Hi Jason,
I am interested to know if it is possible to checkpoint your gan model. Since typical metrics e.g. loss and accuracy do not work for GANs, we have to define custom metrics. Using keras, we can easily do this for a classifier like the disc model, but I don;t know how to do this with the gen model. Please assume that we have a metric to analyze the quality of the generated images.
Not really as loss does not relate to image quality.
You can save after each manually executed epoch if you like.
Hi, thank you for this great tutorial. Is there a way of using more than one condition vector ? could we use multiple condition vectors then concatenate them ?
You’re welcome.
Perhaps. You may need to experiment and/or check the literature for related approaches.
Thanks for teaching me ML. 2 Questions:
I notice train_on_batch is passed a half_batch real & half_batch fake data. Are weights somehow only updated on loading a full batch?
Why would we use such high 50d Embedding for mapping only10 classes?
Weights are updated after each batch update.
50d embedding is common, you can try alternatives.
Hi Jason, thanks for the great tutorial!
I’m trying to create a conditional gan for time series data so my model is using LSTMs instead of CNNs. I’m having trouble understanding how to reshape my input and the labels embeddings.
In my case, instead of a 28×28 image, I have a time-series sample of shape: time_steps, n_features
As you know, an LSTM needs the input to be [n_samples, time_steps, n_features]
but now I also need to add the labels and I will get 4 dimensions instead of 3.
do you have any suggestions on how to do this right?
thanks a lot!
Perhaps this will help:
https://machinelearningmastery.com/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
Hi Jason,
Thanks for your great post.
In you code when generate fake image;
But based on the paper, I see other people use real label inputs(same as from real image sample) and z_input to generator fake image, then test d model weights based on this fake image. But it seems this won’t influence the model. I want to ask which one is correct? Is there any difference?
Thank you!
There are many different types of models.
Perhaps experiment with small modifications and see what works well for your application.
Hi Jason,
I am using the conditional GAN for my time-series data generation. Based on my application, the generator loss converges at certain point and then it increases. How can I include the early stopping in my model such that when g_loss is below certain threshold, the training should get terminated and the model be saved.
Generally GANs do not converge:
https://machinelearningmastery.com/faq/single-faq/why-is-my-gan-not-converging
Hi Jason, I am trying to apply your conditional GAN code to a CT scan dataset with 256×256 input images. I added a few more layers in discriminator and generator models. A sample of generator code changes I made is shown below. The training from this modified code takes hours without showing any errors or results. Any idea what went wrong? Thanks.
# linear multiplication
n_nodes = 4 * 4
li = Dense(n_nodes)(li)
# reshape to additional channel
li = Reshape((4, 4, 1))(li)
# image generator input
in_lat = Input(shape=(latent_dim,))
# foundation for 4×4 image
n_nodes = 1024 * 4 * 4
gen = Dense(n_nodes)(in_lat)
gen = LeakyReLU(alpha=0.2)(gen)
gen = Reshape((4, 4, 1024))(gen)
# merge image gen and label input
merge = Concatenate()([gen, li])
# upsample to 8×8
gen = Conv2DTranspose(512, (5,5), strides=(2,2), padding=’same’)(merge)
gen = LeakyReLU(alpha=0.2)(gen)
# upsample to 16×16
gen = Conv2DTranspose(256, (5,5), strides=(2,2), padding=’same’)(gen)
gen = LeakyReLU(alpha=0.2)(gen)
# upsample to 32×32
gen = Conv2DTranspose(128, (5,5), strides=(2,2), padding=’same’)(gen)
gen = LeakyReLU(alpha=0.2)(gen)
# upsample to 64×64
gen = Conv2DTranspose(64, (5,5), strides=(2,2), padding=’same’)(gen)
gen = LeakyReLU(alpha=0.2)(gen)
# upsample to 128×128
gen = Conv2DTranspose(32, (5,5), strides=(2,2), padding=’same’)(gen)
gen = LeakyReLU(alpha=0.2)(gen)
# upsample to 256×256
gen = Conv2DTranspose(16, (5,5), strides=(2,2), padding=’same’)(gen)
gen = LeakyReLU(alpha=0.2)(gen)
# output
out_layer = Conv2D(1, (256,256), activation=’tanh’, padding=’same’)(gen)
Perhaps some of these suggestions will help:
https://machinelearningmastery.com/faq/single-faq/how-do-i-speed-up-the-training-of-my-model
Hi David, I am a student trying to generate 256×256 images for a project too. Would you be able to share your code for the project you did?
Hi Jason, I have question about load model and continue training. When I end the set epoch, I save the g_model to h5. If I want to use the model for continue training, which model I need. Need to save the d_model and gan model? Thanks.
I suspect you will need to save/load the G and D and composite models.
It help me to continue training. Thanks you for reply.
You’re welcome.
Thanks for your reply. I success to do continue training.
Thanks a lot for all of your works, Jason. Great.
Why didn’t save gan_model and load that one!?
I try to do that in your code and also in mine, but couldn’t!
May you load gan_model and test?
You’re welcome.
The composite model is only used during training, then discarded.
I used a dataset from (http://vision.ucsd.edu/~leekc/ExtYaleDatabase/ExtYaleB.html) and wanted to generate face images with Conditional gan, I referenced the network architecture from (https://github.com/GANs-in-Action/gans-in-action/blob/master/chapter-8/Chapter_8_CGAN.ipynb) and (https://github.com/ mvedang/Conditional-GAN-CIFAR-10) network architecture, but no matter how many times I train it, the resulting image is still noise.
Even if I adjust the parameters of the Discriminator and Generator such as layers, neurons, etc., the generated results are still noise.
Can you help me to correct the Generator and Discriminator models I have constructed? code and result link:https://colab.research.google.com/drive/14ul6BeXpVnlO3TVmfvSiR0kkYUuWfvn-?usp=sharing
Generator :
def build_cgan_generator(z_dim):
z_input = Input(shape=(z_dim,))
label_input = Input(shape=(1,),dtype=’int32′)
label_embedding = Embedding(classes,output_dim=z_dim,input_length=1)(label_input)
label_embedding = Flatten()(label_embedding)
join_represent = Multiply()([z_input,label_embedding])
x = Dense(4*4*256)(join_represent)
x = Reshape((4,4,256))(x)#4*4*256
x = Conv2DTranspose(64,kernel_size=3,padding=’same’,strides=2)(x)#8*8*64
#x = BatchNormalization(momentum=0.8)(x)
x = LeakyReLU(0.01)(x)
x = Conv2DTranspose(128,kernel_size=3,padding=’same’,strides=2)(x)#16*16*128
#x = BatchNormalization(momentum=0.8)(x)
x = LeakyReLU(0.01)(x)
x = Conv2DTranspose(64,kernel_size=3,padding=’same’,strides=2)(x)#32*32*64
#x = BatchNormalization(momentum=0.8)(x)
x = LeakyReLU(0.01)(x)
x = Conv2DTranspose(32,kernel_size=3,padding=’same’,strides=2)(x)#64*64*32
#x = BatchNormalization(momentum=0.8)(x)
x = LeakyReLU(0.01)(x)
x = Conv2DTranspose(3,kernel_size=4,padding=’same’,strides=2)(x)#128*128*3
output = keras.layers.Activation(‘tanh’)(x)
model = keras.Model([z_input,label_input],output)
tf.keras.utils.plot_model(model,to_file=’generator.png’,show_shapes=True)
return model
Discriminator:
def build_cgan_discriminator(img_shape):
img_input = Input(shape=img_shape)
label_input = Input(shape=(1,))
label_embedding = Embedding(classes,output_dim=np.prod((img_shape[0],img_shape[1],1)),input_length=1)(label_input)
label_embedding = Flatten()(label_embedding)
label_embedding = Reshape((img_shape[0],img_shape[1],1))(label_embedding)
concatenated = Concatenate(axis=-1)([img_input, label_embedding])
x=layers.Conv2D(64,kernel_size=3,strides=2,padding=’same’)(concatenated)
x=LeakyReLU(0.01)(x)
x=layers.Conv2D(64,kernel_size=3,strides=2,padding=’same’)(x)
#x = BatchNormalization(momentum=0.8)(x)
x=LeakyReLU(0.01)(x)
x=layers.Conv2D(128,kernel_size=3,strides=2,padding=’same’)(x)
#x = BatchNormalization(momentum=0.8)(x)
x=LeakyReLU(0.01)(x)
x=layers.Conv2D(64,kernel_size=3,strides=2,padding=’same’)(x)
#x = BatchNormalization(momentum=0.8)(x)
x=LeakyReLU(0.01)(x)
x=Flatten()(x)
x=layers.Dropout(0.4)(x)
outputs = layers.Dense(1,activation=’sigmoid’,name=’Output’)(x)
model = keras.Model([img_input,label_input],outputs)
tf.keras.utils.plot_model(model,to_file=’discriminator.png’,show_shapes=True)
return model
Sorry, I don’t have the capacity to review/debug your code. Perhaps these tips will help:
https://machinelearningmastery.com/faq/single-faq/can-you-read-review-or-debug-my-code
Thanks a lot for all.
I implemented cGAN on a different data. But the loss of generator is increasing and accuracy for both generator and discriminator are 100% in different epochs and batch size.
May you help me, why?
Generally, loss is not a good indicator for GAN performance:
https://machinelearningmastery.com/faq/single-faq/why-is-my-gan-not-converging
Perhaps try running the example a few times?
Perhaps try adapting the model configuration?
hi sear,
how can we use cgan for dataset celeba?
Not sure it is appropriate.
Please sear, can you help me; how can i modify this code to use it for celebA data set. can i implement the same as that is RGB and there are various labels for a single picture.
Perhaps this tutorial will help:
https://machinelearningmastery.com/how-to-interpolate-and-perform-vector-arithmetic-with-faces-using-a-generative-adversarial-network/
thank you so much sear
You’re welcome.
Hi Jason, your tutorials are a great help. So I had a silly idea take this example and generate 60000 fake samples and use them to train a Fasion Mnist classification network from your other tutorial, and to my astonishement the generated dataset gave much higher accuracy on a validation set than the real training dataset. I didn’t change anything in the example but the training set, and the result was over 99% accuracy, compared to around 90% in 10 epochs for the real one. This seems too good to be true considering that the best method from the benchmark gets ~96% (https://paperswithcode.com/sota/image-classification-on-fashion-mnist), so I would want to ask if you have any idea why this might have happened?
That might mean your fake samples are not fake enough. This is a difficult problem to solve. But think in this way, if your fake samples are too simple to identify and use it to train, the machine will not learn anything useful. Just like giving you unchallenging exercises to do, even doing a lot, you learned nothing.
Hi Adrian, thanks for reply. But if the fake samples weren’t good enough to substitute the training set, then I would expect the accuracy on the validation set (a portion dataset that GAN generator has never seen) to be much lower. What I’m wondering is why a simple classification network separate to the GAN trained with only fake 60k samples yielded higher accuracy than when trained with the official 60k samples, I imagined it would be the other way around.
Without looking at the data you generated, I cannot really tell. But one possibility to explain is this: If the original sample is a bigger problem (e.g. identify a thousand objects) and the generated samples is only a smaller problem (e.g. identify a dog vs a car), then you will likely see that the accuracy of latter is better than former. One way to prove you are actually not doing any better is to use the generated samples to train your network and use the official samples for validation.
Hope this helps!
I’ve come back to this piece of brilliant work on your part.
What I don’t understand is how the information from the d_model gets transferred to the g_model via the gan_model so quickly. I continue to make modifications and the following is a cryptic piece within the training loop where I exposed and reused some calculations.
[X_real, labels_real], y_real = generate_real_samples(dataset, n_batch)
d_learning_rate = calculate_learning_rate(lr/g_loss, counter)
K.set_value(d_model.optimizer.learning_rate, d_learning_rate)
d_loss1, _ = d_model.train_on_batch([X_real, labels_real], y_real)
z_input, labels = generate_latent_points(latent_dim, n_batch)
X_fake = g_model.predict([z_input, labels])
y_fake = zeros((n_batch, 1))
d_loss2, _ = d_model.train_on_batch([X_fake, labels], y_fake)
y_gan = ones((n_batch, 1))
g_learning_rate = calculate_learning_rate(lr, counter)
K.set_value(gan_model.optimizer.learning_rate, g_learning_rate)
g_loss = gan_model.train_on_batch([z_input, labels], y_gan)
if (j%10==0):
print(‘>%d/%d, %d/%d, d1=%.3f, d2=%.3f g=%.3f’ %
(i+1,n_epochs, j+1, bat_per_epo, d_loss1, d_loss2, g_loss))
You can see I don’t recalculate the latent_points within each loop. It makes little difference in execution time but it illustrates I only need to calculate my latent points at the beginning of each loop and re-use them. All this only deepens the mystery for me. As I understand it, the g_model weights get updated when they are passed through the gan_model (which is the only place they could be updated). So much of this appears to happen in the background.
I also directly manipulate the learning rate and pull back the rate on d_model when gan_model appears to be heading towards a collapse.
def calculate_learning_rate(lr, counter):
lr = lr * 0.998
return lr
This appears to work better than manipulating the weights.
Hopefully I’m not doing anything too far off the charts.
Thanks again for your brilliant work.
Hi Jason, Could this conditional GAN structure be used for the 1D inertial sensor data generation?
Why not? Did you see any issues?
Because most cases are utilized for images generation rather than 1d sensor data. So, I can’t make sure if it works well.
I believe it should work but I can’t see your data. Always the only way to confirm is to experiment!
Thanks a lot for all.
i would like to implemente this code to generate data (data augmentation) in order to balcance data data and then make classification
the probleme how can i modify this code to use it for credit cardt fraud detection data set to generate fraudulant trabsaction classe 1 in .
Thank you, sir, for this nice information. Is it possible to give me the dataset for this code? Thank you very much
Hello Ayat…You may find the datasets at the following location:
http://yann.lecun.com/exdb/mnist/
Regards,
Hello sir,
Your blog has helped me a lot in learning the basics of C-GAN. I am applying C-GAN for a physics model to learn the phase transition in theory.
If I want to generate data (say image pixels in your model) for intermediate labels (not part of training) then how to do that?
thanks
Hi Harry…Thank you for the feedback! You may find the following of interest:
https://www.toptal.com/machine-learning/generative-adversarial-networks
Dear sir,
I have 10 class labels but all of them are in range (0,1) like [0.20169,0.22169,…..] so what number of n_classes shall I take in above code? I tried with n_class=10 but then d_loss became zero and I didn’t get expected output
Hi Shubh,
You may be working on a regression problem and achieve zero prediction errors.
Alternately, you may be working on a classification problem and achieve 100% accuracy.
This is unusual and there are many possible reasons for this, including:
You are evaluating model performance on the training set by accident.
Your hold out dataset (train or validation) is too small or unrepresentative.
You have introduced a bug into your code and it is doing something different from what you expect.
Your prediction problem is easy or trivial and may not require machine learning.
The most common reason is that your hold out dataset is too small or not representative of the broader problem.
This can be addressed by:
Using k-fold cross-validation to estimate model performance instead of a train/test split.
Gather more data.
Use a different split of data for train and test, such as 50/50.
Dear sir,
I have modified above code for my use but I am facing a problem i.e, I have 10 labels which are real numbers between 0 and 1 so when I am using above code I get an error because of embedding layer, How can I resolve it?
Hi Shubh…What is the exact error you are encountering so that I may better assist you? In general I cannot debug your code, however something may stand out immediately if you can provide the exact error message(s).
Hello sir,
Thanks a lot for this blog, it helped me so much. I have a problem when I try to train the gan. I adapted the code to my particular case (images of 6×6), but the output of the train phase is clearly different from yours. Aparently I’ve only changed the input shape and the output (the upsample and down sample are modified too), but nothing more.
My output is:
>1, 1/20, d_loss_real=18834628.000, d_loss_fake=0.696 g_loss=0.690
>1, 2/20, d_loss_real=915644.875, d_loss_fake=0.701 g_loss=0.686
>1, 3/20, d_loss_real=35437.840, d_loss_fake=0.706 g_loss=0.681
>1, 4/20, d_loss_real=0.000, d_loss_fake=0.713 g_loss=0.676
>1, 5/20, d_loss_real=0.000, d_loss_fake=0.719 g_loss=0.669
…
>100, 18/20, d_loss_real=0.000, d_loss_fake=0.023 g_loss=3.808
>100, 19/20, d_loss_real=0.000, d_loss_fake=0.022 g_loss=3.819
>100, 20/20, d_loss_real=0.000, d_loss_fake=0.024 g_loss=3.763
WARNING:tensorflow:Compiled the loaded model, but the compiled metrics have yet to be built.
model.compile_metricswill be empty until you train or evaluate the model.How could I solve it?
Hi Adrian…The following discussion may be of interest to you:
https://stackoverflow.com/questions/67970389/warningtensorflowcompiled-the-loaded-model-but-the-compiled-metrics-have-yet
https://github.com/theAIGuysCode/yolov4-deepsort/issues/79
Hi please tell me How to save images after Images Generation through GAN, Wait for your answer
Hi Ahtisham…The following may be of interest to you:
https://stackoverflow.com/questions/71452209/save-gan-generated-images-one-by-one
Hello Sir,
How can I use images that have a line of text with a different shape in width and height in my dataset such as h=200, w= 2048 and not n×n in as cGan input, I tried using resize, but it got distorted.
Hi M.M…You may find the following resource of interest:
https://machinelearningmastery.com/how-to-load-convert-and-save-images-with-the-keras-api/
Hi, Thank you for replying.
Q/ I am working on a topic (Data Augmentation by using cGAN), for Arabic text handwriting images. The dataset contains images of large sizes and different dimensions (M*N).
I tried to use the code sent by you in order to convert the images to square sizes (N*N), but the result, the images are unclear for reading, can we use this unclear image in cGAN and give a result? To use them in next step in recognition of text ?
– Is there a better way to prevent image distortion when converted it to (N*N),
or
– can I use an image of different sizes in cGAN as input instead of resizing it?
Hi Jason,
Many thanks for this cGAN’s tutorial!
For cGAN, it can accept label (via one-hot encoding) to generate targeted images with the corresponding object. Could you please let me know if it is possible to train a cGAN model to generate images with multiple (e.g., two or three) targeted objects? For example, if we want to generate images containing ‘Dress’, ‘Shirt’ and ‘Bag’, so the input label vector could be [0, 0, 0, 1, 0, 0, 1, 0, 1, 0] (use ‘1’ to activate the object that we want). I am just wondering if this is doable for the cGAN model?
Thank you very much!
Hi Dee…You are very welcome! I would highly recommend the following resources to support your understanding of GANs:
https://machinelearningmastery.com/tour-of-generative-adversarial-network-models/
It’s fantastic! Thanks for this awesome tutorial!
Thank you for the support and feedback Cristian! We greatly appreciate it!
Hello sir, thankyou for this amazing tutorial i really appreciate it.
But i have a question…..i have a task called face emotion generator using GAN. So basically it is a “generator” that can modified the emotion based on 1 static image input. For example, i have an angry image. When i feed it into the “generator”, it can modified into another emotion such like sad, neutral, disgusting, etc.
Is this method (CGAN) the right method for my task?
Anw iam using AffectNet-HQ dataset from Kaggle.
Thankyou sir.
Hi sir, thankyou for making this amazing tutorial.
But i have a question, so i have a task to make a face emotion generator using GAN. Basically this “generator” can create an image face to display in another emotions. For example, from 1 static image of a face, it can be modified so that it displays sad, happy, or other emotions.
My question is this method (CGAN) the right method for my task?
Anw iam using the AffectNet-HQ dataset from kaggle….
Thanks before.
Hi Calvin…You are very welcome! Yes, please proceed with CGAN and let us know what you find.
does the image result can be realistic if i only works with CGAN sir?
Hi sir, thank you so much for providing such an exciting tutorial. But I am a novice in deep learning, can you provide me with some tutorials or blogs to replace the dataset, I want to use your code to train another dataset, please ask what changes are needed in the code. Looking forward to your reply very much!
Hi Roy…You are very welcome! The following resource provides insight into how to apply new data to trained models.
https://machinelearningmastery.com/update-neural-network-models-with-more-data/
Thank you sir, but the data set I want to use tells me that I need to use coco api. How can this be combined with your CGAN code.
Hi David, I am a student trying to generate 256×256 images for a project too. Would you be able to share your code for the project you did?
can i use same code but different dataset will it work? for example dataset to generate numbers
Hi Hithesh…Absolutely! Let us know if you have any questions once you implement your models with new data.
More information regarding GANs can be found here:
https://machinelearningmastery.com/start-here/#gans
how to make sure the condition (i.e. class label in this case) is used. what prevent the network (both d & g) from ignoring the condition and behave like unconditioned case? thanks
Hi Ting…This is a great question! The following resource provides some key insights.
https://openaccess.thecvf.com/content/CVPR2022W/CLVision/papers/Laria_Transferring_Unconditional_to_Conditional_GANs_With_Hyper-Modulation_CVPRW_2022_paper.pdf
How can I use this for timeseries forecasting
Hi MSM…The following resource is a great starting point:
https://dl.acm.org/doi/abs/10.1145/3604237.3626855