Understanding Simple Recurrent Neural Networks in Keras

By Mehreen Saeed on January 6, 2023 in Attention 17

This tutorial is designed for anyone looking for an understanding of how recurrent neural networks (RNN) work and how to use them via the Keras deep learning library. While the Keras library provides all the methods required for solving problems and building applications, it is also important to gain an insight into how everything works. In this article, the computations taking place in the RNN model are shown step by step. Next, a complete end-to-end system for time series prediction is developed.

After completing this tutorial, you will know:

The structure of an RNN
How an RNN computes the output when given an input
How to prepare data for a SimpleRNN in Keras
How to train a SimpleRNN model

Kick-start your project with my book Building Transformer Models with Attention. It provides self-study tutorials with working code to guide you into building a fully-working transformer model that can
translate sentences from one language to another...

Let’s get started.

Understanding simple recurrent neural networks in Keras. Photo by Mehreen Saeed, some rights reserved.

Tutorial Overview

This tutorial is divided into two parts; they are:

The structure of the RNN
1. Different weights and biases associated with different layers of the RNN
2. How computations are performed to compute the output when given an input
A complete application for time series prediction

Prerequisites

It is assumed that you have a basic understanding of RNNs before you start implementing them. An Introduction to Recurrent Neural Networks and the Math That Powers Them gives you a quick overview of RNNs.

Let’s now get right down to the implementation part.

Import Section

To start the implementation of RNNs, let’s add the import section.

from pandas import read_csv
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
import math
import matplotlib.pyplot as plt

from pandas import read_csv

import numpy as np

from keras.models import Sequential

from keras.layers import Dense, SimpleRNN

from sklearn.preprocessing import MinMaxScaler

from sklearn.metrics import mean_squared_error

import math

import matplotlib.pyplot as plt

Want to Get Started With Building Transformer Models with Attention?

Take my free 12-day email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Keras SimpleRNN

The function below returns a model that includes a SimpleRNN layer and a Dense layer for learning sequential data. The input_shape specifies the parameter (time_steps x features). We’ll simplify everything and use univariate data, i.e., one feature only; the time steps are discussed below.

def create_RNN(hidden_units, dense_units, input_shape, activation):
    model = Sequential()
    model.add(SimpleRNN(hidden_units, input_shape=input_shape, 
                        activation=activation[0]))
    model.add(Dense(units=dense_units, activation=activation[1]))
    model.compile(loss='mean_squared_error', optimizer='adam')
    return model

demo_model = create_RNN(2, 1, (3,1), activation=['linear', 'linear'])

def create_RNN(hidden_units, dense_units, input_shape, activation):

model = Sequential()

model.add(SimpleRNN(hidden_units, input_shape=input_shape,

activation=activation[0]))

model.add(Dense(units=dense_units, activation=activation[1]))

model.compile(loss='mean_squared_error', optimizer='adam')

return model

demo_model = create_RNN(2, 1, (3,1), activation=['linear', 'linear'])

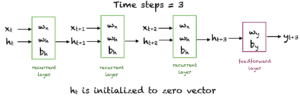
The object demo_model is returned with two hidden units created via the SimpleRNN layer and one dense unit created via the Dense layer. The input_shape is set at 3×1, and a linear activation function is used in both layers for simplicity. Just to recall, the linear activation function $f(x) = x$ makes no change in the input. The network looks as follows:

If we have $m$ hidden units ($m=2$ in the above case), then:

Input: $x \in R$
Hidden unit: $h \in R^m$
Weights for the input units: $w_x \in R^m$
Weights for the hidden units: $w_h \in R^{mxm}$
Bias for the hidden units: $b_h \in R^m$
Weight for the dense layer: $w_y \in R^m$
Bias for the dense layer: $b_y \in R$

Let’s look at the above weights. Note: As the weights are randomly initialized, the results posted here will be different from yours. The important thing is to learn what the structure of each object being used looks like and how it interacts with others to produce the final output.

wx = demo_model.get_weights()[0]
wh = demo_model.get_weights()[1]
bh = demo_model.get_weights()[2]
wy = demo_model.get_weights()[3]
by = demo_model.get_weights()[4]

print('wx = ', wx, ' wh = ', wh, ' bh = ', bh, ' wy =', wy, 'by = ', by)

wx = demo_model.get_weights()[0]

wh = demo_model.get_weights()[1]

bh = demo_model.get_weights()[2]

wy = demo_model.get_weights()[3]

by = demo_model.get_weights()[4]

print('wx = ', wx, ' wh = ', wh, ' bh = ', bh, ' wy =', wy, 'by = ', by)

wx =  [[ 0.18662322 -1.2369459 ]]  wh =  [[ 0.86981213 -0.49338293]
 [ 0.49338293  0.8698122 ]]  bh =  [0. 0.]  wy = [[-0.4635998]
 [ 0.6538409]] by =  [0.]

wx = [[ 0.18662322 -1.2369459 ]] wh = [[ 0.86981213 -0.49338293]

[ 0.49338293 0.8698122 ]] bh = [0. 0.] wy = [[-0.4635998]

[ 0.6538409]] by = [0.]

Now let’s do a simple experiment to see how the layers from a SimpleRNN and Dense layer produce an output. Keep this figure in view.

Layers of a recurrent neural network

We’ll input x for three time steps and let the network generate an output. The values of the hidden units at time steps 1, 2, and 3 will be computed. $h_0$ is initialized to the zero vector. The output $o_3$ is computed from $h_3$ and $w_y$. An activation function is not required as we are using linear units.

x = np.array([1, 2, 3])
# Reshape the input to the required sample_size x time_steps x features 
x_input = np.reshape(x,(1, 3, 1))
y_pred_model = demo_model.predict(x_input)


m = 2
h0 = np.zeros(m)
h1 = np.dot(x[0], wx) + h0 + bh
h2 = np.dot(x[1], wx) + np.dot(h1,wh) + bh
h3 = np.dot(x[2], wx) + np.dot(h2,wh) + bh
o3 = np.dot(h3, wy) + by

print('h1 = ', h1,'h2 = ', h2,'h3 = ', h3)

print("Prediction from network ", y_pred_model)
print("Prediction from our computation ", o3)

x = np.array([1, 2, 3])

# Reshape the input to the required sample_size x time_steps x features

x_input = np.reshape(x,(1, 3, 1))

y_pred_model = demo_model.predict(x_input)

m = 2

h0 = np.zeros(m)

h1 = np.dot(x[0], wx) + h0 + bh

h2 = np.dot(x[1], wx) + np.dot(h1,wh) + bh

h3 = np.dot(x[2], wx) + np.dot(h2,wh) + bh

o3 = np.dot(h3, wy) + by

print('h1 = ', h1,'h2 = ', h2,'h3 = ', h3)

print("Prediction from network ", y_pred_model)

print("Prediction from our computation ", o3)

h1 =  [[ 0.18662322 -1.23694587]] h2 =  [[-0.07471441 -3.64187904]] h3 =  [[-1.30195881 -6.84172557]]
Prediction from network  [[-3.8698118]]
Prediction from our computation  [[-3.86981216]]

h1 = [[ 0.18662322 -1.23694587]] h2 = [[-0.07471441 -3.64187904]] h3 = [[-1.30195881 -6.84172557]]

Prediction from network [[-3.8698118]]

Prediction from our computation [[-3.86981216]]

Running the RNN on Sunspots Dataset

Now that we understand how the SimpleRNN and Dense layers are put together. Let’s run a complete RNN on a simple time series dataset. We’ll need to follow these steps:

Read the dataset from a given URL
Split the data into training and test sets
Prepare the input to the required Keras format
Create an RNN model and train it
Make the predictions on training and test sets and print the root mean square error on both sets
View the result

Step 1, 2: Reading Data and Splitting Into Train and Test

The following function reads the train and test data from a given URL and splits it into a given percentage of train and test data. It returns single-dimensional arrays for train and test data after scaling the data between 0 and 1 using MinMaxScaler from scikit-learn.

# Parameter split_percent defines the ratio of training examples
def get_train_test(url, split_percent=0.8):
    df = read_csv(url, usecols=[1], engine='python')
    data = np.array(df.values.astype('float32'))
    scaler = MinMaxScaler(feature_range=(0, 1))
    data = scaler.fit_transform(data).flatten()
    n = len(data)
    # Point for splitting data into train and test
    split = int(n*split_percent)
    train_data = data[range(split)]
    test_data = data[split:]
    return train_data, test_data, data

sunspots_url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv'
train_data, test_data, data = get_train_test(sunspots_url)

# Parameter split_percent defines the ratio of training examples

def get_train_test(url, split_percent=0.8):

df = read_csv(url, usecols=[1], engine='python')

data = np.array(df.values.astype('float32'))

scaler = MinMaxScaler(feature_range=(0, 1))

data = scaler.fit_transform(data).flatten()

n = len(data)

# Point for splitting data into train and test

split = int(n*split_percent)

train_data = data[range(split)]

test_data = data[split:]

return train_data, test_data, data

sunspots_url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv'

train_data, test_data, data = get_train_test(sunspots_url)

Step 3: Reshaping Data for Keras

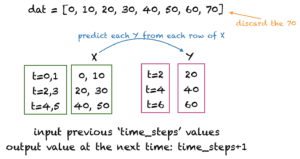
The next step is to prepare the data for Keras model training. The input array should be shaped as: total_samples x time_steps x features.

There are many ways of preparing time series data for training. We’ll create input rows with non-overlapping time steps. An example for time steps = 2 is shown in the figure below. Here, time steps denotes the number of previous time steps to use for predicting the next value of the time series data.

How data is prepared for sunspots example

The following function get_XY() takes a one-dimensional array as input and converts it to the required input X and target Y arrays. We’ll use 12 time_steps for the sunspots dataset as the sunspots generally have a cycle of 12 months. You can experiment with other values of time_steps.

# Prepare the input X and target Y
def get_XY(dat, time_steps):
    # Indices of target array
    Y_ind = np.arange(time_steps, len(dat), time_steps)
    Y = dat[Y_ind]
    # Prepare X
    rows_x = len(Y)
    X = dat[range(time_steps*rows_x)]
    X = np.reshape(X, (rows_x, time_steps, 1))    
    return X, Y

time_steps = 12
trainX, trainY = get_XY(train_data, time_steps)
testX, testY = get_XY(test_data, time_steps)

# Prepare the input X and target Y

def get_XY(dat, time_steps):

# Indices of target array

Y_ind = np.arange(time_steps, len(dat), time_steps)

Y = dat[Y_ind]

# Prepare X

rows_x = len(Y)

X = dat[range(time_steps*rows_x)]

X = np.reshape(X, (rows_x, time_steps, 1))

return X, Y

time_steps = 12

trainX, trainY = get_XY(train_data, time_steps)

testX, testY = get_XY(test_data, time_steps)

Step 4: Create RNN Model and Train

For this step, you can reuse your create_RNN() function that was defined above.

model = create_RNN(hidden_units=3, dense_units=1, input_shape=(time_steps,1), 
                   activation=['tanh', 'tanh'])
model.fit(trainX, trainY, epochs=20, batch_size=1, verbose=2)

model = create_RNN(hidden_units=3, dense_units=1, input_shape=(time_steps,1),

activation=['tanh', 'tanh'])

model.fit(trainX, trainY, epochs=20, batch_size=1, verbose=2)

Step 5: Compute and Print the Root Mean Square Error

The function print_error() computes the mean square error between the actual and predicted values.

def print_error(trainY, testY, train_predict, test_predict):    
    # Error of predictions
    train_rmse = math.sqrt(mean_squared_error(trainY, train_predict))
    test_rmse = math.sqrt(mean_squared_error(testY, test_predict))
    # Print RMSE
    print('Train RMSE: %.3f RMSE' % (train_rmse))
    print('Test RMSE: %.3f RMSE' % (test_rmse))    

# make predictions
train_predict = model.predict(trainX)
test_predict = model.predict(testX)
# Mean square error
print_error(trainY, testY, train_predict, test_predict)

def print_error(trainY, testY, train_predict, test_predict):

# Error of predictions

train_rmse = math.sqrt(mean_squared_error(trainY, train_predict))

test_rmse = math.sqrt(mean_squared_error(testY, test_predict))

# Print RMSE

print('Train RMSE: %.3f RMSE' % (train_rmse))

print('Test RMSE: %.3f RMSE' % (test_rmse))

# make predictions

train_predict = model.predict(trainX)

test_predict = model.predict(testX)

# Mean square error

print_error(trainY, testY, train_predict, test_predict)

Train RMSE: 0.058 RMSE
Test RMSE: 0.077 RMSE

1 2	Train RMSE: 0.058 RMSE Test RMSE: 0.077 RMSE

Step 6: View the Result

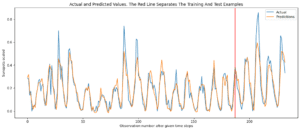
The following function plots the actual target values and the predicted values. The red line separates the training and test data points.

# Plot the result
def plot_result(trainY, testY, train_predict, test_predict):
    actual = np.append(trainY, testY)
    predictions = np.append(train_predict, test_predict)
    rows = len(actual)
    plt.figure(figsize=(15, 6), dpi=80)
    plt.plot(range(rows), actual)
    plt.plot(range(rows), predictions)
    plt.axvline(x=len(trainY), color='r')
    plt.legend(['Actual', 'Predictions'])
    plt.xlabel('Observation number after given time steps')
    plt.ylabel('Sunspots scaled')
    plt.title('Actual and Predicted Values. The Red Line Separates The Training And Test Examples')
plot_result(trainY, testY, train_predict, test_predict)

# Plot the result

def plot_result(trainY, testY, train_predict, test_predict):

actual = np.append(trainY, testY)

predictions = np.append(train_predict, test_predict)

rows = len(actual)

plt.figure(figsize=(15, 6), dpi=80)

plt.plot(range(rows), actual)

plt.plot(range(rows), predictions)

plt.axvline(x=len(trainY), color='r')

plt.legend(['Actual', 'Predictions'])

plt.xlabel('Observation number after given time steps')

plt.ylabel('Sunspots scaled')

plt.title('Actual and Predicted Values. The Red Line Separates The Training And Test Examples')

plot_result(trainY, testY, train_predict, test_predict)

The following plot is generated:

Consolidated Code

Given below is the entire code for this tutorial. Try this out at your end and experiment with different hidden units and time steps. You can add a second SimpleRNN to the network and see how it behaves. You can also use the scaler object to rescale the data back to its normal range.

# Parameter split_percent defines the ratio of training examples
def get_train_test(url, split_percent=0.8):
    df = read_csv(url, usecols=[1], engine='python')
    data = np.array(df.values.astype('float32'))
    scaler = MinMaxScaler(feature_range=(0, 1))
    data = scaler.fit_transform(data).flatten()
    n = len(data)
    # Point for splitting data into train and test
    split = int(n*split_percent)
    train_data = data[range(split)]
    test_data = data[split:]
    return train_data, test_data, data

# Prepare the input X and target Y
def get_XY(dat, time_steps):
    Y_ind = np.arange(time_steps, len(dat), time_steps)
    Y = dat[Y_ind]
    rows_x = len(Y)
    X = dat[range(time_steps*rows_x)]
    X = np.reshape(X, (rows_x, time_steps, 1))    
    return X, Y

def create_RNN(hidden_units, dense_units, input_shape, activation):
    model = Sequential()
    model.add(SimpleRNN(hidden_units, input_shape=input_shape, activation=activation[0]))
    model.add(Dense(units=dense_units, activation=activation[1]))
    model.compile(loss='mean_squared_error', optimizer='adam')
    return model

def print_error(trainY, testY, train_predict, test_predict):    
    # Error of predictions
    train_rmse = math.sqrt(mean_squared_error(trainY, train_predict))
    test_rmse = math.sqrt(mean_squared_error(testY, test_predict))
    # Print RMSE
    print('Train RMSE: %.3f RMSE' % (train_rmse))
    print('Test RMSE: %.3f RMSE' % (test_rmse))    

# Plot the result
def plot_result(trainY, testY, train_predict, test_predict):
    actual = np.append(trainY, testY)
    predictions = np.append(train_predict, test_predict)
    rows = len(actual)
    plt.figure(figsize=(15, 6), dpi=80)
    plt.plot(range(rows), actual)
    plt.plot(range(rows), predictions)
    plt.axvline(x=len(trainY), color='r')
    plt.legend(['Actual', 'Predictions'])
    plt.xlabel('Observation number after given time steps')
    plt.ylabel('Sunspots scaled')
    plt.title('Actual and Predicted Values. The Red Line Separates The Training And Test Examples')

sunspots_url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv'
time_steps = 12
train_data, test_data, data = get_train_test(sunspots_url)
trainX, trainY = get_XY(train_data, time_steps)
testX, testY = get_XY(test_data, time_steps)

# Create model and train
model = create_RNN(hidden_units=3, dense_units=1, input_shape=(time_steps,1), 
                   activation=['tanh', 'tanh'])
model.fit(trainX, trainY, epochs=20, batch_size=1, verbose=2)

# make predictions
train_predict = model.predict(trainX)
test_predict = model.predict(testX)

# Print error
print_error(trainY, testY, train_predict, test_predict)

#Plot result
plot_result(trainY, testY, train_predict, test_predict)

# Parameter split_percent defines the ratio of training examples

def get_train_test(url, split_percent=0.8):

df = read_csv(url, usecols=[1], engine='python')

data = np.array(df.values.astype('float32'))

scaler = MinMaxScaler(feature_range=(0, 1))

data = scaler.fit_transform(data).flatten()

n = len(data)

# Point for splitting data into train and test

split = int(n*split_percent)

train_data = data[range(split)]

test_data = data[split:]

return train_data, test_data, data

# Prepare the input X and target Y

def get_XY(dat, time_steps):

Y_ind = np.arange(time_steps, len(dat), time_steps)

Y = dat[Y_ind]

rows_x = len(Y)

X = dat[range(time_steps*rows_x)]

X = np.reshape(X, (rows_x, time_steps, 1))

return X, Y

def create_RNN(hidden_units, dense_units, input_shape, activation):

model = Sequential()

model.add(SimpleRNN(hidden_units, input_shape=input_shape, activation=activation[0]))

model.add(Dense(units=dense_units, activation=activation[1]))

model.compile(loss='mean_squared_error', optimizer='adam')

return model

def print_error(trainY, testY, train_predict, test_predict):

# Error of predictions

train_rmse = math.sqrt(mean_squared_error(trainY, train_predict))

test_rmse = math.sqrt(mean_squared_error(testY, test_predict))

# Print RMSE

print('Train RMSE: %.3f RMSE' % (train_rmse))

print('Test RMSE: %.3f RMSE' % (test_rmse))

# Plot the result

def plot_result(trainY, testY, train_predict, test_predict):

actual = np.append(trainY, testY)

predictions = np.append(train_predict, test_predict)

rows = len(actual)

plt.figure(figsize=(15, 6), dpi=80)

plt.plot(range(rows), actual)

plt.plot(range(rows), predictions)

plt.axvline(x=len(trainY), color='r')

plt.legend(['Actual', 'Predictions'])

plt.xlabel('Observation number after given time steps')

plt.ylabel('Sunspots scaled')

plt.title('Actual and Predicted Values. The Red Line Separates The Training And Test Examples')

sunspots_url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv'

time_steps = 12

train_data, test_data, data = get_train_test(sunspots_url)

trainX, trainY = get_XY(train_data, time_steps)

testX, testY = get_XY(test_data, time_steps)

# Create model and train

model = create_RNN(hidden_units=3, dense_units=1, input_shape=(time_steps,1),

activation=['tanh', 'tanh'])

model.fit(trainX, trainY, epochs=20, batch_size=1, verbose=2)

# make predictions

train_predict = model.predict(trainX)

test_predict = model.predict(testX)

# Print error

print_error(trainY, testY, train_predict, test_predict)

#Plot result

plot_result(trainY, testY, train_predict, test_predict)

Summary

In this tutorial, you discovered recurrent neural networks and their various architectures.

Specifically, you learned:

The structure of RNNs
How the RNN computes an output from previous inputs
How to implement an end-to-end system for time series forecasting using an RNN

Do you have any questions about RNNs discussed in this post? Ask your questions in the comments below, and I will do my best to answer.

17 Responses to Understanding Simple Recurrent Neural Networks in Keras

tony November 15, 2021 at 8:47 pm #

When I use tensorflow.keras, NotImplementedError is thrown in create_RNN(). What should I update? Thanks.

Reply
- Adrian Tam November 16, 2021 at 2:29 am #
  
  create_RNN() is a function defined here. Which line is triggering the NotImplementedError?
  
  Reply
  - tony November 16, 2021 at 3:12 pm #
    
    In “model.add(SimpleRNN(hidden_units, input_shape=input_shape, activation=activation[0]))”
    
    The error thrown at:
    ~/anaconda3/envs/py38/lib/python3.8/site-packages/tensorflow/python/framework/ops.py in __array__(self)
    850
    851 def __array__(self):
    –> 852 raise NotImplementedError(
    853 “Cannot convert a symbolic Tensor ({}) to a numpy array.”
    854 ” This error may indicate that you’re trying to pass a Tensor to”
    
    NotImplementedError: Cannot convert a symbolic Tensor (simple_rnn/strided_slice:0) to a numpy array. This error may indicate that you’re trying to pass a Tensor to a NumPy call, which is not supported
    
    Python version is 3.8.12
    Tensorflow version is 2.4.1
    
    Thanks.
    
    Reply
Master56^^ December 21, 2021 at 6:40 am #

Error still wasn’t fix NotImplementedError: Cannot convert a symbolic Tensor (simple_rnn_1/strided_slice:0) to a numpy array. This error may indicate that you’re trying to pass a Tensor to a NumPy call, which is not supported

Reply
- James Carmichael December 24, 2021 at 5:58 am #
  
  Hi Master56^^…Please provide a full code listing and a description of your Python coding environment.
  
  Regards,
  
  Reply
Tommy Guo August 9, 2022 at 9:26 am #

Hi Mehran,

Thank you for providing this very insightful post! I had gone through learning materials from other online courses and labs but did not actually grasp what was actually happening in a RNN until I read your post here. It was very well written and elegantly lucid. The code is similarly very easy to follow and I hope to expand on this example to implement an RNN for my research project!

All the best,

Tommy

Reply
- James Carmichael August 9, 2022 at 9:53 am #
  
  Great feedback Tommy! We appreciate your support and feedback!
  
  Reply
Paolo March 3, 2023 at 5:22 am #

really great post!
I might have spotted a little typo:

h1 = np.dot(x[0], wx) + h0 + bh

should be:

h1 = np.dot(x[0], wx) + np.dot(h0, wh) + bh

anyway, the result doesn’t change as h0 is all zeros

Reply
- James Carmichael March 3, 2023 at 9:23 am #
  
  Thank you Paolo! We appreciate the feedback.
  
  Reply
cesiy March 28, 2023 at 5:30 pm #

we want extra information about this and it also execute on copy paste in colab or jupyter

Reply
- James Carmichael March 29, 2023 at 7:16 am #
  
  Hi cesiy…Have you been able to successfully execute the sample code? If not please let us know what is not working or what error messages you are receiving.
  
  Reply
tasos July 10, 2023 at 8:57 pm #

Thank you! How about a sequence with more than one feature per timestep? I tried the following but Keras outputs one value, and the manual computation outputs two values:

# hidden_units, dense_units, input_shape, activation
m = 2
demo_model = create_RNN(m, 1, (3,2), activation=[‘tanh’, ‘linear’])

wx = demo_model.get_weights()[0]
wh = demo_model.get_weights()[1]
bh = demo_model.get_weights()[2]
wy = demo_model.get_weights()[3]
by = demo_model.get_weights()[4]

print(‘wx = ‘, wx, ‘\nwh = ‘, wh, ‘\nbh = ‘, bh, ‘\nwy =’, wy, ‘\nby = ‘, by)

x = np.array([1,0.1, 2,0.2, 3,0.3])
# Reshape the input to the required sample_size x time_steps x features
x_input = np.reshape(x,(1, 3, 2))
print(‘x =’, x)
print(‘x_reshaped = ‘, x_input)
y_pred_model = demo_model.predict(x_input)

h0 = np.zeros(m)
h1 = np.tanh(np.dot(x[0], wx) + np.dot(h0,wh) + bh)
h2 = np.tanh(np.dot(x[1], wx) + np.dot(h1,wh) + bh)
h3 = np.tanh(np.dot(x[2], wx) + np.dot(h2,wh) + bh)
o3 = np.dot(h3, wy) + by

print(‘h1 = ‘, h1, ‘h2 = ‘, h2, ‘h3 = ‘, h3)

print(“Prediction from network “, y_pred_model)
print(“Prediction from our computation “, o3)

Output:
Prediction from network [[0.09162921]]
Prediction from our computation [[ 0.14343597] [-0.27000149]]

Reply
- James Carmichael July 10, 2023 at 11:12 pm #
  
  Hi Tasos…Thank you for your feedback! We will review this scenario.
  
  Reply
Odise October 4, 2023 at 7:05 am #

Hello, im using this dataset at the moment and i have to use a split ( train test validation) where train: from first row until 1965, validation from 1966 to 1975 and test from 1976 to last row. Im currently new to this type of language since i just started using Rstudio and i would like an answer as soon as posible bcuz i don’t seem to find a solution. Thank you very much.

Reply
- James Carmichael October 4, 2023 at 10:04 am #
  
  Hi Odise…The following resource provides best practices when applying training, testing and validation:
  
  https://machinelearningmastery.com/training-validation-test-split-and-cross-validation-done-right/
  
  Reply
Zineb October 20, 2023 at 9:13 pm #

Hi,
In the first example (Keras simpleRNN), you get weights without training the model ( no fit functing after model compilation )

how is that ?

Thanks in advance

Reply
Zineb October 20, 2023 at 10:42 pm #

One more question PLZ

In the first example (Keras Simple RNN);
y_pred_model=demo_model.predict(x_input)
print(“Prediction from network “, y_pred_model)
I obtain : [[-1.1634194]] !!

I just copy and past the code you give

Reply

Navigation

Understanding Simple Recurrent Neural Networks in Keras

Tutorial Overview

Prerequisites

Import Section

Want to Get Started With Building Transformer Models with Attention?

Keras SimpleRNN

Running the RNN on Sunspots Dataset

Step 1, 2: Reading Data and Splitting Into Train and Test

Step 3: Reshaping Data for Keras

Step 4: Create RNN Model and Train

Step 5: Compute and Print the Root Mean Square Error

Step 6: View the Result

Consolidated Code

Further Reading

Books

Articles

Summary

Learn Transformers and Attention!

Teach your deep learning model to read a sentence

Give magical power of understanding human language for
Your Projects

More On This Topic

17 Responses to Understanding Simple Recurrent Neural Networks in Keras

Leave a Reply Click here to cancel reply.

Navigation

Tutorial Overview

Prerequisites

Import Section

Want to Get Started With Building Transformer Models with Attention?

Keras SimpleRNN

Running the RNN on Sunspots Dataset

Step 1, 2: Reading Data and Splitting Into Train and Test

Step 3: Reshaping Data for Keras

Step 4: Create RNN Model and Train

Step 5: Compute and Print the Root Mean Square Error

Step 6: View the Result

Consolidated Code

Further Reading

Books

Articles

Summary

Learn Transformers and Attention!

Teach your deep learning model to read a sentence

Give magical power of understanding human language for Your Projects

More On This Topic

17 Responses to Understanding Simple Recurrent Neural Networks in Keras

Leave a Reply Click here to cancel reply.

Give magical power of understanding human language for
Your Projects