A Gentle Introduction to Positional Encoding in Transformer Models, Part 1

In languages, the order of the words and their position in a sentence really matters. The meaning of the entire sentence can change if the words are re-ordered. When implementing NLP solutions, recurrent neural networks have an inbuilt mechanism that deals with the order of sequences. The transformer model, however, does not use recurrence or convolution and treats each data point as independent of the other. Hence, positional information is added to the model explicitly to retain the information regarding the order of words in a sentence. Positional encoding is the scheme through which the knowledge of the order of objects in a sequence is maintained.

For this tutorial, we’ll simplify the notations used in this remarkable paper, Attention Is All You Need by Vaswani et al. After completing this tutorial, you will know:

• What is positional encoding, and why it’s important
• Positional encoding in transformers
• Code and visualize a positional encoding matrix in Python using NumPy

Kick-start your project with my book Building Transformer Models with Attention. It provides self-study tutorials with working code to guide you into building a fully-working transformer model that can
translate sentences from one language to another...

Let’s get started.

A gentle introduction to positional encoding in transformer models
Photo by Muhammad Murtaza Ghani on Unsplash, some rights reserved

Tutorial Overview

This tutorial is divided into four parts; they are:

1. What is positional encoding
2. Mathematics behind positional encoding in transformers
3. Implementing the positional encoding matrix using NumPy
4. Understanding and visualizing the positional encoding matrix

What Is Positional Encoding?

Positional encoding describes the location or position of an entity in a sequence so that each position is assigned a unique representation. There are many reasons why a single number, such as the index value, is not used to represent an item’s position in transformer models. For long sequences, the indices can grow large in magnitude. If you normalize the index value to lie between 0 and 1, it can create problems for variable length sequences as they would be normalized differently.

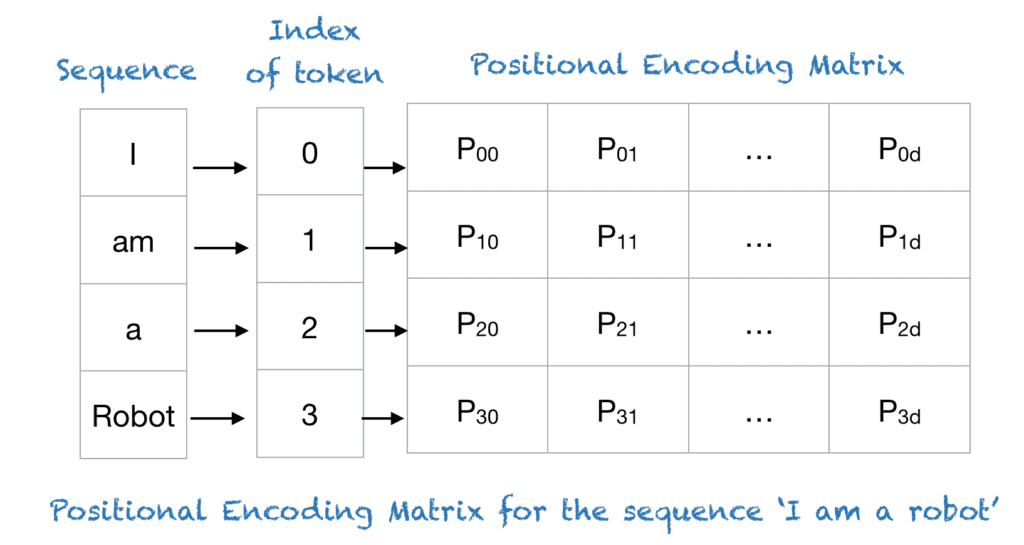
Transformers use a smart positional encoding scheme, where each position/index is mapped to a vector. Hence, the output of the positional encoding layer is a matrix, where each row of the matrix represents an encoded object of the sequence summed with its positional information. An example of the matrix that encodes only the positional information is shown in the figure below.

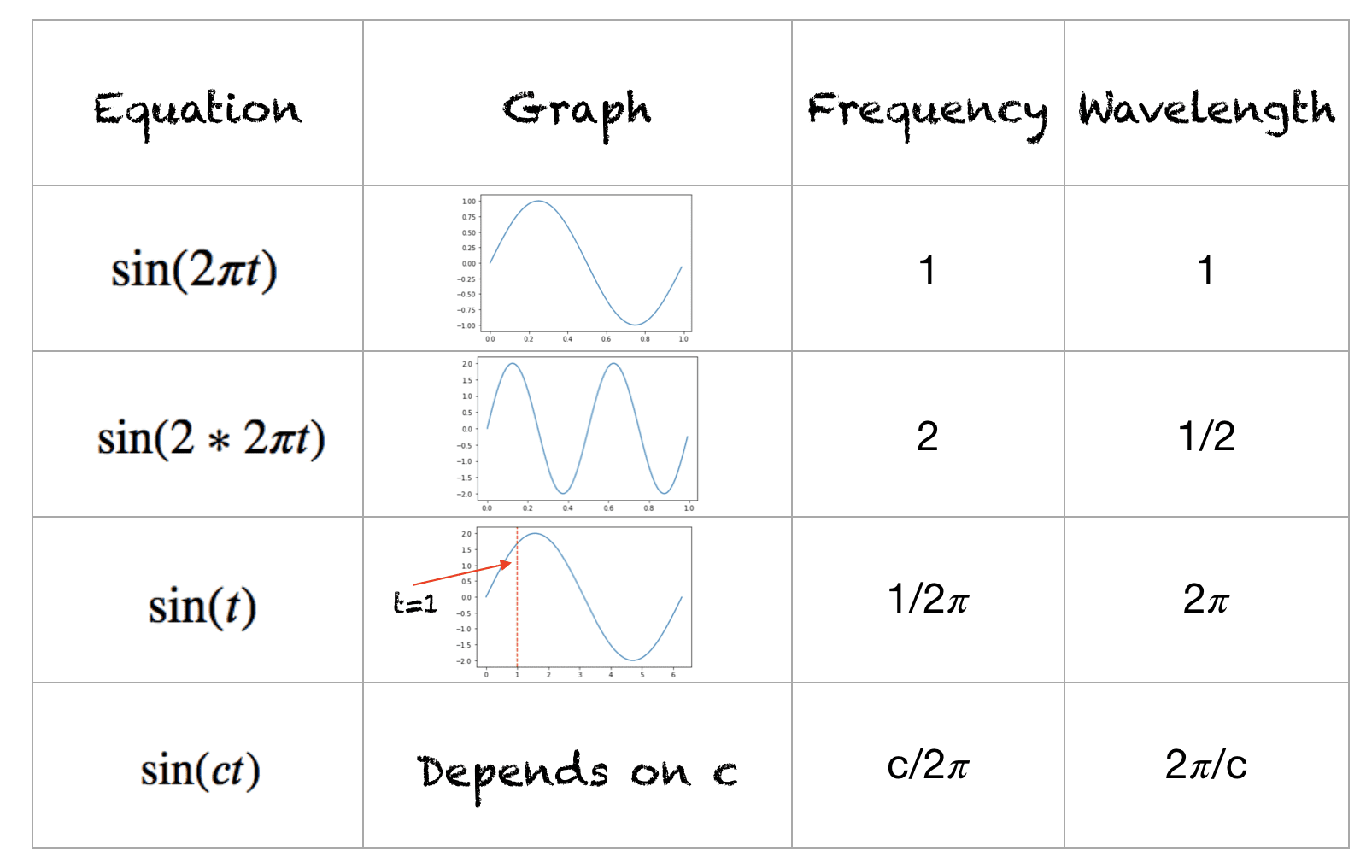
A Quick Run-Through of the Trigonometric Sine Function

This is a quick recap of sine functions; you can work equivalently with cosine functions. The function’s range is [-1,+1]. The frequency of this waveform is the number of cycles completed in one second. The wavelength is the distance over which the waveform repeats itself. The wavelength and frequency for different waveforms are shown below:

Positional Encoding Layer in Transformers

Let’s dive straight into this. Suppose you have an input sequence of length $L$ and require the position of the $k^{th}$ object within this sequence. The positional encoding is given by sine and cosine functions of varying frequencies:

\begin{eqnarray}
P(k, 2i) &=& \sin\Big(\frac{k}{n^{2i/d}}\Big)\\
P(k, 2i+1) &=& \cos\Big(\frac{k}{n^{2i/d}}\Big)
\end{eqnarray}

Here:

$k$: Position of an object in the input sequence, $0 \leq k < L/2$

$d$: Dimension of the output embedding space

$P(k, j)$: Position function for mapping a position $k$ in the input sequence to index $(k,j)$ of the positional matrix

$n$: User-defined scalar, set to 10,000 by the authors of Attention Is All You Need.

$i$: Used for mapping to column indices $0 \leq i < d/2$, with a single value of $i$ maps to both sine and cosine functions

In the above expression, you can see that even positions correspond to a sine function and odd positions correspond to cosine functions.

Example

To understand the above expression, let’s take an example of the phrase “I am a robot,” with n=100 and d=4. The following table shows the positional encoding matrix for this phrase. In fact, the positional encoding matrix would be the same for any four-letter phrase with n=100 and d=4.

Coding the Positional Encoding Matrix from Scratch

Here is a short Python code to implement positional encoding using NumPy. The code is simplified to make the understanding of positional encoding easier.

To understand the positional encoding, let’s start by looking at the sine wave for different positions with n=10,000 and d=512.

Python

def plotSinusoid(k, d=512, n=10000): x = np.arange(0, 100, 1) denominator = np.power(n, 2*x/d) y = np.sin(k/denominator) plt.plot(x, y) plt.title('k = ' + str(k)) fig = plt.figure(figsize=(15, 4)) for i in range(4): plt.subplot(141 + i) plotSinusoid(i*4)

1 2 3 4 5 6 7 8 9 10 11

def plotSinusoid(k, d=512, n=10000):     x = np.arange(0, 100, 1)     denominator = np.power(n, 2*x/d)     y = np.sin(k/denominator)     plt.plot(x, y)     plt.title('k = ' + str(k))   fig = plt.figure(figsize=(15, 4))     for i in range(4):     plt.subplot(141 + i)     plotSinusoid(i*4)

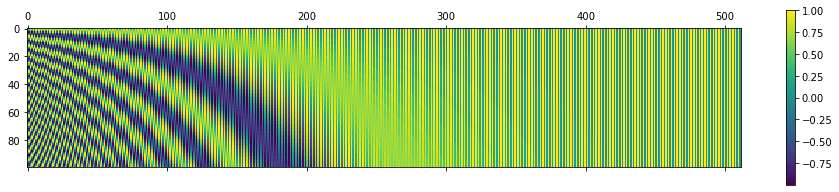
The following figure is the output of the above code:

Sine wave for different position indices

You can see that each position $k$ corresponds to a different sinusoid, which encodes a single position into a vector. If you look closely at the positional encoding function, you can see that the wavelength for a fixed $i$ is given by:

$$
\lambda_{i} = 2 \pi n^{2i/d}
$$

Hence, the wavelengths of the sinusoids form a geometric progression and vary from $2\pi$ to $2\pi n$. The scheme for positional encoding has a number of advantages.

1. The sine and cosine functions have values in [-1, 1], which keeps the values of the positional encoding matrix in a normalized range.
2. As the sinusoid for each position is different, you have a unique way of encoding each position.
3. You have a way of measuring or quantifying the similarity between different positions, hence enabling you to encode the relative positions of words.

Visualizing the Positional Matrix

Let’s visualize the positional matrix on bigger values. Use Python’s matshow() method from the matplotlib library. Setting n=10,000 as done in the original paper, you get the following:

Python

P = getPositionEncoding(seq_len=100, d=512, n=10000) cax = plt.matshow(P) plt.gcf().colorbar(cax)

1 2 3

P = getPositionEncoding(seq_len=100, d=512, n=10000) cax = plt.matshow(P) plt.gcf().colorbar(cax)

The positional encoding matrix for n=10,000, d=512, sequence length=100

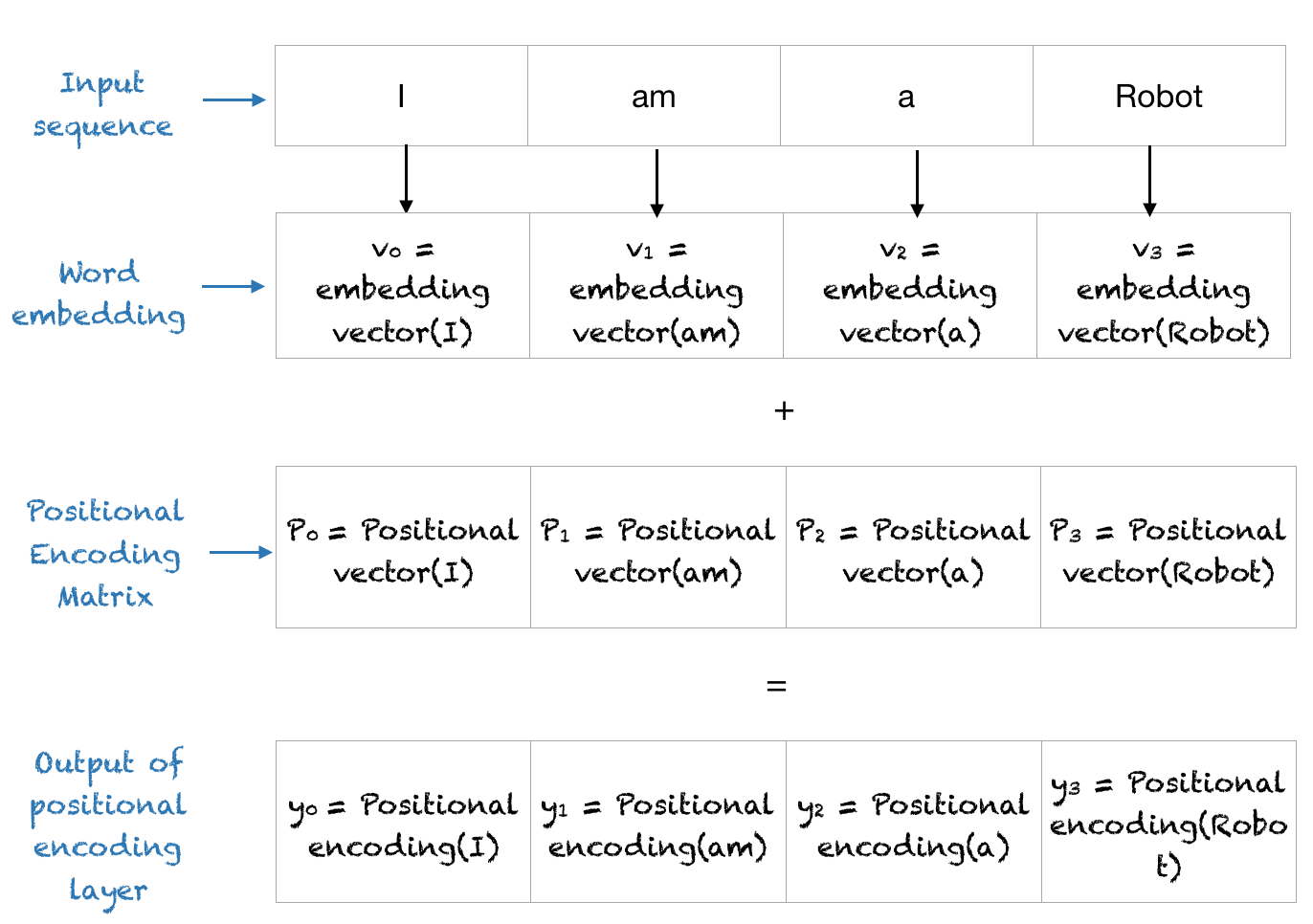
What Is the Final Output of the Positional Encoding Layer?

The positional encoding layer sums the positional vector with the word encoding and outputs this matrix for the subsequent layers. The entire process is shown below.

The positional encoding layer in the transformer

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Books

• Transformers for natural language processing, by Denis Rothman.

Papers

• Attention Is All You Need, 2017.

Articles

• The Transformer Attention Mechanism
• The Transformer Model
• Transformer model for language understanding

Summary

In this tutorial, you discovered positional encoding in transformers.

Specifically, you learned:

• What is positional encoding, and why it is needed.
• How to implement positional encoding in Python using NumPy
• How to visualize the positional encoding matrix

Do you have any questions about positional encoding discussed in this post? Ask your questions in the comments below, and I will do my best to answer.

Learn Transformers and Attention!

Teach your deep learning model to read a sentence

...using transformer models with attention

Discover how in my new Ebook:
Building Transformer Models with Attention

It provides self-study tutorials with working code to guide you into building a fully-working transformer models that can
translate sentences from one language to another...

Give magical power of understanding human language for
Your Projects

See What's Inside