It is important to compare the performance of multiple different machine learning algorithms consistently.
In this post you will discover how you can create a test harness to compare multiple different machine learning algorithms in Python with scikit-learn.
You can use this test harness as a template on your own machine learning problems and add more and different algorithms to compare.
Kick-start your project with my new book Machine Learning Mastery With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Update Mar/2018: Added alternate link to download the dataset as the original appears to have been taken down.

How To Compare Machine Learning Algorithms in Python with scikit-learn
Photo by Michael Knight, some rights reserved.
Choose The Best Machine Learning Model
How do you choose the best model for your problem?
When you work on a machine learning project, you often end up with multiple good models to choose from. Each model will have different performance characteristics.
Using resampling methods like cross validation, you can get an estimate for how accurate each model may be on unseen data. You need to be able to use these estimates to choose one or two best models from the suite of models that you have created.
Compare Machine Learning Models Carefully
When you have a new dataset, it is a good idea to visualize the data using different techniques in order to look at the data from different perspectives.
The same idea applies to model selection. You should use a number of different ways of looking at the estimated accuracy of your machine learning algorithms in order to choose the one or two to finalize.
A way to do this is to use different visualization methods to show the average accuracy, variance and other properties of the distribution of model accuracies.
In the next section you will discover exactly how you can do that in Python with scikit-learn.
Need help with Machine Learning in Python?
Take my free 2-week email course and discover data prep, algorithms and more (with code).
Click to sign-up now and also get a free PDF Ebook version of the course.
Compare Machine Learning Algorithms Consistently
The key to a fair comparison of machine learning algorithms is ensuring that each algorithm is evaluated in the same way on the same data.
You can achieve this by forcing each algorithm to be evaluated on a consistent test harness.
In the example below 6 different algorithms are compared:
- Logistic Regression
- Linear Discriminant Analysis
- K-Nearest Neighbors
- Classification and Regression Trees
- Naive Bayes
- Support Vector Machines
The problem is a standard binary classification dataset called the Pima Indians onset of diabetes problem. The problem has two classes and eight numeric input variables of varying scales.
You can learn more about the dataset here:
The 10-fold cross validation procedure is used to evaluate each algorithm, importantly configured with the same random seed to ensure that the same splits to the training data are performed and that each algorithms is evaluated in precisely the same way.
Each algorithm is given a short name, useful for summarizing results afterward.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# Compare Algorithms import pandas import matplotlib.pyplot as plt from sklearn import model_selection from sklearn.linear_model import LogisticRegression from sklearn.tree import DecisionTreeClassifier from sklearn.neighbors import KNeighborsClassifier from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.naive_bayes import GaussianNB from sklearn.svm import SVC # load dataset url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = pandas.read_csv(url, names=names) array = dataframe.values X = array[:,0:8] Y = array[:,8] # prepare configuration for cross validation test harness seed = 7 # prepare models models = [] models.append(('LR', LogisticRegression())) models.append(('LDA', LinearDiscriminantAnalysis())) models.append(('KNN', KNeighborsClassifier())) models.append(('CART', DecisionTreeClassifier())) models.append(('NB', GaussianNB())) models.append(('SVM', SVC())) # evaluate each model in turn results = [] names = [] scoring = 'accuracy' for name, model in models: kfold = model_selection.KFold(n_splits=10, random_state=seed) cv_results = model_selection.cross_val_score(model, X, Y, cv=kfold, scoring=scoring) results.append(cv_results) names.append(name) msg = "%s: %f (%f)" % (name, cv_results.mean(), cv_results.std()) print(msg) # boxplot algorithm comparison fig = plt.figure() fig.suptitle('Algorithm Comparison') ax = fig.add_subplot(111) plt.boxplot(results) ax.set_xticklabels(names) plt.show() |
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example provides a list of each algorithm short name, the mean accuracy and the standard deviation accuracy.
|
1 2 3 4 5 6 |
LR: 0.769515 (0.048411) LDA: 0.773462 (0.051592) KNN: 0.726555 (0.061821) CART: 0.695232 (0.062517) NB: 0.755178 (0.042766) SVM: 0.651025 (0.072141) |
The example also provides a box and whisker plot showing the spread of the accuracy scores across each cross validation fold for each algorithm.
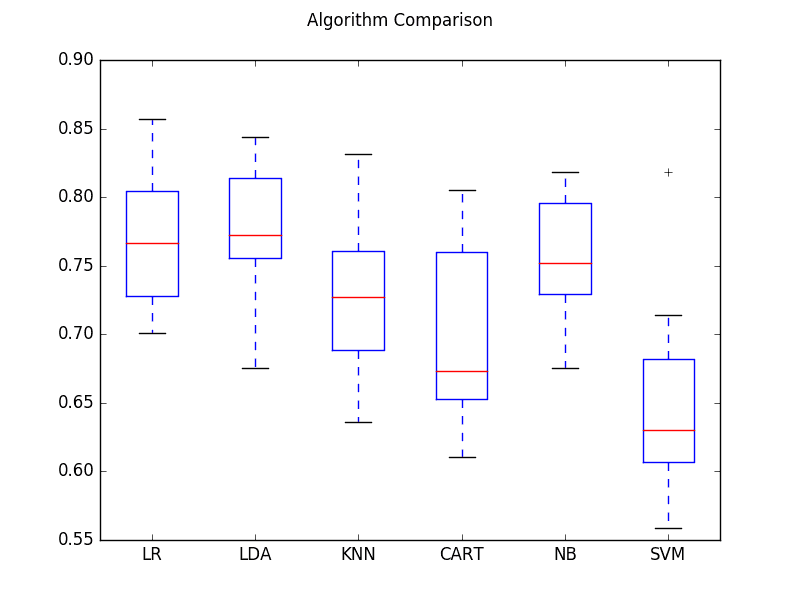
Compare Machine Learning Algorithms
From these results, it would suggest that both logistic regression and linear discriminate analysis are perhaps worthy of further study on this problem.
Summary
In this post you discovered how to evaluate multiple different machine learning algorithms on a dataset in Python with scikit-learn.
You learned how to both use the same test harness to evaluate the algorithms and how to summarize the results both numerically and using a box and whisker plot.
You can use this recipe as a template for evaluating multiple algorithms on your own problems.
Do you have any questions about evaluating machine learning algorithms in Python or about this post? Ask your questions in the comments below and I will do my best to answer them.







Great article! Just a quick question, what do you think is the best method? First optimise hyper-parameters and then compare the algorithms or vice versa. Thanks.
I recommend first spot checking algorithms and comparing them, followed by tuning.
Thank you for your recommendation…
You should not just rely on this. Accuracy is only one portion of a model’s accuracy. Depending on the investigation desired, you should look at Precision and Recall because accuracy may be only a tiny portion. Also, why have you not taken an approach with ANOVA, or the Wilcoxon Test, major tests within the realm of data science and widely accepted? Additionally, 5×2 cross-validation should be done, not 10-fold (this is widely accepted). Last, what I find completely missing in this is that you have not discussed how to actually arrive at a statistically-significant decision. This is not a good representation.
Eric, nobody cares about your phd, whatever it is you did it in. Also, stop calling it ANOVA when all you’re doing is a regression, it doesn’t make you any smarter. And lastly, nobody cares about your phd and your academic research, this is a machine learning article for Data Scientists.
There’s always room for improvement and we have to start/stop somewhere in an introductory piece.
right
How do we compare the prediction with actual post this?
Hi Dr Brownlee,
Big fan of your tutorials. I have a question regarding the compare first then tune approach. When we plot them on a box plot and select the best, this is all based on the default model setting right? But once we have tune the different settings in a given model, would the predictive performance be different?
So the not so good models might even outperform the best model given in the first glance boxplot, if we have trained them more properly. So in this sense, wouldn’t it better to train every module separately, and then say, connect all of them and plot their ROC to see which performs best?
Sure, if you have the resources.
Dear Dr. Bronwlee,
Thank you for all the useful tutorials. I have two questions if you don’t mind.
1- Would it better to normalize data first since some algorithms are sensitive to it? e.g. KNN and Neural Networks.
2- I obtained the following ranking after comparing some algorithms in another dataset:
Before tuning hyperparameters: Random Forest, Decision Tree, Logistic Regression, SVM
After tuning hyperparameters: Random Forest, Logistic Regression, SVM, Decision Tree
Hence, do you think we should first tune hyper-parameters before comparing machine learning algorithms?
Thank you in advance for your answers.
Yes scaling first is a good idea, but test to confirm that it lifts model skill.
Thank you for your answer.
Please, I have one last question.
Since the results also depend on the random state, should we use different values and keep the average accuracy for each machine learning algorithm?
Thanks in advance.
Yes. I explain this more here:
https://machinelearningmastery.com/randomness-in-machine-learning/
And here:
https://machinelearningmastery.com/evaluate-skill-deep-learning-models/
Accuracy is easily readable but, in my opinion, it should be replaced by AUC: AUC is “consistent” and “more discriminating” than accuracy (Ling et al. 2003).
AUC can be examined on an ROC or Precision vs Recall curve. What should happen is weights based on misclassification, in a confusion matrix. In this case, you can tune a model to avoid certain misclassifications, as some may be more valuable to avoid. If you have zero care about which misclassification occurs, ROC is a decent metric for how you should tune parameters. ROC should be examined for hyperparameter decisions.
So go write your own article
hahahahahahhahahahhhahahha this dude seems to hate eric..n since it is annoymus, this might as well be the auther
In the code, “seed = 7” is hard coded. Shouldn’t we have a different seed for each fold?
To answer my own question, it appears that each model is trained and tested for all folds before moving on to the next model. The seed applies to the initial state so for the above, the 10 folds will all be different from one another, but the same data split for each of the 10 folds will be presented to each algorithm.
Yes Tom, the seed ensures we have the same sequence of random numbers. The random numbers ensure we have a random split of the data into the k folds.
Thank you for sharing.
I had to tweak the code a little to make it work with scikit-learn 0.18.
The cross_validation module is deprecated. It’s replaced by model_selection.
The KFold parameters have changed too:
0.17: cross_validation.KFold(n, n_folds=3, shuffle=False, random_state=None)
0.18: model_selection.KFold(n_splits=3, shuffle=False, random_state=None)
I have a question: is it ok to train the classifier before adding it to the list? Like:
lr = LogisticRegression()
lr.fit(X_train, y_train)
models.append((‘LR’,lr))
Thanks Guillaume, I will look at updating the example. I have recently updated all of my books to support the new sklearn.
No, the structure of the example fits and evaluates each model in turn. Your example essentially unrolls the for loop.
What a great article! I learned so much from your writing 🙂
I also read your other article comparing different algorithms in R, and I noticed that you used a lot more techniques in that article:
• Table Summary
• Box and Whisker Plots
• Density Plots
• Dot Plots
• Parallel Plots
• Scatterplot Matrix
• Pairwise xyPlots
• Statistical Significance Tests
I was wondering why you did not provide the same techniques in this Python article? Is it because these functions are more readily available in R?
Thanks so much!
Great question.
These capabilities are available in Python, but are spread through the scipy and statsmodels libs rather than directly available in sklearn.
R is a more technical platform for more technical types, I tend to go into more detail in those examples.
Is this something you would like to see more of Angela?
Hi Jason. Thank you for these great articles. I also read this article of yours (https://goo.gl/v71GPT). What I wonder is the proper validation method. Should we conduct k-fold or repeated n*k-fold cross validation? I recently read a journal article where researchers compare around 50 models under 5*2-folds setting, suggesting it is more robust. How should we proceed while comparing models?
Hi Suleyman,
Using k-fold cross validation is a gold standard. The specific configuration is problem specific, but common configurations of 3,5, 10 do well on many datasets.
On very large datasets, a train-test split may be sufficient. For complex or small datasets, if you have the resources, repeated k-fold cross validation is preferred. Often, we would like to use repeated k-fold cross validation, but the computational expense is too high.
There is no “best”, just lots of options to tune for your given problem.
How do you choose?
Balance your constraints (amount of data, resources, time, ..) against your requirements (robustness of result).
Thank you Jason. That is what I have been doing.
Do stick with 5×2. Nested Cross Validation is widely accepted, and way ahead of regular k-fold.
Hi Jason,
Thanks a lot for this good article.
Could you please give some interpretations of the standard deviation values?
Especially regarding overfitting.
I thought that in case we have a small standard deviation of the cv results, we will have more overfitting, but I am not sure about that.
Thanks
Hi Othmane, great question.
So standard deviation summarizes the spread of the distribution, assuming it is Gaussian.
A tight spread may suggest overfitting or it may not, but we can only be sure by evaluating the model on a hold out dataset.
One use of the stdev is to specify a confidence interval for the result. For example, the performance of the model is x% on unseen data, with the performance in the range of 2 standard deviations of that score (95th percentile).
This might help:
https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule
Thanks for the prompt, this topic of interpreting results is not discussed enough. I plan to write more about it.
Following Othmane’s question, shouldn’t we work with the standard error of the mean instead of the standard deviation? Basically, divide the standard deviations by sqrt(10). This is because “The standard error (SE) of a statistic (most commonly the mean) is the standard deviation of its sampling distribution”. https://en.wikipedia.org/wiki/Standard_error
You can, I have an example of calculating standard error here:
https://machinelearningmastery.com/estimate-number-experiment-repeats-stochastic-machine-learning-algorithms/
I have examples of calculating confidence intervals here:
https://machinelearningmastery.com/report-classifier-performance-confidence-intervals/
and here:
https://machinelearningmastery.com/calculate-bootstrap-confidence-intervals-machine-learning-results-python/
Hi, from the boxplot, we get LR and LDA to have higher accuracy, so we select them as our models.
So now, can I apply train_test_split to check the RMSE and the accuracy for the testing data using both these models. Whichever gives the best result, I will make that my final model?
Hi Dhrubajit,
There are many ways to choose a final model. Often we prefer a model with better average performance rather than better absolute performance, this is because of the natural variance in the estimation of performance of the models on unseen data.
Once you choose a final model, train it on all available data and you can start to use it to make predictions.
Great article! Could you please explain me why this program doesn’t work when Y is float?
Hi Peter,
Classification problems assume the outcome is a label.
great post! thanks for sharing
Thanks Edmond.
Hi Jason,
I have started learning and implementing Machine learning algorithms.
One question – the above blog will tell us which Machine learning algorithm to go with. However, Should we ever check that if we are using Regression, how well the regression fits the data by checking
Autocorrelation, Multicollinearity and normality.
What I have learnt from reading blogs and articles that we all calculate score by using cross validation methodology, and then find out which would fit best. have not seen anyone following traditional ways such as checking Autocorrelation, Multicollinearity and normality. I might be wrong. Please throw some light on the same.
THanks Nitesh
Yes, on time series, an understanding of the autocorrelation is practically required.
When using a linear method, an idea of multicollinearity can be helpful.
I would suggest this type of analysis before investigating models to get a better idea of the structure of your problem.
Hi Jason! First of all thanks for all your blog posts, they are really helping me to better understand how to work with datasets and machine learning algorithms.
I’ve a question related to the scoring method. Before discovering the method you are using here, I was using the .score() method in this way (assume I already have splitted the dataset 80/20 and tranformed the data):
from sklearn.svm import LinearSVC
lin_svc = LinearSVC()
lin_svc.fit(train_set_scaled, train_set_labels)
lin_svc.score(test_set_scaled, test_set_labels)
getting a score that was similar but different to the one I obtain with the method explained in this post. What’s the difference between using score() and using cross_val_score() ?
Thanks!
Good question.
The cross_val_score() function uses the more robust cross validation method to evaluate model skill:
http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html#sklearn.model_selection.cross_val_score
The score() function on a model evaluate the skill of the model on the provided dataset.
http://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html#sklearn.svm.LinearSVC.score
Does that help?
While comparing algorithms by using same code which is mentioned above i got one error ‘could not covert string to float’.
Can you please tell me how to tackle it.
Confirm that you copied the code exactly and that you are using the same data file. Also confirm that all of your Python libraries are up to date.
Thanks Jason.
Actually I am using different dataset. My dataset is about stock related. So what can I do for it while comparing the algorithms.
Hi,
Thank you so much for this tutorial. It really helps one using Machine Learning in sklearn.
One questio: I’mm trying to use this code with my dataset but I have features which are strings and not numbers, as in your dataset.
What can I do to change the code in order for it to work? (I’m getting an error saying “could not convert string to float”
If they are labels, you can use a label encoder.
If you are working with string input, see NLP:
https://machinelearningmastery.com/start-here/#nlp
Hello, Dr. Jason! Thank you so much for this wonderful article. I have a question for you. I noticed you have not mentioned feature selection and feature engineering in the Python mini course. So, my question is that if we were to implement both of these tasks, what should be the order with respect to this present stage of spot checking and comparison of machine learning algorithms? Should we first select one or two best performing models after comparison and then implement feature selection and feature engineering or first implement them and then perform spot checking and model comparison?
Thank you in advanced.
Generally before spot checking.
Thank you for answering! But, that “generally” is really not helping. Can you please explain in which cases it is suggested to do that and in which cases not? I think it’s really important for me to learn.
No, it depends on the data and the project. I have to speak in generalities because I do not have the capacity to get involved in everyones project. Sorry.
Oh, okay. I hope to learn it as I do more projects. Thank you!
Thank you for the brilliant tutorial! If we have split our data in to train and test sets and wanted to know the accuracy of the trained model on the held out test data, could we do:
cv_results = model_selection.cross_val_score(model, X_test, Y_test, cv=kfold, scoring=scoring)
Or would we need to use .fit on the training data before testing on the test data? I hope this makes sense! Thank you.
Generally, we would fit the model on all of the training set, make predictions for the test set, then evaluate the skill of the predictions on the test set.
Ahh OK, so the above method is really just for comparing models? And then we train/ test using e.g. a 0.2 split? Would you ever actually train your model using cross-validation? Thanks so much.
No, you train the model on all data before making predictions. See this post:
https://machinelearningmastery.com/train-final-machine-learning-model/
Thanks for a great tutorial! I can follow the logic, but it seems UCI has taken down the pima indians dataset.
Thanks, I have updated the link to the dataset.
Thank you for the post Jason. I am curious however, how which scores are normally reported when comparing ML models fitted with slightly different features. E.g there is a set of features both models A and B share and A has been fitted a single unique feature and B has one as well, which A is not trained with. When one would evaluate such models for comparing, should we report and compare the scores on the test set or use cross_val_score with all the data?
Interesting.
Perhaps you could pick a measure that is relevant to the general domain, it could be something generic such as model accuracy or prediction error.
Thank you for the response, I was thinking of either using MAE or MSE since mine is a regression problem and see, which model achieves the lowest score.
However I don’t know, what is the general practice, should we compare the two models like:
A: Using cross_val_score to report MSE with the regressor and X, y where X and y is the entire data (no train/test split)
or
B: Doing a train/test split, fitting the model with train data and then making predictions using the test data and compare the MSE scores of the models
The choice and configuration of the test harness is a big part of the challenge of applied machine learning.
It must be tailored to your specific problem.
Hi Dr. Jason,
Thank you for this wonderful post. I have a question about complexity. As we usually use Accuracy to score the performance of Learning Algorithms. Is there any provision made for measuring the time taken(i.e. speed ) for the algorithm to complete the specific task given. I added a timeit function in one of your code i used from your post as follows
%timeit results = cross_val_score(bcancermodelb, X, Y, cv=kfold,scoring=scoring)
print(“Accuracy: %.3f%% (%.3f%%)” % (results.mean()*100.0, results.std()*100.0))
and i end up with the following result
19.2 ms ± 1.08 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Accuracy: 93.420% (3.623%).
Can this be a good measure for the time taken for a particular model?
Generally no. If this is an important consideration in your model, then you can take it into account.
Hi Jason,
I am little confused about the box plot I am getting. I had compared 9 algorithms accuracy on my datasets with more than 90 features. The results I am getting is bit confusing as I only LDA showing more than 90% accuracy than other models, which ranges from 20% h 40%. Is the plot is valid and I can consider LDA as best model?
Perhaps inspect the raw data to confirm the finding.
hi i get this error , why would it be?
ValueError: Input contains NaN, infinity or a value too large for dtype(‘float64’).
Perhaps check that your input data was loaded correctly?
cv_results = model_selection.cross_val_score(model, X, Y, cv=kfold,scoring=scoring)
i probably have error in this line
Ensure you have copied the code exactly, preserving white space.
Hi how did u solve your problem
If I use the code above, I receive the following error message. (Python 3.6 – Spyder)
for name, model in models:
File “”, line 1
for name, model in models:
^
SyntaxError: unexpected EOF while parsing
Looks like you added a “,”.
Be sure to copy the code exactly.
I found the mistake.
Glad to hear it.
explain this: “preg’, ‘plas’, ‘pres’, ‘skin’, ‘test’, ‘mass’, ‘pedi’, ‘age’, ‘class'”
They are explained here:
https://github.com/jbrownlee/Datasets/blob/master/pima-indians-diabetes.names
Hi Jason
how can I get confusion matrix’s per algorithm from Your example? Also TP FP TN and FN to calculate prediction and recall per algorithm? Thanks!
This post explains the confusion matrix and shows how to calculate it:
https://machinelearningmastery.com/confusion-matrix-machine-learning/
Thanks Jason.
Hi, problem is that I know actual value (Y) but cannot find how to gain/print predicted values for each algorithm in this example?
This post explains how to make predictions with sklearn:
https://machinelearningmastery.com/make-predictions-scikit-learn/
Thank you so much for your all posts. They are extremely helpful.
I’m happy they help!
Hello Sir,
The accuracy for my problem is low, will you please suggest me to improve this.
LDA: 0.581771 (0.052691)
KNN: 0.523047 (0.054386)
CART: 0.606641 (0.044246)
NB: 0.562109 (0.089570)
SVM: 0.554167 (0.099744)
Yes, I have have suggestions here:
https://machinelearningmastery.com/machine-learning-performance-improvement-cheat-sheet/
i have a problem in the code.
in this line kfold = model_selection.KFold(n_splits=6, random_state=seed)
my dataset contains 4 nemuric input and two classes.
i need to know what the seeds an n-spilts or they refer for what?
need quick reply please.
Thi sis a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/what-value-should-i-set-for-the-random-number-seed
Hello sir,
I was trying to build a web tool as part of my project. It lets the user upload a dataset and plots accuracy of different algorithms with this code . I tried this code with many datasets and found this code isn’t working for too large datasets like a dataset with 2*10^6 rows and 30 coloumns. Can u tell the approx max size of dataset which could run properly?
I believe it will scale with the amount of RAM available.
For larger datasets, it may be better to use progressive loading or a big data framework.
Thank you, Dr. Brownlee, for this tutorial.
You said that the results would suggest that both logistic regression and linear discriminate analysis are worthy of further study on this problem.
How can we compare two boxplots (logistic regression and linear discriminate analysis for example) to determine which one is better?
Perhaps evaluate each model multiple times and compares the means (mean of means and their distribution).
Thank you for this great post. I’m working on customer churn problem and have performed LR, RF, SVM, KNN and when I applied your code to select the best model which gives below output when I pass test data i.e x_test and y_test instead of X, Y in your code. am I doing it correctly, like which data to pass instead of X and Y? train or test ?? Please response ASAP.
Thank you
LR: 0.762319 (0.024232)
SVM: 0.666667 (0.033747)
KNN: 0.598551 (0.030891)
RF: 0.779710 (0.027430)
Sorry, I don’t understand your question, perhaps you can rephrase it or elaborate?
Hi Jason, thanks for this post. How can I do a hyper-parameter tuning for each model using your template? For example lets assume that I want to tune the “number or neighbors” for KNN, the “depth of tree” for decision tree and so on. I am thinking about having another for loop inside the main one for hyper-parameter tuning. The tricky part for me is how to pass a parameter value to the model?
I would recommend this post for combining spot checking and some tuning:
https://machinelearningmastery.com/spot-check-machine-learning-algorithms-in-python/
Hi , Jason, i wonder if you can do me a favor.
(1)My undergraduate dissertation is about designing an algorithm or several chunks of code based on Neural Network, especially deep neural network.
(2) But i also need to compare deep learning with shallow learning on their performances, like accuracy and other metrics.
So based on these two tasks, do i have some efficient ways to implement them? How about import sth existing from sklearn like you. But I’m not so sure what I can do with sklearn. I had seen my thesis as a task of recreating steamer from scratch. It seems unworthy of my effort, but i’m not so sure. what do you think?
I recommend talking to your research advisor about your concerns.
Hi Jason,
Thanks for the article in comparing the different predictive models in Python. I am currently in the process of comparing the different predictive models using root mean squared percentage error(RMSPE) in a regression problem. Using your cross validation code as follows:
I have gotten the following results:
LM: -8679071434605513.000000 (7381730822398656.000000)
Ridge: -9344356403286348.000000 (5680597868319848.000000)
Lasso: -8214240415834513.000000 (6885019346742973.000000)
RandomForest: -6671926010255401.000000 (5635345468122856.000000)
gbm: -5373061987919916.000000 (5191299686435015.000000)
Can I ask how to convert the following to RMSPE to be represented in boxplots? I have already split my dataset to training and test data. Thanks!
They are very big scores!
You might want to scale data prior to modeling?
The “results” variable is a list that can be plotted directly as a boxplot, you can then have a list of lists for a series of boxplots.
Hi Jason,
Thanks for your reply. However, my features have a mix of categorical and numerical variables. How do I do scaling in this case? Usually I do not have the practice of scaling the data. Thanks!
Only scale the numerical features. Only scale the categorical features if you use an integer encoding.
Thanks for your great post and also for your kindness and response! I’m using Pyspark platform to build the model which able to provide insight from huge datasets and also predict the risk. could you recommend me the parameter I will consider to compare machine learning algorithm for best accuracy and performance by using Pyspark?
Thanks!
I recommend testing a suite of algorithm configurations in order to discover what works best for your specific dataset.
I explain more here:
https://machinelearningmastery.com/faq/single-faq/what-algorithm-config-should-i-use
Great article Dr Brownlee
Please, how can I test and compare different ML algorithms using big data data sets?
Any reference please ! is kuggle considered a good exalemple for big data?
Thanks.
Perhaps you can use a big data framework. I don’t have tutorials on this topic, sorry.
Great post !!!
HI jason ,
i am predicting top 3 skills for a candidate T Comparing Actual vs predicted I am stuck with comparing actual vs predicted values top three classes when we compare and print the results actual vs predicted results, the predicted values are sorted by top probabilities and mapped to classes where as in actual we have only class labels and when we compare the values are deviating. please suggest how to proceed.
Regards,
Naveen
Perhaps your problem is a multi-label classification problem, instead of a multi-class classification problem?
If so, this paper might give you ideas on how to evaluate skill:
https://scholar.google.com/scholar?cluster=11211211207326445005&hl=en&as_sdt=0,5
Hi Jason,
Thank you so much for the wonderful article. I have an issue , in my dataset I have a total of 124414 observation , the dependent variable is binary (0 & 1), however the issue is the dataset has 124388 zeros and only 106 ones. Can you please tell me how to deal with that situation.
Perhaps try a suite of models to see if the problem is learnable?
I tried couple of models . The train and test accuracies are too high. Do you think it sounds good ?
LogisticRegressionCV
0.999153
0.999138
KNeighborsClassifier
1
0.999028
DecisionTreeClassifier
1
0.998766
GaussianNB
0.997454
0.997272
LinearDiscriminantAnalysis
0.994809
0.994139
It many be the case that your problem is easy to solve or the test data is not representative of the broader problem.
Hi Jason,
Wanna ask you hoa to comare my results with a seed and other users results with other seeds which they did not specify them
You can run many times with many different seeds and compare the mean performance across all runs.
Hi Jason,
I would like to ask you, know some measured points, how to fit the curve of two features variables with python, and get the corresponding expression, can you pass sklearn, pass the curve_fit of scipy, thank you, look forward to your reply!
I believe scipy has polynomial models for this, e.g.
https://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html
Hi Jason,
Thanks for your article of comparing different models in python.
In the process of comparing the different predictive models, I am using your cross validation code as follows:
results = []
names = []
scoring = ‘accuracy’
for name, model in models:
kfold = model_selection.KFold(n_splits=10, random_state=seed)
cv_results = model_selection.cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
results.append(cv_results)
names.append(name)
msg = “%s: %f (%f)” % (name, cv_results.mean(), cv_results.std())
print(msg)
But, I am getting a warning message like this “The default value of gamma will change from ‘auto’ to ‘scale’ in version 0.22 to account better for unscaled features. Set gamma explicitly to ‘auto’ or ‘scale’ to avoid this warning”
Please, How to handle it?
Yes, this post shows how to handle it:
https://machinelearningmastery.com/how-to-fix-futurewarning-messages-in-scikit-learn/
Thanks for your quick response. Moreover, the post indeed is very helpful. However, after running the codes i can only have Support Victor Machine short name and the corresponding mean accuracy as well as the standard deviation instead of provides a list of all the algorithms short name, the mean accuracy and the standard deviation accuracy.
Please, what need to be added to solve the issue on ground.
I am pleased for my enthusiastic response.
Thanks in anticipation.
Sorry, I don’t follow. What problem are you having exactly?
Hi Dr. Brownlee, thanks for the article! Would you mind to help me with a problem? I need to compare the performance of 2 different deep learning algorithms on solving the same classification task, using the same dataset. First, I defined the maximum number of parameters and used that number for both models, so, although the models are completely different, they have the same complexity parameter wise. 2) I also considered other hyperparameters such as the dropout rate, number of epochs and batch size. In the end, I got the 2 models with their hyperparameters tuned. Now I’ll compare their performance using the cross-validation results for the optimized cases (mean and std of the metrics) and then check their performance of the test set. Is this methodology correct?
Sounds like a good approach.
Perhaps ensure both methods are tested on the same number of folds and the test procedure is repeated 3-30 times.
Thanks 🙂
You’re welcome.
Hi Dr. Jason
why you don not use statistical test to compare the algorithms?
You can on a large project.
I try to keep each tutorial focuses on one question.
Which test would you suggest to compare the algorithms?
If I have a training set and a testing set.
Can you tell me which situation is correct?
1- I use the EarlyStopping on the training loss while fitting the model on the training set. Then I test the model on the test set.
2- I fit the model on the training set to a certain epoch without using the EarlyStopping. Then I test the model on the testing set.
Thank you
You train on the train set, use early stopping with the validation set, and evaluate the model on a test set.
More here:
https://machinelearningmastery.com/difference-test-validation-datasets/
And here:
https://machinelearningmastery.com/early-stopping-to-avoid-overtraining-neural-network-models/
Thanks Jason for this helpful example. I use it as tamplate for my analysis.
Do you have such example and you use cross validation leave-one-out instead of K-fold?
Thanks
Amora
Well done!
Yes, start here:
https://machinelearningmastery.com/k-fold-cross-validation/
Jason, if I keep K= N ( number of total samples in my data set) does this work like LOO? Other words if I run your above code and change the k from 10 to N (395 N samples in my data set) does this work like the LOO algorithm ?
for name, model in models:
kfold = model_selection.KFold(n_splits=395 random_state=None)
cv_results = model_selection.cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
results.append(cv_results)
names.append(name)
msg = “%s: %f (%f)” % (name, cv_results.mean(), cv_results.std())
print(msg)
Yes, or you can use LOOCV directly:
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.LeaveOneOut.html
Both do the same thing.
Hi Dr.Jason
I am a little confused about how should we proceed after we selected the best model (and after the hyper parametrization). Usually, without cross-validation we compare train score with test score to see if the model is overfitting, for example. However, with cross-validation, I split initially the dataset in train and test, and use the train set for doing cross-validation. What should I do after with the test set? Should I fit the model with the train set and compare the test scores with the score obtained from the cross-validation?
Thanks!
One approach is to use all data for cross validation if the dataset is small and compare scores.
If you have lots of data, select model using cross val on the training data, and perform tuning on the val data.
Hi Dr.,
I have a doubt. From your example, in the evaluation phase for choosing the model, we generally select the one with the highest accuracy (using cross-validation). However, if we get the evaluation accuracy and the training accuracy (I mean print not only the evaluation accuracy but also the training accuracy), sometimes, by the difference between the two values we can infer that the model with the highest evaluation accuracy is overfitting. Should we, in that case, choose a different algorithm, with low accuracy however that we know that does not have overfitting problems?
Thanks for your help!
Ideally you would train the model to the point before overfitting, or use a test harness that prevents overfitting.
Hi Dr.,
I follow your article (a very good article, I must say) and I obtain the following plot:
https://ibb.co/9WcQWFy
I always tried to have the training accuracy for spot eventually signs of overfitting.
My doubt is, I choose the RFC algorithm. However, train accuracy gives me 100%. Since it is the training accuracy this value is normal? What do you suggest? Should I choose another algorithm that doesn’t give 100% accuracy on the train, because RFC is overfitting?
Thanks!
I recommend reviewing hold out test set accuracy, not train set accuracy.
Thanks for the response! Hold-out test set accuracy gives 82%. I think my doubt is what should I compare with the holdout test set, to identify eventually overfitting. Should I compare this value with the 94% obtain from RFC test?
Compare hold out performance of a model to the hold out performance of a naive model:
https://machinelearningmastery.com/faq/single-faq/how-to-know-if-a-model-has-good-performance
How To Compare Machine Learning Algorithms in Python with scikit-learn if the problem dataset is regression not binary classification I mean when the target is ‘continuous’
Use regression algorithms and a different error metric such as mean absolute error.
Hi Jason,
Thanks for the article,
I am wondering what is the best way to compare different deep learning models for the same problem ?
Thanks
With a consistent test harness, such as a train/test split or k-fold cross-validation, ideally with repeated evaluation to overcome the stochastic nature of the learning algorithm.
See this tutorial:
https://machinelearningmastery.com/evaluate-skill-deep-learning-models/
Great article
I have trained a Tiny yolov3 model on my own dataset of images and got a model.h5
I have modified this model and got three different versions of it and trained them as well and got model.h5 for each one. how to compare them like what you did?
Evaluate each on the same hold out test sets and compare a chosen performance metric.
Hi Jason,
Thanks for your tutorials. They have tremendously helped me understanding ML.
I have a sort of question that might look naive to you but I thought you are the most logical approach that I think I have.
I have a binary classification dataset, I used a dozens of ML algorithms to train, test, classify and got my accuracies compared. I observed algorithms and its model perform variably on same as well as different datasets giving me variable feature importance to predict the label.
So, I am trying to get some idea to deal with why ML one algorithms performs better than other and how can I get uniform results.
Any opinion is appreciated.
Thank you for your time.
You’re welcome.
Some algorithms perform better than others by definition, they use different representations and optimization algorithms.
Our job as practitioners is to discover what works best for a given dataset.
I found a similar example here.
https://towardsdatascience.com/quickly-test-multiple-models-a98477476f0
Thanks for sharing.
Hello Jason, If I use the same algorithms (Logistic Regression, Random Forest, etc) and a neural network. How I can compare or add the neural network to compare with the anothers algorithms?
Thank you so much
have a nice day!
Diana
You can estimate the performance of each method using your test harness and compare mean performance of each method directly.
sir, can i use this code to run with my own dataset?
Yes, load your dataset and compare the evaluations.
Hello Sir, Great Explanation. I’m new to this field. can you tell me what should i write to get the f1 score of these algorithms Thank you.
This will help you to calculate the f1:
https://machinelearningmastery.com/fbeta-measure-for-machine-learning/
Hi, Thank you for this tutorial,
I have a question though, I am working on a project “toxic comments detection”, I have 4 classes [hateful, noise, neutral, supportive], the results of my model is the probaility for each class, I want to compare my model to an existing API, this API only returns the class of the comments (not probabilities), for now I’m using accuracy and I don’t think it the best metrics to use, is there a better metric and a fair one to use to compare the two. when I use ROC score I don’t think it’s fair for the API since when it makes an error it’s the maximum error possible (predicting 1 when it’s 0 is worse than predicting 0.8 when it’s 0)
You’re welcome.
ROC score would not be appropriate as you have multiple classes.
Perhaps this will help:
https://machinelearningmastery.com/tour-of-evaluation-metrics-for-imbalanced-classification/
I am getting errors while executing this code can you help me?
Usually I will not help debugging but please post the error message. I will take a quick look.
Hi! how can I compare models if I uded this code 3 times, the first for the original 6 models, the second with oversample of the 6 modeles and the third with undersample of the 6 models, I saved the different scores, and results, (results, results1 and results2) but I can´t find a way to compare the 18 models .
Thanks !
If you get the score, why can’t you compare?
Dr. Brownlee,
Thank you very much for this wonderful tutorial. I have applied it for regression purposes. It worked for LR, SVR, DT, and RF.
I have tried to add Deep Learning. It is not conclusive. See below please.
# Models preparation
models = []
models.append((‘LR’, LinearRegression()))
models.append((‘SVR’, SVR()))
models.append((‘DT’, DecisionTreeRegressor()))
models.append((‘RF’, RandomForestRegressor()))
models.append((‘DL’, KerasRegressor()))
#models.append((‘DL’, Sequential()))
When I added KerasRegressor(), I got the error message: AttributeError: ‘KerasRegressor’ object has no attribute ‘__call__’
When I change KerasRegressor by Sequential(), I received this error message:
TypeError: Cannot clone object ” (type ): it does not seem to be a scikit-learn estimator as it does not implement a ‘get_params’ method.
Maybe I am wrong in doing this. Any help is very appreciated please.
Hi Kim-Ndor…hanks for asking.
I’m eager to help, but I just don’t have the capacity to debug code for you.
I am happy to make some suggestions:
Consider aggressively cutting the code back to the minimum required. This will help you isolate the problem and focus on it.
Consider cutting the problem back to just one or a few simple examples.
Consider finding other similar code examples that do work and slowly modify them to meet your needs. This might expose your misstep.
Consider posting your question and code to StackOverflow.
Dear Dr. Brownlee,
Following my previous post, I want to add the following:
models.append((‘DL’, Sequential())) does not throw an error message in model preparation.
However, when running model evaluation, I got the results for the first four algorithms:
LR: -0.169154 (0.072120)
SVR: -0.101527 (0.040932)
DT: -0.200274 (0.057728)
RF: -0.117059 (0.034939)
plus
.
.
TypeError: Cannot clone object ” (type ): it does not seem to be a scikit-learn estimator as it does not implement a ‘get_params’ method.
models.append((‘DL’, KerasRegressor())) gives AttributeError: ‘KerasRegressor’ object has no attribute ‘__call__’
when running model preparation
Below are all my models:
# Models preparation
models = []
models.append((‘LR’, LinearRegression()))
models.append((‘SVR’, SVR()))
models.append((‘DT’, DecisionTreeRegressor()))
models.append((‘RF’, RandomForestRegressor()))
#models.append((‘DL’, KerasRegressor()))
models.append((‘DL’, Sequential()))
I first used KerasRegressor() then changed by Sequential() to se whether it will work.
Respectfully,
Kim
I
Thank you for the feedback Kim!
Dear Carmichael,
Sorry my first did not appear. I need help in adding deep learning to the first four algorithms. I am running regression problems.
Is it not possible to append KerasRegressor() in this situation? I got the error messages pasted in my previous post when trying. Any help is welcome please.
Below the model preparation.
# Models preparation
models = []
models.append((‘LR’, LinearRegression()))
models.append((‘SVR’, SVR()))
models.append((‘DT’, DecisionTreeRegressor()))
models.append((‘RF’, RandomForestRegressor()))
#models.append((‘DL’, KerasRegressor()))
models.append((‘DL’, Sequential()))
i have a question please, I built Pose Estimation project ,but i don’t add ML algorithm in it yet
i am hesitating about which one i used my problem help person to perform his physical therapy exercises well by calculating angles between key points that apply at input videos
Hi Esraa…Please elaborate on what you mean by having already built the project? Does this mean you have collected your input data and performed preprocessing on it?
What should i do if i want to compute accuracy, precision, recall, F1 score all together at one run using this code
Hi Bhuvaneshwari…The following resource may be of interest to you:
https://machinelearningmastery.com/how-to-calculate-precision-recall-f1-and-more-for-deep-learning-models/
Hello
I have the following Dataframe and i want to plot the boxplots for each metrics of each Model. That is i need 3 boxplots for Accuracy and same for other metrics.
Models Accuracy Sensitivity Specificity MCC
0 ACPred-BMF 80.81 88.37 73.26 62
1 ACP-MHCN 73.00 78.50 67.40 46
2 Proposed Model 95.33 91.65 97.08 88
please i need the code in python
Thanks & Rehgards
Hi Shahid…The following resource is a great starting point with using Matplotlib to create box plots:
https://www.geeksforgeeks.org/box-plot-in-python-using-matplotlib/