The weights of artificial neural networks must be initialized to small random numbers.
This is because this is an expectation of the stochastic optimization algorithm used to train the model, called stochastic gradient descent.
To understand this approach to problem solving, you must first understand the role of nondeterministic and randomized algorithms as well as the need for stochastic optimization algorithms to harness randomness in their search process.
In this post, you will discover the full background as to why neural network weights must be randomly initialized.
After reading this post, you will know:
- About the need for nondeterministic and randomized algorithms for challenging problems.
- The use of randomness during initialization and search in stochastic optimization algorithms.
- That stochastic gradient descent is a stochastic optimization algorithm and requires the random initialization of network weights.
Kick-start your project with my new book Deep Learning With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

Why Initialize a Neural Network with Random Weights?
Photo by lwtt93, some rights reserved.
Overview
This post is divided into 4 parts; they are:
- Deterministic and Non-Deterministic Algorithms
- Stochastic Search Algorithms
- Random Initialization in Neural Networks
- Initialization Methods
Deterministic and Non-Deterministic Algorithms
Classical algorithms are deterministic.
An example is an algorithm to sort a list.
Given an unsorted list, the sorting algorithm, say bubble sort or quick sort, will systematically sort the list until you have an ordered result. Deterministic means that each time the algorithm is given the same list, it will execute in exactly the same way. It will make the same moves at each step of the procedure.
Deterministic algorithms are great as they can make guarantees about best, worst, and average running time. The problem is, they are not suitable for all problems.
Some problems are hard for computers. Perhaps because of the number of combinations; perhaps because of the size of data. They are so hard because a deterministic algorithm cannot be used to solve them efficiently. The algorithm may run, but will continue running until the heat death of the universe.
An alternate solution is to use nondeterministic algorithms. These are algorithms that use elements of randomness when making decisions during the execution of the algorithm. This means that a different order of steps will be followed when the same algorithm is rerun on the same data.
They can rapidly speed up the process of getting a solution, but the solution will be approximate, or “good,” but often not the “best.” Nondeterministic algorithms often cannot make strong guarantees about running time or the quality of the solution found.
This is often fine as the problems are so hard that any good solution will often be satisfactory.
Stochastic Search Algorithms
Search problems are often very challenging and require the use of nondeterministic algorithms that make heavy use of randomness.
The algorithms are not random per se; instead they make careful use of randomness. They are random within a bound and are referred to as stochastic algorithms.
The incremental, or step-wise, nature of the search often means the process and the algorithms are referred to as an optimization from an initial state or position to a final state or position. For example, stochastic optimization problem or a stochastic optimization algorithm.
Some examples include the genetic algorithm, simulated annealing, and stochastic gradient descent.
The search process is incremental from a starting point in the space of possible solutions toward some good enough solution.
They share common features in their use of randomness, such as:
- Use of randomness during initialization.
- Use of randomness during the progression of the search.
We know nothing about the structure of the search space. Therefore, to remove bias from the search process, we start from a randomly chosen position.
As the search process unfolds, there is a risk that we are stuck in an unfavorable area of the search space. Using randomness during the search process gives some likelihood of getting unstuck and finding a better final candidate solution.
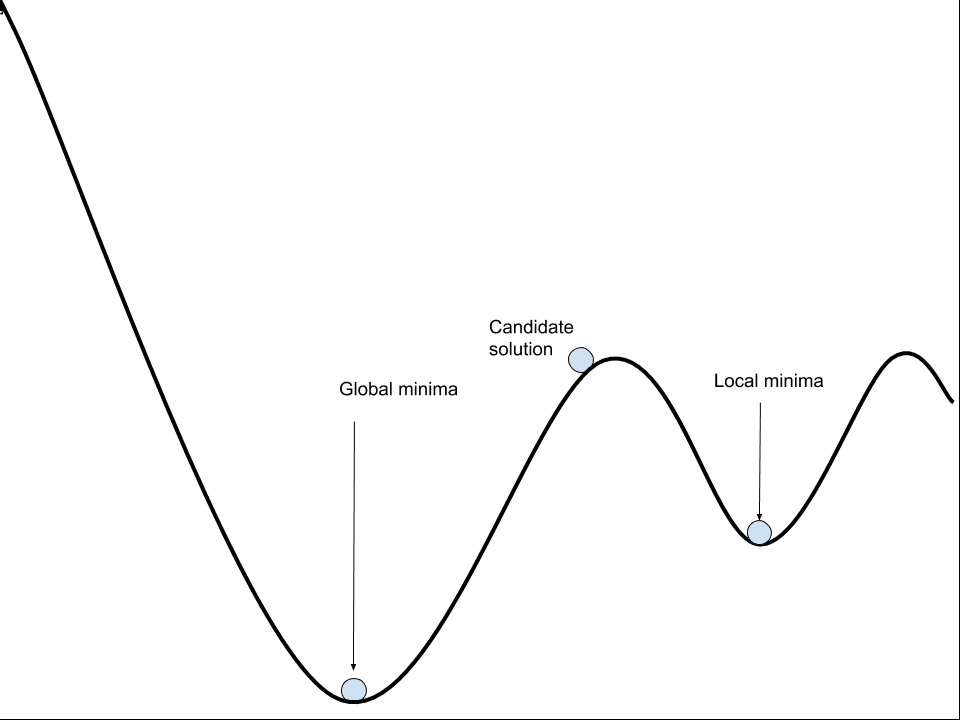
The idea of getting stuck and returning a less-good solution is referred to as getting stuck in a local optima.
These two elements of random initialization and randomness during the search work together.
They work together better if we consider any solution found by the search as provisional, or a candidate, and that the search process can be performed multiple times.
This gives the stochastic search process multiple opportunities to start and traverse the space of candidate solutions in search of a better candidate solution–a so-called global optima.
The navigation of the space of candidate solutions is often described using the analogy of a one- or two-landscape of mountains and valleys (e.g. like a fitness landscape). If we are maximizing a score during the search, we can think of small hills in the landscape as a local optima and the largest hills as the global optima.
This is a fascinating area of research, an area where I have some background. For example, see my book:
Random Initialization in Neural Networks
Artificial neural networks are trained using a stochastic optimization algorithm called stochastic gradient descent.
The algorithm uses randomness in order to find a good enough set of weights for the specific mapping function from inputs to outputs in your data that is being learned. It means that your specific network on your specific training data will fit a different network with a different model skill each time the training algorithm is run.
This is a feature, not a bug.
I write about this issue more in the post:
As described in the previous section, stochastic optimization algorithms such as stochastic gradient descent use randomness in selecting a starting point for the search and in the progression of the search.
Specifically, stochastic gradient descent requires that the weights of the network are initialized to small random values (random, but close to zero, such as in [0.0, 0.1]). Randomness is also used during the search process in the shuffling of the training dataset prior to each epoch, which in turn results in differences in the gradient estimate for each batch.
You can learn more about stochastic gradient descent in this post:
The progression of the search or learning of a neural network is referred to as convergence. The discovering of a sub-optimal solution or local optima is referred to as premature convergence.
Training algorithms for deep learning models are usually iterative in nature and thus require the user to specify some initial point from which to begin the iterations. Moreover, training deep models is a sufficiently difficult task that most algorithms are strongly affected by the choice of initialization.
— Page 301, Deep Learning, 2016.
The most effective way to evaluate the skill of a neural network configuration is to repeat the search process multiple times and report the average performance of the model over those repeats. This gives the configuration the best chance to search the space from multiple different sets of initial conditions. Sometimes this is called a multiple restart or multiple-restart search.
You can learn more about the effective evaluation of neural networks in this post:
Why Not Set Weights to Zero?
We can use the same set of weights each time we train the network; for example, you could use the values of 0.0 for all weights.
In this case, the equations of the learning algorithm would fail to make any changes to the network weights, and the model will be stuck. It is important to note that the bias weight in each neuron is set to zero by default, not a small random value.
Specifically, nodes that are side-by-side in a hidden layer connected to the same inputs must have different weights for the learning algorithm to update the weights.
This is often referred to as the need to break symmetry during training.
Perhaps the only property known with complete certainty is that the initial parameters need to “break symmetry” between different units. If two hidden units with the same activation function are connected to the same inputs, then these units must have different initial parameters. If they have the same initial parameters, then a deterministic learning algorithm applied to a deterministic cost and model will constantly update both of these units in the same way.
— Page 301, Deep Learning, 2016.
When to Initialize to the Same Weights?
We could use the same set of random numbers each time the network is trained.
This would not be helpful when evaluating network configurations.
It may be helpful in order to train the same final set of network weights given a training dataset in the case where a model is being used in a production environment.
You can learn more about fixing the random seed for neural networks developed with Keras in this post:
Initialization Methods
Traditionally, the weights of a neural network were set to small random numbers.
The initialization of the weights of neural networks is a whole field of study as the careful initialization of the network can speed up the learning process.
Modern deep learning libraries, such as Keras, offer a host of network initialization methods, all are variations of initializing the weights with small random numbers.
For example, the current methods are available in Keras at the time of writing for all network types:
- Zeros: Initializer that generates tensors initialized to 0.
- Ones: Initializer that generates tensors initialized to 1.
- Constant: Initializer that generates tensors initialized to a constant value.
- RandomNormal: Initializer that generates tensors with a normal distribution.
- RandomUniform: Initializer that generates tensors with a uniform distribution.
- TruncatedNormal: Initializer that generates a truncated normal distribution.
- VarianceScaling: Initializer capable of adapting its scale to the shape of weights.
- Orthogonal: Initializer that generates a random orthogonal matrix.
- Identity: Initializer that generates the identity matrix.
- lecun_uniform: LeCun uniform initializer.
- glorot_normal: Glorot normal initializer, also called Xavier normal initializer.
- glorot_uniform: Glorot uniform initializer, also called Xavier uniform initializer.
- he_normal: He normal initializer.
- lecun_normal: LeCun normal initializer.
- he_uniform: He uniform variance scaling initializer.
See the documentation for more details.
Out of interest, the default initializers chosen by Keras developers for different layer types are as follows:
- Dense (e.g. MLP): glorot_uniform
- LSTM: glorot_uniform
- CNN: glorot_uniform
You can learn more about “glorot_uniform“, also called “Xavier uniform“, named for the developer of the method Xavier Glorot, in the paper:
There is no single best way to initialize the weights of a neural network.
Modern initialization strategies are simple and heuristic. Designing improved initialization strategies is a difficult task because neural network optimization is not yet well understood. […] Our understanding of how the initial point affects generalization is especially primitive, offering little to no guidance for how to select the initial point.
— Page 301, Deep Learning, 2016.
It is one more hyperparameter for you to explore and test and experiment with on your specific predictive modeling problem.
Do you have a favorite method for weight initialization?
Let me know in the comments below.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
- Deep Learning, 2016.
Articles
- Nondeterministic algorithm on Wikipedia
- Randomized algorithm on Wikipedia
- Stochastic optimization on Wikipedia
- Stochastic gradient descent on Wikipedia
- Fitness landscape on Wikipedia
- Neural Network FAQ
- Keras Weight Initialization
- Understanding the difficulty of training deep feedforward neural networks, 2010.
Discussion
- What are good initial weights in a neural network?
- Why should weights of Neural Networks be initialized to random numbers?
- What are good initial weights in a neural network?
Summary
In this post, you discovered why neural network weights must be randomly initialized.
Specifically, you learned:
- About the need for nondeterministic and randomized algorithms for challenging problems.
- The use of randomness during initialization and search in stochastic optimization algorithms.
- That stochastic gradient descent is a stochastic optimization algorithm and requires the random initialization of network weights.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.





It’s probably worth mentioning pretrained initialization.
E.g. if you’re working with RGB images and using a standard architecture, chances are that pretrained weights for ImageNet exist, and that’s often a better starting point than random.
That’s a great point. Even though I don’t work on image processing I have seen articles where people have used transfer learning very effectively.
I have started to see transfer learning in NLP and time series as well. Highly effective!
Hmmmm regarding ‘Transfer Learning in NLP’.
I know of only one way to do it it effectively; pre-trained word-embedding + manually adding words/vectors. Example: ‘dollares’ is not in word-embedding, but you need it. And ‘dollares’ is a synonym for ‘dollar’. So you manually add in the txt or bin the word ‘dollares’ with the same word vectors (e.g. 300) as for ‘dollar’.
To me, everything else fail in “Transfer Learning in NLP”. Technically, there are other ways of doing it (as you posted in another blog), but in practice, they don’t work when I try them.
Franco
Fitting LSTM language models and using them with a little re-training has worked well for me on some projects as a time saver.
Sir, I thought I’d seek some career guidance from you, that’s why I post the question stated below:
To become a specialist in ML (as you are), is it the path – “BTech /BE in Computer science -> MTech in CS (specialisation in ML) -> PhD” what I should take?? Or is it a Bachelor/ Master of Science or should I go straight away into courses that offer AI/ML in colleges that offer them?? I’m much interested in in understanding ML algorithms, their working, the math behind them and research into new ML algorithms or methods or create them myself. If you can give a more detailed outlook into the factors affecting the course I should take, that’s way better 5han anything, since you’re from the field.
Hi Sam…There are many ways to get started in machine learning.
You need to find the one way that works best for your preferred learning style.
I teach a top-down and results-first approach to machine learning.
The core of my approach is to get you to focus on the end-to-end process of working through a predictive modeling problem. In this context everything (or most things) starts to make sense.
My best advice for getting started is broken down into a 5-step process:
How to get started in applied machine learning
I’m here to help and answer your questions along the way.
Nice, thanks Chris!
3 questions, would it be wise to use a Genetic Algorithm to create initial weights and then plug these in. Can you set initial weights in Keras. Also if you train the net10 times and the average performance is X which you are happy with would it be wise to then use the version that produced the best results
One thing that hasn’t been talked about with neural networks using excess weight parameters is the possible emergence of repetition code error correction. Then slight changes in the input will still result in the expected output, just with a little Gaussian noise added. I think with squashing type activation functions in particular that results in rather strong attractor states.
I view things that way because of my experiments with associative memory:
https://github.com/S6Regen/Associative-Memory-and-Self-Organizing-Maps-Experiments
There is also the question of what is actually happening where “feedback alignment” is used in place of back-propagation.
https://arxiv.org/abs/1609.01596
My theory is that in such a case you are using a deep neural network in associative memory mode. Where the extra layers reduce “crosstalk” between memories. Where crosstalk is quantization/error correction to the wrong result.
I found that crosstalk is a major problem using associative memory on real images, however if you use 2 or more layers of associative memory there are ways of solving the problem, for example using a random intermediate target during training.
Anyway I prefer evolving neural networks and I had this to say about quantization and evolution:
https://groups.google.com/forum/#!topic/artificial-general-intelligence/4aKEE0gGGoA
And here is some code: https://github.com/S6Regen/Thunderbird
I want to mix that deep neural network with associative memory to make an ALife. However, for some reason I always procrastinate. If it is the case that evolution can proceed a million times faster in a crafted digital growth medium than in biological systems then maybe that is introducing a little hesitation.
Thanks for sharing Sean.
Thanks for your lights on these random initializations ! I am not a specialist of ann, and indeed at first, random weights seem a bit weird in the input layers when you input raw, (spatially/temporally) structured signals into them… I have seen ann used on some composite features derived from signals of interest, with no obvious a priori structure (to model beforehand), where a purely stochastic approach may appear more natural, as well as in the deep layers, but I also saw for example raw EEG multichannel signal directly injected into cnn/rnn without any signal transformation / sparsification… these signals have both a temporal / spectral well known structure and they are convolved with hundreds of random matrixes in the first layers… and then I get an optimization problem with millions of parameters / weights… well, not I, Adam does its job, find a low place in an obscure multidimensional categorical cross entropic landscape… and at the end of the heavy training, my GPU makes smoke and, despite the overall recognition performance, I find myself disturbed by such a randomness in the input layers: where is the information learned there ? shouldn’t their kernels / filters be more deterministic so as to mimick / match the signal waveform features ? (old memories of signal processing course ?). So I introduce some regularization term into the landscape to mufle this noise (and also maybe to improve performance transfert), not really knowing where I stand within this landscape, but definitely attracted toward more smoothness, more continuity for my input layer. Or what about directly initializing my input layer kernels with a nice (adapted to the structure of my signals) dictionnary of atoms or wavelets ? Would it be conceivable to initialize more and more randomly our layers as we go deeper in the network ?
The learning process changes the weights from random to regular, in response to the structure in the data and learning the mapping function from inputs to outputs.
What about learning without random initialization. https://arxiv.org/abs/1805.07828
Intersting, I have not read that. Have you? What’s it all about?
In this paper the author use linear algebra methods to train MLP without BP algorithm. Specially, the pseudoinverse operation is used to get initial weight.
Fascinating! I best it has trouble scaling to large models.
https://github.com/sibofeng/PILAE
> — Page 301, Deep Learning, 2016.
I have the book and it’s on the 293 page.
Thanks, I was using the PDF to get the page numbers, they might differ from the hard copy (mines on the shelf).
Awesome,Tnx 🙂
You’re welcome.
“glorot_uniform“, also called “Xavier normal“
shouldn’t this be:
“glorot_uniform“, also called “Xavier uniform“?
Thanks, fixed.
hi, Jason Brownlee.
always thanks for sharing your post.
if you don’t mind, I have a question.
currently I’m using LSTM model and get randomly different result in same model.(loss : RMSLE)
In this case, if I save the lowest ‘RMSLE’ model and weights for reuse, is this right way?
(I’m not using K-fold, just use step ‘fit’ in loop)
always, thanks for your sharing.
Yes, you could try that approach.
Another might be to fit multiple final models and average their predictions, e.g. described here:
https://machinelearningmastery.com/ensemble-methods-for-deep-learning-neural-networks/
you’re awesome!
Thanks.
Hi Jason,
Thank you for the insightful post.
I would appreciate if you can help me with the below.
I have built my MLP model and used ReLu activation function and Xavier weight initialization method. The results were good enough. and the model showed good performance.
But I have been reading so many articles and books on how the weight initialization method is related to the selected activation function. And realized that when using ReLu is it best to use He initialization.
Does this mean it is “wrong” to use Relu with Xavier initialization?
No, not wrong, just different. Use whatever works well or well enough.
Hello Jason,
what I cannot truly grasp is why we have a problem only if we set the initial weights of our ann to zero and not if we set them to another constant value?
Thank you in advance for your time and your work!
It has proven really helpful and full of insight for me!
Because the model will not learn effectively.
Try it and see.
Hallo,
I am trying to read your link of your book “Clever algorithms… “, but 404 comes up.
Any plans to fix it ??
Thanks
I shut it down, you can access the full book as a PDF here:
https://github.com/clever-algorithms/CleverAlgorithms
Thanks for your answer
https://www.mdpi.com/1424-8220/21/14/4772/htm
non random initialization for convolutional networks like to a papet
Thanks for the link. By random, it can mean different things too! For example, drawing random numbers from Gaussain or from uniform distribution can be very different.
Hello Jason,
I am still trying to understand why different initializations could yield roughly the same convergence for the neural network instead of setting off to completely different paths. Is it that there are actually different paths, but just all minimizes the cost function to a degree?
Is it possible to randomly select an initialization that’s particularly bad? For instance, suppose the initialization is such that the weights are identical for each node in the same layer (but are random otherwise), would this NN be essentially only as good as 1 single dense layer with 1 node?
Thanks in advance.
Different initializations give same result is what we expected for “convergence”. But it is not guaranteed. People studied this carefully to find what can easier to bring convergence. In fact, with different initialization, your model will be totally different (check the final network weights), just the result looks similar.
If you want something really bad, try initialize the weight to a large number (e.g., Gaussian(10000,10) or so). You will see exploding/vanishing gradient problem.