In order to build a classifier that accurately classifies the data samples and performs well on test data, you need to initialize the weights in a way that the model converges well. Usually we randomized the weights. But when we use mean square error (MSE) as loss for training a logistic regression model, we may sometimes face a few problems. Before we get into further details, note that the methodology used here also applies to classification models other than logistic regression and it will be used in the upcoming tutorials.
Our model can converge well if the weights are initialized in a proper region. However, if we started the model weights in an unfavorable region, we may see the model difficult to converge or very slow to converge. In this tutorial you’ll learn what happens to the model training if you use MSE loss and model weights are adversely initialized. Particularly, you will learn:
How bad initialization can affect training of a logistic regression model.
How to train a logistic regression model with PyTorch.
How badly initialized weights with MSE loss can significantly reduce the accuracy of the model.
So, let’s get started.
Kick-start your project with my book Deep Learning with PyTorch. It provides self-study tutorials with working code.
Let’s get started.
Initializing Weights for Deep Learning Models. Picture by Priscilla Serneo. Some rights reserved.
Overview
This tutorial is in three parts; they are
Preparing the Data and Building a Model
The Effect of Initial Values of Model Weights
Appropriate Weight Initialization
Preparing the Data and Building a Model
First, let’s prepare some synthetic data for training and evaluating the model.
The data will be predicting a value of 0 or 1 based on a single variable.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch
from torch.utils.data import Dataset
classData(Dataset):
def __init__(self):
self.x=torch.arange(-2,2,0.1).view(-1,1)
self.y=torch.zeros(self.x.shape[0],1)
self.y[self.x[:,0]>0.2]=1
self.len=self.x.shape[0]
def __getitem__(self,idx):
returnself.x[idx],self.y[idx]
def __len__(self):
"get data length"
returnself.len
With this Dataset class, we can create a dataset object.
1
2
# Creating dataset object
data_set=Data()
Now, let’s build a custom module with nn.Module for our logistic regression model. As explained in our previous tutorials, you are going to use the methods and attributes from nn.Module package to build custom modules.
1
2
3
4
5
6
7
8
9
10
# build custom module for logistic regression
classLogisticRegression(torch.nn.Module):
# build the constructor
def __init__(self,n_inputs):
super().__init__()
self.linear=torch.nn.Linear(n_inputs,1)
# make predictions
def forward(self,x):
y_pred=torch.sigmoid(self.linear(x))
returny_pred
You’ll create a model object for logistic regression, as follows.
1
log_regr=LogisticRegression(1)
Want to Get Started With Deep Learning with PyTorch?
Take my free email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
The Effect of Initial Values of Model Weights
In order to prove the point, let’s replace the randomly initialized model weights with other values (or predetermined bad values) that will not let the model converge.
1
2
3
4
# replace the randomly initialized weights with our own values
As you can see, the randomly initialized parameters have been replaced.
You will train this model with stochastic gradient descent and set the learning rate at 2. As you have to check how badly initialized values with MSE loss may impact the model performance, you’ll set this criterion to check the model loss. In training, the data is provided by the dataloader with a batch size of 2.
As you can see, the loss during training remains constant and there isn’t any improvements. This indicates that the model is not learning and it won’t perform well on test data.
Let’s also visualize the plot for model training.
1
2
3
4
5
6
import matplotlib.pyplot asplt
plt.plot(Loss)
plt.xlabel("no. of iterations")
plt.ylabel("total loss")
plt.show()
You shall see the following: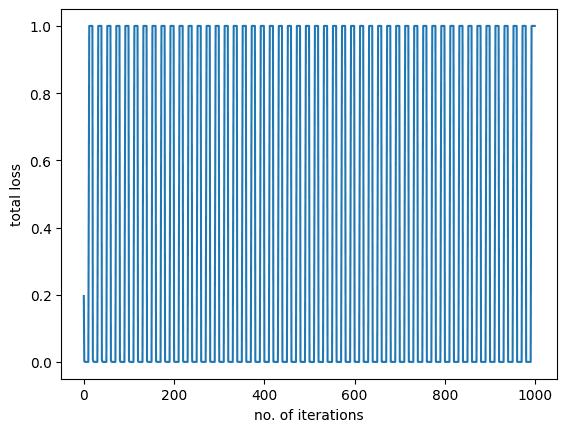The graph also tells us the same story that there wasn’t any change or reduction in the model loss during training.
While our model didn’t do well during training, let’s get the predictions for test data and measure the overall accuracy of the model.
1
2
3
4
5
# get the model predictions on test data
y_pred=log_regr(data_set.x)
label=y_pred>0.5# setting the threshold for classification
The accuracy of the model is around 57 percent only, which isn’t what you would expect. That’s how badly initialized weights with MSE loss may impact the model accuracy. In order to reduce this error, we apply maximum likelihood estimation and cross entropy loss, which will be covered in the next tutorial.
Putting everything together, the following is the complete code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
import matplotlib.pyplot asplt
import torch
from torch.utils.data import Dataset,DataLoader
torch.manual_seed(0)
classData(Dataset):
def __init__(self):
self.x=torch.arange(-2,2,0.1).view(-1,1)
self.y=torch.zeros(self.x.shape[0],1)
self.y[self.x[:,0]>0.2]=1
self.len=self.x.shape[0]
def __getitem__(self,idx):
returnself.x[idx],self.y[idx]
def __len__(self):
"get data length"
returnself.len
# Creating dataset object
data_set=Data()
# build custom module for logistic regression
classLogisticRegression(torch.nn.Module):
# build the constructor
def __init__(self,n_inputs):
super().__init__()
self.linear=torch.nn.Linear(n_inputs,1)
# make predictions
def forward(self,x):
y_pred=torch.sigmoid(self.linear(x))
returny_pred
log_regr=LogisticRegression(1)
# replace the randomly initialized weights with our own values
By default, the initialized weight from PyTorch should give you the correct model. If you modify the code above to comment out the two lines that overwrote the model weigths before training and re-run it, you should see the result works quite well. The reason it works horribly above is because the weights are too far off from the optimal weights, and the use of MSE as loss function in logistic regression problems.
The nature of optimization algorithms such as stochastic gradient descent does not guarantee it to work in all cases. In order to make the optimization algorithms to find the solution, i.e., the model to converge, it is best to have the model weights located at the proximity of the solution. Of course, we would not know where is the proximity before the model converge. But research has found that we should prefer the weights be set such that in a batch of the sample data,
the mean of activation is zero
the variance of the the activation is comparable to the variance of a layer’s input
One popular method is to initialize model weights using Xavier initialization, i.e., set weights randomly according to a Uniform distribution, $U[-\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}]$, where $n$ is the number of input to the layer (in our case is 1).
Another method is normalized Xavier initialization, which is to use the distribution $U[-\sqrt{\frac{6}{n+m}}, \sqrt{\frac{6}{n+m}}]$, for $n$ and $m$ the number of inputs and outputs to the layer. In our case, both are 1.
If we prefer not to use uniform distribution, He initialization suggested to use Gaussian distribution with mean 0 and variance $\sqrt{2/n}$.
It provides self-study tutorials with hundreds of working code to turn you from a novice to expert. It equips you with tensor operation, training, evaluation, hyperparameter optimization,
and much more...
Kick-start your deep learning journey with hands-on exercises
Just a question. After training you say
“While our model didn’t do well during training, let’s get the predictions for test data and measure the overall accuracy of the model.”
But it seems you predict again the training data (data_set.x), as I can not see test data in the example.
Is there something I am not understanding?
Best
The graph also tells us the same story that there wasn’t any change or reduction in the model loss during training.
Hi Muhammad:
Nice and very clear tutorials.
Just a question. After training you say
“While our model didn’t do well during training, let’s get the predictions for test data and measure the overall accuracy of the model.”
But it seems you predict again the training data (data_set.x), as I can not see test data in the example.
Is there something I am not understanding?
Best
Hi Edu…Best practices can be found in the following resource for a train/test split:
https://machinelearningmastery.com/training-validation-test-split-and-cross-validation-done-right/