Calculating Derivatives in PyTorch

Derivatives are one of the most fundamental concepts in calculus. They describe how changes in the variable inputs affect the function outputs. The objective of this article is to provide a high-level introduction to calculating derivatives in PyTorch for those who are new to the framework. PyTorch offers a convenient way to calculate derivatives for user-defined functions.

While we always have to deal with backpropagation (an algorithm known to be the backbone of a neural network) in neural networks, which optimizes the parameters to minimize the error in order to achieve higher classification accuracy; concepts learned in this article will be used in later posts on deep learning for image processing and other computer vision problems.

After going through this tutorial, you’ll learn:

• How to calculate derivatives in PyTorch.
• How to use autograd in PyTorch to perform auto differentiation on tensors.
• About the computation graph that involves different nodes and leaves, allowing you to calculate the gradients in a simple possible manner (using the chain rule).
• How to calculate partial derivatives in PyTorch.
• How to implement the derivative of functions with respect to multiple values.

Kick-start your project with my book Deep Learning with PyTorch. It provides self-study tutorials with working code.

Calculating Derivatives in PyTorch
Picture by Jossuha Théophile. Some rights reserved.

Differentiation in Autograd

The autograd – an auto differentiation module in PyTorch – is used to calculate the derivatives and optimize the parameters in neural networks. It is intended primarily for gradient computations.

Before we start, let’s load up some necessary libraries we’ll use in this tutorial.

Now, let’s use a simple tensor and set the requires_grad parameter to true. This allows us to perform automatic differentiation and lets PyTorch evaluate the derivatives using the given value which, in this case, is 3.0.

We’ll use a simple equation $y=3x^2$ as an example and take the derivative with respect to variable x. So, let’s create another tensor according to the given equation. Also, we’ll apply a neat method .backward on the variable y that forms acyclic graph storing the computation history, and evaluate the result with .grad for the given value.

As you can see, we have obtained a value of 18, which is correct.

Computational Graph

PyTorch generates derivatives by building a backwards graph behind the scenes, while tensors and backwards functions are the graph’s nodes. In a graph, PyTorch computes the derivative of a tensor depending on whether it is a leaf or not.

PyTorch will not evaluate a tensor’s derivative if its leaf attribute is set to True. We won’t go into much detail about how the backwards graph is created and utilized, because the goal here is to give you a high-level knowledge of how PyTorch makes use of the graph to calculate derivatives.

So, let’s check how the tensors x and y look internally once they are created. For x:

and for y:

As you can see, each tensor has been assigned with a particular set of attributes.

The data attribute stores the tensor’s data while the grad_fn attribute tells about the node in the graph. Likewise, the .grad attribute holds the result of the derivative. Now that you have learnt some basics about the autograd and computational graph in PyTorch, let’s take a little more complicated equation $y=6x^2+2x+4$ and calculate the derivative. The derivative of the equation is given by:

$$\frac{dy}{dx} = 12x+2$$

Evaluating the derivative at $x = 3$,

$$\left.\frac{dy}{dx}\right\vert_{x=3} = 12\times 3+2 = 38$$

Now, let’s see how PyTorch does that,

The derivative of the equation is 38, which is correct.

Implementing Partial Derivatives of Functions

PyTorch also allows us to calculate partial derivatives of functions. For example, if we have to apply partial derivation to the following function,

$$f(u,v) = u^3+v^2+4uv$$

Its derivative with respect to $u$ is,

$$\frac{\partial f}{\partial u} = 3u^2 + 4v$$

Similarly, the derivative with respect to $v$ will be,

$$\frac{\partial f}{\partial v} = 2v + 4u$$

Now, let’s do it the PyTorch way, where $u = 3$ and $v = 4$.

We’ll create u, v and f tensors and apply the .backward attribute on f in order to compute the derivative. Finally, we’ll evaluate the derivative using the .grad with respect to the values of u and v.

Derivative of Functions with Multiple Values

What if we have a function with multiple values and we need to calculate the derivative with respect to its multiple values? For this, we’ll make use of the sum attribute to (1) produce a scalar-valued function, and then (2) take the derivative. This is how we can see the ‘function vs. derivative’ plot:

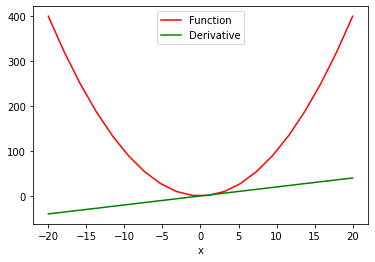
In the two plot() function above, we extract the values from PyTorch tensors so we can visualize them. The .detach method doesn’t allow the graph to further track the operations. This makes it easy for us to convert a tensor to a numpy array.

Summary

In this tutorial, you learned how to implement derivatives on various functions in PyTorch.

Particularly, you learned:

• How to calculate derivatives in PyTorch.
• How to use autograd in PyTorch to perform auto differentiation on tensors.
• About the computation graph that involves different nodes and leaves, allowing you to calculate the gradients in a simple possible manner (using the chain rule).
• How to calculate partial derivatives in PyTorch.
• How to implement the derivative of functions with respect to multiple values.

Get Started on Deep Learning with PyTorch!

Learn how to build deep learning models

...using the newly released PyTorch 2.0 library

Discover how in my new Ebook:
Deep Learning with PyTorch

It provides self-study tutorials with hundreds of working code to turn you from a novice to expert. It equips you with
tensor operation, training, evaluation, hyperparameter optimization, and much more...

Kick-start your deep learning journey with hands-on exercises

See What's Inside