A Gentle Introduction to Function Derivatives

The concept of the derivative is the building block of many topics of calculus. It is important for understanding integrals, gradients, Hessians, and much more.

In this tutorial, you will discover the definition of a derivative, its notation and how you can compute the derivative based upon this definition. You will also discover why the derivative of a function is a function itself.

After completing this tutorial, you will know:

• The definition of the derivative of a function
• How to compute the derivative of a function based upon the definition
• Why some functions do not have a derivative at a point

Let’s get started.

A Gentle Introduction to Function Derivatives Photo by Mehreen Saeed, some rights reserved

Tutorial Overview

This tutorial is divided into three parts; they are:

1. The definition and notation used for derivatives of functions
2. How to compute the derivative of a function using the definition
3. Why some functions do not have a derivative at a point

What is the Derivative of a Function

In very simple words,  the derivative of a function f(x) represents its rate of change and is denoted by either f'(x) or df/dx. Let’s first look at its definition and a pictorial illustration of the derivative.

Illustration of the Definition of a Function Derivative

In the figure, Δx represents a change in the value of x. We keep making the interval between x and (x+Δx) smaller and smaller until it is infinitesimal. Hence, we have the limit (Δ????→0). The numerator f(x+Δx)-f(x) represents the corresponding change in the value of the function f over the interval Δx. This makes the derivative of a function f at a point x, the rate of change of f at that point.

An important point to note is that Δx, the change in x can be negative or positive. Hence:

0<|Δx|< ????,

where ???? is an infinitesimally small value.

About the Notation

The derivative of a function can be denoted by both f'(x) and df/dx. The mathematical giant Newton used f'(x) to denote the derivative of a function. Leibniz, another mathematical hero, used df/dx. So df/dx is a single term, not to be confused with a fraction. It is read as the derivative of a function f with respect to x, and also indicates that x is the independent variable.

Connection with Velocity

One of the most commonly cited examples of derivatives is that of velocity. Velocity is the rate of change of distance w.r.t. time. Hence if f(t) represents the distance travelled at time t, then f'(t) is the velocity at time t. The following sections show various examples of computing the derivative.

Differentiation Examples

The method of finding the derivative of a function is called differentiation. In this section, we’ll see how the definition of the derivative can be used to find the derivative of different functions. Later on, once you are more comfortable with the definition, you can use the defined rules to differentiate a function.

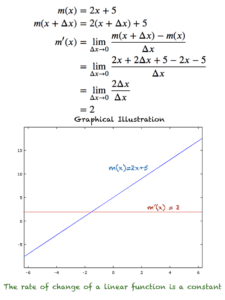
Example 1: m(x) = 2x+5

Let’s start with a simple example of a linear function m(x) = 2x+5. We can see that m(x) changes at a constant rate. We can differentiate this function as follows.

Derivative of m(x) = 2x+5

The above figure shows how the function m(x) is changing and it also shows that no matter which value of x, we choose the rate of change of m(x) always remains a 2.

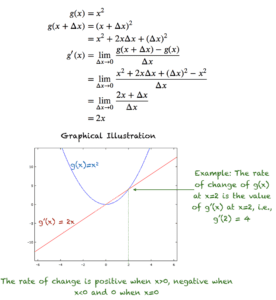
Example 2: g(x) = x^2

Suppose we have the function g(x) given by: g(x) = x^2. The figure below shows how the derivative of g(x) w.r.t. x is calculated. There is also a plot of the function and its derivative in the figure.

Derivative of g(x) = x^2

As g'(x) = 2x, hence g'(0) = 0, g'(1) = 2, g'(2) = 4 and g'(-1) = -2, g'(-2) = -4

From the figure, we can see that the value of g(x) is very large for large negative values of x. When x < 0, increasing x decreases g(x) and hence g'(x) < 0 for x<0. The graph flattens out for x=0, where the derivative or rate of change of g(x) becomes zero. When x>0, g(x) increases quadratically with the increase in x, and hence, the derivative is also positive.

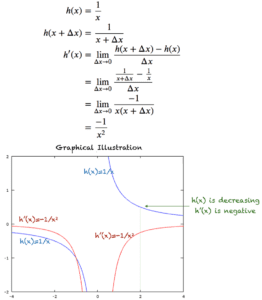
Example 3: h(x) = 1/x

Suppose we have the function h(x) = 1/x. Shown below is the differentiation of h(x) w.r.t. x (for x ≠0) and the figure illustrating the derivative. The blue curve denotes h(x) and the red curve its corresponding derivative.

Derivative of h(x) = 1/x

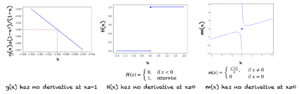
Differentiability and Continuity

For example 3, the function h(x) = 1/x is undefined at the point x=0. Hence, its derivative (-1/x^2) is also not defined at x=0. If a function is not continuous at a point, then it does not have a derivative at that point. Below are a few scenarios, where a function is not differentiable:

1. If the function is not defined at a point
2. Function does not have a limit at that point
3. If the function is not continuous at a point
4. The function has a sudden jump at a point

Following are a few examples:

Examples of Points at Which there is no Derivative

Extensions

This section lists some ideas for extending the tutorial that you may wish to explore.

• Velocity and instantaneous rates of change
• Rules for derivatives
• Integration

If you explore any of these extensions, I’d love to know. Post your findings in the comments below.

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Tutorials

• Limits and continuity
• Evaluating limits

Resources

• Additional resources on Calculus Books for Machine Learning

Books

• Thomas’ Calculus, 14th edition, 2017. (based on the original works of George B. Thomas, revised by Joel Hass, Christopher Heil, Maurice Weir)
• Calculus, 3rd Edition, 2017. (Gilbert Strang)
• Calculus, 8th edition, 2015. (James Stewart)

Summary

In this tutorial, you discovered the function derivatives and the fundamentals of function differentiation.

Specifically, you learned:

• The definition and notation of a function derivative
• How to differentiate a function using the definition
• When a function is not differentiable

Do you have any questions? Ask your questions in the comments below and I will do my best to answer.

Get a Handle on Calculus for Machine Learning!

Feel Smarter with Calculus Concepts

...by getting a better sense on the calculus symbols and terms

Discover how in my new Ebook:
Calculus for Machine Learning

It provides self-study tutorials with full working code on:
differntiation, gradient, Lagrangian mutiplier approach, Jacobian matrix, and much more...

Bring Just Enough Calculus Knowledge to
Your Machine Learning Projects

See What's Inside