Random Subspace Ensemble is a machine learning algorithm that combines the predictions from multiple decision trees trained on different subsets of columns in the training dataset.
Randomly varying the columns used to train each contributing member of the ensemble has the effect of introducing diversity into the ensemble and, in turn, can lift performance over using a single decision tree.
It is related to other ensembles of decision trees such as bootstrap aggregation (bagging) that creates trees using different samples of rows from the training dataset, and random forest that combines ideas from bagging and the random subspace ensemble.
Although decision trees are often used, the general random subspace method can be used with any machine learning model whose performance varies meaningfully with the choice of input features.
In this tutorial, you will discover how to develop random subspace ensembles for classification and regression.
After completing this tutorial, you will know:
- Random subspace ensembles are created from decision trees fit on different samples of features (columns) in the training dataset.
- How to use the random subspace ensemble for classification and regression with scikit-learn.
- How to explore the effect of random subspace model hyperparameters on model performance.
Kick-start your project with my new book Ensemble Learning Algorithms With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

How to Develop a Random Subspace Ensemble With Python
Photo by Marsel Minga, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Random Subspace Ensemble
- Random Subspace Ensemble via Bagging
- Random Subspace Ensemble for Classification
- Random Subspace Ensemble for Regression
- Random Subspace Ensemble Hyperparameters
- Explore Number of Trees
- Explore Number of Features
- Explore Alternate Algorithm
Random Subspace Ensemble
A predictive modeling problem consists of one or more input variables and a target variable.
A variable is a column in the data and is also often referred to as a feature. We can consider all input features together as defining an n-dimensional vector space, where n is the number of input features and each example (input row of data) is a point in the feature space.
This is a common conceptualization in machine learning and as input feature spaces become larger, the distance between points in the space increases, known generally as the curse of dimensionality.
A subset of input features can, therefore, be thought of as a subset of the input feature space, or a subspace.
Selecting features is a way of defining a subspace of the input feature space. For example, feature selection refers to an attempt to reduce the number of dimensions of the input feature space by selecting a subset of features to keep or a subset of features to delete, often based on their relationship to the target variable.
Alternatively, we can select random subsets of input features to define random subspaces. This can be used as the basis for an ensemble learning algorithm, where a model can be fit on each random subspace of features. This is referred to as a random subspace ensemble or the random subspace method.
The training data is usually described by a set of features. Different subsets of features, or called subspaces, provide different views on the data. Therefore, individual learners trained from different subspaces are usually diverse.
— Page 116, Ensemble Methods, 2012.
It was proposed by Tin Kam Ho in the 1998 paper titled “The Random Subspace Method For Constructing Decision Forests” where a decision tree is fit on each random subspace.
More generally, it is a diversity technique for ensemble learning that belongs to a class of methods that change the training dataset for each model in the attempt to reduce the correlation between the predictions of the models in the ensemble.
The procedure is as simple as selecting a random subset of input features (columns) for each model in the ensemble and fitting the model on the model in the entire training dataset. It can be augmented with additional changes, such as using a bootstrap or random sample of the rows in training dataset.
The classifier consists of multiple trees constructed systematically by pseudorandomly selecting subsets of components of the feature vector, that is, trees constructed in randomly chosen subspaces.
— The Random Subspace Method For Constructing Decision Forests, 1998.
As such, the random subspace ensemble is related to bootstrap aggregation (bagging) that introduces diversity by training each model, often a decision tree, on a different random sample of the training dataset, with replacement (e.g. the bootstrap sampling method). The random forest ensemble may also be considered a hybrid of both the bagging and random subset ensemble methods.
Algorithms that use different feature subsets are commonly referred to as random subspace methods …
— Page 21, Ensemble Machine Learning, 2012.
The random subspace method can be used with any machine learning algorithm, although it is well suited to models that are sensitive to large changes to the input features, such as decision trees and k-nearest neighbors.
It is appropriate for datasets that have a large number of input features, as it can result in good performance with good efficiency. If the dataset contains many irrelevant input features, it may be better to use feature selection as a data preparation technique as the prevalence of irrelevant features in subspaces may hurt the performance of the ensemble.
For data with a lot of redundant features, training a learner in a subspace will be not only effective but also efficient.
— Page 116, Ensemble Methods, 2012.
Now that we are familiar with the random subspace ensemble, let’s explore how we can implement the approach.
Want to Get Started With Ensemble Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Random Subspace Ensemble via Bagging
We can implement the random subspace ensemble using bagging in scikit-learn.
Bagging is provided via the BaggingRegressor and BaggingClassifier classes.
We can configure bagging to be a random subspace ensemble by setting the “bootstrap” argument to “False” to turn off sampling of the training dataset rows and setting the maximum number of features to a given value via the “max_features” argument.
The default model for bagging is a decision tree, but it can be changed to any model we like.
We can demonstrate using bagging to implement a random subspace ensemble with decision trees for classification and regression.
Random Subspace Ensemble for Classification
In this section, we will look at developing a random subspace ensemble using bagging for a classification problem.
First, we can use the make_classification() function to create a synthetic binary classification problem with 1,000 examples and 20 input features.
The complete example is listed below.
|
1 2 3 4 5 6 |
# test classification dataset from sklearn.datasets import make_classification # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and summarizes the shape of the input and output components.
|
1 |
(1000, 20) (1000,) |
Next, we can configure a bagging model to be a random subspace ensemble for decision trees on this dataset.
Each model will be fit on a random subspace of 10 input features, chosen arbitrarily.
|
1 2 3 |
... # define the random subspace ensemble model model = BaggingClassifier(bootstrap=False, max_features=10) |
We will evaluate the model using repeated stratified k-fold cross-validation, with three repeats and 10 folds. We will report the mean and standard deviation of the accuracy of the model across all repeats and folds.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# evaluate random subspace ensemble via bagging for classification from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import BaggingClassifier # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5) # define the random subspace ensemble model model = BaggingClassifier(bootstrap=False, max_features=10) # define the evaluation method cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # evaluate the model on the dataset n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) # report performance print('Mean Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the random subspace ensemble with default hyperparameters achieves a classification accuracy of about 85.4 percent on this test dataset.
|
1 |
Mean Accuracy: 0.854 (0.039) |
We can also use the random subspace ensemble model as a final model and make predictions for classification.
First, the ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our binary classification dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# make predictions using random subspace ensemble via bagging for classification from sklearn.datasets import make_classification from sklearn.ensemble import BaggingClassifier # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5) # define the model model = BaggingClassifier(bootstrap=False, max_features=10) # fit the model on the whole dataset model.fit(X, y) # make a single prediction row = [[-4.7705504,-1.88685058,-0.96057964,2.53850317,-6.5843005,3.45711663,-7.46225013,2.01338213,-0.45086384,-1.89314931,-2.90675203,-0.21214568,-0.9623956,3.93862591,0.06276375,0.33964269,4.0835676,1.31423977,-2.17983117,3.1047287]] yhat = model.predict(row) print('Predicted Class: %d' % yhat[0]) |
Running the example fits the random subspace ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Predicted Class: 1 |
Now that we are familiar with using bagging for classification, let’s look at the API for regression.
Random Subspace Ensemble for Regression
In this section, we will look at using bagging for a regression problem.
First, we can use the make_regression() function to create a synthetic regression problem with 1,000 examples and 20 input features.
The complete example is listed below.
|
1 2 3 4 5 6 |
# test regression dataset from sklearn.datasets import make_regression # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and summarizes the shape of the input and output components.
|
1 |
(1000, 20) (1000,) |
Next, we can evaluate a random subspace ensemble via bagging on this dataset.
As before, we must configure bagging to use all rows of the training dataset and specify the number of input features to randomly select.
|
1 2 3 |
... # define the model model = BaggingRegressor(bootstrap=False, max_features=10) |
As we did with the last section, we will evaluate the model using repeated k-fold cross-validation, with three repeats and 10 folds. We will report the mean absolute error (MAE) of the model across all repeats and folds. The scikit-learn library makes the MAE negative so that it is maximized instead of minimized. This means that larger negative MAE are better and a perfect model has a MAE of 0.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# evaluate random subspace ensemble via bagging for regression from numpy import mean from numpy import std from sklearn.datasets import make_regression from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedKFold from sklearn.ensemble import BaggingRegressor # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5) # define the model model = BaggingRegressor(bootstrap=False, max_features=10) # define the evaluation procedure cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) # evaluate the model n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise') # report performance print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the bagging ensemble with default hyperparameters achieves a MAE of about 114.
|
1 |
MAE: -114.630 (10.920) |
We can also use the random subspace ensemble model as a final model and make predictions for regression.
First, the ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our regression dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# random subspace ensemble via bagging for making predictions for regression from sklearn.datasets import make_regression from sklearn.ensemble import BaggingRegressor # define dataset X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5) # define the model model = BaggingRegressor(bootstrap=False, max_features=10) # fit the model on the whole dataset model.fit(X, y) # make a single prediction row = [[0.88950817,-0.93540416,0.08392824,0.26438806,-0.52828711,-1.21102238,-0.4499934,1.47392391,-0.19737726,-0.22252503,0.02307668,0.26953276,0.03572757,-0.51606983,-0.39937452,1.8121736,-0.00775917,-0.02514283,-0.76089365,1.58692212]] yhat = model.predict(row) print('Prediction: %d' % yhat[0]) |
Running the example fits the random subspace ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
|
1 |
Prediction: -157 |
Now that we are familiar with using the scikit-learn API to evaluate and use random subspace ensembles, let’s look at configuring the model.
Random Subspace Ensemble Hyperparameters
In this section, we will take a closer look at some of the hyperparameters you should consider tuning for the random subspace ensemble and their effect on model performance.
Explore Number of Trees
An important hyperparameter for the random subspace method is the number of decision trees used in the ensemble. More trees will stabilize the variance of the model, countering the effect of the number of features selected by each tree that introduces diversity.
The number of trees can be set via the “n_estimators” argument and defaults to 10.
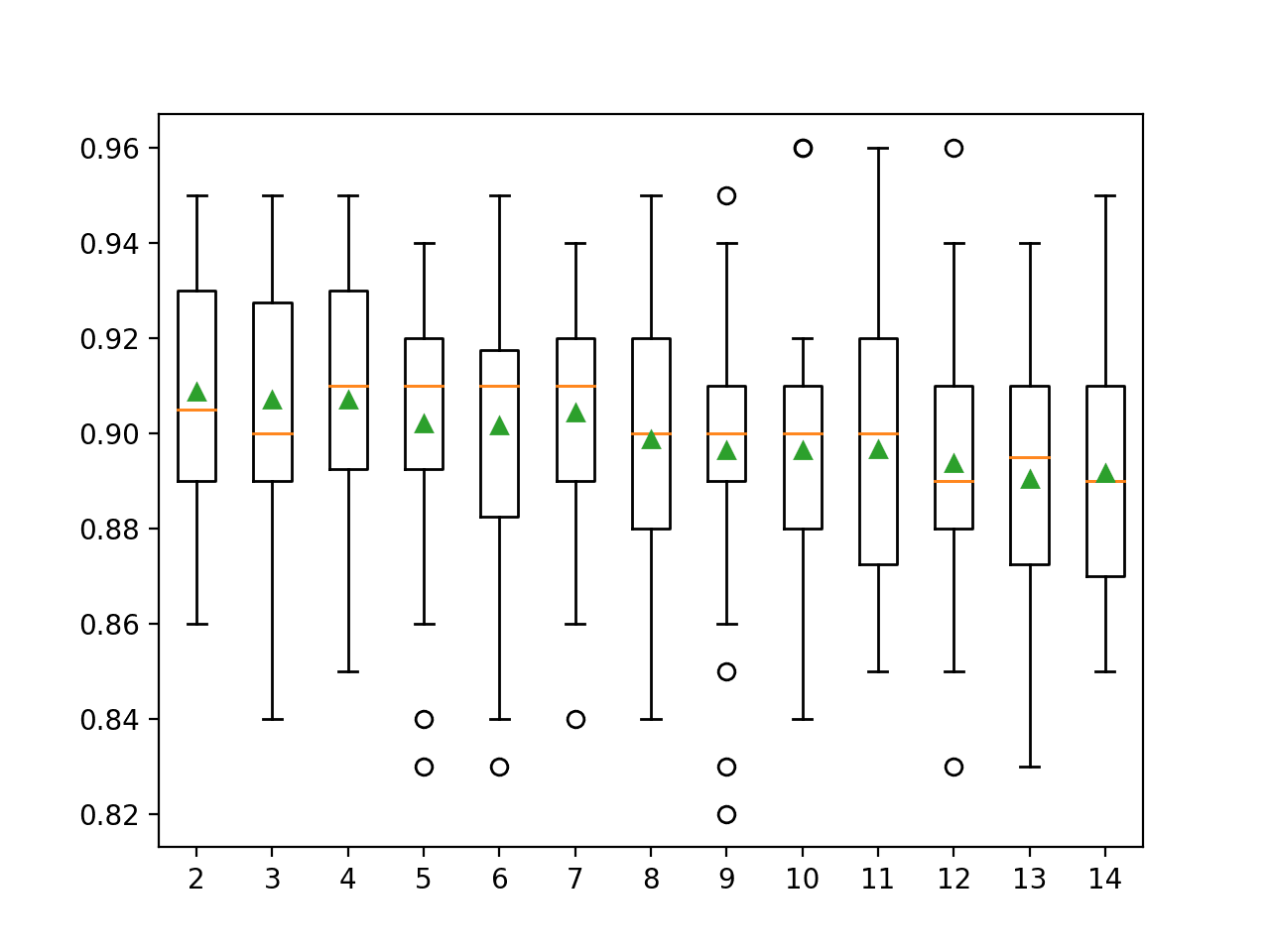
The example below explores the effect of the number of trees with values between 10 to 5,000.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# explore random subspace ensemble number of trees effect on performance from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import BaggingClassifier from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5) return X, y # get a list of models to evaluate def get_models(): models = dict() n_trees = [10, 50, 100, 500, 1000, 5000] for n in n_trees: models[str(n)] = BaggingClassifier(n_estimators=n, bootstrap=False, max_features=10) return models # evaluate a given model using cross-validation def evaluate_model(model): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean accuracy for each configured number of decision trees.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that that performance appears to continue to improve as the number of ensemble members is increased to 5,000.
|
1 2 3 4 5 6 |
>10 0.853 (0.030) >50 0.885 (0.038) >100 0.891 (0.034) >500 0.894 (0.036) >1000 0.894 (0.034) >5000 0.896 (0.033) |
A box and whisker plot is created for the distribution of accuracy scores for each configured number of trees.
We can see the general trend of further improvement with the number of decision trees used in the ensemble.
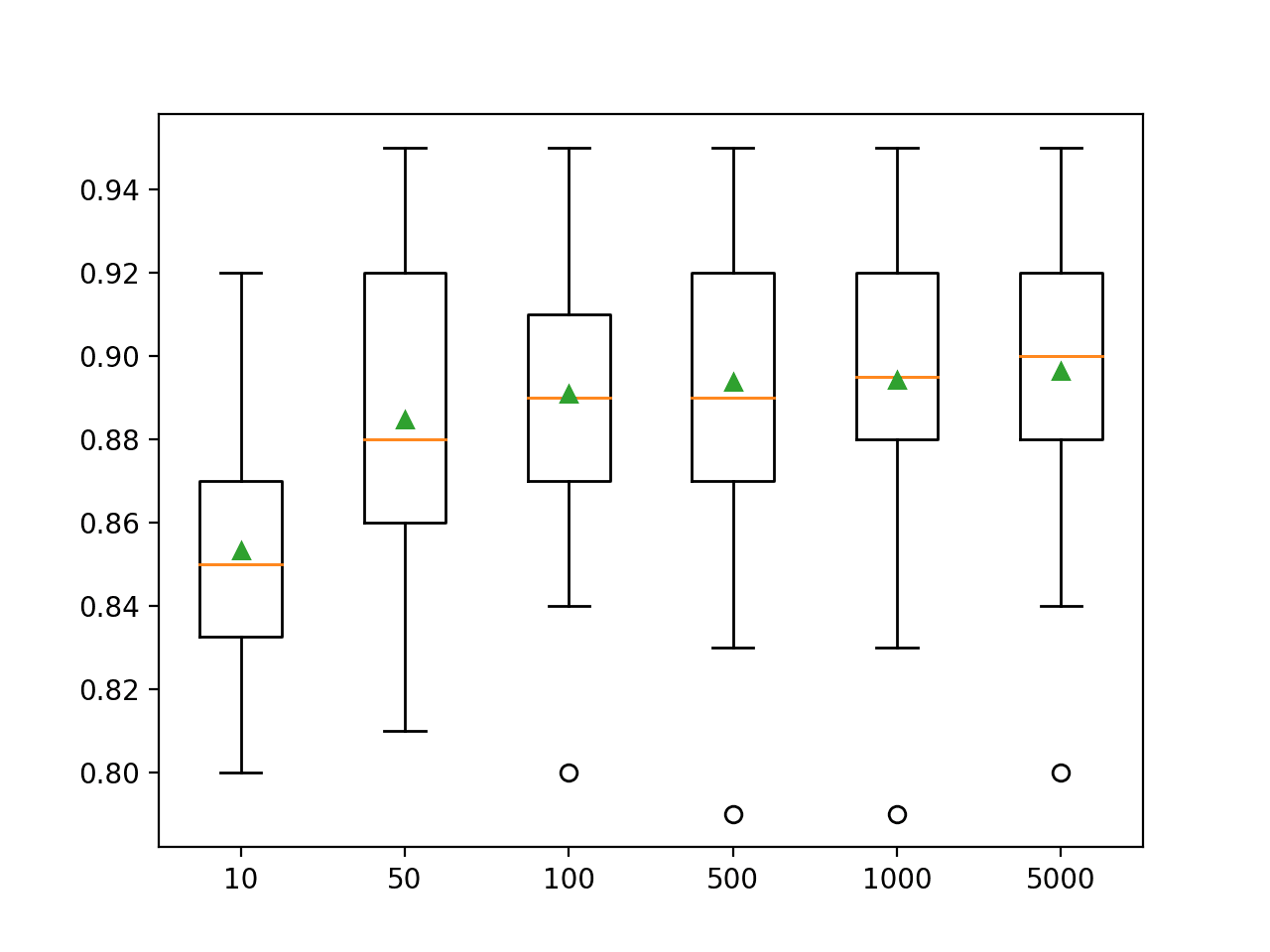
Box Plot of Random Subspace Ensemble Size vs. Classification Accuracy
Explore Number of Features
The number of features selected for each random subspace controls the diversity of the ensemble.
Fewer features mean more diversity, whereas more features mean less diversity. More diversity may require more trees to reduce the variance of predictions made by the model.
We can vary the diversity of the ensemble by varying the number of random features selected by setting the “max_features” argument.
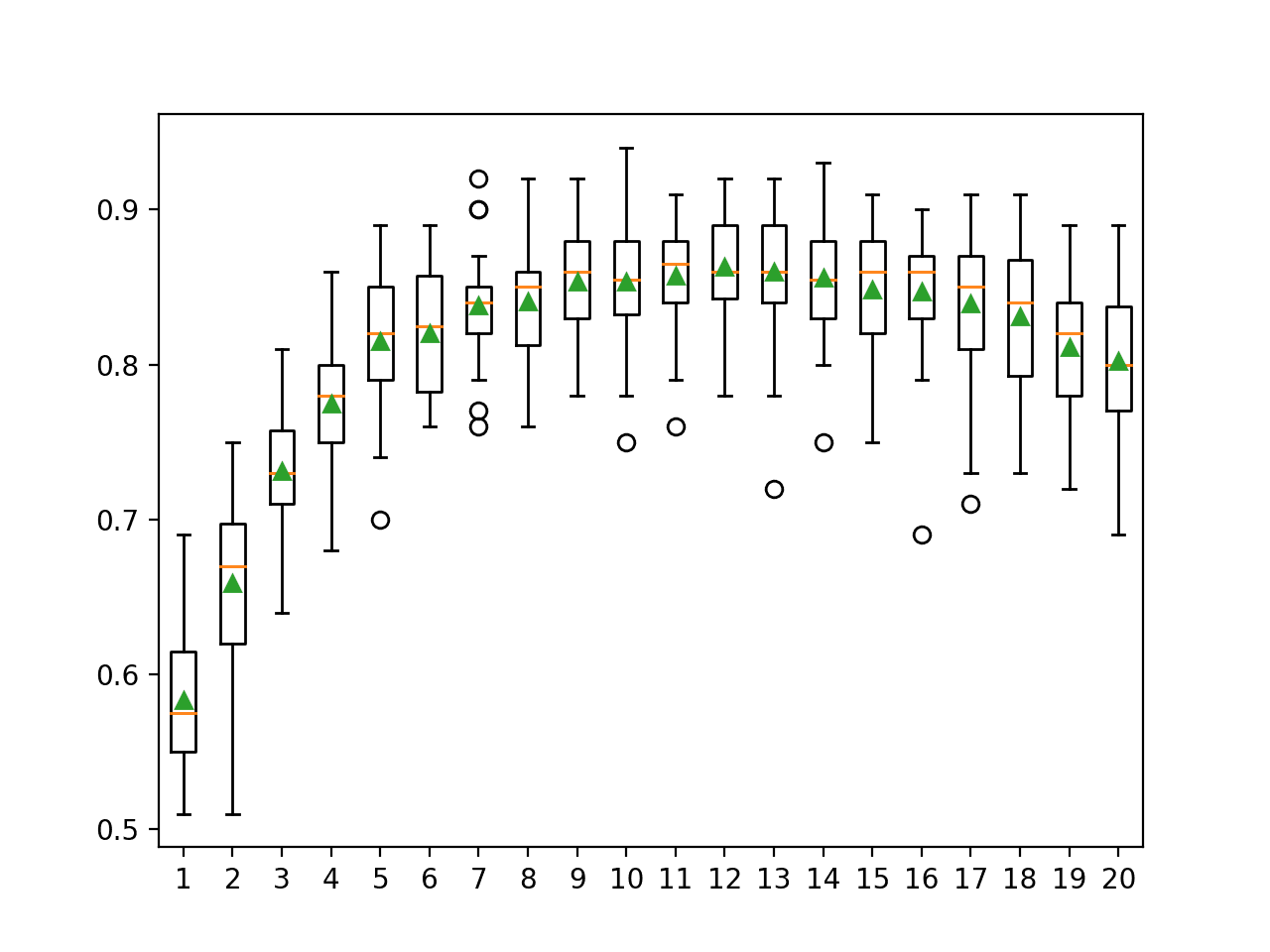
The example below varies the value from 1 to 20 with a fixed number of trees in the ensemble.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# explore random subspace ensemble number of features effect on performance from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import BaggingClassifier from matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5) return X, y # get a list of models to evaluate def get_models(): models = dict() for n in range(1,21): models[str(n)] = BaggingClassifier(n_estimators=100, bootstrap=False, max_features=n) return models # evaluate a given model using cross-validation def evaluate_model(model): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) return scores # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # evaluate the models and store results results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # plot model performance for comparison pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example first reports the mean accuracy for each number of features.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that perhaps using 8 to 11 features in the random subspaces might be appropriate on this dataset when using 100 decision trees. This might suggest increasing the number of trees to a large value first, then tuning the number of features selected in each subset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
>1 0.607 (0.036) >2 0.771 (0.042) >3 0.837 (0.036) >4 0.858 (0.037) >5 0.869 (0.034) >6 0.883 (0.033) >7 0.887 (0.038) >8 0.894 (0.035) >9 0.893 (0.035) >10 0.885 (0.038) >11 0.892 (0.034) >12 0.883 (0.036) >13 0.881 (0.044) >14 0.875 (0.038) >15 0.869 (0.041) >16 0.861 (0.044) >17 0.851 (0.041) >18 0.831 (0.046) >19 0.815 (0.046) >20 0.801 (0.049) |
A box and whisker plot is created for the distribution of accuracy scores for each number of random subset features.
We can see a general trend of increasing accuracy to a point and a steady decrease in performance after 11 features.
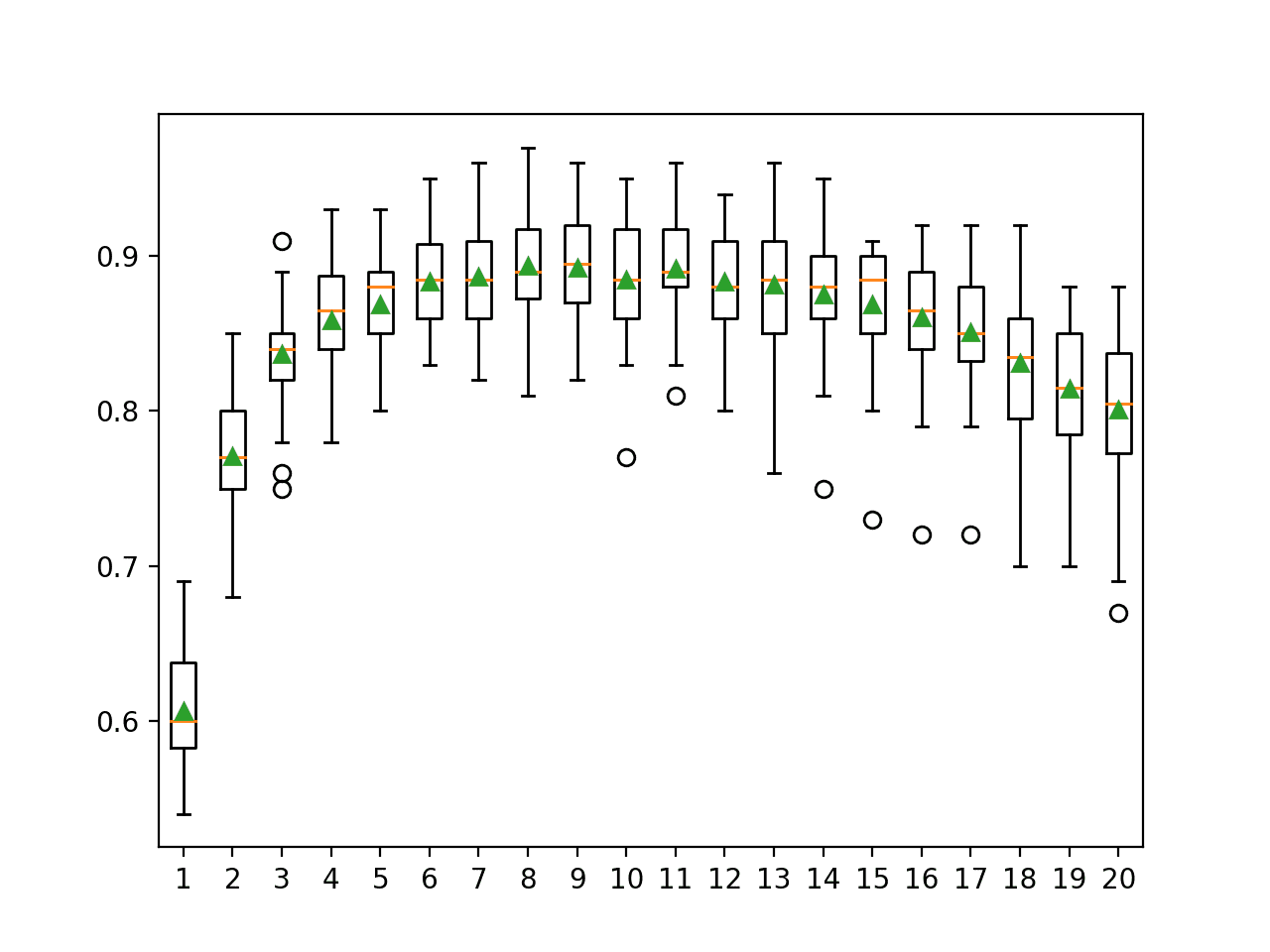
Box Plot of Random Subspace Ensemble Features vs. Classification Accuracy
Explore Alternate Algorithm
Decision trees are the most common algorithm used in a random subspace ensemble.
The reason for this is that they are easy to configure and work well on most problems.
Other algorithms can be used to construct random subspaces and must be configured to have a modestly high variance. One example is the k-nearest neighbors algorithm where the k value can be set to a low value.
The algorithm used in the ensemble is specified via the “base_estimator” argument and must be set to an instance of the algorithm and algorithm configuration to use.
The example below demonstrates using a KNeighborsClassifier as the base algorithm used in the random subspace ensemble via the bagging class. Here, the algorithm is used with default hyperparameters where k is set to 5.
|
1 2 3 |
... # define the model model = BaggingClassifier(base_estimator=KNeighborsClassifier(), bootstrap=False, max_features=10) |
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# evaluate random subspace ensemble with knn algorithm for classification from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.ensemble import BaggingClassifier # define dataset X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5) # define the model model = BaggingClassifier(base_estimator=KNeighborsClassifier(), bootstrap=False, max_features=10) # define the evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # evaluate the model n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # report performance print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the random subspace ensemble with KNN and default hyperparameters achieves a classification accuracy of about 90 percent on this test dataset.
|
1 |
Accuracy: 0.901 (0.032) |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
Books
- Pattern Classification Using Ensemble Methods, 2010.
- Ensemble Methods, 2012.
- Ensemble Machine Learning, 2012.
APIs
Articles
Summary
In this tutorial, you discovered how to develop random subspace ensembles for classification and regression.
Specifically, you learned:
- Random subspace ensembles are created from decision trees fit on different samples of features (columns) in the training dataset.
- How to use the random subspace ensemble for classification and regression with scikit-learn.
- How to explore the effect of random subspace model hyperparameters on model performance.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.



Hi Jason,
I’m thinking about prediction of values based on past information (numerical).
I’ve seen some methods (VAR i.e. Vector Autoregressive Model), or Prophet or neural net using Keras GRU for a Timeseries forecasting for weather prediction (as an example).
I’d like to predict job demand for a prototype.
What is your suggestion?
What are differences between using a VAR vs. a GRU model for a prediction?
Is possibile to apply a GRU model to predict (it seems simpler)?
How many years back (historical data) are necessary to build a prototype?
Thanks,
Marco
I recommend testing a suite of different models and discover what works best for your dataset.
Start with linear models, then try machine learning models, then try deep learning models. All models must out perform a simple persistence model in order to have skill.
Hi Jason,
one more question If I’d like to predict job demand and how many students will graduate and plotting the results using two curves (to show the gap).
Do I have to implement two separate algorithms for predictions?
Which is the easiest way?
Thanks,
Marco
The easiest model is a naive model:
https://machinelearningmastery.com/how-to-grid-search-naive-methods-for-univariate-time-series-forecasting/
Hi Jason,
thanks for the answer above.
What is a linear model?
Is something related to a linear regression?
Why do you say “start with linear model, then try machine learning models”?
I usually used linear regression with sklearn (that is a machine learning
library). You mean implementing a linear regression without any library?
Thanks,
Marco
A linear model is a weighted sum of inputs, like linear regression and logistic regression.
When I suggest starting with a linear model for time series, I mean SARIMA and ETS.
I recommend using libraries, not coding algorithms from scratch – unless your goal is to learn how to code algorithms from scratch.
Hi Jason,
one more question can XGBoost used also for timeseries? Do you have an example?
Thanks,
Marco
Yes, here:
https://machinelearningmastery.com/xgboost-for-time-series-forecasting/
Hi Jason,
one more question what kind of metric is used for time-series with ARIMA and GRU or LSTM model to test model effectiveness?
Thanks,
Marco
mean absolute error is a good starting point.
Jason,
is is possible to use multiple features with ARIMA (so far I’ve seen example
with one feature). Is there any example? On the contrary, I’ve seen example of GRU/ LSTM models with 14 features (e.g. Timeseries forecasting for weather prediction
https://keras.io/examples/timeseries/timeseries_weather_forecasting/).
Thanks,
Marco
Not really. You can have exogenous variables, so called ARIMAX and SARIMAX.
Hello Jason,
I’m working on time series, I wolud like to use with linear models (e.g. SARIMA) and with deep learning (Keras GRU).
I’d like metrics like MAE and RMSE . What is the difference (in simple word) between them? Do you suggest any others metrics?
Marco
MAE: mean absolute error.
RMSE: root mean squared error.
Either of these metrics is a good starting point.
Jason,
is it possible to plot metrics like MAE and RMSE? Do you have any example?
Thanks,
Marco
Plot how?
Jason,
what are main differences between ARIMA and a deep learning (e.g. GRU o LSTM)
in term of accuracy?
ARIMA is a linear model.
Deep learning can learn any function, in theory (given the right architecture and learning configuration).
Jason,
What is easier to use ARIMA vs. GRU / LSTM?
Marco
SARIMA/ARIMA are MUCH easier to use.
Jason,
what Pyhton library suggest to use for ARIMA, SARIMA and SARIMAX?
Thank you,
Marco
Statsmodels.
Jason,
one more question, what are major differences between using XGBRegressor and FBProphet for forecasts based on time series?
Thanks,
Marco
XGBoost is a regression model, not specialised for time series.
Prophet is a time series model.
Jason,
thanks a lot for you answers.
A VAR (Vector Autoregressive Model) is something similar to ARIMA? At the end can they produce similar results?
Thanks,
Marco
Yes, it is an AR model that supports multiple variables, learn more here:
https://machinelearningmastery.com/time-series-forecasting-methods-in-python-cheat-sheet/
Jason,
in order to predict job demand what is better to use VAR o ARIMA models?
Thanks,
Marco
I recommend testing a suite of models and discover what works well or best for your specific dataset.