Simple forecasting methods include naively using the last observation as the prediction or an average of prior observations.
It is important to evaluate the performance of simple forecasting methods on univariate time series forecasting problems before using more sophisticated methods as their performance provides a lower-bound and point of comparison that can be used to determine of a model has skill or not for a given problem.
Although simple, methods such as the naive and average forecast strategies can be tuned to a specific problem in terms of the choice of which prior observation to persist or how many prior observations to average. Often, tuning the hyperparameters of these simple strategies can provide a more robust and defensible lower bound on model performance, as well as surprising results that may inform the choice and configuration of more sophisticated methods.
In this tutorial, you will discover how to develop a framework from scratch for grid searching simple naive and averaging strategies for time series forecasting with univariate data.
After completing this tutorial, you will know:
- How to develop a framework for grid searching simple models from scratch using walk-forward validation.
- How to grid search simple model hyperparameters for daily time series data for births.
- How to grid search simple model hyperparameters for monthly time series data for shampoo sales, car sales, and temperature.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Apr/2019: Updated the links to the datasets.
- Updated Feb/2020: Fixed typo in the selection of the seasonality in last two cases.

How to Grid Search Naive Methods for Univariate Time Series Forecasting
Photo by Rob and Stephanie Levy, some rights reserved.
Tutorial Overview
This tutorial is divided into six parts; they are:
- Simple Forecasting Strategies
- Develop a Grid Search Framework
- Case Study 1: No Trend or Seasonality
- Case Study 2: Trend
- Case Study 3: Seasonality
- Case Study 4: Trend and Seasonality
Simple Forecasting Strategies
It is important and useful to test simple forecast strategies prior to testing more complex models.
Simple forecast strategies are those that assume little or nothing about the nature of the forecast problem and are fast to implement and calculate.
The results can be used as a baseline in performance and used as a point of a comparison. If a model can perform better than the performance of a simple forecast strategy, then it can be said to be skillful.
There are two main themes to simple forecast strategies; they are:
- Naive, or using observations values directly.
- Average, or using a statistic calculated on previous observations.
Let’s take a closer look at both of these strategies.
Naive Forecasting Strategy
A naive forecast involves using the previous observation directly as the forecast without any change.
It is often called the persistence forecast as the prior observation is persisted.
This simple approach can be adjusted slightly for seasonal data. In this case, the observation at the same time in the previous cycle may be persisted instead.
This can be further generalized to testing each possible offset into the historical data that could be used to persist a value for a forecast.
For example, given the series:
|
1 |
[1, 2, 3, 4, 5, 6, 7, 8, 9] |
We could persist the last observation (relative index -1) as the value 9 or persist the second last prior observation (relative index -2) as 8, and so on.
Average Forecast Strategy
One step above the naive forecast is the strategy of averaging prior values.
All prior observations are collected and averaged, either using the mean or the median, with no other treatment to the data.
In some cases, we may want to shorten the history used in the average calculation to the last few observations.
We can generalize this to the case of testing each possible set of n-prior observations to be included into the average calculation.
For example, given the series:
|
1 |
[1, 2, 3, 4, 5, 6, 7, 8, 9] |
We could average the last one observation (9), the last two observations (8, 9), and so on.
In the case of seasonal data, we may want to average the last n-prior observations at the same time in the cycle as the time that is being forecasted.
For example, given the series with a 3-step cycle:
|
1 |
[1, 2, 3, 1, 2, 3, 1, 2, 3] |
We could use a window size of 3 and average the last one observation (-3 or 1), the last two observations (-3 or 1, and -(3 * 2) or 1), and so on.
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Develop a Grid Search Framework
In this section, we will develop a framework for grid searching the two simple forecast strategies described in the previous section, namely the naive and average strategies.
We can start off by implementing a naive forecast strategy.
For a given dataset of historical observations, we can persist any value in that history, that is from the previous observation at index -1 to the first observation in the history at -(len(data)).
The naive_forecast() function below implements the naive forecast strategy for a given offset from 1 to the length of the dataset.
|
1 2 3 |
# one-step naive forecast def naive_forecast(history, n): return history[-n] |
We can test this function out on a small contrived dataset.
|
1 2 3 4 5 6 7 8 9 10 |
# one-step naive forecast def naive_forecast(history, n): return history[-n] # define dataset data = [10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0] print(data) # test naive forecast for i in range(1, len(data)+1): print(naive_forecast(data, i)) |
Running the example first prints the contrived dataset, then the naive forecast for each offset in the historical dataset.
|
1 2 3 4 5 6 7 8 9 10 11 |
[10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0] 100.0 90.0 80.0 70.0 60.0 50.0 40.0 30.0 20.0 10.0 |
We can now look at developing a function for the average forecast strategy.
Averaging the last n observations is straight-forward; for example:
|
1 2 |
from numpy import mean result = mean(history[-n:]) |
We may also want to test out the median in those cases where the distribution of observations is non-Gaussian.
|
1 2 |
from numpy import median result = median(history[-n:]) |
The average_forecast() function below implements this taking the historical data and a config array or tuple that specifies the number of prior values to average as an integer, and a string that describe the way to calculate the average (‘mean‘ or ‘median‘).
|
1 2 3 4 5 6 7 8 |
# one-step average forecast def average_forecast(history, config): n, avg_type = config # mean of last n values if avg_type is 'mean': return mean(history[-n:]) # median of last n values return median(history[-n:]) |
The complete example on a small contrived dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from numpy import mean from numpy import median # one-step average forecast def average_forecast(history, config): n, avg_type = config # mean of last n values if avg_type is 'mean': return mean(history[-n:]) # median of last n values return median(history[-n:]) # define dataset data = [10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0] print(data) # test naive forecast for i in range(1, len(data)+1): print(average_forecast(data, (i, 'mean'))) |
Running the example forecasts the next value in the series as the mean value from contiguous subsets of prior observations from -1 to -10, inclusively.
|
1 2 3 4 5 6 7 8 9 10 11 |
[10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0] 100.0 95.0 90.0 85.0 80.0 75.0 70.0 65.0 60.0 55.0 |
We can update the function to support averaging over seasonal data, respecting the seasonal offset.
An offset argument can be added to the function that when not set to 1 will determine the number of prior observations backwards to count before collecting values from which to include in the average.
For example, if n=1 and offset=3, then the average is calculated from the single value at n*offset or 1*3 = -3. If n=2 and offset=3, then the average is calculated from the values at 1*3 or -3 and 2*3 or -6.
We can also add some protection to raise an exception when a seasonal configuration (n * offset) extends beyond the end of the historical observations.
The updated function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# one-step average forecast def average_forecast(history, config): n, offset, avg_type = config values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # mean of last n values if avg_type is 'mean': return mean(values) # median of last n values return median(values) |
We can test out this function on a small contrived dataset with a seasonal cycle.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
from numpy import mean from numpy import median # one-step average forecast def average_forecast(history, config): n, offset, avg_type = config values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # mean of last n values if avg_type is 'mean': return mean(values) # median of last n values return median(values) # define dataset data = [10.0, 20.0, 30.0, 10.0, 20.0, 30.0, 10.0, 20.0, 30.0] print(data) # test naive forecast for i in [1, 2, 3]: print(average_forecast(data, (i, 3, 'mean'))) |
Running the example calculates the mean values of [10], [10, 10] and [10, 10, 10].
|
1 2 3 4 |
[10.0, 20.0, 30.0, 10.0, 20.0, 30.0, 10.0, 20.0, 30.0] 10.0 10.0 10.0 |
It is possible to combine both the naive and the average forecast strategies together into the same function.
There is a little overlap between the methods, specifically the n-offset into the history that is used to either persist values or determine the number of values to average.
It is helpful to have both strategies supported by one function so that we can test a suite of configurations for both strategies at once as part of a broader grid search of simple models.
The simple_forecast() function below combines both strategies into a single function.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# one-step simple forecast def simple_forecast(history, config): n, offset, avg_type = config # persist value, ignore other config if avg_type == 'persist': return history[-n] # collect values to average values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # check if we can average if len(values) < 2: raise Exception('Cannot calculate average') # mean of last n values if avg_type == 'mean': return mean(values) # median of last n values return median(values) |
Next, we need to build up some functions for fitting and evaluating a model repeatedly via walk-forward validation, including splitting a dataset into train and test sets and evaluating one-step forecasts.
We can split a list or NumPy array of data using a slice given a specified size of the split, e.g. the number of time steps to use from the data in the test set.
The train_test_split() function below implements this for a provided dataset and a specified number of time steps to use in the test set.
|
1 2 3 |
# split a univariate dataset into train/test sets def train_test_split(data, n_test): return data[:-n_test], data[-n_test:] |
After forecasts have been made for each step in the test dataset, they need to be compared to the test set in order to calculate an error score.
There are many popular error scores for time series forecasting. In this case, we will use root mean squared error (RMSE), but you can change this to your preferred measure, e.g. MAPE, MAE, etc.
The measure_rmse() function below will calculate the RMSE given a list of actual (the test set) and predicted values.
|
1 2 3 |
# root mean squared error or rmse def measure_rmse(actual, predicted): return sqrt(mean_squared_error(actual, predicted)) |
We can now implement the walk-forward validation scheme. This is a standard approach to evaluating a time series forecasting model that respects the temporal ordering of observations.
First, a provided univariate time series dataset is split into train and test sets using the train_test_split() function. Then the number of observations in the test set are enumerated. For each we fit a model on all of the history and make a one step forecast. The true observation for the time step is then added to the history, and the process is repeated. The simple_forecast() function is called in order to fit a model and make a prediction. Finally, an error score is calculated by comparing all one-step forecasts to the actual test set by calling the measure_rmse() function.
The walk_forward_validation() function below implements this, taking a univariate time series, a number of time steps to use in the test set, and an array of model configuration.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# walk-forward validation for univariate data def walk_forward_validation(data, n_test, cfg): predictions = list() # split dataset train, test = train_test_split(data, n_test) # seed history with training dataset history = [x for x in train] # step over each time-step in the test set for i in range(len(test)): # fit model and make forecast for history yhat = simple_forecast(history, cfg) # store forecast in list of predictions predictions.append(yhat) # add actual observation to history for the next loop history.append(test[i]) # estimate prediction error error = measure_rmse(test, predictions) return error |
If you are interested in making multi-step predictions, you can change the call to predict() in the simple_forecast() function and also change the calculation of error in the measure_rmse() function.
We can call walk_forward_validation() repeatedly with different lists of model configurations.
One possible issue is that some combinations of model configurations may not be called for the model and will throw an exception.
We can trap exceptions and ignore warnings during the grid search by wrapping all calls to walk_forward_validation() with a try-except and a block to ignore warnings. We can also add debugging support to disable these protections in the case we want to see what is really going on. Finally, if an error does occur, we can return a None result; otherwise, we can print some information about the skill of each model evaluated. This is helpful when a large number of models are evaluated.
The score_model() function below implements this and returns a tuple of (key and result), where the key is a string version of the tested model configuration.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# score a model, return None on failure def score_model(data, n_test, cfg, debug=False): result = None # convert config to a key key = str(cfg) # show all warnings and fail on exception if debugging if debug: result = walk_forward_validation(data, n_test, cfg) else: # one failure during model validation suggests an unstable config try: # never show warnings when grid searching, too noisy with catch_warnings(): filterwarnings("ignore") result = walk_forward_validation(data, n_test, cfg) except: error = None # check for an interesting result if result is not None: print(' > Model[%s] %.3f' % (key, result)) return (key, result) |
Next, we need a loop to test a list of different model configurations.
This is the main function that drives the grid search process and will call the score_model() function for each model configuration.
We can dramatically speed up the grid search process by evaluating model configurations in parallel. One way to do that is to use the Joblib library.
We can define a Parallel object with the number of cores to use and set it to the number of scores detected in your hardware.
|
1 |
executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') |
We can then create a list of tasks to execute in parallel, which will be one call to the score_model() function for each model configuration we have.
|
1 |
tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) |
Finally, we can use the Parallel object to execute the list of tasks in parallel.
|
1 |
scores = executor(tasks) |
That’s it.
We can also provide a non-parallel version of evaluating all model configurations in case we want to debug something.
|
1 |
scores = [score_model(data, n_test, cfg) for cfg in cfg_list] |
The result of evaluating a list of configurations will be a list of tuples, each with a name that summarizes a specific model configuration and the error of the model evaluated with that configuration as either the RMSE or None if there was an error.
We can filter out all scores set to None.
|
1 |
scores = [r for r in scores if r[1] != None] |
We can then sort all tuples in the list by the score in ascending order (best are first), then return this list of scores for review.
The grid_search() function below implements this behavior given a univariate time series dataset, a list of model configurations (list of lists), and the number of time steps to use in the test set. An optional parallel argument allows the evaluation of models across all cores to be tuned on or off, and is on by default.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# grid search configs def grid_search(data, cfg_list, n_test, parallel=True): scores = None if parallel: # execute configs in parallel executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) scores = executor(tasks) else: scores = [score_model(data, n_test, cfg) for cfg in cfg_list] # remove empty results scores = [r for r in scores if r[1] != None] # sort configs by error, asc scores.sort(key=lambda tup: tup[1]) return scores |
We’re nearly done.
The only thing left to do is to define a list of model configurations to try for a dataset.
We can define this generically. The only parameter we may want to specify is the periodicity of the seasonal component in the series (offset), if one exists. By default, we will assume no seasonal component.
The simple_configs() function below will create a list of model configurations to evaluate.
The function only requires the maximum length of the historical data as an argument and optionally the periodicity of any seasonal component, which is defaulted to 1 (no seasonal component).
|
1 2 3 4 5 6 7 8 9 |
# create a set of simple configs to try def simple_configs(max_length, offsets=[1]): configs = list() for i in range(1, max_length+1): for o in offsets: for t in ['persist', 'mean', 'median']: cfg = [i, o, t] configs.append(cfg) return configs |
We now have a framework for grid searching simple model hyperparameters via one-step walk-forward validation.
It is generic and will work for any in-memory univariate time series provided as a list or NumPy array.
We can make sure all the pieces work together by testing it on a contrived 10-step dataset.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
# grid search simple forecasts from math import sqrt from numpy import mean from numpy import median from multiprocessing import cpu_count from joblib import Parallel from joblib import delayed from warnings import catch_warnings from warnings import filterwarnings from sklearn.metrics import mean_squared_error # one-step simple forecast def simple_forecast(history, config): n, offset, avg_type = config # persist value, ignore other config if avg_type == 'persist': return history[-n] # collect values to average values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # check if we can average if len(values) < 2: raise Exception('Cannot calculate average') # mean of last n values if avg_type == 'mean': return mean(values) # median of last n values return median(values) # root mean squared error or rmse def measure_rmse(actual, predicted): return sqrt(mean_squared_error(actual, predicted)) # split a univariate dataset into train/test sets def train_test_split(data, n_test): return data[:-n_test], data[-n_test:] # walk-forward validation for univariate data def walk_forward_validation(data, n_test, cfg): predictions = list() # split dataset train, test = train_test_split(data, n_test) # seed history with training dataset history = [x for x in train] # step over each time-step in the test set for i in range(len(test)): # fit model and make forecast for history yhat = simple_forecast(history, cfg) # store forecast in list of predictions predictions.append(yhat) # add actual observation to history for the next loop history.append(test[i]) # estimate prediction error error = measure_rmse(test, predictions) return error # score a model, return None on failure def score_model(data, n_test, cfg, debug=False): result = None # convert config to a key key = str(cfg) # show all warnings and fail on exception if debugging if debug: result = walk_forward_validation(data, n_test, cfg) else: # one failure during model validation suggests an unstable config try: # never show warnings when grid searching, too noisy with catch_warnings(): filterwarnings("ignore") result = walk_forward_validation(data, n_test, cfg) except: error = None # check for an interesting result if result is not None: print(' > Model[%s] %.3f' % (key, result)) return (key, result) # grid search configs def grid_search(data, cfg_list, n_test, parallel=True): scores = None if parallel: # execute configs in parallel executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) scores = executor(tasks) else: scores = [score_model(data, n_test, cfg) for cfg in cfg_list] # remove empty results scores = [r for r in scores if r[1] != None] # sort configs by error, asc scores.sort(key=lambda tup: tup[1]) return scores # create a set of simple configs to try def simple_configs(max_length, offsets=[1]): configs = list() for i in range(1, max_length+1): for o in offsets: for t in ['persist', 'mean', 'median']: cfg = [i, o, t] configs.append(cfg) return configs if __name__ == '__main__': # define dataset data = [10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0] print(data) # data split n_test = 4 # model configs max_length = len(data) - n_test cfg_list = simple_configs(max_length) # grid search scores = grid_search(data, cfg_list, n_test) print('done') # list top 3 configs for cfg, error in scores[:3]: print(cfg, error) |
Running the example first prints the contrived time series dataset.
Next, the model configurations and their errors are reported as they are evaluated.
Finally, the configurations and the error for the top three configurations are reported.
We can see that the persistence model with a configuration of 1 (e.g. persist the last observation) achieves the best performance of the simple models tested, as would be expected.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
[10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0] > Model[[1, 1, 'persist']] 10.000 > Model[[2, 1, 'persist']] 20.000 > Model[[2, 1, 'mean']] 15.000 > Model[[2, 1, 'median']] 15.000 > Model[[3, 1, 'persist']] 30.000 > Model[[4, 1, 'persist']] 40.000 > Model[[5, 1, 'persist']] 50.000 > Model[[5, 1, 'mean']] 30.000 > Model[[3, 1, 'mean']] 20.000 > Model[[4, 1, 'median']] 25.000 > Model[[6, 1, 'persist']] 60.000 > Model[[4, 1, 'mean']] 25.000 > Model[[3, 1, 'median']] 20.000 > Model[[6, 1, 'mean']] 35.000 > Model[[5, 1, 'median']] 30.000 > Model[[6, 1, 'median']] 35.000 done [1, 1, 'persist'] 10.0 [2, 1, 'mean'] 15.0 [2, 1, 'median'] 15.0 |
Now that we have a robust framework for grid searching simple model hyperparameters, let’s test it out on a suite of standard univariate time series datasets.
The results demonstrated on each dataset provide a baseline of performance that can be used to compare more sophisticated methods, such as SARIMA, ETS, and even machine learning methods.
Case Study 1: No Trend or Seasonality
The ‘daily female births’ dataset summarizes the daily total female births in California, USA in 1959.
The dataset has no obvious trend or seasonal component.
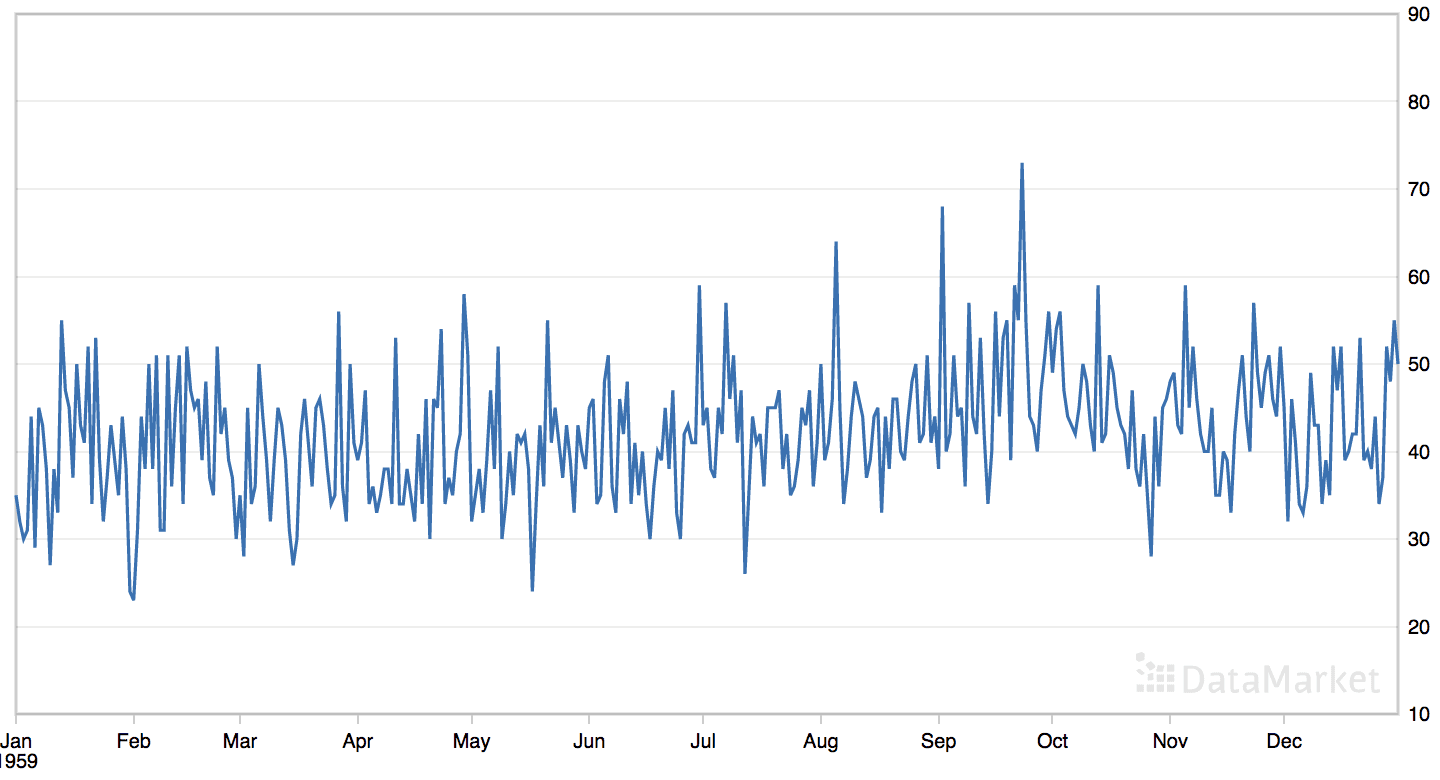
Line Plot of the Daily Female Births Dataset
Download the dataset directly from here:
Save the file with the filename ‘daily-total-female-births.csv‘ in your current working directory.
We can load this dataset as a Pandas series using the function read_csv().
|
1 |
series = read_csv('daily-total-female-births.csv', header=0, index_col=0) |
The dataset has one year, or 365 observations. We will use the first 200 for training and the remaining 165 as the test set.
The complete example grid searching the daily female univariate time series forecasting problem is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
# grid search simple forecast for daily female births from math import sqrt from numpy import mean from numpy import median from multiprocessing import cpu_count from joblib import Parallel from joblib import delayed from warnings import catch_warnings from warnings import filterwarnings from sklearn.metrics import mean_squared_error from pandas import read_csv # one-step simple forecast def simple_forecast(history, config): n, offset, avg_type = config # persist value, ignore other config if avg_type == 'persist': return history[-n] # collect values to average values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # check if we can average if len(values) < 2: raise Exception('Cannot calculate average') # mean of last n values if avg_type == 'mean': return mean(values) # median of last n values return median(values) # root mean squared error or rmse def measure_rmse(actual, predicted): return sqrt(mean_squared_error(actual, predicted)) # split a univariate dataset into train/test sets def train_test_split(data, n_test): return data[:-n_test], data[-n_test:] # walk-forward validation for univariate data def walk_forward_validation(data, n_test, cfg): predictions = list() # split dataset train, test = train_test_split(data, n_test) # seed history with training dataset history = [x for x in train] # step over each time-step in the test set for i in range(len(test)): # fit model and make forecast for history yhat = simple_forecast(history, cfg) # store forecast in list of predictions predictions.append(yhat) # add actual observation to history for the next loop history.append(test[i]) # estimate prediction error error = measure_rmse(test, predictions) return error # score a model, return None on failure def score_model(data, n_test, cfg, debug=False): result = None # convert config to a key key = str(cfg) # show all warnings and fail on exception if debugging if debug: result = walk_forward_validation(data, n_test, cfg) else: # one failure during model validation suggests an unstable config try: # never show warnings when grid searching, too noisy with catch_warnings(): filterwarnings("ignore") result = walk_forward_validation(data, n_test, cfg) except: error = None # check for an interesting result if result is not None: print(' > Model[%s] %.3f' % (key, result)) return (key, result) # grid search configs def grid_search(data, cfg_list, n_test, parallel=True): scores = None if parallel: # execute configs in parallel executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) scores = executor(tasks) else: scores = [score_model(data, n_test, cfg) for cfg in cfg_list] # remove empty results scores = [r for r in scores if r[1] != None] # sort configs by error, asc scores.sort(key=lambda tup: tup[1]) return scores # create a set of simple configs to try def simple_configs(max_length, offsets=[1]): configs = list() for i in range(1, max_length+1): for o in offsets: for t in ['persist', 'mean', 'median']: cfg = [i, o, t] configs.append(cfg) return configs if __name__ == '__main__': # define dataset series = read_csv('daily-total-female-births.csv', header=0, index_col=0) data = series.values print(data) # data split n_test = 165 # model configs max_length = len(data) - n_test cfg_list = simple_configs(max_length) # grid search scores = grid_search(data, cfg_list, n_test) print('done') # list top 3 configs for cfg, error in scores[:3]: print(cfg, error) |
Running the example prints the model configurations and the RMSE are printed as the models are evaluated.
The top three model configurations and their error are reported at the end of the run.
We can see that the best result was an RMSE of about 6.93 births with the following configuration:
- Strategy: Average
- n: 22
- function: mean()
This is surprising given the lack of trend or seasonality, I would have expected either a persistence of -1 or an average of the entire historical dataset to result in the best performance.
|
1 2 3 4 5 6 7 8 9 10 11 |
... > Model[[186, 1, 'mean']] 7.523 > Model[[200, 1, 'median']] 7.681 > Model[[186, 1, 'median']] 7.691 > Model[[187, 1, 'persist']] 11.137 > Model[[187, 1, 'mean']] 7.527 done [22, 1, 'mean'] 6.930411499775709 [23, 1, 'mean'] 6.932293117115201 [21, 1, 'mean'] 6.951918385845375 |
Case Study 2: Trend
The ‘shampoo’ dataset summarizes the monthly sales of shampoo over a three-year period.
The dataset contains an obvious trend but no obvious seasonal component.
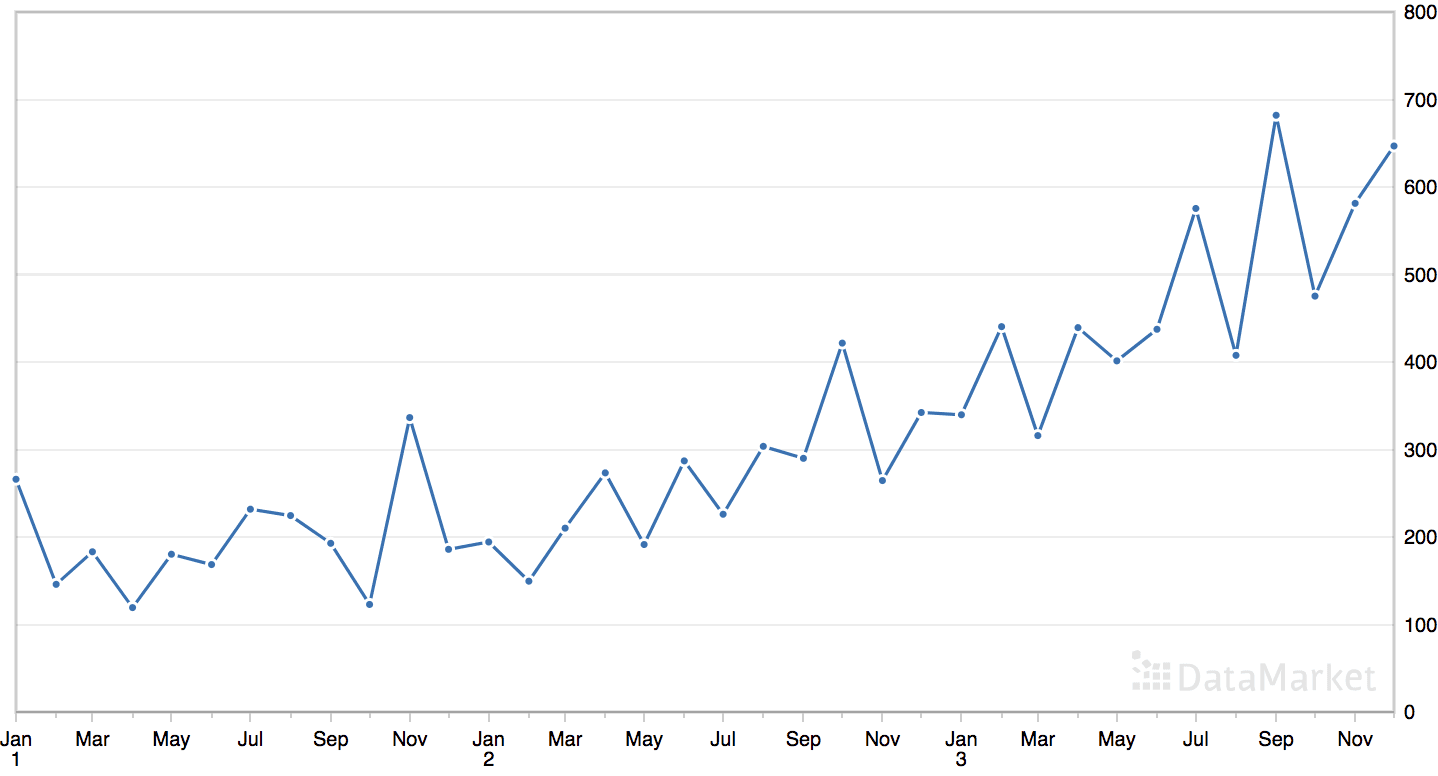
Line Plot of the Monthly Shampoo Sales Dataset
Download the dataset directly from here:
Save the file with the filename ‘shampoo.csv‘ in your current working directory.
We can load this dataset as a Pandas series using the function read_csv().
|
1 2 3 4 5 6 |
# parse dates def custom_parser(x): return datetime.strptime('195'+x, '%Y-%m') # load dataset series = read_csv('shampoo.csv', header=0, index_col=0, date_parser=custom_parser) |
The dataset has three years, or 36 observations. We will use the first 24 for training and the remaining 12 as the test set.
The complete example grid searching the shampoo sales univariate time series forecasting problem is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
# grid search simple forecast for monthly shampoo sales from math import sqrt from numpy import mean from numpy import median from multiprocessing import cpu_count from joblib import Parallel from joblib import delayed from warnings import catch_warnings from warnings import filterwarnings from sklearn.metrics import mean_squared_error from pandas import read_csv from pandas import datetime # one-step simple forecast def simple_forecast(history, config): n, offset, avg_type = config # persist value, ignore other config if avg_type == 'persist': return history[-n] # collect values to average values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # check if we can average if len(values) < 2: raise Exception('Cannot calculate average') # mean of last n values if avg_type == 'mean': return mean(values) # median of last n values return median(values) # root mean squared error or rmse def measure_rmse(actual, predicted): return sqrt(mean_squared_error(actual, predicted)) # split a univariate dataset into train/test sets def train_test_split(data, n_test): return data[:-n_test], data[-n_test:] # walk-forward validation for univariate data def walk_forward_validation(data, n_test, cfg): predictions = list() # split dataset train, test = train_test_split(data, n_test) # seed history with training dataset history = [x for x in train] # step over each time-step in the test set for i in range(len(test)): # fit model and make forecast for history yhat = simple_forecast(history, cfg) # store forecast in list of predictions predictions.append(yhat) # add actual observation to history for the next loop history.append(test[i]) # estimate prediction error error = measure_rmse(test, predictions) return error # score a model, return None on failure def score_model(data, n_test, cfg, debug=False): result = None # convert config to a key key = str(cfg) # show all warnings and fail on exception if debugging if debug: result = walk_forward_validation(data, n_test, cfg) else: # one failure during model validation suggests an unstable config try: # never show warnings when grid searching, too noisy with catch_warnings(): filterwarnings("ignore") result = walk_forward_validation(data, n_test, cfg) except: error = None # check for an interesting result if result is not None: print(' > Model[%s] %.3f' % (key, result)) return (key, result) # grid search configs def grid_search(data, cfg_list, n_test, parallel=True): scores = None if parallel: # execute configs in parallel executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) scores = executor(tasks) else: scores = [score_model(data, n_test, cfg) for cfg in cfg_list] # remove empty results scores = [r for r in scores if r[1] != None] # sort configs by error, asc scores.sort(key=lambda tup: tup[1]) return scores # create a set of simple configs to try def simple_configs(max_length, offsets=[1]): configs = list() for i in range(1, max_length+1): for o in offsets: for t in ['persist', 'mean', 'median']: cfg = [i, o, t] configs.append(cfg) return configs # parse dates def custom_parser(x): return datetime.strptime('195'+x, '%Y-%m') if __name__ == '__main__': # load dataset series = read_csv('shampoo.csv', header=0, index_col=0, date_parser=custom_parser) data = series.values print(data.shape) # data split n_test = 12 # model configs max_length = len(data) - n_test cfg_list = simple_configs(max_length) # grid search scores = grid_search(data, cfg_list, n_test) print('done') # list top 3 configs for cfg, error in scores[:3]: print(cfg, error) |
Running the example prints the configurations and the RMSE are printed as the models are evaluated.
The top three model configurations and their error are reported at the end of the run.
We can see that the best result was an RMSE of about 95.69 sales with the following configuration:
- Strategy: Persist
- n: 2
This is surprising as the trend structure of the data would suggest that persisting the previous value (-1) would be the best approach, not persisting the second last value.
|
1 2 3 4 5 6 7 8 9 10 11 |
... > Model[[23, 1, 'mean']] 209.782 > Model[[23, 1, 'median']] 221.863 > Model[[24, 1, 'persist']] 305.635 > Model[[24, 1, 'mean']] 213.466 > Model[[24, 1, 'median']] 226.061 done [2, 1, 'persist'] 95.69454007413378 [2, 1, 'mean'] 96.01140340258198 [2, 1, 'median'] 96.01140340258198 |
Case Study 3: Seasonality
The ‘monthly mean temperatures’ dataset summarizes the monthly average air temperatures in Nottingham Castle, England from 1920 to 1939 in degrees Fahrenheit.
The dataset has an obvious seasonal component and no obvious trend.
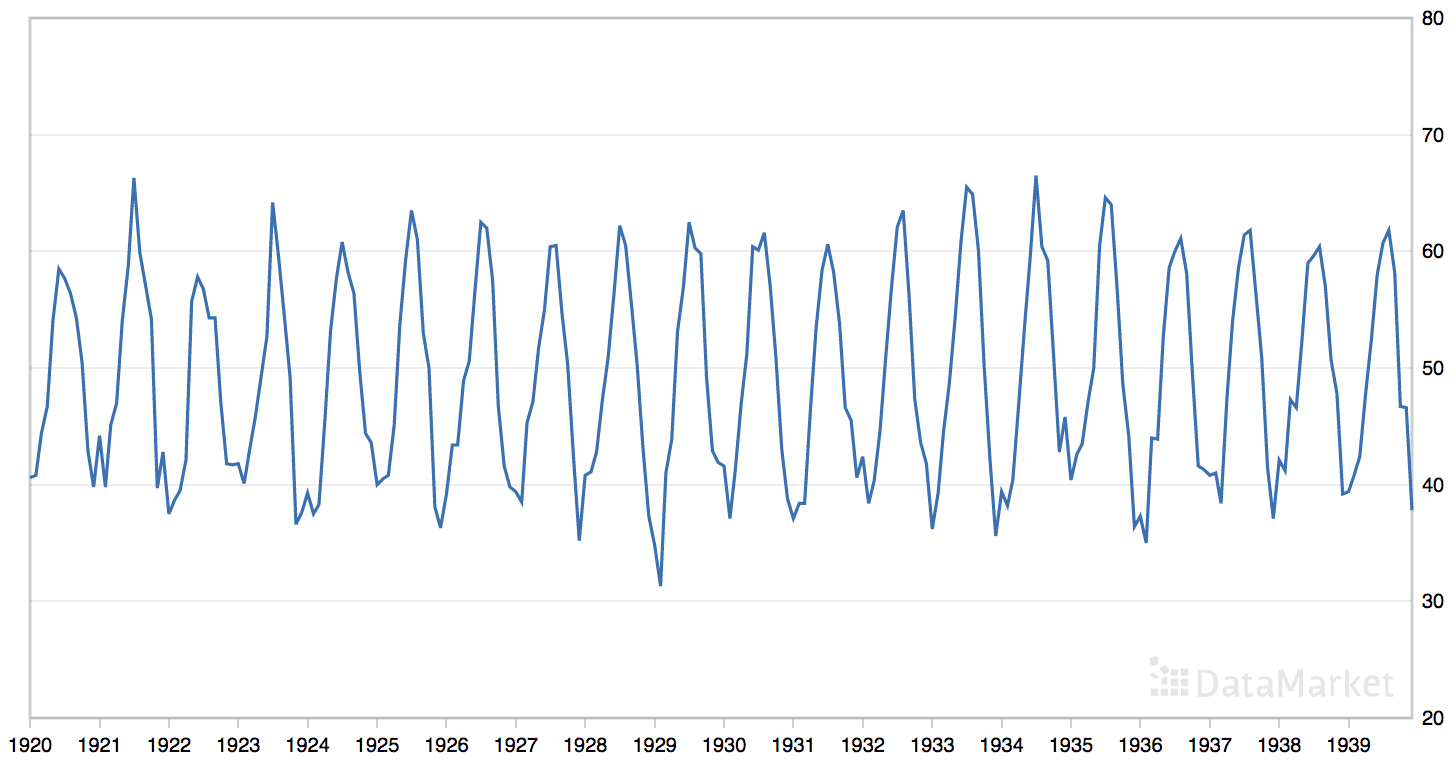
Line Plot of the Monthly Mean Temperatures Dataset
Download the dataset directly from here:
Save the file with the filename ‘monthly-mean-temp.csv‘ in your current working directory.
We can load this dataset as a Pandas series using the function read_csv().
|
1 |
series = read_csv('monthly-mean-temp.csv', header=0, index_col=0) |
The dataset has 20 years, or 240 observations. We will trim the dataset to the last five years of data (60 observations) in order to speed up the model evaluation process and use the last year or 12 observations for the test set.
|
1 2 |
# trim dataset to 5 years data = data[-(5*12):] |
The period of the seasonal component is about one year, or 12 observations. We will use this as the seasonal period in the call to the simple_configs() function when preparing the model configurations.
|
1 2 |
# model configs cfg_list = simple_configs(max_length, offsets=[1,12]) |
The complete example grid searching the monthly mean temperature time series forecasting problem is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
# grid search simple forecast for monthly mean temperature from math import sqrt from numpy import mean from numpy import median from multiprocessing import cpu_count from joblib import Parallel from joblib import delayed from warnings import catch_warnings from warnings import filterwarnings from sklearn.metrics import mean_squared_error from pandas import read_csv # one-step simple forecast def simple_forecast(history, config): n, offset, avg_type = config # persist value, ignore other config if avg_type == 'persist': return history[-n] # collect values to average values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # check if we can average if len(values) < 2: raise Exception('Cannot calculate average') # mean of last n values if avg_type == 'mean': return mean(values) # median of last n values return median(values) # root mean squared error or rmse def measure_rmse(actual, predicted): return sqrt(mean_squared_error(actual, predicted)) # split a univariate dataset into train/test sets def train_test_split(data, n_test): return data[:-n_test], data[-n_test:] # walk-forward validation for univariate data def walk_forward_validation(data, n_test, cfg): predictions = list() # split dataset train, test = train_test_split(data, n_test) # seed history with training dataset history = [x for x in train] # step over each time-step in the test set for i in range(len(test)): # fit model and make forecast for history yhat = simple_forecast(history, cfg) # store forecast in list of predictions predictions.append(yhat) # add actual observation to history for the next loop history.append(test[i]) # estimate prediction error error = measure_rmse(test, predictions) return error # score a model, return None on failure def score_model(data, n_test, cfg, debug=False): result = None # convert config to a key key = str(cfg) # show all warnings and fail on exception if debugging if debug: result = walk_forward_validation(data, n_test, cfg) else: # one failure during model validation suggests an unstable config try: # never show warnings when grid searching, too noisy with catch_warnings(): filterwarnings("ignore") result = walk_forward_validation(data, n_test, cfg) except: error = None # check for an interesting result if result is not None: print(' > Model[%s] %.3f' % (key, result)) return (key, result) # grid search configs def grid_search(data, cfg_list, n_test, parallel=True): scores = None if parallel: # execute configs in parallel executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) scores = executor(tasks) else: scores = [score_model(data, n_test, cfg) for cfg in cfg_list] # remove empty results scores = [r for r in scores if r[1] != None] # sort configs by error, asc scores.sort(key=lambda tup: tup[1]) return scores # create a set of simple configs to try def simple_configs(max_length, offsets=[1]): configs = list() for i in range(1, max_length+1): for o in offsets: for t in ['persist', 'mean', 'median']: cfg = [i, o, t] configs.append(cfg) return configs if __name__ == '__main__': # define dataset series = read_csv('monthly-mean-temp.csv', header=0, index_col=0) data = series.values print(data) # data split n_test = 12 # model configs max_length = len(data) - n_test cfg_list = simple_configs(max_length, offsets=[1,12]) # grid search scores = grid_search(data, cfg_list, n_test) print('done') # list top 3 configs for cfg, error in scores[:3]: print(cfg, error) |
Running the example prints the model configurations and the RMSE are printed as the models are evaluated.
The top three model configurations and their error are reported at the end of the run.
We can see that the best result was an RMSE of about 1.501 degrees with the following configuration:
- Strategy: Average
- n: 4
- offset: 12
- function: mean()
This finding is not too surprising. Given the seasonal structure of the data, we would expect a function of the last few observations at prior points in the yearly cycle to be effective.
|
1 2 3 4 5 6 7 8 9 10 |
... > Model[[227, 12, 'persist']] 5.365 > Model[[228, 1, 'persist']] 2.818 > Model[[228, 1, 'mean']] 8.258 > Model[[228, 1, 'median']] 8.361 > Model[[228, 12, 'persist']] 2.818 done [4, 12, 'mean'] 1.5015616870445234 [8, 12, 'mean'] 1.5794579766489512 [13, 12, 'mean'] 1.586186052546763 |
Case Study 4: Trend and Seasonality
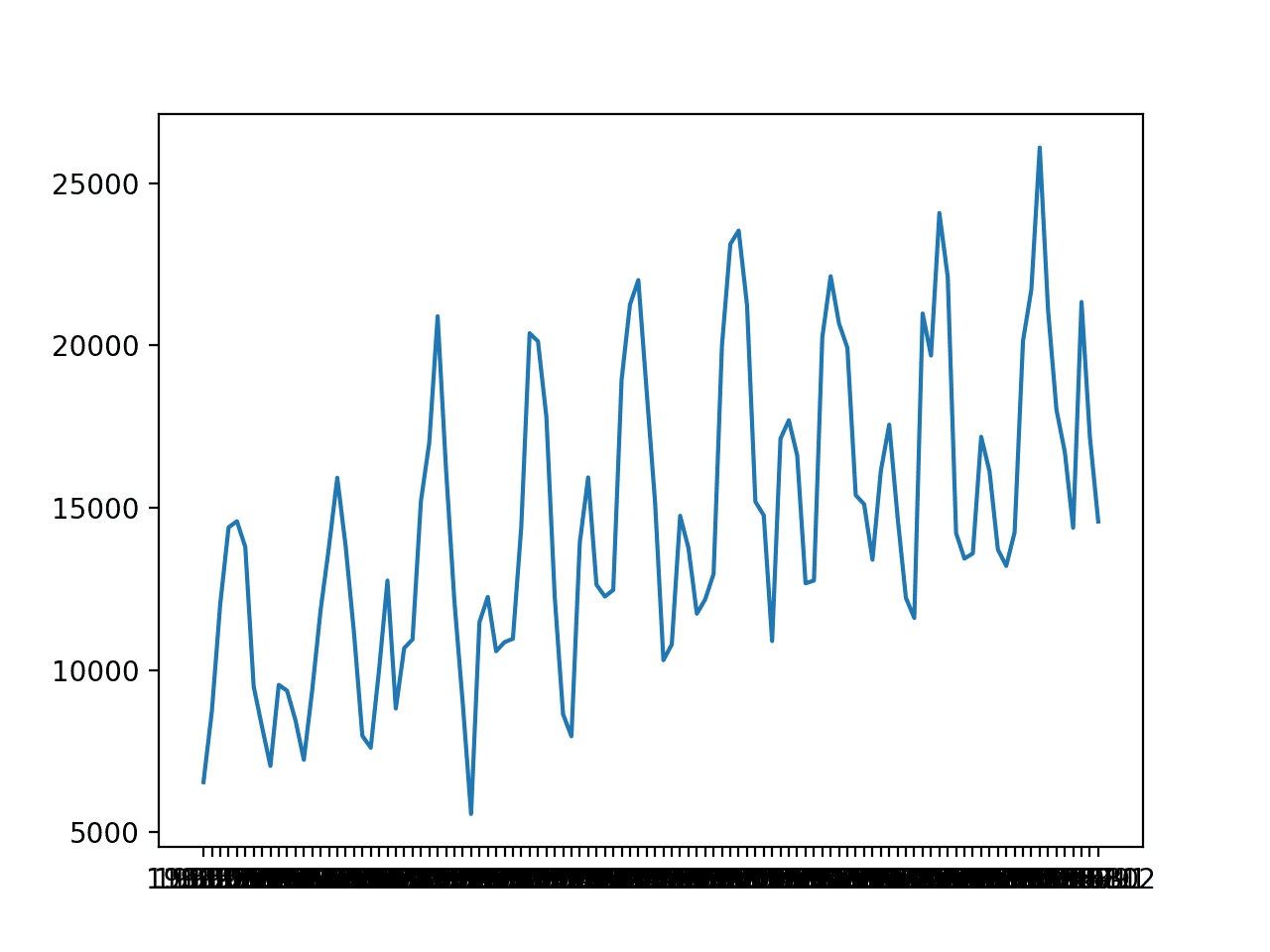
The ‘monthly car sales’ dataset summarizes the monthly car sales in Quebec, Canada between 1960 and 1968.
The dataset has an obvious trend and seasonal component.
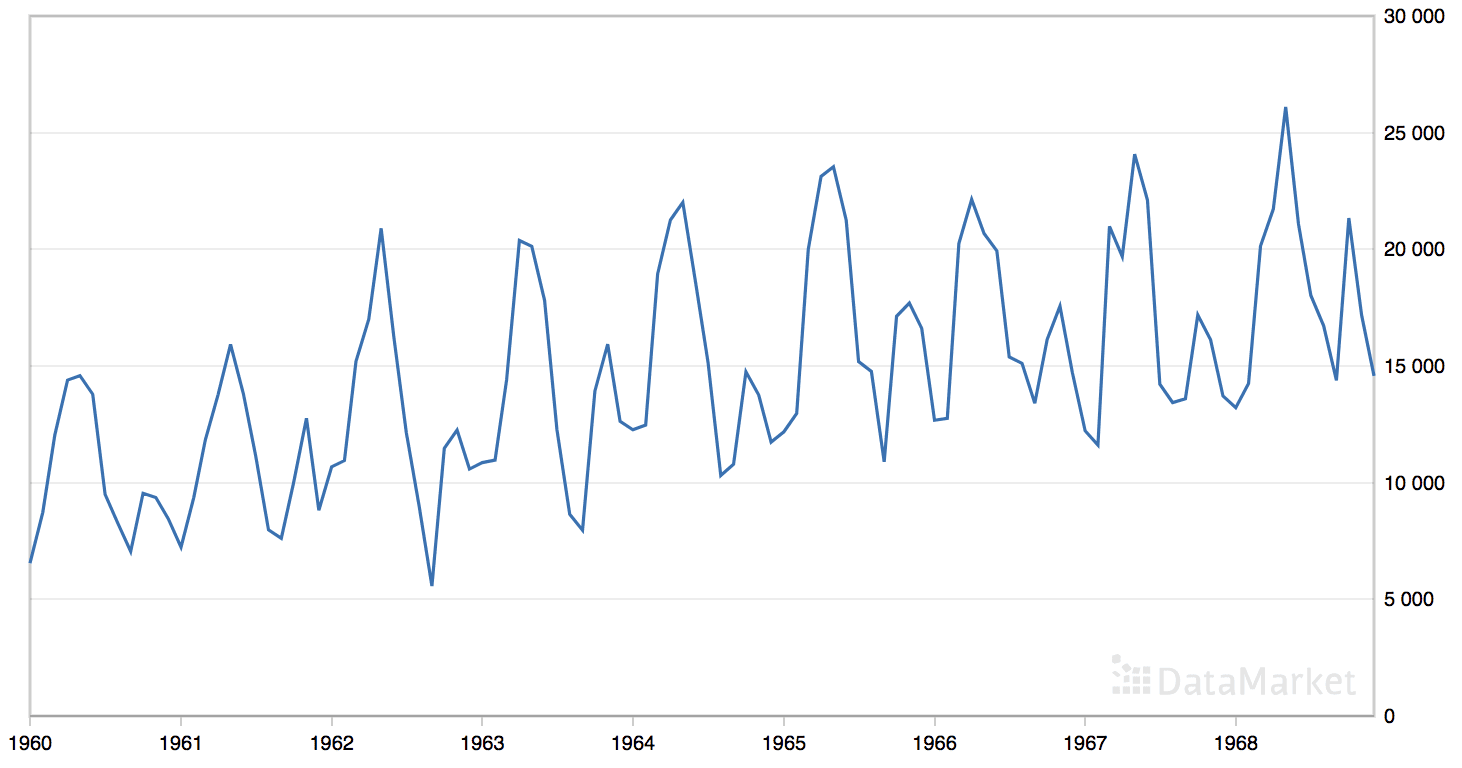
Line Plot of the Monthly Car Sales Dataset
Download the dataset directly from here:
Save the file with the filename ‘monthly-car-sales.csv‘ in your current working directory.
We can load this dataset as a Pandas series using the function read_csv().
|
1 |
series = read_csv('monthly-car-sales.csv', header=0, index_col=0) |
The dataset has 9 years, or 108 observations. We will use the last year or 12 observations as the test set.
The period of the seasonal component could be 12 months. We will try this as the seasonal period in the call to the simple_configs() function when preparing the model configurations.
|
1 2 |
# model configs cfg_list = simple_configs(max_length, offsets=[1,12]) |
The complete example grid searching the monthly car sales time series forecasting problem is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
# grid search simple forecast for monthly car sales from math import sqrt from numpy import mean from numpy import median from multiprocessing import cpu_count from joblib import Parallel from joblib import delayed from warnings import catch_warnings from warnings import filterwarnings from sklearn.metrics import mean_squared_error from pandas import read_csv # one-step simple forecast def simple_forecast(history, config): n, offset, avg_type = config # persist value, ignore other config if avg_type == 'persist': return history[-n] # collect values to average values = list() if offset == 1: values = history[-n:] else: # skip bad configs if n*offset > len(history): raise Exception('Config beyond end of data: %d %d' % (n,offset)) # try and collect n values using offset for i in range(1, n+1): ix = i * offset values.append(history[-ix]) # check if we can average if len(values) < 2: raise Exception('Cannot calculate average') # mean of last n values if avg_type == 'mean': return mean(values) # median of last n values return median(values) # root mean squared error or rmse def measure_rmse(actual, predicted): return sqrt(mean_squared_error(actual, predicted)) # split a univariate dataset into train/test sets def train_test_split(data, n_test): return data[:-n_test], data[-n_test:] # walk-forward validation for univariate data def walk_forward_validation(data, n_test, cfg): predictions = list() # split dataset train, test = train_test_split(data, n_test) # seed history with training dataset history = [x for x in train] # step over each time-step in the test set for i in range(len(test)): # fit model and make forecast for history yhat = simple_forecast(history, cfg) # store forecast in list of predictions predictions.append(yhat) # add actual observation to history for the next loop history.append(test[i]) # estimate prediction error error = measure_rmse(test, predictions) return error # score a model, return None on failure def score_model(data, n_test, cfg, debug=False): result = None # convert config to a key key = str(cfg) # show all warnings and fail on exception if debugging if debug: result = walk_forward_validation(data, n_test, cfg) else: # one failure during model validation suggests an unstable config try: # never show warnings when grid searching, too noisy with catch_warnings(): filterwarnings("ignore") result = walk_forward_validation(data, n_test, cfg) except: error = None # check for an interesting result if result is not None: print(' > Model[%s] %.3f' % (key, result)) return (key, result) # grid search configs def grid_search(data, cfg_list, n_test, parallel=True): scores = None if parallel: # execute configs in parallel executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing') tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list) scores = executor(tasks) else: scores = [score_model(data, n_test, cfg) for cfg in cfg_list] # remove empty results scores = [r for r in scores if r[1] != None] # sort configs by error, asc scores.sort(key=lambda tup: tup[1]) return scores # create a set of simple configs to try def simple_configs(max_length, offsets=[1]): configs = list() for i in range(1, max_length+1): for o in offsets: for t in ['persist', 'mean', 'median']: cfg = [i, o, t] configs.append(cfg) return configs if __name__ == '__main__': # define dataset series = read_csv('monthly-car-sales.csv', header=0, index_col=0) data = series.values print(data) # data split n_test = 12 # model configs max_length = len(data) - n_test cfg_list = simple_configs(max_length, offsets=[1,12]) # grid search scores = grid_search(data, cfg_list, n_test) print('done') # list top 3 configs for cfg, error in scores[:3]: print(cfg, error) |
Running the example prints the model configurations and the RMSE are printed as the models are evaluated.
The top three model configurations and their error are reported at the end of the run.
We can see that the best result was an RMSE of about 1841.155 sales with the following configuration:
- Strategy: Average
- n: 3
- offset: 12
- function: median()
It is not surprising that the chosen model is a function of the last few observations at the same point in prior cycles, although the use of the median instead of the mean may not have been immediately obvious and the results were much better than the mean.
|
1 2 3 4 5 6 7 8 9 10 |
... > Model[[79, 1, 'median']] 5124.113 > Model[[91, 12, 'persist']] 9580.149 > Model[[79, 12, 'persist']] 8641.529 > Model[[92, 1, 'persist']] 9830.921 > Model[[92, 1, 'mean']] 5148.126 done [3, 12, 'median'] 1841.1559321976688 [3, 12, 'mean'] 2115.198495632485 [4, 12, 'median'] 2184.37708988932 |
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Plot Forecast. Update the framework to re-fit a model with the best configuration and forecast the entire test dataset, then plot the forecast compared to the actual observations in the test set.
- Drift Method. Implement the drift method for simple forecasts and compare the results to the average and naive methods.
- Another Dataset. Apply the developed framework to an additional univariate time series problem.
If you explore any of these extensions, I’d love to know.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Summary
In this tutorial, you discovered how to develop a framework from scratch for grid searching simple naive and averaging strategies for time series forecasting with univariate data.
Specifically, you learned:
- How to develop a framework for grid searching simple models from scratch using walk-forward validation.
- How to grid search simple model hyperparameters for daily time series data for births.
- How to grid search simple model hyperparameters for monthly time series data for shampoo sales, car sales, and temperature.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.




sir It is one of the nice blog about learning.I am also writing blogs related to machine learning and block chain, if you could help me out
I don’t know about block chain, sorry.
Hi Jason,
I’m trying to add multi-step forecast functionality to your code based on the hint you gave below:
“If you are interested in making multi-step predictions, you can change the call to predict() in the simple_forecast() function and also change the calculation of error in the measure_rmse() function”.
However, I did not see a predict()in the simple_forecast() function to change, that would effect the calculation of the measure_rmse().
I was only changing the cfg configuration in simple_configs() and could not trust my results.
Could you please give more hints on the multi-step forecast functionality
Thank you in advance
When it comes to naive methods, you must develop your own predict function.
A naive forecast for a multi-step forecast may involve predicting the last observation n times forward, where n is the number of time steps to predict.
If this is challenging for you, a good place to get started with time series forecasting is here:
https://machinelearningmastery.com/start-here/#timeseries
OK. Thanks