Error-Correcting Output Codes (ECOC) for Machine Learning

By Jason Brownlee on April 27, 2021 in Ensemble Learning 4

Machine learning algorithms, like logistic regression and support vector machines, are designed for two-class (binary) classification problems.

As such, these algorithms must either be modified for multi-class (more than two) classification problems or not used at all. The Error-Correcting Output Codes method is a technique that allows a multi-class classification problem to be reframed as multiple binary classification problems, allowing the use of native binary classification models to be used directly.

Unlike one-vs-rest and one-vs-one methods that offer a similar solution by dividing a multi-class classification problem into a fixed number of binary classification problems, the error-correcting output codes technique allows each class to be encoded as an arbitrary number of binary classification problems. When an overdetermined representation is used, it allows the extra models to act as “error-correction” predictions that can result in better predictive performance.

In this tutorial, you will discover how to use error-correcting output codes for classification.

After completing this tutorial, you will know:

Error-correcting output codes is a technique for using binary classification models on multi-class classification prediction tasks.
How to fit, evaluate, and use error-correcting output codes classification models to make predictions.
How to tune and evaluate different values for the number of bits per class hyperparameter used by error-correcting output codes.

Kick-start your project with my new book Ensemble Learning Algorithms With Python, including step-by-step tutorials and the Python source code files for all examples.

Let’s get started.

Error-Correcting Output Codes (ECOC) for Machine Learning
Photo by Fred Hsu, some rights reserved.

Tutorial Overview

This tutorial is divided into three parts; they are:

Error-Correcting Output Codes
Evaluate and Use ECOC Classifiers
Tune Number of Bits Per Class

Error-Correcting Output Codes

Classification tasks are those where a label is predictive for a given input variable.

Binary classification tasks are those classification problems where the target contains two values, whereas multi-class classification problems are those that have more than two target class labels.

Many machine learning models have been developed for binary classification, although they may require modification to work with multi-class classification problems. For example, logistic regression and support vector machines were specifically designed for binary classification.

Several machine learning algorithms, such as SVM, were originally designed to solve only binary classification tasks.

— Page 133, Pattern Classification Using Ensemble Methods, 2010.

Rather than limiting the choice of algorithms or adapting the algorithms for multi-class problems, an alternative approach is to reframe the multi-class classification problem as multiple binary classification problems. Two common methods that can be used to achieve this include the one-vs-rest (OvR) and one-vs-one (OvO) techniques.

OvR: splits a multi-class problem into one binary problem per class.
OvO: splits a multi-class problem into one binary problem per each pair of classes.

Once split into subtasks, a binary classification model can be fit on each task and the model with the largest response can be taken as the prediction.

Both the OvR and OvO may be thought of as a type of ensemble learning model given that multiple separate models are fit for a predictive modeling task and used in concert to make a prediction. In both cases, the prediction of the “ensemble members” is a simple winner take all approach.

… convert the multiclass task into an ensemble of binary classification tasks, whose results are then combined.

— Page 134, Pattern Classification Using Ensemble Methods, 2010.

For more on one-vs-rest and one-vs-one models, see the tutorial:

How to Use One-vs-Rest and One-vs-One for Multi-Class Classification

A related approach is to prepare a binary encoding (e.g. a bitstring) to represent each class in the problem. Each bit in the string can be predicted by a separate binary classification problem. Arbitrarily, length encodings can be chosen for a given multi-class classification problem.

To be clear, each model receives the full input pattern and only predicts one position in the output string. During training, each model can be trained to produce the correct 0 or 1 output for the binary classification task. A prediction can then be made for new examples by using each model to make a prediction for the input to create the binary string, then compare the binary string to each class’s known encoding. The class encoding that has the smallest distance to the prediction is then chosen as the output.

A codeword of length l is ascribed to each class. Commonly, the size of the codewords has more bits than needed in order to uniquely represent each class.

— Page 138, Pattern Classification Using Ensemble Methods, 2010.

It is an interesting approach that allows the class representation to be more elaborate than is required (perhaps overdetermined) as compared to a one-hot encoding and introduces redundancy into the representation and modeling of the problem. This is intentional as the additional bits in the representation act like error-correcting codes to fix, correct, or improve the prediction.

… the idea is that the redundant “error-correcting” bits allow for some inaccuracies, and can improve performance.

— Page 606, The Elements of Statistical Learning, 2016.

This gives the technique its name: error-correcting output codes, or ECOC for short.

Error-Correcting Output Codes (ECOC) is a simple yet powerful approach to deal with a multi-class problem based on the combination of binary classifiers.

— Page 90, Ensemble Methods, 2012.

Care can be taken to ensure that each encoded class has a very different binary string encoding. A suite of different encoding schemes has been explored as well as specific methods for constructing the encodings to ensure they are sufficiently far apart in the encoding space. Interestingly, random encodings have been found to work perhaps just as well.

… analyzed the ECOC approach, and showed that random code assignment worked as well as the optimally constructed error-correcting codes

— Page 606, The Elements of Statistical Learning, 2016.

For a detailed review of the various different encoding schemes and methods for mapping predicted strings to encoded classes, I recommend Chapter 6 “Error Correcting Output Codes” of the book “Pattern Classification Using Ensemble Methods“.

Want to Get Started With Ensemble Learning?

Take my free 7-day email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Evaluate and Use ECOC Classifiers

The scikit-learn library provides an implementation of ECOC via the OutputCodeClassifier class.

The class takes as an argument the model to use to fit each binary classifier, and any machine learning model can be used. In this case, we will use a logistic regression model, intended for binary classification.

The class also provides the “code_size” argument that specifies the size of the encoding for the classes as a multiple of the number of classes, e.g. the number of bits to encode for each class label.

For example, if we wanted an encoding with bit strings with a length of 6 bits, and we had three classes, then we can specify the coding size as 2:

encoding_length = code_size * num_classes
encoding_length = 2 * 3
encoding_length = 6

The example below demonstrates how to define an example of the OutputCodeClassifier with 2 bits per class and using a LogisticRegression model for each bit in the encoding.

...
# define the binary classification model
model = LogisticRegression()
# define the ecoc model
ecoc = OutputCodeClassifier(model, code_size=2, random_state=1)

...

# define the binary classification model

model = LogisticRegression()

# define the ecoc model

ecoc = OutputCodeClassifier(model, code_size=2, random_state=1)

Although there are many sophisticated ways to construct the encoding for each class, the OutputCodeClassifier class selects a random bit string encoding for each class, at least at the time of writing.

We can explore the use of the OutputCodeClassifier on a synthetic multi-class classification problem.

We can use the make_classification() function to define a multi-class classification problem with 1,000 examples, 20 input features, and three classes.

The example below demonstrates how to create the dataset and summarize the number of rows, columns, and classes in the dataset.

# multi-class classification dataset
from collections import Counter
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)
# summarize the dataset
print(X.shape, y.shape)
# summarize the number of classes
print(Counter(y))

# multi-class classification dataset

from collections import Counter

from sklearn.datasets import make_classification

# define dataset

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)

# summarize the dataset

print(X.shape, y.shape)

# summarize the number of classes

print(Counter(y))

Running the example creates the dataset and reports the number of rows and columns, confirming the dataset was created as expected.

The number of examples in each class is then reported, showing a nearly equal number of cases for each of the three configured classes.

(1000, 20) (1000,)
Counter({2: 335, 1: 333, 0: 332})

1 2	(1000, 20) (1000,) Counter({2: 335, 1: 333, 0: 332})

Next, we can evaluate an error-correcting output codes model on the dataset.

We will use a logistic regression with 2 bits per class as we defined above. The model will then be evaluated using repeated stratified k-fold cross-validation with three repeats and 10 folds. We will summarize the performance of the model using the mean and and standard deviation of classification accuracy across all repeats and folds.

...
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model and collect the scores
n_scores = cross_val_score(ecoc, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# summarize the performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

...

# define the evaluation procedure

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

# evaluate the model and collect the scores

n_scores = cross_val_score(ecoc, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

# summarize the performance

print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

Tying this together, the complete example is listed below.

# evaluate error-correcting output codes for multi-class classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OutputCodeClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)
# define the binary classification model
model = LogisticRegression()
# define the ecoc model
ecoc = OutputCodeClassifier(model, code_size=2, random_state=1)
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model and collect the scores
n_scores = cross_val_score(ecoc, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# summarize the performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

# evaluate error-correcting output codes for multi-class classification

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.multiclass import OutputCodeClassifier

# define dataset

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)

# define the binary classification model

model = LogisticRegression()

# define the ecoc model

ecoc = OutputCodeClassifier(model, code_size=2, random_state=1)

# define the evaluation procedure

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

# evaluate the model and collect the scores

n_scores = cross_val_score(ecoc, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

# summarize the performance

print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

Running the example defines the model and evaluates it on our synthetic multi-class classification dataset using the defined test procedure.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

In this case, we can see that the model achieved a mean classification accuracy of about 76.6 percent.

Accuracy: 0.766 (0.037)

1	Accuracy: 0.766 (0.037)

We may choose to use this as our final model.

This requires that we fit the model on all available data and use it to make predictions on new data.

The example below provides a full example of how to fit and use an error-correcting output model as a final model.

# use error-correcting output codes model as a final model and make a prediction
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OutputCodeClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)
# define the binary classification model
model = LogisticRegression()
# define the ecoc model
ecoc = OutputCodeClassifier(model, code_size=2, random_state=1)
# fit the model on the whole dataset
ecoc.fit(X, y)
# make a single prediction
row = [[0.04339387, 2.75542632, -3.79522705, -0.71310994, -3.08888853, -1.2963487, -1.92065166, -3.15609907, 1.37532356, 3.61293237, 1.00353523, -3.77126962, 2.26638828, -10.22368666, -0.35137382, 1.84443763, 3.7040748, 2.50964286, 2.18839505, -2.31211692]]
yhat = ecoc.predict(row)
print('Predicted Class: %d' % yhat[0])

# use error-correcting output codes model as a final model and make a prediction

from sklearn.datasets import make_classification

from sklearn.linear_model import LogisticRegression

from sklearn.multiclass import OutputCodeClassifier

# define dataset

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)

# define the binary classification model

model = LogisticRegression()

# define the ecoc model

ecoc = OutputCodeClassifier(model, code_size=2, random_state=1)

# fit the model on the whole dataset

ecoc.fit(X, y)

# make a single prediction

row = [[0.04339387, 2.75542632, -3.79522705, -0.71310994, -3.08888853, -1.2963487, -1.92065166, -3.15609907, 1.37532356, 3.61293237, 1.00353523, -3.77126962, 2.26638828, -10.22368666, -0.35137382, 1.84443763, 3.7040748, 2.50964286, 2.18839505, -2.31211692]]

yhat = ecoc.predict(row)

print('Predicted Class: %d' % yhat[0])

Running the example fits the ECOC model on the entire dataset and uses the model to predict the class label for a single row of data.

In this case, we can see that the model predicted the class label 0.

Predicted Class: 0

1	Predicted Class: 0

Now that we are familiar with how to fit and use the ECOC model, let’s take a closer look at how to configure it.

Tune Number of Bits Per Class

The key hyperparameter for the ECOC model is the encoding of class labels.

This includes properties such as:

The choice of representation (bits, real numbers, etc.)
The encoding of each class label (random, etc.)
The length of representation (number of bits, etc.)
How predictions are mapped to classes (distance, etc.)

The OutputCodeClassifier scikit-learn implementation does not currently provide a lot of control over these elements.

The element it does give control over is the number of bits used to encode each class label.

In this section, we can perform a manual grid search across different numbers of bits per class label and compare the results. This provides a template that you can adapt and use on your own project.

First, we can define a function to create and return the dataset.

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)
	return X, y

# get the dataset

def get_dataset():

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)

return X, y

We can then define a function that will create a collection of models to evaluate.

Each model will be an example of the OutputCodeClassifier using a LogisticRegression for each binary classification problem. We will configure the code_size of each model to be different, with values ranging from 1 to 20.

# get a list of models to evaluate
def get_models():
	models = dict()
	for i in range(1,21):
		# create model
		model = LogisticRegression()
		# create error correcting output code classifier
		models[str(i)] = OutputCodeClassifier(model, code_size=i, random_state=1)
	return models

# get a list of models to evaluate

def get_models():

models = dict()

for i in range(1,21):

# create model

model = LogisticRegression()

# create error correcting output code classifier

models[str(i)] = OutputCodeClassifier(model, code_size=i, random_state=1)

return models

We can evaluate each model using related k-fold cross-validation as we did in the previous section to give a sample of classification accuracy scores.

# evaluate a give model using cross-validation
def evaluate_model(model):
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# evaluate a give model using cross-validation

def evaluate_model(model):

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

return scores

We can report the mean and standard deviation of the scores for each configuration and plot the distributions as box and whisker plots side by side to visually compare the results.

...
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	scores = evaluate_model(model)
	results.append(scores)
	names.append(name)
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

...

# evaluate the models and store results

results, names = list(), list()

for name, model in models.items():

scores = evaluate_model(model)

results.append(scores)

names.append(name)

print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))

# plot model performance for comparison

pyplot.boxplot(results, labels=names, showmeans=True)

pyplot.show()

Tying this all together, the complete example of comparing ECOC classification with a grid of the number of bits per class is listed below.

# compare the number of bits per class for error-correcting output code classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OutputCodeClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	for i in range(1,21):
		# create model
		model = LogisticRegression()
		# create error correcting output code classifier
		models[str(i)] = OutputCodeClassifier(model, code_size=i, random_state=1)
	return models

# evaluate a give model using cross-validation
def evaluate_model(model):
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	scores = evaluate_model(model)
	results.append(scores)
	names.append(name)
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

# compare the number of bits per class for error-correcting output code classification

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.multiclass import OutputCodeClassifier

from matplotlib import pyplot

# get the dataset

def get_dataset():

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)

return X, y

# get a list of models to evaluate

def get_models():

models = dict()

for i in range(1,21):

# create model

model = LogisticRegression()

# create error correcting output code classifier

models[str(i)] = OutputCodeClassifier(model, code_size=i, random_state=1)

return models

# evaluate a give model using cross-validation

def evaluate_model(model):

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

return scores

# define dataset

X, y = get_dataset()

# get the models to evaluate

models = get_models()

# evaluate the models and store results

results, names = list(), list()

for name, model in models.items():

scores = evaluate_model(model)

results.append(scores)

names.append(name)

print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))

# plot model performance for comparison

pyplot.boxplot(results, labels=names, showmeans=True)

pyplot.show()

Running the example first evaluates each model configuration and reports the mean and standard deviation of the accuracy scores.

In this case, we can see that perhaps 5 or 6 bits per class results in the best performance with reported mean accuracy scores of about 78.2 percent and 78.0 percent respectively. We also see good results for 9, 13, 17, and 20 bits per class, with perhaps 17 bits per class giving the best result of about 78.5 percent.

>1 0.545 (0.032)
>2 0.766 (0.037)
>3 0.776 (0.036)
>4 0.769 (0.035)
>5 0.782 (0.037)
>6 0.780 (0.037)
>7 0.776 (0.039)
>8 0.775 (0.036)
>9 0.782 (0.038)
>10 0.779 (0.036)
>11 0.770 (0.033)
>12 0.777 (0.037)
>13 0.781 (0.037)
>14 0.779 (0.039)
>15 0.771 (0.033)
>16 0.769 (0.035)
>17 0.785 (0.034)
>18 0.776 (0.038)
>19 0.776 (0.034)
>20 0.780 (0.038)

>1 0.545 (0.032)

>2 0.766 (0.037)

>3 0.776 (0.036)

>4 0.769 (0.035)

>5 0.782 (0.037)

>6 0.780 (0.037)

>7 0.776 (0.039)

>8 0.775 (0.036)

>9 0.782 (0.038)

>10 0.779 (0.036)

>11 0.770 (0.033)

>12 0.777 (0.037)

>13 0.781 (0.037)

>14 0.779 (0.039)

>15 0.771 (0.033)

>16 0.769 (0.035)

>17 0.785 (0.034)

>18 0.776 (0.038)

>19 0.776 (0.034)

>20 0.780 (0.038)

A figure is created showing the box and whisker plots for the accuracy scores for each model configuration.

We can see that besides a value of 1, the number of bits per class delivers similar results in terms of spread and mean accuracy scores that cluster around 77 percent. This suggests that the approach is reasonably stable across configurations.

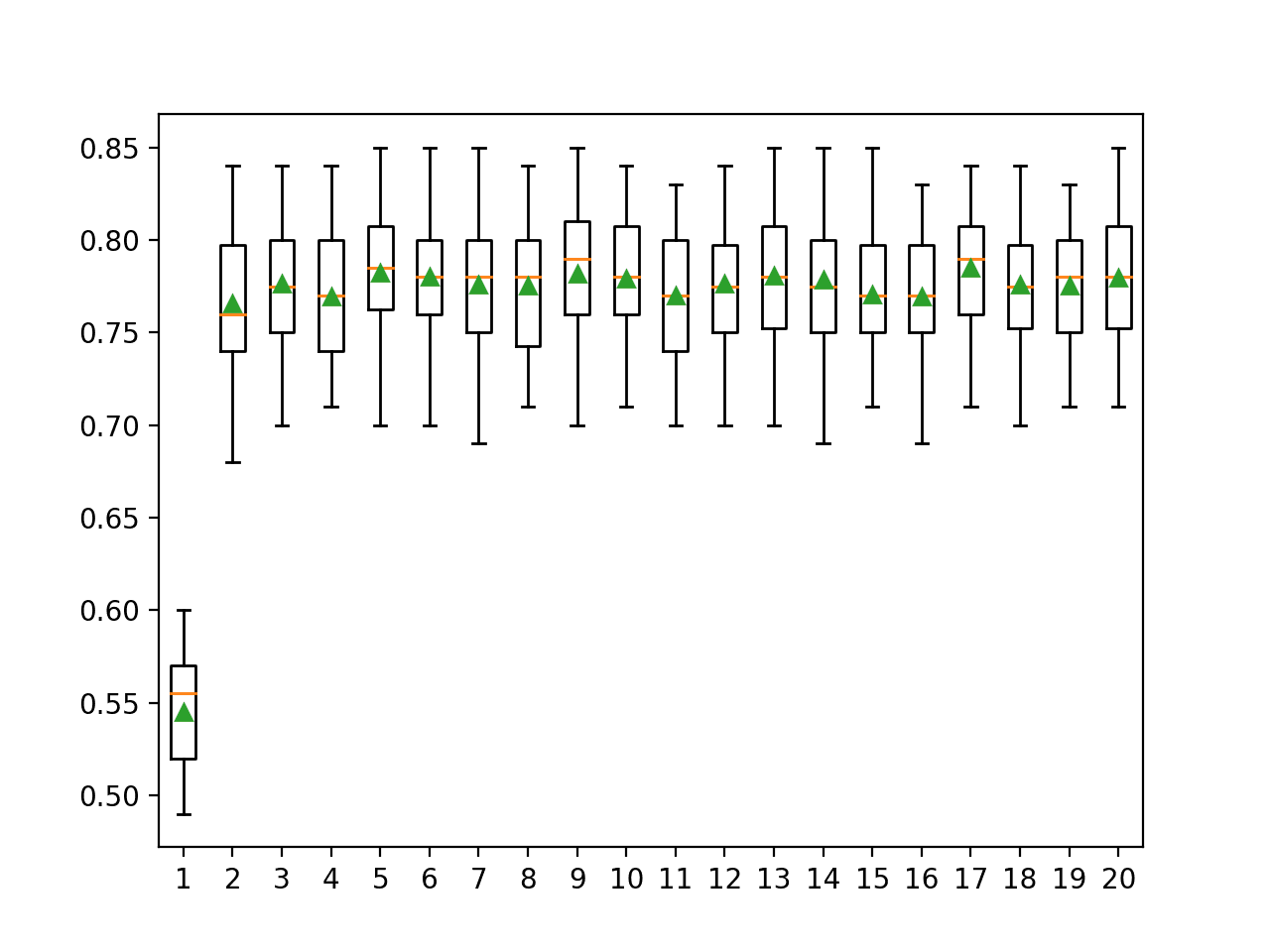
Box and Whisker Plots of Bits Per Class vs. Distribution of Classification Accuracy for ECOC

Summary

In this tutorial, you discovered how to use error-correcting output codes for classification.

Specifically, you learned:

Error-correcting output codes is a technique for using binary classification models on multi-class classification prediction tasks.
How to fit, evaluate, and use error-correcting output codes classification models to make predictions.
How to tune and evaluate different values for the number of bits per class hyperparameter used by error-correcting output codes.

Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

4 Responses to Error-Correcting Output Codes (ECOC) for Machine Learning

Anthony The Koala December 16, 2020 at 1:09 pm #

Dear Dr Jason,
Two questions please, one on meaning of error and other correcting codes.
(1) Where is the correction being performed.
(2) is the tutorial’s concept of ECOC related to error correcting codes? That is there is a signal made of 0s and1s consisting of data and error correcting information. The signal is subject to noise and the receiver decodes the correct data using the error correcting information.
That is, is the ECOC the same as error correcting systems where a digital signal is subject to noise and the most likely data is decoded using the error correcting information in the data stream?
Thank you,
Anthony of Sydney

- Jason Brownlee December 16, 2020 at 1:43 pm #
  
  The overdetermined representation acts like an error correcting code. Like error-correcting bits. Perhaps re-read section 1 “Error-Correcting Output Codes”.
  
  No, it is not the same as error correcting code, it is inspired by the technique.
  
Neda July 5, 2023 at 4:45 am #

Dear Dr. Jason,
First,I want to thank you for this article. It really helped me.

I have one question:
if I want to tune other parameters other than “code_size”, what should I do?

- James Carmichael July 5, 2023 at 7:22 am #
  
  Hi Neda…You may find the concept of hyperparameter optimization beneficial:
  
  https://machinelearningmastery.com/combined-algorithm-selection-and-hyperparameter-optimization/

Navigation

Error-Correcting Output Codes (ECOC) for Machine Learning

Tutorial Overview

Error-Correcting Output Codes

Want to Get Started With Ensemble Learning?

Evaluate and Use ECOC Classifiers

Tune Number of Bits Per Class

Further Reading

Related Tutorials

Papers

Books

APIs

Summary

Get a Handle on Modern Ensemble Learning!

Improve Your Predictions in Minutes

Bring Modern Ensemble Learning Techniques to
Your Machine Learning Projects

More On This Topic

4 Responses to Error-Correcting Output Codes (ECOC) for Machine Learning

Leave a Reply Click here to cancel reply.

Navigation

Tutorial Overview

Error-Correcting Output Codes

Want to Get Started With Ensemble Learning?

Evaluate and Use ECOC Classifiers

Tune Number of Bits Per Class

Further Reading

Related Tutorials

Papers

Books

APIs

Summary

Get a Handle on Modern Ensemble Learning!

Improve Your Predictions in Minutes

Bring Modern Ensemble Learning Techniques to Your Machine Learning Projects

More On This Topic

4 Responses to Error-Correcting Output Codes (ECOC) for Machine Learning

Leave a Reply Click here to cancel reply.

Bring Modern Ensemble Learning Techniques to
Your Machine Learning Projects