Bagging is an ensemble machine learning algorithm that combines the predictions from many decision trees.
It is also easy to implement given that it has few key hyperparameters and sensible heuristics for configuring these hyperparameters.
Bagging performs well in general and provides the basis for a whole field of ensemble of decision tree algorithms such as the popular random forest and extra trees ensemble algorithms, as well as the lesser-known Pasting, Random Subspaces, and Random Patches ensemble algorithms.
In this tutorial, you will discover how to develop Bagging ensembles for classification and regression.
After completing this tutorial, you will know:
Bagging ensemble is an ensemble created from decision trees fit on different samples of a dataset.
How to use the Bagging ensemble for classification and regression with scikit-learn.
How to explore the effect of Bagging model hyperparameters on model performance.
Kick-start your project with my new book Ensemble Learning Algorithms With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
Update Aug/2020: Added a common questions section.
How to Develop a Bagging Ensemble in Python Photo by daveynin, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
Bagging Ensemble Algorithm
Bagging Scikit-Learn API
Bagging for Classification
Bagging for Regression
Bagging Hyperparameters
Explore Number of Trees
Explore Number of Samples
Explore Alternate Algorithm
Bagging Extensions
Pasting Ensemble
Random Subspaces Ensemble
Random Patches Ensemble
Common Questions
Bagging Ensemble Algorithm
Bootstrap Aggregation, or Bagging for short, is an ensemble machine learning algorithm.
Specifically, it is an ensemble of decision tree models, although the bagging technique can also be used to combine the predictions of other types of models.
As its name suggests, bootstrap aggregation is based on the idea of the “bootstrap” sample.
A bootstrap sample is a sample of a dataset with replacement. Replacement means that a sample drawn from the dataset is replaced, allowing it to be selected again and perhaps multiple times in the new sample. This means that the sample may have duplicate examples from the original dataset.
The bootstrap sampling technique is used to estimate a population statistic from a small data sample. This is achieved by drawing multiple bootstrap samples, calculating the statistic on each, and reporting the mean statistic across all samples.
An example of using bootstrap sampling would be estimating the population mean from a small dataset. Multiple bootstrap samples are drawn from the dataset, the mean calculated on each, then the mean of the estimated means is reported as an estimate of the population.
Surprisingly, the bootstrap method provides a robust and accurate approach to estimating statistical quantities compared to a single estimate on the original dataset.
This same approach can be used to create an ensemble of decision tree models.
This is achieved by drawing multiple bootstrap samples from the training dataset and fitting a decision tree on each. The predictions from the decision trees are then combined to provide a more robust and accurate prediction than a single decision tree (typically, but not always).
Bagging predictors is a method for generating multiple versions of a predictor and using these to get an aggregated predictor. […] The multiple versions are formed by making bootstrap replicates of the learning set and using these as new learning sets
Predictions are made for regression problems by averaging the prediction across the decision trees. Predictions are made for classification problems by taking the majority vote prediction for the classes from across the predictions made by the decision trees.
The bagged decision trees are effective because each decision tree is fit on a slightly different training dataset, which in turn allows each tree to have minor differences and make slightly different skillful predictions.
Technically, we say that the method is effective because the trees have a low correlation between predictions and, in turn, prediction errors.
Decision trees, specifically unpruned decision trees, are used as they slightly overfit the training data and have a high variance. Other high-variance machine learning algorithms can be used, such as a k-nearest neighbors algorithm with a low k value, although decision trees have proven to be the most effective.
If perturbing the learning set can cause significant changes in the predictor constructed, then bagging can improve accuracy.
Bagging does not always offer an improvement. For low-variance models that already perform well, bagging can result in a decrease in model performance.
The evidence, both experimental and theoretical, is that bagging can push a good but unstable procedure a significant step towards optimality. On the other hand, it can slightly degrade the performance of stable procedures.
Both models operate the same way and take the same arguments that influence how the decision trees are created.
Randomness is used in the construction of the model. This means that each time the algorithm is run on the same data, it will produce a slightly different model.
When using machine learning algorithms that have a stochastic learning algorithm, it is good practice to evaluate them by averaging their performance across multiple runs or repeats of cross-validation. When fitting a final model, it may be desirable to either increase the number of trees until the variance of the model is reduced across repeated evaluations, or to fit multiple final models and average their predictions.
Let’s take a look at how to develop a Bagging ensemble for both classification and regression.
Bagging for Classification
In this section, we will look at using Bagging for a classification problem.
First, we can use the make_classification() function to create a synthetic binary classification problem with 1,000 examples and 20 input features.
Running the example creates the dataset and summarizes the shape of the input and output components.
1
(1000, 20) (1000,)
Next, we can evaluate a Bagging algorithm on this dataset.
We will evaluate the model using repeated stratified k-fold cross-validation, with three repeats and 10 folds. We will report the mean and standard deviation of the accuracy of the model across all repeats and folds.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# evaluate bagging algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the Bagging ensemble with default hyperparameters achieves a classification accuracy of about 85 percent on this test dataset.
1
Accuracy: 0.856 (0.037)
We can also use the Bagging model as a final model and make predictions for classification.
First, the Bagging ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our binary classification dataset.
1
2
3
4
5
6
7
8
9
10
11
12
13
# make predictions using bagging for classification
Running the example fits the Bagging ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
1
Predicted Class: 1
Now that we are familiar with using Bagging for classification, let’s look at the API for regression.
Bagging for Regression
In this section, we will look at using Bagging for a regression problem.
First, we can use the make_regression() function to create a synthetic regression problem with 1,000 examples and 20 input features.
Running the example creates the dataset and summarizes the shape of the input and output components.
1
(1000, 20) (1000,)
Next, we can evaluate a Bagging algorithm on this dataset.
As we did with the last section, we will evaluate the model using repeated k-fold cross-validation, with three repeats and 10 folds. We will report the mean absolute error (MAE) of the model across all repeats and folds. The scikit-learn library makes the MAE negative so that it is maximized instead of minimized. This means that larger negative MAE are better and a perfect model has a MAE of 0.
The complete example is listed below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# evaluate bagging ensemble for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the Bagging ensemble with default hyperparameters achieves a MAE of about 100.
1
MAE: -101.133 (9.757)
We can also use the Bagging model as a final model and make predictions for regression.
First, the Bagging ensemble is fit on all available data, then the predict() function can be called to make predictions on new data.
The example below demonstrates this on our regression dataset.
1
2
3
4
5
6
7
8
9
10
11
12
13
# bagging ensemble for making predictions for regression
Running the example fits the Bagging ensemble model on the entire dataset and is then used to make a prediction on a new row of data, as we might when using the model in an application.
1
Prediction: -134
Now that we are familiar with using the scikit-learn API to evaluate and use Bagging ensembles, let’s look at configuring the model.
Bagging Hyperparameters
In this section, we will take a closer look at some of the hyperparameters you should consider tuning for the Bagging ensemble and their effect on model performance.
Explore Number of Trees
An important hyperparameter for the Bagging algorithm is the number of decision trees used in the ensemble.
Typically, the number of trees is increased until the model performance stabilizes. Intuition might suggest that more trees will lead to overfitting, although this is not the case. Bagging and related ensemble of decision trees algorithms (like random forest) appear to be somewhat immune to overfitting the training dataset given the stochastic nature of the learning algorithm.
The number of trees can be set via the “n_estimators” argument and defaults to 100.
The example below explores the effect of the number of trees with values between 10 to 5,000.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# explore bagging ensemble number of trees effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example first reports the mean accuracy for each configured number of decision trees.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that that performance improves on this dataset until about 100 trees and remains flat after that.
1
2
3
4
5
6
>10 0.855 (0.037)
>50 0.876 (0.035)
>100 0.882 (0.037)
>500 0.885 (0.041)
>1000 0.885 (0.037)
>5000 0.885 (0.038)
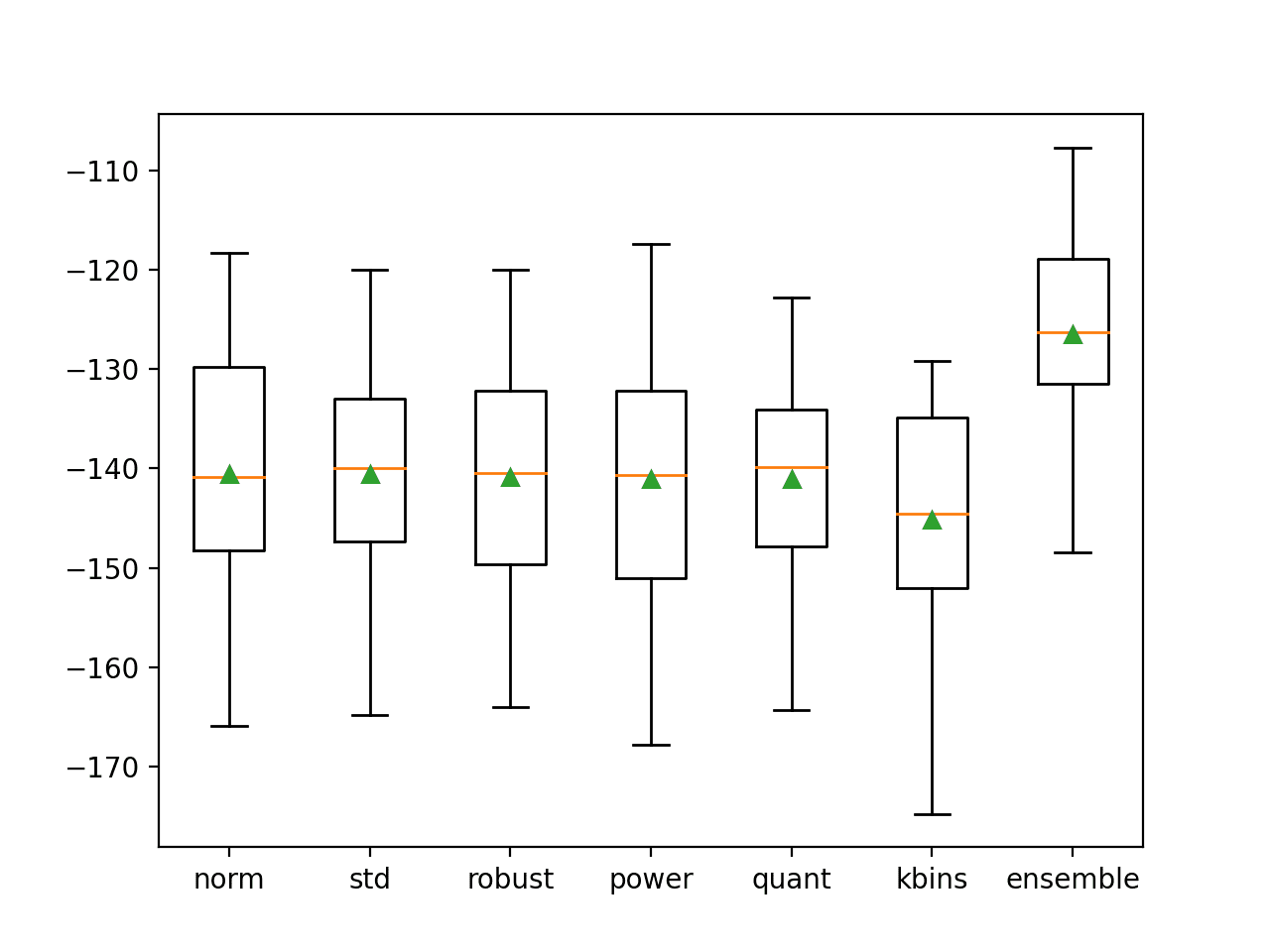
A box and whisker plot is created for the distribution of accuracy scores for each configured number of trees.
We can see the general trend of no further improvement beyond about 100 trees.
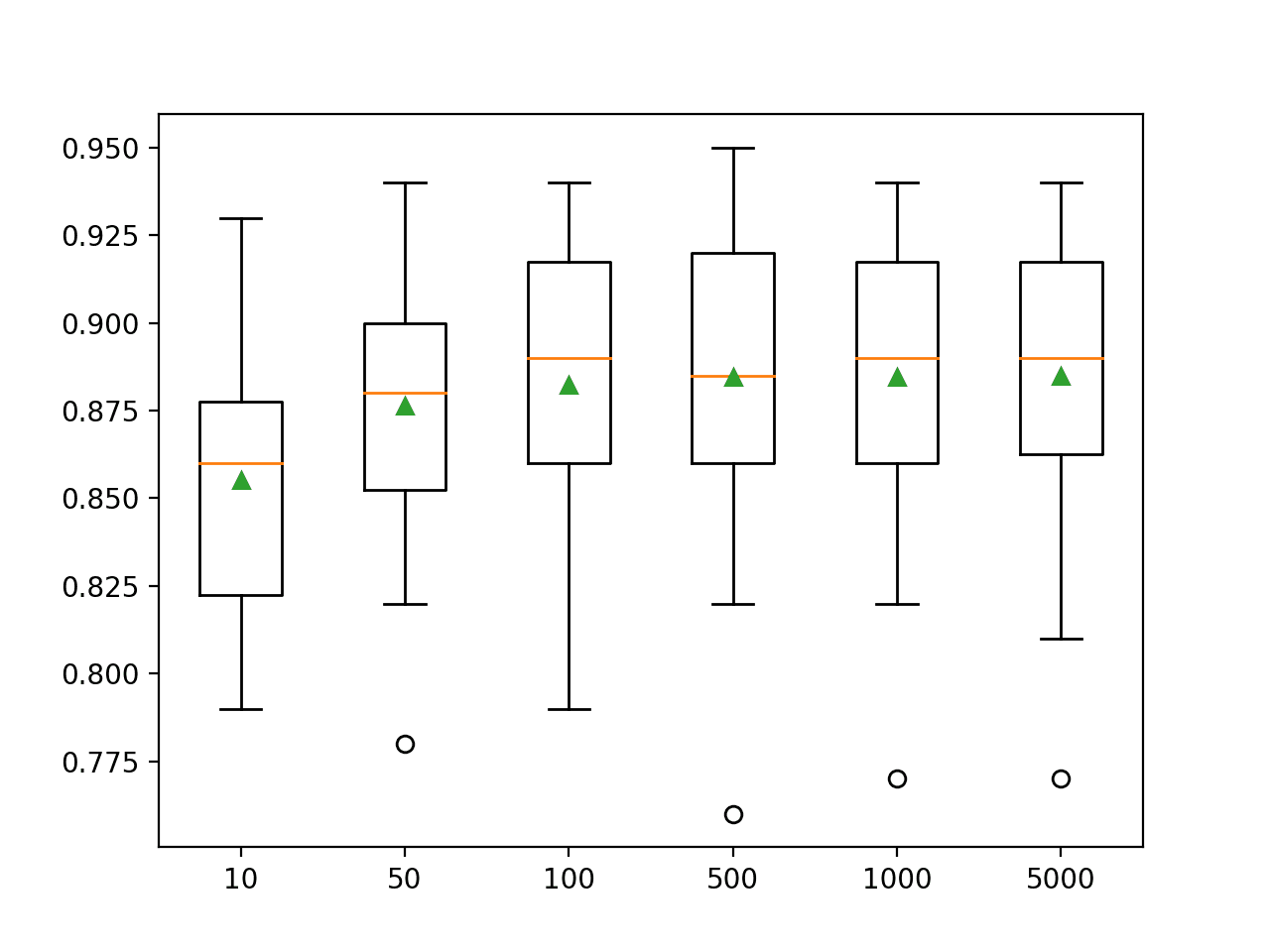
Box Plot of Bagging Ensemble Size vs. Classification Accuracy
Explore Number of Samples
The size of the bootstrap sample can also be varied.
The default is to create a bootstrap sample that has the same number of examples as the original dataset. Using a smaller dataset can increase the variance of the resulting decision trees and could result in better overall performance.
The number of samples used to fit each decision tree is set via the “max_samples” argument.
The example below explores different sized samples as a ratio of the original dataset from 10 percent to 100 percent (the default).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# explore bagging ensemble number of samples effect on performance
from numpy import mean
from numpy import std
from numpy import arange
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example first reports the mean accuracy for each sample set size.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, the results suggest that performance generally improves with an increase in the sample size, highlighting that the default of 100 percent the size of the training dataset is sensible.
It might also be interesting to explore a smaller sample size with a corresponding increase in the number of trees in an effort to reduce the variance of the individual models.
1
2
3
4
5
6
7
8
9
10
>0.1 0.810 (0.036)
>0.2 0.836 (0.044)
>0.3 0.844 (0.043)
>0.4 0.843 (0.041)
>0.5 0.852 (0.034)
>0.6 0.855 (0.042)
>0.7 0.858 (0.042)
>0.8 0.861 (0.033)
>0.9 0.866 (0.041)
>1.0 0.864 (0.042)
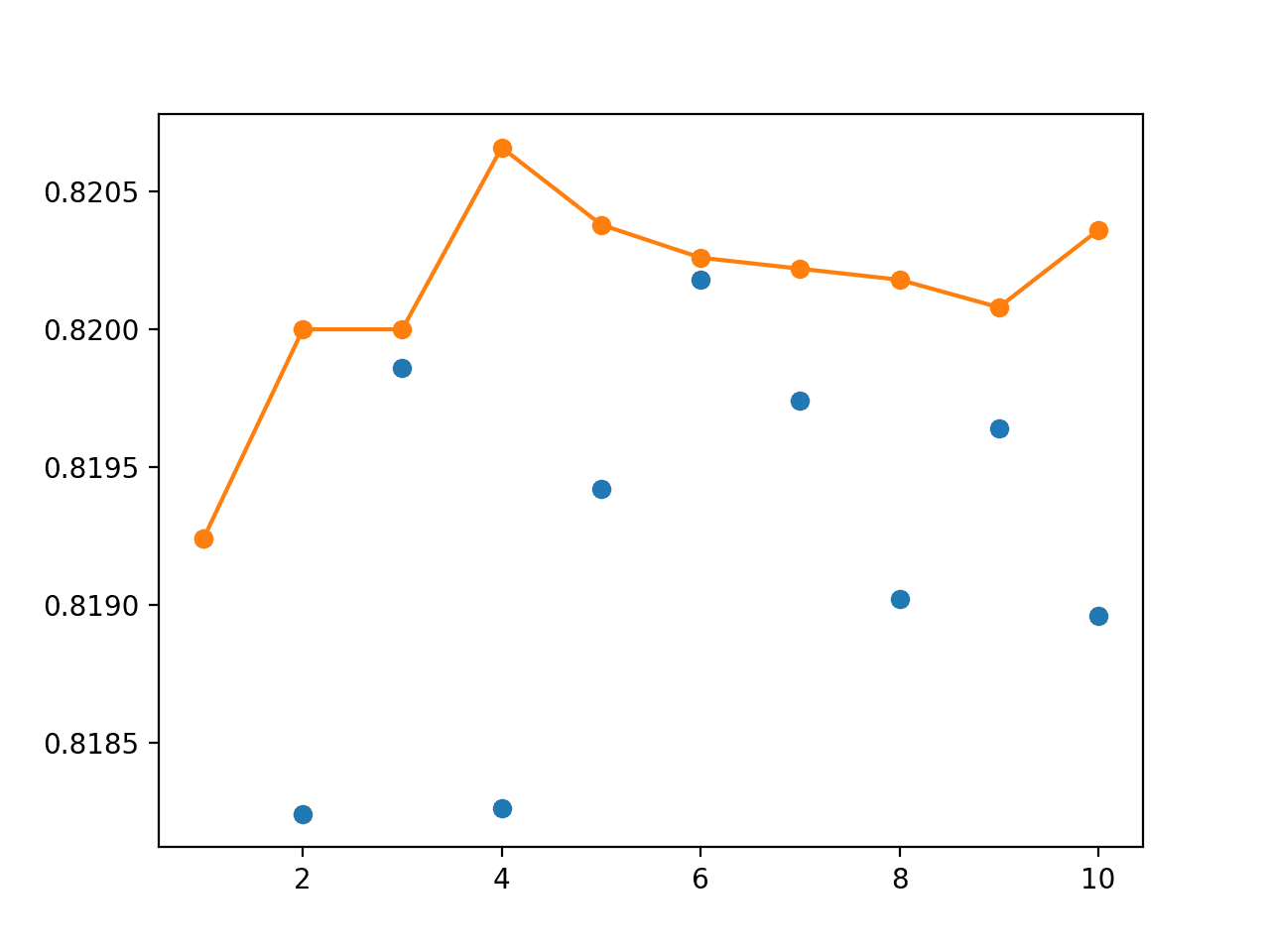
A box and whisker plot is created for the distribution of accuracy scores for each sample size.
We see a general trend of increasing accuracy with sample size.
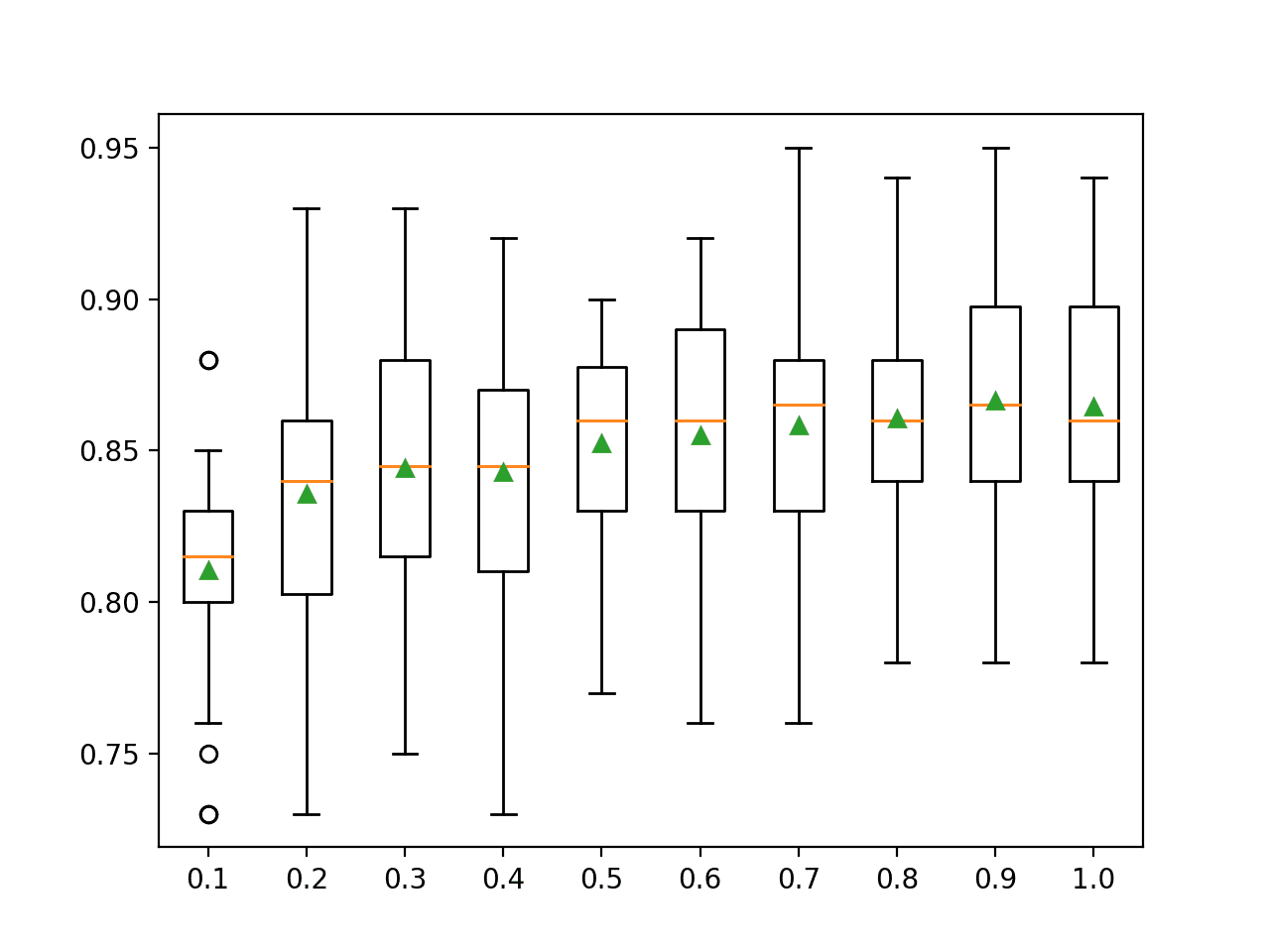
Box Plot of Bagging Sample Size vs. Classification Accuracy
Explore Alternate Algorithm
Decision trees are the most common algorithm used in a bagging ensemble.
The reason for this is that they are easy to configure to have a high variance and because they perform well in general.
Other algorithms can be used with bagging and must be configured to have a modestly high variance. One example is the k-nearest neighbors algorithm where the k value can be set to a low value.
The algorithm used in the ensemble is specified via the “base_estimator” argument and must be set to an instance of the algorithm and algorithm configuration to use.
The example below demonstrates using a KNeighborsClassifier as the base algorithm used in the bagging ensemble. Here, the algorithm is used with default hyperparameters where k is set to 5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# evaluate bagging with knn algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the Bagging ensemble with KNN and default hyperparameters achieves a classification accuracy of about 88 percent on this test dataset.
1
Accuracy: 0.888 (0.036)
We can test different values of k to find the right balance of model variance to achieve good performance as a bagged ensemble.
The below example tests bagged KNN models with k values between 1 and 20.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# explore bagging ensemble k for knn effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
Running the example first reports the mean accuracy for each k value.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, the results suggest a small k value such as two to four results in the best mean accuracy when used in a bagging ensemble.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
>1 0.884 (0.025)
>2 0.890 (0.029)
>3 0.886 (0.035)
>4 0.887 (0.033)
>5 0.878 (0.037)
>6 0.879 (0.042)
>7 0.877 (0.037)
>8 0.877 (0.036)
>9 0.871 (0.034)
>10 0.877 (0.033)
>11 0.876 (0.037)
>12 0.877 (0.030)
>13 0.874 (0.034)
>14 0.871 (0.039)
>15 0.875 (0.034)
>16 0.877 (0.033)
>17 0.872 (0.034)
>18 0.873 (0.036)
>19 0.876 (0.034)
>20 0.876 (0.037)
A box and whisker plot is created for the distribution of accuracy scores for each k value.
We see a general trend of increasing accuracy with sample size in the beginning, then a modest decrease in performance as the variance of the individual KNN models used in the ensemble is increased with larger k values.
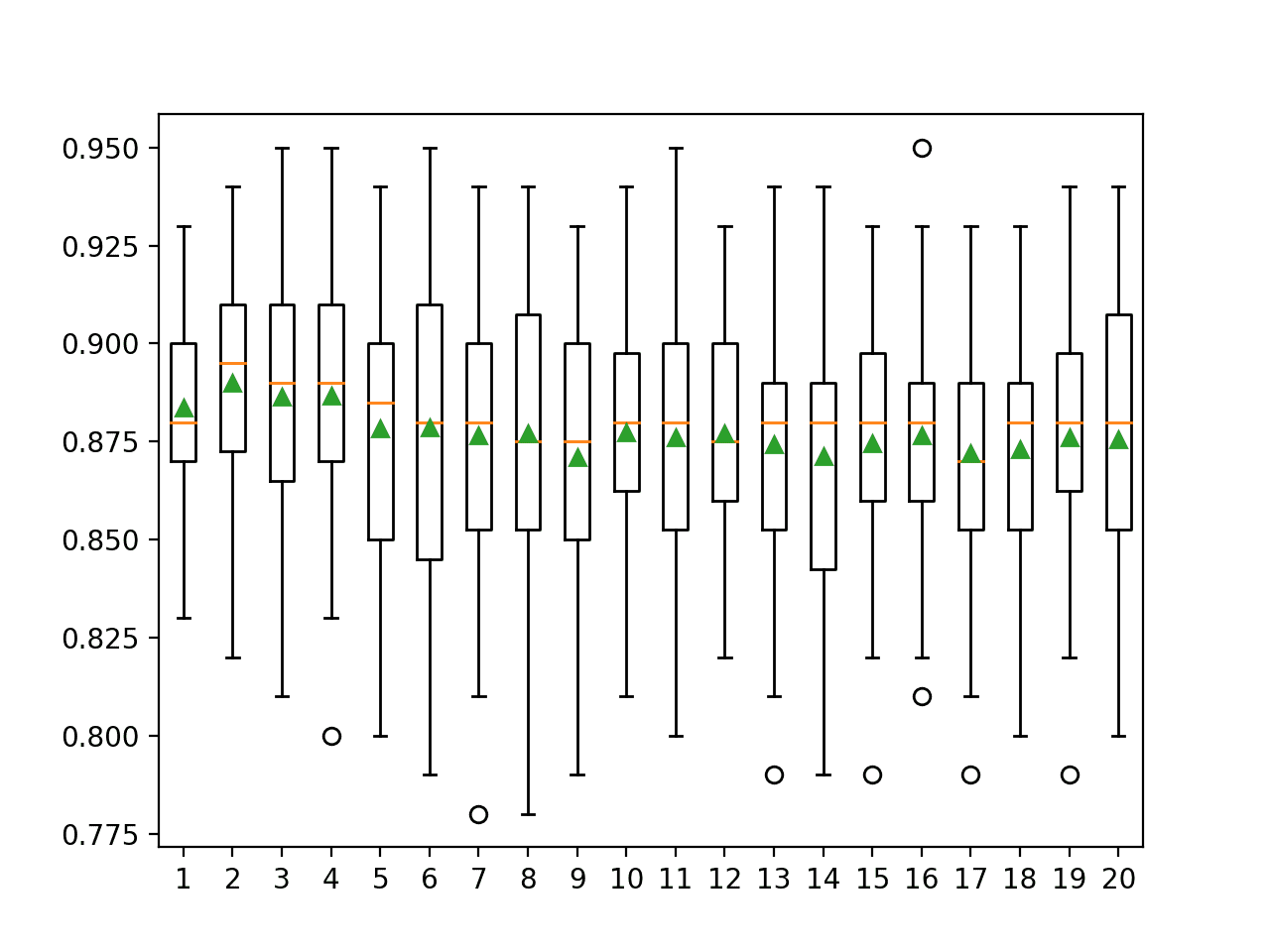
Box Plot of Bagging KNN Number of Neighbors vs. Classification Accuracy
Bagging Extensions
There are many modifications and extensions to the bagging algorithm in an effort to improve the performance of the approach.
There is a number of less famous, although still effective, extensions to bagging that may be interesting to investigate.
This section demonstrates some of these approaches, such as pasting ensemble, random subspace ensemble, and the random patches ensemble.
We are not racing these extensions on the dataset, but rather providing working examples of how to use each technique that you can copy-paste and try with your own dataset.
Pasting Ensemble
The Pasting Ensemble is an extension to bagging that involves fitting ensemble members based on random samples of the training dataset instead of bootstrap samples.
The approach is designed to use smaller sample sizes than the training dataset in cases where the training dataset does not fit into memory.
The procedure takes small pieces of the data, grows a predictor on each small piece and then pastes these predictors together. A version is given that scales up to terabyte data sets. The methods are also applicable to on-line learning.
The example below demonstrates the Pasting ensemble by setting the “bootstrap” argument to “False” and setting the number of samples used in the training dataset via “max_samples” to a modest value, in this case, 50 percent of the training dataset size.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# evaluate pasting ensemble algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the Pasting ensemble achieves a classification accuracy of about 84 percent on this dataset.
1
Accuracy: 0.848 (0.039)
Random Subspaces Ensemble
A Random Subspace Ensemble is an extension to bagging that involves fitting ensemble members based on datasets constructed from random subsets of the features in the training dataset.
It is similar to the random forest except the data samples are random rather than a bootstrap sample and the subset of features is selected for the entire decision tree rather than at each split point in the tree.
The classifier consists of multiple trees constructed systematically by pseudorandomly selecting subsets of components of the feature vector, that is, trees constructed in randomly chosen subspaces.
The example below demonstrates the Random Subspace ensemble by setting the “bootstrap” argument to “False” and setting the number of features used in the training dataset via “max_features” to a modest value, in this case, 10.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# evaluate random subspace ensemble algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the Random Subspace ensemble achieves a classification accuracy of about 86 percent on this dataset.
1
Accuracy: 0.862 (0.040)
We would expect that there would be a number of features in the random subspace that provides the right balance of model variance and model skill.
The example below demonstrates the effect of using different numbers of features in the random subspace ensemble from 1 to 20.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# explore random subspace ensemble ensemble number of features effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example first reports the mean accuracy for each number of features.
In this case, the results suggest that using about half the number of features in the dataset (e.g. between 9 and 13) might give the best results for the random subspace ensemble on this dataset.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
>1 0.583 (0.047)
>2 0.659 (0.048)
>3 0.731 (0.038)
>4 0.775 (0.045)
>5 0.815 (0.044)
>6 0.820 (0.040)
>7 0.838 (0.034)
>8 0.841 (0.035)
>9 0.854 (0.036)
>10 0.854 (0.041)
>11 0.857 (0.034)
>12 0.863 (0.035)
>13 0.860 (0.043)
>14 0.856 (0.038)
>15 0.848 (0.043)
>16 0.847 (0.042)
>17 0.839 (0.046)
>18 0.831 (0.044)
>19 0.811 (0.043)
>20 0.802 (0.048)
A box and whisker plot is created for the distribution of accuracy scores for each random subspace size.
We see a general trend of increasing accuracy with the number of features to about 10 to 13 where it is approximately level, then a modest decreasing trend in performance after that.
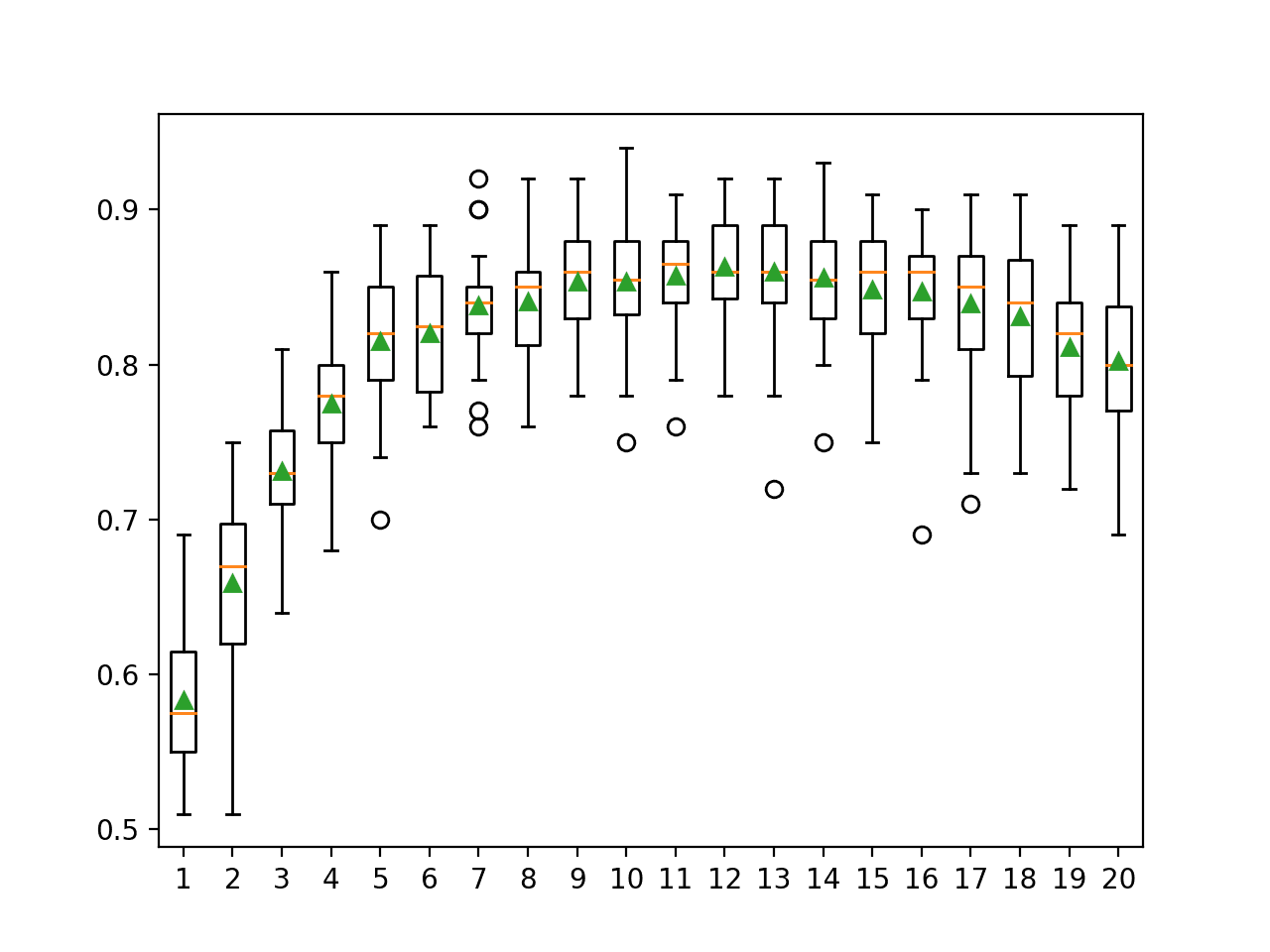
Box Plot of Random Subspace Ensemble Number of Features vs. Classification Accuracy
Random Patches Ensemble
The Random Patches Ensemble is an extension to bagging that involves fitting ensemble members based on datasets constructed from random subsets of rows (samples) and columns (features) of the training dataset.
It does not use bootstrap samples and might be considered an ensemble that combines both the random sampling of the dataset of the Pasting ensemble and the random sampling of features of the Random Subspace ensemble.
We investigate a very simple, yet effective, ensemble framework that builds each individual model of the ensemble from a random patch of data obtained by drawing random subsets of both instances and features from the whole dataset.
The example below demonstrates the Random Patches ensemble with decision trees created from a random sample of the training dataset limited to 50 percent of the size of the training dataset, and with a random subset of 10 features.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# evaluate random patches ensemble algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
Running the example reports the mean and standard deviation accuracy of the model.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see the Random Patches ensemble achieves a classification accuracy of about 84 percent on this dataset.
1
Accuracy: 0.845 (0.036)
Common Questions
In this section we will take a closer look at some common sticking points you may have with the bagging ensemble procedure.
Q. What algorithm should be used in the ensemble?
The algorithm should have a moderate variance, meaning it is moderately dependent upon the specific training data.
The decision tree is the default model to use because it works well in practice. Other algorithms can be used as long as they are configured to have a moderate variance.
The chosen algorithm should be moderately stable, not unstable like a decision stump and not very stable like a pruned decision tree, typically an unpruned decision tree is used.
… it is well known that Bagging should be used with unstable learners, and generally, the more unstable, the larger the performance improvement.
Thank you for the tutorials!!They are all valuable:))
Can I ask you, shouldn’t we take the fit method only in the train set? Why do you take it to all the dataset(X, y) ??
To clarify my understanding, you work with the train/test from the available data during the “ML evaluation phase.” Still, when considering to deploy the best algorithm (found in previous “phase”), you create a model trained with all available data and evaluate new/unseen examples a posteriori, right?
We use something like cross-validation to estimate the performance of each model/pipeline and choose one. Now we know how well it will perform on average on new data.
We then fit this model on all data and start using it. No need to evaluate it again.
Breiman in his article written about two kinds of pasting: Rvote and Ivote.
I assume that you implemented Ivote Pasting with bootstrap=False and ‘max_samples=0.5’
But how I can implement Rvote Pasting?
One can also use scores.mean() and scores.std() for calculating average and standard deviation of the scores without invoking numpy mean and std functions.
Thanks for the tutorial.
I tried to apply hyper parameter tuning for number of samples for regression problem, but I ran into this error:”Supported target types are: (‘binary’, ‘multiclass’). Got ‘continuous’ instead.”.
I don’t know why, I’m using randomforestregressor function, and when the code wants to evaluate model and take the models from the defined dic, this error comes up.
Would appreciate it if you could give me a heads up.
Yes, add “base_estimator=RandomForestClassifier()” to the BaggingClassier() call will make it. But this will be very slow as you are now having a lot of decision trees to fit.
Thank you for the tutorials!!They are all valuable:))
Can I ask you, shouldn’t we take the fit method only in the train set? Why do you take it to all the dataset(X, y) ??
You’re welcome.
Yes, models are only fit on the training dataset.
To clarify my understanding, you work with the train/test from the available data during the “ML evaluation phase.” Still, when considering to deploy the best algorithm (found in previous “phase”), you create a model trained with all available data and evaluate new/unseen examples a posteriori, right?
Not quite.
We use something like cross-validation to estimate the performance of each model/pipeline and choose one. Now we know how well it will perform on average on new data.
We then fit this model on all data and start using it. No need to evaluate it again.
Breiman in his article written about two kinds of pasting: Rvote and Ivote.
I assume that you implemented Ivote Pasting with
bootstrap=Falseand ‘max_samples=0.5’But how I can implement Rvote Pasting?
Perhaps you can adapt the above example for your needs.
Hi Jason,
One can also use scores.mean() and scores.std() for calculating average and standard deviation of the scores without invoking numpy mean and std functions.
Ron
Yes, I typically for get that. Thank you for the reminder!
Thanks for the tutorial.
I tried to apply hyper parameter tuning for number of samples for regression problem, but I ran into this error:”Supported target types are: (‘binary’, ‘multiclass’). Got ‘continuous’ instead.”.
I don’t know why, I’m using randomforestregressor function, and when the code wants to evaluate model and take the models from the defined dic, this error comes up.
Would appreciate it if you could give me a heads up.
Perhaps the above model does not support regression. I expect that this is the case.
Hi why is n_informative=15 and n_redundant=5? 🙂
These parameters are just an example. You may need to change it for your specific problem to solve.
can we use random forest as parameter for baggin classifier ?
Yes, add “base_estimator=RandomForestClassifier()” to the BaggingClassier() call will make it. But this will be very slow as you are now having a lot of decision trees to fit.
Don’t you need to scale your data to use KNN?
Yes, that would be better especially if each feature is in a different order of magnitude.