Building a Single Layer Neural Network in PyTorch

By Muhammad Asad Iqbal Khan on April 8, 2023 in Deep Learning with PyTorch 3

A neural network is a set of neuron nodes that are interconnected with one another. The neurons are not just connected to their adjacent neurons but also to the ones that are farther away.

The main idea behind neural networks is that every neuron in a layer has one or more input values, and they produce output values by applying some mathematical functions to the input. The outputs of the neurons in one layer become the inputs for the next layer.

A single layer neural network is a type of artificial neural network where there is only one hidden layer between the input and output layers. This is the classic architecture before the deep learning became popular. In this tutorial, you will get a chance to build a neural network with only a single hidden layer. Particularly, you will learn:

How to build a single layer neural network in PyTorch.
How to train a single layer neural network with PyTorch.
How to classify one-dimensional data using a single layer neural network.

Kick-start your project with my book Deep Learning with PyTorch. It provides self-study tutorials with working code.

Let’s get started.

Building a Single Layer Neural Network in PyTorch.
Picture by Tim Cheung. Some rights reserved.

Overview

This tutorial is in three parts; they are

- Preparing the Dataset
- Build the Model
- Train the Model

Preparing the Data

A neural network simply a function that approximates other functions with some parameters. Let’s build some data and see how our single layer neural network approximates the function to make the data linearly separable. Later in this tutorial, you will visualize the function during training to see how the approximated function overlaps over the given set of data points.

import torch
import matplotlib.pyplot as plt

# generate synthetic the data
X = torch.arange(-30, 30, 1).view(-1, 1).type(torch.FloatTensor)
Y = torch.zeros(X.shape[0])
Y[(X[:, 0] <= -10)] = 1.0
Y[(X[:, 0] > -10) & (X[:, 0] < 10)] = 0.5
Y[(X[:, 0] > 10)] = 0

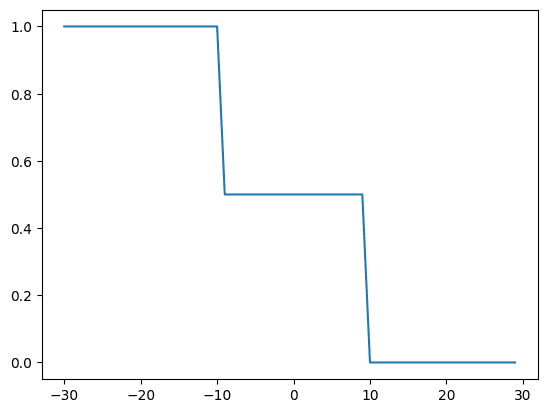
import torch

import matplotlib.pyplot as plt

# generate synthetic the data

X = torch.arange(-30, 30, 1).view(-1, 1).type(torch.FloatTensor)

Y = torch.zeros(X.shape[0])

Y[(X[:, 0] <= -10)] = 1.0

Y[(X[:, 0] > -10) & (X[:, 0] < 10)] = 0.5

Y[(X[:, 0] > 10)] = 0

The data, as plotted using matplotlib, looks like the following.

...
plt.plot(X, Y)
plt.show()

...

plt.plot(X, Y)

plt.show()

Want to Get Started With Deep Learning with PyTorch?

Take my free email crash course now (with sample code).

Click to sign-up and also get a free PDF Ebook version of the course.

Build the Model with `nn.Module`

Next, let’s build our custom module for single layer neural network with nn.Module. Please check previous tutorials of the series if you need more information on nn.Module.

This neural network features an input layer, a hidden layer with two neurons, and an output layer. After each layer, a sigmoid activation function is applied. Other kind of activation functions are available in PyTorch but the classic design for this network is to use sigmoid function.

Here is how your single layer neural network looks like in code.

...

# Define the class for single layer NN
class one_layer_net(torch.nn.Module):    
    # Constructor
    def __init__(self, input_size, hidden_neurons, output_size):
        super(one_layer_net, self).__init__()
        # hidden layer 
        self.linear_one = torch.nn.Linear(input_size, hidden_neurons)
        self.linear_two = torch.nn.Linear(hidden_neurons, output_size) 
        # defining layers as attributes
        self.layer_in = None
        self.act = None
        self.layer_out = None
    # prediction function
    def forward(self, x):
        self.layer_in = self.linear_one(x)
        self.act = torch.sigmoid(self.layer_in)
        self.layer_out = self.linear_two(self.act)
        y_pred = torch.sigmoid(self.linear_two(self.act))
        return y_pred

...

# Define the class for single layer NN

class one_layer_net(torch.nn.Module):

# Constructor

def __init__(self, input_size, hidden_neurons, output_size):

super(one_layer_net, self).__init__()

# hidden layer

self.linear_one = torch.nn.Linear(input_size, hidden_neurons)

self.linear_two = torch.nn.Linear(hidden_neurons, output_size)

# defining layers as attributes

self.layer_in = None

self.act = None

self.layer_out = None

# prediction function

def forward(self, x):

self.layer_in = self.linear_one(x)

self.act = torch.sigmoid(self.layer_in)

self.layer_out = self.linear_two(self.act)

y_pred = torch.sigmoid(self.linear_two(self.act))

return y_pred

Let’s also instantiate a model object.

# create the model 
model = one_layer_net(1, 2, 1)  # 2 represents two neurons in one hidden layer

1 2	# create the model model = one_layer_net(1, 2, 1) # 2 represents two neurons in one hidden layer

Train the Model

Before starting the training loop, let’s define loss function and optimizer for the model. You will write a loss function for the cross entropy loss and use stochastic gradient descent for parameter optimization.

def criterion(y_pred, y):
    out = -1 * torch.mean(y * torch.log(y_pred) + (1 - y) * torch.log(1 - y_pred))
    return out
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

def criterion(y_pred, y):

out = -1 * torch.mean(y * torch.log(y_pred) + (1 - y) * torch.log(1 - y_pred))

return out

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

Now you have all components to train the model. Let’s train the model for 5000 epochs. You will see a plot of how the neural network approximates the function after every 1000 epochs.

# Define the training loop
epochs=5000
cost = []
total=0
for epoch in range(epochs):
    total=0
    epoch = epoch + 1
    for x, y in zip(X, Y):
        yhat = model(x)
        loss = criterion(yhat, y)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        # get total loss 
        total+=loss.item() 
    cost.append(total)
    if epoch % 1000 == 0:
        print(str(epoch)+ " " + "epochs done!") # visualze results after every 1000 epochs   
        # plot the result of function approximator
        plt.plot(X.numpy(), model(X).detach().numpy())
        plt.plot(X.numpy(), Y.numpy(), 'm')
        plt.xlabel('x')
        plt.show()

# Define the training loop

epochs=5000

cost = []

total=0

for epoch in range(epochs):

total=0

epoch = epoch + 1

for x, y in zip(X, Y):

yhat = model(x)

loss = criterion(yhat, y)

loss.backward()

optimizer.step()

optimizer.zero_grad()

# get total loss

total+=loss.item()

cost.append(total)

if epoch % 1000 == 0:

print(str(epoch)+ " " + "epochs done!") # visualze results after every 1000 epochs

# plot the result of function approximator

plt.plot(X.numpy(), model(X).detach().numpy())

plt.plot(X.numpy(), Y.numpy(), 'm')

plt.xlabel('x')

plt.show()

After 1000 epochs, the model approximated the function like the following:

But after 5000 epochs, it improves to the following: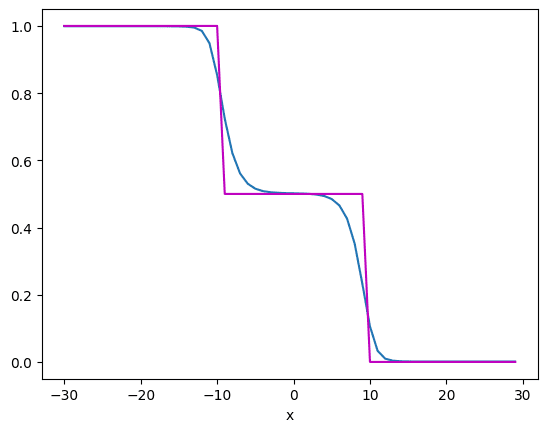

From which, you can see the approximation in blue is closer to the data in purple. As you can see, the neural network approximates the functions quite nicely. If the function is more complex, you may need more hidden layers or more neurons in the hidden layer, i.e., a more complex model.

Let’s also plot to see how the loss reduced during training.

# plot the cost
plt.plot(cost)
plt.xlabel('epochs')
plt.title('cross entropy loss')
plt.show()

# plot the cost

plt.plot(cost)

plt.xlabel('epochs')

plt.title('cross entropy loss')

plt.show()

You should see: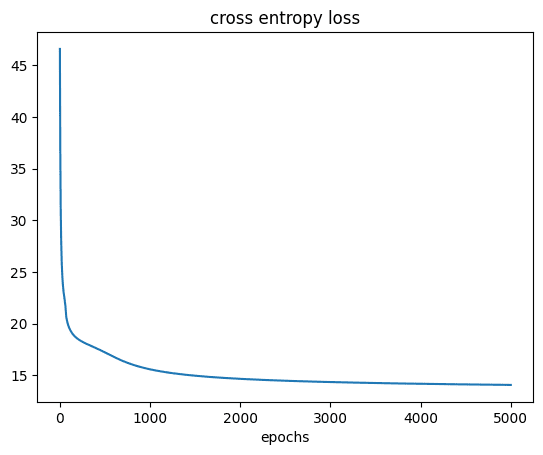

Putting everything together, the following is the complete code:

import torch
import matplotlib.pyplot as plt

# generate synthetic the data
X = torch.arange(-30, 30, 1).view(-1, 1).type(torch.FloatTensor)
Y = torch.zeros(X.shape[0])
Y[(X[:, 0] <= -10)] = 1.0
Y[(X[:, 0] > -10) & (X[:, 0] < 10)] = 0.5
Y[(X[:, 0] > 10)] = 0

plt.plot(X, Y)
plt.show()

# Define the class for single layer NN
class one_layer_net(torch.nn.Module):    
    # Constructor
    def __init__(self, input_size, hidden_neurons, output_size):
        super(one_layer_net, self).__init__()
        # hidden layer 
        self.linear_one = torch.nn.Linear(input_size, hidden_neurons)
        self.linear_two = torch.nn.Linear(hidden_neurons, output_size) 
        # defining layers as attributes
        self.layer_in = None
        self.act = None
        self.layer_out = None
    # prediction function
    def forward(self, x):
        self.layer_in = self.linear_one(x)
        self.act = torch.sigmoid(self.layer_in)
        self.layer_out = self.linear_two(self.act)
        y_pred = torch.sigmoid(self.linear_two(self.act))
        return y_pred

# create the model 
model = one_layer_net(1, 2, 1)  # 2 represents two neurons in one hidden layer

def criterion(y_pred, y):
    out = -1 * torch.mean(y * torch.log(y_pred) + (1 - y) * torch.log(1 - y_pred))
    return out
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# Define the training loop
epochs=5000
cost = []
total=0
for epoch in range(epochs):
    total=0
    epoch = epoch + 1
    for x, y in zip(X, Y):
        yhat = model(x)
        loss = criterion(yhat, y)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        # get total loss 
        total+=loss.item() 
    cost.append(total)
    if epoch % 1000 == 0:
        print(str(epoch)+ " " + "epochs done!") # visualze results after every 1000 epochs   
        # plot the result of function approximator
        plt.plot(X.numpy(), model(X).detach().numpy())
        plt.plot(X.numpy(), Y.numpy(), 'm')
        plt.xlabel('x')
        plt.show()

# plot the cost
plt.plot(cost)
plt.xlabel('epochs')
plt.title('cross entropy loss')
plt.show()

import torch

import matplotlib.pyplot as plt

# generate synthetic the data

X = torch.arange(-30, 30, 1).view(-1, 1).type(torch.FloatTensor)

Y = torch.zeros(X.shape[0])

Y[(X[:, 0] <= -10)] = 1.0

Y[(X[:, 0] > -10) & (X[:, 0] < 10)] = 0.5

Y[(X[:, 0] > 10)] = 0

plt.plot(X, Y)

plt.show()

# Define the class for single layer NN

class one_layer_net(torch.nn.Module):

# Constructor

def __init__(self, input_size, hidden_neurons, output_size):

super(one_layer_net, self).__init__()

# hidden layer

self.linear_one = torch.nn.Linear(input_size, hidden_neurons)

self.linear_two = torch.nn.Linear(hidden_neurons, output_size)

# defining layers as attributes

self.layer_in = None

self.act = None

self.layer_out = None

# prediction function

def forward(self, x):

self.layer_in = self.linear_one(x)

self.act = torch.sigmoid(self.layer_in)

self.layer_out = self.linear_two(self.act)

y_pred = torch.sigmoid(self.linear_two(self.act))

return y_pred

# create the model

model = one_layer_net(1, 2, 1) # 2 represents two neurons in one hidden layer

def criterion(y_pred, y):

out = -1 * torch.mean(y * torch.log(y_pred) + (1 - y) * torch.log(1 - y_pred))

return out

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# Define the training loop

epochs=5000

cost = []

total=0

for epoch in range(epochs):

total=0

epoch = epoch + 1

for x, y in zip(X, Y):

yhat = model(x)

loss = criterion(yhat, y)

loss.backward()

optimizer.step()

optimizer.zero_grad()

# get total loss

total+=loss.item()

cost.append(total)

if epoch % 1000 == 0:

print(str(epoch)+ " " + "epochs done!") # visualze results after every 1000 epochs

# plot the result of function approximator

plt.plot(X.numpy(), model(X).detach().numpy())

plt.plot(X.numpy(), Y.numpy(), 'm')

plt.xlabel('x')

plt.show()

# plot the cost

plt.plot(cost)

plt.xlabel('epochs')

plt.title('cross entropy loss')

plt.show()

Summary

In this tutorial, you learned how you can build and train a neural network and estimate the function. Particularly, you learned:

How to build a single layer neural network in PyTorch.
How to train a single layer neural network with PyTorch.
How to classify one-dimensional data using a single layer neural network.

3 Responses to Building a Single Layer Neural Network in PyTorch

Anthony the Koala January 14, 2023 at 10:57 am #

I have followed Mr Khan’s tutorials.

First, they are clearly written and secondly a by-product of his tutorials are the application of instatiating classes and inheritance from superior classes and implementaion of inherited classes.

Thank you,
Anthony of Sydney

Alex.A January 14, 2023 at 9:40 pm #

Hi, followed the code, using jupyter notebook, works well.

The epochs calculations takes time. How can I convert the code to run with CUDA, to accelarate the speed?

- James Carmichael January 15, 2023 at 8:38 am #
  
  Hi Alex.A…The following resource is a great starting point:
  
  https://www.vincent-lunot.com/post/an-introduction-to-cuda-in-python-part-1/

Navigation

Building a Single Layer Neural Network in PyTorch

Overview

Preparing the Data

Want to Get Started With Deep Learning with PyTorch?

Build the Model with `nn.Module`

Train the Model

Summary

Get Started on Deep Learning with PyTorch!

Learn how to build deep learning models

Kick-start your deep learning journey with hands-on exercises

More On This Topic

3 Responses to Building a Single Layer Neural Network in PyTorch

Leave a Reply Click here to cancel reply.

Navigation

Overview

Preparing the Data

Want to Get Started With Deep Learning with PyTorch?

Build the Model with nn.Module

Train the Model

Summary

Get Started on Deep Learning with PyTorch!

Learn how to build deep learning models

Kick-start your deep learning journey with hands-on exercises

More On This Topic

3 Responses to Building a Single Layer Neural Network in PyTorch

Leave a Reply Click here to cancel reply.

Build the Model with `nn.Module`