Test-time augmentation, or TTA for short, is a technique for improving the skill of predictive models.
It is typically used to improve the predictive performance of deep learning models on image datasets where predictions are averaged across multiple augmented versions of each image in the test dataset.
Although popular with image datasets and neural network models, test-time augmentation can be used with any machine learning algorithm on tabular datasets, such as those often seen in regression and classification predictive modeling problems.
In this tutorial, you will discover how to use test-time augmentation for tabular data in scikit-learn.
After completing this tutorial, you will know:
- Test-time augmentation is a technique for improving model performance and is commonly used for deep learning models on image datasets.
- How to implement test-time augmentation for regression and classification tabular datasets in Python with scikit-learn.
- How to tune the number of synthetic examples and amount of statistical noise used in test-time augmentation.
Kick-start your project with my new book Data Preparation for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

Test-Time Augmentation With Scikit-Learn
Photo by barnimages, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Test-Time Augmentation
- Standard Model Evaluation
- Test-Time Augmentation Example
Test-Time Augmentation
Test-time augmentation, or TTA for short, is a technique for improving the skill of a predictive model.
It is a procedure implemented when using a fit model to make predictions, such as on a test dataset or on new data. The procedure involves creating multiple slightly modified copies of each example in the dataset. A prediction is made for each modified example and the predictions are averaged to give a more accurate prediction for the original example.
TTA is often used with image classification, where image data augmentation is used to create multiple modified versions of each image, such as crops, zooms, rotations, and other image-specific modifications. As such, the technique results in a lift in the performance of image classification algorithms on standard datasets.
In their 2015 paper that achieved then state-of-the-art results on the ILSVRC dataset titled “Very Deep Convolutional Networks for Large-Scale Image Recognition,” the authors use horizontal flip test-time augmentation:
We also augment the test set by horizontal flipping of the images; the soft-max class posteriors of the original and flipped images are averaged to obtain the final scores for the image.
— Very Deep Convolutional Networks for Large-Scale Image Recognition, 2015.
For more on test-time augmentation with image data, see the tutorial:
Although often used for image data, test-time augmentation can also be used for other data types, such as tabular data (e.g. rows and columns of numbers).
There are many ways that TTA can be used with tabular data. One simple approach involves creating copies of rows of data with small Gaussian noise added. The predictions from the copied rows can then be averaged to result in an improved prediction for regression or classification.
We will explore how this might be achieved using the scikit-learn Python machine learning library.
First, let’s define a standard approach for evaluating a model.
Want to Get Started With Data Preparation?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Standard Model Evaluation
In this section, we will explore the typical way of evaluating a machine learning model before we introduce test-time augmentation in the next section.
First, let’s define a synthetic classification dataset.
We will use the make_classification() function to create a dataset with 100 examples, each with 20 input variables.
The example creates and summarizes the dataset.
|
1 2 3 4 5 6 |
# test classification dataset from sklearn.datasets import make_classification # define dataset X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # summarize the dataset print(X.shape, y.shape) |
Running the example creates the dataset and confirms the number of rows and columns of the dataset.
|
1 |
(100, 20) (100,) |
This is a binary classification task and we will fit and evaluate a linear model, specifically, a logistic regression model.
A good practice when evaluating machine learning models is to use repeated k-fold cross-validation. When the dataset is a classification problem, it is important to ensure that a stratified version of k-fold cross-validation is used. As such, we will use repeated stratified k-fold cross-validation with 10 folds and 5 repeats.
|
1 2 3 |
... # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) |
We will enumerate the folds and repeats manually so that later we can perform test-time augmentation.
Each loop, we must define and fit the model, then use the fit model to make a prediction, evaluate the predictions, and store the result.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # fit model model = LogisticRegression() model.fit(X_train, y_train) # evaluate model y_hat = model.predict(X_test) acc = accuracy_score(y_test, y_hat) scores.append(acc) |
At the end, we can report the mean classification accuracy across all folds and repeats.
|
1 2 3 |
... # report performance print('Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
Tying this together, the complete example of evaluating a logistic regression model on the synthetic binary classification dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# evaluate logistic regression using repeated stratified k-fold cross-validation from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # create dataset X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # fit model model = LogisticRegression() model.fit(X_train, y_train) # evaluate model y_hat = model.predict(X_test) acc = accuracy_score(y_test, y_hat) scores.append(acc) # report performance print('Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
Running the example evaluates the logistic regression using repeated stratified k-fold cross-validation.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the model achieved the mean classification accuracy of 79.8 percent.
|
1 |
Accuracy: 0.798 (0.110) |
Next, let’s explore how we might update this example to use test-time augmentation.
Test-Time Augmentation Example
Implementing test-time augmentation involves two steps.
The first step is to select a method for creating modified versions of each row in the test set.
In this tutorial, we will add Gaussian random noise to each feature. An alternate approach might be to add uniformly random noise or even copy feature values from examples in the test dataset.
The normal() NumPy function will be used to create a vector of random Gaussian values with a zero mean and small standard deviation. The standard deviation should be proportional to the distribution for each variable in the training dataset. In this case, we will keep the example simple and use a value of 0.02.
|
1 2 3 4 5 |
... # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss |
Given a row of data from the test set, we can create a given number of modified copies. It is a good idea to use an odd number of copies, such as 3, 5, or 7, as when we average the labels assigned to each later, we want to break ties automatically.
The create_test_set() function below implements this; given a row of data, it will return a test set that contains the row as well as “n_cases” modified copies, defaulting to 3 (so the test set size is 4).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# create a test set for a row of real data with an unknown label def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set |
An improvement to this approach would be to standardize or normalize the train and test datasets each loop and then use a standard deviation for the normal() that is consistent across features meaningful to the standard normal. This is left as an exercise for the reader.
The second setup is to make use of the create_test_set() for each example in the test set, make a prediction for the constructed test set, and record the predicted label using a summary statistic across the predictions. Given that the prediction is categorical, the statistical mode would be appropriate, via the mode() scipy function. If the dataset was regression or we were predicting probabilities, the mean or median would be more appropriate.
|
1 2 3 4 5 6 7 |
... # create the test set test_set = create_test_set(row) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) |
The test_time_augmentation() function below implements this; given a model and a test set, it returns an array of predictions where each prediction was made using test-time augmentation.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# make predictions using test-time augmentation def test_time_augmentation(model, X_test): # evaluate model y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat |
Tying all of this together, the complete example of evaluating the logistic regression model on the dataset using test-time augmentation is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
# evaluate logistic regression using test-time augmentation from numpy.random import seed from numpy.random import normal from numpy import mean from numpy import std from scipy.stats import mode from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # create a test set for a row of real data with an unknown label def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set # make predictions using test-time augmentation def test_time_augmentation(model, X_test): # evaluate model y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat # initialize numpy random number generator seed(1) # create dataset X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # fit model model = LogisticRegression() model.fit(X_train, y_train) # make predictions using test-time augmentation y_hat = test_time_augmentation(model, X_test) # calculate the accuracy for this iteration acc = accuracy_score(y_test, y_hat) # store the result scores.append(acc) # report performance print('Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
Running the example evaluates the logistic regression using repeated stratified k-fold cross-validation and test-time augmentation.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the model achieved the mean classification accuracy of 81.0 percent, which is better than the test harness that does not use test-time augmentation that achieved an accuracy of 79.8 percent.
|
1 |
Accuracy: 0.810 (0.114) |
It might be interesting to grid search the number of synthetic examples created each time a prediction is made during test-time augmentation.
The example below explores values between 1 and 20 and plots the results.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
# compare the number of synthetic examples created during the test-time augmentation from numpy.random import seed from numpy.random import normal from numpy import mean from numpy import std from scipy.stats import mode from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score from matplotlib import pyplot # create a test set for a row of real data with an unknown label def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set # make predictions using test-time augmentation def test_time_augmentation(model, X_test, cases): # evaluate model y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row, n_cases=cases) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat # evaluate different number of synthetic examples created at test time examples = range(1, 21) results = list() for e in examples: # initialize numpy random number generator seed(1) # create dataset X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # fit model model = LogisticRegression() model.fit(X_train, y_train) # make predictions using test-time augmentation y_hat = test_time_augmentation(model, X_test, e) # calculate the accuracy for this iteration acc = accuracy_score(y_test, y_hat) # store the result scores.append(acc) # report performance print('>%d, acc: %.3f (%.3f)' % (e, mean(scores), std(scores))) results.append(mean(scores)) # plot the results pyplot.plot(examples, results) pyplot.show() |
Running the example reports the accuracy for different numbers of synthetic examples created during test-time augmentation.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Recall that we used three examples in the previous example.
In this case, it looks like a value of three might be optimal for this test harness, as all other values seem to result in lower performance.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
>1, acc: 0.800 (0.118) >2, acc: 0.806 (0.114) >3, acc: 0.810 (0.114) >4, acc: 0.798 (0.105) >5, acc: 0.802 (0.109) >6, acc: 0.798 (0.107) >7, acc: 0.800 (0.111) >8, acc: 0.802 (0.110) >9, acc: 0.806 (0.105) >10, acc: 0.802 (0.110) >11, acc: 0.798 (0.112) >12, acc: 0.806 (0.110) >13, acc: 0.802 (0.110) >14, acc: 0.802 (0.109) >15, acc: 0.798 (0.110) >16, acc: 0.796 (0.111) >17, acc: 0.806 (0.112) >18, acc: 0.796 (0.111) >19, acc: 0.800 (0.113) >20, acc: 0.804 (0.109) |
A line plot of number of examples vs. classification accuracy is created showing that perhaps odd numbers of examples generally result in better performance than even numbers of examples.
This might be expected due to their ability to break ties when using the mode of the predictions.
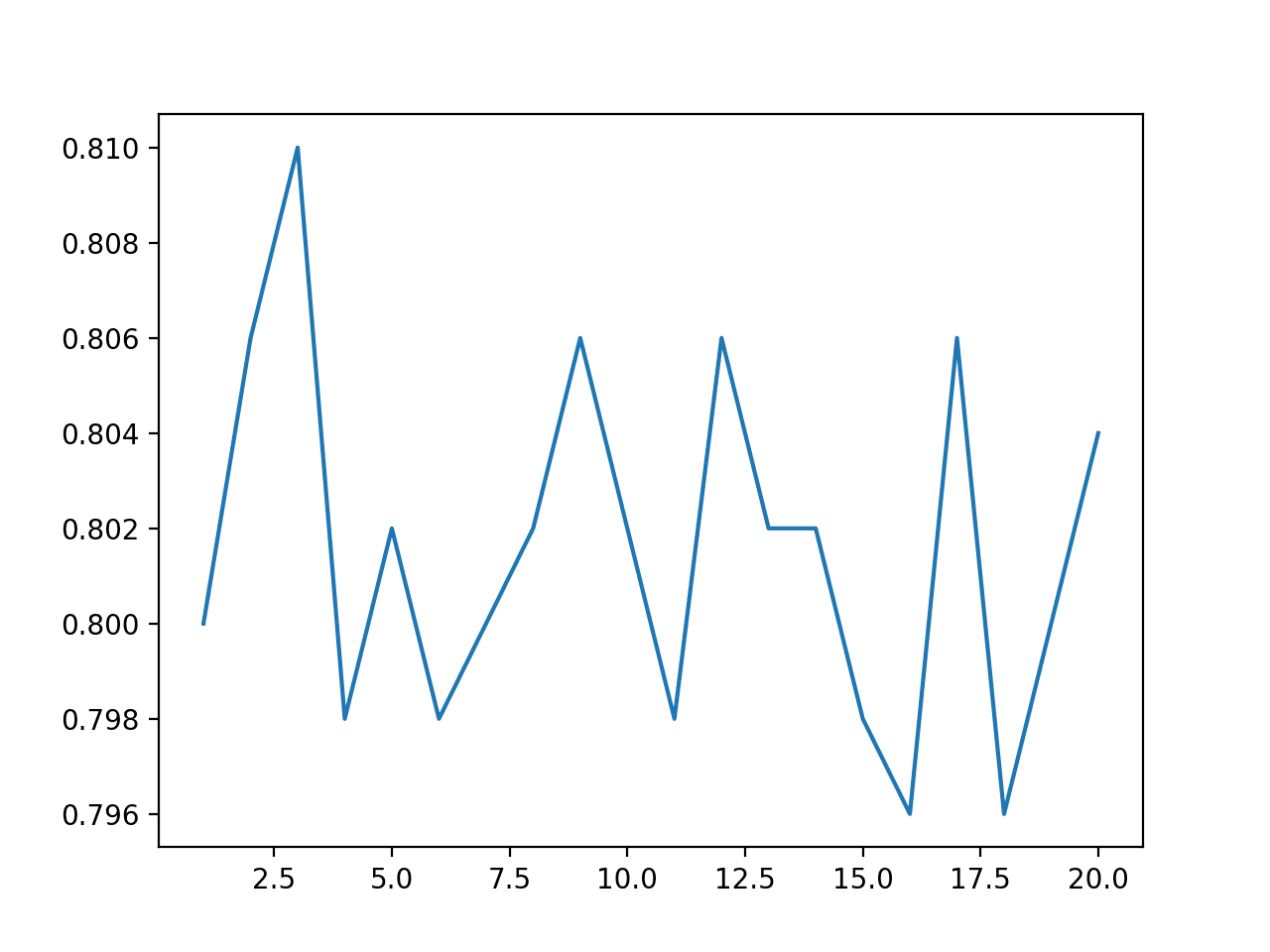
Line Plot of Number of Synthetic Examples in TTA vs. Classification Accuracy
We can also perform the same sensitivity analysis with the amount of random noise added to examples in the test set during test-time augmentation.
The example below demonstrates this with noise values between 0.01 and 0.3 with a grid of 0.01.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
# compare amount of noise added to examples created during the test-time augmentation from numpy.random import seed from numpy.random import normal from numpy import arange from numpy import mean from numpy import std from scipy.stats import mode from sklearn.datasets import make_classification from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score from matplotlib import pyplot # create a test set for a row of real data with an unknown label def create_test_set(row, n_cases=3, feature_scale=0.2): test_set = list() test_set.append(row) # make copies of row for _ in range(n_cases): # create vector of random gaussians gauss = normal(loc=0.0, scale=feature_scale, size=len(row)) # add to test case new_row = row + gauss # store in test set test_set.append(new_row) return test_set # make predictions using test-time augmentation def test_time_augmentation(model, X_test, noise): # evaluate model y_hat = list() for i in range(X_test.shape[0]): # retrieve the row row = X_test[i] # create the test set test_set = create_test_set(row, feature_scale=noise) # make a prediction for all examples in the test set labels = model.predict(test_set) # select the label as the mode of the distribution label, _ = mode(labels) # store the prediction y_hat.append(label) return y_hat # evaluate different number of synthetic examples created at test time noise = arange(0.01, 0.31, 0.01) results = list() for n in noise: # initialize numpy random number generator seed(1) # create dataset X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # prepare the cross-validation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=5, random_state=1) scores = list() for train_ix, test_ix in cv.split(X, y): # split the data X_train, X_test = X[train_ix], X[test_ix] y_train, y_test = y[train_ix], y[test_ix] # fit model model = LogisticRegression() model.fit(X_train, y_train) # make predictions using test-time augmentation y_hat = test_time_augmentation(model, X_test, n) # calculate the accuracy for this iteration acc = accuracy_score(y_test, y_hat) # store the result scores.append(acc) # report performance print('>noise=%.3f, acc: %.3f (%.3f)' % (n, mean(scores), std(scores))) results.append(mean(scores)) # plot the results pyplot.plot(noise, results) pyplot.show() |
Running the example reports the accuracy for different amounts of statistical noise added to examples created during test-time augmentation.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Recall that we used a standard deviation of 0.02 in the first example.
In this case, it looks like a value of about 0.230 might be optimal for this test harness, resulting in a slightly higher accuracy of 81.2 percent.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
>noise=0.010, acc: 0.798 (0.110) >noise=0.020, acc: 0.798 (0.110) >noise=0.030, acc: 0.798 (0.110) >noise=0.040, acc: 0.800 (0.113) >noise=0.050, acc: 0.802 (0.112) >noise=0.060, acc: 0.804 (0.111) >noise=0.070, acc: 0.806 (0.108) >noise=0.080, acc: 0.806 (0.108) >noise=0.090, acc: 0.806 (0.108) >noise=0.100, acc: 0.806 (0.108) >noise=0.110, acc: 0.806 (0.108) >noise=0.120, acc: 0.806 (0.108) >noise=0.130, acc: 0.806 (0.108) >noise=0.140, acc: 0.806 (0.108) >noise=0.150, acc: 0.808 (0.111) >noise=0.160, acc: 0.808 (0.111) >noise=0.170, acc: 0.808 (0.111) >noise=0.180, acc: 0.810 (0.114) >noise=0.190, acc: 0.810 (0.114) >noise=0.200, acc: 0.810 (0.114) >noise=0.210, acc: 0.810 (0.114) >noise=0.220, acc: 0.810 (0.114) >noise=0.230, acc: 0.812 (0.114) >noise=0.240, acc: 0.812 (0.114) >noise=0.250, acc: 0.812 (0.114) >noise=0.260, acc: 0.812 (0.114) >noise=0.270, acc: 0.810 (0.114) >noise=0.280, acc: 0.808 (0.116) >noise=0.290, acc: 0.808 (0.116) >noise=0.300, acc: 0.808 (0.116) |
A line plot of the amount of noise added to examples vs. classification accuracy is created, showing that perhaps a small range of noise around a standard deviation of 0.250 might be optimal on this test harness.
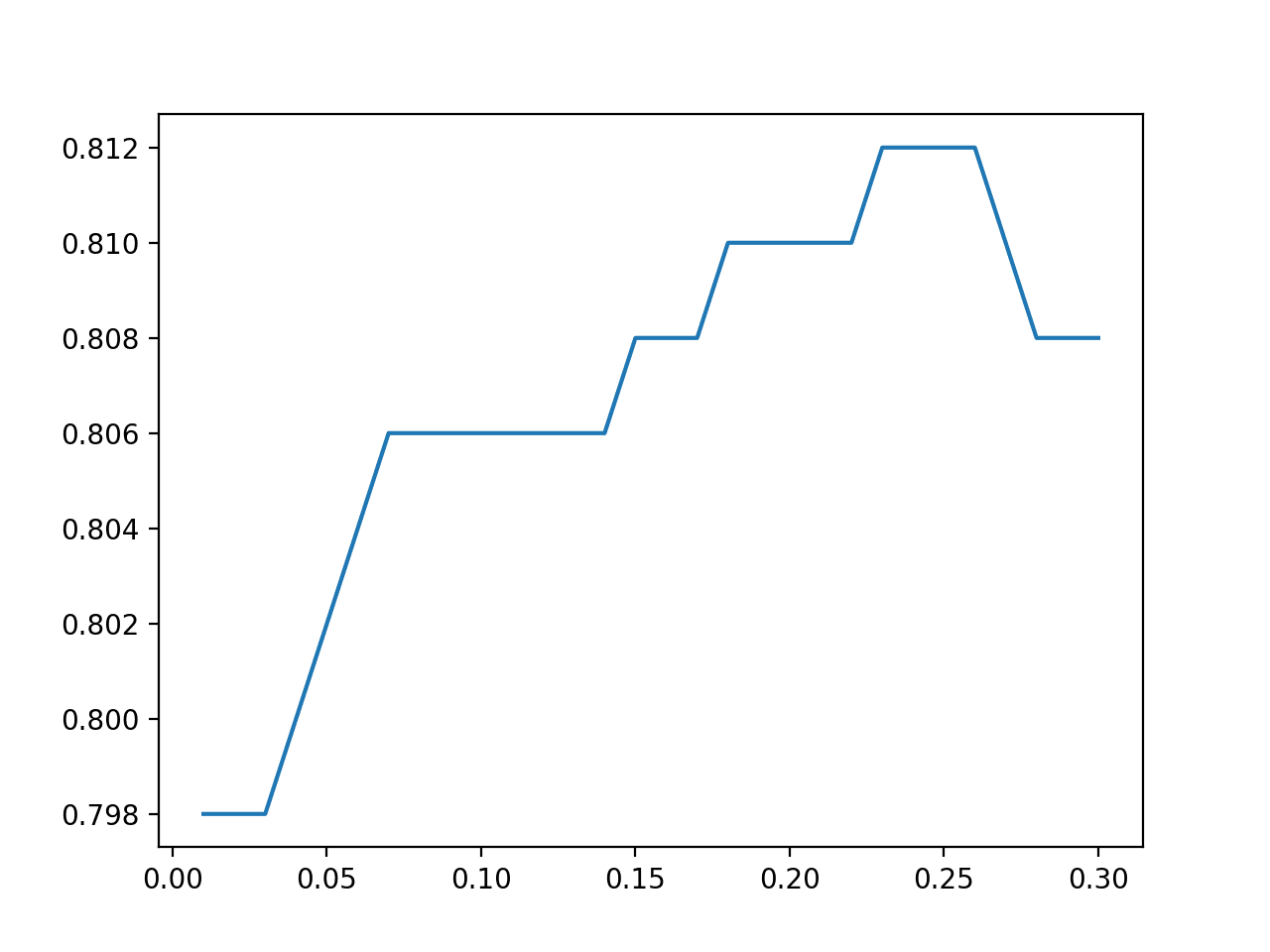
Line Plot of Statistical Noise Added to Examples in TTA vs. Classification Accuracy
Why not use an oversampling method like SMOTE?
SMOTE is a popular oversampling method for rebalancing observations for each class in a training dataset. It can create synthetic examples but requires knowledge of the class labels which does not make it easy for use in test-time augmentation.
One approach might be to take a given example for which a prediction is required and assume it belongs to a given class. Then generate synthetic samples from the training dataset using the new example as the focal point of the synthesis, and classify them. This is then repeated for each class label. The total or average classification response (perhaps probability) can be tallied for each class group and the group with the largest response can be taken as the prediction.
This is just off the cuff, I have not actually tried this approach. Have a go and let me know if it works.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
- How to Use Test-Time Augmentation to Make Better predictions
- How to Generate Random Numbers in Python
APIs
- sklearn.datasets.make_classification API.
- sklearn.model_selection.RepeatedStratifiedKFold API.
- numpy.random.normal API.
- scipy.stats.mode API.
Summary
In this tutorial, you discovered how to use test-time augmentation for tabular data in scikit-learn.
Specifically, you learned:
- Test-time augmentation is a technique for improving model performance and is commonly used for deep learning models on image datasets.
- How to implement test-time augmentation for regression and classification tabular datasets in Python with scikit-learn.
- How to tune the number of synthetic examples and amount of statistical noise used in test-time augmentation.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.






sir is we apply test time augmentation after optimization technique .for eg after hyper-parameter optimization of deep learning
Yes, it used with a fit model. Not during training.
sir is test time augmentation is used with deep learning model
It can be, here is an example for image data:
https://machinelearningmastery.com/how-to-use-test-time-augmentation-to-improve-model-performance-for-image-classification/
sir is u have papers on test time augmentation
Sorry, I do not.
sir please provide test time augmentation on tabular data with deep learning.
Thanks for the suggestion.
You can adapt the above examples directly for use with deep learning models.
I understand test time augmentation but I need to understand how to apply oversampling in augmentation in other research
What do you mean exactly?
I have a paper in breast cancer the author applying augmentation. I don’t know how the author apply it on the dataset.
Perhaps contact the author via email and ask?
Posting image specific techniques for numeric dataset is of great help.
Is it possible to use augmentation on one-class numerical training dataset to generate the other class and then apply ML algorithms on test dataset with two class.
Perhaps, maybe try it – prototype it and see.
It has no email contact
Perhaps search for the author via google.
OK thanks
Dr Jason,
In the section headed “Standard Model Evaluation”, I wanted to count how many iterations were in the loop
when I set RepeatedStratifiedIKFold’s n_splits and n_repeats.
Setting n_splits=10,n_repeats=5:
There were 50 iterations of the loop
Changing the parameters to n_splits=100, n_repeats=5:
There were 500 iterations.
code to replicate:
Why is count = n_iterations * n_repeat?
I thought the loop counted the number of repeats.
.
Thank you,
Anthony of Sydney
If there are 10 folds and 5 repeats, then we would expected folds * repeats or 500 iterations and in turn results.
Dear Dr Jason,
Thank you for the reply. I understand why the number of iterations is no_of_folds*repeats.
To paraphrase:
We have a dataset. We split the dataset into k folds. That is we take k random samples from the dataset. For each fold we split the dataset into train and test samples. The train is used to train the model and the test is used to test the model.
The “repeat” means repeating k folds “repeat” times.
Hence the total number of iterations is no_of_folds*repeats.
Source: subheading What is K-Fold Cross Validation?, https://medium.com/datadriveninvestor/k-fold-cross-validation-6b8518070833 .
You may yourself, “…what is train_ix and test_ix?
Answer: train_ix, is an array of indices from the selections from the set of train_X and set of train_y. Similarly test_ix is an array of indices from the selections of set of test_X and set of test_y.
Thank you,
Anthony of Sydney
Thanks for the help on TTA for Tabular. Very very useful. I look forward to applying this at work and kaggle!
You’re welcome, let me know how you go!
congratulations you are good
Thanks!
Jason is this tecnique included in your book about data preparation?
No, it is a little to specalized for the book.
Hi Jason, I have a class imbalance problem. SMOTE on training data worked for me. Since the correct method to do a train-test split for an imbalanced approach is to use a stratified approach, my test data is also imbalanced.
I read the last paragraph of this article. If I do a SMOTE on train data separately and test data separately, would this be a correct approach to augment test data? This takes care that the training data information is not leaked to the test data. So I believe this would be correct. Can you please share your thoughts?
It would not be appropriate to apply SMOTE to the test dataset. It must only be applied to the training dataset.
Hi Jason, I would really appreciate if you can also explain the reason as it will help me understand.
SMOTE should be not be applied on complete data set because this will leak the test data information during training. I agree totally with this.
However, as I mentioned earlier, the SMOTE is being applied separately on training and test data after the split. Needed to understand, why this cannot be done.
Also I would like to add here that I am using different SMOTE techniques for train and test set as the goal is to purely augment the test set based only on its own nature of the data to give a chance to the algorithm to try and predict more test samples.
Pasting code:
oversample_train = ADASYN(sampling_strategy = ‘all’, random_state = 0)
X_train, y_train = oversample_train.fit_resample(X_train, y_train)
oversample_test = SMOTE(sampling_strategy = ‘all’, random_state = 0)
X_test, y_test = oversample_test.fit_resample(X_test, y_test)
Changing the training set with smote biases the training of the model – which is good – it performs better.
The test set is designed to evaluate the performance of a model on data not used during training. If the test set is changed, such as changing the distribution, then the evaluation of any model on that test set would not be a valid.
Never apply smote to a test set.
Thanks Jason!
Thank you very much for your great post.
In your example, all the features are numerical features. If there are some categorical features in the training set and testing set, how to use Test-Time Augmentation method? Is this method also suitable for the regression problems?
You’re welcome.
I don’t think the approach is appropriate for categorical inputs, unless they have an ordinal relationship – in which case you could use a multinomial probability distribution to sample their values, perhaps. Or just don’t resample the categorical inputs.
Yes, I suspect you could use this approach for regression.
Thank you very much for your great post.
can I apply this technique for a complete numerical dataset?
Why you think you cannot?
For my project work, I want to use the data augmentation process. I already use the Variational Autoencoder method. If I can use it, I can compare two methods.
Also, my output is not a classification.