Many imbalanced classification tasks require a skillful model that predicts a crisp class label, where both classes are equally important.
An example of an imbalanced classification problem where a class label is required and both classes are equally important is the detection of oil spills or slicks in satellite images. The detection of a spill requires mobilizing an expensive response, and missing an event is equally expensive, causing damage to the environment.
One way to evaluate imbalanced classification models that predict crisp labels is to calculate the separate accuracy on the positive class and the negative class, referred to as sensitivity and specificity. These two measures can then be averaged using the geometric mean, referred to as the G-mean, that is insensitive to the skewed class distribution and correctly reports on the skill of the model on both classes.
In this tutorial, you will discover how to develop a model to predict the presence of an oil spill in satellite images and evaluate it using the G-mean metric.
After completing this tutorial, you will know:
- How to load and explore the dataset and generate ideas for data preparation and model selection.
- How to evaluate a suite of probabilistic models and improve their performance with appropriate data preparation.
- How to fit a final model and use it to predict class labels for specific cases.
Kick-start your project with my new book Imbalanced Classification with Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Jan/2021: Updated links for API documentation.

Develop an Imbalanced Classification Model to Detect Oil Spills
Photo by Lenny K Photography, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
- Oil Spill Dataset
- Explore the Dataset
- Model Test and Baseline Result
- Evaluate Models
- Evaluate Probabilistic Models
- Evaluate Balanced Logistic Regression
- Evaluate Resampling With Probabilistic Models
- Make Prediction on New Data
Oil Spill Dataset
In this project, we will use a standard imbalanced machine learning dataset referred to as the “oil spill” dataset, “oil slicks” dataset or simply “oil.”
The dataset was introduced in the 1998 paper by Miroslav Kubat, et al. titled “Machine Learning for the Detection of Oil Spills in Satellite Radar Images.” The dataset is often credited to Robert Holte, a co-author of the paper.
The dataset was developed by starting with satellite images of the ocean, some of which contain an oil spill and some that do not. Images were split into sections and processed using computer vision algorithms to provide a vector of features to describe the contents of the image section or patch.
The input to [the system] is a raw pixel image from a radar satellite Image processing techniques are used […] The output of the image processing is a fixed-length feature vector for each suspicious region. During normal operation these feature vectors are fed into a classier to decide which images and which regions within an image to present for human inspection.
— Machine Learning for the Detection of Oil Spills in Satellite Radar Images, 1998.
The task is given a vector that describes the contents of a patch of a satellite image, then predicts whether the patch contains an oil spill or not, e.g. from the illegal or accidental dumping of oil in the ocean.
There are 937 cases. Each case is comprised of 48 numerical computer vision derived features, a patch number, and a class label.
A total of nine satellite images were processed into patches. Cases in the dataset are ordered by image and the first column of the dataset represents the patch number for the image. This was provided for the purposes of estimating model performance per-image. In this case, we are not interested in the image or patch number and this first column can be removed.
The normal case is no oil spill assigned the class label of 0, whereas an oil spill is indicated by a class label of 1. There are 896 cases for no oil spill and 41 cases of an oil spill.
The second critical feature of the oil spill domain can be called an imbalanced training set: there are very many more negative examples lookalikes than positive examples oil slicks. Against the 41 positive examples we have 896 negative examples the majority class thus comprises almost 96% of the data.
— Machine Learning for the Detection of Oil Spills in Satellite Radar Images, 1998.
We do not have access to the program used to prepare computer vision features from the satellite images, therefore we are restricted to work with the extracted features that were collected and made available.
Next, let’s take a closer look at the data.
Want to Get Started With Imbalance Classification?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Explore the Dataset
First, download the dataset and save it in your current working directory with the name “oil-spill.csv”
Review the contents of the file.
The first few lines of the file should look as follows:
|
1 2 3 4 5 6 |
1,2558,1506.09,456.63,90,6395000,40.88,7.89,29780,0.19,214.7,0.21,0.26,0.49,0.1,0.4,99.59,32.19,1.84,0.16,0.2,87.65,0,0.47,132.78,-0.01,3.78,0.22,3.2,-3.71,-0.18,2.19,0,2.19,310,16110,0,138.68,89,69,2850,1000,763.16,135.46,3.73,0,33243.19,65.74,7.95,1 2,22325,79.11,841.03,180,55812500,51.11,1.21,61900,0.02,901.7,0.02,0.03,0.11,0.01,0.11,6058.23,4061.15,2.3,0.02,0.02,87.65,0,0.58,132.78,-0.01,3.78,0.84,7.09,-2.21,0,0,0,0,704,40140,0,68.65,89,69,5750,11500,9593.48,1648.8,0.6,0,51572.04,65.73,6.26,0 3,115,1449.85,608.43,88,287500,40.42,7.34,3340,0.18,86.1,0.21,0.32,0.5,0.17,0.34,71.2,16.73,1.82,0.19,0.29,87.65,0,0.46,132.78,-0.01,3.78,0.7,4.79,-3.36,-0.23,1.95,0,1.95,29,1530,0.01,38.8,89,69,1400,250,150,45.13,9.33,1,31692.84,65.81,7.84,1 4,1201,1562.53,295.65,66,3002500,42.4,7.97,18030,0.19,166.5,0.21,0.26,0.48,0.1,0.38,120.22,33.47,1.91,0.16,0.21,87.65,0,0.48,132.78,-0.01,3.78,0.84,6.78,-3.54,-0.33,2.2,0,2.2,183,10080,0,108.27,89,69,6041.52,761.58,453.21,144.97,13.33,1,37696.21,65.67,8.07,1 5,312,950.27,440.86,37,780000,41.43,7.03,3350,0.17,232.8,0.15,0.19,0.35,0.09,0.26,289.19,48.68,1.86,0.13,0.16,87.65,0,0.47,132.78,-0.01,3.78,0.02,2.28,-3.44,-0.44,2.19,0,2.19,45,2340,0,14.39,89,69,1320.04,710.63,512.54,109.16,2.58,0,29038.17,65.66,7.35,0 ... |
We can see that the first column contains integers for the patch number. We can also see that the computer vision derived features are real-valued with differing scales such as thousands in the second column and fractions in other columns.
All input variables are numeric, and there are no missing values marked with a “?” character.
Firstly, we can load the CSV dataset and confirm the number of rows and columns.
The dataset can be loaded as a DataFrame using the read_csv() Pandas function, specifying the location and the fact that there is no header line.
|
1 2 3 4 5 |
... # define the dataset location filename = 'oil-spill.csv' # load the csv file as a data frame dataframe = read_csv(filename, header=None) |
Once loaded, we can summarize the number of rows and columns by printing the shape of the DataFrame.
|
1 2 3 |
... # summarize the shape of the dataset print(dataframe.shape) |
We can also summarize the number of examples in each class using the Counter object.
|
1 2 3 4 5 6 7 |
... # summarize the class distribution target = dataframe.values[:,-1] counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
Tying this together, the complete example of loading and summarizing the dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# load and summarize the dataset from pandas import read_csv from collections import Counter # define the dataset location filename = 'oil-spill.csv' # load the csv file as a data frame dataframe = read_csv(filename, header=None) # summarize the shape of the dataset print(dataframe.shape) # summarize the class distribution target = dataframe.values[:,-1] counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
Running the example first loads the dataset and confirms the number of rows and columns.
The class distribution is then summarized, confirming the number of oil spills and non-spills and the percentage of cases in the minority and majority classes.
|
1 2 3 |
(937, 50) Class=1, Count=41, Percentage=4.376% Class=0, Count=896, Percentage=95.624% |
We can also take a look at the distribution of each variable by creating a histogram for each.
With 50 variables, it is a lot of plots, but we might spot some interesting patterns. Also, with so many plots, we must turn off the axis labels and plot titles to reduce the clutter. The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# create histograms of each variable from pandas import read_csv from matplotlib import pyplot # define the dataset location filename = 'oil-spill.csv' # load the csv file as a data frame dataframe = read_csv(filename, header=None) # create a histogram plot of each variable ax = dataframe.hist() # disable axis labels for axis in ax.flatten(): axis.set_title('') axis.set_xticklabels([]) axis.set_yticklabels([]) pyplot.show() |
Running the example creates the figure with one histogram subplot for each of the 50 variables in the dataset.
We can see many different distributions, some with Gaussian-like distributions, others with seemingly exponential or discrete distributions.
Depending on the choice of modeling algorithms, we would expect scaling the distributions to the same range to be useful, and perhaps the use of some power transforms.
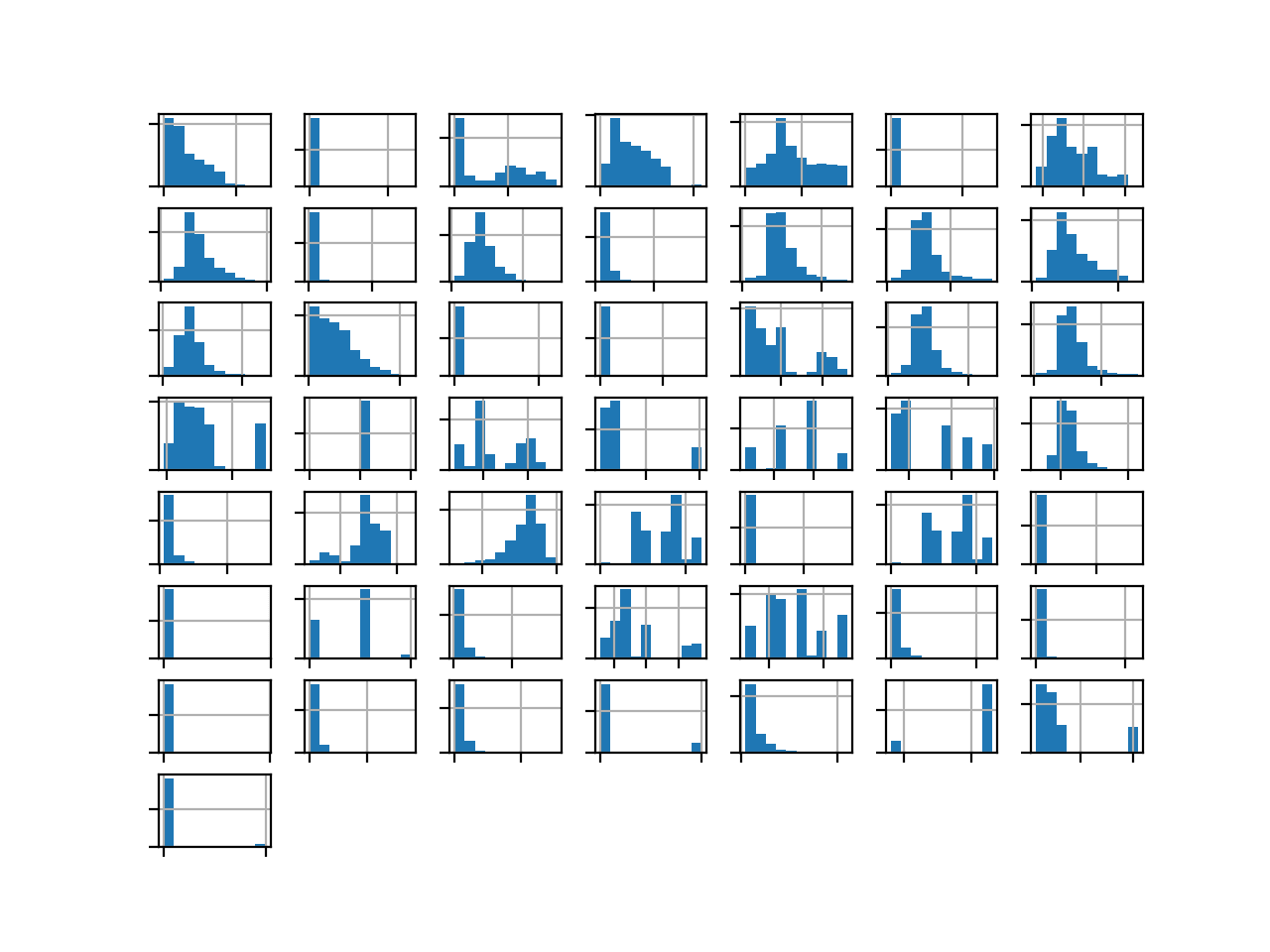
Histogram of Each Variable in the Oil Spill Dataset
Now that we have reviewed the dataset, let’s look at developing a test harness for evaluating candidate models.
Model Test and Baseline Result
We will evaluate candidate models using repeated stratified k-fold cross-validation.
The k-fold cross-validation procedure provides a good general estimate of model performance that is not too optimistically biased, at least compared to a single train-test split. We will use k=10, meaning each fold will contain about 937/10 or about 94 examples.
Stratified means that each fold will contain the same mixture of examples by class, that is about 96% to 4% non-spill and spill. Repeated means that the evaluation process will be performed multiple times to help avoid fluke results and better capture the variance of the chosen model. We will use three repeats.
This means a single model will be fit and evaluated 10 * 3, or 30, times and the mean and standard deviation of these runs will be reported.
This can be achieved using the RepeatedStratifiedKFold scikit-learn class.
We are predicting class labels of whether a satellite image patch contains a spill or not. There are many measures we could use, although the authors of the paper chose to report the sensitivity, specificity, and the geometric mean of the two scores, called the G-mean.
To this end, we have mainly used the geometric mean (g-mean) […] This measure has the distinctive property of being independent of the distribution of examples between classes, and is thus robust in circumstances where this distribution might change with time or be different in the training and testing sets.
— Machine Learning for the Detection of Oil Spills in Satellite Radar Images, 1998.
Recall that the sensitivity is a measure of the accuracy for the positive class and specificity is a measure of the accuracy of the negative class.
- Sensitivity = TruePositives / (TruePositives + FalseNegatives)
- Specificity = TrueNegatives / (TrueNegatives + FalsePositives)
The G-mean seeks a balance of these scores, the geometric mean, where poor performance for one or the other results in a low G-mean score.
- G-Mean = sqrt(Sensitivity * Specificity)
We can calculate the G-mean for a set of predictions made by a model using the geometric_mean_score() function provided by the imbalanced-learn library.
First, we can define a function to load the dataset and split the columns into input and output variables. We will also drop column 22 because the column contains a single value, and the first column that defines the image patch number. The load_dataset() function below implements this.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, :-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y |
We can then define a function that will evaluate a given model on the dataset and return a list of G-Mean scores for each fold and repeat.
The evaluate_model() function below implements this, taking the dataset and model as arguments and returning the list of scores.
|
1 2 3 4 5 6 7 8 9 |
# evaluate a model def evaluate_model(X, y, model): # define evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # evaluate model scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores |
Finally, we can evaluate a baseline model on the dataset using this test harness.
A model that predicts the majority class label (0) or the minority class label (1) for all cases will result in a G-mean of zero. As such, a good default strategy would be to randomly predict one class label or another with a 50% probability and aim for a G-mean of about 0.5.
This can be achieved using the DummyClassifier class from the scikit-learn library and setting the “strategy” argument to ‘uniform‘.
|
1 2 3 |
... # define the reference model model = DummyClassifier(strategy='uniform') |
Once the model is evaluated, we can report the mean and standard deviation of the G-mean scores directly.
|
1 2 3 4 5 |
... # evaluate the model result_m, result_s = evaluate_model(X, y, model) # summarize performance print('Mean G-Mean: %.3f (%.3f)' % (result_m, result_s)) |
Tying this together, the complete example of loading the dataset, evaluating a baseline model and reporting the performance is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# test harness and baseline model evaluation from collections import Counter from numpy import mean from numpy import std from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from imblearn.metrics import geometric_mean_score from sklearn.metrics import make_scorer from sklearn.dummy import DummyClassifier # load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, :-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y # evaluate a model def evaluate_model(X, y, model): # define evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # evaluate model scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores # define the location of the dataset full_path = 'oil-spill.csv' # load the dataset X, y = load_dataset(full_path) # summarize the loaded dataset print(X.shape, y.shape, Counter(y)) # define the reference model model = DummyClassifier(strategy='uniform') # evaluate the model scores = evaluate_model(X, y, model) # summarize performance print('Mean G-Mean: %.3f (%.3f)' % (mean(scores), std(scores))) |
Running the example first loads and summarizes the dataset.
We can see that we have the correct number of rows loaded, and that we have 47 computer vision derived input variables, with the constant value column (index 22) and the patch number column (index 0) removed.
Importantly, we can see that the class labels have the correct mapping to integers with 0 for the majority class and 1 for the minority class, customary for imbalanced binary classification dataset.
Next, the average of the G-Mean scores is reported.
In this case, we can see that the baseline algorithm achieves a G-Mean of about 0.47, close to the theoretical maximum of 0.5. This score provides a lower limit on model skill; any model that achieves an average G-Mean above about 0.47 (or really above 0.5) has skill, whereas models that achieve a score below this value do not have skill on this dataset.
|
1 2 |
(937, 47) (937,) Counter({0: 896, 1: 41}) Mean G-Mean: 0.478 (0.143) |
It is interesting to note that a good G-mean reported in the paper was about 0.811, although the model evaluation procedure was different. This provides a rough target for “good” performance on this dataset.
Now that we have a test harness and a baseline in performance, we can begin to evaluate some models on this dataset.
Evaluate Models
In this section, we will evaluate a suite of different techniques on the dataset using the test harness developed in the previous section.
The goal is to both demonstrate how to work through the problem systematically and to demonstrate the capability of some techniques designed for imbalanced classification problems.
The reported performance is good, but not highly optimized (e.g. hyperparameters are not tuned).
What score can you get? If you can achieve better G-mean performance using the same test harness, I’d love to hear about it. Let me know in the comments below.
Evaluate Probabilistic Models
Let’s start by evaluating some probabilistic models on the dataset.
Probabilistic models are those models that are fit on the data under a probabilistic framework and often perform well in general for imbalanced classification datasets.
We will evaluate the following probabilistic models with default hyperparameters in the dataset:
- Logistic Regression (LR)
- Linear Discriminant Analysis (LDA)
- Gaussian Naive Bayes (NB)
Both LR and LDA are sensitive to the scale of the input variables, and often expect and/or perform better if input variables with different scales are normalized or standardized as a pre-processing step.
In this case, we will standardize the dataset prior to fitting each model. This will be achieved using a Pipeline and the StandardScaler class. The use of a Pipeline ensures that the StandardScaler is fit on the training dataset and applied to the train and test sets within each k-fold cross-validation evaluation, avoiding any data leakage that might result in an optimistic result.
We can define a list of models to evaluate on our test harness as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
... # define models models, names, results = list(), list(), list() # LR models.append(Pipeline(steps=[('t', StandardScaler()),('m',LogisticRegression(solver='liblinear'))])) names.append('LR') # LDA models.append(Pipeline(steps=[('t', StandardScaler()),('m',LinearDiscriminantAnalysis())])) names.append('LDA') # NB models.append(GaussianNB()) names.append('NB') |
Once defined, we can enumerate the list and evaluate each in turn. The mean and standard deviation of G-mean scores can be printed during evaluation and the sample of scores can be stored.
Algorithms can be compared directly based on their mean G-mean score.
|
1 2 3 4 5 6 7 8 |
... # evaluate each model for i in range(len(models)): # evaluate the model and store results scores = evaluate_model(X, y, models[i]) results.append(scores) # summarize and store print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) |
At the end of the run, we can use the scores to create a box and whisker plot for each algorithm.
Creating the plots side by side allows the distributions to be compared both with regard to the mean score, but also the middle 50 percent of the distribution between the 25th and 75th percentiles.
|
1 2 3 4 |
... # plot the results pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Tying this together, the complete example comparing three probabilistic models on the oil spill dataset using the test harness is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# compare probabilistic model on the oil spill dataset from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.naive_bayes import GaussianNB from imblearn.metrics import geometric_mean_score from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler # load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, :-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y # evaluate a model def evaluate_model(X, y, model): # define evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # evaluate model scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores # define the location of the dataset full_path = 'oil-spill.csv' # load the dataset X, y = load_dataset(full_path) # define models models, names, results = list(), list(), list() # LR models.append(Pipeline(steps=[('t', StandardScaler()),('m',LogisticRegression(solver='liblinear'))])) names.append('LR') # LDA models.append(Pipeline(steps=[('t', StandardScaler()),('m',LinearDiscriminantAnalysis())])) names.append('LDA') # NB models.append(GaussianNB()) names.append('NB') # evaluate each model for i in range(len(models)): # evaluate the model and store results scores = evaluate_model(X, y, models[i]) results.append(scores) # summarize and store print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # plot the results pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example evaluates each of the probabilistic models on the dataset.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
You may see some warnings from the LDA algorithm such as “Variables are collinear“. These can be safely ignored for now, but suggests that the algorithm could benefit from feature selection to remove some of the variables.
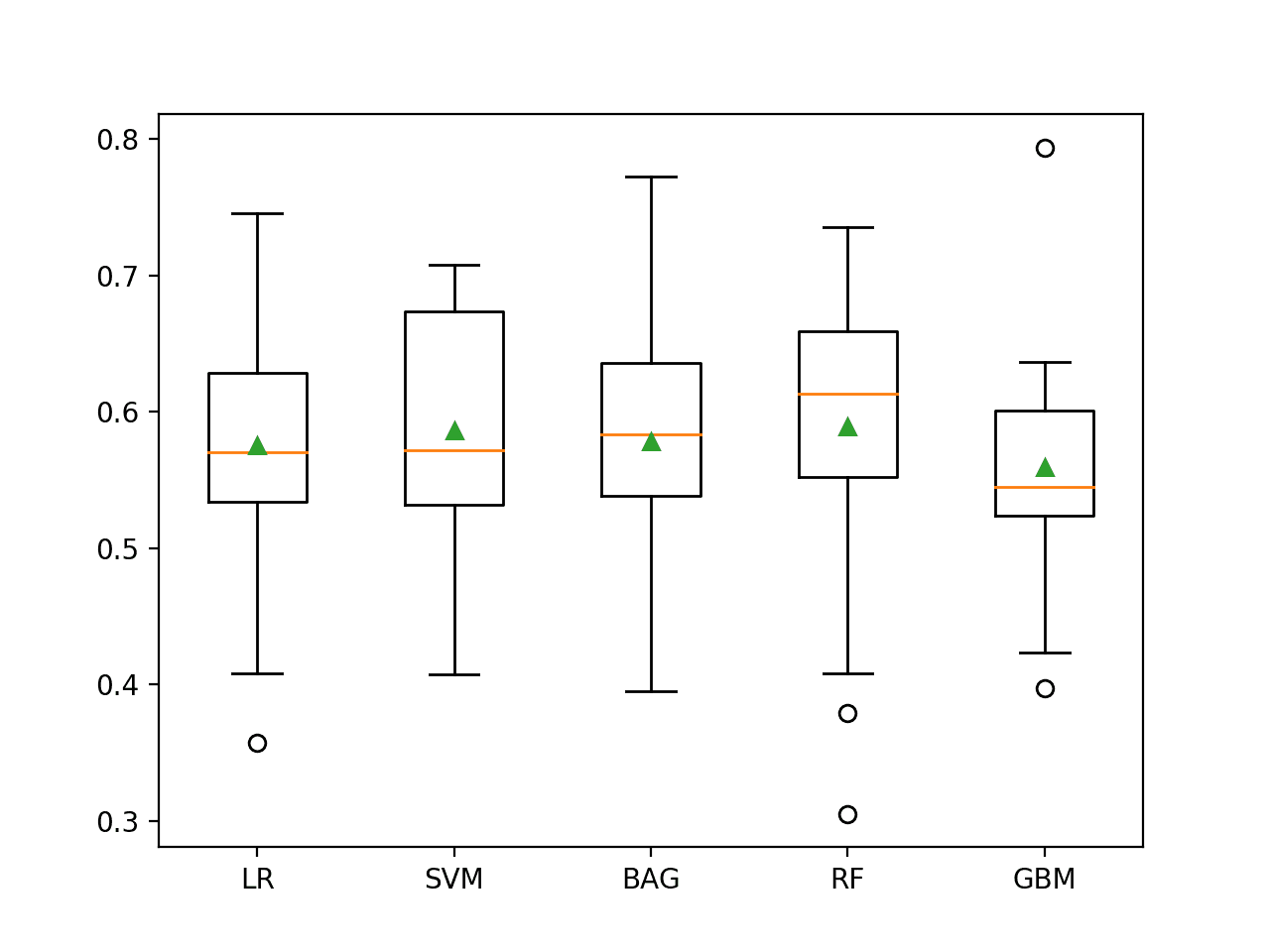
In this case, we can see that each algorithm has skill, achieving a mean G-mean above 0.5. The results suggest that an LDA might be the best performing of the models tested.
|
1 2 3 |
>LR 0.621 (0.261) >LDA 0.741 (0.220) >NB 0.721 (0.197) |
The distribution of the G-mean scores is summarized using a figure with a box and whisker plot for each algorithm. We can see that the distribution for both LDA and NB is compact and skillful and that the LR may have a few results during the run where the method performed poorly, pushing the distribution down.
This highlights that it is not just the mean performance, but also the consistency of the model that should be considered when selecting a model.
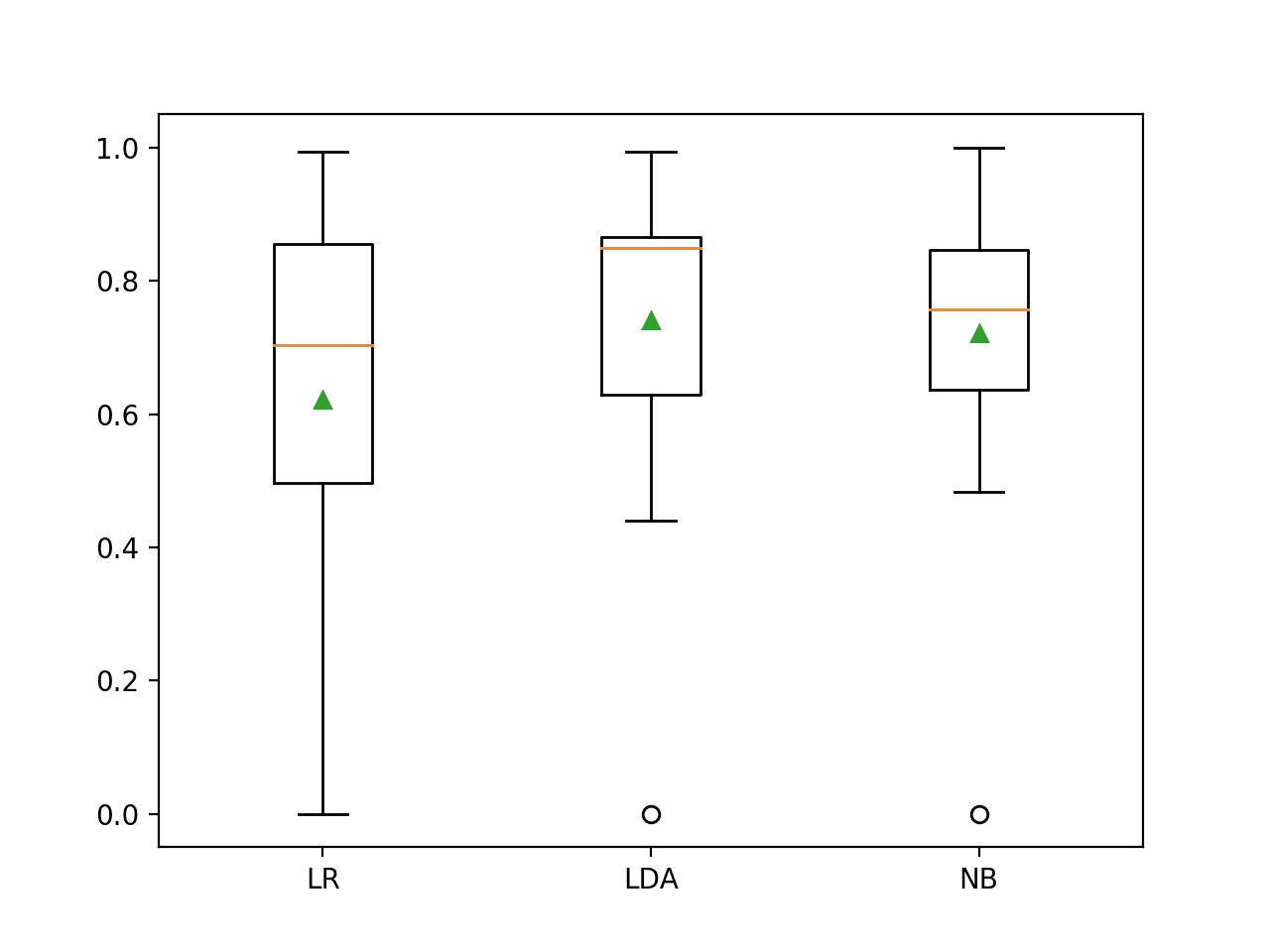
Box and Whisker Plot of Probabilistic Models on the Imbalanced Oil Spill Dataset
We’re off to a good start, but we can do better.
Evaluate Balanced Logistic Regression
The logistic regression algorithm supports a modification that adjusts the importance of classification errors to be inversely proportional to the class weighting.
This allows the model to better learn the class boundary in favor of the minority class, which might help overall G-mean performance. We can achieve this by setting the “class_weight” argument of the LogisticRegression to ‘balanced‘.
|
1 2 |
... LogisticRegression(solver='liblinear', class_weight='balanced') |
As mentioned, logistic regression is sensitive to the scale of input variables and can perform better with normalized or standardized inputs; as such it is a good idea to test both for a given dataset. Additionally, a power distribution can be used to spread out the distribution of each input variable and make those variables with a Gaussian-like distribution more Gaussian. This can benefit models like Logistic Regression that make assumptions about the distribution of input variables.
The power transom will use the Yeo-Johnson method that supports positive and negative inputs, but we will also normalize data prior to the transform. Also, the PowerTransformer class used for the transform will also standardize each variable after the transform.
We will compare a LogisticRegression with a balanced class weighting to the same algorithm with three different data preparation schemes, specifically normalization, standardization, and a power transform.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # define models models, names, results = list(), list(), list() # LR Balanced models.append(LogisticRegression(solver='liblinear', class_weight='balanced')) names.append('Balanced') # LR Balanced + Normalization models.append(Pipeline(steps=[('t', MinMaxScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Norm') # LR Balanced + Standardization models.append(Pipeline(steps=[('t', StandardScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Std') # LR Balanced + Power models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Power') |
Tying this together, the comparison of balanced logistic regression with different data preparation schemes is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
# compare balanced logistic regression on the oil spill dataset from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from imblearn.metrics import geometric_mean_score from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import PowerTransformer # load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, :-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y # evaluate a model def evaluate_model(X, y, model): # define evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # evaluate model scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores # define the location of the dataset full_path = 'oil-spill.csv' # load the dataset X, y = load_dataset(full_path) # define models models, names, results = list(), list(), list() # LR Balanced models.append(LogisticRegression(solver='liblinear', class_weight='balanced')) names.append('Balanced') # LR Balanced + Normalization models.append(Pipeline(steps=[('t', MinMaxScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Norm') # LR Balanced + Standardization models.append(Pipeline(steps=[('t', StandardScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Std') # LR Balanced + Power models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Power') # evaluate each model for i in range(len(models)): # evaluate the model and store results scores = evaluate_model(X, y, models[i]) results.append(scores) # summarize and store print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # plot the results pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example evaluates each version of the balanced logistic regression model on the dataset.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
You may see some warnings from the first balanced LR model, such as “Liblinear failed to converge“. These warnings can be safely ignored for now but suggest that the algorithm could benefit from feature selection to remove some of the variables.
In this case, we can see that the balanced version of logistic regression performs much better than all of the probabilistic models evaluated in the previous section.
The results suggest that perhaps the use of balanced LR with data normalization for pre-processing performs the best on this dataset with a mean G-mean score of about 0.852. This is in the range or better than the results reported in the 1998 paper.
|
1 2 3 4 |
>Balanced 0.846 (0.142) >Balanced-Norm 0.852 (0.119) >Balanced-Std 0.843 (0.124) >Balanced-Power 0.847 (0.130) |
A figure is created with box and whisker plots for each algorithm, allowing the distribution of results to be compared.
We can see that the distribution for the balanced LR is tighter in general than the non-balanced version in the previous section. We can also see that the median result (orange line) for the normalized version is higher than the mean, above 0.9, which is impressive. A mean different from the median suggests a skewed distribution for the results, pulling the mean down with a few bad outcomes.
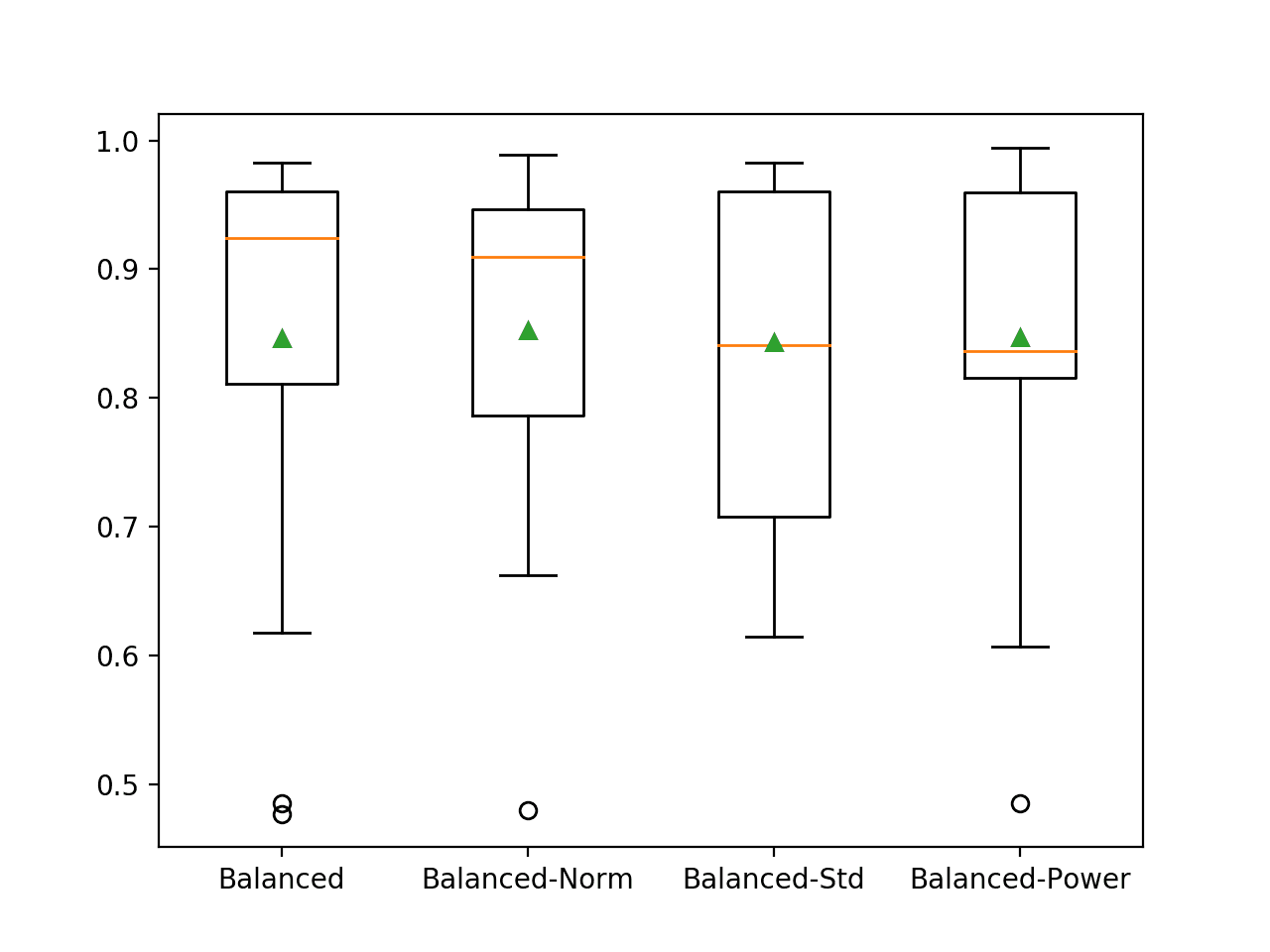
Box and Whisker Plot of Balanced Logistic Regression Models on the Imbalanced Oil Spill Dataset
We now have excellent results with little work; let’s see if we can take it one step further.
Evaluate Data Sampling With Probabilistic Models
Data sampling provides a way to better prepare the imbalanced training dataset prior to fitting a model.
Perhaps the most popular data sampling is the SMOTE oversampling technique for creating new synthetic examples for the minority class. This can be paired with the edited nearest neighbor (ENN) algorithm that will locate and remove examples from the dataset that are ambiguous, making it easier for models to learn to discriminate between the two classes.
This combination is called SMOTE-ENN and can be implemented using the SMOTEENN class from the imbalanced-learn library; for example:
|
1 2 3 |
... # define SMOTE-ENN data sampling method e = SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))) |
SMOTE and ENN both work better when the input data is scaled beforehand. This is because both techniques involve using the nearest neighbor algorithm internally and this algorithm is sensitive to input variables with different scales. Therefore, we will require the data to be normalized as a first step, then sampled, then used as input to the (unbalanced) logistic regression model.
As such, we can use the Pipeline class provided by the imbalanced-learn library to create a sequence of data transforms including the data sampling method, and ending with the logistic regression model.
We will compare four variations of the logistic regression model with data sampling, specifically:
- SMOTEENN + LR
- Normalization + SMOTEENN + LR
- Standardization + SMOTEENN + LR
- Normalization + Power + SMOTEENN + LR
The expectation is that LR will perform better with SMOTEENN, and that SMOTEENN will perform better with standardization or normalization. The last case does a lot, first normalizing the dataset, then applying the power transform, standardizing the result (recall that the PowerTransformer class will standardize the output by default), applying SMOTEENN, then finally fitting a logistic regression model.
These combinations can be defined as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # SMOTEENN models.append(Pipeline(steps=[('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('LR') # SMOTEENN + Norm models.append(Pipeline(steps=[('t', MinMaxScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Norm') # SMOTEENN + Std models.append(Pipeline(steps=[('t', StandardScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Std') # SMOTEENN + Power models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Power') |
Tying this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
# compare data sampling with logistic regression on the oil spill dataset from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from imblearn.metrics import geometric_mean_score from sklearn.preprocessing import PowerTransformer from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from imblearn.pipeline import Pipeline from imblearn.combine import SMOTEENN from imblearn.under_sampling import EditedNearestNeighbours # load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, :-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y # evaluate a model def evaluate_model(X, y, model): # define evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # evaluate model scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores # define the location of the dataset full_path = 'oil-spill.csv' # load the dataset X, y = load_dataset(full_path) # define models models, names, results = list(), list(), list() # SMOTEENN models.append(Pipeline(steps=[('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('LR') # SMOTEENN + Norm models.append(Pipeline(steps=[('t', MinMaxScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Norm') # SMOTEENN + Std models.append(Pipeline(steps=[('t', StandardScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Std') # SMOTEENN + Power models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Power') # evaluate each model for i in range(len(models)): # evaluate the model and store results scores = evaluate_model(X, y, models[i]) # summarize and store print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) results.append(scores) # plot the results pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
Running the example evaluates each version of the SMOTEENN with logistic regression model on the dataset.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the addition of SMOTEENN improves the performance of the default LR algorithm, achieving a mean G-mean of 0.852 compared to 0.621 seen in the first set of experimental results. This is even better than balanced LR without any data scaling (previous section) that achieved a G-mean of about 0.846.
The results suggest that perhaps the final combination of normalization, power transform, and standardization achieves a slightly better score than the default LR with SMOTEENN with a G-mean of about 0.873, although the warning messages suggest some problems that need to be ironed out.
|
1 2 3 4 |
>LR 0.852 (0.105) >Norm 0.838 (0.130) >Std 0.849 (0.113) >Power 0.873 (0.118) |
The distribution of results can be compared with box and whisker plots. We can see the distributions all roughly have the same tight spread and that the difference in means of the results can be used to select a model.
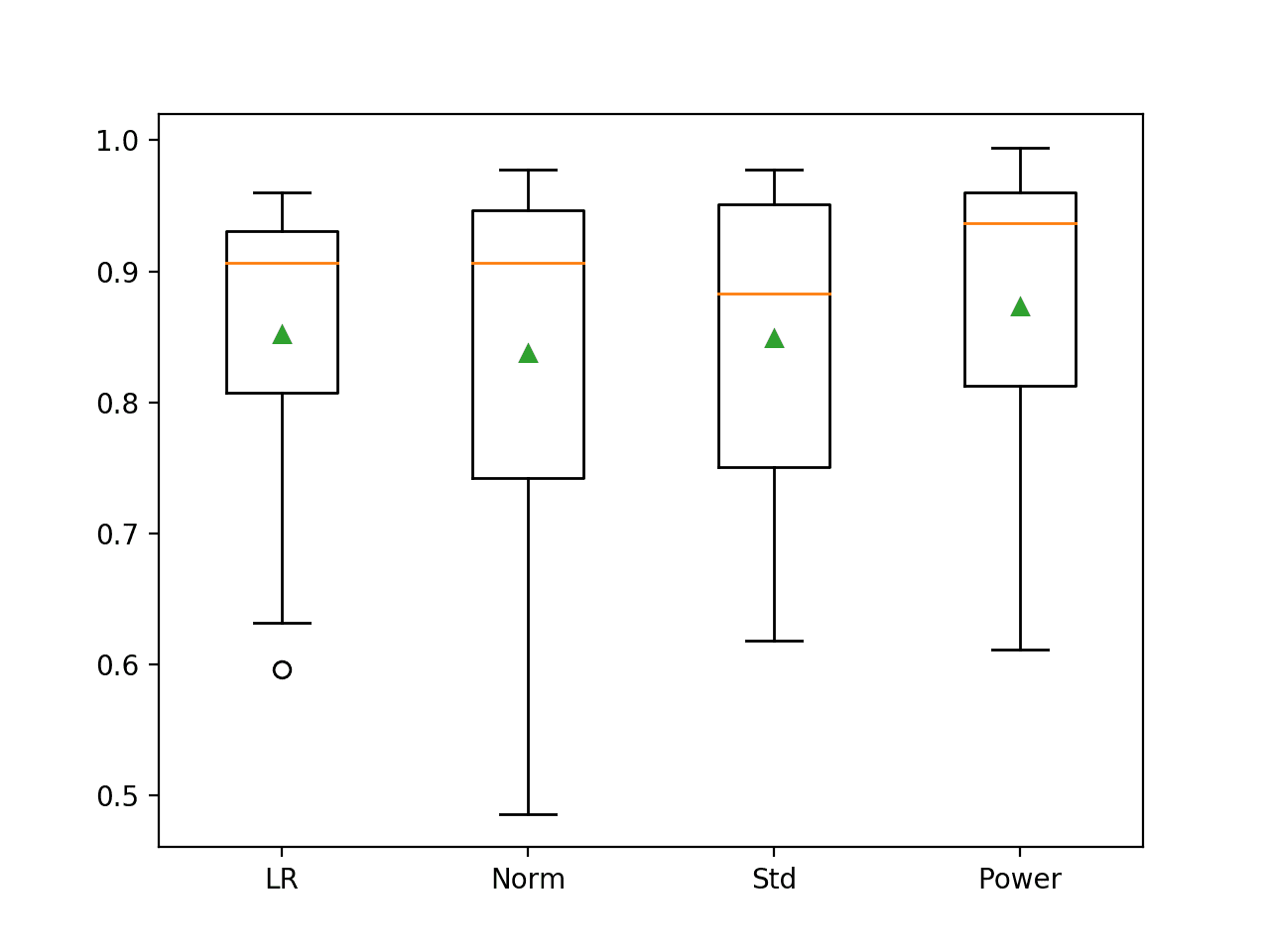
Box and Whisker Plot of Logistic Regression Models with Data Sampling on the Imbalanced Oil Spill Dataset
Make Prediction on New Data
The use of SMOTEENN with Logistic Regression directly without any data scaling probably provides the simplest and well-performing model that could be used going forward.
This model had a mean G-mean of about 0.852 on our test harness.
We will use this as our final model and use it to make predictions on new data.
First, we can define the model as a pipeline.
|
1 2 3 4 5 |
... # define the model smoteenn = SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority')) model = LogisticRegression(solver='liblinear') pipeline = Pipeline(steps=[('e', smoteenn), ('m', model)]) |
Once defined, we can fit it on the entire training dataset.
|
1 2 3 |
... # fit the model pipeline.fit(X, y) |
Once fit, we can use it to make predictions for new data by calling the predict() function. This will return the class label of 0 for no oil spill, or 1 for an oil spill.
For example:
|
1 2 3 4 5 6 7 |
... # define a row of data row = [...] # make prediction yhat = pipeline.predict([row]) # get the label label = yhat[0] |
To demonstrate this, we can use the fit model to make some predictions of labels for a few cases where we know there is no oil spill, and a few where we know there is.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# fit a model and make predictions for the on the oil spill dataset from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.linear_model import LogisticRegression from imblearn.pipeline import Pipeline from imblearn.combine import SMOTEENN from imblearn.under_sampling import EditedNearestNeighbours # load the dataset def load_dataset(full_path): # load the dataset as a numpy array data = read_csv(full_path, header=None) # retrieve numpy array data = data.values # split into input and output elements X, y = data[:, 1:-1], data[:, -1] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder().fit_transform(y) return X, y # define the location of the dataset full_path = 'oil-spill.csv' # load the dataset X, y = load_dataset(full_path) # define the model smoteenn = SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority')) model = LogisticRegression(solver='liblinear') pipeline = Pipeline(steps=[('e', smoteenn), ('m', model)]) # fit the model pipeline.fit(X, y) # evaluate on some non-spill cases (known class 0) print('Non-Spill Cases:') data = [[329,1627.54,1409.43,51,822500,35,6.1,4610,0.17,178.4,0.2,0.24,0.39,0.12,0.27,138.32,34.81,2.02,0.14,0.19,75.26,0,0.47,351.67,0.18,9.24,0.38,2.57,-2.96,-0.28,1.93,0,1.93,34,1710,0,25.84,78,55,1460.31,710.63,451.78,150.85,3.23,0,4530.75,66.25,7.85], [3234,1091.56,1357.96,32,8085000,40.08,8.98,25450,0.22,317.7,0.18,0.2,0.49,0.09,0.41,114.69,41.87,2.31,0.15,0.18,75.26,0,0.53,351.67,0.18,9.24,0.24,3.56,-3.09,-0.31,2.17,0,2.17,281,14490,0,80.11,78,55,4287.77,3095.56,1937.42,773.69,2.21,0,4927.51,66.15,7.24], [2339,1537.68,1633.02,45,5847500,38.13,9.29,22110,0.24,264.5,0.21,0.26,0.79,0.08,0.71,89.49,32.23,2.2,0.17,0.22,75.26,0,0.51,351.67,0.18,9.24,0.27,4.21,-2.84,-0.29,2.16,0,2.16,228,12150,0,83.6,78,55,3959.8,2404.16,1530.38,659.67,2.59,0,4732.04,66.34,7.67]] for row in data: # make prediction yhat = pipeline.predict([row]) # get the label label = yhat[0] # summarize print('>Predicted=%d (expected 0)' % (label)) # evaluate on some spill cases (known class 1) print('Spill Cases:') data = [[2971,1020.91,630.8,59,7427500,32.76,10.48,17380,0.32,427.4,0.22,0.29,0.5,0.08,0.42,149.87,50.99,1.89,0.14,0.18,75.26,0,0.44,351.67,0.18,9.24,2.5,10.63,-3.07,-0.28,2.18,0,2.18,164,8730,0,40.67,78,55,5650.88,1749.29,1245.07,348.7,4.54,0,25579.34,65.78,7.41], [3155,1118.08,469.39,11,7887500,30.41,7.99,15880,0.26,496.7,0.2,0.26,0.69,0.11,0.58,118.11,43.96,1.76,0.15,0.18,75.26,0,0.4,351.67,0.18,9.24,0.78,8.68,-3.19,-0.33,2.19,0,2.19,150,8100,0,31.97,78,55,3471.31,3059.41,2043.9,477.23,1.7,0,28172.07,65.72,7.58], [115,1449.85,608.43,88,287500,40.42,7.34,3340,0.18,86.1,0.21,0.32,0.5,0.17,0.34,71.2,16.73,1.82,0.19,0.29,87.65,0,0.46,132.78,-0.01,3.78,0.7,4.79,-3.36,-0.23,1.95,0,1.95,29,1530,0.01,38.8,89,69,1400,250,150,45.13,9.33,1,31692.84,65.81,7.84]] for row in data: # make prediction yhat = pipeline.predict([row]) # get the label label = yhat[0] # summarize print('>Predicted=%d (expected 1)' % (label)) |
Running the example first fits the model on the entire training dataset.
Then the fit model used to predict the label of an oil spill for cases where we know there is none, chosen from the dataset file. We can see that all cases are correctly predicted.
Then some cases of actual oil spills are used as input to the model and the label is predicted. As we might have hoped, the correct labels are again predicted.
|
1 2 3 4 5 6 7 8 |
Non-Spill Cases: >Predicted=0 (expected 0) >Predicted=0 (expected 0) >Predicted=0 (expected 0) Spill Cases: >Predicted=1 (expected 1) >Predicted=1 (expected 1) >Predicted=1 (expected 1) |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
APIs
- pandas.read_csv API.
- sklearn.model_selection.RepeatedStratifiedKFold API.
- sklearn.dummy.DummyClassifier API.
- imblearn.metrics.geometric_mean_score API.
- sklearn.pipeline.Pipeline API.
- sklearn.linear_model.LogisticRegression API.
- imblearn.combine.SMOTEENN API.
Articles
Summary
In this tutorial, you discovered how to develop a model to predict the presence of an oil spill in satellite images and evaluate it using the G-mean metric.
Specifically, you learned:
- How to load and explore the dataset and generate ideas for data preparation and model selection.
- How to evaluate a suite of probabilistic models and improve their performance with appropriate data preparation.
- How to fit a final model and use it to predict class labels for specific cases.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.





Hi Jason,
Your article is excellent.
Congratulations.
Thanks.
Hi Jason,
Thanks for the article.
I want help with the book I have to buy.
I have a classic imbalance problem: predicting credit defaults for large corporations.
But I don’t want to treat this problem with classic methods (like logistic regression or LDA).
I saw in an article that the heterogeneous set (medium weight set) did an excellent job on a similar problem.
Which book is the most advisable?
Thank you.
#Heterogeneous ensembles(Weighted average ensemble)
This one:
https://machinelearningmastery.com/imbalanced-classification-with-python/
Excellent work! I love it 😀
hi sir…nice work in the field of Machine learning…actually I am now pursuing My PhD….Kindly suggest me some kind of the research components to carry out my research work….
This is a common question that I answer here:
https://machinelearningmastery.com/faq/single-faq/what-research-topic-should-i-work-on
Hey ,Jason Brownlee
Will you please write an eloberated article on text summerisation NLP .
Thanks for the suggestion.
I want to know how to deal with the data which is not Normal for the regression task. LIke price prediction where data is not normally distributed. How can we deal with that?
Try modeling it directly as a baseline. Then perhaps try power transform and other transforms and review any change/lift in performance.
Seems typo in smoteenn code:
SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy=’minority’))
Thanks, what is the typo exactly?
Hi Jason,
Thanks again for you detailed and excellent explanation of each step in building the model.
Did you choose, a logistic regression model for the sake of reproducibility with the paper?. Just curious if with a Boosting algorithm you could get a higher accuracy.
Thanks!
Carlos.
No, I tested a ton of algorithms and found that it performed well.
Thanks for this presentation.
I am quite uncomfortable about estimating the performance using the resampled dataset. I mean using the output dataset of the resampling function (Smoteenn in this article). I would prefer to use the original data.
Nevertheless, if we expect the a smoothed boundary to the function to be estimate, the resampling makes the boundary more “visible” also possibly more noisy.
In the other hand, one advandtave of smoteenn is the removing step that approximatly keep the resampled dataset in a convex space (almost).
Still, I don’t have a clear overview of this, do you ?
Thanks,
Jérémie
I think you misunderstand data resampling.
We fit on resampled data, but we estimate on raw data.
I am agree with this strategy : fit on resampled data, and estimate on raw data.
Nevertheless, I don’t understand where in the whole code from section “Evaluate Data Sampling With Probabilistic Models”, the performance estimation is computed only on raw data.
In the cross-validation loop “cross_val_score”, you give the raw data (X, y) to the pipeline that contains the resampling method. Do you mean that the cross_val_score apply the resampling only for the training step and keep the raw data for the prediction/evaluation ? I don’t think it is the case.
Thanks!
Correct, the tutorial enumerates different strategies in order to discover what works best for this dataset.
Yes, the reason we use a Pipeline is because it is aware of only performing data sampling transforms on training data and NOT to test data during cross-validation. Learn more here:
https://imbalanced-learn.readthedocs.io/en/stable/generated/imblearn.pipeline.Pipeline.html
Indeed, I saw that in the pipeline.py code of the imbalearn library : https://github.com/scikit-learn-contrib/imbalanced-learn/blob/12b2e0d2858a30d4687fbf910372b8f416b33998/imblearn/pipeline.py#L319
Thanks!
You’re welcome.
Great tutorial, as always!
I have a question regarding the PowerTransformer step in the pipeline.
I would imagine than only some of the features, not all, need this kind of transformation to have a more “Gaussian-like” distribution.
Doesn’t it hurt other features when we apply this transformation to the whole dataset?
Would there be a way, within the pipeline, to tell PowerTransformer to apply the transformation only to certain features and not others?
Update : I tried to achieve this by defining a custom function which fits the transformer to selected columns only. I’m not sure if that makes sense or not. It doesn’t have any impact on the score at all…
def powtransf():
pt = PowerTransformer()
columns=[0,1,2,4,7,9,15,16,21,26,30,32,33,38,39,40,41,42,43,44,45,46]
return pt.fit(X[:,columns])
[…]
models.append(Pipeline(steps=[(‘t’, MinMaxScaler()),(‘p’,powtransf()),(‘m’, LogisticRegression(solver=’liblinear’, class_weight = ‘balanced’))]))
If no impact on score, it is not needed on this task, might be useful on other projects…
Very likely.
Ideally, we would check each feature in turn.
Hello, I would like to ask, what are the digitized image features, I can not find 50 so many, what way do you get so many digital features?
You can see the paper “Machine Learning for the Detection of Oil Spills in Satellite Radar Images.” linked in the tutorial that explains the data.
Hi, thanks for sharing this, I am novice in Machine Learning. My question is: How could I apply this model to a new image? I don’t really understand what the features are and how to convert satellite images to use this model.
You would have to extract features from the new image then feed those features into a model.
In this case, we don’t have the tools used to extract features from images.