Last Updated on October 11, 2019
The Frechet Inception Distance score, or FID for short, is a metric that calculates the distance between feature vectors calculated for real and generated images.
The score summarizes how similar the two groups are in terms of statistics on computer vision features of the raw images calculated using the inception v3 model used for image classification. Lower scores indicate the two groups of images are more similar, or have more similar statistics, with a perfect score being 0.0 indicating that the two groups of images are identical.
The FID score is used to evaluate the quality of images generated by generative adversarial networks, and lower scores have been shown to correlate well with higher quality images.
In this tutorial, you will discover how to implement the Frechet Inception Distance for evaluating generated images.
After completing this tutorial, you will know:
- The Frechet Inception Distance summarizes the distance between the Inception feature vectors for real and generated images in the same domain.
- How to calculate the FID score and implement the calculation from scratch in NumPy.
- How to implement the FID score using the Keras deep learning library and calculate it with real images.
Kick-start your project with my new book Generative Adversarial Networks with Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Updated Oct 2019: Fixed minor typo in the description of the method.
How to Implement the Frechet Inception Distance (FID) From Scratch for Evaluating Generated Images
Photo by dronepicr, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
- What Is the Frechet Inception Distance?
- How to Calculate the Frechet Inception Distance
- How to Implement the Frechet Inception Distance With NumPy
- How to Implement the Frechet Inception Distance With Keras
- How to Calculate the Frechet Inception Distance for Real Images
What Is the Frechet Inception Distance?
The Frechet Inception Distance, or FID for short, is a metric for evaluating the quality of generated images and specifically developed to evaluate the performance of generative adversarial networks.
The FID score was proposed and used by Martin Heusel, et al. in their 2017 paper titled “GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium.”
The score was proposed as an improvement over the existing Inception Score, or IS.
For the evaluation of the performance of GANs at image generation, we introduce the “Frechet Inception Distance” (FID) which captures the similarity of generated images to real ones better than the Inception Score.
— GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium, 2017.
The inception score estimates the quality of a collection of synthetic images based on how well the top-performing image classification model Inception v3 classifies them as one of 1,000 known objects. The scores combine both the confidence of the conditional class predictions for each synthetic image (quality) and the integral of the marginal probability of the predicted classes (diversity).
The inception score does not capture how synthetic images compare to real images. The goal in developing the FID score was to evaluate synthetic images based on the statistics of a collection of synthetic images compared to the statistics of a collection of real images from the target domain.
Drawback of the Inception Score is that the statistics of real world samples are not used and compared to the statistics of synthetic samples.
— GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium, 2017.
Like the inception score, the FID score uses the inception v3 model. Specifically, the coding layer of the model (the last pooling layer prior to the output classification of images) is used to capture computer-vision-specific features of an input image. These activations are calculated for a collection of real and generated images.
The activations are summarized as a multivariate Gaussian by calculating the mean and covariance of the images. These statistics are then calculated for the activations across the collection of real and generated images.
The distance between these two distributions is then calculated using the Frechet distance, also called the Wasserstein-2 distance.
The difference of two Gaussians (synthetic and real-world images) is measured by the Frechet distance also known as Wasserstein-2 distance.
— GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium, 2017.
The use of activations from the Inception v3 model to summarize each image gives the score its name of “Frechet Inception Distance.”
A lower FID indicates better-quality images; conversely, a higher score indicates a lower-quality image and the relationship may be linear.
The authors of the score show that lower FID scores correlate with better-quality images when systematic distortions were applied such as the addition of random noise and blur.
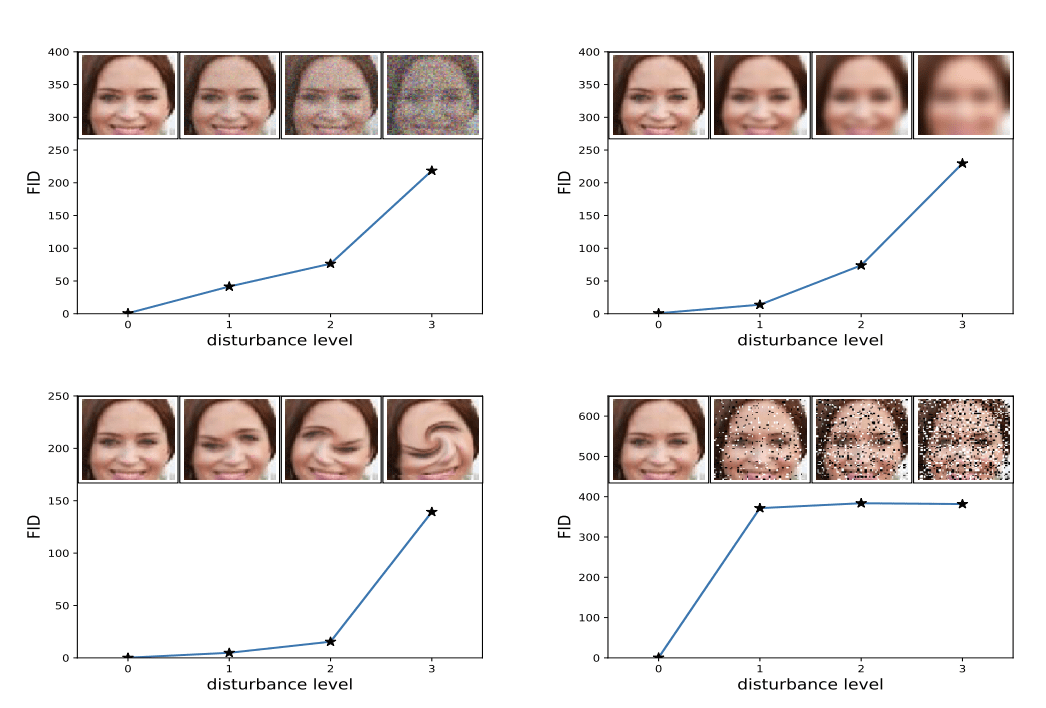
Example of How Increased Distortion of an Image Correlates with High FID Score.
Taken from: GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium.
How to Calculate the Frechet Inception Distance
The FID score is calculated by first loading a pre-trained Inception v3 model.
The output layer of the model is removed and the output is taken as the activations from the last pooling layer, a global spatial pooling layer.
This output layer has 2,048 activations, therefore, each image is predicted as 2,048 activation features. This is called the coding vector or feature vector for the image.
A 2,048 feature vector is then predicted for a collection of real images from the problem domain to provide a reference for how real images are represented. Feature vectors can then be calculated for synthetic images.
The result will be two collections of 2,048 feature vectors for real and generated images.
The FID score is then calculated using the following equation taken from the paper:
- d^2 = ||mu_1 – mu_2||^2 + Tr(C_1 + C_2 – 2*sqrt(C_1*C_2))
The score is referred to as d^2, showing that it is a distance and has squared units.
The “mu_1” and “mu_2” refer to the feature-wise mean of the real and generated images, e.g. 2,048 element vectors where each element is the mean feature observed across the images.
The C_1 and C_2Â are the covariance matrix for the real and generated feature vectors, often referred to as sigma.
The ||mu_1 – mu_2||^2 refers to the sum squared difference between the two mean vectors. Tr refers to the trace linear algebra operation, e.g. the sum of the elements along the main diagonal of the square matrix.
The sqrt is the square root of the square matrix, given as the product between the two covariance matrices.
The square root of a matrix is often also written as M^(1/2), e.g. the matrix to the power of one half, which has the same effect. This operation can fail depending on the values in the matrix because the operation is solved using numerical methods. Commonly, some elements in the resulting matrix may be imaginary, which often can be detected and removed.
Want to Develop GANs from Scratch?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
How to Implement the Frechet Inception Distance With NumPy
Implementing the calculation of the FID score in Python with NumPy arrays is straightforward.
First, let’s define a function that will take a collection of activations for real and generated images and return the FID score.
The calculate_fid() function listed below implements the procedure.
Here, we implement the FID calculation almost directly. It is worth noting that the official implementation in TensorFlow implements elements of the calculation in a slightly different order, likely for efficiency, and introduces additional checks around the matrix square root to handle possible numerical instabilities.
I recommend reviewing the official implementation and extending the implementation below to add these checks if you experience problems calculating the FID on your own datasets.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# calculate frechet inception distance def calculate_fid(act1, act2): # calculate mean and covariance statistics mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False) mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False) # calculate sum squared difference between means ssdiff = numpy.sum((mu1 - mu2)**2.0) # calculate sqrt of product between cov covmean = sqrtm(sigma1.dot(sigma2)) # check and correct imaginary numbers from sqrt if iscomplexobj(covmean): covmean = covmean.real # calculate score fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean) return fid |
We can then test out this function to calculate the inception score for some contrived feature vectors.
Feature vectors will probably contain small positive values and will have a length of 2,048 elements. We can construct two lots of 10 images worth of feature vectors with small random numbers as follows:
|
1 2 3 4 5 6 |
... # define two collections of activations act1 = random(10*2048) act1 = act1.reshape((10,2048)) act2 = random(10*2048) act2 = act2.reshape((10,2048)) |
One test would be to calculate the FID between a set of activations and itself, which we would expect to have a score of 0.0.
We can then calculate the distance between the two sets of random activations, which we would expect to be a large number.
|
1 2 3 4 5 6 7 |
... # fid between act1 and act1 fid = calculate_fid(act1, act1) print('FID (same): %.3f' % fid) # fid between act1 and act2 fid = calculate_fid(act1, act2) print('FID (different): %.3f' % fid) |
Tying this all together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# example of calculating the frechet inception distance import numpy from numpy import cov from numpy import trace from numpy import iscomplexobj from numpy.random import random from scipy.linalg import sqrtm # calculate frechet inception distance def calculate_fid(act1, act2): # calculate mean and covariance statistics mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False) mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False) # calculate sum squared difference between means ssdiff = numpy.sum((mu1 - mu2)**2.0) # calculate sqrt of product between cov covmean = sqrtm(sigma1.dot(sigma2)) # check and correct imaginary numbers from sqrt if iscomplexobj(covmean): covmean = covmean.real # calculate score fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean) return fid # define two collections of activations act1 = random(10*2048) act1 = act1.reshape((10,2048)) act2 = random(10*2048) act2 = act2.reshape((10,2048)) # fid between act1 and act1 fid = calculate_fid(act1, act1) print('FID (same): %.3f' % fid) # fid between act1 and act2 fid = calculate_fid(act1, act2) print('FID (different): %.3f' % fid) |
Running the example first reports the FID between the act1 activations and itself, which is 0.0 as we expect (Note: the sign of the score can be ignored).
The distance between the two collections of random activations is also as we expect: a large number, which in this case was 358.
|
1 2 |
FID (same): -0.000 FID (different): 358.927 |
You may want to experiment with the calculation of the FID score and test other pathological cases.
How to Implement the Frechet Inception Distance With Keras
Now that we know how to calculate the FID score and to implement it in NumPy, we can develop an implementation in Keras.
This involves the preparation of the image data and using a pretrained Inception v3 model to calculate the activations or feature vectors for each image.
First, we can load the Inception v3 model in Keras directly.
|
1 2 3 |
... # load inception v3 model model = InceptionV3() |
This will prepare a version of the inception model for classifying images as one of 1,000 known classes. We can remove the output (the top) of the model via the include_top=False argument. Painfully, this also removes the global average pooling layer that we require, but we can add it back via specifying the pooling=’avg’ argument.
When the output layer of the model is removed, we must specify the shape of the input images, which is 299x299x3 pixels, e.g. the input_shape=(299,299,3) argument.
Therefore, the inception model can be loaded as follows:
|
1 2 3 |
... # prepare the inception v3 model model = InceptionV3(include_top=False, pooling='avg', input_shape=(299,299,3)) |
This model can then be used to predict the feature vector for one or more images.
Our images are likely to not have the required shape. We will use the scikit-image library to resize the NumPy array of pixel values to the required size. The scale_images() function below implements this.
|
1 2 3 4 5 6 7 8 9 |
# scale an array of images to a new size def scale_images(images, new_shape): images_list = list() for image in images: # resize with nearest neighbor interpolation new_image = resize(image, new_shape, 0) # store images_list.append(new_image) return asarray(images_list) |
Note, you may need to install the scikit-image library. This can be achieved as follows:
|
1 |
sudo pip install scikit-image |
Once resized, the image pixel values will also need to be scaled to meet the expectations for inputs to the inception model. This can be achieved by calling the preprocess_input() function.
We can update our calculate_fid() function defined in the previous section to take the loaded inception model and two NumPy arrays of image data as arguments, instead of activations. The function will then calculate the activations before calculating the FID score as before.
The updated version of the calculate_fid() function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# calculate frechet inception distance def calculate_fid(model, images1, images2): # calculate activations act1 = model.predict(images1) act2 = model.predict(images2) # calculate mean and covariance statistics mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False) mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False) # calculate sum squared difference between means ssdiff = numpy.sum((mu1 - mu2)**2.0) # calculate sqrt of product between cov covmean = sqrtm(sigma1.dot(sigma2)) # check and correct imaginary numbers from sqrt if iscomplexobj(covmean): covmean = covmean.real # calculate score fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean) return fid |
We can then test this function with some contrived collections of images, in this case, 10 32×32 images with random pixel values in the range [0,255].
|
1 2 3 4 5 6 |
... # define two fake collections of images images1 = randint(0, 255, 10*32*32*3) images1 = images1.reshape((10,32,32,3)) images2 = randint(0, 255, 10*32*32*3) images2 = images2.reshape((10,32,32,3)) |
We can then convert the integer pixel values to floating point values and scale them to the required size of 299×299 pixels.
|
1 2 3 4 5 6 7 |
... # convert integer to floating point values images1 = images1.astype('float32') images2 = images2.astype('float32') # resize images images1 = scale_images(images1, (299,299,3)) images2 = scale_images(images2, (299,299,3)) |
Then the pixel values can be scaled to meet the expectations of the Inception v3 model.
|
1 2 3 4 |
... # pre-process images images1 = preprocess_input(images1) images2 = preprocess_input(images2) |
Then calculate the FID scores, first between a collection of images and itself, then between the two collections of images.
|
1 2 3 4 5 6 7 |
... # fid between images1 and images1 fid = calculate_fid(model, images1, images1) print('FID (same): %.3f' % fid) # fid between images1 and images2 fid = calculate_fid(model, images1, images2) print('FID (different): %.3f' % fid) |
Tying all of this together, the complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# example of calculating the frechet inception distance in Keras import numpy from numpy import cov from numpy import trace from numpy import iscomplexobj from numpy import asarray from numpy.random import randint from scipy.linalg import sqrtm from keras.applications.inception_v3 import InceptionV3 from keras.applications.inception_v3 import preprocess_input from keras.datasets.mnist import load_data from skimage.transform import resize # scale an array of images to a new size def scale_images(images, new_shape): images_list = list() for image in images: # resize with nearest neighbor interpolation new_image = resize(image, new_shape, 0) # store images_list.append(new_image) return asarray(images_list) # calculate frechet inception distance def calculate_fid(model, images1, images2): # calculate activations act1 = model.predict(images1) act2 = model.predict(images2) # calculate mean and covariance statistics mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False) mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False) # calculate sum squared difference between means ssdiff = numpy.sum((mu1 - mu2)**2.0) # calculate sqrt of product between cov covmean = sqrtm(sigma1.dot(sigma2)) # check and correct imaginary numbers from sqrt if iscomplexobj(covmean): covmean = covmean.real # calculate score fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean) return fid # prepare the inception v3 model model = InceptionV3(include_top=False, pooling='avg', input_shape=(299,299,3)) # define two fake collections of images images1 = randint(0, 255, 10*32*32*3) images1 = images1.reshape((10,32,32,3)) images2 = randint(0, 255, 10*32*32*3) images2 = images2.reshape((10,32,32,3)) print('Prepared', images1.shape, images2.shape) # convert integer to floating point values images1 = images1.astype('float32') images2 = images2.astype('float32') # resize images images1 = scale_images(images1, (299,299,3)) images2 = scale_images(images2, (299,299,3)) print('Scaled', images1.shape, images2.shape) # pre-process images images1 = preprocess_input(images1) images2 = preprocess_input(images2) # fid between images1 and images1 fid = calculate_fid(model, images1, images1) print('FID (same): %.3f' % fid) # fid between images1 and images2 fid = calculate_fid(model, images1, images2) print('FID (different): %.3f' % fid) |
Running the example first summarizes the shapes of the fabricated images and their rescaled versions, matching our expectations.
Note: the first time the InceptionV3 model is used, Keras will download the model weights and save them into the ~/.keras/models/ directory on your workstation. The weights are about 100 megabytes and may take a moment to download depending on the speed of your internet connection.
The FID score between a given set of images and itself is 0.0, as we expect, and the distance between the two collections of random images is about 35.
|
1 2 3 4 |
Prepared (10, 32, 32, 3) (10, 32, 32, 3) Scaled (10, 299, 299, 3) (10, 299, 299, 3) FID (same): -0.000 FID (different): 35.495 |
How to Calculate the Frechet Inception Distance for Real Images
It may be useful to calculate the FID score between two collections of real images.
The Keras library provides a number of computer vision datasets, including the CIFAR-10 dataset. These are color photos with the small size of 32×32 pixels and is split into train and test elements and can be loaded as follows:
|
1 2 3 |
... # load cifar10 images (images1, _), (images2, _) = cifar10.load_data() |
The training dataset has 50,000 images, whereas the test dataset has only 10,000 images. It may be interesting to calculate the FID score between these two datasets to get an idea of how representative the test dataset is of the training dataset.
Scaling and scoring 50K images takes a long time, therefore, we can reduce the “training set” to a 10K random sample as follows:
|
1 2 3 |
... shuffle(images1) images1 = images1[:10000] |
Tying this all together, we can calculate the FID score between a sample of the train and the test dataset as follows.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
# example of calculating the frechet inception distance in Keras for cifar10 import numpy from numpy import cov from numpy import trace from numpy import iscomplexobj from numpy import asarray from numpy.random import shuffle from scipy.linalg import sqrtm from keras.applications.inception_v3 import InceptionV3 from keras.applications.inception_v3 import preprocess_input from keras.datasets.mnist import load_data from skimage.transform import resize from keras.datasets import cifar10 # scale an array of images to a new size def scale_images(images, new_shape): images_list = list() for image in images: # resize with nearest neighbor interpolation new_image = resize(image, new_shape, 0) # store images_list.append(new_image) return asarray(images_list) # calculate frechet inception distance def calculate_fid(model, images1, images2): # calculate activations act1 = model.predict(images1) act2 = model.predict(images2) # calculate mean and covariance statistics mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False) mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False) # calculate sum squared difference between means ssdiff = numpy.sum((mu1 - mu2)**2.0) # calculate sqrt of product between cov covmean = sqrtm(sigma1.dot(sigma2)) # check and correct imaginary numbers from sqrt if iscomplexobj(covmean): covmean = covmean.real # calculate score fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean) return fid # prepare the inception v3 model model = InceptionV3(include_top=False, pooling='avg', input_shape=(299,299,3)) # load cifar10 images (images1, _), (images2, _) = cifar10.load_data() shuffle(images1) images1 = images1[:10000] print('Loaded', images1.shape, images2.shape) # convert integer to floating point values images1 = images1.astype('float32') images2 = images2.astype('float32') # resize images images1 = scale_images(images1, (299,299,3)) images2 = scale_images(images2, (299,299,3)) print('Scaled', images1.shape, images2.shape) # pre-process images images1 = preprocess_input(images1) images2 = preprocess_input(images2) # calculate fid fid = calculate_fid(model, images1, images2) print('FID: %.3f' % fid) |
Running the example may take some time depending on the speed of your workstation.
At the end of the run, we can see that the FID score between the train and test datasets is about five.
|
1 2 3 |
Loaded (10000, 32, 32, 3) (10000, 32, 32, 3) Scaled (10000, 299, 299, 3) (10000, 299, 299, 3) FID: 5.492 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
- GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium, 2017.
- Are GANs Created Equal? A Large-Scale Study, 2017.
- Pros and Cons of GAN Evaluation Measures, 2018.
Code Projects
- Official Implementation in TensorFlow, GitHub.
- Frechet Inception Distance (FID score) in PyTorch, GitHub.
API
- numpy.trace API.
- numpy.cov API.
- numpy.iscomplexobj API.
- Keras Inception v3 Model
- scikit-image Library
Articles
- Frechet Inception Distance, 2017.
- Frechet Inception Distance, 2018.
- Frechet distance, Wikipedia.
- Covariance matrix, Wikipedia.
- Square root of a matrix, Wikipedia.
Summary
In this tutorial, you discovered how to implement the Frechet Inception Distance for evaluating generated images.
Specifically, you learned:
- The Frechet Inception Distance summarizes the distance between the Inception feature vectors for real and generated images in the same domain.
- How to calculate the FID score and implement the calculation from scratch in NumPy.
- How to implement the FID score using the Keras deep learning library and calculate it with real images.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
Develop Generative Adversarial Networks Today!
Develop Your GAN Models in Minutes
...with just a few lines of python codeDiscover how in my new Ebook:
Generative Adversarial Networks with Python
It provides self-study tutorials and end-to-end projects on:
DCGAN, conditional GANs, image translation, Pix2Pix, CycleGAN
and much more...
Hi Jason,
Thanks a lot for your tutorials and keep touching lives with your awesome tutorials.
Thanks, I’m glad the help!
Hi Jason,
May I know is this method suitable to measure for synthetic time series data? Or is there any suitable approach to measure?
No.
I’m not sure off the cuff, sorry.
Hi, Thnx for valuable tutorial. Suppose i have generated data for two classes from two classes Positive & Negative, by running GAN two times. Then should i have to measure FID by taking same classes i.e. Positive original vs Positive Generated and same for negative. Or i have to mix the classes i.e. (Positive original + Negative Original) vs (Positive Generate + negative Generated).
Not sure I follow, sorry.
FID is run on generated images regardless of “class”.
hello
thanks for this great tutorial
its important to consider a batch size?
in other implementation i see batch size for calculating fid
how to add this feature?
thank you in advance
I guess it does not matter for the calculation, but does for the efficiency of the calculation – e.g. running batches of images through the model.
thank you for your replay
i have a another question
when i want to calculate fid score between real and genereated images
i must use test dataset or train dataset or both is allowed ???
thank you very much
You are generating new images, there is no train/test dataset in this case.
hello
thank you for replay
consider a conditinal gan such as Pix2Pix
for calculating FID we need two directory of images (real and fake images)
this image(input images to generator and target images) must be from test dataset?
Thank you very much for explaining
Ah yes, I see. I forgot how fid worked. It’s been a year.
Hey Jason, great tutorials as usual. I have got a custom dataset with a dimension of 64*64*1(grayscale) per image. In order to scale it up with the Inception model, should I convert it to the RGB color-space?
Hmmm, I don’t have a good off the cuff answer. Perhaps try it and see what happens.
Hey Jason, I tried it but got an error stating that the input image depth must be 3. So I did an np.dstack((img, img, img)) on my dataset to make it as per the model requirements and it worked. As usual, thanks for your amazing blogs, they are really helping me implement my projects.
Well done!
Amazing Work Once Again, I am using the CelebA dataset, how many images will be enough to generate for calculating FID.
Thanks.
Hundreds or perhaps thousands.
thank you, i did apply your FID implementation with some modification on 4000+ images, the quality of the images is ok, yet i get an FID score of 20000+, while the same images gives FID of 200+ on other implementations, probably my modification and addition of ImageDataGenerator might be responsible for that.
Interesting.
Thank you so much , for everything that i’m searching about GAN you have a tutorial with awesome code explanations .Keep Going
Thanks!
Thanks a lot. I’m doing my thesis on GANs and you’re saving me!
You’re welcome!
Thank you for all your great tutorials on GANs.
A question that crosses my mind is whether IS or FID scores are just metrics or we can use them as loss functions too ( 1 – FID)?
Off the cuff, they are just metrics.
Hi Jason,
You will have to check, but skimage resize automatically changes the range from 0-255 to 0-1. So the output of the function will be (299, 299, 3) between 0-1. You then apply preprocess_input, which is defined as:
def preprocess_input(x):
x /= 255.
x -= 0.5
x *= 2.
return x
Presumably you are double scaling. You can add preserve_range=True in resize to avoid that.
When doing anything except classification with pretrained networks they tend to be kind of robusts to details like these, but then of course, that it what makes them terrible in terms of adversarial robustness.
Thanks for the tip Simon! I’ll investigate.
resize() does not appear to change the range of the pixel values.
Hi Jason,
How do we calculate the FID score if the dataset size is less than 2048 images?
2048 is not related to the number of images used to calculate the score.
Hi Jason,
In the Official Implementation in TensorFlow, GitHub – they say:
IMPORTANT: The number of samples to calculate the Gaussian statistics (mean and covariance) should be greater than the dimension of the coding layer, here 2048 for the Inception pool 3 layer. Otherwise the covariance is not full rank resulting in complex numbers and nans by calculating the square root.
We recommend using a minimum sample size of 10,000 to calculate the FID otherwise the true FID of the generator is underestimated.
In my case I do not have that many samples. Is it still Ok to calculate the FID on very little samples (<2048)?
Fair enough.
Perhaps don’t use the official implementation to meet the requirements you listd.
Dear Jason,
I have finished the first two parts of your book “GAN with Python”. I have written a review about it:
http://questioneurope.blogspot.com/2020/09/generative-adversarial-networks-with.html
Kind regards,
Dominique
Well done!
Dear Dr. Jason
Hello,thank you for wonderful works.
I have a question. Could I use this to calculate fid value between datasets in my local path to another datasets in my local path?
I used like this:
images1 = list(glob(str(“real images path”)))
shuffle(images1)
images1 = images1[:1000]
images1 = DataFrame(images1)
images2 = DataFrame(list(glob(str(“generated images path”))))
But I got a error like this:
ValueError: Input 0 of layer conv2d_846 is incompatible with the layer: : expected min_ndim=4, found ndim=2. Full shape received: (None, 1)
You’re welcome.
Sorry, I don’t know why you got this error. Perhaps you can post your entire code listing and error to stackoverflow.com
Hi Jason, thanks for the tutorials. Does the FID score have value when applied to a GAN generating images which don’t belong to any of the 1000 classes that inception v3 was trained on?
It will give a score, not sure that it will be as useful.
Hi Jason,
Firstly , thanks a lot for sharing your knowledge. Truly appreciate it.
I tried using your codes on 10000 images. No problem.
It was also alright to compare 20000 images.
however, from 30000 images onwards, memory issues begin to come up.
It’s almost impossible to calculate FID for 50000 images as recommended to get reliable FID values. Even when I used on a system with 117 GB memory.
How could we get around memory issues?
Perhaps you can try using a machine with more memory, e.g. in the cloud?
Perhaps you can try using fewer images?
Perhaps you can try scaling down the image sizes?
Okay thanks Jason.
Hi Jason, amazing job. Can the feature vector for evaluating the FID score be extracted for another network, e.g., a Residual Network?
Thanks.
Perhaps.
Dear Jason,
Thank you very much for your sharing. Your tutorials help me a lot.
There is a question I want to seek your suggestions about FID. Can we use it in different other datasets, for example, my own dataset?
Best regards,
Rui Guo
I think so, perhaps experiment.
Hello Jason,
Thank you very much for your sharing.
I found that the ‘calculate_fid’ function may not suitable for calculating only a one-pair comparison. As the variable name implies ‘images1’, the numpy function will fail with only input one pair image.
Since the covariance matrix is a single value, the msqrt, trace will not work properly.
For example.
act_1, act_2 = model.predict(im_1), model.predict(im_2)
one_sigma_val_1 = cov(act1, rowvar=False)
one_sigma_val_2 = cov(act2, rowvar=False)
…
covmean = sqrtm(one_sigma_val_1.dot(one_sigma_val_2 )) // error this line.
Best regards,
Josef Huang
Thanks.
HI . did you find solution for this error
Hi Jason
Thank you for the great tutorial
Can FID be useful for non image and 1D data sets, like generating “gene expression” data ?
Hey, thanks for this! why do we assume that the dist. of hte features of both fakes and reals is gaussian?
Hi Rachel…The following resource may add clarity:
https://www.itl.nist.gov/div898/handbook/pmd/section4/pmd445.htm
Hi Jason,
May I know what is the recommended number of samples for calculating FID score?
Hi Mohamed..The following resource may be of interest:
https://openaccess.thecvf.com/content_CVPR_2020/papers/Chong_Effectively_Unbiased_FID_and_Inception_Score_and_Where_to_Find_CVPR_2020_paper.pdf
Hi, there’s a problem with the link to the paper. I found the working link as of now: https://arxiv.org/abs/1706.08500#
Thank you Kien!
Nice post!
Thank you!
Hi Naooooooo…You are very welcome! Thank you for the feedback and support!
Thank you for sharing this informative article on implementing the Frechet Inception Distance (FID) for evaluating GANs. It provides a clear and detailed explanation of what FID is and how to calculate it from scratch using NumPy and with the Keras deep learning library. This will be a valuable resource for anyone working with generative adversarial networks.
Thank you for your feedback and support Brandi! We greatly support it!