A problem with gradient boosted decision trees is that they are quick to learn and overfit training data.
One effective way to slow down learning in the gradient boosting model is to use a learning rate, also called shrinkage (or eta in XGBoost documentation).
In this post you will discover the effect of the learning rate in gradient boosting and how to tune it on your machine learning problem using the XGBoost library in Python.
After reading this post you will know:
- The effect learning rate has on the gradient boosting model.
- How to tune learning rate on your machine learning on your problem.
- How to tune the trade-off between the number of boosted trees and learning rate on your problem.
Kick-start your project with my new book XGBoost With Python, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Update Jan/2017: Updated to reflect changes in scikit-learn API version 0.18.1.

Tune Learning Rate for Gradient Boosting with XGBoost in Python
Photo by Robert Hertel, some rights reserved.
Need help with XGBoost in Python?
Take my free 7-day email course and discover xgboost (with sample code).
Click to sign-up now and also get a free PDF Ebook version of the course.
Slow Learning in Gradient Boosting with a Learning Rate
Gradient boosting involves creating and adding trees to the model sequentially.
New trees are created to correct the residual errors in the predictions from the existing sequence of trees.
The effect is that the model can quickly fit, then overfit the training dataset.
A technique to slow down the learning in the gradient boosting model is to apply a weighting factor for the corrections by new trees when added to the model.
This weighting is called the shrinkage factor or the learning rate, depending on the literature or the tool.
Naive gradient boosting is the same as gradient boosting with shrinkage where the shrinkage factor is set to 1.0. Setting values less than 1.0 has the effect of making less corrections for each tree added to the model. This in turn results in more trees that must be added to the model.
It is common to have small values in the range of 0.1 to 0.3, as well as values less than 0.1.
Let’s investigate the effect of the learning rate on a standard machine learning dataset.
Problem Description: Otto Dataset
In this tutorial we will use the Otto Group Product Classification Challenge dataset.
This dataset is available for free from Kaggle (you will need to sign-up to Kaggle to be able to download this dataset). You can download the training dataset train.csv.zip from the Data page and place the unzipped train.csv file into your working directory.
This dataset describes the 93 obfuscated details of more than 61,000 products grouped into 10 product categories (e.g. fashion, electronics, etc.). Input attributes are counts of different events of some kind.
The goal is to make predictions for new products as an array of probabilities for each of the 10 categories and models are evaluated using multiclass logarithmic loss (also called cross entropy).
This competition was completed in May 2015 and this dataset is a good challenge for XGBoost because of the nontrivial number of examples, the difficulty of the problem and the fact that little data preparation is required (other than encoding the string class variables as integers).
Tuning Learning Rate in XGBoost
When creating gradient boosting models with XGBoost using the scikit-learn wrapper, the learning_rate parameter can be set to control the weighting of new trees added to the model.
We can use the grid search capability in scikit-learn to evaluate the effect on logarithmic loss of training a gradient boosting model with different learning rate values.
We will hold the number of trees constant at the default of 100 and evaluate of suite of standard values for the learning rate on the Otto dataset.
|
1 |
learning_rate = [0.0001, 0.001, 0.01, 0.1, 0.2, 0.3] |
There are 6 variations of learning rate to be tested and each variation will be evaluated using 10-fold cross validation, meaning that there is a total of 6×10 or 60 XGBoost models to be trained and evaluated.
The log loss for each learning rate will be printed as well as the value that resulted in the best performance.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
# XGBoost on Otto dataset, Tune learning_rate from pandas import read_csv from xgboost import XGBClassifier from sklearn.model_selection import GridSearchCV from sklearn.model_selection import StratifiedKFold from sklearn.preprocessing import LabelEncoder import matplotlib matplotlib.use('Agg') from matplotlib import pyplot # load data data = read_csv('train.csv') dataset = data.values # split data into X and y X = dataset[:,0:94] y = dataset[:,94] # encode string class values as integers label_encoded_y = LabelEncoder().fit_transform(y) # grid search model = XGBClassifier() learning_rate = [0.0001, 0.001, 0.01, 0.1, 0.2, 0.3] param_grid = dict(learning_rate=learning_rate) kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7) grid_search = GridSearchCV(model, param_grid, scoring="neg_log_loss", n_jobs=-1, cv=kfold) grid_result = grid_search.fit(X, label_encoded_y) # summarize results print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_)) means = grid_result.cv_results_['mean_test_score'] stds = grid_result.cv_results_['std_test_score'] params = grid_result.cv_results_['params'] for mean, stdev, param in zip(means, stds, params): print("%f (%f) with: %r" % (mean, stdev, param)) # plot pyplot.errorbar(learning_rate, means, yerr=stds) pyplot.title("XGBoost learning_rate vs Log Loss") pyplot.xlabel('learning_rate') pyplot.ylabel('Log Loss') pyplot.savefig('learning_rate.png') |
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running this example prints the best result as well as the log loss for each of the evaluated learning rates.
|
1 2 3 4 5 6 7 |
Best: -0.001156 using {'learning_rate': 0.2} -2.155497 (0.000081) with: {'learning_rate': 0.0001} -1.841069 (0.000716) with: {'learning_rate': 0.001} -0.597299 (0.000822) with: {'learning_rate': 0.01} -0.001239 (0.001730) with: {'learning_rate': 0.1} -0.001156 (0.001684) with: {'learning_rate': 0.2} -0.001158 (0.001666) with: {'learning_rate': 0.3} |
Interestingly, we can see that the best learning rate was 0.2.
This is a high learning rate and it suggest that perhaps the default number of trees of 100 is too low and needs to be increased.
We can also plot the effect of the learning rate of the (inverted) log loss scores, although the log10-like spread of chosen learning_rate values means that most are squashed down the left-hand side of the plot near zero.
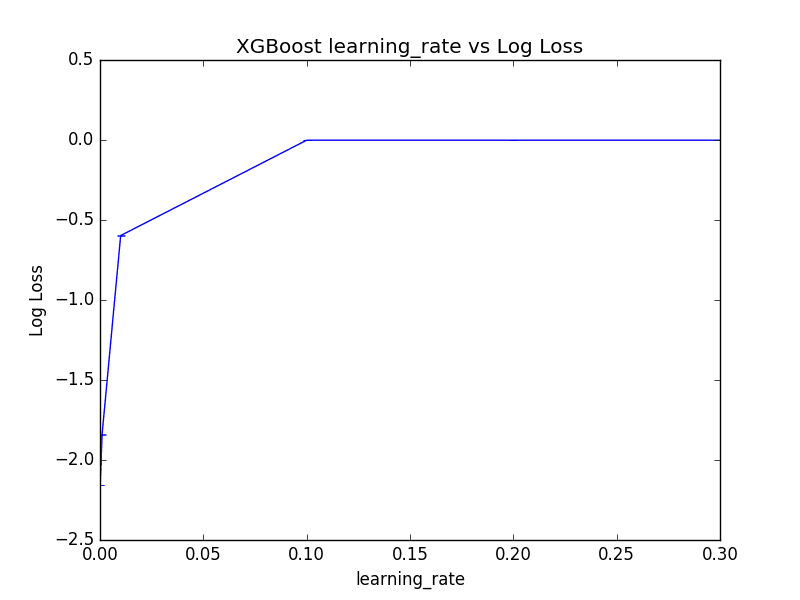
Tune Learning Rate in XGBoost
Next, we will look at varying the number of trees whilst varying the learning rate.
Tuning Learning Rate and the Number of Trees in XGBoost
Smaller learning rates generally require more trees to be added to the model.
We can explore this relationship by evaluating a grid of parameter pairs. The number of decision trees will be varied from 100 to 500 and the learning rate varied on a log10 scale from 0.0001 to 0.1.
|
1 2 |
n_estimators = [100, 200, 300, 400, 500] learning_rate = [0.0001, 0.001, 0.01, 0.1] |
There are 5 variations of n_estimators and 4 variations of learning_rate. Each combination will be evaluated using 10-fold cross validation, so that is a total of 4x5x10 or 200 XGBoost models that must be trained and evaluated.
The expectation is that for a given learning rate, performance will improve and then plateau as the number of trees is increased. The full code listing is provided below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# XGBoost on Otto dataset, Tune learning_rate and n_estimators from pandas import read_csv from xgboost import XGBClassifier from sklearn.model_selection import GridSearchCV from sklearn.model_selection import StratifiedKFold from sklearn.preprocessing import LabelEncoder import matplotlib matplotlib.use('Agg') from matplotlib import pyplot import numpy # load data data = read_csv('train.csv') dataset = data.values # split data into X and y X = dataset[:,0:94] y = dataset[:,94] # encode string class values as integers label_encoded_y = LabelEncoder().fit_transform(y) # grid search model = XGBClassifier() n_estimators = [100, 200, 300, 400, 500] learning_rate = [0.0001, 0.001, 0.01, 0.1] param_grid = dict(learning_rate=learning_rate, n_estimators=n_estimators) kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7) grid_search = GridSearchCV(model, param_grid, scoring="neg_log_loss", n_jobs=-1, cv=kfold) grid_result = grid_search.fit(X, label_encoded_y) # summarize results print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_)) means = grid_result.cv_results_['mean_test_score'] stds = grid_result.cv_results_['std_test_score'] params = grid_result.cv_results_['params'] for mean, stdev, param in zip(means, stds, params): print("%f (%f) with: %r" % (mean, stdev, param)) # plot results scores = numpy.array(means).reshape(len(learning_rate), len(n_estimators)) for i, value in enumerate(learning_rate): pyplot.plot(n_estimators, scores[i], label='learning_rate: ' + str(value)) pyplot.legend() pyplot.xlabel('n_estimators') pyplot.ylabel('Log Loss') pyplot.savefig('n_estimators_vs_learning_rate.png') |
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Running the example prints the best combination as well as the log loss for each evaluated pair.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Best: -0.001152 using {'n_estimators': 300, 'learning_rate': 0.1} -2.155497 (0.000081) with: {'n_estimators': 100, 'learning_rate': 0.0001} -2.115540 (0.000159) with: {'n_estimators': 200, 'learning_rate': 0.0001} -2.077211 (0.000233) with: {'n_estimators': 300, 'learning_rate': 0.0001} -2.040386 (0.000304) with: {'n_estimators': 400, 'learning_rate': 0.0001} -2.004955 (0.000373) with: {'n_estimators': 500, 'learning_rate': 0.0001} -1.841069 (0.000716) with: {'n_estimators': 100, 'learning_rate': 0.001} -1.572384 (0.000692) with: {'n_estimators': 200, 'learning_rate': 0.001} -1.364543 (0.000699) with: {'n_estimators': 300, 'learning_rate': 0.001} -1.196490 (0.000713) with: {'n_estimators': 400, 'learning_rate': 0.001} -1.056687 (0.000728) with: {'n_estimators': 500, 'learning_rate': 0.001} -0.597299 (0.000822) with: {'n_estimators': 100, 'learning_rate': 0.01} -0.214311 (0.000929) with: {'n_estimators': 200, 'learning_rate': 0.01} -0.080729 (0.000982) with: {'n_estimators': 300, 'learning_rate': 0.01} -0.030533 (0.000949) with: {'n_estimators': 400, 'learning_rate': 0.01} -0.011769 (0.001071) with: {'n_estimators': 500, 'learning_rate': 0.01} -0.001239 (0.001730) with: {'n_estimators': 100, 'learning_rate': 0.1} -0.001153 (0.001702) with: {'n_estimators': 200, 'learning_rate': 0.1} -0.001152 (0.001704) with: {'n_estimators': 300, 'learning_rate': 0.1} -0.001153 (0.001708) with: {'n_estimators': 400, 'learning_rate': 0.1} -0.001153 (0.001708) with: {'n_estimators': 500, 'learning_rate': 0.1} |
We can see that the best result observed was a learning rate of 0.1 with 300 trees.
It is hard to pick out trends from the raw data and small negative log loss results. Below is a plot of each learning rate as a series showing log loss performance as the number of trees is varied.
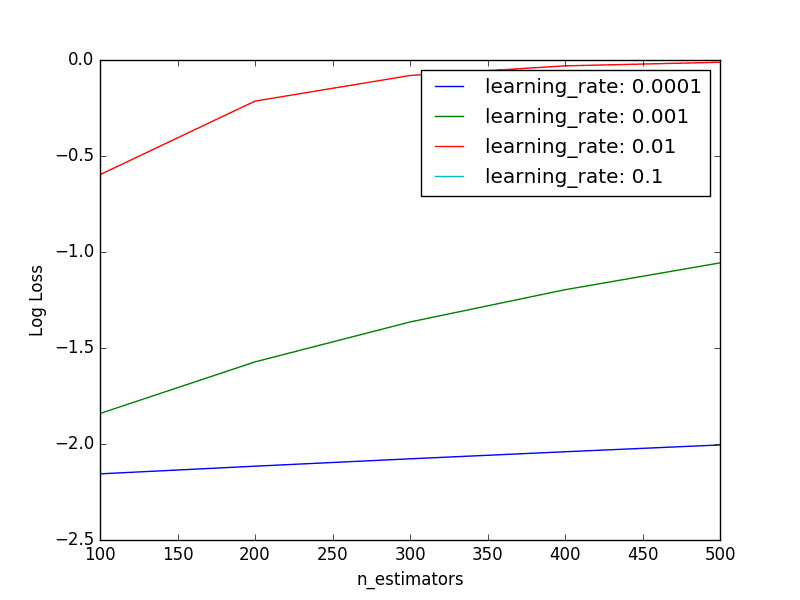
Tuning Learning Rate and Number of Trees in XGBoost
We can see that the expected general trend holds, where the performance (inverted log loss) improves as the number of trees is increased.
Performance is generally poor for the smaller learning rates, suggesting that a much larger number of trees may be required. We may need to increase the number of trees to many thousands which may be quite computationally expensive.
The results for learning_rate=0.1 are obscured due the large y-axis scale of the graph. We can extract the performance measure for just learning_rate=0.1 and plot them directly.
|
1 2 3 4 5 6 7 8 9 |
# Plot performance for learning_rate=0.1 from matplotlib import pyplot n_estimators = [100, 200, 300, 400, 500] loss = [-0.001239, -0.001153, -0.001152, -0.001153, -0.001153] pyplot.plot(n_estimators, loss) pyplot.xlabel('n_estimators') pyplot.ylabel('Log Loss') pyplot.title('XGBoost learning_rate=0.1 n_estimators vs Log Loss') pyplot.show() |
Running this code shows the increased performance as the number of trees are added, followed by a plateau in performance across 400 and 500 trees.
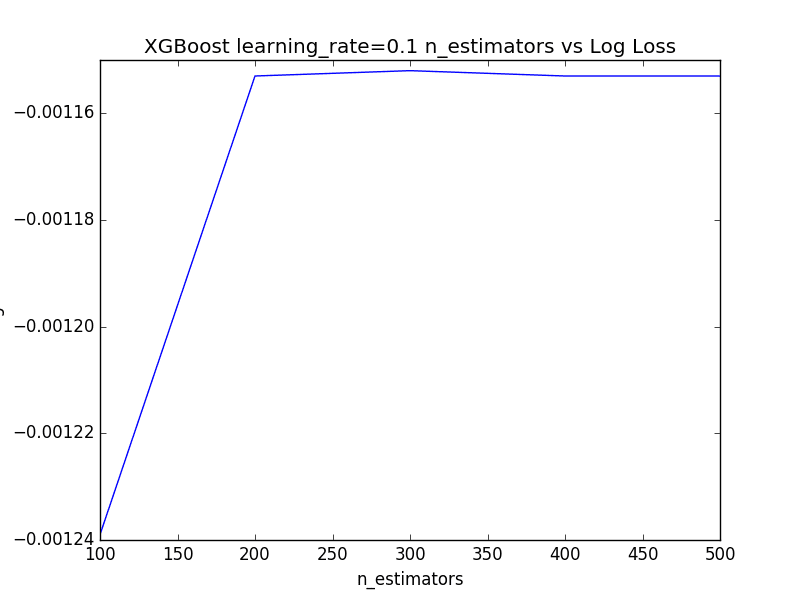
Plot of Learning Rate=0.1 and varying the Number of Trees in XGBoost
Summary
In this post you discovered the effect of weighting the addition of new trees to a gradient boosting model, called shrinkage or the learning rate.
Specifically, you learned:
- That adding a learning rate is intended to slow down the adaptation of the model to the training data.
- How to evaluate a range of learning rate values on your machine learning problem.
- How to evaluate the relationship of varying both the number of trees and the learning rate on your problem.
Do you have any questions regarding shrinkage in gradient boosting or about this post? Ask your questions in the comments and I will do my best to answer them.






Hi! How long does it take to run the first part “Tuning the Learning Rate” and what system are you running it on? Thanks.
I ran the examples on a large AWS instance, for example:
https://machinelearningmastery.com/train-xgboost-models-cloud-amazon-web-services/
Sorry, I do not recall how long it took. I believe no example took longer than a few hours.
Great! Thanks for the info!
“Tuning Learning Rate and the Number of Trees in XGBoost” Running this part is taking more time for me (completed 6 hours but still running).
Ouch, I think I may have run it on a large AWS instance with 32 cores.
What is the use of learning rate and what does it represent? can you please tell me any intuitive explanation?
The learning rate makes the boosting process more or less conservative, e.g. to correct or boost more or less based on the results of the previously added tree.
Excellent and userful article. I applied it on my data, It helped me to choose learning rate and n_estimators prefectly because of which Results imporoved a lot.
Thanks,
Thanks, well done!
the first colum of csv is ID, Isn’t this feature useless?
Thank you
Yes, it often is.
How to do make predictions on the tuned xg_boost model? Do you just pass the learning rate and number of trees as parameters in XGBClassifier? Could you add that code also to the article?
After the model is fit, you can save it and use it to start making predictions.
This is called creating a final model, more here:
https://machinelearningmastery.com/train-final-machine-learning-model/
Hi.. Is it possible to show how the tree is built for gradient boosted tree for binary class problem?.. I am curious how exactly the tree is built.. Using what function to determine the split.. And how the results from each tree being added to compute the prediction class. If possible .. Use simple example.. With learning rate 0.1.. . I am familiar with single cart tree… But till now not able to get the understanding for gradient boosted tree.. Only recently i realized that for gradient boosted tree.. The tree is builtbusing regression tree.. And the classification is converted using probability value. I would appreciate a lot if u can show one example as requested … Thanks
Thanks for the suggestion.
Hey, can you please tell me why we are even going for learning rate or shrinkage parameter in GB while we already have number of base learners as hyperparameter and we even having thepre-computed γ m through gradient minimization technique, so how does this learning rate adds more value in this?
This is a shrinkage factor, it is explained in the post. Perhaps a re-read is in order?
Instead of having discrete values for learning rate, an approach with lower and upper bounds can be tried as well. So, something similar to learning_rate = scipy.stats.uniform(lower_bound, upper_bound)
Thanks.
Hi, I have a question here.
I read some paper and it seems that we need to find the best learning rate (minimize our loss function) after we fit the base learner. Does it mean in Python library, we don’t need to find the best learning rate and we just simply set it as a constant number?
never mind. I abused notation here.
No problem.
how evaluate the accuracy,precision and recall after tuning the parameter
You can calculate any metrics you wish using the scikit-learn library:
https://scikit-learn.org/stable/modules/classes.html#module-sklearn.metrics
grid_search
after executing grid_search i got the result as mentioned below
GridSearchCV(cv=StratifiedKFold(n_splits=5, random_state=7, shuffle=True),
error_score=’raise-deprecating’,
estimator=XGBClassifier(base_score=0.5, booster=’gbtree’, colsample_bylevel=1,
colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=0,
max_depth=3, min_child_weight=1, missing=None, n_estimators=100,
n_jobs=1, nthread=None, objective=’binary:logistic’, random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=True, subsample=1),
fit_params=None, iid=’warn’, n_jobs=-1,
param_grid={‘learning_rate’: [0.0001, 0.001, 0.01, 0.1, 0.2, 0.3]},
pre_dispatch=’2*n_jobs’, refit=True, return_train_score=’warn’,
scoring=’neg_log_loss’, verbose=0)
but when i am trying to execute “grid_result = grid_search.fit(X, label_encoded_y)” it will shows this error can you suggest the solution
JoblibValueError Traceback (most recent call last)
in ()
—-> 1 grid_result = grid_search.fit(X, label_encoded_y)
/home/gopal/.local/lib/python2.7/site-packages/sklearn/model_selection/_search.pyc in fit(self, X, y, groups, **fit_params)
721 return results_container[0]
722
–> 723 self._run_search(evaluate_candidates)
724
725 results = results_container[0]
/home/gopal/.local/lib/python2.7/site-packages/sklearn/model_selection/_search.pyc in _run_search(self, evaluate_candidates)
1190 def _run_search(self, evaluate_candidates):
1191 “””Search all candidates in param_grid”””
-> 1192 evaluate_candidates(ParameterGrid(self.param_grid))
1193
1194
/home/gopal/.local/lib/python2.7/site-packages/sklearn/model_selection/_search.pyc in evaluate_candidates(candidate_params)
710 for parameters, (train, test)
711 in product(candidate_params,
–> 712 cv.split(X, y, groups)))
713
714 all_candidate_params.extend(candidate_params)
/home/gopal/.local/lib/python2.7/site-packages/sklearn/externals/joblib/parallel.pyc in __call__(self, iterable)
932
933 with self._backend.retrieval_context():
–> 934 self.retrieve()
935 # Make sure that we get a last message telling us we are done
936 elapsed_time = time.time() – self._start_time
/home/gopal/.local/lib/python2.7/site-packages/sklearn/externals/joblib/parallel.pyc in retrieve(self)
860 this_report = format_outer_frames(context=10,
861 stack_start=1)
–> 862 raise exception.unwrap(this_report)
863 else:
864 raise
JoblibValueError: JoblibValueError
Sorry to hear that, I have some suggestions here:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
hi Jason
For grid search cross validation , i got RMSE=1066 ,MAE=749.49 but for normal cross validation the RMSE =1052 ,MAE= 739.03 so i am confused that after tuning the parameter still the rmse value is more than the normal cross validatio rmse value for big mart dataset. please guide me on this aslo sugesst me how to calculate accuracy based rmse and mae value
The difference might be due to the stochastic nature of the learning algorithm.
Perhaps try repeated cross-validation to get a more stable evaluation?
Hi Jason
As per my knowledge log loss is nothingh but a cross entropy , which ranges 0 to 1 but here your graph showing negative value for log loss in every time i.e log loss vs learning rate and other graph as well as. Also i am getting same negative values for logloss , please clarify me why i got the negative value for log loss?
Yes, sklearn inverts loss scores to make all scores maximize instead of minimize.
You see this with negative MSE as well.
why it so sir, if loss score is maximize then the model will not treat as good model i think
What do you mean exactly?
i mean if log loss score is maximized instead of minimize in sklearn .how do i interpret the model whether is good or bad model. also what is the significance negative value of log loss .
A model has skill if you evaluate it using a metric, like accuracy, and compare it to a naive model and it performs better.
This will help:
https://machinelearningmastery.com/faq/single-faq/how-to-know-if-a-model-has-good-performance
There seems to be a point for the learning rate above which you get a normal range of predictions between 0 and 1 but below which you get a limited range of predictions from XGBoost (e.g., all records are between .49 and .51 for example). Have you noticed this and can you explain what is happening? The lower learning rate with the limited prediction range yields lower precision and recall but has much better capture rate for top 3 deciles in validation results in every case.
Fascinating.
No, I have not seen that before. It maybe the case that the model fails to converge.
Any insights on the math behind the learning rate? Is a value of 0.1 something like a weight?
It controls the amount of update to the model or contribution of a given tree to the prediction. Smaller means less contribution and more trees will be required most likely.
Use trial and error to configure for a given dataset.
Does XGBoost perform better than neural networks?
Depends on the specific dataset.
For tabular data, yes often it does.
Hi Jason,
In Kaggle Competition Notebooks people tuning upto 4 decimals for XGB parameters like
params = {'classify__estimator__colsample_bytree': 0.6522,
'classify__estimator__gamma': 3.6975,
'classify__estimator__learning_rate': 0.0503,
'classify__estimator__max_delta_step': 2.0706,
'classify__estimator__max_depth': 10,
'classify__estimator__min_child_weight': 31.5800,
'classify__estimator__n_estimators': 166,
'classify__estimator__subsample': 0.8639
}
May i know how it is possible?
I found some using hyperopt library, but accuracy wise its not good when compared with the tuning results between hyperopt and gridsearch, gridsearch giving more accuracy than hyperopt.
Dont understand why lower accuracy with hyperopt
hyperopt is just another way to search the space of possible hyperparameters, it is not the “best”. There is no “best” way to search, given the no free lunch theorem:
https://machinelearningmastery.com/faq/single-faq/what-is-the-no-free-lunch-theorem
Yes, that can happen if you use a good grid.
Sorry, I don’t understand the problem, it seems fine to me.
What do you mean exactly, can you please elaborate?
Thanks Jason, Understood
HI Jason,
My teacher actually used this example and exact set up in our class example. I am now trying to apply (the exact same setup) to my own model but I am getting error that says ”
ValueError: Invalid parameter learning_rate for estimator ” (I have posted the full error below). What does this mean? When I first got the error I was using the number you have listed above for n_estimator and learning rate. I then I tried increase the learning rate but I am still getting the same error.
—————————————————————————
_RemoteTraceback Traceback (most recent call last)
_RemoteTraceback:
“””
Traceback (most recent call last):
File “C:\Users\cyrra\anaconda3\lib\site-packages\joblib\externals\loky\process_executor.py”, line 431, in _process_worker
r = call_item()
File “C:\Users\cyrra\anaconda3\lib\site-packages\joblib\externals\loky\process_executor.py”, line 285, in __call__
return self.fn(*self.args, **self.kwargs)
File “C:\Users\cyrra\anaconda3\lib\site-packages\joblib\_parallel_backends.py”, line 595, in __call__
return self.func(*args, **kwargs)
File “C:\Users\cyrra\anaconda3\lib\site-packages\joblib\parallel.py”, line 262, in __call__
return [func(*args, **kwargs)
File “C:\Users\cyrra\anaconda3\lib\site-packages\joblib\parallel.py”, line 262, in
return [func(*args, **kwargs)
File “C:\Users\cyrra\anaconda3\lib\site-packages\sklearn\utils\fixes.py”, line 222, in __call__
return self.function(*args, **kwargs)
File “C:\Users\cyrra\anaconda3\lib\site-packages\sklearn\model_selection\_validation.py”, line 581, in _fit_and_score
estimator = estimator.set_params(**cloned_parameters)
File “C:\Users\cyrra\anaconda3\lib\site-packages\sklearn\base.py”, line 230, in set_params
raise ValueError(‘Invalid parameter %s for estimator %s. ‘
ValueError: Invalid parameter learning_rate for estimator GridSearchCV(cv=StratifiedKFold(n_splits=4, random_state=7, shuffle=True),
estimator=XGBClassifier(base_score=0.5, booster=’gbtree’,
colsample_bylevel=1, colsample_bynode=1,
colsample_bytree=1, gamma=0, gpu_id=-1,
importance_type=’gain’,
interaction_constraints=”,
learning_rate=0.300000012,
max_delta_step=0, max_depth=6,
min_child_weight=1, missing=nan,
monotone_constraints='()’,
n_estimators=100, n_jobs=8,
num_parallel_tree=1,
objective=’multi:softprob’, random_state=0,
reg_alpha=0, reg_lambda=1,
scale_pos_weight=None, subsample=1,
tree_method=’exact’, validate_parameters=1,
verbosity=None),
n_jobs=-1,
param_grid={‘max_depth’: [2, 4, 6, 8],
‘n_estimators’: [50, 100, 150, 200]},
scoring=’neg_log_loss’, verbose=1). Check the list of available parameters with
estimator.get_params().keys().“””
The above exception was the direct cause of the following exception:
ValueError Traceback (most recent call last)
in
—-> 1 grid_result_m = grid_search_m.fit(X, ym)
~\anaconda3\lib\site-packages\sklearn\utils\validation.py in inner_f(*args, **kwargs)
61 extra_args = len(args) – len(all_args)
62 if extra_args 63 return f(*args, **kwargs)
64
65 # extra_args > 0
~\anaconda3\lib\site-packages\sklearn\model_selection\_search.py in fit(self, X, y, groups, **fit_params)
839 return results
840
–> 841 self._run_search(evaluate_candidates)
842
843 # multimetric is determined here because in the case of a callable
~\anaconda3\lib\site-packages\sklearn\model_selection\_search.py in _run_search(self, evaluate_candidates)
1286 def _run_search(self, evaluate_candidates):
1287 “””Search all candidates in param_grid”””
-> 1288 evaluate_candidates(ParameterGrid(self.param_grid))
1289
1290
~\anaconda3\lib\site-packages\sklearn\model_selection\_search.py in evaluate_candidates(candidate_params, cv, more_results)
793 n_splits, n_candidates, n_candidates * n_splits))
794
–> 795 out = parallel(delayed(_fit_and_score)(clone(base_estimator),
796 X, y,
797 train=train, test=test,
~\anaconda3\lib\site-packages\joblib\parallel.py in __call__(self, iterable)
1052
1053 with self._backend.retrieval_context():
-> 1054 self.retrieve()
1055 # Make sure that we get a last message telling us we are done
1056 elapsed_time = time.time() – self._start_time
~\anaconda3\lib\site-packages\joblib\parallel.py in retrieve(self)
931 try:
932 if getattr(self._backend, ‘supports_timeout’, False):
–> 933 self._output.extend(job.get(timeout=self.timeout))
934 else:
935 self._output.extend(job.get())
~\anaconda3\lib\site-packages\joblib\_parallel_backends.py in wrap_future_result(future, timeout)
540 AsyncResults.get from multiprocessing.”””
541 try:
–> 542 return future.result(timeout=timeout)
543 except CfTimeoutError as e:
544 raise TimeoutError from e
~\anaconda3\lib\concurrent\futures\_base.py in result(self, timeout)
437 raise CancelledError()
438 elif self._state == FINISHED:
–> 439 return self.__get_result()
440 else:
441 raise TimeoutError()
~\anaconda3\lib\concurrent\futures\_base.py in __get_result(self)
386 def __get_result(self):
387 if self._exception:
–> 388 raise self._exception
389 else:
390 return self._result
ValueError: Invalid parameter learning_rate for estimator GridSearchCV(cv=StratifiedKFold(n_splits=4, random_state=7, shuffle=True),
estimator=XGBClassifier(base_score=0.5, booster=’gbtree’,
colsample_bylevel=1, colsample_bynode=1,
colsample_bytree=1, gamma=0, gpu_id=-1,
importance_type=’gain’,
interaction_constraints=”,
learning_rate=0.300000012,
max_delta_step=0, max_depth=6,
min_child_weight=1, missing=nan,
monotone_constraints='()’,
n_estimators=100, n_jobs=8,
num_parallel_tree=1,
objective=’multi:softprob’, random_state=0,
reg_alpha=0, reg_lambda=1,
scale_pos_weight=None, subsample=1,
tree_method=’exact’, validate_parameters=1,
verbosity=None),
n_jobs=-1,
param_grid={‘max_depth’: [2, 4, 6, 8],
‘n_estimators’: [50, 100, 150, 200]},
scoring=’neg_log_loss’, verbose=1). Check the list of available parameters with
estimator.get_params().keys().I’m sorry to hear that you’re having trouble, perhaps some of these tips will help:
https://machinelearningmastery.com/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
I’m confused about how you have gone about choosing the optimal learning rate. In the graph the log loss is plotted. We want to minimize the loss. Since logarithm is a monotonic transformation, this means we also want to choose the value of the learning rate that minimizes this log-loss, so the optimal learning rate is actually 0.0001. This also backs up the theory that XGBoost generalizes better with as small learning rate as possible.
Hi Dom…the following may be of interest to you:
https://towardsdatascience.com/selecting-optimal-parameters-for-xgboost-model-training-c7cd9ed5e45e