Having seen how to implement the scaled dot-product attention and integrate it within the multi-head attention of the Transformer model, let’s progress one step further toward implementing a complete Transformer model by applying its encoder. Our end goal remains to apply the complete model to Natural Language Processing (NLP).
In this tutorial, you will discover how to implement the Transformer encoder from scratch in TensorFlow and Keras.
After completing this tutorial, you will know:
- The layers that form part of the Transformer encoder.
- How to implement the Transformer encoder from scratch.
Kick-start your project with my book Building Transformer Models with Attention. It provides self-study tutorials with working code to guide you into building a fully-working transformer model that can
translate sentences from one language to another...
Let’s get started.

Implementing the transformer encoder from scratch in TensorFlow and Keras
Photo by ian dooley, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Recap of the Transformer Architecture
- The Transformer Encoder
- Implementing the Transformer Encoder From Scratch
- The Fully Connected Feed-Forward Neural Network and Layer Normalization
- The Encoder Layer
- The Transformer Encoder
- Testing Out the Code
Prerequisites
For this tutorial, we assume that you are already familiar with:
- The Transformer model
- The scaled dot-product attention
- The multi-head attention
- The Transformer positional encoding
Recap of the Transformer Architecture
Recall having seen that the Transformer architecture follows an encoder-decoder structure. The encoder, on the left-hand side, is tasked with mapping an input sequence to a sequence of continuous representations; the decoder, on the right-hand side, receives the output of the encoder together with the decoder output at the previous time step to generate an output sequence.
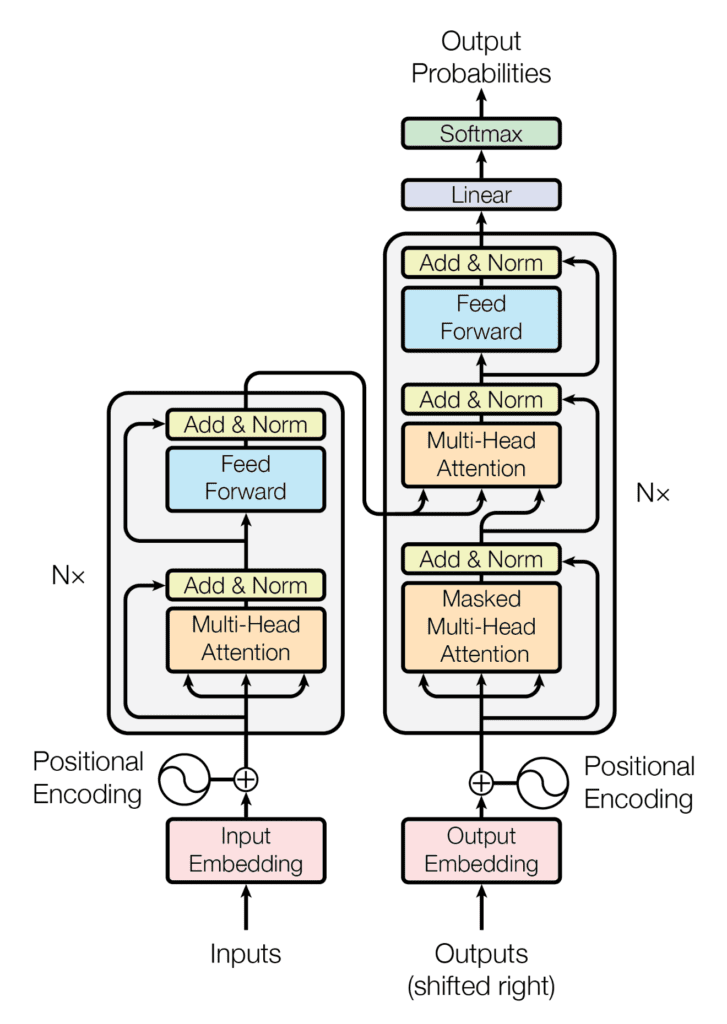
The encoder-decoder structure of the Transformer architecture
Taken from “Attention Is All You Need“
In generating an output sequence, the Transformer does not rely on recurrence and convolutions.
You have seen that the decoder part of the Transformer shares many similarities in its architecture with the encoder. In this tutorial, you will focus on the components that form part of the Transformer encoder.
The Transformer Encoder
The Transformer encoder consists of a stack of $N$ identical layers, where each layer further consists of two main sub-layers:
- The first sub-layer comprises a multi-head attention mechanism that receives the queries, keys, and values as inputs.
- A second sub-layer comprises a fully-connected feed-forward network.
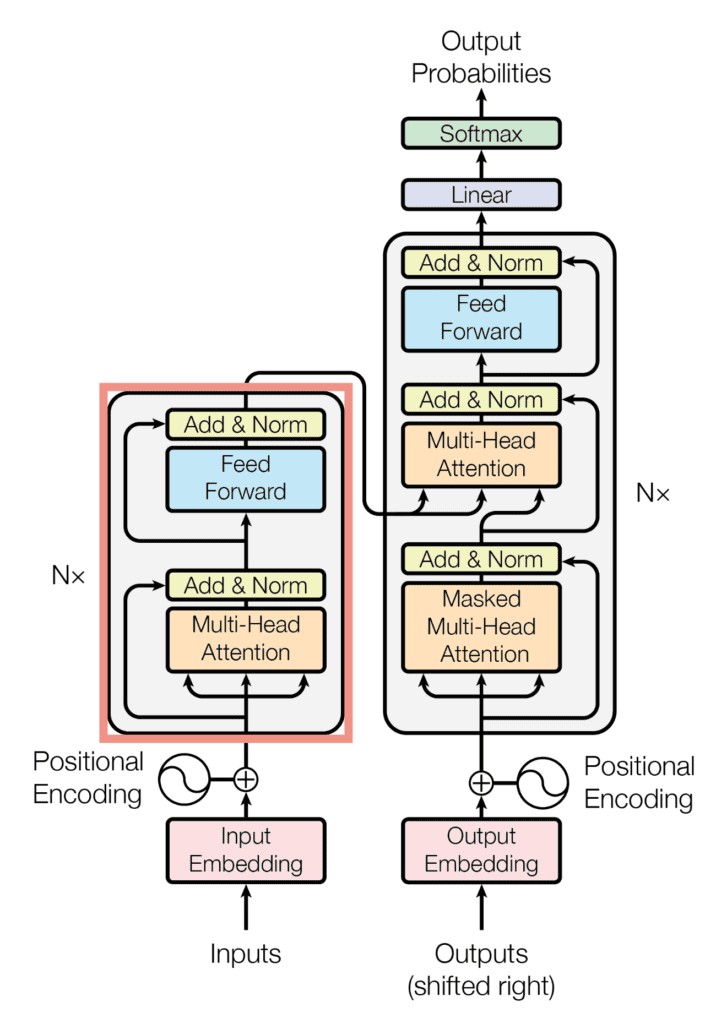
The encoder block of the Transformer architecture
Taken from “Attention Is All You Need“
Following each of these two sub-layers is layer normalization, into which the sub-layer input (through a residual connection) and output are fed. The output of each layer normalization step is the following:
LayerNorm(Sublayer Input + Sublayer Output)
In order to facilitate such an operation, which involves an addition between the sublayer input and output, Vaswani et al. designed all sub-layers and embedding layers in the model to produce outputs of dimension, $d_{\text{model}}$ = 512.
Also, recall the queries, keys, and values as the inputs to the Transformer encoder.
Here, the queries, keys, and values carry the same input sequence after this has been embedded and augmented by positional information, where the queries and keys are of dimensionality, $d_k$, and the dimensionality of the values is $d_v$.
Furthermore, Vaswani et al. also introduce regularization into the model by applying a dropout to the output of each sub-layer (before the layer normalization step), as well as to the positional encodings before these are fed into the encoder.
Let’s now see how to implement the Transformer encoder from scratch in TensorFlow and Keras.
Want to Get Started With Building Transformer Models with Attention?
Take my free 12-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Implementing the Transformer Encoder from Scratch
The Fully Connected Feed-Forward Neural Network and Layer Normalization
Let’s begin by creating classes for the Feed Forward and Add & Norm layers that are shown in the diagram above.
Vaswani et al. tell us that the fully connected feed-forward network consists of two linear transformations with a ReLU activation in between. The first linear transformation produces an output of dimensionality, $d_{ff}$ = 2048, while the second linear transformation produces an output of dimensionality, $d_{\text{model}}$ = 512.
For this purpose, let’s first create the class FeedForward that inherits from the Layer base class in Keras and initialize the dense layers and the ReLU activation:
|
1 2 3 4 5 6 7 |
class FeedForward(Layer): def __init__(self, d_ff, d_model, **kwargs): super(FeedForward, self).__init__(**kwargs) self.fully_connected1 = Dense(d_ff) # First fully connected layer self.fully_connected2 = Dense(d_model) # Second fully connected layer self.activation = ReLU() # ReLU activation layer ... |
We will add to it the class method, call(), that receives an input and passes it through the two fully connected layers with ReLU activation, returning an output of dimensionality equal to 512:
|
1 2 3 4 5 6 |
... def call(self, x): # The input is passed into the two fully-connected layers, with a ReLU in between x_fc1 = self.fully_connected1(x) return self.fully_connected2(self.activation(x_fc1)) |
The next step is to create another class, AddNormalization, that also inherits from the Layer base class in Keras and initialize a Layer normalization layer:
|
1 2 3 4 5 |
class AddNormalization(Layer): def __init__(self, **kwargs): super(AddNormalization, self).__init__(**kwargs) self.layer_norm = LayerNormalization() # Layer normalization layer ... |
In it, include the following class method that sums its sub-layer’s input and output, which it receives as inputs, and applies layer normalization to the result:
|
1 2 3 4 5 6 7 |
... def call(self, x, sublayer_x): # The sublayer input and output need to be of the same shape to be summed add = x + sublayer_x # Apply layer normalization to the sum return self.layer_norm(add) |
The Encoder Layer
Next, you will implement the encoder layer, which the Transformer encoder will replicate identically $N$ times.
For this purpose, let’s create the class, EncoderLayer, and initialize all the sub-layers that it consists of:
|
1 2 3 4 5 6 7 8 9 10 |
class EncoderLayer(Layer): def __init__(self, h, d_k, d_v, d_model, d_ff, rate, **kwargs): super(EncoderLayer, self).__init__(**kwargs) self.multihead_attention = MultiHeadAttention(h, d_k, d_v, d_model) self.dropout1 = Dropout(rate) self.add_norm1 = AddNormalization() self.feed_forward = FeedForward(d_ff, d_model) self.dropout2 = Dropout(rate) self.add_norm2 = AddNormalization() ... |
Here, you may notice that you have initialized instances of the FeedForward and AddNormalization classes, which you just created in the previous section, and assigned their output to the respective variables, feed_forward and add_norm (1 and 2). The Dropout layer is self-explanatory, where the rate defines the frequency at which the input units are set to 0. You created the MultiHeadAttention class in a previous tutorial, and if you saved the code into a separate Python script, then do not forget to import it. I saved mine in a Python script named multihead_attention.py, and for this reason, I need to include the line of code from multihead_attention import MultiHeadAttention.
Let’s now proceed to create the class method, call(), that implements all the encoder sub-layers:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
... def call(self, x, padding_mask, training): # Multi-head attention layer multihead_output = self.multihead_attention(x, x, x, padding_mask) # Expected output shape = (batch_size, sequence_length, d_model) # Add in a dropout layer multihead_output = self.dropout1(multihead_output, training=training) # Followed by an Add & Norm layer addnorm_output = self.add_norm1(x, multihead_output) # Expected output shape = (batch_size, sequence_length, d_model) # Followed by a fully connected layer feedforward_output = self.feed_forward(addnorm_output) # Expected output shape = (batch_size, sequence_length, d_model) # Add in another dropout layer feedforward_output = self.dropout2(feedforward_output, training=training) # Followed by another Add & Norm layer return self.add_norm2(addnorm_output, feedforward_output) |
In addition to the input data, the call() method can also receive a padding mask. As a brief reminder of what was said in a previous tutorial, the padding mask is necessary to suppress the zero padding in the input sequence from being processed along with the actual input values.
The same class method can receive a training flag which, when set to True, will only apply the Dropout layers during training.
The Transformer Encoder
The last step is to create a class for the Transformer encoder, which should be named Encoder:
|
1 2 3 4 5 6 7 |
class Encoder(Layer): def __init__(self, vocab_size, sequence_length, h, d_k, d_v, d_model, d_ff, n, rate, **kwargs): super(Encoder, self).__init__(**kwargs) self.pos_encoding = PositionEmbeddingFixedWeights(sequence_length, vocab_size, d_model) self.dropout = Dropout(rate) self.encoder_layer = [EncoderLayer(h, d_k, d_v, d_model, d_ff, rate) for _ in range(n)] ... |
The Transformer encoder receives an input sequence after this would have undergone a process of word embedding and positional encoding. In order to compute the positional encoding, let’s make use of the PositionEmbeddingFixedWeights class described by Mehreen Saeed in this tutorial.
As you have similarly done in the previous sections, here, you will also create a class method, call(), that applies word embedding and positional encoding to the input sequence and feeds the result to $N$ encoder layers:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
... def call(self, input_sentence, padding_mask, training): # Generate the positional encoding pos_encoding_output = self.pos_encoding(input_sentence) # Expected output shape = (batch_size, sequence_length, d_model) # Add in a dropout layer x = self.dropout(pos_encoding_output, training=training) # Pass on the positional encoded values to each encoder layer for i, layer in enumerate(self.encoder_layer): x = layer(x, padding_mask, training) return x |
The code listing for the full Transformer encoder is the following:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
from tensorflow.keras.layers import LayerNormalization, Layer, Dense, ReLU, Dropout from multihead_attention import MultiHeadAttention from positional_encoding import PositionEmbeddingFixedWeights # Implementing the Add & Norm Layer class AddNormalization(Layer): def __init__(self, **kwargs): super(AddNormalization, self).__init__(**kwargs) self.layer_norm = LayerNormalization() # Layer normalization layer def call(self, x, sublayer_x): # The sublayer input and output need to be of the same shape to be summed add = x + sublayer_x # Apply layer normalization to the sum return self.layer_norm(add) # Implementing the Feed-Forward Layer class FeedForward(Layer): def __init__(self, d_ff, d_model, **kwargs): super(FeedForward, self).__init__(**kwargs) self.fully_connected1 = Dense(d_ff) # First fully connected layer self.fully_connected2 = Dense(d_model) # Second fully connected layer self.activation = ReLU() # ReLU activation layer def call(self, x): # The input is passed into the two fully-connected layers, with a ReLU in between x_fc1 = self.fully_connected1(x) return self.fully_connected2(self.activation(x_fc1)) # Implementing the Encoder Layer class EncoderLayer(Layer): def __init__(self, h, d_k, d_v, d_model, d_ff, rate, **kwargs): super(EncoderLayer, self).__init__(**kwargs) self.multihead_attention = MultiHeadAttention(h, d_k, d_v, d_model) self.dropout1 = Dropout(rate) self.add_norm1 = AddNormalization() self.feed_forward = FeedForward(d_ff, d_model) self.dropout2 = Dropout(rate) self.add_norm2 = AddNormalization() def call(self, x, padding_mask, training): # Multi-head attention layer multihead_output = self.multihead_attention(x, x, x, padding_mask) # Expected output shape = (batch_size, sequence_length, d_model) # Add in a dropout layer multihead_output = self.dropout1(multihead_output, training=training) # Followed by an Add & Norm layer addnorm_output = self.add_norm1(x, multihead_output) # Expected output shape = (batch_size, sequence_length, d_model) # Followed by a fully connected layer feedforward_output = self.feed_forward(addnorm_output) # Expected output shape = (batch_size, sequence_length, d_model) # Add in another dropout layer feedforward_output = self.dropout2(feedforward_output, training=training) # Followed by another Add & Norm layer return self.add_norm2(addnorm_output, feedforward_output) # Implementing the Encoder class Encoder(Layer): def __init__(self, vocab_size, sequence_length, h, d_k, d_v, d_model, d_ff, n, rate, **kwargs): super(Encoder, self).__init__(**kwargs) self.pos_encoding = PositionEmbeddingFixedWeights(sequence_length, vocab_size, d_model) self.dropout = Dropout(rate) self.encoder_layer = [EncoderLayer(h, d_k, d_v, d_model, d_ff, rate) for _ in range(n)] def call(self, input_sentence, padding_mask, training): # Generate the positional encoding pos_encoding_output = self.pos_encoding(input_sentence) # Expected output shape = (batch_size, sequence_length, d_model) # Add in a dropout layer x = self.dropout(pos_encoding_output, training=training) # Pass on the positional encoded values to each encoder layer for i, layer in enumerate(self.encoder_layer): x = layer(x, padding_mask, training) return x |
Testing Out the Code
You will work with the parameter values specified in the paper, Attention Is All You Need, by Vaswani et al. (2017):
|
1 2 3 4 5 6 7 8 9 10 |
h = 8 # Number of self-attention heads d_k = 64 # Dimensionality of the linearly projected queries and keys d_v = 64 # Dimensionality of the linearly projected values d_ff = 2048 # Dimensionality of the inner fully connected layer d_model = 512 # Dimensionality of the model sub-layers' outputs n = 6 # Number of layers in the encoder stack batch_size = 64 # Batch size from the training process dropout_rate = 0.1 # Frequency of dropping the input units in the dropout layers ... |
As for the input sequence, you will work with dummy data for the time being until you arrive at the stage of training the complete Transformer model in a separate tutorial, at which point you will be using actual sentences:
|
1 2 3 4 5 6 |
... enc_vocab_size = 20 # Vocabulary size for the encoder input_seq_length = 5 # Maximum length of the input sequence input_seq = random.random((batch_size, input_seq_length)) ... |
Next, you will create a new instance of the Encoder class, assigning its output to the encoder variable, subsequently feeding in the input arguments, and printing the result. You will set the padding mask argument to None for the time being, but you will return to this when you implement the complete Transformer model:
|
1 2 3 |
... encoder = Encoder(enc_vocab_size, input_seq_length, h, d_k, d_v, d_model, d_ff, n, dropout_rate) print(encoder(input_seq, None, True)) |
Tying everything together produces the following code listing:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from numpy import random enc_vocab_size = 20 # Vocabulary size for the encoder input_seq_length = 5 # Maximum length of the input sequence h = 8 # Number of self-attention heads d_k = 64 # Dimensionality of the linearly projected queries and keys d_v = 64 # Dimensionality of the linearly projected values d_ff = 2048 # Dimensionality of the inner fully connected layer d_model = 512 # Dimensionality of the model sub-layers' outputs n = 6 # Number of layers in the encoder stack batch_size = 64 # Batch size from the training process dropout_rate = 0.1 # Frequency of dropping the input units in the dropout layers input_seq = random.random((batch_size, input_seq_length)) encoder = Encoder(enc_vocab_size, input_seq_length, h, d_k, d_v, d_model, d_ff, n, dropout_rate) print(encoder(input_seq, None, True)) |
Running this code produces an output of shape (batch size, sequence length, model dimensionality). Note that you will likely see a different output due to the random initialization of the input sequence and the parameter values of the Dense layers.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
tf.Tensor( [[[-0.4214715 -1.1246173 -0.8444572 ... 1.6388322 -0.1890367 1.0173352 ] [ 0.21662089 -0.61147404 -1.0946581 ... 1.4627445 -0.6000164 -0.64127874] [ 0.46674493 -1.4155326 -0.5686513 ... 1.1790234 -0.94788337 0.1331717 ] [-0.30638126 -1.9047263 -1.8556844 ... 0.9130118 -0.47863355 0.00976158] [-0.22600567 -0.9702025 -0.91090447 ... 1.7457147 -0.139926 -0.07021569]] ... [[-0.48047638 -1.1034104 -0.16164204 ... 1.5588069 0.08743562 -0.08847156] [-0.61683714 -0.8403657 -1.0450369 ... 2.3587787 -0.76091915 -0.02891812] [-0.34268388 -0.65042275 -0.6715749 ... 2.8530657 -0.33631966 0.5215888 ] [-0.6288677 -1.0030932 -0.9749813 ... 2.1386387 0.0640307 -0.69504136] [-1.33254 -1.2524267 -0.230098 ... 2.515467 -0.04207756 -0.3395423 ]]], shape=(64, 5, 512), dtype=float32) |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
Papers
Summary
In this tutorial, you discovered how to implement the Transformer encoder from scratch in TensorFlow and Keras.
Specifically, you learned:
- The layers that form part of the Transformer encoder
- How to implement the Transformer encoder from scratch
Do you have any questions?
Ask your questions in the comments below, and I will do my best to answer.








Hi Stefania,
Thanks for the wonderful post. I am also reading the book “Building Transformer Models with Attention”. I have a question from “chapter 14.4 Positional Encoding in Transformers”.
Here, I did not get the reason why you are using
word_embedding_matrix = self.get_position_encoding(vocab_size, output_dim)
in order to initialize the word_embedding_matrix quoting the paper “Attention Is All You Need”.
I did not understand how this method “get_position_encoding” represents the words as embeddings. Can you please help me here?
Thanks!!
It may be confusing but try to think about that as a way to generate a random matrix. The word embedding matrix is simply to encode words (which is in the order of 10,000 or them) into a shorter vector (e.g., 50 floats). We do not want two unrelated, distinct words to share the same vector. Hence the embedding matrix is best to be randomized, but also guaranteed not to “collide”. It happens that the positional encoding fulfilled this property and hence it is abused here.
In fact, you can also use numpy.random to generate a random matrix. But in this case, it is best to set “trainable=True” too to let Keras to fine-tune it to avoid unwanted collision.
Okay, this makes sense now. Thanks for the clarification, Adrian. MachineLearningMastery is always been my best tutor in learning Data Science. Keep it up!!!
hi sir, i am trying to apply above code for univariate wind power data. is it possible to alter the above code for wind power (time series ) data?
Hi Bashir…Yes this is possible. Please proceed and let us know if you have any questions!