We have already familiarized ourselves with the theory behind the Transformer model and its attention mechanism. We have already started our journey of implementing a complete model by seeing how to implement the scaled-dot product attention. We shall now progress one step further into our journey by encapsulating the scaled-dot product attention into a multi-head attention mechanism, which is a core component. Our end goal remains to apply the complete model to Natural Language Processing (NLP).
In this tutorial, you will discover how to implement multi-head attention from scratch in TensorFlow and Keras.
After completing this tutorial, you will know:
- The layers that form part of the multi-head attention mechanism.
- How to implement the multi-head attention mechanism from scratch.
Kick-start your project with my book Building Transformer Models with Attention. It provides self-study tutorials with working code to guide you into building a fully-working transformer model that can
translate sentences from one language to another...
Let’s get started.

How to implement multi-head attention from scratch in TensorFlow and Keras
Photo by Everaldo Coelho, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Recap of the Transformer Architecture
- The Transformer Multi-Head Attention
- Implementing Multi-Head Attention From Scratch
- Testing Out the Code
Prerequisites
For this tutorial, we assume that you are already familiar with:
- The concept of attention
- The Transfomer attention mechanism
- The Transformer model
- The scaled dot-product attention
Recap of the Transformer Architecture
Recall having seen that the Transformer architecture follows an encoder-decoder structure. The encoder, on the left-hand side, is tasked with mapping an input sequence to a sequence of continuous representations; the decoder, on the right-hand side, receives the output of the encoder together with the decoder output at the previous time step to generate an output sequence.
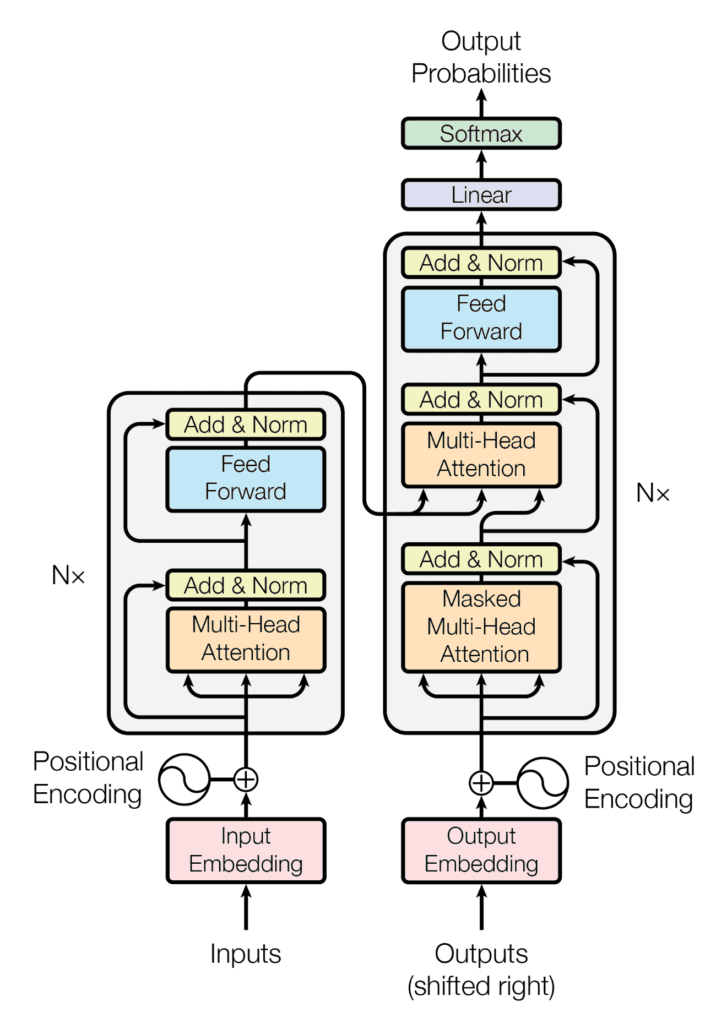
The encoder-decoder structure of the Transformer architecture
Taken from “Attention Is All You Need“
In generating an output sequence, the Transformer does not rely on recurrence and convolutions.
You have seen that the decoder part of the Transformer shares many similarities in its architecture with the encoder. One of the core mechanisms that both the encoder and decoder share is the multi-head attention mechanism.
The Transformer Multi-Head Attention
Each multi-head attention block is made up of four consecutive levels:
- On the first level, three linear (dense) layers that each receive the queries, keys, or values
- On the second level, a scaled dot-product attention function. The operations performed on both the first and second levels are repeated h times and performed in parallel, according to the number of heads composing the multi-head attention block.
- On the third level, a concatenation operation that joins the outputs of the different heads
- On the fourth level, a final linear (dense) layer that produces the output
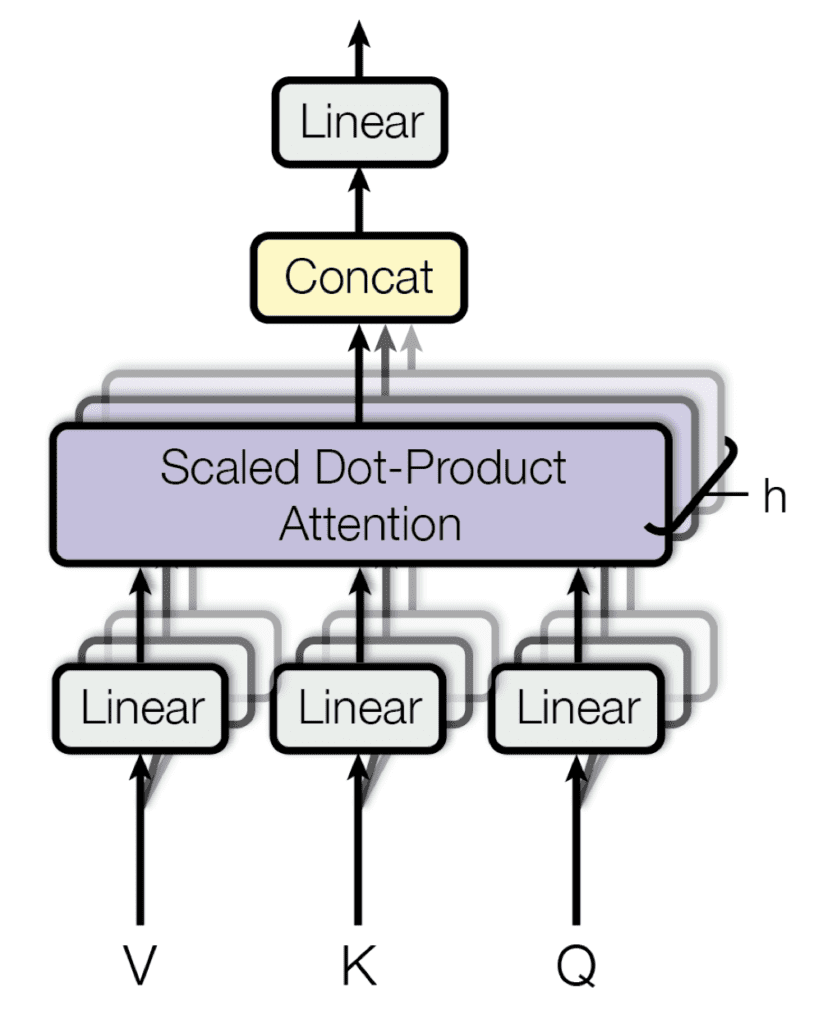
Multi-head attention
Taken from “Attention Is All You Need“
Recall as well the important components that will serve as building blocks for your implementation of the multi-head attention:
- The queries, keys, and values: These are the inputs to each multi-head attention block. In the encoder stage, they each carry the same input sequence after this has been embedded and augmented by positional information. Similarly, on the decoder side, the queries, keys, and values fed into the first attention block represent the same target sequence after this would have also been embedded and augmented by positional information. The second attention block of the decoder receives the encoder output in the form of keys and values, and the normalized output of the first decoder attention block as the queries. The dimensionality of the queries and keys is denoted by $d_k$, whereas the dimensionality of the values is denoted by $d_v$.
- The projection matrices: When applied to the queries, keys, and values, these projection matrices generate different subspace representations of each. Each attention head then works on one of these projected versions of the queries, keys, and values. An additional projection matrix is also applied to the output of the multi-head attention block after the outputs of each individual head would have been concatenated together. The projection matrices are learned during training.
Let’s now see how to implement the multi-head attention from scratch in TensorFlow and Keras.
Implementing Multi-Head Attention from Scratch
Let’s start by creating the class, MultiHeadAttention, which inherits from the Layer base class in Keras and initialize several instance attributes that you shall be working with (attribute descriptions may be found in the comments):
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class MultiHeadAttention(Layer): def __init__(self, h, d_k, d_v, d_model, **kwargs): super(MultiHeadAttention, self).__init__(**kwargs) self.attention = DotProductAttention() # Scaled dot product attention self.heads = h # Number of attention heads to use self.d_k = d_k # Dimensionality of the linearly projected queries and keys self.d_v = d_v # Dimensionality of the linearly projected values self.W_q = Dense(d_k) # Learned projection matrix for the queries self.W_k = Dense(d_k) # Learned projection matrix for the keys self.W_v = Dense(d_v) # Learned projection matrix for the values self.W_o = Dense(d_model) # Learned projection matrix for the multi-head output ... |
Here note that an instance of the DotProductAttention class that was implemented earlier has been created, and its output was assigned to the variable attention. Recall that you implemented the DotProductAttention class as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from tensorflow import matmul, math, cast, float32 from tensorflow.keras.layers import Layer from keras.backend import softmax # Implementing the Scaled-Dot Product Attention class DotProductAttention(Layer): def __init__(self, **kwargs): super(DotProductAttention, self).__init__(**kwargs) def call(self, queries, keys, values, d_k, mask=None): # Scoring the queries against the keys after transposing the latter, and scaling scores = matmul(queries, keys, transpose_b=True) / math.sqrt(cast(d_k, float32)) # Apply mask to the attention scores if mask is not None: scores += -1e9 * mask # Computing the weights by a softmax operation weights = softmax(scores) # Computing the attention by a weighted sum of the value vectors return matmul(weights, values) |
Next, you will be reshaping the linearly projected queries, keys, and values in such a manner as to allow the attention heads to be computed in parallel.
The queries, keys, and values will be fed as input into the multi-head attention block having a shape of (batch size, sequence length, model dimensionality), where the batch size is a hyperparameter of the training process, the sequence length defines the maximum length of the input/output phrases, and the model dimensionality is the dimensionality of the outputs produced by all sub-layers of the model. They are then passed through the respective dense layer to be linearly projected to a shape of (batch size, sequence length, queries/keys/values dimensionality).
The linearly projected queries, keys, and values will be rearranged into (batch size, number of heads, sequence length, depth), by first reshaping them into (batch size, sequence length, number of heads, depth) and then transposing the second and third dimensions. For this purpose, you will create the class method, reshape_tensor, as follows:
|
1 2 3 4 5 6 7 8 9 10 |
def reshape_tensor(self, x, heads, flag): if flag: # Tensor shape after reshaping and transposing: (batch_size, heads, seq_length, -1) x = reshape(x, shape=(shape(x)[0], shape(x)[1], heads, -1)) x = transpose(x, perm=(0, 2, 1, 3)) else: # Reverting the reshaping and transposing operations: (batch_size, seq_length, d_model) x = transpose(x, perm=(0, 2, 1, 3)) x = reshape(x, shape=(shape(x)[0], shape(x)[1], -1)) return x |
The reshape_tensor method receives the linearly projected queries, keys, or values as input (while setting the flag to True) to be rearranged as previously explained. Once the multi-head attention output has been generated, this is also fed into the same function (this time setting the flag to False) to perform a reverse operation, effectively concatenating the results of all heads together.
Hence, the next step is to feed the linearly projected queries, keys, and values into the reshape_tensor method to be rearranged, then feed them into the scaled dot-product attention function. In order to do so, let’s create another class method, call, as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def call(self, queries, keys, values, mask=None): # Rearrange the queries to be able to compute all heads in parallel q_reshaped = self.reshape_tensor(self.W_q(queries), self.heads, True) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Rearrange the keys to be able to compute all heads in parallel k_reshaped = self.reshape_tensor(self.W_k(keys), self.heads, True) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Rearrange the values to be able to compute all heads in parallel v_reshaped = self.reshape_tensor(self.W_v(values), self.heads, True) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Compute the multi-head attention output using the reshaped queries, keys and values o_reshaped = self.attention(q_reshaped, k_reshaped, v_reshaped, self.d_k, mask) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) ... |
Note that the reshape_tensor method can also receive a mask (whose value defaults to None) as input, in addition to the queries, keys, and values.
Recall that the Transformer model introduces a look-ahead mask to prevent the decoder from attending to succeeding words, such that the prediction for a particular word can only depend on known outputs for the words that come before it. Furthermore, since the word embeddings are zero-padded to a specific sequence length, a padding mask also needs to be introduced to prevent the zero values from being processed along with the input. These look-ahead and padding masks can be passed on to the scaled-dot product attention through the mask argument.
Once you have generated the multi-head attention output from all the attention heads, the final steps are to concatenate back all outputs together into a tensor of shape (batch size, sequence length, values dimensionality) and passing the result through one final dense layer. For this purpose, you will add the next two lines of code to the call method.
|
1 2 3 4 5 6 7 8 |
... # Rearrange back the output into concatenated form output = self.reshape_tensor(o_reshaped, self.heads, False) # Resulting tensor shape: (batch_size, input_seq_length, d_v) # Apply one final linear projection to the output to generate the multi-head attention # Resulting tensor shape: (batch_size, input_seq_length, d_model) return self.W_o(output) |
Putting everything together, you have the following implementation of the multi-head attention:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
from tensorflow import math, matmul, reshape, shape, transpose, cast, float32 from tensorflow.keras.layers import Dense, Layer from keras.backend import softmax # Implementing the Scaled-Dot Product Attention class DotProductAttention(Layer): def __init__(self, **kwargs): super(DotProductAttention, self).__init__(**kwargs) def call(self, queries, keys, values, d_k, mask=None): # Scoring the queries against the keys after transposing the latter, and scaling scores = matmul(queries, keys, transpose_b=True) / math.sqrt(cast(d_k, float32)) # Apply mask to the attention scores if mask is not None: scores += -1e9 * mask # Computing the weights by a softmax operation weights = softmax(scores) # Computing the attention by a weighted sum of the value vectors return matmul(weights, values) # Implementing the Multi-Head Attention class MultiHeadAttention(Layer): def __init__(self, h, d_k, d_v, d_model, **kwargs): super(MultiHeadAttention, self).__init__(**kwargs) self.attention = DotProductAttention() # Scaled dot product attention self.heads = h # Number of attention heads to use self.d_k = d_k # Dimensionality of the linearly projected queries and keys self.d_v = d_v # Dimensionality of the linearly projected values self.d_model = d_model # Dimensionality of the model self.W_q = Dense(d_k) # Learned projection matrix for the queries self.W_k = Dense(d_k) # Learned projection matrix for the keys self.W_v = Dense(d_v) # Learned projection matrix for the values self.W_o = Dense(d_model) # Learned projection matrix for the multi-head output def reshape_tensor(self, x, heads, flag): if flag: # Tensor shape after reshaping and transposing: (batch_size, heads, seq_length, -1) x = reshape(x, shape=(shape(x)[0], shape(x)[1], heads, -1)) x = transpose(x, perm=(0, 2, 1, 3)) else: # Reverting the reshaping and transposing operations: (batch_size, seq_length, d_k) x = transpose(x, perm=(0, 2, 1, 3)) x = reshape(x, shape=(shape(x)[0], shape(x)[1], self.d_k)) return x def call(self, queries, keys, values, mask=None): # Rearrange the queries to be able to compute all heads in parallel q_reshaped = self.reshape_tensor(self.W_q(queries), self.heads, True) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Rearrange the keys to be able to compute all heads in parallel k_reshaped = self.reshape_tensor(self.W_k(keys), self.heads, True) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Rearrange the values to be able to compute all heads in parallel v_reshaped = self.reshape_tensor(self.W_v(values), self.heads, True) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Compute the multi-head attention output using the reshaped queries, keys and values o_reshaped = self.attention(q_reshaped, k_reshaped, v_reshaped, self.d_k, mask) # Resulting tensor shape: (batch_size, heads, input_seq_length, -1) # Rearrange back the output into concatenated form output = self.reshape_tensor(o_reshaped, self.heads, False) # Resulting tensor shape: (batch_size, input_seq_length, d_v) # Apply one final linear projection to the output to generate the multi-head attention # Resulting tensor shape: (batch_size, input_seq_length, d_model) return self.W_o(output) |
Want to Get Started With Building Transformer Models with Attention?
Take my free 12-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Testing Out the Code
You will be working with the parameter values specified in the paper, Attention Is All You Need, by Vaswani et al. (2017):
|
1 2 3 4 5 6 |
h = 8 # Number of self-attention heads d_k = 64 # Dimensionality of the linearly projected queries and keys d_v = 64 # Dimensionality of the linearly projected values d_model = 512 # Dimensionality of the model sub-layers' outputs batch_size = 64 # Batch size from the training process ... |
As for the sequence length and the queries, keys, and values, you will be working with dummy data for the time being until you arrive at the stage of training the complete Transformer model in a separate tutorial, at which point you will be using actual sentences:
|
1 2 3 4 5 6 7 |
... input_seq_length = 5 # Maximum length of the input sequence queries = random.random((batch_size, input_seq_length, d_k)) keys = random.random((batch_size, input_seq_length, d_k)) values = random.random((batch_size, input_seq_length, d_v)) ... |
In the complete Transformer model, values for the sequence length and the queries, keys, and values will be obtained through a process of word tokenization and embedding. We will be covering this in a separate tutorial.
Returning to the testing procedure, the next step is to create a new instance of the MultiHeadAttention class, assigning its output to the multihead_attention variable:
|
1 2 3 |
... multihead_attention = MultiHeadAttention(h, d_k, d_v, d_model) ... |
Since the MultiHeadAttention class inherits from the Layer base class, the call() method of the former will be automatically invoked by the magic __call()__ method of the latter. The final step is to pass in the input arguments and print the result:
|
1 2 |
... print(multihead_attention(queries, keys, values)) |
Tying everything together produces the following code listing:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
from numpy import random input_seq_length = 5 # Maximum length of the input sequence h = 8 # Number of self-attention heads d_k = 64 # Dimensionality of the linearly projected queries and keys d_v = 64 # Dimensionality of the linearly projected values d_model = 512 # Dimensionality of the model sub-layers' outputs batch_size = 64 # Batch size from the training process queries = random.random((batch_size, input_seq_length, d_k)) keys = random.random((batch_size, input_seq_length, d_k)) values = random.random((batch_size, input_seq_length, d_v)) multihead_attention = MultiHeadAttention(h, d_k, d_v, d_model) print(multihead_attention(queries, keys, values)) |
Running this code produces an output of shape (batch size, sequence length, model dimensionality). Note that you will likely see a different output due to the random initialization of the queries, keys, and values and the parameter values of the dense layers.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
tf.Tensor( [[[-0.02185373 0.32784638 0.15958631 ... -0.0353895 0.6645204 -0.2588266 ] [-0.02272229 0.32292002 0.16208754 ... -0.03644213 0.66478664 -0.26139447] [-0.01876744 0.32900316 0.16190802 ... -0.03548665 0.6645842 -0.26155376] [-0.02193783 0.32687354 0.15801215 ... -0.03232524 0.6642926 -0.25795174] [-0.02224652 0.32437912 0.1596448 ... -0.0340827 0.6617497 -0.26065096]] ... [[ 0.05414441 0.27019292 0.1845745 ... 0.0809482 0.63738805 -0.34231138] [ 0.05546578 0.27191412 0.18483458 ... 0.08379208 0.6366671 -0.34372014] [ 0.05190979 0.27185103 0.18378328 ... 0.08341806 0.63851804 -0.3422392 ] [ 0.05437043 0.27318984 0.18792395 ... 0.08043509 0.6391771 -0.34357914] [ 0.05406848 0.27073097 0.18579456 ... 0.08388947 0.6376929 -0.34230167]]], shape=(64, 5, 512), dtype=float32) |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
Papers
Summary
In this tutorial, you discovered how to implement multi-head attention from scratch in TensorFlow and Keras.
Specifically, you learned:
- The layers that form part of the multi-head attention mechanism
- How to implement the multi-head attention mechanism from scratch
Do you have any questions?
Ask your questions in the comments below, and I will do my best to answer.







Hi. Very good explanation! I have a little doubt. Why do you need to reshape the input and then calculate the transpose instead of just reshaping it to (batch size, heads, sequence lenght, -1)? Thanks.
Hi Moises…You may certainly proceed with your suggestion. Let us know what you find.
Awesome tutorial. Thanks for pulling all this together!
You are very welcome Brett!
if we reshape the data, does that not mean that we still perform regular dot attention (1 head), but now reshape it as if it were 8 heads? I’m not seeing extra dimensions being created when I print out the reshaped query, key, value matrices’ shapes
Hi Diego…The following series may be of interest to you:
https://towardsdatascience.com/transformers-explained-visually-part-3-multi-head-attention-deep-dive-1c1ff1024853
I think
self.W_q (d_k)
self.W_k (d_k)
self.W_v (d_v)
should not have a static d_k value, but instead should be:
self.head_dim = self.d_model // self.heads
self.W_q (self.head_dim)
self.W_k (self.head_dim)
self.W_v (self.head_dim)
otherwise your q,k,v matrices are not related to the embed space and the number of heads, but just to a preset value of the d_k dimensionality
I agree. This needs to be explicitly pointed out.
In the last block of code:
queries = random.random((batch_size, input_seq_length, d_k))
Should it be this instead:
queries = random.random((batch_size, input_seq_length, d_model)) ?
In the article you wrote:
“The queries, keys, and values will be fed as input into the multi-head attention block having a shape of (batch size, sequence length, model dimensionality), where the batch size is a hyperparameter of the training process, the sequence length defines the maximum length of the input/output phrases, and the model dimensionality is the dimensionality of the outputs produced by all sub-layers of the model. They are then passed through the respective dense layer to be linearly projected to a shape of (batch size, sequence length, queries/keys/values dimensionality).”
In particular you said “model dimensionality” in the above quote, which is d_model, not d_k.
In other words, I think W_q is a matrix of dimension 512 x 64. Where input dim = d_model = 512, output dim = d_k = 64.
Am I mistaken? This is very confusing to me…. thanks if someone can clarify this for me.
Hi Cybernetic1, thank you for the interest.
What I meant by, “The queries, keys, and values will be fed as input into the multi-head attention block having a shape of (batch size, sequence length, model dimensionality)…”, is that the output of the multi-head attention block is of shape (batch size, sequence length, model dimensionality) rather than the queries, keys or values. Otherwise, it may be confirmed from Vaswani’s paper that the queries and keys are of dimensionality d_k, and the values are of dimensionality d_v, where Vaswani et al. set d_k and d_v to a value that differs from that for d_model.
I agree with Cybernetic1.
d_k is the dimensionality of the linearly projected queries and keys. But in this code ‘queries = random.random((batch_size, input_seq_length, d_k))’, queries is the input of the multihead_attention which have not been projected yet. They will be projected in the call function of MultiHeadAttention which is done by this code ‘q_reshaped = self.reshape_tensor(self.W_q(queries), self.heads, True)’. So in the first line of code, the last dimensionality should be d_model or d_k * h.
There is a mistake in the code itself. The multihead class should be:
class MultiHeadAttention(Layer):
def __init__(self, h, d_model, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.attention = DotProductAttention() # Scaled dot product attention
self.heads = h # Number of attention heads to use
assert d_model % h = 0
d_k= d_model//h # d_k should be calculated from d_model and h
self.d_k = d_k # Dimensionality of the linearly projected queries and keys
self.d_v = d_k # Dimensionality of the linearly projected values
self.d_model = d_model # Dimensionality of the model
#units of projection matrices should be d_model instead of d_k/d_v
self.W_q = Dense(d_model) # Learned projection matrix for the queries
self.W_k = Dense(d_model) # Learned projection matrix for the keys
self.W_v = Dense(d_model) # Learned projection matrix for the values
self.W_o = Dense(d_model) # Learned projection matrix for the multi-head output
The other portion of the code seems to be ok.
this is the correct answer
Agree with Cybernetic1, but I really appreciate author’s effort putting these together!
Queries and Keys must have same dimensions, to be able successfully compute MatMul in DotProductAttention.
Queries: (batch, time, d_q)
Keys: (batch, time, d_k)
To calculate DotProduct(Queries, Keys) = Queries @ Keys.T (d_q must be EQUAL to d_k)
Thank you for your feedback Ivan!
Hello,
In PDF-version.
def reshape_tensor…..
…..
—- False branch
x = reshape(x, shape=(shape(x)[0], shape(x)[1], self.d_k))
…..
IMO d_k is incorrect , should be d_v. Due to reverse reshaping is done on Values, not on keys/queries.
Book version throws exception is d_k not the same as d_v
Thank you for your feedback Ivan!
Over-regularization at a scaled dot-product attention.
In chapter 3.2.1 of the paper “Attention is all you need” there is a footer explaining the effect of regularization term (dk**-1/2)
—
To illustrate why the dot products get large, assume that the components of q and k are independent random variables with mean 0 and variance 1. Then their dot product, q · k, has mean 0 and variance dk.
—
We can observe this behavior:
q = tf.random.normal([2,3,16,8])
k = tf.random.normal([2,3,16,8])
qk = q@tf.transpose(k, perm=[0,1,3,2])
tf.math.reduce_variance(qk)
# ——— almost equal to last dimension
qk2 = q@tf.transpose(k, perm=[0,1,3,2])/tf.math.sqrt(8.)
# ——— add regularization term
tf.math.reduce_variance(qk2)
# ——— dot-prod variance is close to variance of q and k
Back to the Book.
In the code MultiHeadAttention.call()
…
# Compute the multi-head attention output using the reshaped queries, keys and values
o_reshaped = self.attention(q_reshaped, k_reshaped, v_reshaped, self.d_k, mask)
# Resulting tensor shape: (batch_size, heads, input_seq_length, -1)
…
self.d_k could be two values:
1-st option) before reshape: d_k = number of heads * query size
2-nd option) after reshape: d_k = query size
In the book “1-st option” is used. Which makes dot-product over-regularized and slows down the training, due to gradients are equal across all tokens.
To implement 2-nd option, in MultiHeadAttention.call replace
o_reshaped = self.attention(q_reshaped, k_reshaped, v_reshaped, self.d_k, mask)
# to the next line
o_reshaped = self.attention(q_reshaped, k_reshaped, v_reshaped, self.d_k / self.heads, mask)
To investigate scores-values you can set breakpoint immediately after score calculations in the DotProductAttention.call and add per-head-variance of keys, queries and scores to a watch window:
math.reduce_variance(keys, axis=[0,2,3])
math.reduce_variance(queries, axis=[0,2,3])
math.reduce_variance(scores, axis=[0,2,3])
Observations with current code (1-st option):
keys and queries variances are close to each other, but scores-variance is order of magnitude smaller. Scores variance is around 0.1.
With 2-nd option implemented all three variances are in the same ball-park.
Over-regularization influences softmax distribution, with each term is almost equal to each other and gradients flow will be equally distributed across all terms.
Thank you for your feedback Ivan! Let us know if we can address any specific questions regarding our content.
I think this is the correct code:
o_reshaped = self.attention(q_reshaped, k_reshaped, v_reshaped, self.d_k / self.heads, mask)
Hi! And thank you for your detailed and very clear introduction to Transformer models.
I just wanted to point out a confusing typo. In the “Implementing Multi-Head Attention from Scratch” sub-section, you write “Note that the reshape_tensor method can also receive a mask”, but I think you are talking about the attention method, instead.
Cheers,
Florian
You are very welcome Florian! We appreciate the support, feedback and suggestions!
Florian’s correction is an important one. I have seen this in many places on this website, where a consequential typo is pointed out or an important correction is made and you just thank them. Also instead of giving detailed responses you link to generic (sometimes useful) pages and “encourage” commenters to “try it out” and “let us know what you find”.
I purchased the eBook and I am grateful for it. But I use the comments on this website as a much-needed “errata” section. It is a bit disappointing that you are not actively engaging with your readers or making corrections when errors are pointed out.
How to use this with after Keras Bi-LSTM layer?
Hi Gabriel…The following resource may be of interest to you:
https://keras.io/api/layers/attention_layers/multi_head_attention/
Why would I pass query, key and value as input to the multihead attention? The input to the multihead attention should be the training data right if dimension [batch_dim, max_token_length, embedding_dim]?
Hi Kishan…The following resource may be of interest to you:
https://paperswithcode.com/method/multi-head-attention