The Bayes Optimal Classifier is a probabilistic model that makes the most probable prediction for a new example.
It is described using the Bayes Theorem that provides a principled way for calculating a conditional probability. It is also closely related to the Maximum a Posteriori: a probabilistic framework referred to as MAP that finds the most probable hypothesis for a training dataset.
In practice, the Bayes Optimal Classifier is computationally expensive, if not intractable to calculate, and instead, simplifications such as the Gibbs algorithm and Naive Bayes can be used to approximate the outcome.
In this post, you will discover Bayes Optimal Classifier for making the most accurate predictions for new instances of data.
After reading this post, you will know:
- Bayes Theorem provides a principled way for calculating conditional probabilities, called a posterior probability.
- Maximum a Posteriori is a probabilistic framework that finds the most probable hypothesis that describes the training dataset.
- Bayes Optimal Classifier is a probabilistic model that finds the most probable prediction using the training data and space of hypotheses to make a prediction for a new data instance.
Kick-start your project with my new book Probability for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.

A Gentle Introduction to the Bayes Optimal Classifier
Photo by Nate Loper, some rights reserved.
Overview
This tutorial is divided into three parts; they are:
- Bayes Theorem
- Maximum a Posteriori (MAP)
- Bayes Optimal Classifier
Bayes Theorem
Recall that the Bayes theorem provides a principled way of calculating a conditional probability.
It involves calculating the conditional probability of one outcome given another outcome, using the inverse of this relationship, stated as follows:
- P(A | B) = (P(B | A) * P(A)) / P(B)
The quantity that we are calculating is typically referred to as the posterior probability of A given B and P(A) is referred to as the prior probability of A.
The normalizing constant of P(B) can be removed, and the posterior can be shown to be proportional to the probability of B given A multiplied by the prior.
- P(A | B) is proportional to P(B | A) * P(A)
Or, simply:
- P(A | B) = P(B | A) * P(A)
This is a helpful simplification as we are not interested in estimating a probability, but instead in optimizing a quantity. A proportional quantity is good enough for this purpose.
For more on the topic of Bayes Theorem, see the post:
Now that we are up to speed on Bayes Theorem, let’s also take a look at the Maximum a Posteriori framework.
Maximum a Posteriori (MAP)
Machine learning involves finding a model (hypothesis) that best explains the training data.
There are two probabilistic frameworks that underlie many different machine learning algorithms.
They are:
- Maximum a Posteriori (MAP), a Bayesian method.
- Maximum Likelihood Estimation (MLE), a frequentist method.
The objective of both of these frameworks in the context of machine learning is to locate the hypothesis that is most probable given the training dataset.
Specifically, they answer the question:
What is the most probable hypothesis given the training data?
Both approaches frame the problem of fitting a model as optimization and involve searching for a distribution and set of parameters for the distribution that best describes the observed data.
MLE is a frequentist approach, and MAP provides a Bayesian alternative.
A popular replacement for maximizing the likelihood is maximizing the Bayesian posterior probability density of the parameters instead.
— Page 306, Information Theory, Inference and Learning Algorithms, 2003.
Given the simplification of Bayes Theorem to a proportional quantity, we can use it to estimate the proportional hypothesis and parameters (theta) that explain our dataset (X), stated as:
- P(theta | X) = P(X | theta) * P(theta)
Maximizing this quantity over a range of theta solves an optimization problem for estimating the central tendency of the posterior probability (e.g. the model of the distribution).
As such, this technique is referred to as “maximum a posteriori estimation,” or MAP estimation for short, and sometimes simply “maximum posterior estimation.”
- maximize P(X | theta) * P(theta)
For more on the topic of Maximum a Posteriori, see the post:
Now that we are familiar with the MAP framework, we can take a closer look at the related concept of the Bayes optimal classifier.
Bayes Optimal Classifier
The Bayes optimal classifier is a probabilistic model that makes the most probable prediction for a new example, given the training dataset.
This model is also referred to as the Bayes optimal learner, the Bayes classifier, Bayes optimal decision boundary, or the Bayes optimal discriminant function.
- Bayes Classifier: Probabilistic model that makes the most probable prediction for new examples.
Specifically, the Bayes optimal classifier answers the question:
What is the most probable classification of the new instance given the training data?
This is different from the MAP framework that seeks the most probable hypothesis (model). Instead, we are interested in making a specific prediction.
In general, the most probable classification of the new instance is obtained by combining the predictions of all hypotheses, weighted by their posterior probabilities.
— Page 175, Machine Learning, 1997.
The equation below demonstrates how to calculate the conditional probability for a new instance (vi) given the training data (D), given a space of hypotheses (H).
- P(vj | D) = sum {h in H} P(vj | hi) * P(hi | D)
Where vj is a new instance to be classified, H is the set of hypotheses for classifying the instance, hi is a given hypothesis, P(vj | hi) is the posterior probability for vi given hypothesis hi, and P(hi | D) is the posterior probability of the hypothesis hi given the data D.
Selecting the outcome with the maximum probability is an example of a Bayes optimal classification.
- max sum {h in H} P(vj | hi) * P(hi | D)
Any model that classifies examples using this equation is a Bayes optimal classifier and no other model can outperform this technique, on average.
Any system that classifies new instances according to [the equation] is called a Bayes optimal classifier, or Bayes optimal learner. No other classification method using the same hypothesis space and same prior knowledge can outperform this method on average.
— Page 175, Machine Learning, 1997.
We have to let that sink in.
It is a big deal.
It means that any other algorithm that operates on the same data, the same set of hypotheses, and same prior probabilities cannot outperform this approach, on average. Hence the name “optimal classifier.”
Although the classifier makes optimal predictions, it is not perfect given the uncertainty in the training data and incomplete coverage of the problem domain and hypothesis space. As such, the model will make errors. These errors are often referred to as Bayes errors.
The Bayes classifier produces the lowest possible test error rate, called the Bayes error rate. […] The Bayes error rate is analogous to the irreducible error …
— Page 38, An Introduction to Statistical Learning with Applications in R, 2017.
Because the Bayes classifier is optimal, the Bayes error is the minimum possible error that can be made.
- Bayes Error: The minimum possible error that can be made when making predictions.
Further, the model is often described in terms of classification, e.g. the Bayes Classifier. Nevertheless, the principle applies just as well to regression: that is, predictive modeling problems where a numerical value is predicted instead of a class label.
It is a theoretical model, but it is held up as an ideal that we may wish to pursue.
In theory we would always like to predict qualitative responses using the Bayes classifier. But for real data, we do not know the conditional distribution of Y given X, and so computing the Bayes classifier is impossible. Therefore, the Bayes classifier serves as an unattainable gold standard against which to compare other methods.
— Page 39, An Introduction to Statistical Learning with Applications in R, 2017.
Because of the computational cost of this optimal strategy, we instead can work with direct simplifications of the approach.
Two of the most commonly used simplifications use a sampling algorithm for hypotheses, such as Gibbs sampling, or to use the simplifying assumptions of the Naive Bayes classifier.
- Gibbs Algorithm. Randomly sample hypotheses biased on their posterior probability.
- Naive Bayes. Assume that variables in the input data are conditionally independent.
For more on the topic of Naive Bayes, see the post:
Nevertheless, many nonlinear machine learning algorithms are able to make predictions are that are close approximations of the Bayes classifier in practice.
Despite the fact that it is a very simple approach, KNN can often produce classifiers that are surprisingly close to the optimal Bayes classifier.
— Page 39, An Introduction to Statistical Learning with Applications in R, 2017.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Posts
- A Gentle Introduction to Maximum a Posteriori (MAP) for Machine Learning
- A Gentle Introduction to Bayes Theorem for Machine Learning
- How to Develop a Naive Bayes Classifier from Scratch in Python
Books
- Section 6.7 Bayes Optimal Classifier, Machine Learning, 1997.
- Section 2.4.2 Bayes error and noise, Foundations of Machine Learning, 2nd edition, 2018.
- Section 2.2.3 The Classification Setting, An Introduction to Statistical Learning with Applications in R, 2017.
- Information Theory, Inference and Learning Algorithms, 2003.
Papers
- The Multilayer Perceptron As An Approximation To A Bayes Optimal Discriminant Function, 1990.
- Bayes Optimal Multilabel Classification via Probabilistic Classifier Chains, 2010.
- Restricted bayes optimal classifiers, 2000.
- Bayes Classifier And Bayes Error, 2013.
Summary
In this post, you discovered the Bayes Optimal Classifier for making the most accurate predictions for new instances of data.
Specifically, you learned:
- Bayes Theorem provides a principled way for calculating conditional probabilities, called a posterior probability.
- Maximum a Posteriori is a probabilistic framework that finds the most probable hypothesis that describes the training dataset.
- Bayes Optimal Classifier is a probabilistic framework that finds the most probable prediction using the training data and space of hypotheses to make a prediction for a new data instance.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.



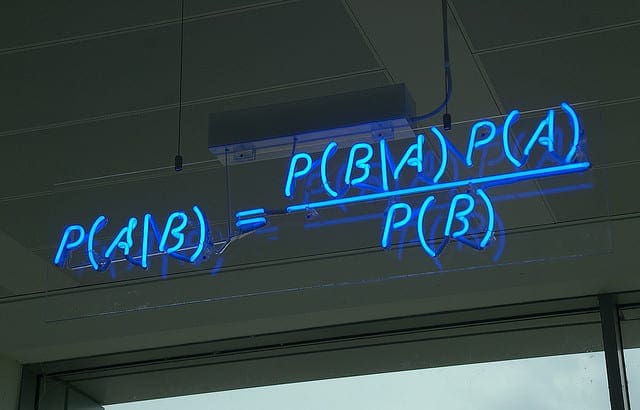




Hello Jason,
Is there any way to figure out in Keras if an algorithm is a linear regression if there aren’t any kind of metrics?
Thanks
Marco
You can look at the model was it was defined to confirm what type of model it is.
You cannot tell from the predictions or evaluation metrics.
Hi
I’ve got a hard time to understand the difference between Naive Bayes and Bayes Optimal Classifier.
Is it true that the naive assumption about the independence of the given features X1, X2, …, Xn being made by Naive Bayes is NOT made anymore by the Bayes Optimal Classifier?
Thanks
Great question!
Correct.
Naive bayes is a simplification of the optimal classifier that is tractable to implement/use.
In Tom Mitchel Machine Learning book at page 175 in the discussion of ‘Bayes Optimal Classifier’ gives an example with h1, h2, and h3. Are these three hypotheses indicate three methods like MAP, ML? If I calculate Naive Bayes classification for a problem based on MAP and ML, How can I calculate ‘Bayes Optimal Classifies?
We typically cannot calculate the bayes optimal classifier directly – we don’t know enough, but we can approximate it with other methods, like naive bayes.
Dear Json
In Bayes’ formula,
P(vj | D) = sum {h in H} P(vj | hi) * P(hi | D)
vj is a class of dataset; not an instance to be classified. This is a typo.
Thanks
Thanks.
Hi Jason.
P(theta | X) = P(X | theta) * P(theta)
is wrong.
$P(\theta | X) = P(X | \theta) * P(\theta) / P(X)$. Am I missing something?
The denominator is often dropped as a normalizing constant.
I might discuss this here:
https://machinelearningmastery.com/bayes-theorem-for-machine-learning/
Hi Jason,
On ISLR book 2nd ed., on page 39, there is a statement: ‘But for real data, we do not know the conditional distribution of Y given X, and so computing the Bayes classifier is impossible”. This makes me confuse because on page 40 looking at Figure 2.15 they plot 2 decision boundaries, one for KNN and the other for Bayesian Classifier. How did they do this? it seems to contradict the statement, or do they mean Naive Bayes instead?
Thanks.
Hi Andi…I am not following your question. Could you rephrase it so that we may better assist you.