Naive Bayes is a very simple classification algorithm that makes some strong assumptions about the independence of each input variable.
Nevertheless, it has been shown to be effective in a large number of problem domains. In this post you will discover the Naive Bayes algorithm for categorical data. After reading this post, you will know.
- How to work with categorical data for Naive Bayes.
- How to prepare the class and conditional probabilities for a Naive Bayes model.
- How to use a learned Naive Bayes model to make predictions.
This post was written for developers and does not assume a background in statistics or probability. Open a spreadsheet and follow along. If you have any questions about Naive Bayes ask in the comments and I will do my best to answer.
Kick-start your project with my new book Master Machine Learning Algorithms, including step-by-step tutorials and the Excel Spreadsheet files for all examples.
Let’s get started.
Naive Bayes Tutorial for Machine Learning
Photo by Beshef, some rights reserved.
Tutorial Dataset
The dataset is contrived. It describes two categorical input variables and a class variable that has two outputs.
|
1 2 3 4 5 6 7 8 9 10 11 |
Weather Car Class sunny working go-out rainy broken go-out sunny working go-out sunny working go-out sunny working go-out rainy broken stay-home rainy broken stay-home sunny working stay-home sunny broken stay-home rainy broken stay-home |
We can convert this into numbers. Each input has only two values and the output class variable has two values. We can convert each variable to binary as follows:
Variable: Weather
- sunny = 1
- rainy = 0
Variable: Car
- working = 1
- broken = 0
Variable: Class
- go-out = 1
- stay-home = 0
Therefore, we can restate the dataset as:
|
1 2 3 4 5 6 7 8 9 10 11 |
Weather Car Class 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 |
This can make the data easier to work with in a spreadsheet or code if you are following along.
Get your FREE Algorithms Mind Map
Sample of the handy machine learning algorithms mind map.
I've created a handy mind map of 60+ algorithms organized by type.
Download it, print it and use it.
Also get exclusive access to the machine learning algorithms email mini-course.
Learn a Naive Bayes Model
There are two types of quantities that need to be calculated from the dataset for the naive Bayes model:
- Class Probabilities.
- Conditional Probabilities.
Let’s start with the class probabilities.
Calculate the Class Probabilities
The dataset is a two class problem and we already know the probability of each class because we contrived the dataset.
Nevertheless, we can calculate the class probabilities for classes 0 and 1 as follows:
- P(class=1) = count(class=1) / (count(class=0) + count(class=1))
- P(class=0) = count(class=0) / (count(class=0) + count(class=1))
or
- P(class=1) = 5 / (5 + 5)
- P(class=0) = 5 / (5 + 5)
This works out to be a probability of 0.5 for any given data instance belonging to class 0 or class 1.
Calculate the Conditional Probabilities
The conditional probabilities are the probability of each input value given each class value.
The conditional probabilities for the dataset can be calculated as follows:
Weather Input Variable
- P(weather=sunny|class=go-out) = count(weather=sunny and class=go-out) / count(class=go-out)
- P(weather=rainy|class=go-out) = count(weather=rainy and class=go-out) / count(class=go-out)
- P(weather=sunny|class=stay-home) = count(weather=sunny and class=stay-home) / count(class=stay-home)
- P(weather=rainy|class=stay-home) = count(weather=rainy and class=stay-home) / count(class=stay-home)
Plugging in the numbers we get:
- P(weather=sunny|class=go-out) = 0.8
- P(weather=rainy|class=go-out) = 0.2
- P(weather=sunny|class=stay-home) = 0.4
- P(weather=rainy|class=stay-home) = 0.6
Car Input Variable
- P(car=working|class=go-out) = count(car=working and class=go-out) / count(class=go-out)
- P(car=broken|class=go-out) = count(car=brokenrainy and class=go-out) / count(class=go-out)
- P(car=working|class=stay-home) = count(car=working and class=stay-home) / count(class=stay-home)
- P(car=broken|class=stay-home) = count(car=brokenrainy and class=stay-home) / count(class=stay-home)
Plugging in the numbers we get:
- P(car=working|class=go-out) = 0.8
- P(car=broken|class=go-out) = 0.2
- P(car=working|class=stay-home) = 0.2
- P(car=broken|class=stay-home) = 0.8
We now have every thing we need to make predictions using the Naive Bayes model.
Make Predictions with Naive Bayes
We can make predictions using Bayes Theorem.
P(h|d) = (P(d|h) * P(h)) / P(d)
Where:
- P(h|d) is the probability of hypothesis h given the data d. This is called the posterior probability.
- P(d|h) is the probability of data d given that the hypothesis h was true.
- P(h) is the probability of hypothesis h being true (regardless of the data). This is called the prior probability of h.
- P(d) is the probability of the data (regardless of the hypothesis).
In fact, we don’t need a probability to predict the most likely class for a new data instance. We only need the numerator and the class that gives the largest response, which will be the predicted output.
MAP(h) = max(P(d|h) * P(h))
Let’s take the first record from our dataset and use our learned model to predict which class we think it belongs.
weather=sunny, car=working
We plug the probabilities for our model in for both classes and calculate the response. Starting with the response for the output “go-out”. We multiply the conditional probabilities together and multiply it by the probability of any instance belonging to the class.
- go-out = P(weather=sunny|class=go-out) * P(car=working|class=go-out) * P(class=go-out)
- go-out = 0.8 * 0.8 * 0.5
- go-out = 0.32
We can perform the same calculation for the stay-home case:
- stay-home = P(weather=sunny|class=stay-home) * P(car=working|class=stay-home) * P(class=stay-home)
- stay-home = 0.4 * 0.2 * 0.5
- stay-home = 0.04
We can see that 0.32 is greater than 0.04, therefore we predict “go-out” for this instance, which is correct.
We can repeat this operation for the entire dataset, as follows:
|
1 2 3 4 5 6 7 8 9 10 11 |
Weather Car Class out? home? Prediction sunny working go-out 0.32 0.04 go-out rainy broken go-out 0.02 0.24 stay-home sunny working go-out 0.32 0.04 go-out sunny working go-out 0.32 0.04 go-out sunny working go-out 0.32 0.04 go-out rainy broken stay-home 0.02 0.24 stay-home rainy broken stay-home 0.02 0.24 stay-home sunny working stay-home 0.32 0.04 go-out sunny broken stay-home 0.08 0.16 stay-home rainy broken stay-home 0.02 0.24 stay-home |
If we tally up the predictions compared to the actual class values, we get an accuracy of 80%, which is excellent given that there are conflicting examples in the dataset.
Summary
In this post you discovered exactly how to implement Naive Bayes from scratch. You learned:
- How to work with categorical data with Naive Bayes.
- How to calculate class probabilities from training data.
- How to calculate conditional probabilities from training data.
- How to use a learned Naive Bayes model to make predictions on new data.
Do you have any questions about Naive Bayes or this post.
Ask your question by leaving a comment and I will do my best to answer it.
Discover How Machine Learning Algorithms Work!
See How Algorithms Work in Minutes
...with just arithmetic and simple examples
Discover how in my new Ebook:
Master Machine Learning Algorithms
It covers explanations and examples of 10 top algorithms, like:
Linear Regression, k-Nearest Neighbors, Support Vector Machines and much more...
Finally, Pull Back the Curtain on
Machine Learning Algorithms
Skip the Academics. Just Results.
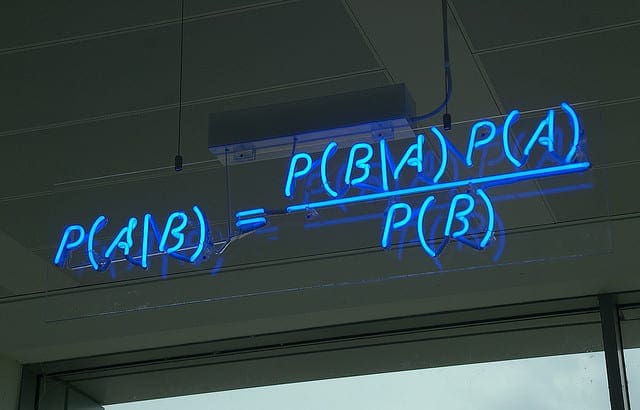
You really need to add MathJax to your blog for proper math.
You are probably right, but but not using crisp equations it might make them less intimidating to developers.
Hi Jason, I’m very happy with how accessible your articles are to beginners! This one was very clear and simple, so thanks!
I was wondering how this Naive Bayes classifier might be used to make *predictions*? For example, your original data set does not include the following combination:
– weather=rainy
– car=working.
How might you use the model to predict the probability of each class given these two inputs?
Thanks Ben,
The section in the post titled “Make Predictions with Naive Bayes” explains how to make a prediction given a new observation.
Your codes are giving these errors:
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 103, in
main()
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 93, in main
dataset = loadCsv(filename)
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 12, in loadCsv
dataset[i] = [float(x) for x in dataset[i]]
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 12, in
dataset[i] = [float(x) for x in dataset[i]]
ValueError: could not convert string to float:
>>>
Hello,
I could not find the SVM in Algorithm Mind Map! To which category it belongs?
Thanks a lot!
Perhaps instance-based methods?
Hi it is great entry article especially for those who are not strong in math as me (on wiki it looks much more strange hard than here), however, may be i get it wrong, but are the conditioned probabilities correct?
P(weather=sunny|class=go-out) = count(weather=sunny and class=go-out) / count(class=go-out)
Let’s take another example. Let’s say that that input will be profession, and output will be introvert/extrovert. Let’s say I will ask 100 people what’s their profession and if they are introverted or extroverted.
Now, let’s say i will meet only 3 IT workers, and all will be introverts. Rest 97 will be another professions and introverts too (just for case of simplicity).
Now, if i will follow your example, then probaility that IT worker is introvert is:
P(profession=IT|class=introvert) = count(profession=IT=introvert) / count(class=introvert)
That is:
3 / 100 = 3% of IT workers are introverts. But is it correct? We asked 3 IT people and all said yes. Should not it be:
P(profession=IT|class=introvert) = count(profession=IT=introvert) / count(profession=IT) ?
Now we will get 100% which reflects our sample. Or? Maybe with the weather sample it is similar?
And it should be
P(weather=sunny|class=go-out) = count(weather=sunny and class=go-out) / count(weather=sunny) ?
Best, Luky
Maybe both ratios have some meanings, but your ratio seems to be more vulnerable to structure of data. Let’s say i will have only 3 IT workers from 10k people, then ratio of IT introverts will be 3/10k introverts (let’s say) which will be very low number, while the second ratio (IT introverts / IT workers) isn’t vulnerable to unequal distributed data sample. (it says 100% even in case of 3 IT workers). But that’s just my opinion, i am curious about your view of thing :).
The math is right. But you are asking different questions.
What is the probability of working in IT and being an introvert versus, what is the probability of being an introvert given that we know the person works in IT.
Correction: “3% of IT workers are introverts” = 3% chance that IT worker is introvert.
But now i see that when following the article ratio probabilities than in my case the extrovert probability would be 0, and that would be beaten by 4% introvert thus resulting in introvert and thats correct prediction.. so it has some sense.. 🙂 bah. math and logic is scary 😛
Stick with it!
Great post — so well explained!
Please give me a pointer to how I can predict a class when there are more than two input variables, such as “got a novel to finish” and “feeling tired”, in addition to the weather and car.
How does one extend the method in such cases?
Consider using the built-in naive bayes in scikit-learn instead of developing your own from scratch:
https://machinelearningmastery.com/spot-check-classification-machine-learning-algorithms-python-scikit-learn/
Hi
I need to use Naive Bayes to detect and prevent SQL Injection
what is the best model for this purpose?
And lets the classifier return the request from client as SQL Injection attack what’s should be happen after that? am I redirect request to another page or make timeout in server of pass the request to the proxy ?
thank’s ^_^
I don’t know, perhaps perform some searches on the topic, or perhaps use this framework to frame and explore the problem:
https://machinelearningmastery.com/how-to-define-your-machine-learning-problem/
Hi!
Weldon Dr. Browwnlee. But still I need your assist to show me how I can calculate conditional probability of a training data like Pima Indian Diabetes Dataset?
hello!
did you happen to find the best model for detecting sql injection?
Try a suite of models on your specific dataset and discover what works best.
Jason,
This blog is written in very funny and crisp manner to get understand by almost everyone. However, how we can leverage your method to continous variable.
Thanks.
You can use Gaussian distribution to approximate the probability distribution of the variable.
This is called Gaussian Naive Bayes.
this method looks simple , but how can i figure out using it for a tablr with many variable values like 2000 records. For examplr assume i have a variable Voltage and time for charge and discharge of a battery, and and i want to find the remaining useful life, having set the threshold at 1.4V, and batttery voltage is 2.1V. How can i use Bayes, given thousands of data for the variables?
Perhaps start with a clear definition of the problem:
https://machinelearningmastery.com/how-to-define-your-machine-learning-problem/
Thanks for the nice overview of Naive Bayes classifier!
You’re welcome.
Hi Dr. Jason Brownlee
I am new in Payton programming language and Machine Learning, I am practicing Machine Learning algorithms so in an exercise where I use the algorithm of Chapter 12 “Naive Bayes” of the Book “machine_learning_algorithms_from_scratch” works well with the dataset of “Iris.csv” but when doing the exercise with another dataset of “Abseinteeism_at_work.csv” it tells me an error “ZeroDivisionError: float division by zero”. And I looked for how to solve the error on the internet, and I already invested some days, but I can not find the solution in the overflow link either. You could help me solve the problem and continue with my learning in this field.
Perhaps there is something specific in the data that is causing the problem?
Perhaps try removing each input column in turn and see how that impacts the model and whether it addresses the issue. That will help you narrow down the problem.
Let me know how you go.
Dear sir thanx a lot . do you have any method of imputation in the NB method.
I don’t believe so.
What problem are you having exactly?
Hi Jason,
I’m getting these errors
Traceback (most recent call last):
File “”, line 17, in
main()
File “”, line 9, in main
summaries = summarizeByClass(trainingSet)
File “”, line 43, in summarizeByClass
for classValue, instances in separated.iteritems():
AttributeError: ‘dict’ object has no attribute ‘iteritems’
Sorry, got it
Glad to hear it.
thanks jason sir
You’re welcome.
Hi Jason and thanks for the clear tutorial!
However, there is one potential issue:
P(h|d) = (P(d|h) * P(h)) / P(d)
If we count P(d) where d = weather is sunny and car is working, we get 0.6 * 0.5 = 0.3
But (P(d|h) * P(h)) = 0.32.
Therefore P(h|d) = 0.32 / 0.3 that is higher than 1.
Can the probability be higher than one?
Thanks for your reply in advance!
No, probabilities must be between 0 and 1.
Then there is an issue. When h=go-out, d=(weather is sunny and car is working):
P(h|d) = 0.32 / 0.3 = 1.0666…
Do you have any ideas regarding this?
Please note that “|” means “given”, it does not mean “divide”.
Thanks for reply.
By ‘ / ‘ I mean the division sign in this formula:
P(h|d) = (P(d|h) * P(h)) / P(d)
I know that we do not necessary need this division for Naive Bayes algorithm, however, I still was curious enough to count the P(h|d).
And I found that:
P(h|d) = (P(d|h) * P(h)) / P(d) = 0.8 * 0.8 * 0.5 / 0.3 = 0.32 / 0.3 = 1.0666…
h = go-out
d = (weather is good, car is working)
P(d) = P(weather is good, car is working) = P(weather is good) * P(car is working) = 0.6 * 0.5 = 0.3
Therefore, P(h|d) = 1.0666… And that is impossible from the one side. However, from the another side I cannot find the issue in counting of probabilities.
I see, thanks.
Hi Jason,
I am really thankful to you for making machine learning so easy for non technical professionals. The way you have explained naive bayes is very easy to understand. I have read tons of blogs and courses but I have found that I learn easily when I learn from your blogs. You have made machine learning very interesting and simpler for me. Thanks a ton!
Thanks!
Hi Jason,
Why do we need to count those probabilities at all?
We want to get P(class=go-out | weather=sunny, car=working), therefore, we can find it directly from your table without making any naive assumptions.
There are 5 cases when class=go-out, and 4 of them appears when weather=sunny and car=working. This simply means:
P(class=go-out | weather=sunny, car=working) = 4/5
Then we can get P(class=stay-home | weather=sunny, car=working) in analogical way. There are 5 cases with class=stay-home, and only 1 of them appears given weather=sunny and car=working. Therefore:
P(class=stay-home | weather=sunny, car=working) = 1/5
And that’s all. So why do we need all your calculations? Thanks in advance if you know the answer.
Good question, I guess in this case I am trying to demonstrate the naive bayes method which operates on probabilities.
Hi Jason, thank you for the helpful tutorials! How would you implement it using few categories instead of binary (sunny, rainy, partly cloudy, snowy..) without using external packages? Do you know any useful method transform the categories to numeric ones? Thanks again!
The above example generalizes to multiple categories directly, e.g. going from a binomial to multinomial probability distribution.
Hello Jason,
You conclude that this contrived dataset has a class probability for any of the classes, i.e. 50%.
( ==> 5 / (5+ 5).
But, there are 6 sunnies and 4 rainies for the first class (sunny or rainy).
Do I suppose correctly that a mistake has been made?
I changed the 6th sunny into a rainy (if counting from the top of the column).
Just FYI, the layout of your tutorial is very simple and easy to follow. Thank you.
It is helping to motivate me to stay the machine learning course. Doesn’t seem so difficult, after all.
Thank you for the feedback Muso! You are correct!